Experimental Research on the Flexural Performance of RC Rectangular Beams Strengthened by Reverse-Arch Method
Abstract
:1. Introduction
2. Materials and Methods
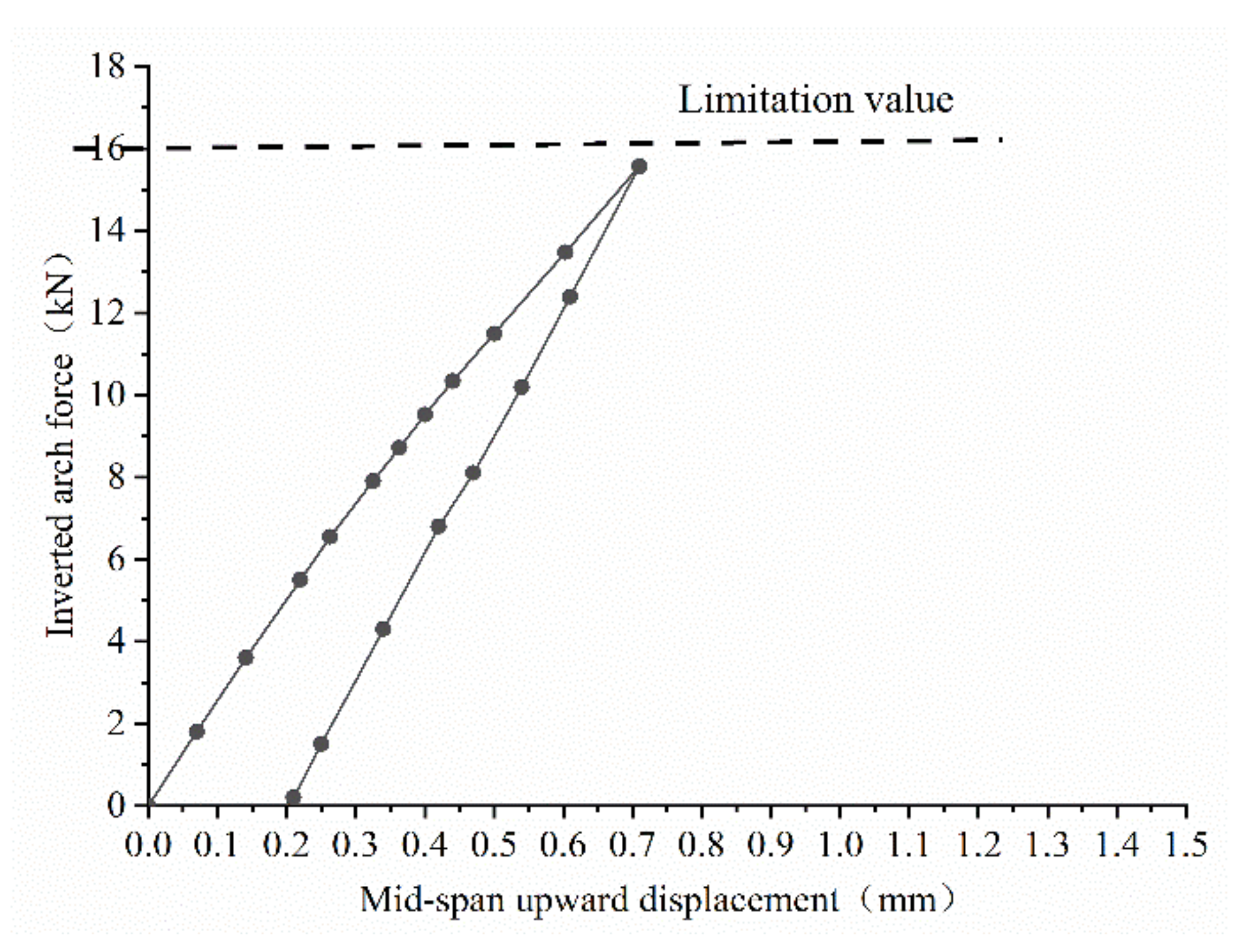
2.1. Reverse-Arch Method Strengthening Reinforced Concrete Beam
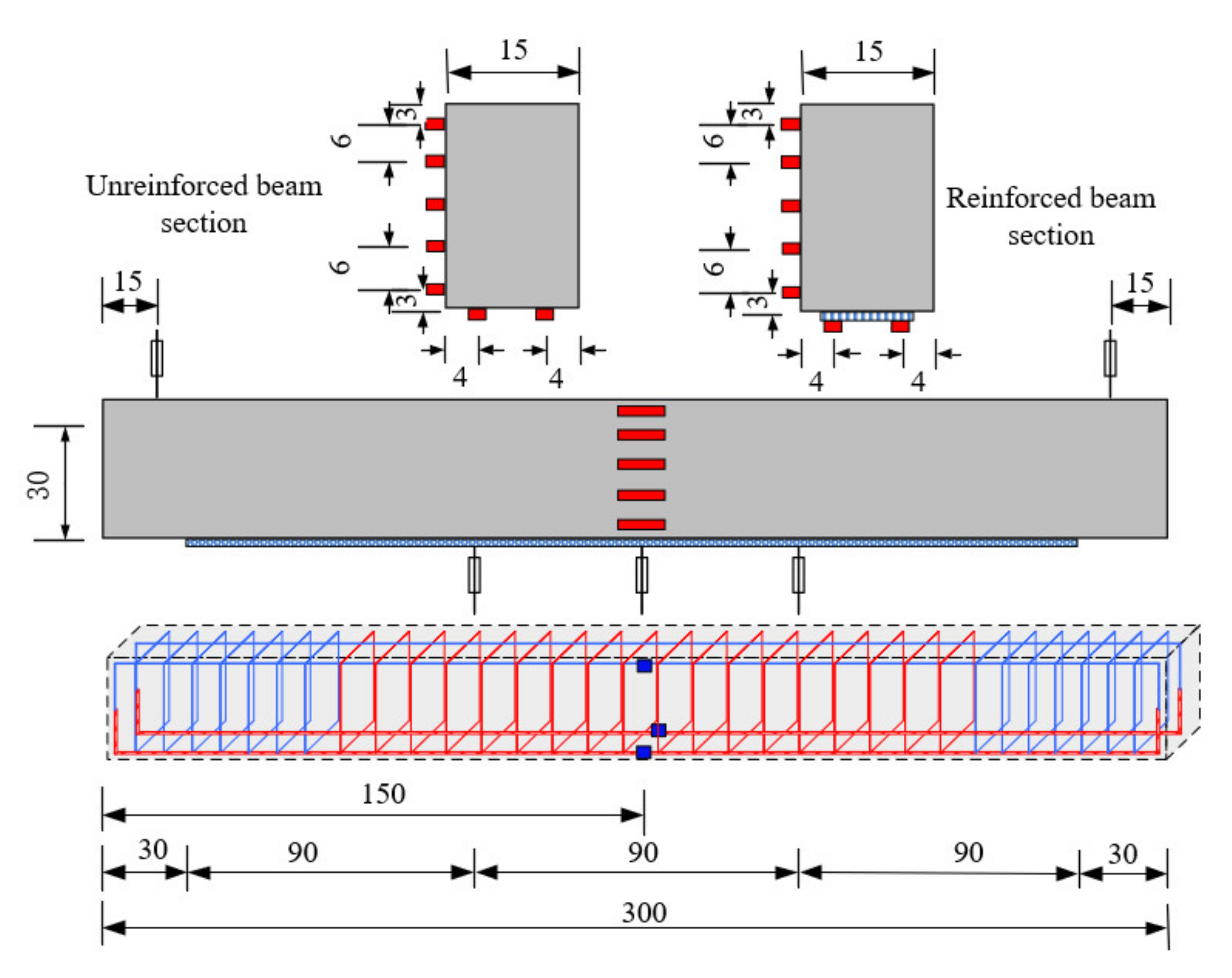
2.2. Test Beam Design
2.2.1. Reinforcement Design
2.2.2. Material Performance
2.2.3. Test Plan and Measuring Point Layout
3. Results and Discussions
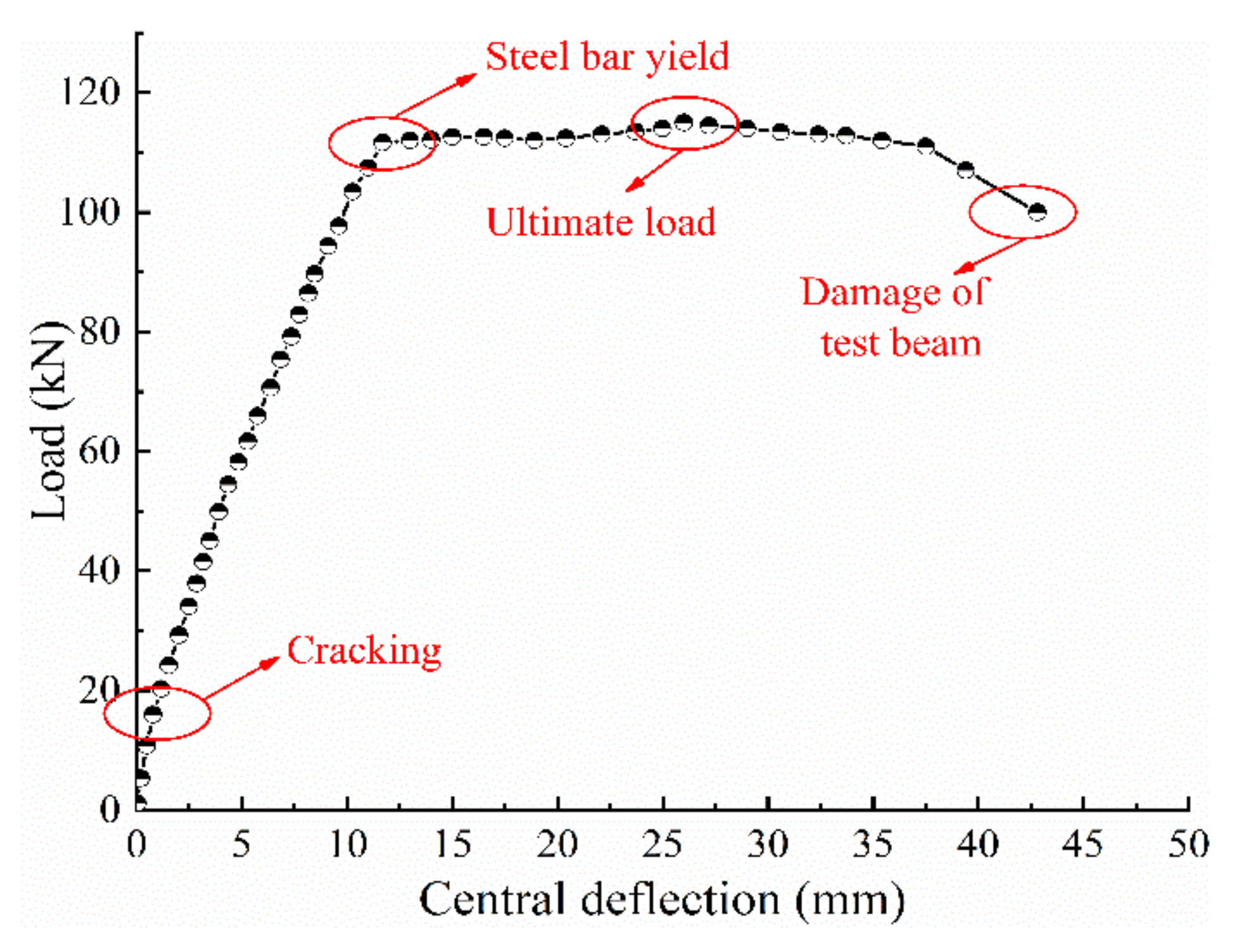
3.1. Test Results and Analysis of R0 Beam’s Flexural Bearing Capacity
3.2. Strengthening Beam Test Results and Analysis
3.2.1. Main Damage Phenomenon and Process
- (1)
- CFRP-R1 beam
- (2)
- CFRP- R2 beam
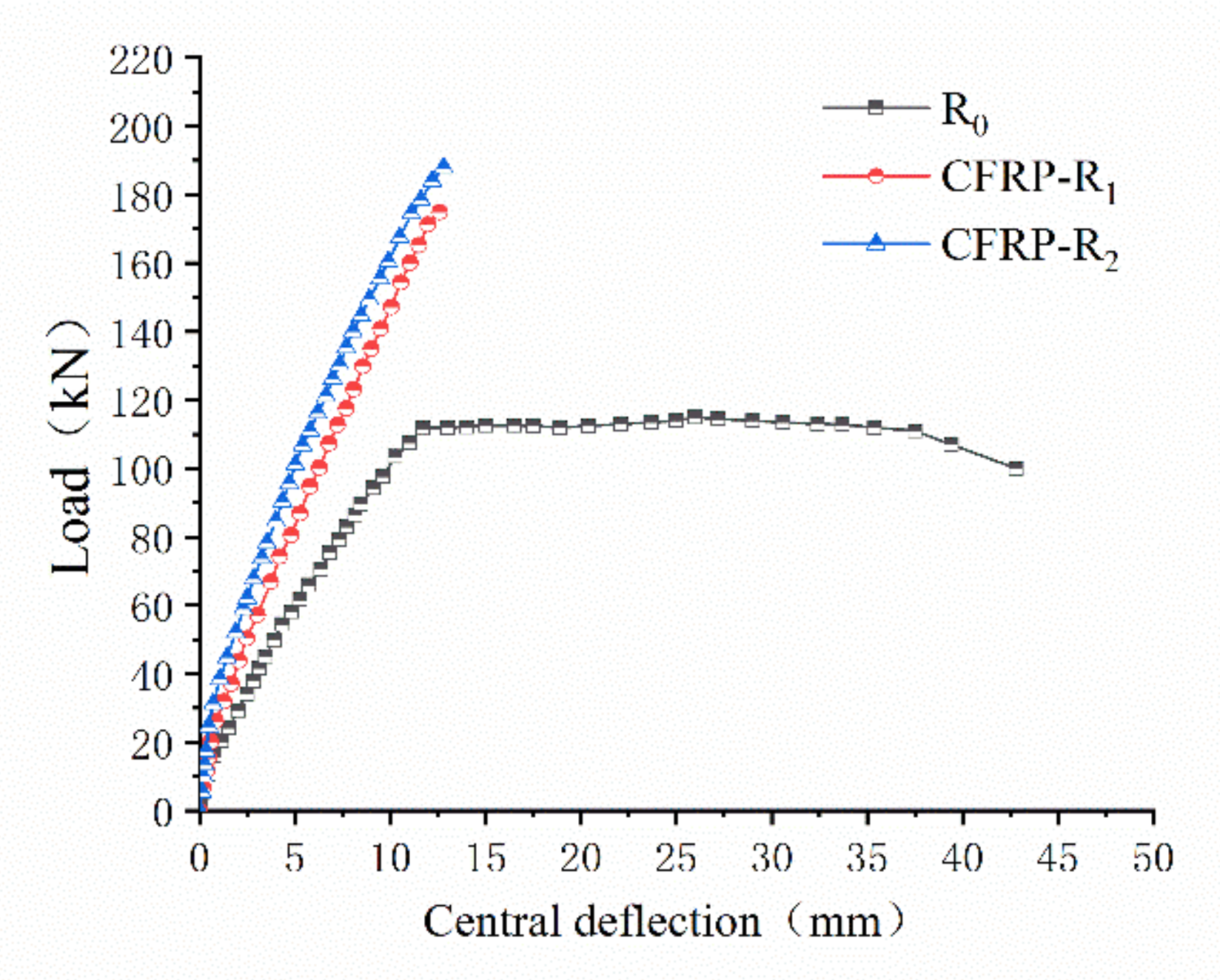
3.2.2. Deflection Analysis
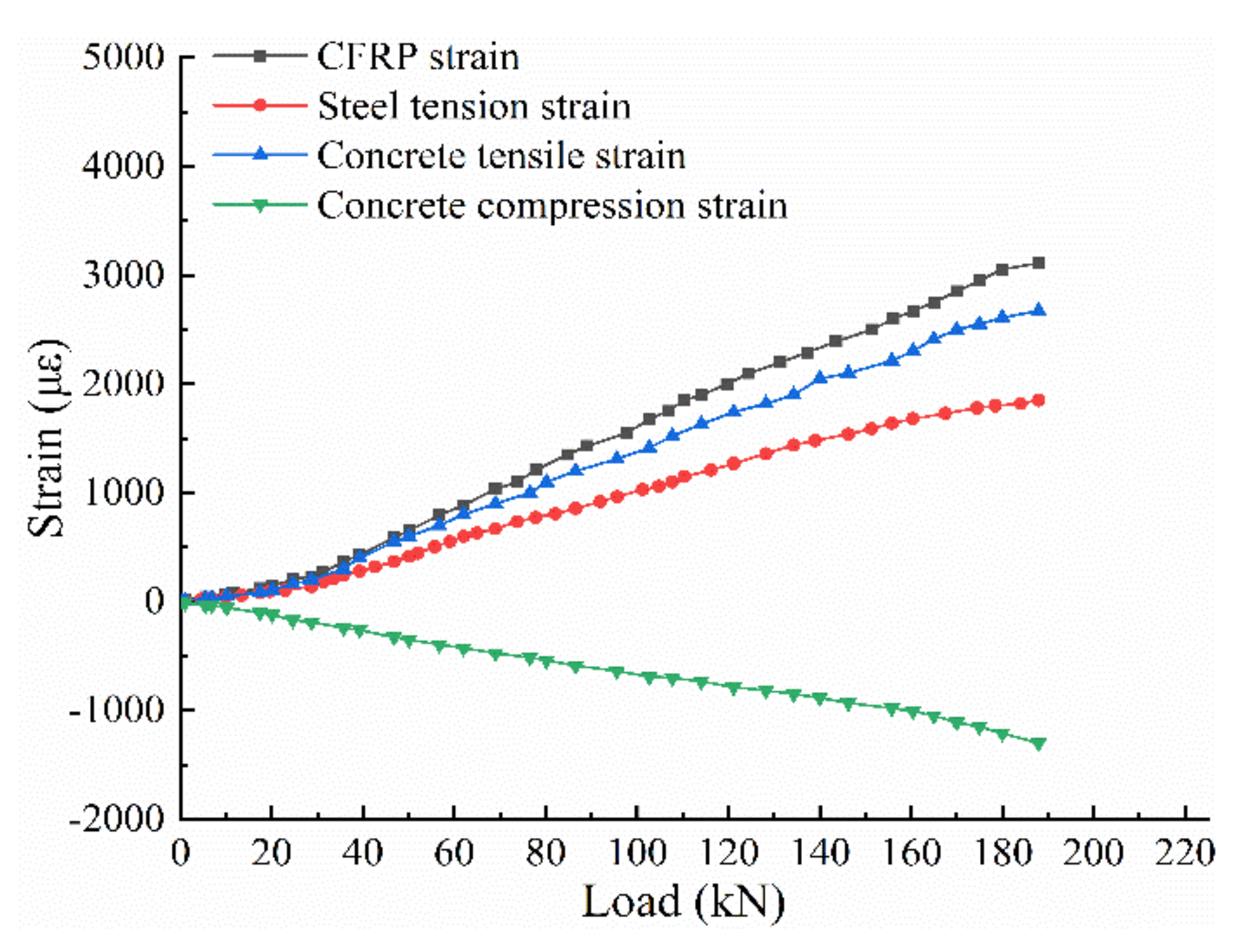
3.2.3. Strain Analysis
- (1)
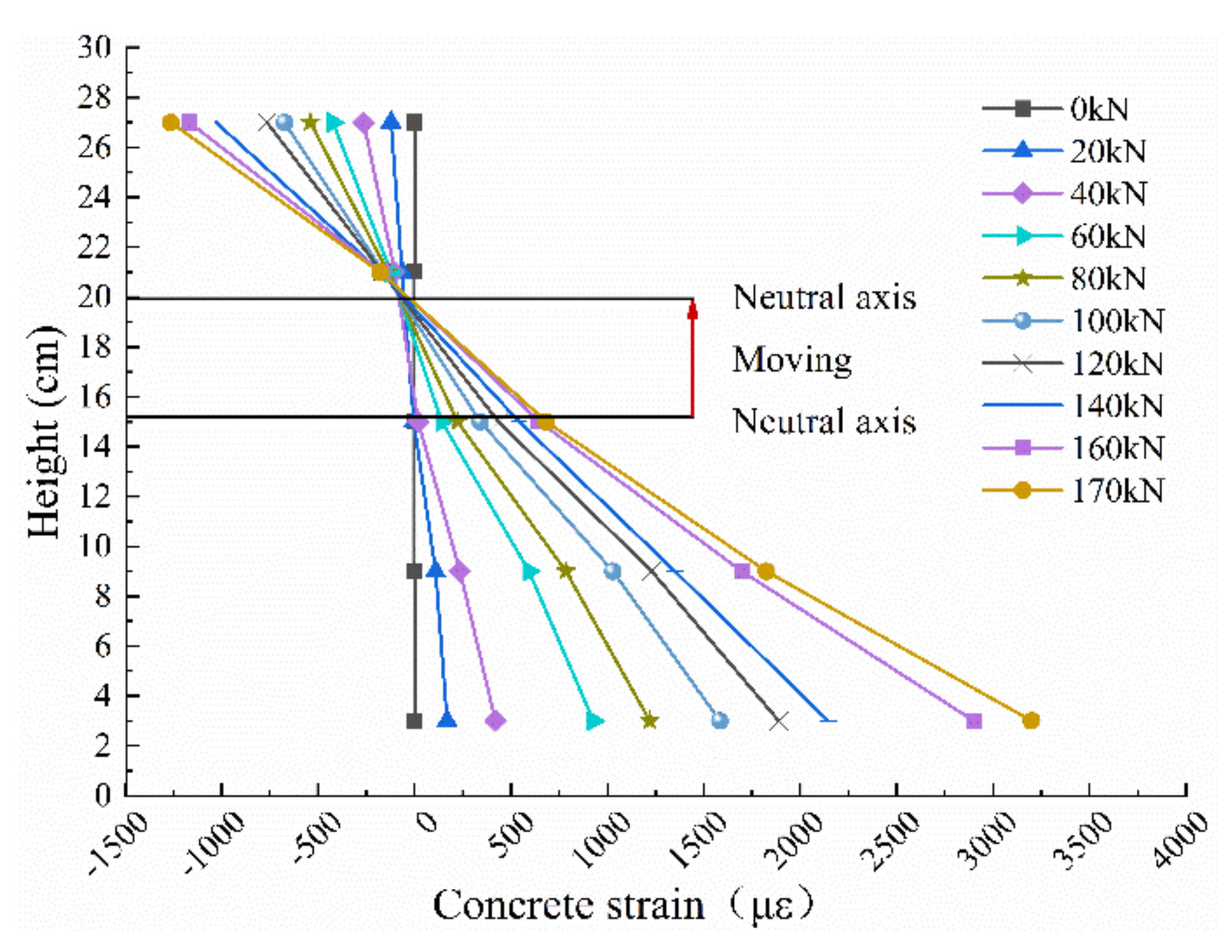
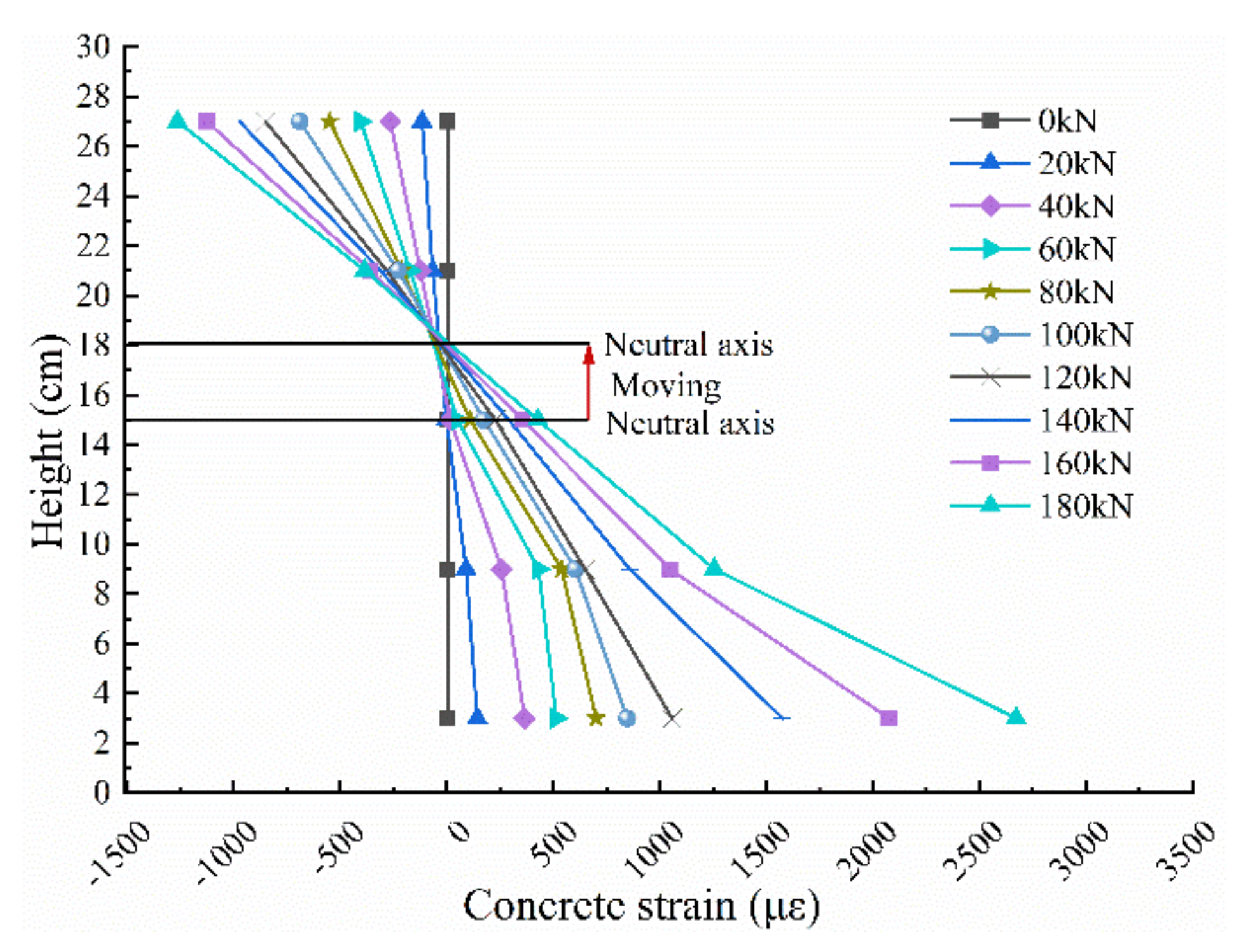
- Analysis of High Strain of Concrete Along Beam
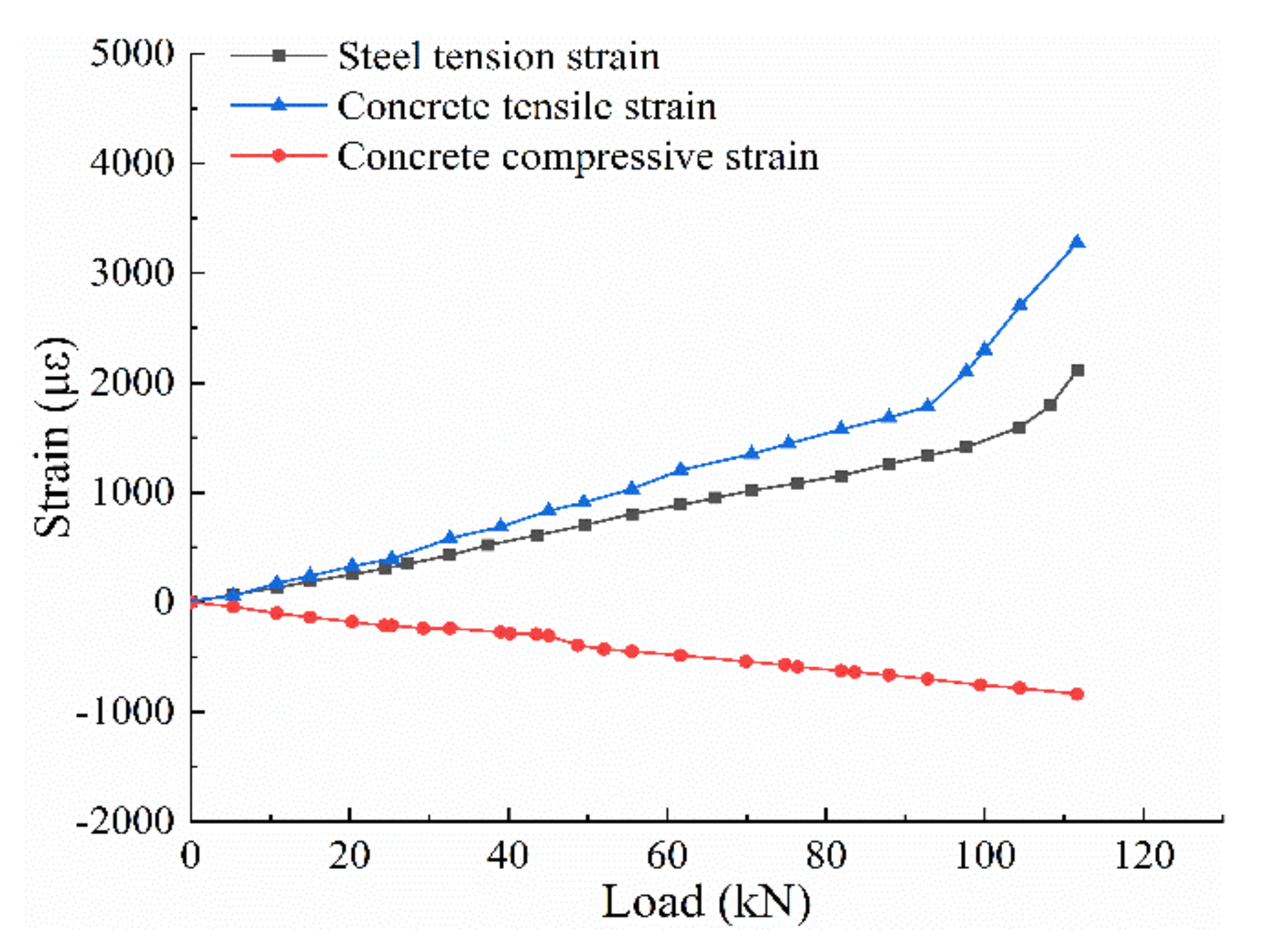
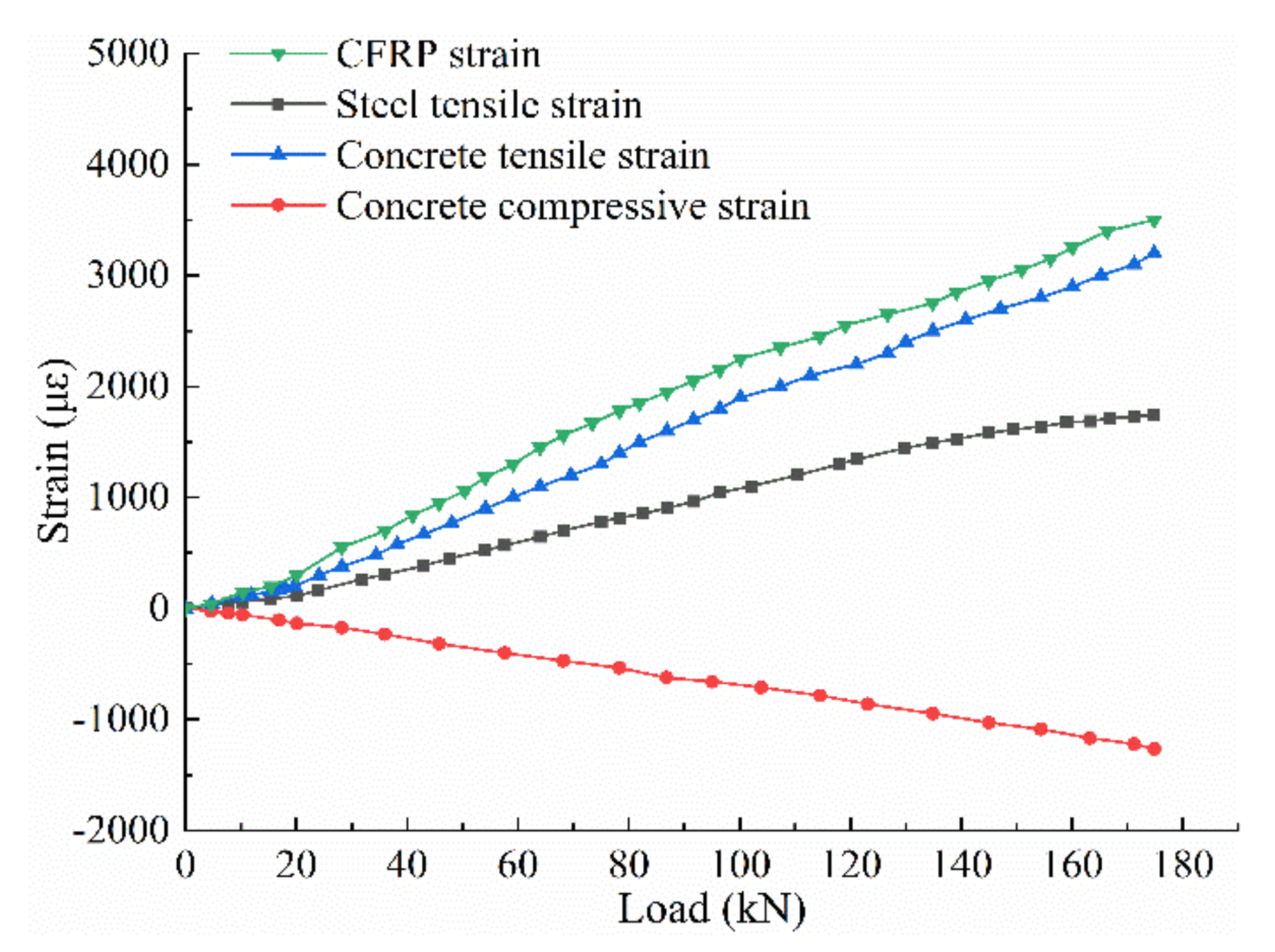
- (2)
- Strain analysis of the steel bar, concrete, and CFRP plate
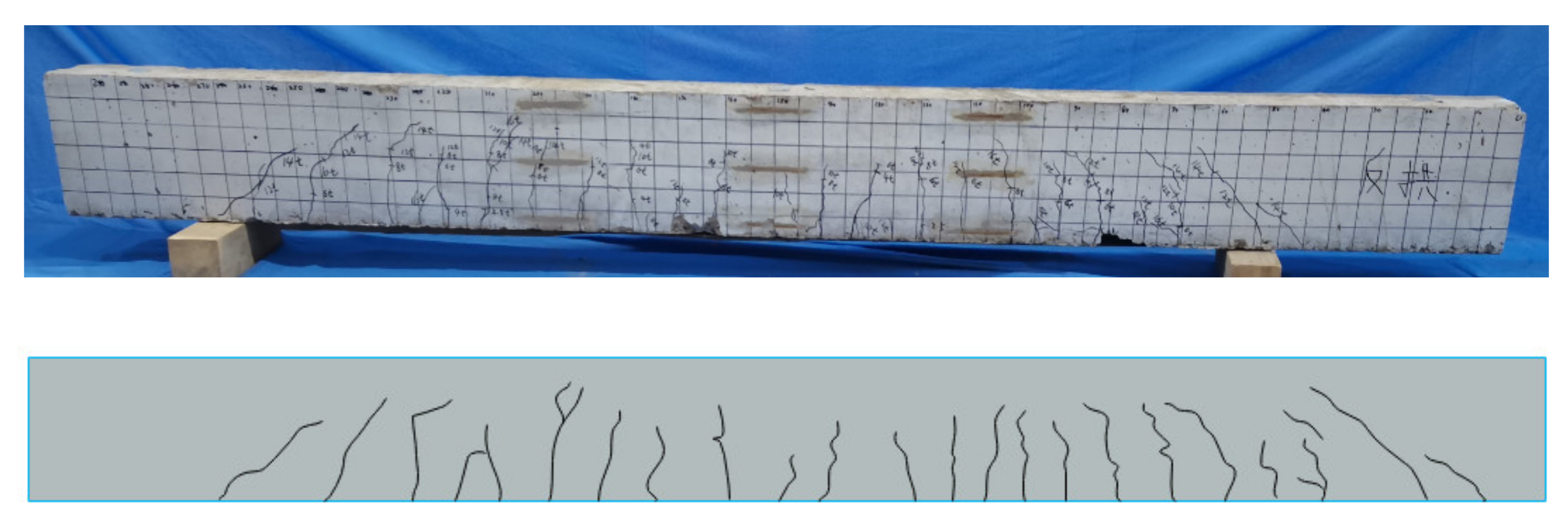
3.2.4. Crack Analysis
- (1)
- R0 beam
- (2)
- CFRP-R1 beam
- (3)
- CFRP-R2 beam
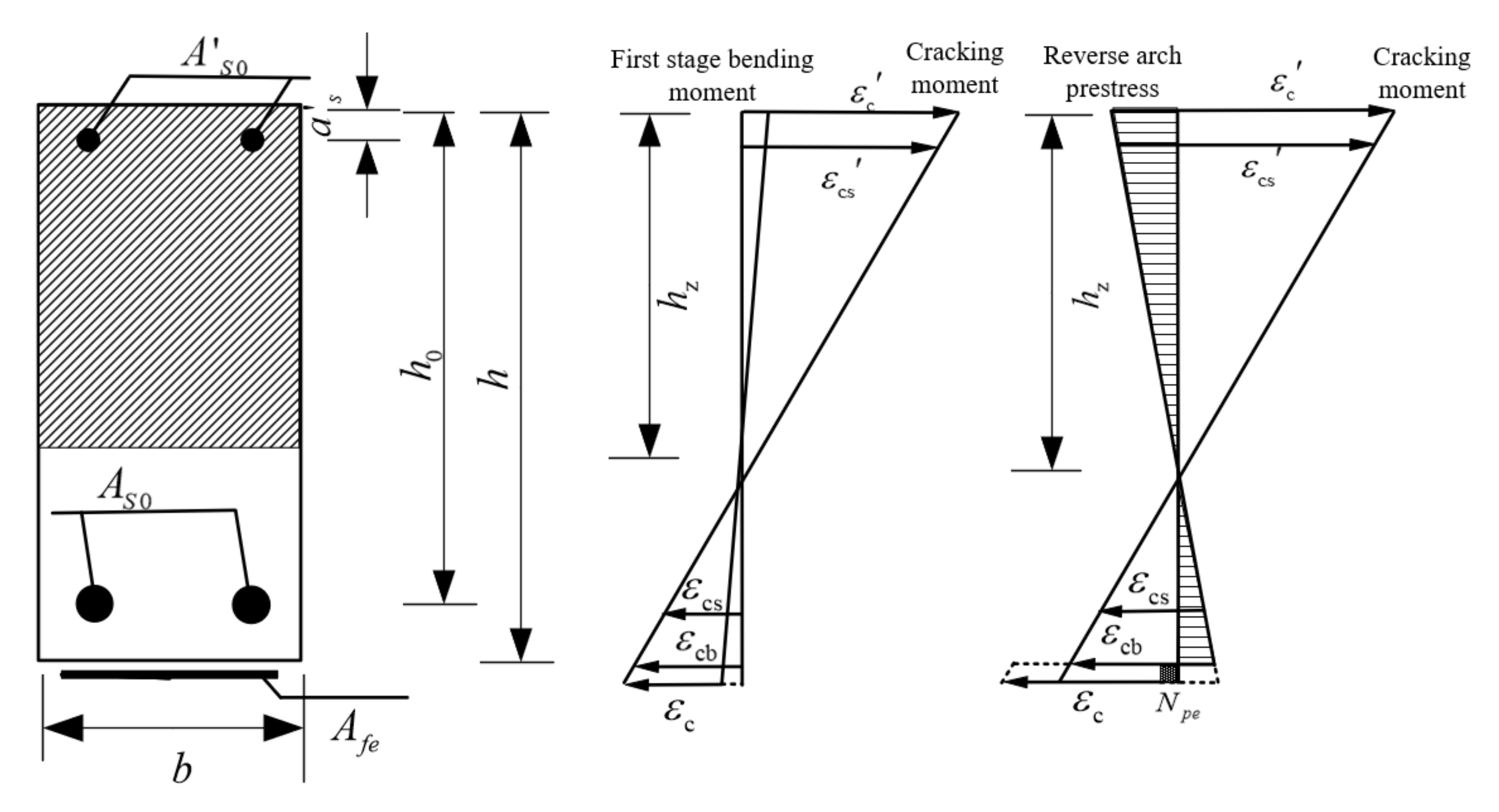
4. Analysis of Reinforced Structure Cracking and Bearing Capacity
4.1. Carrying Capacity
4.2. Cracking Load
5. Conclusions
- (1)
- Through the analysis of the test data, it can be seen that the cracking load and ultimate load are improved compared with the reinforcement of the CFRP plate by the reverse-arch method and the reinforcement by the direct adhesion of the CFRP plate. The RC beam can effectively increase the cracking load of the beam body. Compared with the original beam, the cracking load of the reverse-arch method of attaching the CFRP plate and the direct pasting of the CFRP plate is increased by 25% and 56%, respectively;
- (2)
- The reverse-arch method of pasting the CFRP plate to strengthen the test beam obtained the inverted arch deformation during the early loading stage, which produced the prestress effect. As a result, the test beam and the pasted CFRP plate are under the same force at the beginning of loading, avoiding the secondary stress of the CFRP plate, thereby improving the ultimate load-bearing capacity of the beam. Compared with the original beam, the inverse arch method-pasted CFRP plate reinforcement can increase the ultimate load-carrying capacity by 63%;
- (3)
- The reverse-arch method-pasted CFRP plate reinforcement can effectively improve the rigidity of the beam. When the applied load is less than the cracking load, the deflection growth rate provided by the inverse arch method of pasting the CFRP plate is similar to that of directly pasting the CFRP plate. When the loading load exceeds the cracking load, the increased rate of the deflection of the test beam is more gentle when the reverse-arch method of pasting the CFRP plate is compared with directly pasting the CFRP plate. Compared with the original beam, the deflection growth rate provided by the reverse-arch method of pasting the CFRP plate and the direct pasting of the CFRP plate is smaller in the whole test process;
- (4)
- The reverse-arch method-pasted CFRP plate reinforcement can effectively limit the development of cracks. Under the same load, the length of cracks in the beams reinforced by the reverse-arch method with CFRP plate is shorter than that of the beam reinforced with carbon fiber board directly, and the appearance time is later. When the test beam reaches yield, the crack width of the beam strengthened by directly pasting the CFRP plate is reduced by 11.9% compared with the original beam. The reverse-arch method pastes the CFRP plate to strengthen the original beam. When the test beam yields, the crack width is reduced by 26%;
- (5)
- The calculation of the flexural bearing capacity of the CFRP board reinforced by the inverted arch method is in good agreement with the test results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodhew, P.J.; Clarke, A.J.; Bailey, J.E. A Review of the Fabrication and Properties of Carbon Fibers; Elsevier: Amsterdam, The Netherlands, 1975; Volume 17. [Google Scholar] [CrossRef]
- Jumaat, M.Z.; Rahman, M.M.; Rahman, M.A. Review on bonding techniques of CFRP in strengthening concrete structures. Int. J. Phys. Sci. 2011, 6, 3567–3575. [Google Scholar] [CrossRef]
- Amran, Y.H.M.; Alyousef, R.; Rashid, R.S.M.; Alabduljabbar, H.; Hung, C.-C. Properties and applications of FRP in strengthening RC structures: A review. Structures 2018, 16. [Google Scholar] [CrossRef]
- Wang, H.; Xian, G. Shear capacity of RC beams strengthened with flax fiber sheets grafted with nano-TiO2. Materials 2020, 13, 1430. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boothby, T.E.; Bakis, C.E. Durability of externally bonded fiber-reinforced polymer (FRP) composite systems. In Strengthening and Rehabilitation of Civil Infrastructures Using Fibre-Reinforced Polymer (FRP) Composites; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Eva, O.; Mireia, P.; Antonio, M. Contribution of externally bonded FRP shear reinforcement to the shear strength of RC beams. Compos. Part B 2019, 164. [Google Scholar] [CrossRef]
- Azam, R. CFRP grid embedded in mortar for strengthening of shear-critical RC beams. Mag. Concr. Res. 2018. [Google Scholar] [CrossRef]
- Deng, L.; Luo, R.; Qian, X.; Ma, J.; Huang, X. Experimental study on intelligent carbon fiber slab embedded reinforced concrete beam with rectangular section. Build. Struct. 2019, 49, 92–97. [Google Scholar]
- Aslam, M.; Shafigh, P.; Jumaat, M.Z.; Shah, S.N.R. Strengthening of RC beams using prestressed fiber reinforced polymers–A review. Constr. Build. Mater. 2015, 82, 235–256. [Google Scholar] [CrossRef]
- Wang, H.-L.; Jin, W.-L.; Cleland, D.J.; Zhang, A.-H. Strengthening an in-service reinforcement concrete bridge with prestressed CFRP bar. J. Zhejiang Univ. Sci. A 2009, 10, 635–644. [Google Scholar] [CrossRef]
- Mohee, F.M.; Al-Mayah, A.; Plumtree, A. Development of a novel prestressing anchor for CFRP plates: Experimental investigations. Compos. Struct. 2017, 176, 20–32. [Google Scholar] [CrossRef]
- Rashid, K.; Li, X.; Deng, J.; Xie, Y.; Wang, Y.; Chen, S. Experimental and analytical study on the flexural performance of CFRP-strengthened RC beams at various prestressing levels. Compos. Struct. 2019, 227. [Google Scholar] [CrossRef]
- Xu, F.; Li, D.; Zhao, J.; Huang, J. Experimental research on reinforced concrete beams strengthened by prestressing CFRP plate. Build. Struct. 2010, 40, 372–375. [Google Scholar]
- Kang, K.; Zhang, P.; Deng, L. Experimental research on flexural behavior of reinforced RC beams strengthened with prestressed CFRP plates anchored at both ends. J. Lanzhou Univ. Technol. 2011, 37, 110–115. [Google Scholar]
- Deng, L.; Chen, H.; Zhang, P. Study on calculation methods for flexural capacity of normal section of concrete beams strengthened with prestressed CFRP plates. Build. Sci. 2009, 25, 74–77. [Google Scholar]
- Moshiri, N.; Czaderski, C.; Mostofinejad, D.; Hosseini, A.; Sanginabadi, K.; Breveglieri, M.; Motavalli, M. Flexural strengthening of RC slabs with nonprestressed and prestressed CFRP strips using the EBROG method. Compos. Part B 2020, 201. [Google Scholar] [CrossRef]
- Xiao, X. Study on the Flexural Behavior of RC Beams Strengthened Wi-Thprestressed CFRP under Secondary Load; Hunan University: Changsha, China, 2016. [Google Scholar]
- Chen, D.G.; Yao, Y.; Deng, Y.J. Simulation calculation analysis of RC beam strengthened with carbon-fiber by reverse-arch method. Adv. Mater. Res. 2011, 1269. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, J.; Jin, G.; Sun, B. Analysis on the “reverse-arch prestressed technique” and the improved bearing capacity for steel structure strengthened by carbon-fibre. Steel Constr. 2002, 51–54. [Google Scholar]
- Liang, D.; Sun, J.; Li, Y. Theoretical analysis of Pre-CFRP reinforcement based on anti-arch deflection. J. Univ. Jinan Sci. Technol. 2014, 28, 316–320. [Google Scholar]
- Lin, Q.; Wang, L. Experimental study on concrete beams strengthened with CFRP using reverse arch method. Build. Struct. 2020, 50, 86–89. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standards for the Test of Mechanical Properties of Ordinary Concrete (GB/T 50081-2011); China Architecture & Building Press: Beijing, China, 2011. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard Test Method for Tensile Testing of Metallic Materials (GB/T 228-2010); China Architecture & Building Press: Beijing, China, 2010. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Test Methods of Concrete Structures GB/T50 152-2012; China Construction Industry Press: Beijing, China, 2012. [Google Scholar]
- Pan, Y.; Hu, W.; Guo, R.; Ren, Y. Experimental study on flexural performance of RC beams strengthened with CFRP grid-PCM. J. Build. Struct. 2020, 41, 119–128. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Design Code for Reinforcement of Concrete structures: GB 50367-2013; China Construction Industry Press: Beijing, China, 2014. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Design Code for Concrete Structures: GB 50010-2010; China Construction Industry Press: Beijing, China, 2011. [Google Scholar]
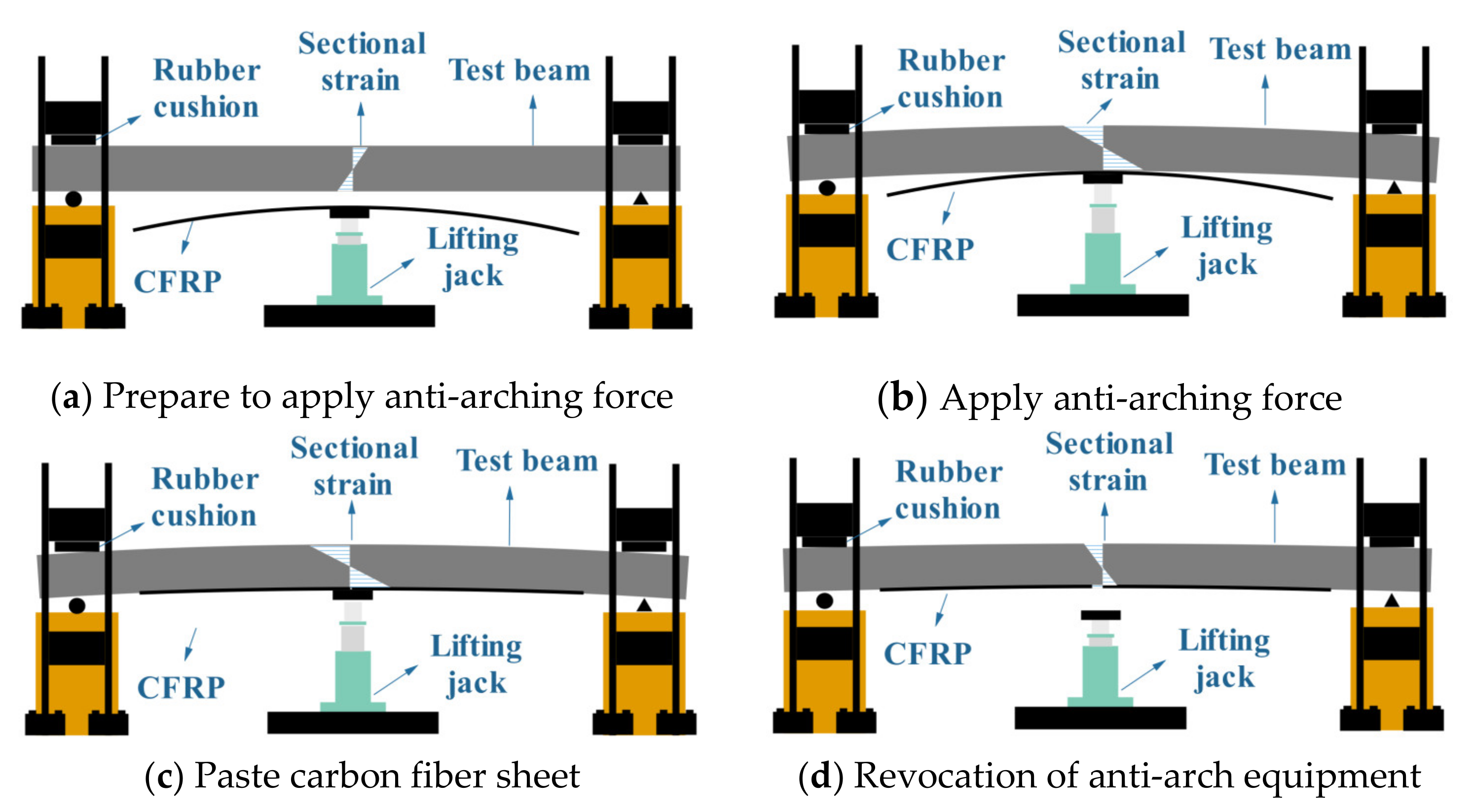
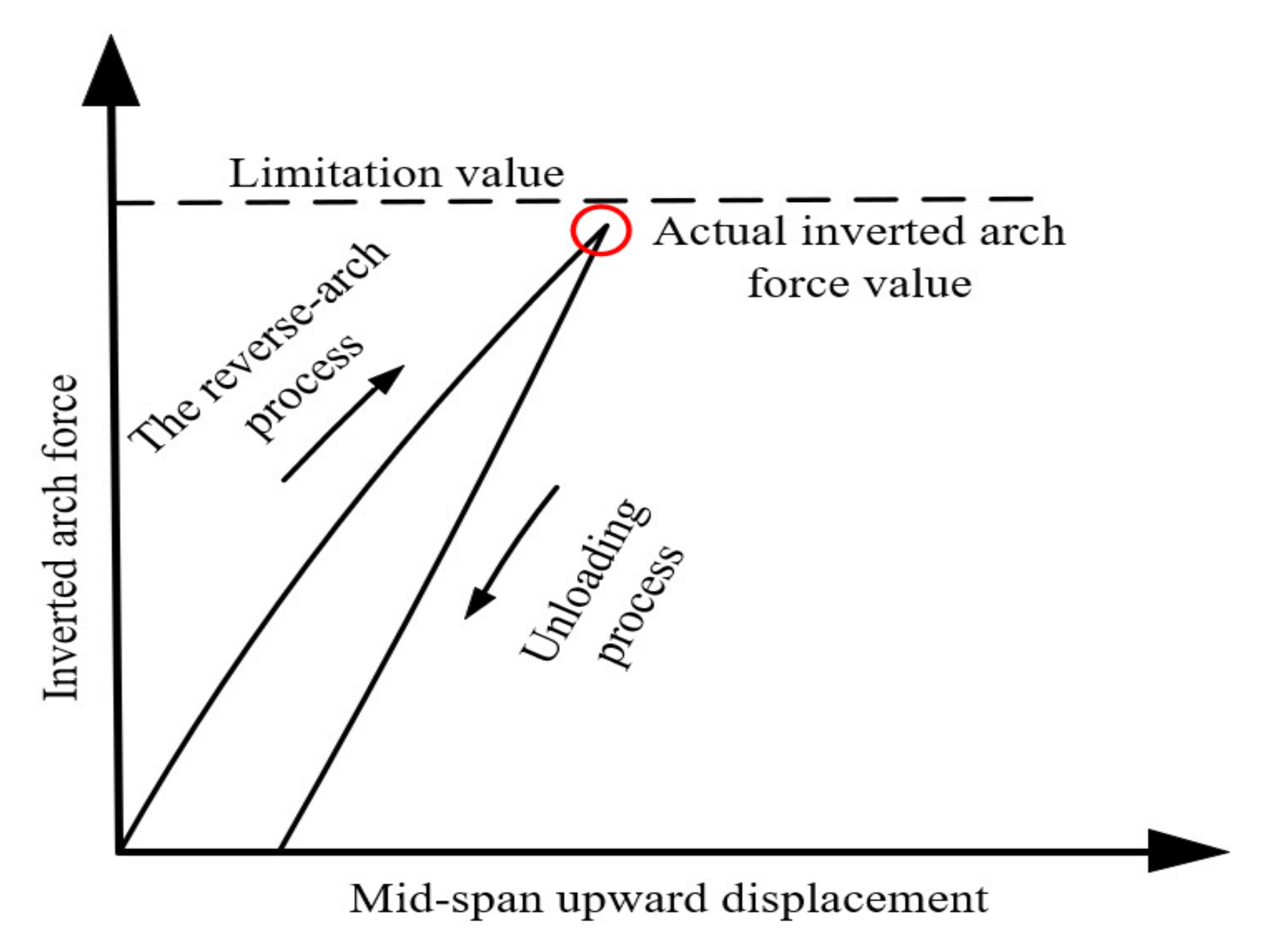
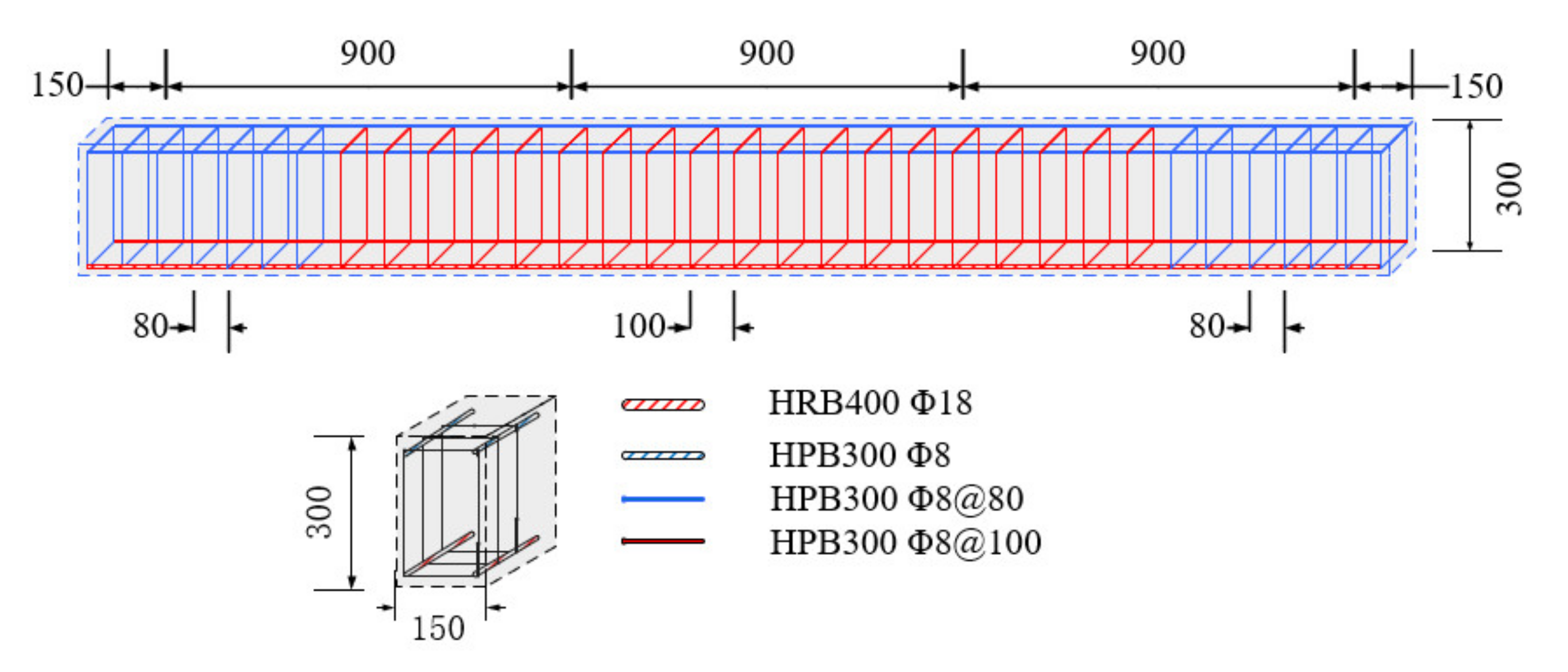



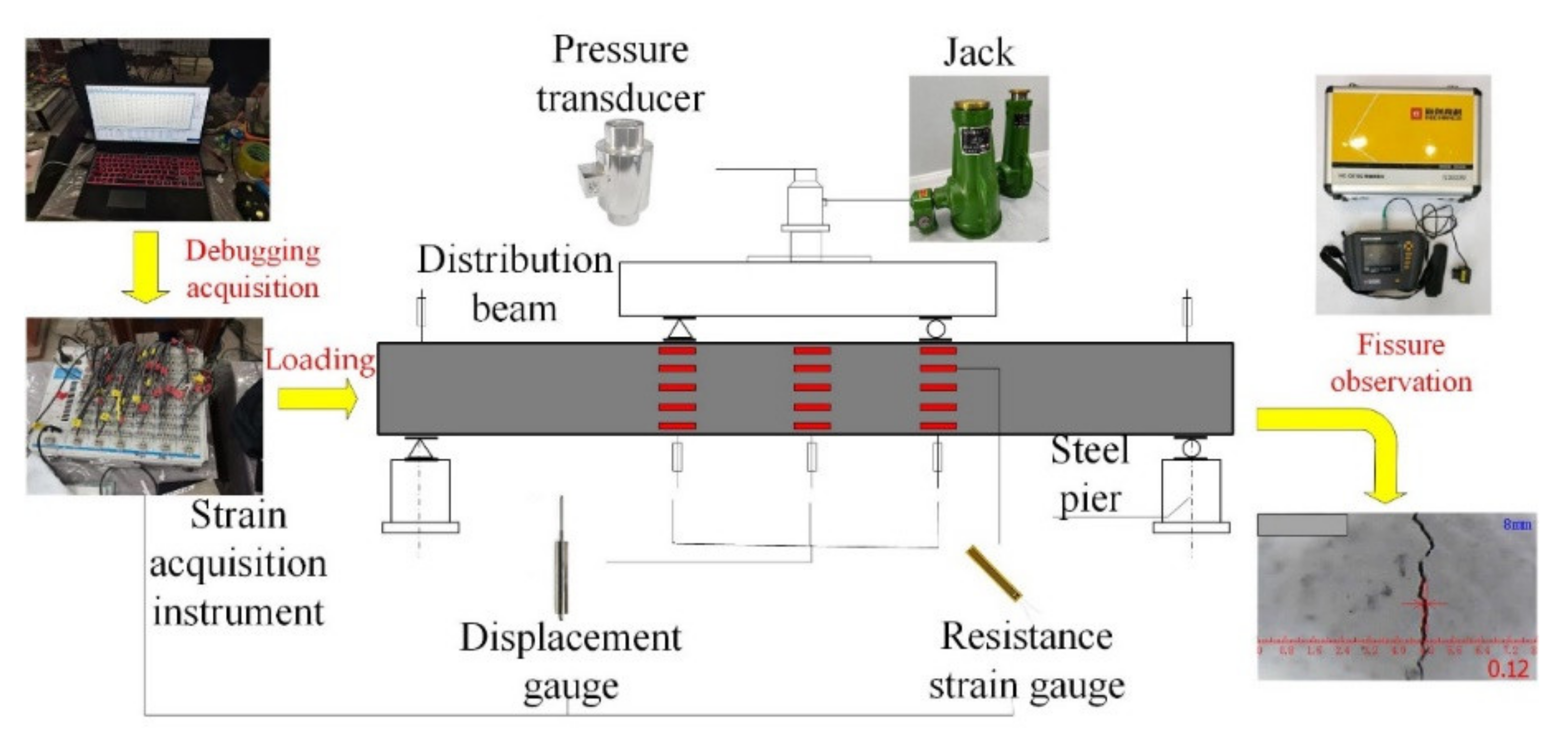









| Testing Specimens | Notation | Concrete Strength | Length (mm) | Section Dimensions (mm) | Paste Method |
|---|---|---|---|---|---|
| Concrete beam | R0 | C30 | 300 | 30 × 15 | / |
| Paste CFRP concrete beam | CFRP-R1 | C30 | 300 | 30 × 15 | Directly pasting |
| Paste CFRP concrete beam | CFRP-R2 | C30 | 300 | 30 × 15 | Reverse-arch method |
| Rebar Type | Yield Strength (MPa) | Tensile Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|
| HRB400 | 412.2 | 6610.8 | 202 |
| HPB300 | 314.8 | 512.7 | 208 |
| Material | Width (mm) | Thickness (mm) | Tensile Strength (mm) | Concrete Tensile Modulus (MPa) | Interlaminar Shear Strength (MPa) | Compressive Strength (MPa) | Elongation (%) |
|---|---|---|---|---|---|---|---|
| CFRP Plate | 100 | 2 | 2617.8 | 1.9 × 105 | 54.1 | / | 1.7 |
| CFRP plate glue | / | / | 49.2 | 4543 | / | 108.4 | 1.64 |
| Size (mm) | Specs | Appropriate Temperature (°C) | Resistance Values (Ω) | Sensitivity Coefficient (%) | Mechanical Hysteresis (μm/m) | Maximum Strain Limit (μm/m) | Supply Voltage (V) |
|---|---|---|---|---|---|---|---|
| 5 × 3 | BX120-100AA | −30–70 | 120 ± 1 | 2.1±2 | 1.2 | 20,000 | 3–10 |
| 100 × 3 | BX120-1AA | −30–70 | 120 ± 1 | 2.1 ± 2 | 1.2 | 20,000 | 3–10 |
| Test Beam | Cracking Load (kN) | Cracking Displacement (mm) | Yield Load (kN) | Yield Displacement (mm) | Ultimate Load (kN) | Ultimate Displacement (mm) | Improved Carrying Capacity (%) |
|---|---|---|---|---|---|---|---|
| R0 | 16 | 0.78 | 111 | 11.70 | 115 | 26.00 | / |
| CFRP-R1 | 20 | 0.59 | 175 | 12.60 | 175 | 12.60 | 52 |
| CFRP-R2 | 25 | 0.49 | 188 | 12.80 | 188 | 12.80 | 63 |
| Test Piece | Test Value of Cracking Load (kN) | The Calculated Value of Cracking Load (kN) | Error (%) | Test Value of Flexural Capacity (kN) | The Calculated Value of Flexural Capacity (kN) | Error (%) |
|---|---|---|---|---|---|---|
| R0 | 16 | 16.2 | 1.23 | 115 | 117 | 1.71 |
| CFRP-R1 | 20 | 20.7 | 3.38 | 176 | 178 | 1.12 |
| CFRP-R2 | 25 | 24.3 | −2.88 | 188 | 185 | −1.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Sun, Q.; Li, C.; Liu, Y. Experimental Research on the Flexural Performance of RC Rectangular Beams Strengthened by Reverse-Arch Method. Symmetry 2021, 13, 1666. https://doi.org/10.3390/sym13091666
Yu T, Sun Q, Li C, Liu Y. Experimental Research on the Flexural Performance of RC Rectangular Beams Strengthened by Reverse-Arch Method. Symmetry. 2021; 13(9):1666. https://doi.org/10.3390/sym13091666
Chicago/Turabian StyleYu, Tao, Quansheng Sun, Chunwei Li, and Yancheng Liu. 2021. "Experimental Research on the Flexural Performance of RC Rectangular Beams Strengthened by Reverse-Arch Method" Symmetry 13, no. 9: 1666. https://doi.org/10.3390/sym13091666
APA StyleYu, T., Sun, Q., Li, C., & Liu, Y. (2021). Experimental Research on the Flexural Performance of RC Rectangular Beams Strengthened by Reverse-Arch Method. Symmetry, 13(9), 1666. https://doi.org/10.3390/sym13091666






