Modular Version of Edge Irregularity Strength for Fan and Wheel Graphs

Abstract

A k-labeling from the vertex set of a simple graph $G=(V,E)$ to a set of integers $\{1,2,\dots ,k\}$ is defined to be a modular edge irregular if, for every couple of distinct edges, their modular edge weights are distinct. The modular edge weight is the remainder of the division of the sum of end vertex labels by modulo $\left|E\right(G\left)\right|$. The modular edge irregularity strength of a graph is known as the maximal vertex label k, minimized over all modular edge irregular k-labelings of the graph. In this paper we describe labeling schemes with symmetrical distribution of even and odd edge weights and investigate the existence of (modular) edge irregular labelings of joins of paths and cycles with isolated vertices. We estimate the bounds of the (modular) edge irregularity strength for the join graphs $P_n+\overline{K_m}$ and $C_n+\overline{K_m}$ and determine the corresponding exact value of the (modular) edge irregularity strength for some fan graphs and wheel graphs in order to prove the sharpness of the presented bounds.

1. Introduction

Consider a simple graph $G=(V,E)$ with the vertex set $V\left(G\right)$ and the edge set $E\left(G\right)$. Ahmad et al. in [1] introduced the concept of the edge irregular labeling of graphs as a modification of the well-known concept of irregular assignments defined by Chartrand et al. in [2].

A vertex labeling $\phi :V\left(G\right)\to \{1,2,\dots ,k\}$ of a graph G is called an edge irregular k-labeling if for any couple of distinct edges $uv,u^{\prime }{v}^{\prime }\in E\left(G\right)$ their edge weights are distinct, that is, $w{t}_{\phi }\left(uv\right)=\phi \left(u\right)+\phi \left(v\right)\ne \phi \left(u^{\prime }\right)+\phi \left(v^{\prime }\right)=w{t}_{\phi }\left(u^{\prime }{v}^{\prime }\right)$. The edge irregularity strength, $\mathrm{es}\left(G\right)$, of G is known as the maximal vertex label k, minimized over all edge irregular k-labelings.

The lower bound of the edge irregularity strength proved in [1] is given by the following formula:

$$\begin{array}{c}\hfill \mathrm{es}\left(G\right)\ge max\left\{⌈\frac{\left|E\right(G\left)\right|+1}{2}⌉,\mathsf{\Delta }\left(G\right)\right\},\end{array}$$

(1)

where $\mathsf{\Delta }\left(G\right)$ is the maximum degree of G. The precise value of the edge irregularity strength for paths, stars, double stars and Cartesian product of two paths is determined in [1] and for Toeplitz graphs in [3]. The exact value of the edge irregularity strength for triangular grid graphs is proven in [4] and for some classes of plane graphs is presented in [5].

Koam et al. in [6] introduced a modular version of the edge irregular labeling which is a modification of the modular irregular labeling defined by Bača et al. in [7], and it was investigated in [8,9,10,11,12].

For a graph $G=(V,E)$ of size q, a vertex labeling $\phi :V\left(G\right)\to \{1,2,\dots ,k\}$ is called a modular edge irregular k-labeling if the edge weight function $\rho :E\left(G\right)\to {\mathbb{Z}}_q$ defined by $\rho \left(uv\right)=w{t}_{\phi }\left(uv\right)=\phi \left(u\right)+\phi \left(v\right)$ is bijective, and is referred to as the modular edge weight of the edge $uv$, where ${\mathbb{Z}}_q$ is the group of integers modulo q. In [6], a new graph invariant was introduced, namely the modular edge irregularity strength, $\mathrm{mes}\left(G\right)$, as the minimum k for which G has a modular edge irregular k-labeling. If no such labeling of G exists, then $\mathrm{mes}\left(G\right)=\infty$.

2. Relationship between $\mathbf{es}\mathbf{\left(}\mathit{G}\mathbf{\right)}$ and $\mathbf{mes}\mathbf{\left(}\mathit{G}\mathbf{\right)}$

Certainly, every modular edge irregular labeling of a graph is also its edge irregular labeling. This gives a lower bound of the modular edge irregularity strength, i.e., for any simple graph G

$$\begin{array}{c}\hfill \mathrm{es}\left(G\right)\le \mathrm{mes}\left(G\right).\end{array}$$

(2)

The converse of (2) does not hold. However, it is interesting to find families of graphs for which the equality holds. The validity of the following claim is obvious.

Theorem 1

([6]). Let G be a simple graph with $\mathrm{es}\left(G\right)=k$. If edge weights under a corresponding edge irregular k-labeling constitute a set of consecutive integers, then

$$\begin{array}{c}\hfill \mathrm{es}\left(G\right)=\mathrm{mes}\left(G\right)=k.\end{array}$$

In [6] the authors estimated the bounds on the modular edge irregularity strength for caterpillars, cycles, friendship graphs and n-suns. They determined the precise values of this parameter for the friendship graph of order $2n+1$, except for $n\equiv 0(mod4)$.

The results in this paper are mostly based on the following theorem.

Theorem 2.

Let f be an edge irregular k-labeling of a graph G. Let W be a subset of the vertices of G such that the labels of all vertices in W are pairwise distinct, where $w_1\in W$ has the smallest label. Let $w{t}_{f,max}\left(G\right)$ be the maximal edge weight of an edge in G under the labeling f. Let $G_W$ be the graph obtained from G by joining all vertices in W with an isolated vertex. Then,

$$\mathrm{es}\left(G_W\right)\le max\{k,w{t}_{f,max}\left(G\right)+1-f\left(w_1\right)\}.$$

Moreover, if all the induced weights of edges in G under the labeling f are consecutive numbers and the labels of the vertices in W are consecutive numbers, then

$$\mathrm{mes}\left(G_W\right)\le max\{k,w{t}_{f,max}\left(G\right)+1-f\left(w_1\right)\}.$$

Proof. 

Let f be an edge irregular k-labeling of a graph G. Let $W=\{w_1,w_2,\dots ,w_t\}$ be a subset of the vertices of G such that

$$\begin{array}{c}\hfill f\left(w_i\right)<f\left(w_{i+1}\right)\mathrm{for}1\le i\le t-1.\end{array}$$

(3)

Let $w{t}_{f,max}\left(G\right)$ be the maximal edge weight of an edge in G under the labeling f. Let $G_W$ be the graph with the vertex set $V\left(G_W\right)=V\left(G\right)\cup \left\{x\right\}$ and the edge set $E\left(G_W\right)=E\left(G\right)\cup \{x{w}_i:1\le i\le t\}$.

We define a vertex labeling g of $G_W$ such that

$$\begin{array}{c}\hfill g\left(v\right)=\left\{\begin{array}{cc}f\left(v\right),\hfill & \mathrm{if}v\in V\left(G\right),\hfill \\ w{t}_{f,max}\left(G\right)+1-f\left(w_1\right),\hfill & \mathrm{if}v=x.\hfill \end{array}\right.\end{array}$$

Thus, the maximal vertex label is the maximum of the numbers k and $w{t}_{f,max}\left(G\right)+1-f\left(w_1\right)$. For the weights of edges in $G_W$ under the labeling g, we have the following. If $uv\in E\left(G\right)$, then

$$w{t}_g\left(uv\right)=g\left(u\right)+g\left(v\right)=f\left(u\right)+f\left(v\right)=w{t}_f\left(uv\right).$$

For the edges $x{w}_i$, $1\le i\le t$ we obtain

$$\begin{array}{cc}\hfill w{t}_g\left(x{w}_i\right)=& g\left(x\right)+g\left(w_i\right)=\left(w{t}_{f,max}\left(G\right)+1-f\left(w_1\right)\right)+f\left(w_i\right).\hfill \end{array}$$

(4)

Thus, $w{t}_g\left(x{w}_1\right)=w{t}_{f,max}\left(G\right)+1$, and according to (3) we obtain that for every $1\le i\le t-1$

$$\begin{array}{c}\hfill w{t}_g\left(x{w}_i\right)<w{t}_g\left(x{w}_{i+1}\right).\end{array}$$

Thus, as f is an edge irregular labeling we have that all edge weights are distinct. This implies

$$\begin{array}{c}\hfill \mathrm{es}\left(G_W\right)\le max\{k,w{t}_{f,max}\left(G\right)+1-f\left(w_1\right)\}.\end{array}$$

Now suppose that the set of induced edge weights under the labeling f consists of consecutive numbers, i.e.,

$$\begin{array}{c}\hfill \{w{t}_f\left(e\right):e\in E\left(G\right)\}=\{w{t}_{f,max}\left(G\right)+1-j:j=1,2,\dots ,\left|E\left(G\right)\right|\},\end{array}$$

(5)

and let $W=\{w_1,w_2,\dots ,w_t\}$ such that for $i=1,2,\dots ,t$

$$f\left(w_i\right)=f\left(w_1\right)+i-1.$$

Then, (4) becomes

$$\begin{array}{cc}\hfill w{t}_g\left(x{w}_i\right)=& \left(w{t}_{f,max}\left(G\right)+1-f\left(w_1\right)\right)+\left(f\left(w_1\right)+i-1\right)=w{t}_{f,max}\left(G\right)+i.\hfill \end{array}$$

Combining this with (5) implies that the weights of edges in $G_W$ under the labeling g are consecutive numbers. Thus,

$$\mathrm{mes}\left(G_W\right)\le max\{k,w{t}_{f,max}\left(G\right)+1-f\left(w_1\right)\}.$$

This concludes the proof. □

The previous theorem allows us to construct (modular) edge irregular labelings of some graphs obtained by joining isolated vertices to a given graph. Let $G\cup H$ denote the union of two disjoint graphs G and H. The join $G+H$ of graphs G and H is the graph $G\cup H$ together with all the edges joining vertices of G and vertices of H. By the symbol $\overline{G}$ we denote the complement of the graph G.

In this paper we describe labeling schemes with symmetrical distribution of even and odd edge weights, and we investigate the existence of edge irregular and modular edge irregular labelings of joins of paths and cycles with isolated vertices. We estimate the bounds of the edge irregularity strength and modular edge irregularity strength for the join graphs $P_n+\overline{K_m}$ and $C_n+\overline{K_m}$ and determine the corresponding exact value of the (modular) edge irregularity strength for some fan graphs and wheel graphs in order to prove the sharpness of the presented bounds.

3. Fan Graphs

A fan graph $F_n$, $n\ge 2$, is a graph obtained by joining all vertices of a path $P_n$ on n vertices to a further vertex, called the centre. Thus, $F_n$ is isomorphic to the join $P_n+K_1$. The fan graph $F_n$ contains $n+1$ vertices (e.g., $v_1,v_2,\dots ,v_n$, u) and $2n-1$ edges (e.g., $v_i{v}_{i+1}$, $1\le i\le n-1$, and $v_{i}u$, $1\le i\le n$).

The next lemma gives a lower bound of the edge irregularity strength for the fan graphs.

Lemma 1.

Let $F_n$, $n\ge 2$, be a fan graph of order $n+1$. Then

$$\begin{array}{c}\hfill \mathrm{es}\left(F_n\right)\ge n+1.\end{array}$$

Proof. 

Since $\left|E\right(F_n\left)\right|=2n-1$ and the maximum degree $\mathsf{\Delta }\left(F_n\right)=n$, then from (1) it follows that $\mathrm{es}\left(F_n\right)\ge n$. However, it is not difficult to see that any edge irregular labeling $\phi$ of the fan graph $F_n$ has to be injective. Evidently, for any two vertices in $V\left(F_n\right)$ their common neighborhood is not an empty set. This means that if $\phi \left(x\right)=\phi \left(y\right)$ for a couple of distinct vertices $x,y\in V\left(F_n\right)$, then $\phi \left(x\right)+\phi \left(z\right)=\phi \left(y\right)+\phi \left(z\right)$, where z is a common neighbor of x and y. This contradicts the fact that $\phi$ is irregular. Hence, $\mathrm{es}\left(F_n\right)\ge n+1$. □

Theorem 3 shows that the lower bound of the edge irregularity strength of fan graphs $F_n$ given in Lemma 1 is tight for some values of the parameter n. To prove the equality we use the following auxiliary lemma.

Lemma 2.

Let f be a (modular) edge irregular k-labeling of a graph G. Then, the vertex labeling g defined such that

$$g\left(u\right)=k+1-f\left(u\right)\mathit{for}\mathit{every}u\in V\left(G\right)$$

is also a (modular) edge irregular k-labeling of a graph G.

Proof. 

Let f be a (modular) edge irregular k-labeling of a graph G and let the labeling g be defined such that

$$g\left(u\right)=k+1-f\left(u\right)\mathrm{for}\mathrm{every}u\in V\left(G\right).$$

Evidently, the maximal vertex label under the labeling g is k, and is obtained on vertices labeled by 1 under the labeling f. If $uv$ is an edge in G, then

$$\begin{array}{cc}\hfill w{t}_g\left(uv\right)& =g\left(u\right)+g\left(v\right)=\left(k+1-f\left(u\right)\right)+\left(k+1-f\left(v\right)\right)=2k+2-\left(f\left(u\right)+f\left(v\right)\right)\hfill \\ \hfill & =2k+2-w{t}_f\left(uv\right).\hfill \end{array}$$

As the edge weights under the labeling f are distinct, we obtain that the edge weights under the labeling g are also distinct.

Moreover, if f is modular edge irregular, i.e., the corresponding modular edge weights are $0,1,\dots ,\left|E\right(G\left)\right|-1$, it is a well established mathematical convention that the modular edge weights under the labeling g are also $0,1,\dots ,\left|E\right(G\left)\right|-1$. This concludes the proof. □

Theorem 3.

The fan graph $F_n$ of order $n+1$, $n\ge 2$, admits an edge irregular $(n+1)$-labeling with consecutive edge weights if and only if $n\in \{2,3,4,5,6\}$.

Proof. 

Let $\phi :V\left(F_n\right)\to \{1,2,\dots ,n+1\}$ be an edge irregular vertex $(n+1)$-labeling with consecutive edge weights $t,t+1,\dots ,t+2n-2$. Clearly, $t\ge 3$ as the sum of the two smallest vertex labels 1 and 2. Since the largest edge weight can be at most $2n+1$ as sum of the two largest vertex labels n and $n+1$, then $t+2n-2\le 2n+1$ and thus $t\le 3$. This means that under the labeling $\phi$ the corresponding edge weights successively attain consecutive values $3,4,\dots ,2n+1$.

We will consider three cases depending on the value of the centre vertex u.

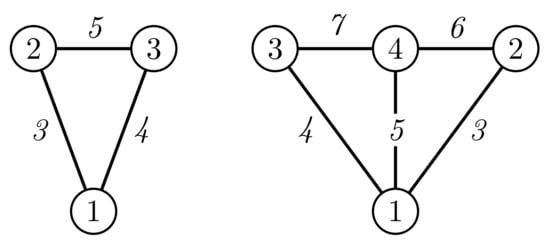
• Case (i). If $\phi \left(u\right)=1$, i.e., $\{\phi \left(v_i\right):1\le i\le n\}=\{2,3,\dots ,n+1\}$, then the weights of edges $v_{i}u$, $1\le i\le n$, receive consecutive values from the set $A_1=\{3,4,\dots ,n+2\}$ and the weights of edges $v_i{v}_{i+1}$, $1\le i\le n-1$, attain values from the set $A_2=\{n+3,n+4,\dots ,2n+1\}$. The sum of the numbers in the set $A_2$ equals to the sum of the corresponding end vertex labels of edges, $v_i{v}_{i+1}$, $1\le i\le n-1$. The labels of vertices $v_1$ and $v_n$ are only counted once, while the labels of the vertices $v_2,v_3,\dots ,v_{n-1}$ are counted twice. We obtain the following:

  $$\begin{array}{c}\hfill 2\sum _{i=1}^n\phi \left(v_i\right)-\phi \left(v_1\right)-\phi \left(v_n\right)=\sum _{i=1}^{n-1}w{t}_{\phi }\left(v_i{v}_{i+1}\right),\end{array}$$

  thus

  $$\begin{array}{c}\hfill 2(2+3+\dots +(n+1))-\phi \left(v_1\right)-\phi \left(v_n\right)=(n+3)+(n+4)+\dots +(2n+1)\end{array}$$

  and

  $$\begin{array}{c}\hfill \phi \left(v_1\right)+\phi \left(v_n\right)=\frac{-n^2+5n+4}{2}.\end{array}$$

  (6)

  Since $\phi \left(v_1\right)+\phi \left(v_n\right)$ is at least 5 and at most $2n+1$, then (6) gives

  $$\begin{array}{c}\hfill 5\le \frac{-n^2+5n+4}{2}\le 2n+1.\end{array}$$

  (7)

  The separation of the compound inequality (7) gives the system of two quadratic inequalities

  $$(n-3)(n-2)\le 0\mathrm{and}(n-2)(n+1)\ge 0,$$

  which has only two integer solutions, $n=2$ and $n=3$. The corresponding edge irregular $(n+1)$-labelings of $F_n$ for $n=2$ and $n=3$ are illustrated in Figure 1.
• Case (ii). If $\phi \left(u\right)=n+1$, i.e., $\{\phi \left(v_i\right):1\le i\le n\}=\{1,2,\dots ,n\}$, then by Lemma 2 this case is analogous to Case (i).
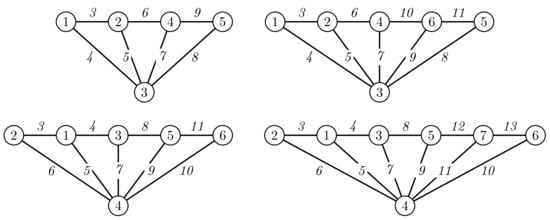
• Case (iii). Assume $\phi \left(u\right)=s$, $1<s<n+1$. Now, the set of labels of vertices $v_1,v_2,\dots ,v_n$ consists of two subsets $C=\{1,2,\dots ,s-1\}$ and $D=\{s+1,s+2,\dots ,n+1\}$. Then, corresponding weights of edges $v_{i}u$ form the set $W=\{wt\left(v_{i}u\right):1\le i\le n\}=\{s+1,s+2,\dots ,2s-2,2s-1,2s+1,2s+2,\dots ,s+n,s+n+1\}$.

We can see that only the vertex labels from the subset C can create the set of the smallest edge weights $W_C=\{3,4,\dots ,s\}$, and only the vertex labels from the subset D can create the set of the largest edge weights $W_D=\{s+n+2,s+n+3,\dots ,2n+1\}$. It is an easy observation that the missing edge weight $2s$ in the set W cannot be obtained as the sum of two vertex labels, neither both from the set C nor both from the set D. Certainly, the edge weight $2s$ must be the sum of two vertex labels (e.g., c and d). Without loss of generality, suppose that c and $\phi \left(v_1\right)$ belong to the set C, and that d with $\phi \left(v_n\right)$ belong to the set D.

Since the sum of all edge weights in the set $W_C$ is equal to the sum of all vertex labels in the subset C (both labels c and $\phi \left(v_1\right)$ are counted once, while the values of the other vertices are counted twice), then

$$\begin{array}{c}\hfill 3+4+\dots +s=2\left(1+2+\dots +(s-1)\right)-c-\phi \left(v_1\right)\end{array}$$

and

$$\begin{array}{c}\hfill c+\phi \left(v_1\right)=\frac{s^2-3s+6}{2}.\end{array}$$

As the value $c+\phi \left(v_1\right)$ is at most $2s-3$ we obtain the inequality $\frac{s^2-3s+6}{2}\le 2s-3$, which has only two integer solutions, $s=3$ or $s=4$.

Analogously, the sum of all edge weights in the set $W_D$ is equal to the sum of all vertex labels in the subset D, where the vertex labels d and $\phi \left(v_n\right)$ are counted once each and the values of constituent vertices are counted twice each. Thus,

$$\begin{array}{c}\hfill (s+n+2)+(s+n+3)+\dots +(2n+1)=2\left[(s+1)+(s+2)+\dots +(n+1)\right]-d-\phi \left(v_n\right)\end{array}$$

and

$$\begin{array}{c}\hfill d+\phi \left(v_n\right)=\frac{-n^2+2ns+3n+s-s^2+4}{2}.\end{array}$$

(8)

Because the numbers d and $\phi \left(v_n\right)$ are from the set D, their sum cannot be smaller than $2s+3$ and cannot be greater than $2n+1$. Thus, (8) leads to the following compound inequality:

$$\begin{array}{c}\hfill 2s+3\le \frac{-n^2+2ns+3n+s-s^2+4}{2}\le 2n+1.\end{array}$$

(9)

Putting $s=3$ to (9) leads to

$$\begin{array}{c}\hfill 18\le -n^2+9n-2\le 4n+2,\end{array}$$

which is equivalent to the following system of two quadratic inequalities:

$$(n-5)(n-4)\le 0\mathrm{and}(n-4)(n-1)\ge 0.$$

By direct calculation we obtain two integer solutions, $n=4$ and $n=5$.

On the other hand, if $s=4$ then (9) gives

$$\begin{array}{c}\hfill 22\le -n^2+11n-8\le 4n+2\end{array}$$

separated to

$$(n-6)(n-5)\le 0\mathrm{and}(n-5)(n-2)\ge 0$$

and their common integer solutions $n=5$ and $n=6$.

The corresponding edge irregular $(n+1)$-labelings of $F_n$ for $(n,s)=(4,3)$, $(n,s)=(5,3)$, $(n,s)=(5,4)$ and $(n,s)=(6,4)$ are illustrated in Figure 2. □

Let us note that from Lemma 1 and Theorem 3 it follows that $\mathrm{es}\left(F_n\right)>n+1$ for $n\ge 7$.

With respect to Theorem 1 and Theorem 3 we obtain the following corollary.

Corollary 1.

Let $F_n$ be a fan graph of order $n+1$. If $n\in \{2,3,4,5,6\}$ then $\mathrm{mes}\left(F_n\right)=n+1$.

The next theorem gives a lower bound and an upper bound for the modular edge irregularity strength of fan graphs $F_n$.

Theorem 4.

Let $F_n$, $n\ge 2$, be a fan graph of order $n+1$. Then,

$$\begin{array}{c}\hfill n+1\le \mathrm{mes}\left(F_n\right)\le n+⌊\frac{n}{2}⌋.\end{array}$$

Proof. 

To obtain the lower bound for the modular edge irregularity strength of fan graphs we need only combine (2) and Lemma 1. From Corollary 1 it follows that $\mathrm{mes}\left(F_n\right)=n+1$ for $n\in \{2,3,4,5,6\}$. Thus, the presented lower bound of the modular edge irregularity strength of $F_n$ is tight.

To obtain the upper bound of the parameter $\mathrm{mes}\left(F_n\right)$ for $n\ge 7$, we consider the vertex labeling $\psi$ of the path $P_n=v_1{v}_2\dots v_n$, defined as follows:

$$\begin{array}{cc}\hfill \psi \left(v_i\right)& =\left\{\begin{array}{cc}⌊\frac{n}{2}⌋+\frac{i+1}{2},\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},1\le i\le n,\hfill \\ \frac{i}{2},\hfill & \mathrm{if}i\mathrm{is}\mathrm{even},2\le i\le n.\hfill \end{array}\right.\hfill \end{array}$$

Thus, all vertex labels are consecutive numbers $1,2,\dots ,n$ and the set of weights of edges $v_i{v}_{i+1}$, $1\le i\le n-1$, consists of consecutive numbers, more precisely,

$$\begin{array}{c}\hfill w{t}_{\psi }\left(v_i{v}_{i+1}\right)=\psi \left(v_i\right)+\psi \left(v_{i+1}\right)=⌊\frac{n}{2}⌋+1+i.\end{array}$$

This means that the maximal edge weight under the labeling $\psi$ is $⌊\frac{3n}{2}⌋$. According to Theorem 2 the labeling $\psi$ can be extended to a modular edge irregular $⌊\frac{3n}{2}⌋$-labeling of the graph ${\left(P_n\right)}_{V\left(P_n\right)}$ which is isomorphic to the fan graph $F_n$. □

Note that we can apply Theorem 2 on $F_n$ recursively, and we can obtain an upper bound for the modular edge irregularity strength of the join of a path $P_n$ with m isolated vertices for $m\ge 1$ in the form

$$\begin{array}{c}\hfill \mathrm{mes}(P_n+\overline{K_m})\le nm+⌊\frac{n}{2}⌋.\end{array}$$

However, we can prove even better the upper bound.

Theorem 5.

Let $P_n$ be a path of order n, $n\ge 2$, and let $m\ge 2$ be an integer. Then,

$$\begin{array}{c}\hfill ⌈\frac{n(m+1)}{2}⌉\le \mathrm{mes}(P_n+\overline{K_m})\le nm.\end{array}$$

Proof. 

Let $V(P_n+\overline{K_m})=\{v_i:1\le i\le n\}\cup \{u_j:1\le j\le m\}$ and $E(P_n+\overline{K_m})=\{v_i{v}_{i+1}:1\le i\le n-1\}\cup \{v_i{u}_j:1\le i\le n,1\le j\le m\}$.

For $n,m\ge 2$ the lower bound follows from (1) and (2). For the upper bound, consider the labeling $\phi$ defined such that

$$\begin{array}{cc}\hfill \phi \left(v_i\right)& =\left\{\begin{array}{cc}n(m-1)+\frac{i+1}{2},\hfill & \mathrm{if}i\mathrm{is}\mathrm{odd},1\le i\le n,\hfill \\ n(m-1)-⌊\frac{n}{2}⌋+\frac{i}{2},\hfill & \mathrm{if}i\mathrm{is}\mathrm{even},2\le i\le n,\hfill \end{array}\right.\hfill \\ \hfill \phi \left(u_j\right)& =\left\{\begin{array}{cc}1+(j-1)n,\hfill & \mathrm{if}1\le j\le m-1,\hfill \\ nm,\hfill & \mathrm{if}j=m.\hfill \end{array}\right.\hfill \end{array}$$

Evidently, the labeling $\phi$ is an $nm$-labeling and

$$\begin{array}{c}\hfill \{\phi \left(v_i\right):1\le i\le n\}=\{n(m-1)-⌊\frac{n}{2}⌋+1,n(m-1)-⌊\frac{n}{2}⌋+2,\dots ,n(m-1)+⌈\frac{n}{2}⌉\}.\end{array}$$

(10)

Now we evaluate the corresponding edge weights. For $1\le i\le n-1$ we have

$$\begin{array}{c}\hfill w{t}_{\phi }\left(v_i{v}_{i+1}\right)=\phi \left(v_i\right)+\phi \left(v_{i+1}\right)=2n(m-1)-⌊\frac{n}{2}⌋+1+i,\end{array}$$

thus the weights of the edges $v_i{v}_{i+1}$ for $1\le i\le n-1$ are

$$2n(m-1)-⌊\frac{n}{2}⌋+2,2n(m-1)-⌊\frac{n}{2}⌋+3,\dots ,n(2m-1)-⌊\frac{n}{2}⌋.$$

According to (10), for $1\le j\le m-1$ we obtain

$$\begin{array}{cc}\hfill \{w{t}_{\phi }\left(v_i{u}_j\right)& =\phi \left(v_i\right)+\phi \left(u_j\right):1\le i\le n\}\hfill \\ \hfill & =\{n(m+j-2)-⌊\frac{n}{2}⌋+2,n(m+j-2)-⌊\frac{n}{2}⌋+3,\dots ,n(m+j-2)+⌈\frac{n}{2}⌉+1\}.\hfill \end{array}$$

This means that the weights of edges $v_i{u}_j$ for $1\le i\le n$, $1\le j\le m-1$ are the consecutive numbers

$$n(m-1)-⌊\frac{n}{2}⌋+2,n(m-1)-⌊\frac{n}{2}⌋+3,\dots ,2n(m-1)-⌊\frac{n}{2}⌋+1.$$

Finally, again using (10) we have

$$\begin{array}{cc}\hfill \{w{t}_{\phi }\left(v_i{u}_m\right)& =\phi \left(v_i\right)+\phi \left(u_m\right):1\le i\le n\}\hfill \\ \hfill & =\{n(2m-1)-⌊\frac{n}{2}⌋+1,n(2m-1)-⌊\frac{n}{2}⌋+2,\dots ,n(2m-1)+⌈\frac{n}{2}⌉\}.\hfill \end{array}$$

Thus, the set of all edge weights consists of consecutive integers

$$n(m-1)-⌊\frac{n}{2}⌋+2,n(m-1)-⌊\frac{n}{2}⌋+3,\dots ,n(2m-1)+⌈\frac{n}{2}⌉.$$

This implies that $\phi$ is a modular edge irregular $nm$-labeling of $P_n+\overline{K_m}$ for $n,m\ge 2$. This concludes the proof. □

Combining (1), (2), Lemma 1 and Theorems 4, 5, we obtain the following corollary.

Corollary 2.

For $n\ge 2$

$$\begin{array}{c}\hfill n+1\le \mathrm{es}(P_n+K_1)\le n+⌊\frac{n}{2}⌋\end{array}$$

and for $n,m\ge 2$

$$\begin{array}{c}\hfill ⌈\frac{n(m+1)}{2}⌉\le \mathrm{es}(P_n+\overline{K_m})\le nm.\end{array}$$

Note that some partial results for $\mathrm{es}(P_n+\overline{K_m})$ for $3\le n\le 6$ and $m\ge 3$ are proved in [13].

4. Wheels

A wheel $W_n$, $n\ge 3$, is a graph of order $n+1$ and size $2n$ obtained by joining vertices $v_1$ and $v_n$ in a fan graph $F_n$. Alternatively, the wheel $W_n$ is obtained as a join of a cycle $C_n$ on n vertices with $K_1$. Let us start by determining a lower bound of the edge irregularity strength for wheels.

Lemma 3.

Let $W_n$, $n\ge 3$, be a wheel of order $n+1$. Then,

$$\begin{array}{c}\hfill \mathrm{es}\left(W_n\right)\ge n+2.\end{array}$$

Proof. 

According to (1) we obtain that $\mathrm{es}\left(W_n\right)\ge n+1$. Suppose that $\phi$ is an edge irregular $(n+1)$-labeling of $W_n$. Evidently, $\phi$ must be a bijection. Thus, the edge weights are not smaller than 3 and are not greater than $2n+1$. However, the number of integers from 3 to $2n+1$ is $2n-1$, but this is a contradiction as $\left|E\right(W_n\left)\right|=2n$. □

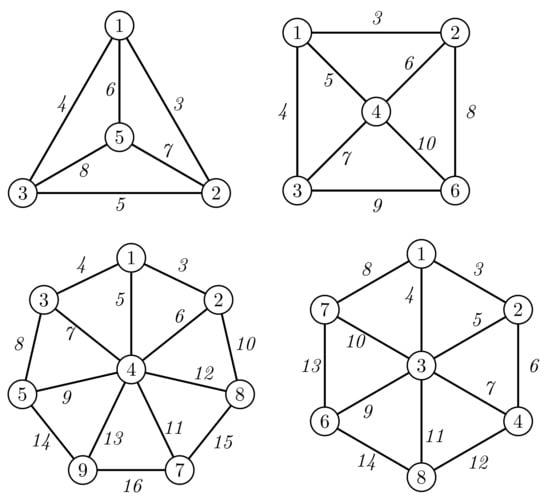
Figure 3 illustrates appropriate modular edge irregular $(n+2)$-labelings for wheels $W_n$ when $n=3,4,6,7$. This proves tightness of the lower bound from Lemma 3.

The next theorem shows that the modular edge irregularity strength of wheels $W_n$ for $n\ge 5$ odd is at most $\frac{3n+1}{2}$.

Theorem 6.

Let $W_n$ be a wheel of order $n+1$. If n is odd, $n\ge 5$, then

$$\begin{array}{c}\hfill n+2\le \mathrm{mes}\left(W_n\right)\le \frac{3n+1}{2}.\end{array}$$

Proof. 

Let $V\left(W_n\right)=\{v_i:1\le i\le n\}\cup \left\{u\right\}$ and $E\left(W_n\right)=\{v_i{v}_{i+1}:1\le i\le n-1\}\cup \left\{v_1{v}_n\right\}\cup \{v_{i}u:1\le i\le n\}$. We obtain the lower bound combining (2) and Lemma 3. For odd n, $n\ge 5$, we construct a vertex $\frac{3n+1}{2}$-labeling $\psi$ of the cycle $C_n=v_1{v}_2\dots v_n{v}_1$ in the following way:

$$\begin{array}{cc}\hfill \psi \left(v_i\right)& =\left\{\begin{array}{cc}\frac{i+1}{2},\hfill & \mathrm{if}i=1,3,\dots ,n,\hfill \\ \frac{n+1+i}{2},\hfill & \mathrm{if}i=2,4,\dots ,n-1.\hfill \end{array}\right.\hfill \end{array}$$

The weights of the edges of the cycle $C_n$ attain values from $\frac{n+3}{2}$ to $\frac{3n+1}{2}$. More precisely,

$$\begin{array}{cc}\hfill w{t}_{\psi }\left(v_i{v}_{i+1}\right)& =\frac{n+3}{2}+i,\mathrm{if}1\le i\le n-1,\hfill \\ \hfill w{t}_{\psi }\left(v_n{v}_1\right)& =\frac{n+3}{2}.\hfill \end{array}$$

As the vertices are labeled by the consecutive numbers $1,2,\dots ,n$, using Theorem 2 we obtain that the graph ${\left(C_n\right)}_{V\left(C_n\right)}$ admits a modular edge irregular $\frac{3n+1}{2}$-labeling. As the graph ${\left(C_n\right)}_{V\left(C_n\right)}$ is isomorphic to the wheel $W_n$, the proof is complete. □

It is easy to prove that $\mathrm{mes}\left(W_5\right)\ne 7$. Thus, according to Theorem 6 we obtain $\mathrm{mes}\left(W_5\right)=8$, which proves that the upper bound given in Theorem 6 is tight.

The next theorems present results for the join of a cycle with m isolates, $m\ge 2$.

Theorem 7.

Let $C_n$ be a cycle of order n, $n\ge 3$ odd, and let $m\ge 2$ be an integer. Then,

$$\begin{array}{c}\hfill ⌈\frac{n(m+1)+1}{2}⌉\le \mathrm{mes}(C_n+\overline{K_m})\le nm+1.\end{array}$$

Proof. 

Let $V(C_n+\overline{K_m})=\{v_i:1\le i\le n\}\cup \{u_j:1\le j\le m\}$ and $E(C_n+\overline{K_m})=\{v_i{v}_{i+1}:1\le i\le n-1\}\cup \left\{v_1{v}_n\right\}\cup \{v_i{u}_j:1\le i\le n,1\le j\le m\}$.

As $n\ge 3$ and $m\ge 2$, we obtain the lower bound combining (1) and (2). For odd n we consider the following labeling $\psi$:

$$\begin{array}{cc}\hfill \psi \left(v_i\right)& =\left\{\begin{array}{cc}nm-\frac{3n-1}{2}+\frac{i+1}{2},\hfill & \mathrm{if}i=1,3,\dots ,n,\hfill \\ nm-n+1+\frac{i}{2},\hfill & \mathrm{if}i=2,4,\dots ,n-1,\hfill \end{array}\right.\hfill \\ \hfill \psi \left(u_j\right)& =\left\{\begin{array}{cc}1+(j-1)n,\hfill & \mathrm{if}1\le j\le m-1,\hfill \\ nm+1,\hfill & \mathrm{if}j=m.\hfill \end{array}\right.\hfill \end{array}$$

The labeling $\psi$ is an $(nm+1)$-labeling and

$$\begin{array}{c}\hfill \{\psi \left(v_i\right):1\le i\le n\}=\{nm-\frac{3n-1}{2}+1,nm-\frac{3n-1}{2}+2,\dots ,nm-\frac{3n-1}{2}+n\}.\end{array}$$

(11)

The weights of the edges $v_i{v}_{i+1}$ for $1\le i\le n-1$ and $v_n{v}_1$ attain the values from $2nm-\frac{5n-5}{2}$ to $2nm-\frac{3n-3}{2}$, as

$$\begin{array}{cc}\hfill w{t}_{\psi }\left(v_i{v}_{i+1}\right)& =2nm-\frac{5n-5}{2}+i,\mathrm{if}1\le i\le n-1,\hfill \\ \hfill w{t}_{\psi }\left(v_n{v}_1\right)& =2nm-\frac{5n-5}{2}.\hfill \end{array}$$

According to (11), for $1\le j\le m-1$ we obtain

$$\begin{array}{cc}\hfill \{w{t}_{\psi }\left(v_i{u}_j\right)& =\psi \left(v_i\right)+\psi \left(u_j\right):1\le i\le n\}\hfill \\ \hfill & =\{nm-\frac{3n-1}{2}+(j-1)n+2,nm-\frac{3n-1}{2}+(j-1)n+3,\dots ,nm-\frac{3n-1}{2}+jn+1\}.\hfill \end{array}$$

Thus, the weights of edges $v_i{u}_j$ for $1\le i\le n$, $1\le j\le m-1$ are the consecutive numbers

$$nm-\frac{3n-5}{2},nm-\frac{3n-7}{2},\dots ,2nm-\frac{5n-3}{2}.$$

Moreover, as

$$\begin{array}{cc}\hfill \{w{t}_{\psi }\left(v_i{u}_m\right)& =\psi \left(v_i\right)+\psi \left(u_m\right):1\le i\le n\}\hfill \\ \hfill & =\{2nm-\frac{3n-1}{2}+2,2nm-\frac{3n-1}{2}+3,\dots ,2nm-\frac{n-3}{2}\},\hfill \end{array}$$

we obtain that the set of all edge weights consists of the numbers

$$nm-\frac{3n-5}{2},nm-\frac{3n-7}{2},\dots ,2nm-\frac{n-3}{2}.$$

Thus, $\psi$ is a modular edge irregular $(nm+1)$-labeling of $C_n+\overline{K_m}$ for odd n with $n\ge 3$ and $m\ge 2$. This means that $\mathrm{mes}(C_n+\overline{K_m})\le nm+1$ in this case. □

For even n we can determine only an upper bound for the edge irregularity strength.

Theorem 8.

Let $W_n$ be a wheel of order $n+1$. If n is even, $n\ge 8$, then

$$\begin{array}{c}\hfill n+2\le \mathrm{es}\left(W_n\right)\le 2n-1.\end{array}$$

Proof. 

We follow the notation used in Theorem 6. Hartsfield and Ringel [14] proved that the even cycle $C_n$ is antimagic, i.e., it is possible to label its edges with the numbers $1,2,\dots ,n$ such that the sums of labels of incident edges (called the vertex weights) are pairwise distinct. Moreover, they constructed the corresponding antimagic labeling of $C_n$, say f, such that the maximal vertex weight is $2n-1$.

For even n, $n\ge 8$, consider a vertex labeling $\psi$ of $C_n$ defined such that

$$\begin{array}{cc}\hfill \psi \left(v_i\right)& =\left\{\begin{array}{cc}f\left(v_i{v}_{i+1}\right),\hfill & \mathrm{if}1\le i\le n-1,\hfill \\ f\left(v_n{v}_1\right),\hfill & \mathrm{if}i=n.\hfill \end{array}\right.\hfill \end{array}$$

Because f is an antimagic labeling, the weights of edges of $C_n$ under the labeling $\psi$ are pairwise distinct and not greater than $2n-1$. Moreover, as under the labeling $\psi$ the vertices $v_1,v_2,\dots ,v_n$ are labeled with the consecutive numbers $1,2,\dots ,n$, applying Theorem 2 we obtain the desired result. □

Repeated use of Theorem 2 gives the following result.

Theorem 9.

Let $C_n$ be a cycle of order n, $n\ge 8$ even, and let m be an integer. Then,

$$\begin{array}{c}\hfill ⌈\frac{n(m+1)+1}{2}⌉\le \mathrm{es}(C_n+\overline{K_m})\le n(m+1)-1.\end{array}$$

5. Conclusions

In this paper we investigated the existence of modular edge irregular labelings of fan and wheel related graphs in order to determine the corresponding exact value of the modular edge irregularity strength. In both cases we estimated the lower and upper bounds of the modular edge irregularity strength and proved the sharpness of the lower bound for a few values of n.

For further investigation of the existence of modular edge irregular labelings of fan related graphs, we propose the following open problem.

Problem 1.

For the fan graph $F_n$ of order $n+1$ and $n\ge 7$, determine the exact value of the modular edge irregularity strength.

Problem 2.

For $n,m\ge 2$ determine the exact value of the modular edge irregularity strength of the fan related graph $P_n+\overline{K_m}$.

We conclude the paper with the following open problems for wheels and wheel related graphs.

Problem 3.

For the wheel $W_n$ of order $n+1$ and $n\ge 8$ determine the exact value of the modular edge irregularity strength.

Problem 4.

For $n\ge 3$, $m\ge 2$, determine the exact value of the modular edge irregularity strength of the wheel related graph $C_n+\overline{K_m}$.