A Search for Cosmic Ray Bursts at 0.1 PeV with a Small Air Shower Array
Abstract
:1. Introduction
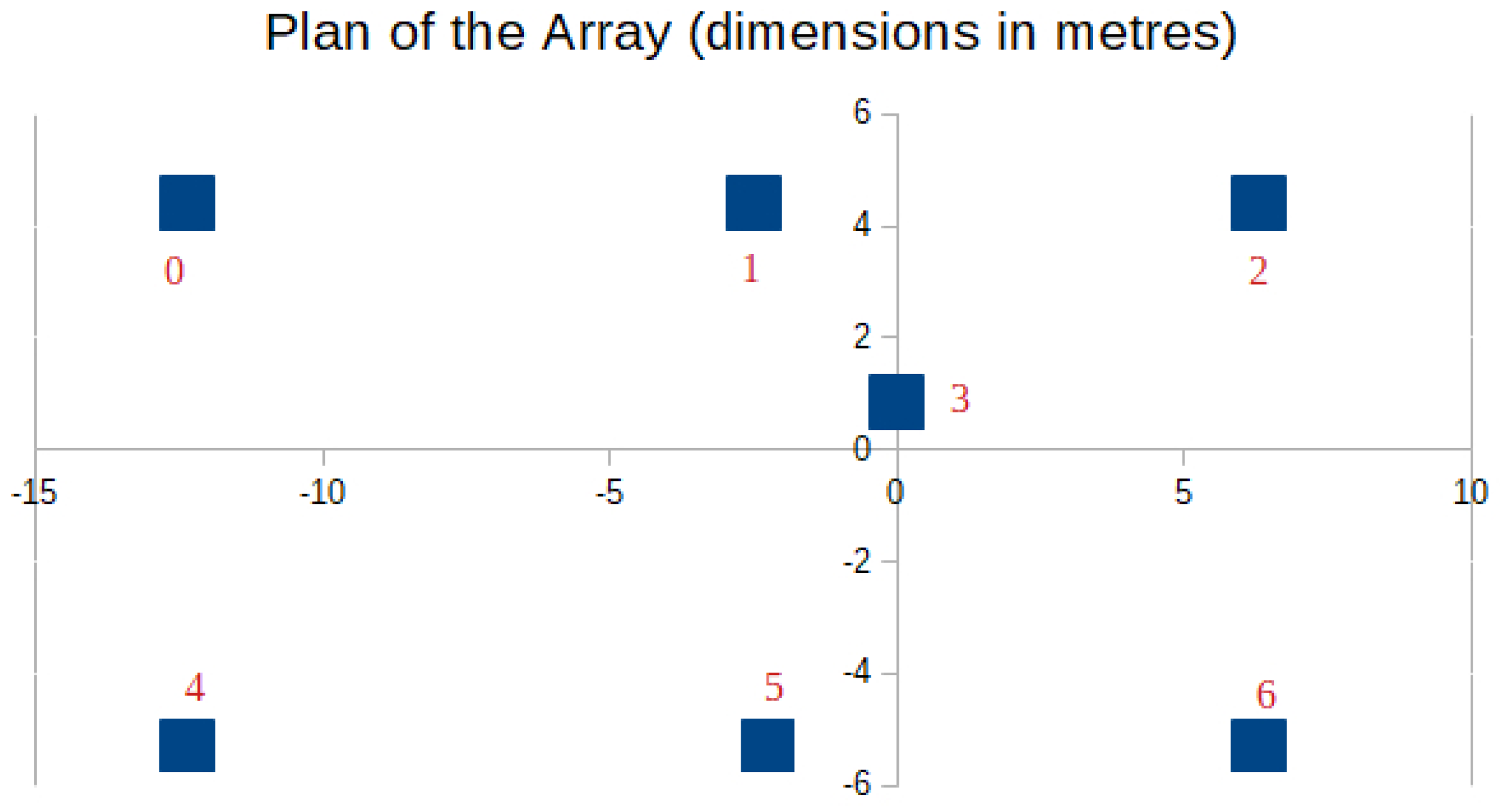
2. Materials and Methods
3. Results
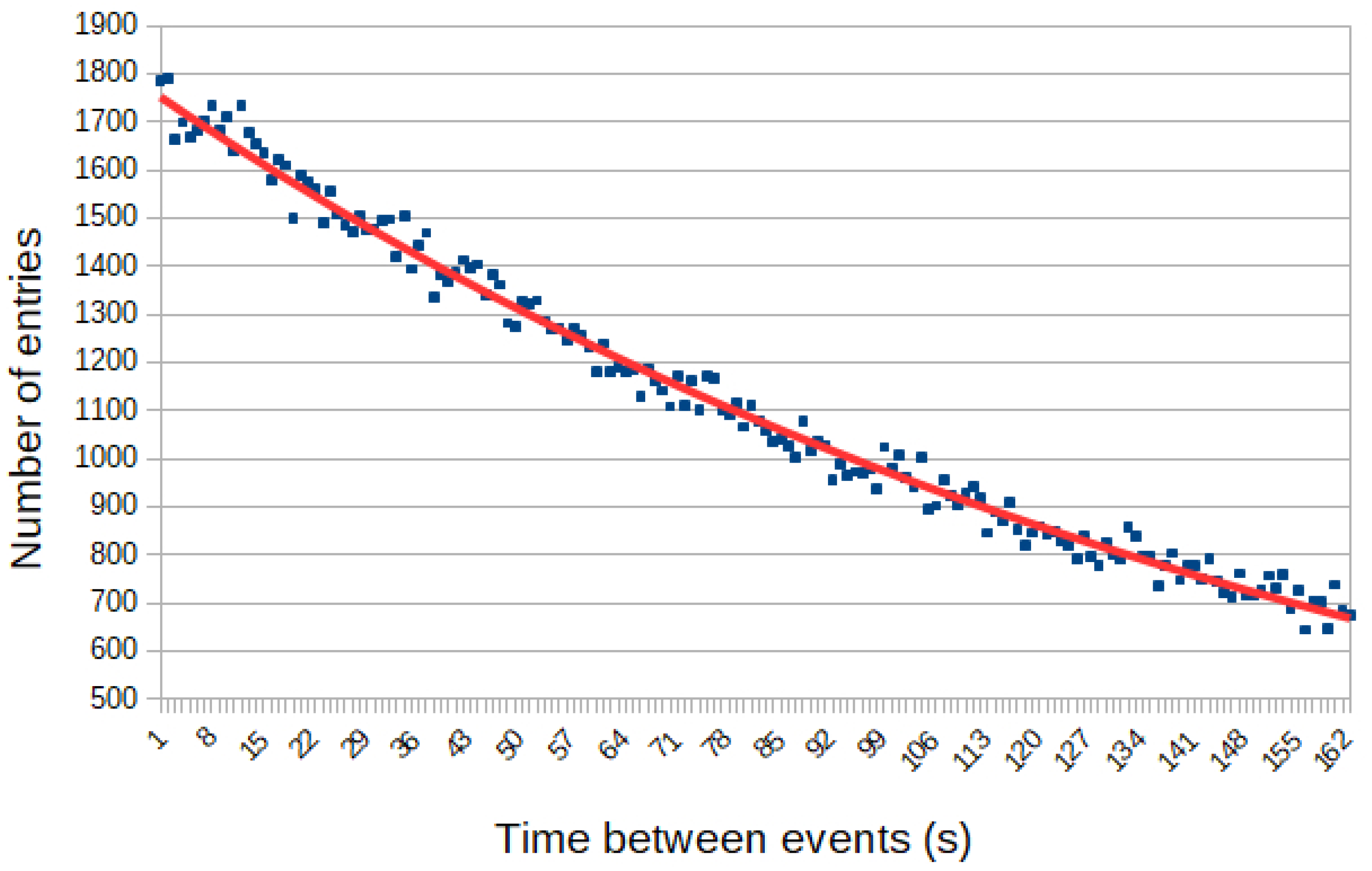
3.1. Event Spacing Distributions
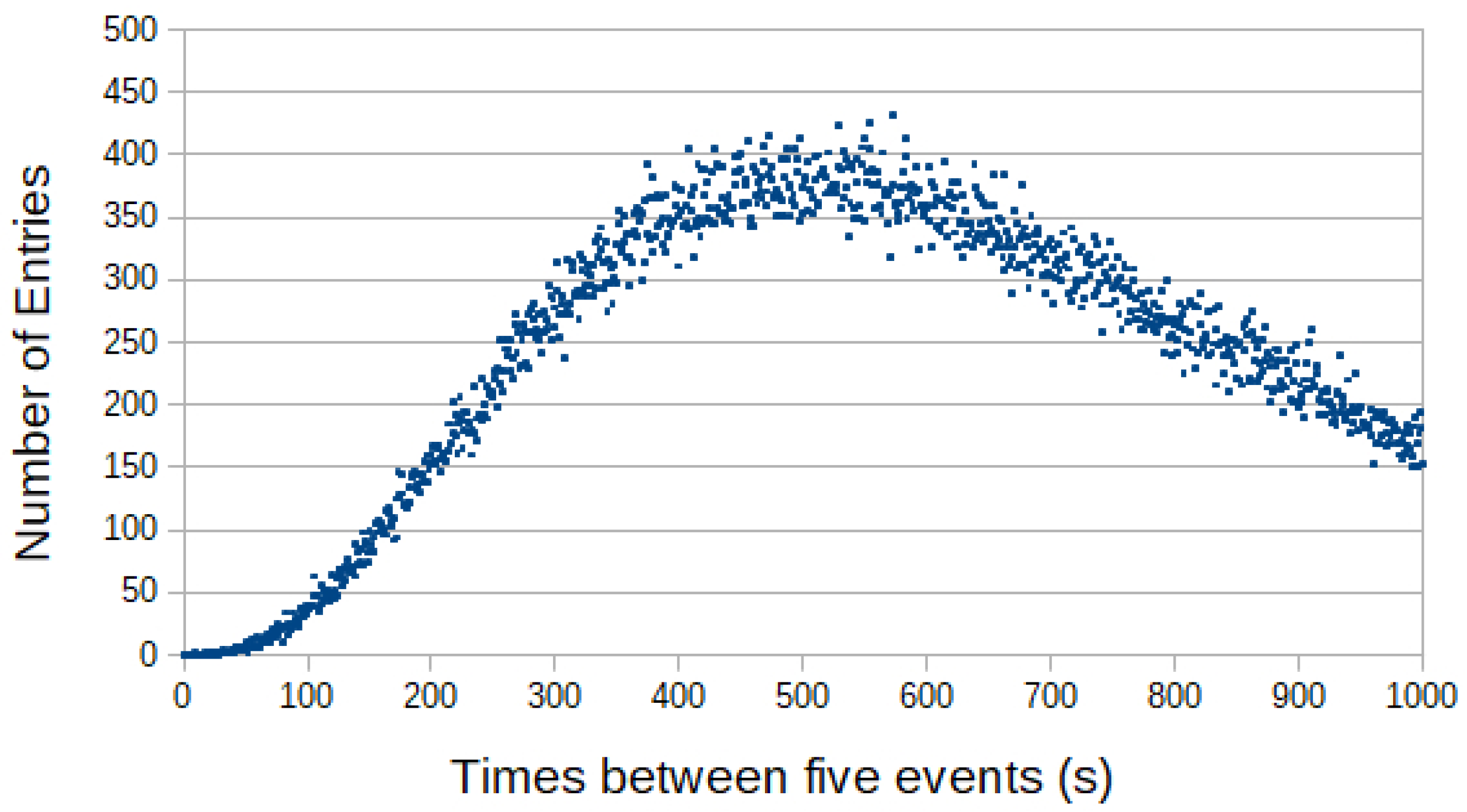
3.2. Examining Five Event Time Spacings at Small Intervals
4. Discussion
4.1. Interpreting the Bursts
4.2. Detector Timing Data
4.3. Burst Directions
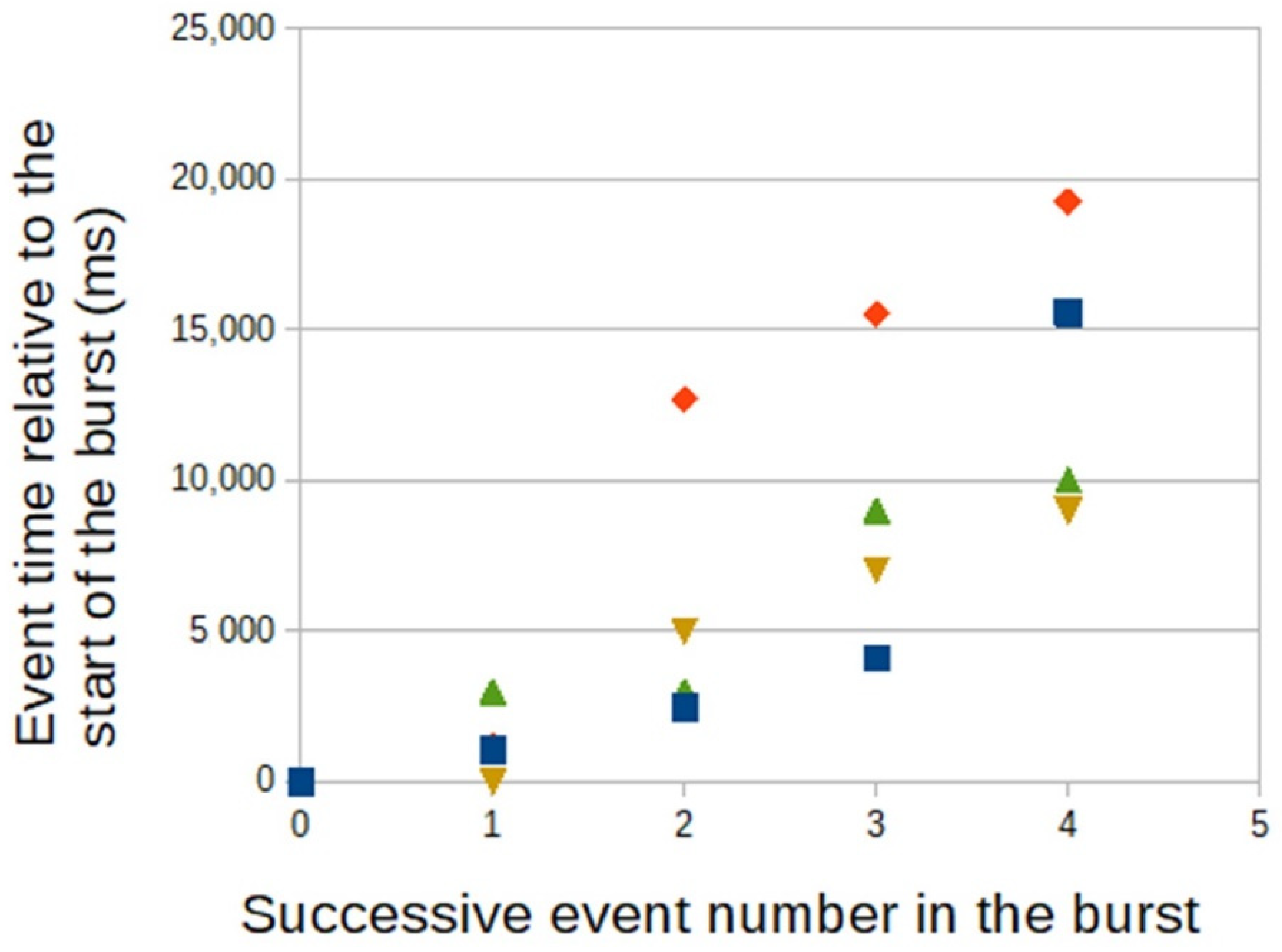
4.4. Event Times within the Bursts
4.5. Interpretation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Homola, P.; Beznosko, D.; Bhatta, G.; Bibrzycki, Ł.; Borczyńska, M.; Bratek, Ł.; Budnev, N.; Burakowski, D.; Alvarez-Castillo, D.; Cheminant, K.A.; et al. Cosmic-Ray Extremely Distributed Observatory. Symmetry 2020, 12, 1835. [Google Scholar] [CrossRef]
- Auger, P.; Ehrenfest, P.; Maze, R.; Daudin, J.; Fréon, R.A. Extensive Cosmic-Ray Showers. Rev. Mod. Phys. 1939, 11, 288–291. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. The Pierre Auger Cosmic Ray Observatory. Nucl. Instrum. Meth. A 2015, 798, 172. [Google Scholar] [CrossRef]
- Klebesadel, R.W.; Strong, I.B.; Olson, R.A. Observations of Gamma-Ray Bursts of Cosmic Origin. Astrophys. J. Lett. 1973, 182, L85. [Google Scholar] [CrossRef]
- Hawking, S.W. Black hole explosions? Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Fegan, D.J.; McBreen, B.; O’Sullivan, C. Observation of a burst of cosmic rays at energies above 7 × 1013 eV. Phys. Rev. Lett. 1983, 51, 2341. [Google Scholar] [CrossRef]
- Smith, G.R.; Ogmen, M.; Buller, E.; Standil, S. Possible Observation of a Burst of Cosmic-Ray Events in the Form of Extensive Air Showers. Phys. Rev. Lett. 1983, 50, 2110–2111. [Google Scholar] [CrossRef]
- Carrel, O.; Martin, M. Observation of time correlations in cosmic rays. Phys. Lett. B 1994, 325, 526. [Google Scholar] [CrossRef] [Green Version]
- Aglietta, M.; Alessandro, B.; Antonioli, P.; Arneodo, F.; Bergamasco, L.; Bertaina, M.E.; Castagnoli, C.; Castellina, A.; Chiavassa, A.; Cini, G.; et al. Search for chaotic features in the arrival times of air showers. Eur. Lett. 1996, 34, 231–2361. [Google Scholar] [CrossRef]
- Kitamura, T.; Ohara, S.; Konishi, T.; Tsuji, K.; Chikawa, M.; Unno, W.; Masaki, I.; Urata, K.; Kato, Y. Chaos in cosmic air showers. Astropart. Phys. 1997, 6, 279. [Google Scholar] [CrossRef]
- Clay, R.W.; Dawson, B.R. A Southern Hemisphere Search for a Nonrandom Component of Cosmic Rays. Aust. J. Phys. 1981, 34, 591. [Google Scholar] [CrossRef] [Green Version]
- Clay, R.; Singh, J. A Search for Bursts at 0.1 PeV with a small air shower array. In Proceedings of the 37th International Cosmic Ray Conference (ICRC2021), Berlin, Germany, 12–23 July 2021; Volume 298. [Google Scholar]
- McBreen, B.; Lambert, C.J. Interactions of high-energy (E > 5 × 1019 eV) photons in the Earth’s magnetic field. Phys. Rev. D 1981, 24, 2536. [Google Scholar] [CrossRef]
- Albert, A.; Alfaro, R.; Alvarez, C.; Camacho, J.R.A.; Arteaga-Velázquez, J.C.; Arunbabu, K.P.; Rojas, D.A.; Solares, H.A.A.; Baghmanyan, V.; Belmont-Moreno, E.; et al. Evidence of 200 TeV Photons from HAWC J1825-134. Astrophys. J. Lett. 2021, 907, L30. [Google Scholar] [CrossRef]
- Cao, Z.; Aharonian, F.; An, Q.; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; Cai, H.; et al. Discovery of the Ultra-high energy gamma-ray source LHASSO J2108+5157. Astrophys. J. Lett. 2021, 919, L22. [Google Scholar] [CrossRef]


| Date and Time (UTC) | Mean RA (deg) | Mean Dec. (deg) |
|---|---|---|
| 19 July 2019 18:48:06 | 25.8 ± 16 | −37 ± 12 |
| 25 March 2021 04:05:16 | 16.5 ± 16 | −55 ± 4 |
| 1 September 2021 14:30:49 | 173.7 ± 17 | −29 ± 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clay, R.; Singh, J.; Homola, P.; Bar, O.; Beznosko, D.; Bhatt, A.; Bhatta, G.; Bibrzycki, Ł.; Budnev, N.; Alvarez-Castillo, D.E.; et al. A Search for Cosmic Ray Bursts at 0.1 PeV with a Small Air Shower Array. Symmetry 2022, 14, 501. https://doi.org/10.3390/sym14030501
Clay R, Singh J, Homola P, Bar O, Beznosko D, Bhatt A, Bhatta G, Bibrzycki Ł, Budnev N, Alvarez-Castillo DE, et al. A Search for Cosmic Ray Bursts at 0.1 PeV with a Small Air Shower Array. Symmetry. 2022; 14(3):501. https://doi.org/10.3390/sym14030501
Chicago/Turabian StyleClay, Roger, Jassimar Singh, Piotr Homola, Olaf Bar, Dmitry Beznosko, Apoorva Bhatt, Gopal Bhatta, Łukasz Bibrzycki, Nikolay Budnev, David E. Alvarez-Castillo, and et al. 2022. "A Search for Cosmic Ray Bursts at 0.1 PeV with a Small Air Shower Array" Symmetry 14, no. 3: 501. https://doi.org/10.3390/sym14030501
APA StyleClay, R., Singh, J., Homola, P., Bar, O., Beznosko, D., Bhatt, A., Bhatta, G., Bibrzycki, Ł., Budnev, N., Alvarez-Castillo, D. E., Dhital, N., Duffy, A. R., Frontczak, M., Góra, D., Gupta, A. C., Łozowski, B., Medvedev, M. V., Mędrala, J., Miszczyk, J., ... Wibig, T. (2022). A Search for Cosmic Ray Bursts at 0.1 PeV with a Small Air Shower Array. Symmetry, 14(3), 501. https://doi.org/10.3390/sym14030501













