Heat Flow Characteristics of Ferrofluid in Magnetic Field Patterns for Electric Vehicle Power Electronics Cooling

Abstract

The ferrofluid is a kind of nanofluid that has magnetization properties in addition to excellent thermophysical properties, which has resulted in an effective performance trend in cooling applications. In the present study, experiments are conducted to investigate the heat flow characteristics of ferrofluid based on thermomagnetic convection under the influence of different magnetic field patterns. The temperature and heat dissipation characteristics are compared for ferrofluid under the influence of no-magnet, I, L, and T magnetic field patterns. The results reveal that the heat gets accumulated within ferrofluid near the heating part in the case of no magnet, whereas the heat flows through ferrofluid under the influence of different magnetic field patterns without any external force. Owing to the thermomagnetic convection characteristic of ferrofluid, the heat dissipates from the heating block and reaches the cooling block by following the path of the I magnetic field pattern. However, in the case of the L and T magnetic field patterns, the thermomagnetic convection characteristic of ferrofluid drives the heat from the heating block to the endpoint location of the pattern instead of the cooling block. The asymmetrical heat dissipation in the case of the L magnetic field pattern and the symmetrical heat dissipation in the case of the T magnetic field pattern are observed following the magnetization path of ferrofluid in the respective cases. The results confirm that the direction of heat flow could be controlled based on the type of magnetic field pattern and its path by utilizing the thermomagnetic behavior of ferrofluid. The proposed lab-scale experimental set-up and results database could be utilized to design an automatic energy transport system for the cooling of power conversion devices in electric vehicles.

1. Introduction

In the last few decades, the need for advanced cooling fluids which surpass the traditional fluids is increasing to improve the efficiency and lifespan of electronic devices [1]. A nanofluid is a colloidal fluid comprised of nano-sized particles dispersed into base fluids. Owing to the Brownian motion of nanoparticles, the thermal conductivity of nanofluids is superior compared to base fluids [2,3]. The heat transfer performance of nanofluids improves with the uniform distribution of nanoparticles in base fluids, hence dispersants have been used to enhance the stability of nanofluids [4].

Patrizi et al. [5] have studied the performance of DC–DC converters under temperature variations by considering thermal cycling, temperature step, and high-temperature tests. The input ripple increases from 80 mV to 85 mV when the temperature approaches 80 °C and the efficiency of the converter reduces by a maximum of 7% with an increase in temperature from 20 °C to 120 °C. A significant amount of heat loss occurs in high-flux-density power electronic devices, which results in an increase in operating temperature. The higher temperature of such devices degrades their efficiency and operating life. Furthermore, the higher temperature of power electronics creates performance issues in the gate threshold voltage shift, a decrease in switching speed, a decrease in mobility, and a decrease in noise margin [6]. The thermal stresses are induced owing to the increase in temperature, which causes the failure of power electronics devices, and hence, the effective thermal management of these devices is requisite for cost-effective and reliable energy conversion [7].

Garud et al. [8] have studied the heat transfer performance characteristics of single- and hybrid-particle nanofluids and concluded that Al₂O₃/Cu nanofluid shows the highest performance evaluation criteria of 1.12. Here, the performance evaluation criteria stand for a ratio of the Nusselt number of nanofluid over the base fluid to the friction factor of the nanofluid over the base fluid. Furthermore, Garud et al. have shown that Al₂O₃/Cu nanofluid with oblate spheroid-shaped nanoparticles depict enhanced first- and second-law characteristics compared to those with spherical-, prolate spheroid-, blade-, cylinder-, platelet-, and brick-shaped nanoparticles [9]. Ghadiri et al. [10] have studied experimentally the cooling performance of a photovoltaic thermal (PVT) system with Fe₃O₄–water ferrofluid coolant under the influence of constant and alternating magnetic fields. The enhanced exergy of 48 W is extracted from the PVT system with 3% ferrofluid under an alternating magnetic field.

Nanofluids depict magnetic characteristics because of the dispersion of ferromagnetic nanoparticles into the base fluid, in which case the nanofluids are named as ferrofluids. The flow control for ferrofluids could be achieved by using its magnetism properties, which were first discovered by NASA in a state of zero gravity [11]. The magnetization performance of ferrofluid changes with temperature, and it is strongest in the saturation magnetization. As the temperature of the fluid increases, it gradually weakens, and when the intrinsic Curie temperature of the fluid is reached, a permanent loss of magnetization performance occurs [12]. Therefore, when a temperature field is generated due to heat transfer in the ferrofluid, the non-equilibrium of magnetization occurs inside because of the local temperature change of the ferrofluid. When the ferrofluid is exposed to a magnetic field environment, the fluid in a relatively low temperature area is induced to the magnetic field, which results in fluid flow, which is called thermomagnetic convection. Thus, the ferrofluid can flow without a special transport device, such as a coolant pump.

Ferrofluid has the property of being magnetized in response to a magnetic field in addition to the properties of existing nanofluids, which leads to a sustainable amount of research on heat transfer systems using the magnetization properties of ferrofluids [13]. Lian et al. [14] have conducted a study on the flow rate according to the thermal load and magnetic field distribution of a ferrofluid. The flow rate was measured through the visualization of the flow pattern by using micro-PIV (particle image velocimetry), and the temperature of the ferrofluid was measured according to the output of the heat source. Through the experiment, the correlation between the thermal load and the flow velocity of the ferrofluid was established, and as a result, it was confirmed that the flow velocity of the ferrofluid increases as the thermal load increases. Xuan et al. [15] have developed a lab-scale cooling device and have tested its cooling performance using ferrofluid under the influence of a magnetic field. The cooling capacity of 5 W is achieved by utilizing only the magnetization characteristics of the ferroflui. Heiazian et al. [16] have proposed a numerical model to simulate the heat transfer performance of ferrofluid under the influence of a magnetic field and presented a consistent validation of the numerical model with the experimental results. Koji et al. [17] have analyzed the heat transfer performance according to the change in flow rate and under the application of a magnetic field. The results confirm that the slower the ferrofluid flow rate, the higher the heat transfer performance of the ferrofluid when forced convection occurs by the magnetic field. Seo et al. [18] have investigated the heat transfer and illuminance characteristics of a high-power LED cooling system with ferrofluid according to magnetic field intensity and the volume fraction of nanoparticles. Yamaguchi et al. [19] have investigated the heat transportation characteristics of a magnetically driven cooling device with ferrofluid as a coolant and depicted the thermal energy transportation of 35.8 W with a heat transfer distance of 5 m. Furthermore, M.S. Pattanaik et al. [20] have shown a similar ferrofluid-based magnetically driven cooling device, which depicts the heat transport distance of 8 m.

Sustainable research has been conducted on ferrofluid as a cooling fluid by utilizing its thermomagnetic convection characteristics when exposed to the magnetic field environment, along with its improved heat transfer performance. By utilizing the thermal–magnetic convection characteristics of the ferrofluid, it is possible to control the thermal flow direction of the ferrofluid through symmetrical and asymmetrical magnetic field patterns, and it is determined that this can be applied to a cooling system. However, most of the prior studies are focused on the unidirectional flow of thermomagnetic convection through a simple arrangement of permanent magnets or a low-power of solenoid coil, which enables the magnetization characteristics of ferrofluid. Research related to the directional control of the heat flow using the thermomagnetic convection of ferrofluid under the application of symmetrical and asymmetrical magnetic fields has not yet been explored. In this study, in order to achieve the effective cooling performance for a ferrofluid-based cooling device, the heat dissipation characteristics of ferrofluid under influences of three magnetic field patterns (with symmetrical and asymmetrical magnet arrangements) are experimentally investigated. The database generated from the lab-scale experiments will be applied to design a cooling system with ferrofluid coolant for the thermal management of high-flux-density devices in electric vehicles.

2. Experimental Method

2.1. Problem Conceptualization

The ferrofluid has the ability to react with an applied magnetic field owing to the magnetic property of dispersed nanoparticles. In order to study the behavior of ferrofluid under the influence of a magnetic field, the ferrofluid-based heat transfer system has been designed in the present work. In the open literature, the concept of an automatic energy transport device has been already proposed, based on which the ferrofluid circulates in the direction of the applied magnetic field. Using this concept, the present system is fabricated such that ferrofluid is filled in a cavity whose one side is exposed to a heating device and whose other side is exposed to a cooling device. The different shapes of magnetic field patterns have been applied to this system. Thus, under the applied temperature difference and magnetic field, the behavior of ferrofluid is observed by conducting several experiments. The details of the experimental set-up, procedure, and parameters are explained in Section 2.2 and Section 2.3.

2.2. Experimental Set-Up Description

Figure 1 shows the schematic diagram of the experimental set-up and the actual image. The experimental set-up comprises of two acryl plates at the top and bottom and two aluminum blocks, one with a ceramic heater and the other with a cooling fan. The experiments are performed in constant temperature and humidity test chambers with an ambient temperature of 25 °C [21]. The small gap is created at the bottom acryl plate to fill the ferrofluid such that the ferrofluid is sandwiched between two acryl plates. The top plate is provided with small holes to insert the thermocouples inside the ferrofluid and one big hole at corner is provided to insert the ferrofluid. To ensure the tight contact between both acryl plates and to avoid the leakage of ferrofluid, both acryl plates are tightly sealed using silicon. The ceramic heater and cooling fan are attached to the respective aluminum blocks using heat-resistant silicon (LC179). The DC power supply is connected with a heater and cooling fan. The ceramic heater for heating has a leakage current of less than 0.5 mA and the voltage is a fixed voltage of 10V through a DC power supply considering the maximum operating temperature of the ferrofluid [22]. The heater is powered using a DC power supply with a voltage and current of 10 V and 0.75 A, respectively, which results in a power input of 7.5 W based on power = voltage $\times$ current for the heater at the heating block. The cooling block is provided with natural convection cooling and fan cooling. The cooling fan is operated with a voltage and current of 10 V and 0.07 A, which results in a power input of 0.7 W. The dimensions of each experimental component are depicted in

Table 1. Dimensions of experiment parts.

Part (Length × Width × Thickness) (mm)	Dimensions
Acrylic plate	200 × 200 × 10
Ferrofluid injection space inside acrylic plate	180 × 180 × 1.8
Ceramic heater	10 × 10 × 1.2
Aluminum block (outside)	20 × 20 × 3
Aluminum block (inside)	10 × 10 × 5
Cooling fan	40 × 40 × 10

[14]. As shown in Figure 1, 33 T-type thermocouples are used to measure the ferrofluid temperature at different locations and two T-type thermocouples (T3 and T33) are used to measure the heating and cooling aluminum blocks’ temperatures. All thermocouples are connected to a data logger (GL840, GL820, GRAPHTEC) for continuously monitoring the temperature data.

To enable the various magnetic field patterns, cylindrical neodymium magnets (N35, EMAGNET) with dimensions of 10 mm × 10 mm are used. The magnetic flux density of each magnet is evaluated as 440 mT by using a Gauss meter (K-6333A, EXSO Co. Ltd., Korea) with an accuracy of ±5% [23,24]. The magnets in different patterns are attached at the lower side of the bottom acryl plate. The heat dissipation characteristics for ferrofluid are compared in three magnet field patterns namely, I magnet field pattern, L magnet field pattern, and T magnet field pattern. The schematic representation of no magnet, I magnet field pattern, L magnet field pattern, and T magnet field pattern is shown in Figure 2. The thermal imaging camera TE-V1 (Sensitivity: <50 mk, Thermal expert) is installed at the center-bottom side of experimental set-up to capture the heat flow distribution in ferrofluid at regular time intervals. By comparing the experimental results of the no-magnet pattern and the I magnet field pattern, the basic heat flow characteristics according to the thermomagnetic convection of the ferrofluid are confirmed. Through the L magnetic field pattern, it is observed whether the heat flow is transferred along the direction of this pattern at the corner where the shape of the pattern is at a right angle, and finally, through the T magnetic field pattern, it is confirmed whether heat is dispersed in the opposite direction based on the magnetic field pattern during the heat flow. Furthermore, the L and T magnetic field patterns are formed to analyze the asymmetrical and symmetrical heat distribution within ferrofluid. The experiments are conducted for a time duration of 30 min. The specifications of the measuring devices are presented in

Table 2. Specifications of measuring devices.

Items	Conditions
Cooling fan	KF0410B1MS-R (JAMICON Co., New Taipei City, Taiwan)
Data logger	GL840, GL820 (GRAPHTEC Co., Yokohama, Japan)
DC power supply	K-6333A (EXSO Co. Ltd., Busan, Korea)
Magnetic field meter	MG-3002 (LUTRON Co., Coopersburg, PA, USA)
Thermal imaging camera	TE-V1 (I3-system, Inc., Daejeon, Korea)
Thermocouple	T-type (Accuracy ±0.1 °C)

. The ferrofluid used in the experiment is HC50 (Taiho, Tokyo, Japan), and its thermal properties are shown in

Table 3. Thermal properties of HC50 ferrofluid.

Properties	Conditions
Specific gravity (at 25 °C)	1.388
Viscosity (at 25 °C)	10 mPa·s
Surface tension (at 25 °C)	26 ± 2 dyne
Saturation magnetization	47.5 ± 3 mT
Boiling point (at 760 mmHg)	150~250 °C
Operating temperature range	−20~120 °C

[25]. The HC50 ferrofluid comprises of a dispersion of Fe₃O₄ nanoparticles in kerosene as a base fluid. The appearance of this ferrofluid is black in liquid form and dark brown when it is dried. When an external magnetic field is applied to HC50 ferrofluid, the nanoparticles get attracted toward the location of the applied magnetic force.

2.3. Experimental Procedure and Uncertainty Analysis

The heat is generated at the heater block by enabling the 10 V DC supply to the heater. At the start of the experiment, the heat is generated at the heater, which is then dissipated to the aluminum block through conduction. As the time passes, the lower surface of the heater block gets heated, which then transfers the heat to the ferrofluid through convection. In the case of the no-magnet experiment, the magnetic field is disabled, hence heat dissipation through ferrofluid will occur based on asymmetrical convection. In the case of the I magnetic field pattern, the magnets are arranged in a straight path by connecting heating and cooling blocks. The magnets are arranged asymmetrically by connecting the heating block and one side’s right-angle corner in the case of the L magnetic field pattern, and those are arranged symmetrically by connecting the heating block and both sides’ right-angle corners in the case of the T magnetic field pattern. All magnetic field patterns enable the magnetic field, which results in the heat flow in the ferrofluid based on thermomagnetic convection. The enabled magnetic field creates non-equilibrium magnetization, which results in ferrofluid circulation based on temperature difference. As the low-temperature ferrofluid responds to the magnetic field and concentrates on the magnet, the high-temperature ferrofluid is transported along the magnet pattern provided on the acrylic plate. The experiments are conducted in a sequence of no-magnet, I, L, and T magnetic field patterns, respectively. The temperatures of the heating and cooling blocks, and ambient and various locations in the ferrofluid are measured at regular time steps using thermocouples and a data logger. Furthermore, the heat distribution in ferrofluid for no-magnet and different magnetic field patterns are visualized by capturing thermal images at regular time steps. The measured temperatures and captured thermal images are compared for no-magnet and various magnetic field patterns to analyze the heat flow characteristics of ferrofluid. The uncertainty associated with any parameter results in the deviation between its measured value and actual value. The uncertainties in the measuring parameters are produced due to the inaccuracies of the measuring devices and errors in the measurements. Therefore, the uncertainty analysis has been performed to ensure the accuracy and reliability of experimental results in the present study. The concept of linearized fraction approximation as presented by Equation (1) is used to calculate the uncertainty in measuring parameters [26]. The measuring parameter in the present experiments is temperature. The accuracies of the thermocouple and data logger are ±0.1 °C and ±0.25%, respectively. The uncertainty in the measured temperature is evaluated as ±0.97% for the conducted experiments.

$$U_R={[{(\frac{\partial R}{\partial X_1}{U}_1)}^2+{(\frac{\partial R}{\partial X_2}{U}_2)}^2+{(\frac{\partial R}{\partial X_3}{U}_3)}^2\dots +{(\frac{\partial R}{\partial X_n}{U}_n)}^2]}^{\frac{1}{2}}$$

(1)

Here, $X_1$, $X_2$, $X_3$,…$X_n$ present dependent quantities, $R$ presents independent quantity, $U_1$, $U_2$, $U_3$,…$U_n$ present uncertainty in independent quantities, and $U_R$ presents uncertainty in dependent quantity.

3. Results & Discussion

Figure 3 shows a comparison of the heat dissipation characteristics of ferrofluid under no-magnet and I magnetic field patterns at various time steps. In the case of no magnet, the heat cannot dissipate within ferrofluid in any direction due to absence of a thermomagnetic convection effect, which results in an increase in temperature near the heating block as time passes, as shown in Figure 3a. The heat gets accumulated near the heating block and the maximum temperature results around this location at the end time of the experiment. The ferrofluid exhibits convection similar to a non-magnetic particle-based nanofluid in an environment where no external magnetic field is applied, and the temperature distribution of the ferrofluid in the heating part remains circular without heat transfer in a specific direction, even after 30 minutes have elapsed from the start of the experiment [27].

In the case of the I magnetic field pattern, the heat dissipates in the direction of the magnetic field generated due to the thermomagnetic convection effect, as shown in Figure 3b. At the starting time of the experiment, the heat is generated near the heating block and as the time passes it dissipates in a straight path to the cooling block because the magnetic field pattern is enabled in the I path connecting the heating and cooling blocks. After a time duration of 10 min, the heat dissipation from the heating block to the cooling block increases in the direction of a straight path. The ferrofluid interferes with the flow of thermomagnetic convection according to the temperature difference and the direction of the external magnetic field to control the direction of heat transfer [28].

Figure 4 depicts the ferrofluid temperatures at different locations along the path of the I magnetic field pattern over the experimental duration. The temperatures of heating and cooling blocks are presented as T3 and T33 curves, whereas temperatures between these two blocks in the straight path are presented as T8, T13, T18, T23, and T28. The highest temperature of 65.3 °C is measured for location T3, which is the heating block temperature. The temperature gradually decreases as the heat transfers along the path of the magnetic field pattern. The heat moves away from the heating block and gets collected as the cooling block, which results in the final cooling block temperature at location T33 of 30.9 °C. The final cooling block temperature is 5.9 °C higher than the ambient temperature, which confirms that the heat is transferred due to the presence of the I magnetic field pattern as a result of thermomagnetic convection. In the case of intermediate locations, the temperature decreases in the order of T8, T13, T18, T23, and T28, respectively, because the distance of these locations increases in the same order from the heating block. The magnetization performance of ferrofluid is strongest in the saturation magnetization and changes with temperature. The ferrofluid losses magnetization characteristics permanently when ferrofluid approaches the Curie temperature [12]. With the increase in temperature, the magnetization characteristic of ferrofluid degrades; therefore, the heat dissipation along the path of the I magnetic field pattern decreases. This results in less variation in ferrofluid temperatures for heating and cooling blocks as well as all locations within the I magnetic field pattern at the end of experiment, when the temperature is high.

The locations T2 and T4 are near the heating block, where the maximum temperature approaches 37.35 °C because the heat is not accumulated around the heating block, which is similar to the no-magnet case. The heat dissipates along the path of the I magnetic field pattern, which results in less heat accumulation around the heating block. The locations T32 and T34 around the cooling block show the temperatures of 27.7 °C and 28.5 °C, respectively, which is higher than the ambient temperature. This indicates that the heat follows the magnetic field pattern path and heats up the cooling block, as well as the heat dissipating around the cooling block. The temperature of ferrofluid does not deviate above 0.5 °C with respect to ambient temperature in all locations except the heating and cooling blocks and locations within the I magnetic field pattern path.

The temperature variation comparison of the heating block with times for no-magnet and I magnetic field patterns is depicted in Figure 5. At the end of the experiment, the temperature of the heating block is measured as 87.4 °C in the case of no magnet and as 65.3 °C in the case of the I magnetic field pattern. The I magnetic field pattern shows a 22.1 °C lower temperature for the heating block compared to the no-magnet case. This indicates that the presence of a magnetic field governs the heat flow following the path of the magnetic field pattern due to the thermomagnetic convection characteristic of ferrofluid. At the start of the experiment, the temperature field is not significantly formed, so the temperature of the heating block is measured similarly in both cases of the no-magnet and I magnetic field patterns. In the case of the no-magnet experiment, the temperature of the heating block continues to rise until the experiment is finished. In the case of the I magnetic field pattern experiment, as the temperature of the heating part rises and the thermal–magnetic convection becomes active, the heating part is cooled by the convection of the ferrofluid [12]. The heat flow occurs along the pattern path, and the rate of increase in the temperature of the heating block decreases. Beyond 20 min, the temperature of the heating block is maintained at a steady-state point in the case of the I magnetic field pattern.

Figure 6 shows the comparison of heat dissipation in ferrofluid for the L and T magnetic field patterns at various time steps over the experimental duration. As shown in Figure 6a, the heat follows the L magnetic field pattern path and heat gets collected at the right-angle corner instead of the cooling block. Despite temperature differences between heating and cooling blocks, the heat is dissipated in the direction of the L magnetic field pattern due to dominance of the thermomagnetic convection effect in ferrofluid generated by the L magnetic field pattern. As the time passes, the dissipation of heat from the heating block to the corner increases along the path of the L magnetic field pattern. The heat is dissipated in both right-angle corners in the case of the T magnetic field pattern, as shown in Figure 6b. In this case, also, the heat dissipated from the heating block gets collected at both corners instead of the cooling block due to the thermomagnetic convection generated by the T magnetic field pattern dominating the temperature difference. The heat distribution increases as time passes and symmetrical heat distribution results along the T magnetic field pattern path at each time step.

Figure 7 shows the comparison of the steady-state temperature of the heating block, cooling block, and endpoint location of the magnetic field patterns. In the case of the I magnetic field pattern, the magnetic field pattern path connects the heating and cooling blocks, which results in the transfer of heat from the heating block to cooling block. However, in the case of the L and T magnetic field patterns, the magnetic field pattern paths connect to both sides’ right-angle corners, which results in the transfer of heat from the heating block to these corners instead of the cooling block. Therefore, in case of the I magnetic field pattern, the cooling block temperature, and in the case of the L and T magnetic field patterns, the endpoint location (both right-angle corners), are depicted in Figure 7. Furthermore, the cooling block is provided with natural convection cooling and with a fan in the case of the I magnetic field pattern. In the case of the no-magnet experiment, the temperature of the heating block is 87.4 °C, which is the highest temperature compared to all magnetic field patterns. The temperature of the cooling block in the case of no magnet is 25.6 °C, which is the lowest temperature compared to the magnetic field patterns. This results in larger temperature differences between the heating and cooling blocks compared to the considered magnetic field patterns and, hence, confirms that the heat is not dissipating in the case of the no-magnet experiment. In the case of the I magnetic field pattern without a fan at the cooling block, the temperatures of the heating and cooling blocks are 66.7 °C and 35.3 °C, respectively. However, the temperatures of the heating and cooling blocks are measured as 65.3 °C and 30.9 °C when a cooling block is provided with a fan. The temperatures of the heating and cooling blocks are lower by 1.4 °C and 4.4 °C, respectively, in the case of the cooling block with a fan compared to that without a fan. This indicates that the ferrofluid has transferred heat to the cooling part, and the cooling performance can be improved by increasing the heat transfer coefficient [14,15]. In the case of the L magnetic field pattern, the temperature at location T16 is presented as the endpoint location of the pattern. In the case of the T magnetic field pattern, the average temperature of locations T16 and T20 is considered as the endpoint location of the pattern. In the case of the L magnetic field pattern experiment, the temperatures of the heating block and the endpoint location of the pattern are measured as 67.1 °C and 41.1 °C, respectively. Whereas, in the case of the T magnetic field pattern, the temperatures of the heating block and the endpoint location of the pattern are measured as 65.8 °C and 36.4 °C, which are lower by 1.3 °C and 4.7 °C, respectively, compared to those in the case of the L magnetic field pattern. Thus, it confirms that the heat dissipation is better in the case of the T magnetic field pattern compared to the L magnetic field pattern. All magnetic field patterns show lower heating block temperatures and higher temperatures for the cooling block and the endpoint location of the pattern compared to the heating and cooling blocks’ temperatures in the case of the no-magnet experiment. These results confirm that by using the thermomagnetic convection effect of ferrofluid, the direction of heat flow could be controlled under the influence of different magnetic field patterns [14,15,16,17,18,19].

The direction of heat flow could be controlled in the presence of a magnetic field using the thermomagnetic convection characteristic of ferrofluid. There is no external work applied to control the heat dissipation direction in ferrofluid. This concept would be used to design a ferrofluid-based cooling system to dissipate the heat from high-flux-density power electronics in electric vehicles. The heat from power electronics devices could be distributed to cooling parts using these magnetic patterns by arranging the magnets in symmetrical and asymmetrical paths. Except the magnetic force imposed by the magnetic field, there is no external pumping power required for such a cooling system. For example, the heat from high-power-density LEDs or inverters in electric vehicles could be absorbed by ferrofluid as a primary coolant, and by using the effective magnetic patterns, the heat from the ferrofluid could be dumped into the cooling part with a secondary coolant (air, water, or any other conventional working fluid) without using any pumping source. Instead of a convectional working fluid, ferrofluid with improved thermophysical properties could be used to dissipate the heat from high-flux-density devices, which could result in improved heat dissipation. Furthermore, despite the high viscosity and density of ferrofluid, this system does not require any external force for ferrofluid circulation, which could reduce the pumping power cost.

4. Conclusions

This experimental study is proposed to control the heat flow direction under the influence of various magnetic field patterns utilizing the thermomagnetic convection characteristics of ferrofluid. The following key findings have been drawn from the conducted study.

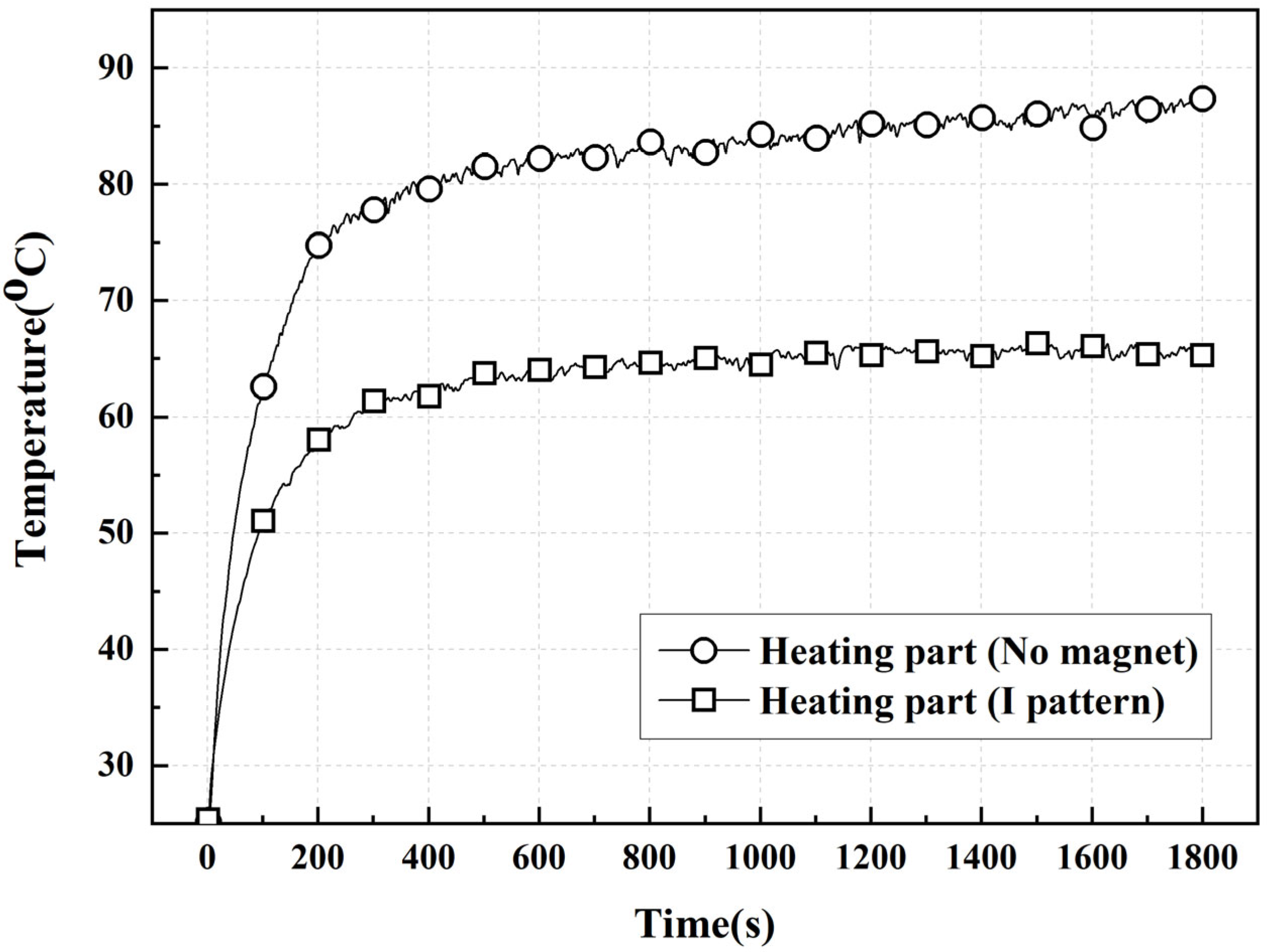
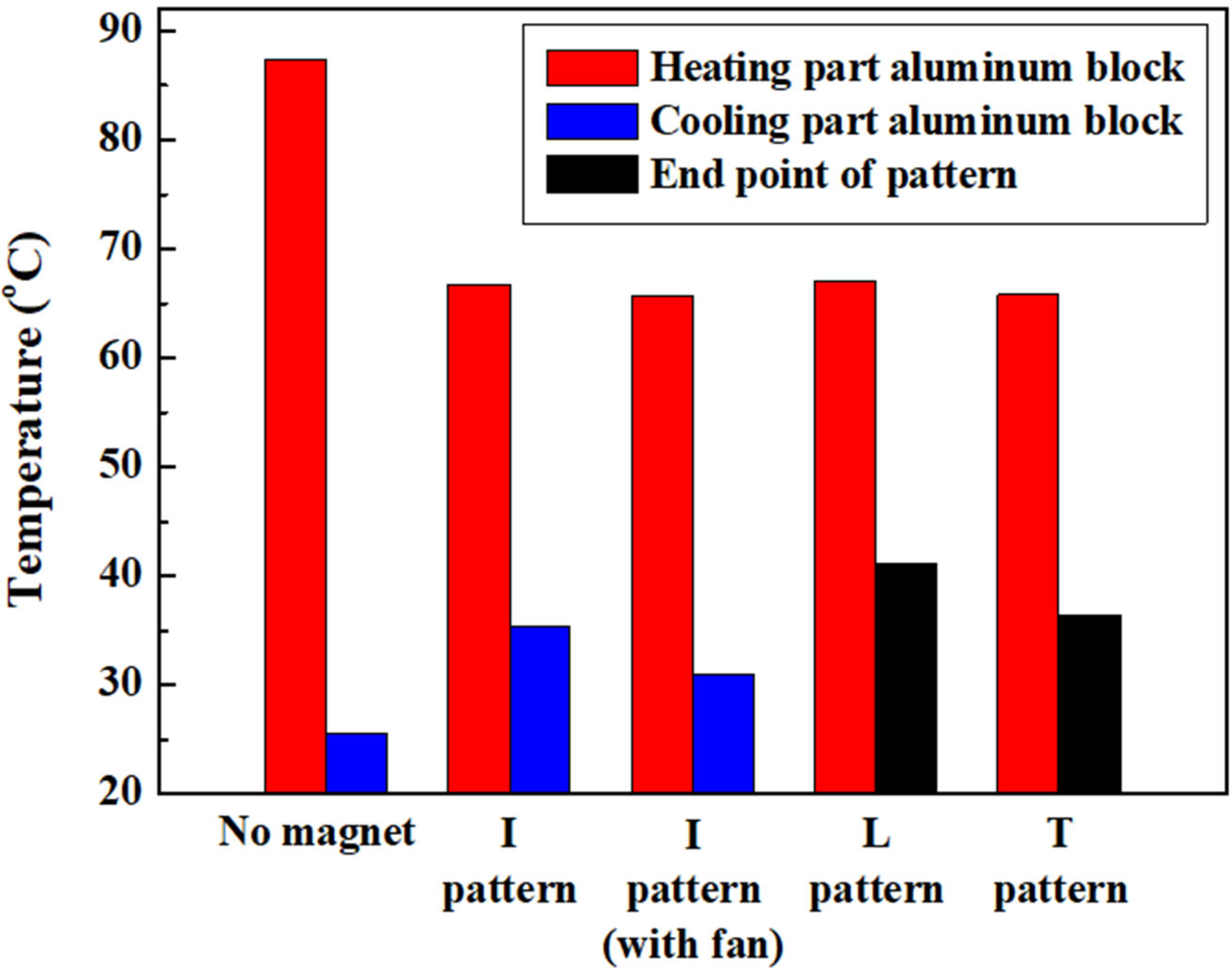
• The temperatures of heating and cooling blocks are evaluated as 87.4 °C and 25.6 °C, respectively, in the case of the no-magnet experiment. This indicates that the heat is not dissipated within ferrofluid, and it gets accumulated near the heating block due to the absence of thermomagnetic convection;
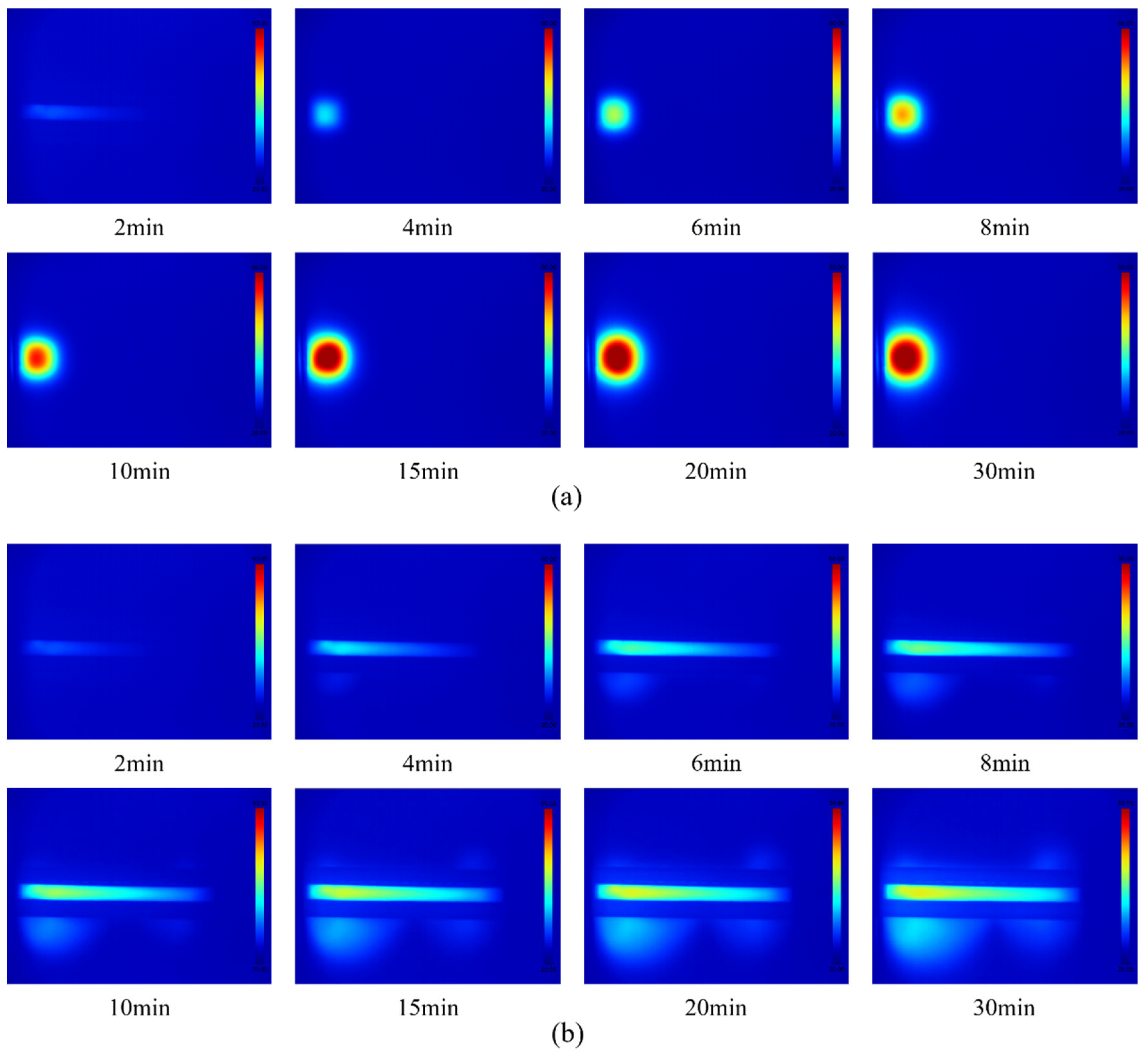
• In the case of the I magnetic field pattern, the heat flows from the heating block to the cooling block along the path of the magnetic field pattern. The thermomagnetic convection of ferrofluid drives the heat in the presence of the magnetic field and the heat dissipation rate increases as time passes;
• The temperatures of the heating and cooling blocks are measured as 66.7 °C and 35.3 °C for the I magnetic field pattern without a cooling fan and as 65.3 °C and 30.9 °C for the I magnetic field pattern with a cooling fan;
• When the fan is used with cooling block in the case of the I magnetic field pattern, the temperature of the heating block lowers by 22.1 °C compared to the heating block temperature in the case of no magnet. Furthermore, the heating and cooling blocks’ temperatures are lower by 1.4 °C and 4.4 °C, respectively, for the cooling block with a fan compared to that without a fan, which indicates that the thermomagnetic convection is sensitive to the temperature difference;
• The heat from the heating block flows to one side’s right-angle corner in the case of the L magnetic field pattern and flows symmetrically to both sides’ right-angle corners in the case of the T magnetic field pattern. In both magnetic field patterns, the heat dissipates along the respective paths of the magnetic field patterns;
• The temperatures of the heating block and the endpoint of the pattern are measured as 67.1 °C and 41.1 °C, respectively, in the case of the L magnetic field pattern and 65.8 °C and 36.4 °C, respectively, in the case of the T magnetic field pattern. In the case of the T magnetic field pattern, the temperatures of the heating block and the endpoint of the pattern are lower by 1.3 °C and 4.7 °C, respectively, compared to the L magnetic field pattern. This indicates a superior heat dissipation performance in the case of the T magnetic field pattern;
• The direction and path of heat flow could be controlled using the magnetization properties of ferrofluid by enabling thermomagnetic convection using various magnetic field patterns. This concept and results database could be referred to as the guidelines to design a ferrofluid-based cooling system with heat dissipation direction control characteristics. This system could be used in electric vehicles to dissipate the heat from high-flux-density power electronics devices.