The Estimation of Bent Line Expectile Regression Model Based on a Smoothing Technique

Abstract

A bent line expectile regression model can describe the effect of a covariate on the response variable with two different straight lines, which intersect at an unknown change-point. Due to the existence of the change-point, the objective function of the model is not differentiable with respect to the change-point, so it cannot be solved by the method of the traditional linear expectile regression model. For this model, a new estimation method is proposed by a smoothing technique, that is, using Gaussian kernel function to approximate the indicator function in the objective function. It can not only estimate the regression coefficients and change-point location simultaneously, but also have better estimation effect, which compensates for the insufficiency of the previous estimation methods. Under the given regularity conditions, the theoretical proofs of the consistency and asymptotic normality of the proposed estimators are derived. There are two parts of numerical simulations in this paper. Simulation 1 discusses various error distributions at different expectile levels under different conditions, the results show that the mean values of the biases of the estimation method in this paper, and other indicators, are very small, which indicates the robust property of the new method. Simulation 2 considers the symmetric and asymmetric bent lien expectile regression models, the results show that the estimated values of the estimation method in this paper are similar to the true values, which indicates the estimation effect and large sample performance of the proposed method are excellent. In the application research, the method in this paper is applied to the Arctic annual average temperature data and the Nile annual average flow data. The research shows that the standard errors of the estimation method in this paper are very similar to 0, indicating that the parameter estimation accuracy of the new method is very high, and the location of the change-point can be accurately estimated, which further confirms that the new method is effective and feasible.

1. Introduction

When performing regression analysis on data in the fields of financial economics [1,2], biomedicine [3,4] and environmental science [5,6], it is inevitable to encounter changes in the data structure. The point corresponding to the change in the data structure is called a change-point [7]. Establishing piecewise linear regression model to study the change-point problem is one of the hot issues in recent years. At present, there have been a large number of literature studies on the piecewise linear regression model, which has been widely used in various fields [8,9,10,11]. According to whether the regression function of the piecewise linear regression model is continuous at the change-point, Bhattacharya [12] divided the model into two categories. One is that the regression function of the model is continuous at the change-point, which is called continuous threshold regression model, and the corresponding change-point is called continuous change-point. On the contrary, the other is called discontinuous piecewise linear regression model, and the corresponding change-point is called discontinuous change-point. This paper is to study the continuous threshold regression model.

In the aspect of change-point detection, Chan [13] extended the log-likelihood ratio test statistics to the piecewise autoregressive model to detect the existence of the change-point. Liu and Qian [14] introduced an empirical likelihood ratio test statistics for continuous change-point in the regression model. Lee et al. [15] proposed general statistics for change-point detection in the regression model, namely sup-likelihood ratio test statistics, which shows that the asymptotic distribution of the test statistics under null assumption is non-standard. In addition, some scholars have studied the change-point detection problem of non-random covariates, mainly focusing on the analysis of time series data, specific references can be referred to Hansen [16] and Cho and White [17], among others. It should be emphasized that the main research goal of this paper is to propose a new estimation method for the continuous threshold expectile regression model, rather than detecting the existence of the change-point. Therefore, this paper is based on the assumption of the existence of the change-point.

In some practical applications, except the conditional expectation of the response variable, we want to have more complete information on the response variable. The expectile regression model proposed by Newey and Powell [18] can not only provide complete information on the response variable through tail expectation, but also have loose application conditions and no strict assumptions for error terms. More importantly, its loss function is differentiable, so it is convenient to calculate. It is a good supplement and expansion to the traditional mean regression model and quantile regression model. Zhang and Li [19] firstly introduced a continuous threshold expectile regression model, also known as bent line expectile regression model, and proposed a formal test for the existence of the change-point at given expectile levels. Similar to Lerman [20], Zhang and Li [19] proposed a grid search method to estimate the regression coefficients and change-point parameter, respectively. The main idea of the grid search method is to search over all possible values under the domain of the change-point and then to select the best one. Nevertheless, the grid search method estimates the regression coefficients and change-point location separately. Not only that, it requires a finer grid to identify the change-point location more precisely, which could result in expensive computation. Furthermore, it is not realistic for this method by assuming that the change-point only occurs at discrete grid points. Motivated by these issues, Zhou and Zhang [21] extended the linearization technique proposed by Yan et al. [22] to the bent line expectile regression model and constructed the interval estimation of the estimators through the theory of the standard linear expectile regression model and the delta technique. Nonetheless, estimation obtained by using the linearization technique in general may underestimate the change-point.

Smoothing technique is to use Gaussian kernel function to approximate the indicator function in the objective function, so as to achieve the purpose of smoothing the change-point locally. Then the objective function is continuous and differentiable with respect to all parameters after being smoothed, so we can easily estimate all parameters in the model. This paper is to propose a new estimation method for the bent line expectile regression model through a smoothing technique, which can simultaneously compensate for the insufficiency of the grid search method of Zhang and Li [19] and the linearization method of Zhou and Zhang [21]. In addition, the theoretical proofs of the consistency and asymptotic normality of the proposed estimators are derived. The numerical simulations under the different conditions show the good performance of the new estimation method proposed in this paper. Finally, the research based on the Arctic annual average temperature data and the Nile annual average flow data show that the new method is effective and feasible.

The remainder of this paper is structured as follows. Section 2 introduces the bent line expectile regression model and proposes a new estimation method for the model based on a smoothing technique. At the same time, we also establish the asymptotic properties of the estimators. In Section 3, simulation studies are conducted to investigate the finite sample performance of the estimation method proposed in this paper. Section 4 applies the model and the estimation method to analyze two real data. Section 5 concludes the paper.

2. Methodology

In this section, we first introduce the bent line expectile regression model, and then point out the insufficiency of the grid search method and linearization method to introduce the smoothing method proposed in this paper. Finally, we prove the consistency and asymptotic normality of the proposed estimators obtained by this new method.

2.1. Model Introduction

Let $\left(Y_i, X_i,{\mathit{Z}}_i\right), i=1,\dots ,n$ be the independent identically distributed random samples from the population $\left(Y,X,\mathit{Z}\right)$. Given $0<\tau <1$, Zhang and Li [19] proposed a bent line expectile regression model:

$$Q_{\tau }\left(Y|X,\mathit{Z}\right)={\beta }_0+{\beta }_{1}X+{\beta }_2{\left(X-t\right)}_{+}+{\mathit{\gamma }}^{⊺}\mathit{Z}$$

(1)

where $Y$ is the response variable, $X$ is the scalar covariate with a change-point, $\mathit{Z}$ is a $p\times 1$-dimensional vector of linear covariates with constant slopes, $Q_{\tau }\left(Y|X,\mathit{Z}\right)$ is the $\tau$th conditional expectile of the response variable $Y$ given $X$ and $\mathit{Z}$, $u_{+}=uI (u>0)$ and $I\left(\cdot \right)$ is the indicator function, $t$ is an unknown change-point, $\mathit{\xi }={\left({\beta }_0,{\beta }_1,{\beta }_2,{\mathit{\gamma }}^{⊺}\right)}^{⊺}$ are the regression coefficients with the exception of $t$. In model (1), the linear expectile regression model $Q_{\tau }\left(Y|X,\mathit{Z}\right)$ is continuous on the covariate $X$ at the change-point location $t$, but $X$ has segmented effects on the expectile of $Y$ through the unknown change-point $t$. More specifically, the slope of $X$ is ${\beta }_1$ below the change-point $t$, whereas it is ${\beta }_1+{\beta }_2$ above that point $t$. For the identifiability of the change-point, it is commonly assumed that ${\beta }_2\ne 0$.

To estimate all the regression parameters of the model $\mathit{\theta }={\left({\mathit{\xi }}^{⊺},t\right)}^{⊺}$ at given expectile levels $\tau \in \left(0,1\right)$, an estimator for $\mathit{\theta }$ can be obtained by minimizing the following objective function:

$$l_{n,\tau }\left(\mathit{\theta }\right)=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\rho }_{\tau }\left\{Y_i-{\beta }_0-{\beta }_1{X}_i-{\beta }_2{\left(X_i-t\right)}_{+}-{\mathit{\gamma }}^{⊺}{\mathit{Z}}_i\right\}$$

(2)

where ${\rho }_{\tau }\left(u\right)=u^2\left|\tau -I\left(u<0\right)\right|$ is the asymmetric least square (ALS) loss function.

2.2. The Proposed Method

However, due to the existence of the change-point $t$, the objective function (2) is not differentiable with respect to $t$, which leads to the non-smoothness problem of the objective function, so it cannot be solved by the method of the traditional linear expectile regression model. In this regard, Zhang and Li [19] proposed the grid search method to circumvent the non-smoothness problem of the objective function. The main idea of the grid search method is to fix the location of the change-point on the grid in advance, then estimate the regression coefficients, and finally use the grid search algorithm to select the optimal point on the grid as the estimation of the change-point parameter. To be specific, for a fixed $t$, the parameter vector $\mathit{\xi }$ can be estimated by,

$$\widehat{\mathit{\xi }}\left(t\right)=\underset{\mathit{\xi }}{arg min}\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\rho }_{\tau }\left\{Y_i-{\mathit{U}}_i\left(t\right)\mathit{\xi }\right\}$$

where ${\mathit{U}}_i\left(t\right)=\left(1,X_i,{\left(X_i-t\right)}_{+},{\mathit{Z}}_i{}^{⊺}\right)$. Then, the change-point $t$ can be estimated by

$$\widehat{t}=\underset{t}{arg min}\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\rho }_{\tau }\left\{Y_i-{\mathit{U}}_i\left(t\right)\widehat{\mathit{\xi }}\left(t\right)\right\}$$

Therefore, the estimator of $\mathit{\theta }$ is $\widehat{\mathit{\theta }}={\left(\widehat{\mathit{\xi }}{\left(t\right)}^{⊺},\widehat{t}\right)}^{⊺}$.

Although the grid search method has become the mainstream estimation method of the change-point model, it has its limitations: the grid search method estimates the regression coefficients and change-point location separately; it requires a finer grid to identify the change-point location more precisely, which could result in expensive computation; it is not realistic for this method by assuming that the change-point only occurs at discrete grid points. In order to overcome these defects of the grid search method, Zhou and Zhang [21] extended the linearization technique proposed by Yan et al. [22] to the bent line expectile regression model, converted the bent line expectile regression model into a standard linear expectile regression model, and then obtained the estimations of the regression coefficients and change-point parameter in the model (1) simultaneously through an iterative algorithm. The specific approach is to approximate the non-linear term by a first-order Taylor expansion around an initial value $t^{\left(0\right)}$,

$${\left(X_i-t\right)}_{+}\approx {\left(X_i-t^{\left(0\right)}\right)}_{+}+\left(-1\right)I(X_i>t^{\left(0\right)})\left(t-t^{\left(0\right)}\right)$$

where $\left(-1\right)I(X_i>t^{\left(0\right)})$ is the first-order derivative of ${\left(X_i-t\right)}_{+}$ at $t^{\left(0\right)}$.

Although the estimation method proposed by Zhou and Zhang [21] makes up for the shortcomings of the grid search method, their method may also have a certain drawback, that is, estimation obtained by using the linearization technique in general may underestimate the change-point. Therefore, our next research content is to propose a better estimation method for the bent line expectile regression model, which can make up for the shortcomings of the grid search method and linearization method simultaneously.

Gaussian kernel function is not only simple in mathematical form and differentiable, that can make calculation easier, but also smooth, which can make the final model smoother. Therefore, we consider to use Gaussian kernel function $\mathsf{\Phi }\left(\frac{X-t}{h}\right)$ to approximate the indicator function $I(X>t)$, where $\mathsf{\Phi }\left(\cdot \right)$ is a standard normal distribution function, $h>0$ is a bandwidth and $h\to 0$ when $n$ tends to infinity. Consequently, the objective function (2) can be approximated by,

$$𝓁\left(\mathit{\theta }\right)=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\rho }_{\tau }\left\{Y_i-{\beta }_0-{\beta }_1{X}_i-{\beta }_2\left(X_i-t\right)\mathsf{\Phi }\left(\frac{X_i-t}{h}\right)-{\mathit{\gamma }}^{⊺}{\mathit{Z}}_i\right\}$$

(3)

Note that the function in the bracket of (3) is continuous and differentiable with respect to all parameters $\mathit{\theta }$, including the change-point $t$. Therefore, we can easily estimate the change-point parameter $t$ and the regression parameters $\mathit{\xi }$ in the model by minimizing the smoothed objective function.

2.3. Asymptotic Properties

To simplify notations, let,

$$g\left({\mathit{w}}_i,\mathit{\theta }\right)={\beta }_0+{\beta }_1{X}_i+{\beta }_2\left(X_i-t\right)\mathsf{\Phi }\left(\frac{X_i-t}{h}\right)+{\mathit{\gamma }}^{⊺}{\mathit{Z}}_i$$

where ${\mathit{w}}_i={\left(1,X_i,{\mathit{Z}}_i^{\top }\right)}^{\top }$, $\mathit{\theta }={\left({\beta }_0,{\beta }_1,{\beta }_2,{\mathit{\gamma }}^{\top },t\right)}^{\top }$. Then the parameters $\mathit{\theta }$ can be estimated by minimizing the following objective function:

$${𝓁}_{\mathsf{\tau }}\left(\mathit{\theta }\right)=\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\rho }_{\tau }\{Y_i-g\left({\mathit{w}}_i,\mathit{\theta }\right)\}$$

(4)

that is,

$${\widehat{\mathit{\theta }}}_n=\underset{\mathit{\theta }}{arg min}{𝓁}_{\mathsf{\tau }}\left(\mathit{\theta }\right)=\underset{\mathit{\theta }}{arg min}\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\rho }_{\tau }\{Y_i-g\left({\mathit{w}}_i,\mathit{\theta }\right)\}$$

(5)

To obtain the asymptotic properties of the estimator ${\widehat{\mathit{\theta }}}_n$, we introduce more notations:

$$\begin{gathered} q\left({\mathit{w}}_i,\mathit{\theta }\right)=\frac{\partial g\left({\mathit{w}}_i,\mathit{\theta }\right)}{\partial \mathit{\theta }} \\ ={\left[1,X_i,\left(X_i-t\right)\mathsf{\Phi }\left(\frac{X_i-t}{h}\right),{\mathit{Z}}_i^{\top },-{\beta }_2\mathsf{\Phi }\left(\frac{X_i-t}{h}\right)-\frac{{\beta }_2\left(X_i-t\right)}{h} \mathsf{\Phi } \prime \left(\frac{X_i-t}{h}\right)\right]}^{\top } \\ {C}_h\left({\mathit{\theta }}_0\right)=\frac{\left[\left(1-2\tau \right)F_i\left(g\left({\mathit{w}}_i,{\mathit{\theta }}_0\right)\right)+\tau \right]}{n}{\displaystyle \sum }_{i=1}^{n}q\left({\mathit{w}}_i,{\mathit{\theta }}_0\right)q^{\top }\left({\mathit{w}}_i,{\mathit{\theta }}_0\right) \\ {D}_h\left({\mathit{\theta }}_0\right)=-\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left\{q\left({\mathit{w}}_i,{\mathit{\theta }}_0\right)q^{\top }\left({\mathit{w}}_i,{\mathit{\theta }}_0\right)\left[\left(1-2\tau \right)F_i\left(g\left({\mathit{w}}_i,{\mathit{\theta }}_0\right)\right)+\tau \right]\right\} \end{gathered}$$

where ${\mathit{\theta }}_0$ is the true parameter, $F_i\left(g\left({\mathit{w}}_i,{\mathit{\theta }}_0\right)\right)$ is the distribution function of $Y_i$.

Obviously, minimizing the objective function (4) is equivalent to solving the equation,

$${\displaystyle \sum }_{i=1}^n{\psi }_{\tau }\left\{Y_i-g\left({\mathit{w}}_i,\mathit{\theta }\right)\right\}q\left({\mathit{w}}_i,\mathit{\theta }\right)=0$$

(6)

where ${\psi }_{\tau }\left(u\right)=u\left|\tau -I(u<0)\right|$ is the kernel of the first-order derivative of the function ${\rho }_{\tau }\left(u\right)$. Solving the equation yields the estimators of the parameters.

The following theorem gives the asymptotic properties of the estimator ${\widehat{\mathit{\theta }}}_n$.

Theorem 1 (Asymptotic Properties).

Let ${\mathit{\theta }}_0$be the true parameter, and ${\widehat{\mathit{\theta }}}_n$ is the estimator of the estimation method in this paper. Under the regularity conditions in theAppendix A, we have ${\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0=O_p\left(n^{-1/2}\right)$, and $\sqrt{n}\left({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0\right)$ is asymptotically normally distributed with mean zero and the covariance matrix of $\Sigma =\tau \left(1-\tau \right)D_h^{-1}\left({\mathit{\theta }}_0\right)C_h\left({\mathit{\theta }}_0\right)D_h^{-\top }\left({\mathit{\theta }}_0\right)$.

The matrices $C_h\left({\mathit{\theta }}_0\right)$ and $D_h\left({\mathit{\theta }}_0\right)$ in the covariance matrix can be estimated by the following formulas:

$$\begin{gathered} {\widehat{C}}_h\left({\widehat{\mathit{\theta }}}_n\right)=\frac{1}{n}{\displaystyle \sum }_{i=1}^{n}q\left({\mathit{w}}_i,{\widehat{\mathit{\theta }}}_n\right)q^{\top }\left({\mathit{w}}_i,{\widehat{\mathit{\theta }}}_n\right) \\ {\widehat{D}}_h\left({\widehat{\mathit{\theta }}}_n\right)=-\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left\{\left[\left(1-2\tau \right){\widehat{F}}_i\left(g\left({\mathit{w}}_i,{\mathit{\theta }}_0\right)\right)+\tau \right]q\left({\mathit{w}}_i,{\widehat{\mathit{\theta }}}_n\right)q^{\top }\left({\mathit{w}}_i,{\widehat{\mathit{\theta }}}_n\right)\right\} \end{gathered}$$

where ${\widehat{F}}_i\left(g\left({\mathit{w}}_i,{\mathit{\theta }}_0\right)\right)$ is the empirical distribution function of $Y_i$.

Note that the estimation of $\mathit{\theta }={\left({\beta }_0,{\beta }_1,{\beta }_2,{\mathit{\gamma }}^{\top },t\right)}^{\top }$ is based on the choice of bandwidth $h$. Therefore, the choice of bandwidth is crucial. We use the cross-validation (CV) criterion to choose the bandwidth $h$. Specifically, let,

$$CV\left(h\right)={\displaystyle \sum }_{i=1}^n{\rho }_{\tau }\left\{Y_i-{\widehat{Q}}_{Y_{-i}}\left(\tau ,\mathit{\theta }{X}_i,{\mathit{Z}}_i\right)\right\}$$

where ${\widehat{Q}}_{Y_{-i}}$ is the estimator of the model after removing the $i$th observation $\left(Y_i,X_i,{\mathit{Z}}_i\right)$. The bandwidth $h$ that minimizes the value of $CV\left(h\right)$ is optimal.

3. Simulation Studies

There are two parts of numerical simulations in this section to verify the finite sample performance of the estimation method in this paper. The first simulation is to evaluate the robust properties of the proposed estimators with three different types of error. Another simulation considers the symmetric and asymmetric bent line expectile regression models.

3.1. Simulation 1

Considering that the independent identically distribution assumption can greatly reduce the case of individual cases in the sample, which makes the sample data more representative in general, we consider the scenario of independent identically distribution. However, in many practical studies, the assumption of independent identically distribution is usually not satisfied, so corresponding to this, we consider the scenario of heteroscedasticity. On the other hand, there are many possible cases for the error term of the model. We discuss the two opposite cases that the error term obeys normal distribution and non-normal distribution. Furthermore, we study the mixed distribution which contains both normal distribution and non-normal distribution.

The simulation data in this section come from the following two scenarios:

(I)

Independent identically distribution (IID): $Y={\beta }_0+{\beta }_{1}X+{\beta }_2{\left(X-t\right)}_{+}+\mathit{\gamma }\mathit{Z}+e$

(II)

Heteroscedasticity: $Y={\beta }_0+{\beta }_{1}X+{\beta }_2{\left(X-t\right)}_{+}+\mathit{\gamma }\mathit{Z}+\left(1+0.3X\right)e$

where $X~\mathit{U}\left(-2,5\right)$, $\mathit{Z}~B\left(1,0.5\right)$. The $\tau$th expectile of the random error term $e$ is 0, that is, $e=\tilde{e}-Q_{\tau }\left(\tilde{e}\right)$, where $Q_{\tau }\left(\tilde{e}\right)$ is the $\tau$th expectile of $\tilde{e}$.

For each scenario, we consider the following three different error cases:

(1)

a standard normal distribution: $\tilde{e}~N\left(0,1\right)$

(2)

a t-distribution with three degrees of freedom: $\tilde{e}~t_3$

(3)

a contaminated standard normal distribution: $\tilde{e}~0.9N\left(0,1\right)+0.1t_3$

The regression coefficients are set as $\left({\beta }_0,{\beta }_1,{\beta }_2,\mathit{\gamma }\right)=\left(1,3,-2,1\right)$ and the change-point is $t=1.5$. For each case, we conduct 200 repetitions with sample sizes $n=200$.

In order to compare the proposed method with that of Zhou and Zhang [21], we also consider the linearization method. Table A1, Table A2, Table A3, Table A4, Table A5 and Table A6 show the simulation results of the linearization method (“seg”) and the proposed method in this paper (“proposed”) at the different expectile levels $\tau =0.1,0.3,0.5,0.7,0.9$. It should be noted that the data in the tables represent biases (estimated value $-$ true value), that is, $bias={\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0$. It can be seen from the tables that the mean values (“Mean”) of the biases of the proposed method in this paper are very similar to 0 at different expectile levels of various error distributions, and for some parameters, this indicator is even equal to 0 in some cases, for example, for the independent identically distribution model with $\tilde{e}~t_3$, the mean value (“Mean”) of the bias of $\mathit{\gamma }$ is 0 when $\tau =0.5$. In addition, this indicator of the method in this paper is far less than the linearization method. On the other hand, the sum of squared errors (“SSE”) of the biases of the two estimation methods are very similar to 0, indicating that the fitting results of the two methods are so satisfying. Further, we find that this indicator of the method in this paper is only about half of that of the linearization method through comparison, which indicates that the method in this paper is more suitable for data fitting. In addition, the minimums (“Min”) and the maximums (“Max”) of the biases of the proposed method are similar to those of the linearization method, and the value ranges of the minimums (“Min”) and the maximums (“Max”) of the two methods are generally $\left(0,1\right)$, just for the case of $\tilde{e}~t_3$, there are more cases where the two indicators are greater than 1 in the two methods, but this situation is also normal. In addition, the upper quartiles (“IQ1”), the medians (“Median”) and the lower quartiles (“IQ3”) of the biases of the proposed method are slightly smaller than those of the linearization method, which is especially evident at the tail expectile levels (e.g., $\tau =0.1,0.9$). It shows that estimation obtained by using the linearization technique indeed underestimates the change-point. All in all, the estimation method in this paper is better than the linearization method.

3.2. Simulation 2

Considering that the location of the change-point may be different, we divide the sources of the simulation data into symmetric and asymmetric cases, which could ensure the rigor and comprehensiveness of the study.

The simulation data in this section come from the following two scenarios:

Symmetric scenario:

$$Y=0+{\beta }_{1}X-2{\beta }_1{\left(X-5\right)}_{+}+c_1\left(X\right)e$$

Asymmetric scenario:

$$Y=4.5-{\beta }_1+{\beta }_{1}X-\left({\beta }_1+0.5\right){\left(X-2\right)}_{+}+c_2\left(X\right)e$$

where $c_1\left(X\right)=0.5+0.1X$, $c_2\left(X\right)=0.5+0.02X$, $e$ is standard normal distribution and its $\tau$th expectile is 0.

In the symmetric scenario, the scalar covariate $X~\mathit{U}\left(0,10\right)$, and the change-point is the median of $X$ which is $t=5$. Then corresponding to the model in this paper, we set $({\beta }_0,{\beta }_1,{\beta }_2,t)=\left(0,{\beta }_1,-2{\beta }_1,5\right)$. In the asymmetric scenario, the scalar covariate $X$ is a mixture distribution that uniformly on $\left(0,1\right)$ with probability 0.1 and uniformly on $\left(0,10\right)$ with probability 0.9, that is, $X~0.1\mathit{U}\left(0,1\right)+0.9\mathit{U}\left(0,10\right)$, the change-point is $t=2$. Then corresponding to the model in this paper, we set $({\beta }_0,{\beta }_1,{\beta }_2,t)=\left(4.5-{\beta }_1,{\beta }_1,-{\beta }_1-0.5,2\right)$.

For each scenario, we set the parameter ${\beta }_1=0.5$, and we conduct 200 repetitions with sample sizes $n=200$ by applying the linearization method (“seg”) and our method (“proposed”). Table A7 and Table A8 record the simulation results at different expectile levels $\tau =0.1,0.3,0.5,0.7,0.9$. It is also worth noting that the data in the tables also represent biases. It can be seen from the tables that the results obtained by the method in this paper and the linearization method are very similar, and their indicators are relatively small, which also shows that the estimated values of both methods are similar to the true values. Not only that, we discover that the mean values (“Mean”), the sum of squared errors (“SSE”), the minimums (“Min”), the upper quartiles (“IQ1”), the medians (“Median”), the lower quartiles (“IQ3”) and the maximums (“Max”) of the biases of the two methods increase with $\tau$, which indicates that the fitting effect is better while the expectile is smaller. In addition, when $\tau$ is small (e.g., $\tau =0.1,0.3$), these indicators of the method in this paper are slightly smaller than those of the linearization method. However, when $\tau$ is larger (e.g., $\tau =0.7,0.9$), these indicators of the proposed method are slightly larger than those of the linearization method. In general, the estimation effect and large sample performance of the proposed method are good.

4. Empirical Applications

There are two parts of practical applications in this section. We apply the proposed method in this paper to the Arctic annual average temperature data and the Nile annual average flow data separately to illustrate the practical utility of the new method.

4.1. Application 1

The latest evidence shows that the earth has been warming over the past 50 years, and this trend has not changed. Scientists from many countries have contributed to the study of global climate change, among which the warming of the Arctic climate is one of the important aspects of the study of global climate change.

In this section, we mainly focus on the annual average temperature data in the Arctic region (90 N–23.6 N) from 1940 to 2021. This dataset is available from NASA Goddard Institute for Space Studies (www.giss.nasa.gov (accessed on 15 March 2022)). Based on the scatter diagram provided by the institute, we can roughly learn that the annual average temperature in the Arctic region remained almost stable between 1940 and 1975, and then increased rapidly after 1975. Therefore, we guess the annual average temperature in the Arctic region changed in 1975. Therefore, we fit the following model to the Arctic annual average temperature data:

$$Q_{\tau }\left(Y|X\right)={\beta }_0+{\beta }_{1}X+{\beta }_2{\left(X-t\right)}_{+}$$

where $Y$ is the annual average temperature in the Arctic region, $X$ is the continuous time and $X_1<X_2<\dots <X_n$, $n=82$ is the sample size. We consider $\tau =0.2,0.3,0.5,0.7,0.8$ these five different expectile levels. Table A9 summarizes the estimations (“Estimate”) of the parameters and their standard errors (“SE”) of the grid search method, linearization method and smoothing method proposed in this paper. It can be seen from the table that the parameter estimation accuracy of the smoothing method proposed in this paper is exactly the same as that of the grid search method, the standard errors of all parameters except ${\beta }_2$ are equal to 0, and the standard error of ${\beta }_2$ is also very similar to 0, which indicates that the parameter estimation accuracy of the two methods are all very high. This is not difficult to explain, although the grid search method is complex and its computation is very large, as long as the fine grid is divided to a certain degree, the optimal value can be obtained, which also shows the good performance and practical utility of the smoothing method proposed in this paper. Moreover, we find that the parameter estimation accuracy of the smoothing method and the grid search method is slightly higher than that of the linearization method. On the other hand, as far as our dataset is concerned, the smoothing method and linearization method can save about a quarter of computation and time compared with the grid search method, which greatly improves the computational efficiency. Most importantly, we can intuitively see the change-point $t\approx 1975$, that is, the annual average temperature in the Arctic region changed significantly in 1975, which also verifies our conjecture.

4.2. Application 2

The Nile dataset is the internal dataset in R, which represents the measurements of the annual average flow (in unit ${10}^8 {\mathrm{m}}^3$) of the River Nile at Aswan between 1871 and 1970. In this section, we mainly focus on the annual average flow data of the Nile from 1871 to 1970. Based on the scatter diagram in Figure 1, we can roughly learn that the annual average flow of the River Nile showed a downward trend before 1914, then increased rapidly after 1914. In addition, it should be noted that the number 1 in the abscissa of the graph represents 1871, and so on.

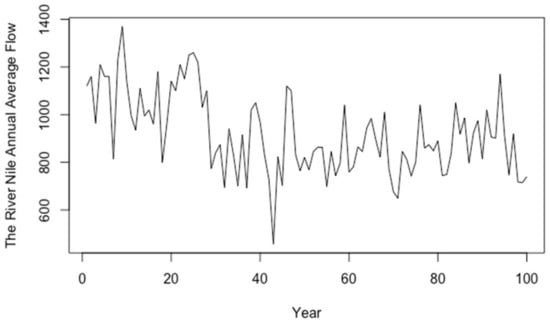
Figure 1. The scatter diagram of the annual average flow of the River Nile.

Therefore, we fit the following model to the Nile annual average flow data:

$$Q_{\tau }\left(Y|X\right)={\beta }_0+{\beta }_{1}X+{\beta }_2{\left(X-t\right)}_{+}$$

where $Y$ is the annual average flow of the River Nile, $X$ is the continuous time and $X_1<X_2<\dots <X_n$, $n=100$ is the sample size. We consider $\tau =0.2,0.3,0.5,0.7,0.8$ these five different expectile levels. Table A10 summarizes the estimations (“Estimate”) of the parameters and their standard errors (“SE”) of the grid search method, linearization method and smoothing method proposed in this paper. It can be seen from the table that the parameter estimation accuracy of the smoothing method proposed in this paper is very similar to that of the grid search method, and both of them are very high. Not only that, we find this indicator of the proposed method and grid search method is slightly higher than that obtained by the linearization method. On the other hand, as far as our dataset is concerned, compared with the grid search method, the smoothing method and linearization method have smaller computation and less operation time. In addition, we can intuitively see $t\approx 1914$ obtained by the proposed method when $\tau =0.2,0.3,0.5$, that is, the annual average flow of the River Nile changed significantly in 1914. It also shows that $t\approx 1924$ when $\tau =0.7,0.8$, and this situation is also acceptable.

5. Conclusions

In this paper, we study the problem of statistical inference of the change-point and other regression coefficients of the bent line expectile regression model. Due to the existence of the change-point, the objective function of the model is not differentiable with respect to the change-point, which brings a huge challenge to our calculation. In order to compensate for the insufficiency of the previous estimation methods, we propose a new estimation method by a smoothing technique, that is, using Gaussian kernel function to approximate the indicator function in the objective function, which can not only estimate the regression coefficients and change-point location simultaneously, greatly reduce the computation, but also improve the accuracy of the parameter estimation. At the same time, we give the large sample properties of the estimation method in this paper, the estimator ${\widehat{\mathit{\theta }}}_n$ converges to the true parameter ${\mathit{\theta }}_0$ at a speed of $n^{-1/2}$ in probability, and the bias ${\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0$ is asymptotically normally distributed. Through the numerical simulation analysis, we find that all the indicators of the biases of the parameter estimations are almost equal to 0, which shows that the new method proposed in this paper has a very good estimation effect and verifies the large sample performance of the new method. Finally, we also apply the model and the method in this paper to the analysis of two actual data and find that the estimated values of the parameters obtained by the new method proposed in this paper are almost equal to the true values, which shows the practical utility of the new method. It not only improves the accuracy of the parameter estimation, but also greatly improves the computational efficiency compared with the grid search method.

The model studied in this paper is the continuous threshold expectile regression model with a single change-point, but in practical applications, it is very meaningful to consider a continuous threshold expectile regression model with multiple change-points. In this regard, we can consider extending the current research work to the multiple change-points situation, which is believed to be a very interesting topic.