Lagrangian Zero Truncated Poisson Distribution: Properties Regression Model and Applications
Abstract
:1. Introduction
2. Some Preliminaries
2.1. Basics on the Discrete Lagrangian Family
2.2. Importance of the Lagrangian Family
3. Lagrangian Zero Truncated Poisson Distribution (LZTPD)
4. Finite Mixtures of Lagrangian Zero Truncated Poisson Distribution
5. Estimation
5.1. Maximum Likelihood
5.2. Method of Moments
6. Generalized Likelihood Ratio Test
7. Simulation Study
8. Lagrangian Zero Truncated Poisson Regression Model
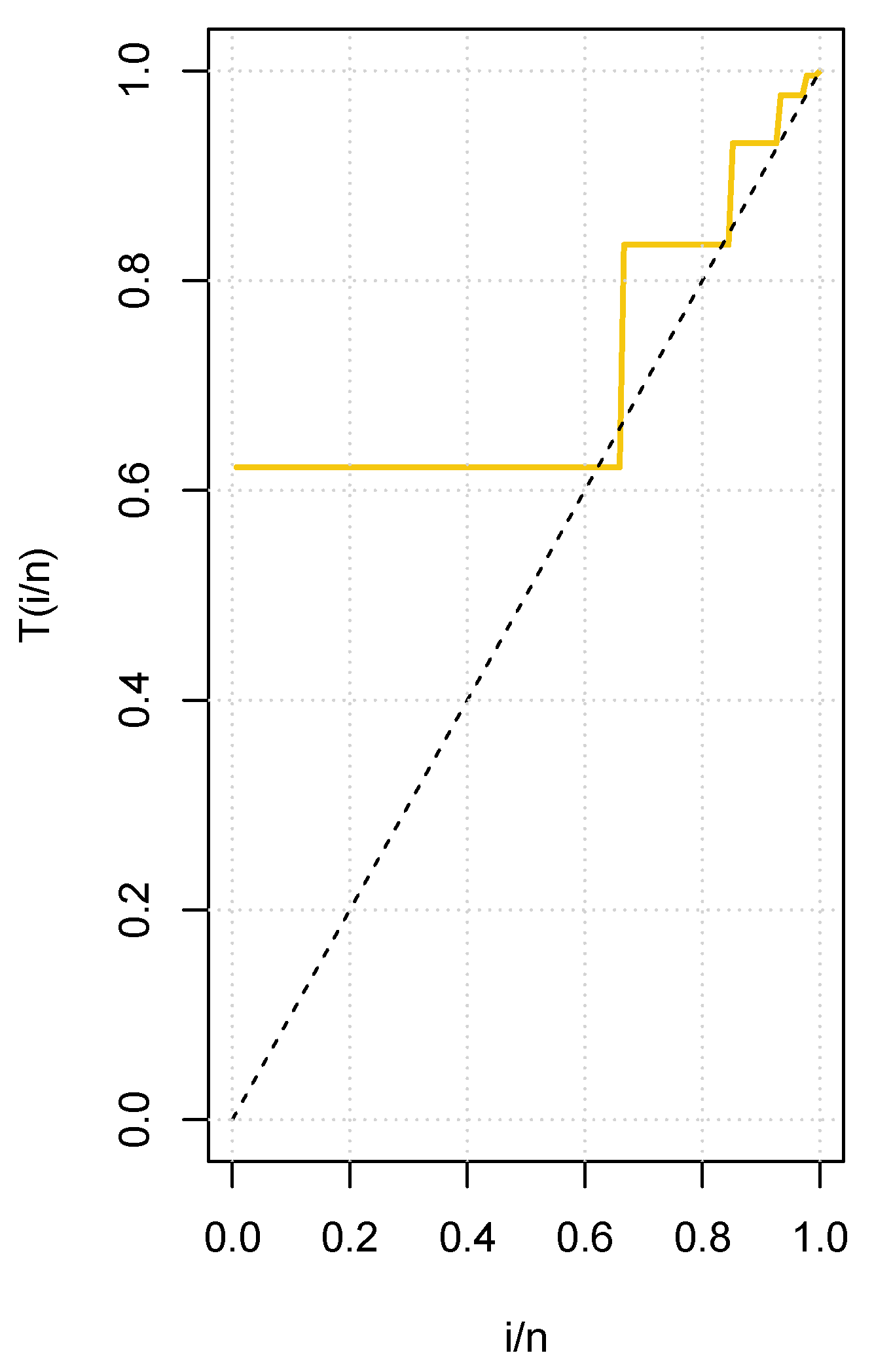
9. Applications and Empirical Study
- The ZTPD proposed by [1], and defined by the following pmf:with .
- The ZTGPD proposed by [21], and specified by the following pmf:wih .
- The IPD elaborated by [3], and indicated by the following pmf:with and .
- The zero truncated discrete Shankar distribution (ZTDSD) proposed by [34], and defined by the following pmf:with .
- The two-parameter zero truncated Poisson-Lindley distribution (ZTPLD) introduced by [35], and indicated by the following pmf:with .
- The zero truncated generalized negative binomial distribution (ZTGNBD) proposed by [36], and defined by the following pmf:with and .
9.1. University Course Enrollments
9.2. Demographic Data
9.3. Biological Science
10. Discussion
10.1. Brief Summary
10.2. This Work
10.3. Contributions and Limitations
10.4. Future Work
11. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LZTPD | Lagrangian Zero Truncated Poisson Distribution |
| ZTPD | Zero Truncated Poisson Distribution |
| IPD | Intervened Poisson Distribution |
| LF | Lagrangian Family |
| DLF | Discrete Lagrangian Family |
| LZTPRM | Lagrangian Zero Truncated Poisson Regression Model |
| ZTPRM | Zero Truncated Poisson Regression Model |
| ZTGPRM | Zero Truncated Generalized Poisson Regression Model |
| IPRM | Intervened Poisson Regression Model |
| pmf | Probability Mass Function |
| hrf | Hazard Rate Function |
| Index Of Dispersion | |
| pgf | Probability Generating Function |
| mgf | Moment Generating Function |
| cgf | Cumulant Generating Function |
| Coefficient of Variation | |
| iid | independent and identically distributed |
| rv | random variable |
| ML | Maximum Likelihood |
| MLEs | Maximum Likelihood Estimates |
| MM | Method of Moments |
| MMEs | Method of Moments Estimates |
| GLRT | Generalized Likelihood Ratio Test |
| MSE | Mean Squared Error |
| LZTPMDg | Lagrangian Zero Truncated Poisson Mixture Distribution with g components |
| TTT | Total Time on Test |
| ZTGPD | Zero Truncated Generalized Poisson Distribution |
| ZTDSD | Zero Truncated Discrete Shankar Distribution |
| ZTPLD | Zero Truncated Poisson Lindley Distribution |
| ZTGNBD | Zero Truncated Generalized Negative Binomial Distribution |
| AIC | Akaike Information Criterion |
| BIC | Bayesian Information Criterion |
| IQR | Inter Quartile Range |
| Md | Median |
| min | Minimum |
| max | Maximum |
| SE | Standard Error |
Appendix A
References
- Cohen, A.C. Estimating parameters in a conditional Poisson distribution. Biometrics 1960, 16, 203–211. [Google Scholar] [CrossRef]
- Singh, J. A characterization of positive Poisson distribution and its application. SIAM J. Appl. Math. 1978, 34, 545–548. [Google Scholar] [CrossRef]
- Shanmugam, R. An intervened Poisson distribution and its medical application. Biometrics 1985, 41, 1025–1029. [Google Scholar] [CrossRef] [PubMed]
- Shanmugam, R. An inferential procedure for the Poisson intervention parameter. Biometrics 1992, 48, 559–565. [Google Scholar] [CrossRef] [PubMed]
- Kumar, C.S.; Shibu, D.S. Modified intervened Poisson distribution. Statistica 2011, 71, 489–499. [Google Scholar]
- Singh, B.P.; Dixit, S.; Shukla, U. An alternative to intervened Poisson distribution for prevalence reduction. J. Math. Stat. Sci. 2016, 2016, 730–740. [Google Scholar]
- Lagrange, J.L. Mécanique Analytique; Jacques Gabay: Paris, France, 1788. [Google Scholar]
- Consul, P.C.; Shenton, L.R. Use of Lagrange expansion for generating generalized probability distributions. SIAM J. Appl. Math. 1972, 23, 239–248. [Google Scholar] [CrossRef]
- Consul, P.C.; Shenton, L.R. Some interesting properties of Lagrangian distributions. Commun. Stat. 1973, 2, 263–272. [Google Scholar] [CrossRef]
- Mohanty, S.G. On a generalized two- coin tossing problem. Biom. Z. 1966, 8, 266–272. [Google Scholar] [CrossRef]
- Consul, P.C.; Famoye, F. Lagrangian Katz family of distributions. Commun. Stat. Theory Methods 1996, 25, 415–434. [Google Scholar] [CrossRef]
- Berg, K.; Nowicki, K. Statistical inference for a class of modified power series distribution with applications to random mapping theory. J. Stat. Plan. Inference 1991, 28, 247–261. [Google Scholar] [CrossRef]
- Li, S.; Black, D.; Lee, C.; Famoye, F. Dependence models arising from the Lagrangian probability distributions. Commun. Stat. Theory Methods 2010, 29, 1729–1742. [Google Scholar] [CrossRef]
- Innocenti, A.R.; Fox, O.; Chibbaro, S. A Lagrangian probability density-function model for collisional turbulent fluid particle flows i. Model derivation. J. Fluid Mech. 2019, 862, 449–489. [Google Scholar] [CrossRef]
- Dobson, A.J.; Dobson, A. An Introduction to Generalized Linear Models, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Long, J.S.; Freese, J. Regression Models for Categorical Dependent Variables Using Stata, 2nd ed.; Stata Press: College Station, TX, USA, 2005. [Google Scholar]
- Shaw, D. On-site samples regression problems of non-negative integers, truncation, and endogenous stratification. J. Econom. 2005, 37, 211–223. [Google Scholar] [CrossRef]
- Shibu, D.S. On Intervened Poisson Distribution and Its Generalization. Ph.D. Thesis, University of Kerala, Thiruvananthapuram, India, 2013. [Google Scholar]
- Janardan, K.G.; Rao, B.R. Lagrangian distributions of second kind and weighted distributions. SIAM J. Appl. Math. 1983, 43, 302–313. [Google Scholar] [CrossRef]
- Janardan, K.G. A wider class of Lagrange distributions of the second kind. Commun. Stat. Theory Methods 1997, 26, 2087–2097. [Google Scholar] [CrossRef]
- Consul, P.C.; Famoye, F. The truncated generalized Poisson distribution and its estimation. Commun. Stat. Theory Methods 1989, 18, 3635–3648. [Google Scholar] [CrossRef]
- Jain, G.C. A Linear function Poisson distribution. Biom. J. 1975, 17, 501–506. [Google Scholar] [CrossRef]
- Consul, P.C.; Famoye, F. Lagrangian Probability Distributions; Birkhaüser: New York, NY, USA, 2006. [Google Scholar]
- Consul, P.C.; Jain, G.C. A generalization of the Poisson distribution. Technometrics 1973, 15, 791–799. [Google Scholar] [CrossRef]
- Gupta, R.C. Modified power series distribution and some of its applications. Sankhya Ser. B 1974, 35, 288–298. [Google Scholar]
- McLachlan, G.; Peel, D. Finite Mixture Models; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Kumar, C.S.; Shibu, D.S. On finite mixtures of modified intervened Poisson distribution and its applications. J. Stat. Theory Appl. 2014, 13, 344–355. [Google Scholar] [CrossRef]
- Titterington, D.M.; Smith, A.F.; Markov, U.E. Statistical Analysis of Finite Mixture Distributions; Wiley: Hoboken, NJ, USA, 1985. [Google Scholar]
- Rao, C.R. Minimum variance and the estimation of several parameters. Math. Proc. Camb. Philos. 1947, 43, 280–283. [Google Scholar] [CrossRef]
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria. Available online: https://www.R-project.org/ (accessed on 6 September 2021).
- Hardin, J.; Hilbe, J. Generalized Linear Models and Extensions, 2nd ed.; StatCorp LP Texas: College Station, TX, USA, 2007. [Google Scholar]
- Hilbe, J.M. Negative Binomial Regression; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Aarset, M.V. How to identify a bathtub hazard rate. IEEE Trans Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]
- Borah, M.; Saikaia, K.R. Zero- tuncated discrete Shankar distribution and its applications. Biom. Biostat. Int. J. 2017, 5, 232–237. [Google Scholar]
- Shanker, R.; Shukla, K.K. A zero- truncated two-parameter Poisson-Lindley distribution with an application to biological science. Turk. Klin. J. Biostat. 2017, 9, 85–95. [Google Scholar] [CrossRef]
- Famoye, F.; Consul, P.C. The truncated generalized negative binomial distribution. J. Appl. Stat. Sci. 1993, 1, 141–157. [Google Scholar]
- Huang, M.; Fung, K.Y. Intervened truncated Poisson distribution. Sankhya Ser. B 1989, 51, 302–310. [Google Scholar]
- Shanker, R.; Fesshaye, H.; Selvaraj, S.; Yemane, A. On zero-truncation of Poisson and Poisson-Lindley distributions and their applications. Biom. Biostat. Int. J. 2015, 2, 168–181. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ong, M.; Liu, H. Compare Predicted Counts between Groups of Zero Truncated Poisson Regression Model based on Recycled Predictions Method. In Proceedings of the Section on Statistics in Epidemiology—JSM 2011, Miami Beach, FL, USA, 30 July–4 August 2011. [Google Scholar]
- Zhao, W.; Feng, Y.; Li, Z. Zero-truncated generalized Poisson regression model and its score tests. J. East China Norm. Univ. Sci. 2010, 1, 17–23. [Google Scholar]




| Mean | Variance | Median | Mode | Skewness | Kurtosis | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.05 | 1.4045 | 1.0797 | 1 | 1 | 0.7687 | 0.7398 | 1.4039 | 5.1257 |
| 0.1 | 1.5531 | 1.3000 | 1 | 1 | 0.8370 | 0.7341 | 1.9099 | 7.8036 | |
| 0.2 | 1.9061 | 1.9476 | 1 | 1 | 1.0217 | 0.7321 | 2.0265 | 10.0765 | |
| 0.3 | 2.3599 | 3.0631 | 2 | 1 | 1.2979 | 0.7416 | 1.3564 | 14.9253 | |
| 0.4 | 2.9650 | 5.1144 | 2 | 1 | 1.7248 | 0.7627 | 2.8461 | 15.4684 | |
| 0.5 | 3.8122 | 9.2482 | 3 | 1 | 2.4259 | 0.7977 | 3.5461 | 17.4684 | |
| 1 | 0.05 | 1.6652 | 2.4915 | 1 | 1 | 1.4962 | 0.9478 | 1.9810 | 5.1030 |
| 0.1 | 1.7577 | 2.8956 | 2 | 1 | 1.6473 | 0.9680 | 2.0319 | 9.7862 | |
| 0.2 | 1.9774 | 4.0345 | 2 | 1 | 2.0402 | 1.0157 | 2.4052 | 10.8162 | |
| 0.3 | 2.2599 | 5.9023 | 2 | 1 | 2.6117 | 1.0750 | 2.9737 | 12.2294 | |
| 0.4 | 2.6366 | 9.1847 | 3 | 1 | 3.4835 | 1.1494 | 3.1804 | 15.0489 | |
| 0.5 | 3.1639 | 15.5245 | 4 | 1 | 4.9066 | 1.2453 | 3.6804 | 17.0489 | |
| 2 | 0.05 | 2.3739 | 6.7172 | 2 | 2 | 2.8296 | 1.0917 | 2.0589 | 6.1850 |
| 0.1 | 2.4415 | 7.6566 | 2 | 2 | 3.1359 | 1.1333 | 2.8669 | 9.0253 | |
| 0.2 | 2.6021 | 10.2187 | 3 | 2 | 3.9270 | 1.2284 | 3.1943 | 11.4901 | |
| 0.3 | 2.8086 | 14.2461 | 3 | 2 | 5.0721 | 1.3438 | 3.5848 | 15.2456 | |
| 0.4 | 3.0840 | 21.0251 | 4 | 2 | 6.8173 | 1.4867 | 3.8983 | 16.0534 | |
| 0.5 | 3.4695 | 33.5493 | 5 | 2 | 9.6696 | 1.6694 | 3.9983 | 17.0534 | |
| 3 | 0.05 | 3.2125 | 13.0707 | 3 | 3 | 4.0686 | 1.1253 | 1.4589 | 6.9185 |
| 0.1 | 3.2741 | 14.7966 | 3 | 3 | 4.5192 | 1.1748 | 1.9866 | 10.0253 | |
| 0.2 | 3.4202 | 19.4386 | 4 | 3 | 5.6833 | 1.2890 | 2.6943 | 11.4901 | |
| 0.3 | 3.6082 | 26.5960 | 5 | 3 | 7.3709 | 1.4292 | 2.9848 | 13.2456 | |
| 0.4 | 3.8587 | 38.3929 | 5 | 4 | 9.9494 | 1.6057 | 3.1983 | 16.7534 | |
| 0.5 | 4.2095 | 59.6845 | 7 | 4 | 14.1782 | 1.8352 | 3.8983 | 18.0534 |
| Parameter Set | Sample Size | Parameters | Estimates | MSE | Bias |
|---|---|---|---|---|---|
| 0.7554 | 0.0598 | −0.2464 | |||
| 0.0379 | 0.0031 | −0.0590 | |||
| 0.7592 | 0.0579 | −0.2488 | |||
| 0.4490 | 0.0026 | −0.0510 | |||
| 0.7801 | 0.0483 | −0.2199 | |||
| 0.4601 | 0.0015 | −0.0399 | |||
| 0.8023 | 0.0390 | −0.1977 | |||
| 0.4780 | 0.0004 | −0.0220 | |||
| 0.9567 | 0.0018 | −0.0433 | |||
| 0.4901 | 0.0001 | −0.0099 | |||
| 0.3646 | 0.0183 | −0.1354 | |||
| 0.0300 | 0.0049 | −0.0700 | |||
| 0.3699 | 0.0169 | −0.1301 | |||
| 0.0542 | 0.0020 | −0.0458 | |||
| 0.3978 | 0.0104 | −0.1022 | |||
| 0.0801 | 0.0003 | −0.0199 | |||
| 0.4736 | 0.0006 | −0.0264 | |||
| 0.0891 | 0.0001 | −0.0109 | |||
| 0.4983 | 0.00001 | −0.0017 | |||
| 0.0940 | 0.00003 | −0.0060 |
| Statistics | n | min | Md | max | IQR | ||
|---|---|---|---|---|---|---|---|
| Values | 56 | 1 | 4 | 7 | 17 | 37 | 13 |
| Model | MLEs | AIC | BIC | ||
|---|---|---|---|---|---|
| ZTPD | 300.1443 | 2997.476 | 602.2886 | 604.3140 | |
| IPD | 300.1443 | 2998.871 | 604.2886 | 608.3393 | |
| ZTDSD | 187.8862 | 144.3541 | 377.7725 | 381.7978 | |
| ZTPLD | 187.856 | 144.7294 | 379.7121 | 383.7628 | |
| ZTGPD | 186.8137 | 154.0068 | 377.6273 | 381.6780 | |
| ZTGNBD | 186.8197 | 153.9518 | 379.6394 | 385.7154 | |
| LZTPD | 186.7358 | 126.0983 | 377.4716 | 381.5223 | |
| Statistics | n | min | Md | max | IQR | ||
|---|---|---|---|---|---|---|---|
| Values | 135 | 1 | 1 | 1 | 2 | 6 | 1 |
| Model | MLEs | AIC | BIC | ||
|---|---|---|---|---|---|
| ZTPD | 150.0619 | 7.9012 | 302.12 | 305.029 | |
| IPD | 150.0619 | 14.863 | 304.70 | 309.93 | |
| ZTDSD | 148.8624 | 12.1887 | 299.7248 | 302.6301 | |
| ZTPLD | 143.8747 | 2.8235 | 291.7493 | 297.5599 | |
| ZTGPD | 143.3546 | 1.746 | 290.709 | 296.520 | |
| ZTGNBD | 143.2366 | 1.5554 | 292.4731 | 301.189 | |
| = 0.5281 | |||||
| LZTPD | 143.0373 | 1.304 | 290.6747 | 296.4852 | |
| Covariates | ZTPRM | ZTGPRM | IPRM | LZTPRM | ||||
|---|---|---|---|---|---|---|---|---|
| Estimate | p-Value | Estimate | p-Value | Estimate | p-Value | Estimate | p-Value | |
| 1.2367 | <0.001 | 1.1961 | <0.001 | 1.1981 | <0.001 | 2.0181 | <0.001 | |
| (0.0213) | (0.0160) | (0.0019) | (0.0021) | |||||
| 0.5609 | <0.001 | 0.5931 | <0.001 | 0.5751 | <0.001 | 0.1361 | <0.001 | |
| (0.0305) | (0.0280) | (0.0345) | (0.0145) | |||||
| −0.0739 | <0.001 | −0.0781 | <0.001 | −0.0766 | <0.001 | −0.0141 | <0.001 | |
| (0.0365) | (0.0156) | (0.0019) | (0.0232) | |||||
| 0.1452 | <0.001 | 0.1499 | <0.001 | 0.2908 | <0.001 | 0.0982 | <0.001 | |
| (0.0168) | (0.0255) | (0.0217) | (0.0251) | |||||
| 0.0934 | <0.001 | 0.0991 | <0.001 | 0.1352 | <0.001 | 0.0142 | <0.001 | |
| (0.0134) | (0.0346) | (0.0109) | (0.0019) | |||||
| 6921.34 | 6629.25 | 6579.37 | 6494.85 | |||||
| AIC | 13854.68 | 13272.50 | 13172.74 | 13003.70 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irshad, M.R.; Chesneau, C.; Shibu, D.S.; Monisha, M.; Maya, R. Lagrangian Zero Truncated Poisson Distribution: Properties Regression Model and Applications. Symmetry 2022, 14, 1775. https://doi.org/10.3390/sym14091775
Irshad MR, Chesneau C, Shibu DS, Monisha M, Maya R. Lagrangian Zero Truncated Poisson Distribution: Properties Regression Model and Applications. Symmetry. 2022; 14(9):1775. https://doi.org/10.3390/sym14091775
Chicago/Turabian StyleIrshad, Muhammed Rasheed, Christophe Chesneau, Damodaran Santhamani Shibu, Mohanan Monisha, and Radhakumari Maya. 2022. "Lagrangian Zero Truncated Poisson Distribution: Properties Regression Model and Applications" Symmetry 14, no. 9: 1775. https://doi.org/10.3390/sym14091775
APA StyleIrshad, M. R., Chesneau, C., Shibu, D. S., Monisha, M., & Maya, R. (2022). Lagrangian Zero Truncated Poisson Distribution: Properties Regression Model and Applications. Symmetry, 14(9), 1775. https://doi.org/10.3390/sym14091775






