Experimental Study on Bending Resistance of New Type Joint of Prestressed Concrete Pipe Pile
Abstract
:1. Introduction
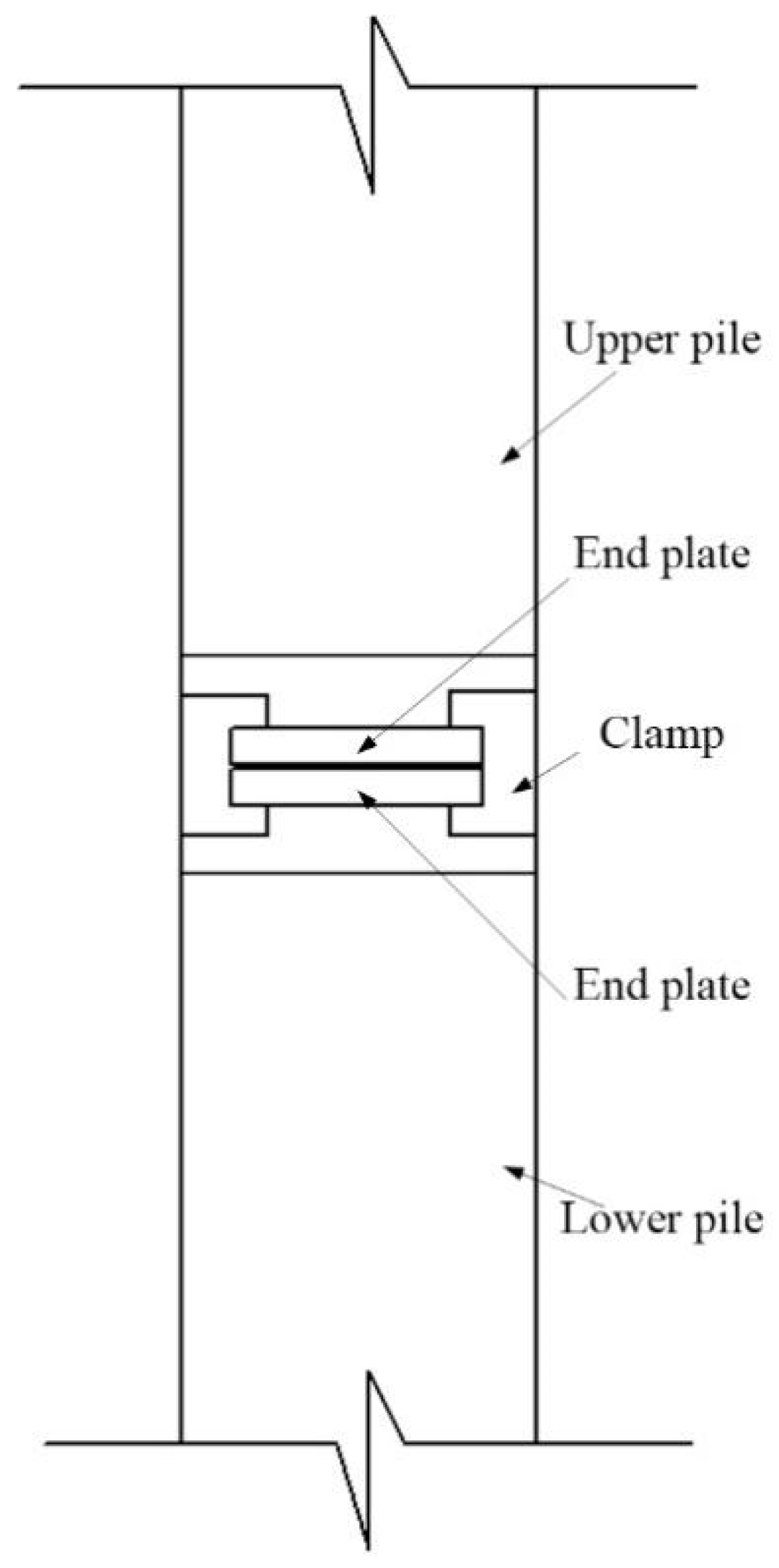
2. New Joint
2.1. Introduction of the New Joint
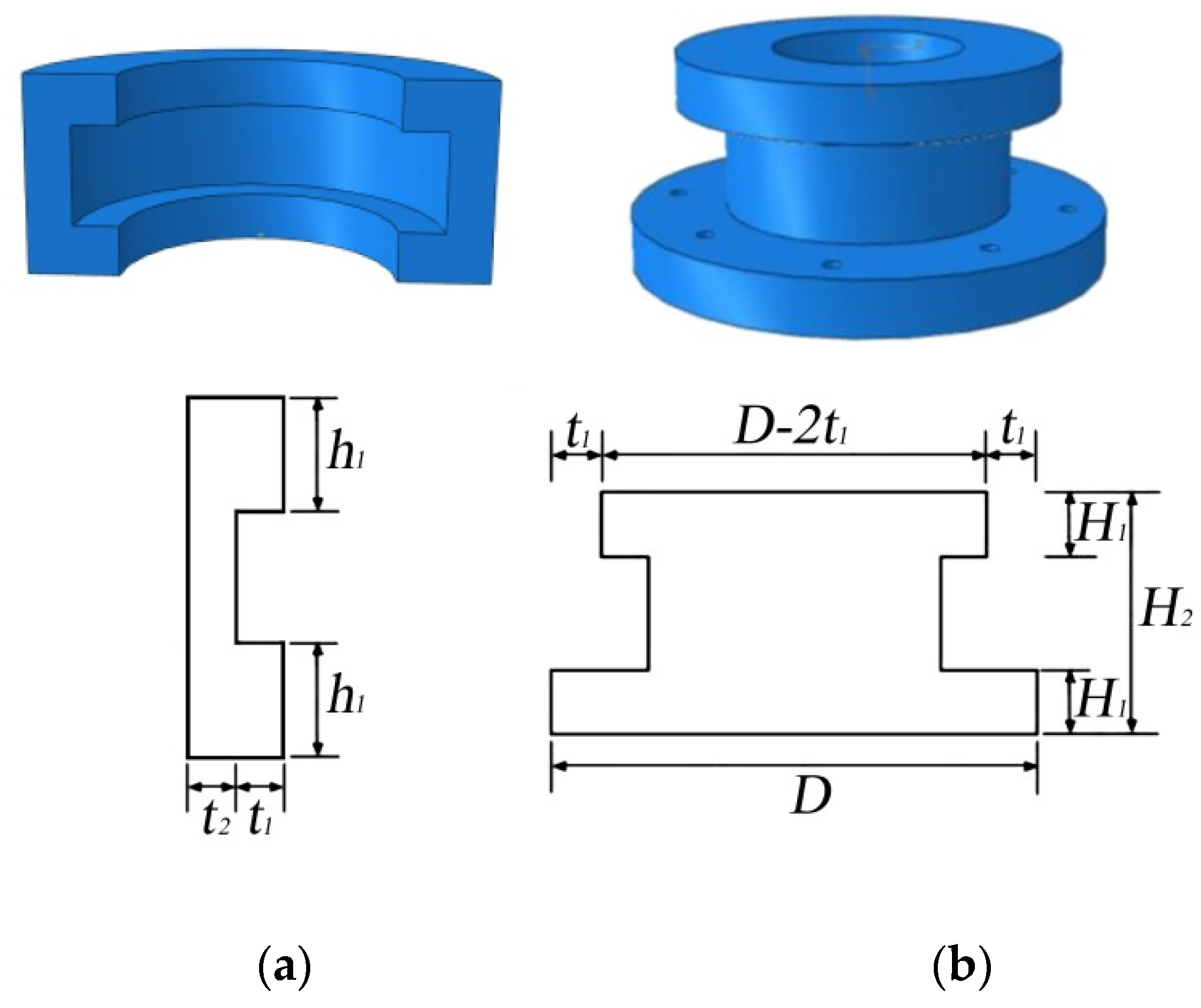
2.2. Determining the Size of the New Joint
3. Test Scheme
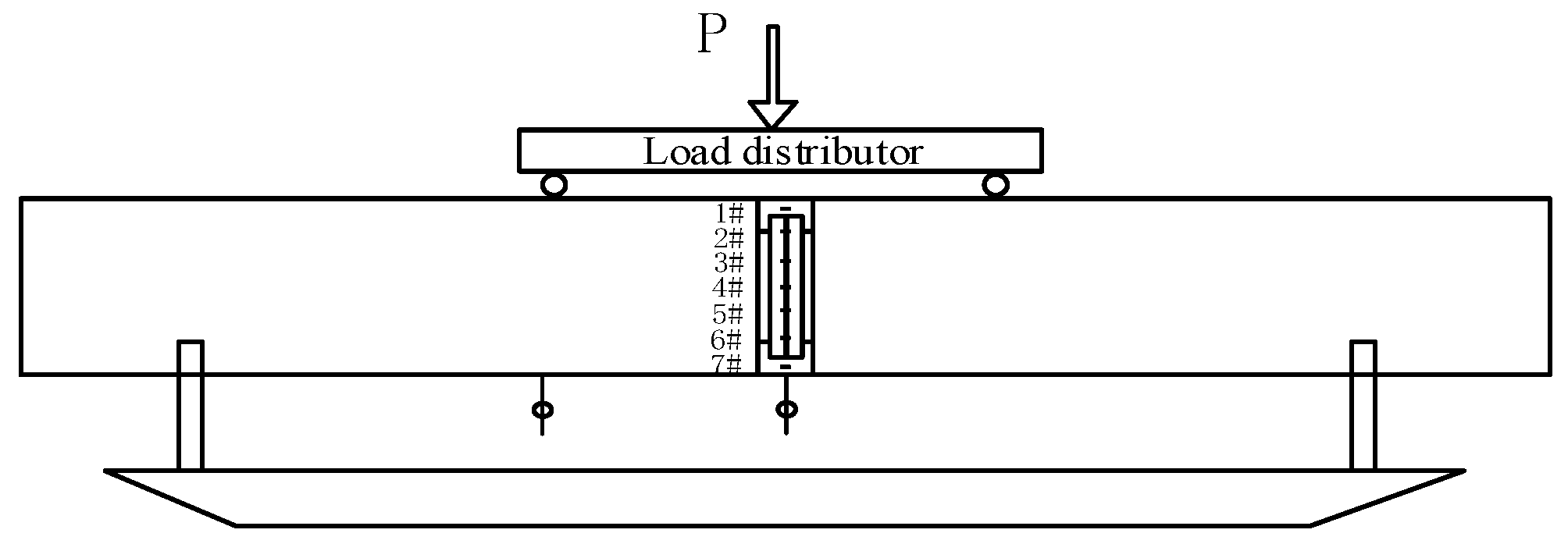
3.1. Experimental Setup
3.2. Load Scheme
- (1)
- First, according to the finite element simulation results, the ultimate flexural bearing capacity of the prestressed concrete pile is predicted. The loading process adopts monotonic graded loading with a consistent loading time interval of 2–3 min.
- (2)
- Before loading, 10% of the estimated ultimate load is applied to the specimen to preload the test apparatus and to eliminate the gap between the device and the specimen.
- (3)
- The load at each level of formal loading is 5% of the predicted ultimate load, which is loaded at a uniform speed, and the next level of loading is carried out after the deformation stabilizes.
- (4)
- When the oil pump readings show a significant retracement and the deformation continues to increase, the specimen is considered to be damaged and reaches the limit state.
4. Test Phenomenon
5. Test Results
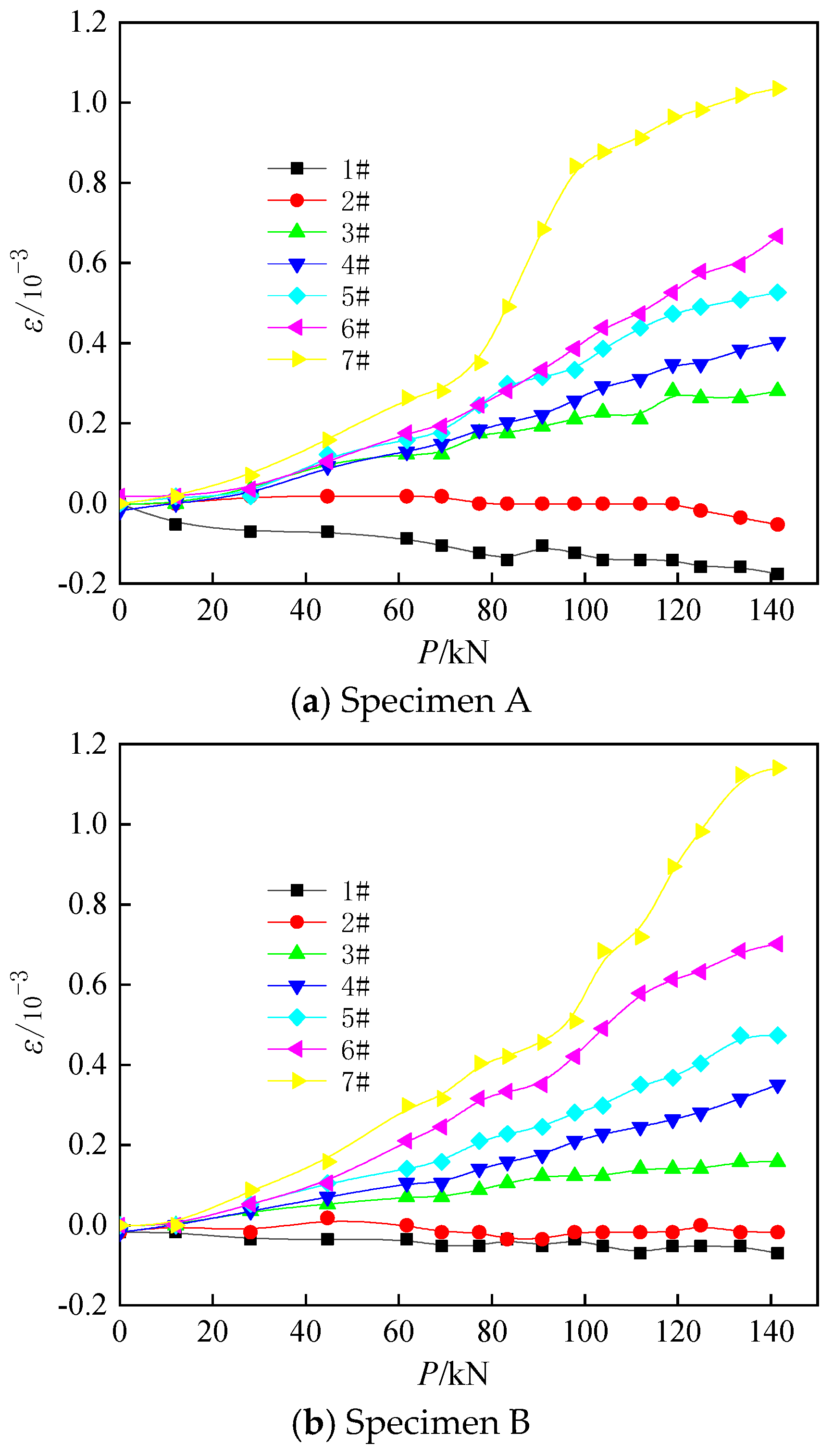
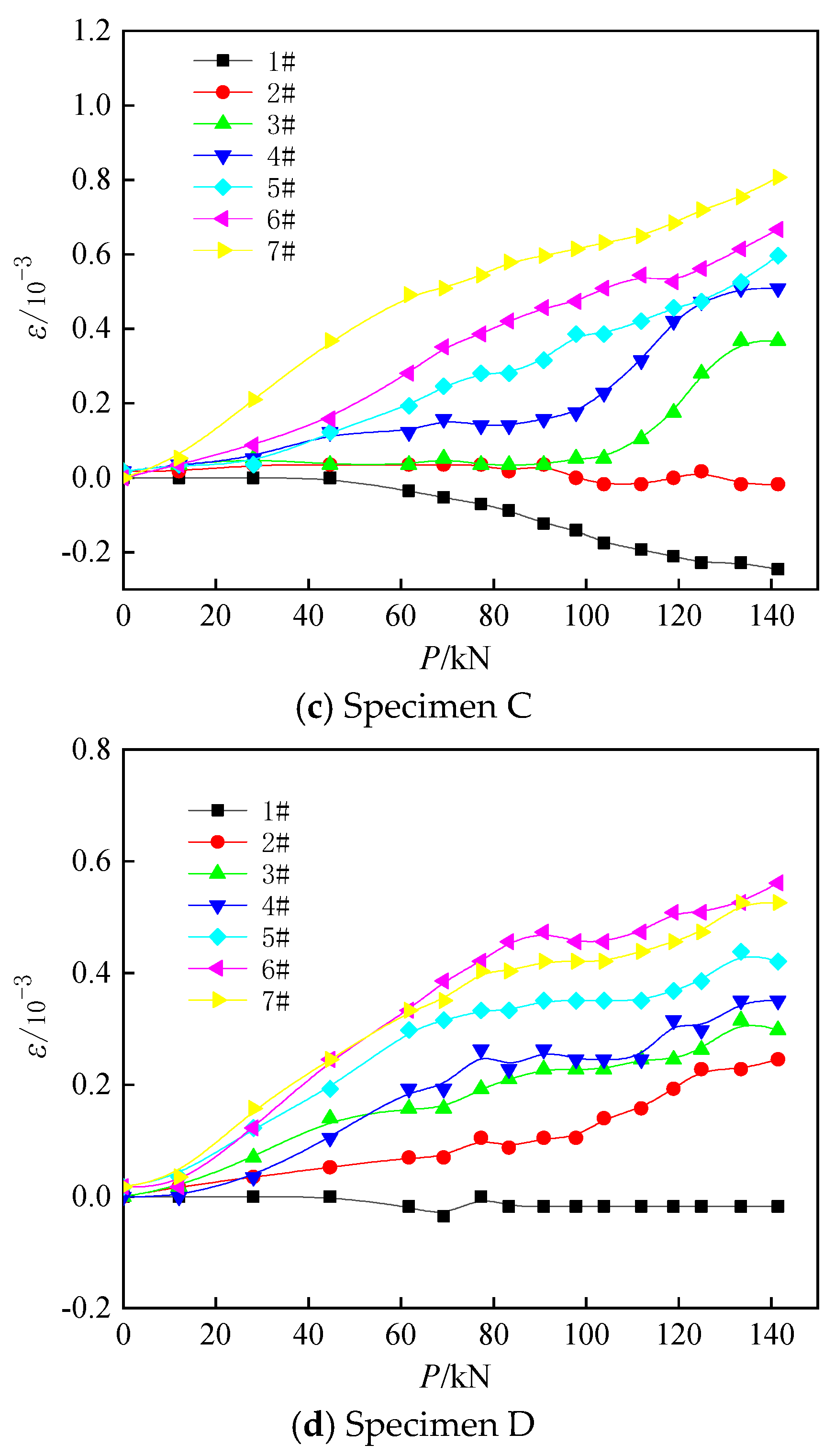
5.1. Strain Analysis
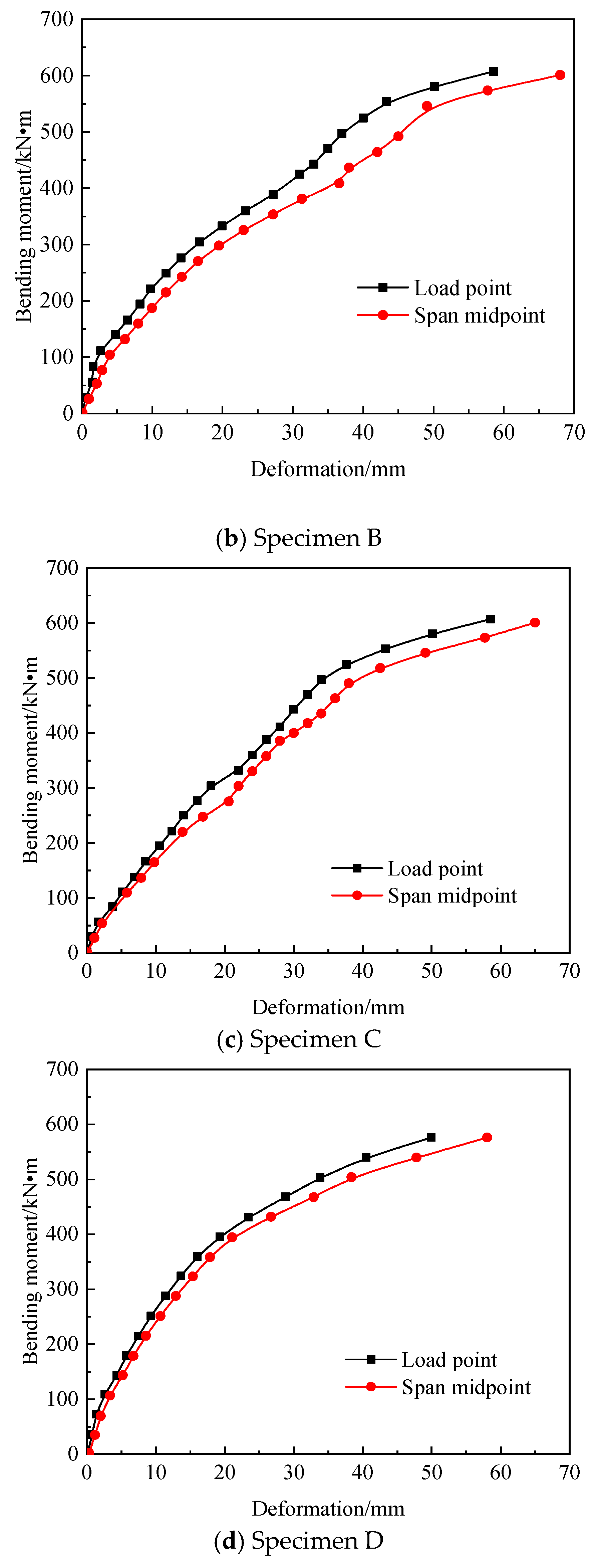
5.2. Flexural Capacity
6. Comparison with FEM
6.1. Material Constitutive Model and Parameters
6.2. Contact Relation and Loading Method of Element Type
6.3. Comparison of Numerical Values and Test Results
7. Conclusions
- (1)
- By observing the crack pattern of the stirrup joint specimens, we determined that cracks are mainly distributed in the pure bending section under pure bending load. Due to the high bearing capacity of the joint, the pile body first develops cracks and fails with an increase in load.
- (2)
- By analyzing the distribution law of the joint strain of the specimen, we found that it is mainly subject to tension under the action of a pure bending load. With an increase in load, the values of tensile and compressive strains increase.
- (3)
- By analyzing the bending moment distribution of the pure bending section of the specimen, it can be determined that when the bending moment is small, the mid-span deflection of all specimens is basically the same as the loading point; however, as the bending moment increases, under the same bending moment, all the specimens span medium deflection, which is greater than the deflection at the loading point.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, F. Experimental research on load transfer mechanism of pretensioned high strength spun concrete piles. Chin. J. Geotech. Eng. 2004, 26, 95–99. [Google Scholar]
- Lv, W.T.; Wang, Y.H.; Leng, W.M. Testing and numerical analysis of load transfer mechanism of PHC pile. Rock Soil Mech. 2006, 27, 466–470. [Google Scholar]
- Ruan, X. Experimental Research on Bearing Behavior of Jacked PHC Pipe Piles. J. Kunming Univ. Sci. Technol. 2011, 36, 33. [Google Scholar]
- Guo, Y.; Cui, W. Experimental study on application of PHC piles in paleo-clay area. Chin. J. Geotech. Eng. 2011, 33, 108–115. [Google Scholar]
- Kang, J.W.; Zang, S.Z.; Gan, Y. Vertical bearing capacity of driven PHC piles in the Chengdu gravel foundation. Chin. J. Geotech. Eng. 2010, 32, 107–110. [Google Scholar]
- Zong, Z.L. Study on Load Transfer Mechanism of PHC Piles under the Silting Geological Condition. Build. Sci. 2011, 27, 22–24. [Google Scholar]
- Liu, F.; Zheng, J.G. Immersion tests on PHC piles in collapsible loess. Chin. J. Geotech. Eng. 2011, 33, 362–366. [Google Scholar]
- Liu, Z.H.; Zheng, J.G.; Yu, Y.T. Vertical bearing behaviors of PHC piles in collapsible loess. Chin. J. Geotech. Eng. 2010, 32, 111–114. [Google Scholar]
- Chen, Z.S.; Rui, R.; Xia, Y.Y. Analysis of Pile-Soil Relative Displacements of Soft Soil Roadbed Reinforced by Prestressed Tubular Piles. Highway 2005, 8, 280–284. [Google Scholar]
- Shen, Y.P.; Mao, Y.F.; Jing, P.; Cheng, W.H. Experimental effect contrast between PHC and CFG pile-raft composite foundation in high speed railway base treatment. Chin. J. Rock Mech. Eng. 2014, 33, 4174–4180. [Google Scholar]
- Cao, X.; Dai, G.; Gong, W.; Tang, J. Experimental study on the seismic behavior of new PHC piles. Arab. J. Geosci. 2020, 13, 778. [Google Scholar] [CrossRef]
- Cao, X.; Dai, G.; Gong, W.; Zhou, F.; Xu, J. Resistance of saturated soil to a laterally vibrating pile. Soil Dyn. Earthq. Eng. 2020, 141, 106496. [Google Scholar]
- Cao, X.; Wang, S.; Gong, W.; Wu, W.; Dai, G.; Zhou, F. Experimental and theoretical study on dynamic stiffness of floating single pile and pile groups in multi-layered soil. Soil Dyn. Earthq. Eng. 2022, 157, 107282. [Google Scholar] [CrossRef]
- Yang, Z.J.; Li, G.C.; Wang, W.J.; Lv, Y.J. Study on the flexural performance of prestressed high strength concrete pile. KSCE J. Civ. Eng. 2018, 22, 4073–4082. [Google Scholar] [CrossRef]
- Banerjee, S.; Stanton, J.F.; Hawkins, N.M. Seismic performance of precast prestressed concrete piles. J. Struct. Eng. 1987, 113, 381–396. [Google Scholar] [CrossRef]
- Wang, T.C.; Yang, Z.J.; Zhao, H.L.; Wang, W.J. Seismic performance of prestressed high strength concrete piles. Mater. Res. Innov. 2014, 18, 515–521. [Google Scholar] [CrossRef]
- Au, F.T.K.; Leung, C.C.Y.; Kwan, A.K.H. Flexural ductility and deformability of reinforced and prestressed concrete sections. Comput. Concr. 2011, 8, 473–489. [Google Scholar] [CrossRef]
- Wang, Y.F.; Chen, G.; Xu, Q.B.; Gong, S.F.; Xiao, Z.B.; Fan, H. Study on Tensile Behavior of Prestressed Concrete Square Pile Connection Joint with Resilient Clamping. J. Disaster Prev. Mitig. Eng. 2018, 38, 1003–1011. [Google Scholar]
- Lu, L.H.; Han, S.; Chen, Z.X.; Wang, G. Study on bending performance of prefabricated square pile with socket and spigot joint. J. Build. Struct. 2018, 39, 153–161. [Google Scholar]
- Zhu, B.; Zhang, F.W.; Zhu, H.S. Wear resistance test on steel joint anticorrosion coating for precast square piles. Eng. J. Wuhan Univ. 2017, S1, 299–302. [Google Scholar]
- Dai, X.F. A New Type of Mechanical Connection Joint of Pre-Stressed Concrete Pipe Pile. Ph.D. Thesis, Zhejiang University of Technology, Hangzhou, China, 2015. [Google Scholar]
- Xu, Q.B.; Chen, G.; He, J.F.; Gong, S.F. Flexural performance experiment of connection joint for composite reinforcement concrete prefabricated square piles. J. Zhejiang Univ. 2017, 51, 1300–1308. [Google Scholar]
- Chen, J.S.; Mo, H.H. Three-dimensional FEM Analysis on Flexural Rigidity of Segment Joints in Shield Tunnel. J. China Railw. Soc. 2009, 31, 87–91. [Google Scholar]
- Zeng, D.Y.; He, C. Numerical Simulation of Segment Joint Bending Stiffness of Metro Shield Tunnel. J. Southwest Jiaotong Univ. 2004, 6, 744–748. [Google Scholar]
- Song, K.Z.; Yuan, D.J.; Wang, M.S. Dynamic performance detection of CFRP composite pipes based on quasi-distributed optical fiber sensing techniques. Rock Soil Mech. 2008, 29, 619–623. [Google Scholar]
- He, C.; Zhang, J.G.; Yang, Z. Model test study on the mechanical characteristics of segment lining for the Wuhan Yangtze River tunnel. China Civ. Eng. J. 2008, 12, 85–90. [Google Scholar]
- Li, Z.P.; Wang, C.; Su, H.F.; Shi, S. Mechanical Property of Tenon-Groove Joints for Metro Station Constructed by Prefabricated Structure. China Railw. Sci. 2015, 36, 7–11. [Google Scholar]
- Liu, J.H. Study on the Design Optimization of the Fabricated Structure of the Subway Station of the Constructed by Open-Cut Method and the Mechanical Behavior of Construction. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2007. [Google Scholar]
- Guner, S.; Chiluwal, S. Cyclic load behavior of helical pile-to-pile cap connections subjected to uplift loads. Eng. Struct. 2021, 243, 112667. [Google Scholar] [CrossRef]
- Xu, Y.; Zeng, Z.; Wang, Z.; Ge, J. Experimental studies of embedment length of precast bridge pier with socket connection to pile cap. Eng. Struct. 2021, 233, 111906. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, W. Experimental and numerical investigation on the behaviour of prestressed high strength concrete pile-to-pile cap connections. KSCE J. Civ. Eng. 2016, 20, 1903–1912. [Google Scholar] [CrossRef]
- Wang, T.; Yang, Z.; Zhao, H.; Wang, W. Seismic Performance of Prestressed High Strength Concrete Pile to Pile Cap Connections. Adv. Struct. Eng. 2014, 17, 1329–1342. [Google Scholar] [CrossRef]
- Joen, P.H. Seismic Performance of Prestressed Concrete Piles and Pile-Pile Cap Connections. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1987. [Google Scholar]
- Chiluwal, S.; Guner, S. Helical Pile-to-Pile Cap Connections Subjected to Uplift Forces: Improving Future Practice. In Proceedings of the Deep Foundations Institute 44th Annual Conference, Chicago, IL, USA, 15–18 October 2019. [Google Scholar]
- Guo, Z.; He, W.; Bai, X.; Chen, Y.F. Seismic Performance of Pile-Cap Connections of Prestressed High-Strength Concrete Pile with Different Details. Struct. Eng. Int. 2017, 27, 546–557. [Google Scholar] [CrossRef]
- Wang, H.; Chen, H.; Chen, C.; Zhao, H.; Jiang, H.; Song, T.; Feng, S. The Structural Performance of CFRP Composite Plates Assembled with Fiber Bragg Grating Sensors. Symmetry 2021, 13, 1631. [Google Scholar] [CrossRef]
- Wang, H.; Song, T.; Yan, J.; Xiang, P.; Feng, S.; Hui, D. Improved analytical method for interfacial-slip control design of steel-concrete composite structures. Symmetry 2021, 13, 1225. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, L.; Xiang, P. Improving the durability of the optical fiber sensor based on strain transfer analysis. Opt. Fiber Technol. 2018, 42, 97–104. [Google Scholar] [CrossRef]
- Sasy, C.; Yung, W.; Hua-Ping, W.; Ping, X. Optical Fiber Sensors for Monitoring Railway Infrastructures: A Review towards Smart Concept. Symmetry 2021, 13, 2251. [Google Scholar] [CrossRef]
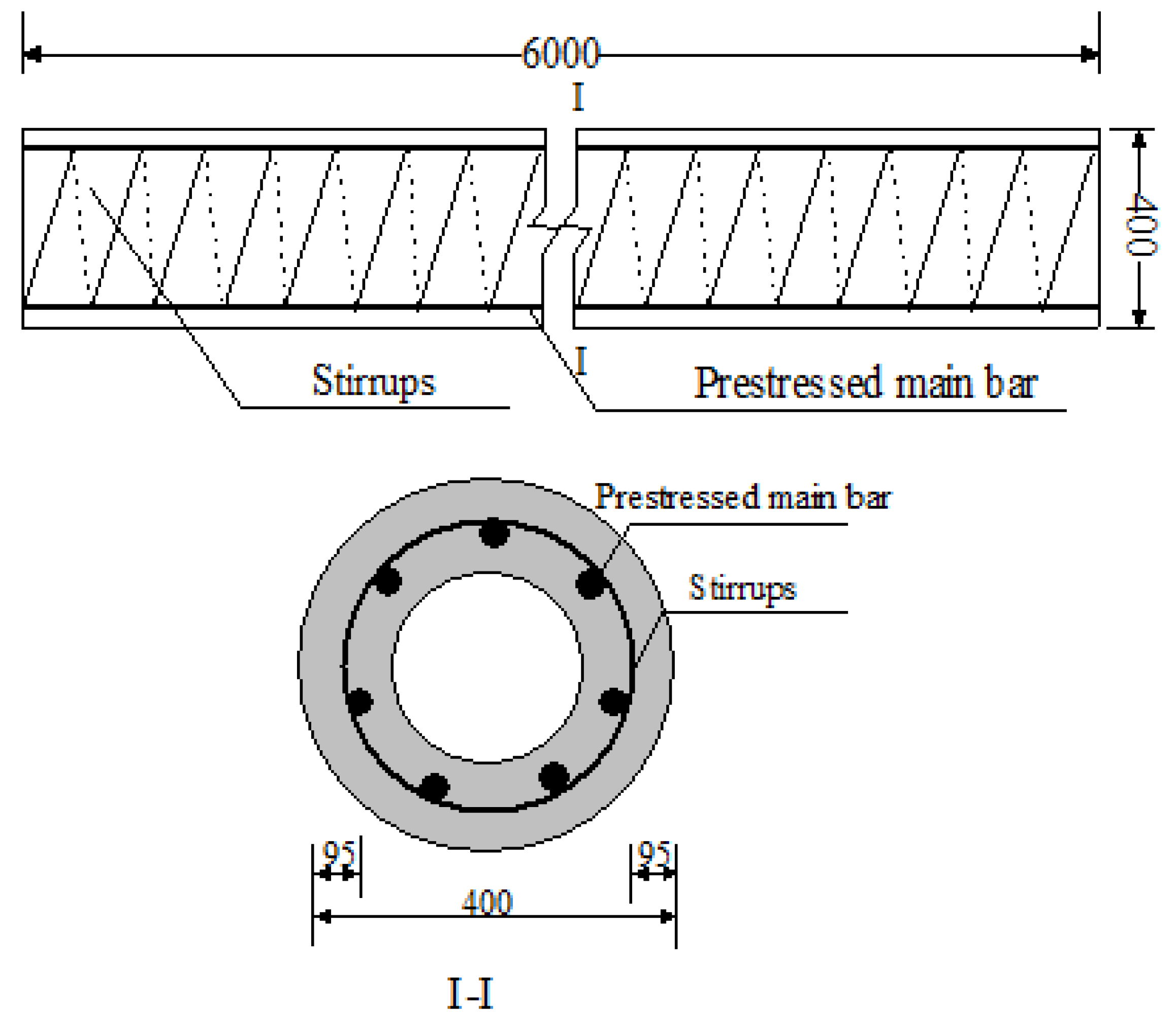









| Number | Pile Type | Pile Diameter (mm) | Wall Thickness (mm) | Prestressed Main Reinforcement | Hoop Reinforcement | σc (MPa) |
|---|---|---|---|---|---|---|
| A | AB | 400 | 95 | 7A10.7 | Ab5@80 | 6.48 |
| B | AB | 400 | 100 | 7A10.7 | Ab5@80 | 6.48 |
| C | AB | 500 | 95 | 7A10.7 | Ab5@80 | 6.48 |
| D | AB | 500 | 100 | 7A10.7 | Ab5@80 | 6.48 |
| Model Material | Volumetric Weight (kN/m3) | Tensile Modulus (GPa) | Yield Strength (MPa) | Compressive Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| Steel bar | 78.5 | 206 | 335 | - | 0.23 |
| Concrete | 25 | 38 | - | 80 | 0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Qi, L.; Yang, Y. Experimental Study on Bending Resistance of New Type Joint of Prestressed Concrete Pipe Pile. Symmetry 2022, 14, 1920. https://doi.org/10.3390/sym14091920
Wang B, Qi L, Yang Y. Experimental Study on Bending Resistance of New Type Joint of Prestressed Concrete Pipe Pile. Symmetry. 2022; 14(9):1920. https://doi.org/10.3390/sym14091920
Chicago/Turabian StyleWang, Bo, Lei Qi, and Yongdong Yang. 2022. "Experimental Study on Bending Resistance of New Type Joint of Prestressed Concrete Pipe Pile" Symmetry 14, no. 9: 1920. https://doi.org/10.3390/sym14091920
APA StyleWang, B., Qi, L., & Yang, Y. (2022). Experimental Study on Bending Resistance of New Type Joint of Prestressed Concrete Pipe Pile. Symmetry, 14(9), 1920. https://doi.org/10.3390/sym14091920





