Exact Solutions to Some Nonlinear Time-Fractional Evolution Equations Using the Generalized Kudryashov Method in Mathematical Physics
Abstract
:1. Introduction
2. Brief Idea of the Conformable Fractional Derivative
- for all ;
- for all ;
- , for all constant functions ;
- ;
- ;
- If, in addition, ϖ is differentiable, then
3. The Generalized Kudryashov Method
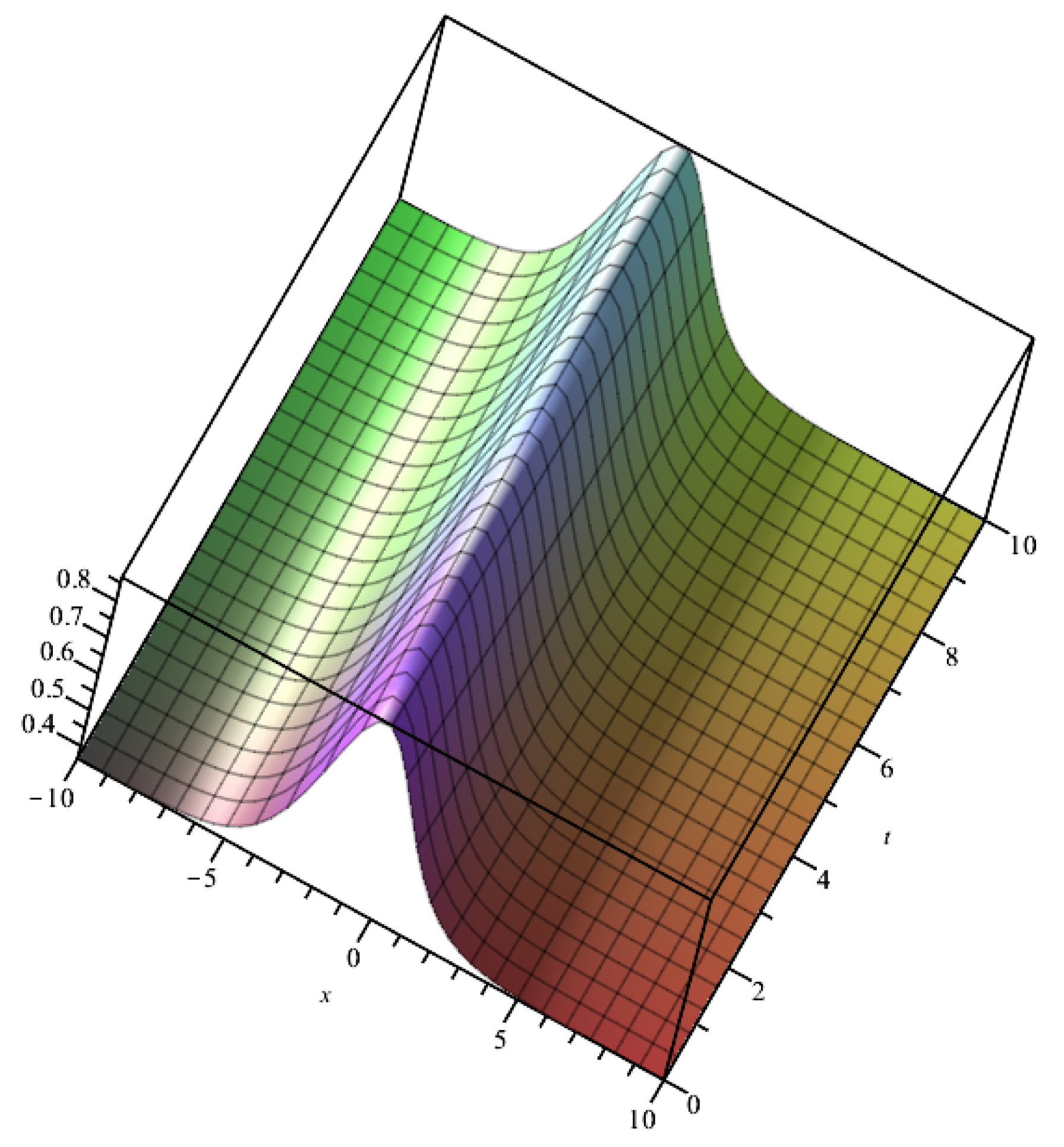
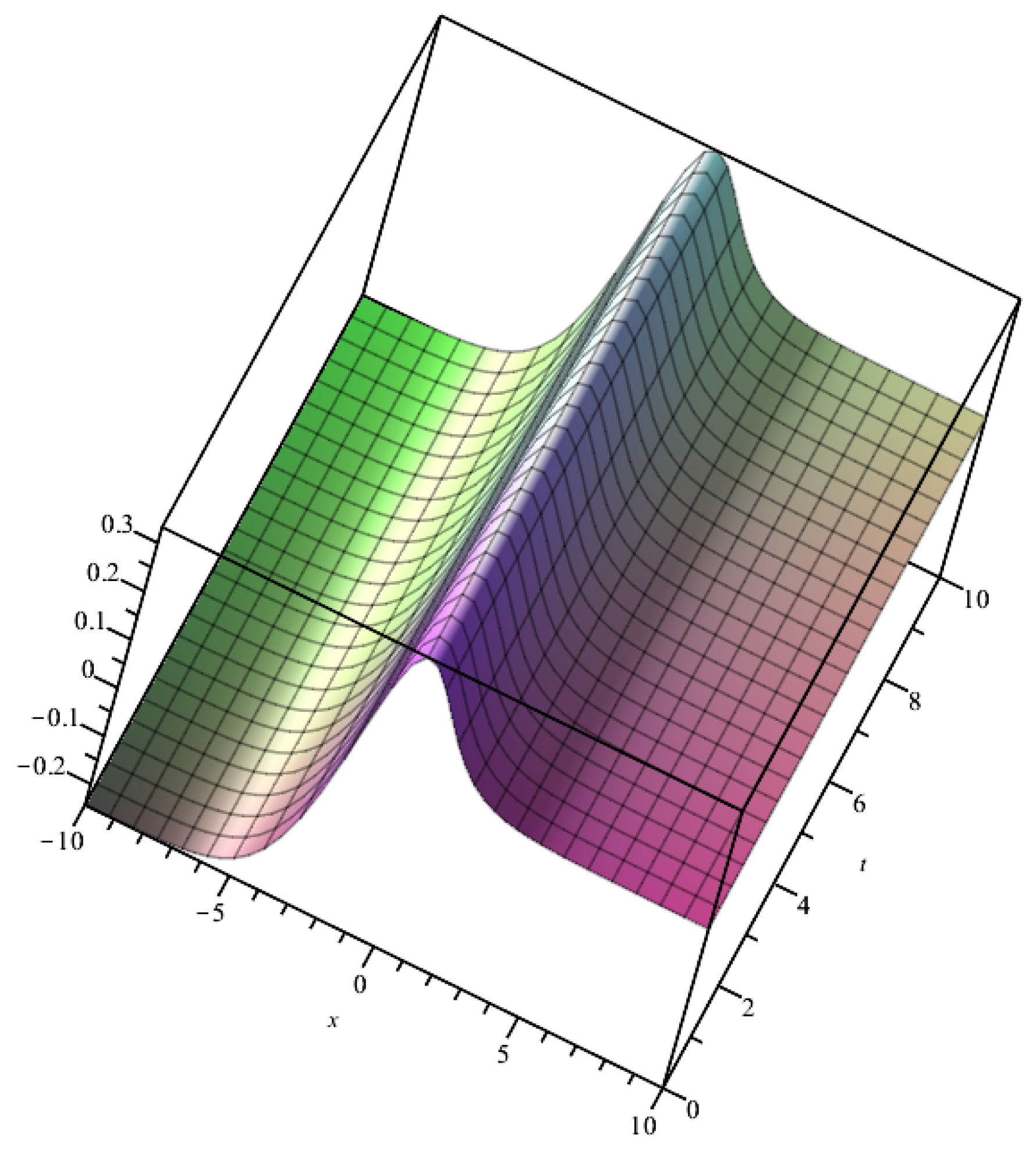
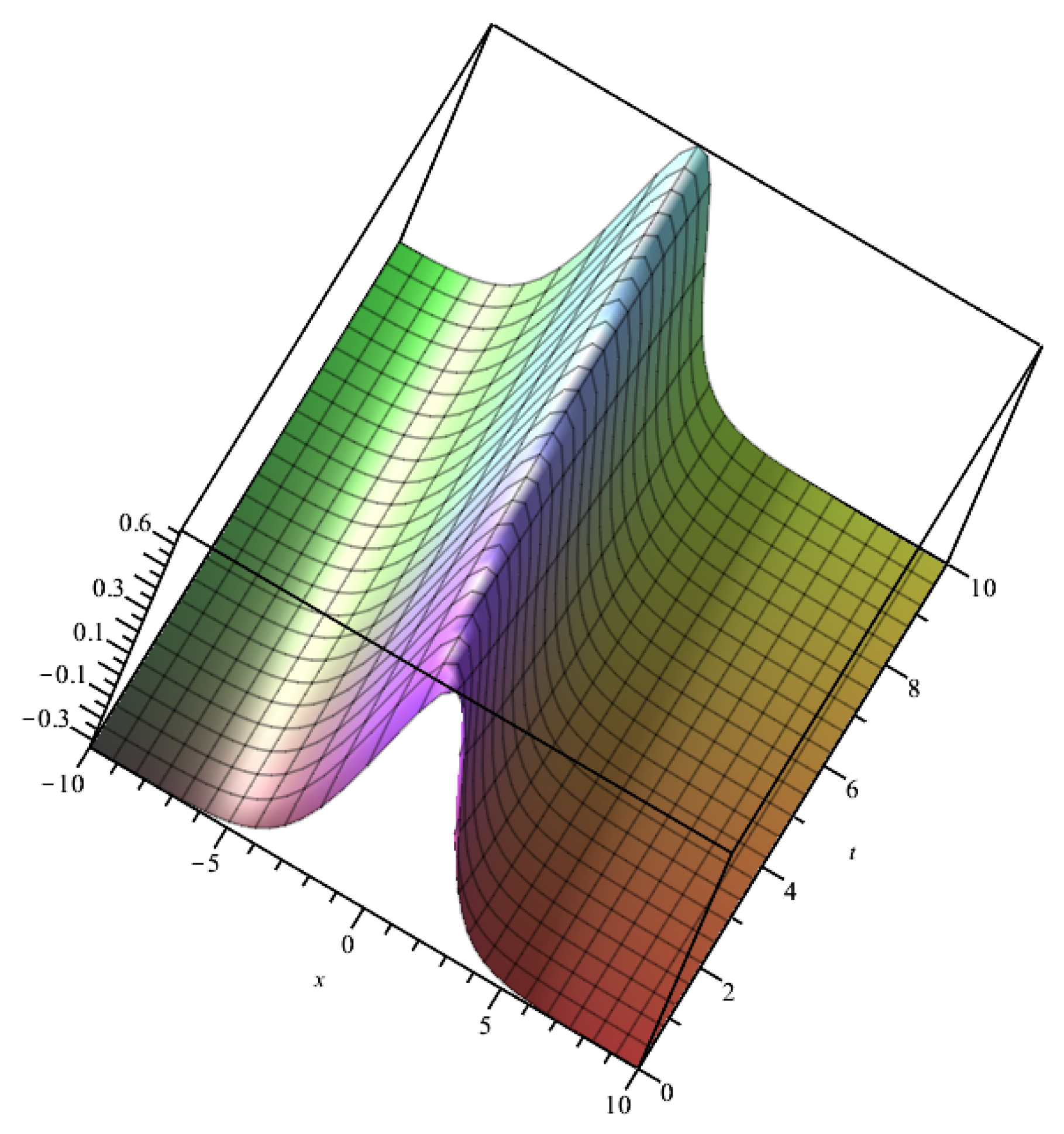
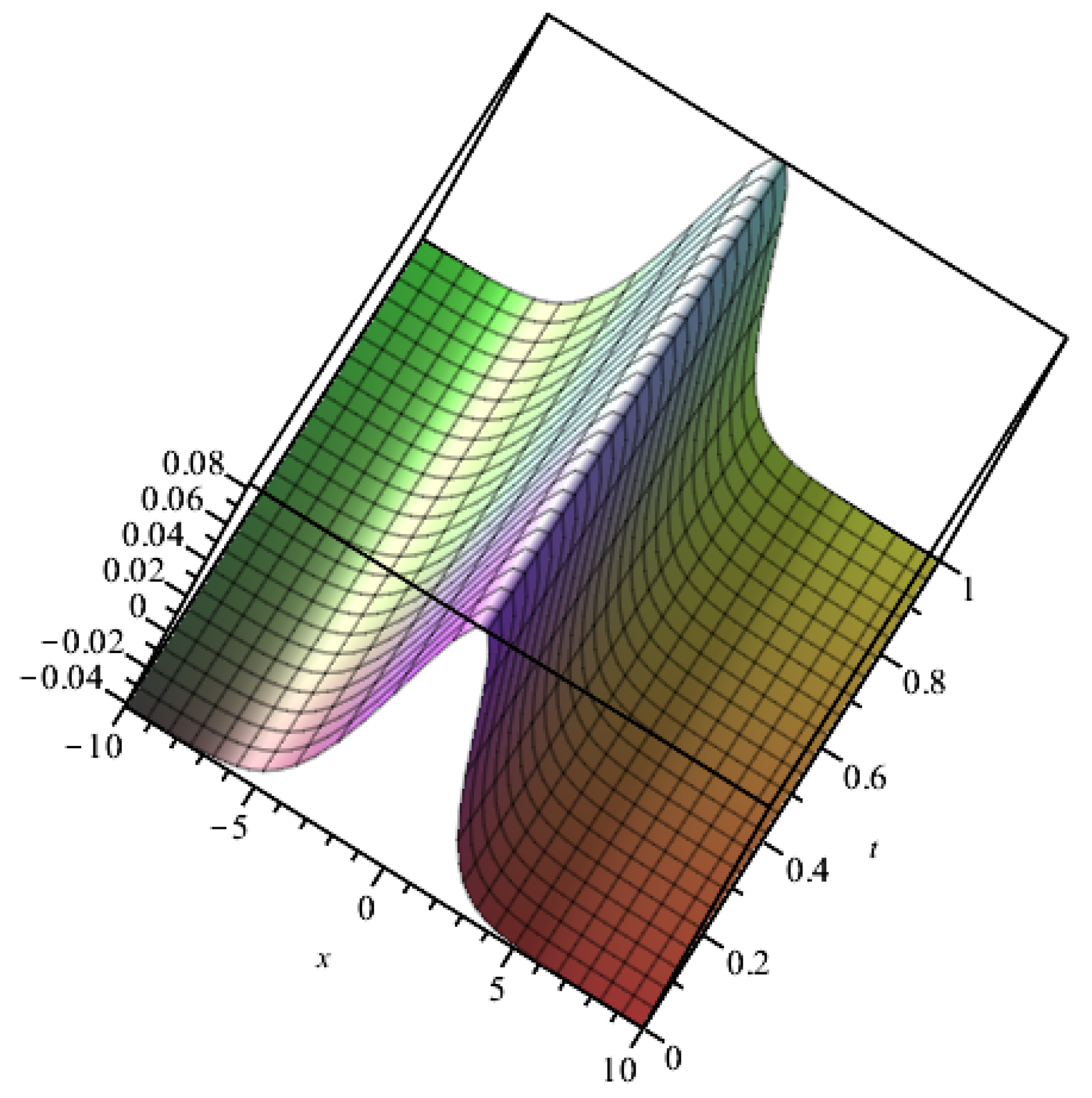
4. Application of the Method
4.1. The Time-Fractional Caudrey–Dodd–Gibbon–Sawada–Kotera Equation
4.2. The Time-Fractional Seventh Order Sawada–Kotera–Ito Equation
4.3. The Seventh-Order Time-Fractional Kaup–Kupershmidt Equation
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- El-Sayed, A.M.A.; Gaber, M. The Adomian decomposition method for solving partial differential equations of fractal order in finite domains. Phys. Lett. A 2006, 359, 175–182. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; Behiry, S.H.; Raslan, W.E. Adomian’s decomposition method for solving an intermediate fractional advection–dispersion equation. Comput. Math. Appl. 2010, 59, 1759–1765. [Google Scholar]
- Odibat, Z.; Momani, S. A generalized differential transform method for linear partial differential equations of fractional order. Appl. Math. Lett. 2008, 21, 194–199. [Google Scholar] [CrossRef]
- Ekici, M.; Ayaz, F. Solution of model equation of completely passive natural convection by improved differential transform method. Res. Eng. Struct. Mater. 2017, 3, 1–10. [Google Scholar] [CrossRef]
- Tian, Q.; Yang, X.; Zhang, H.; Xu, D. An implicit robust numerical scheme with graded meshes for the modified Burgers model with nonlocal dynamic properties. Comput. Appl. Math. 2023, 42, 246. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, Y.; Li, Z. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Zhang, S.; Tong, J.L.; Wang, W. A generalized-expansion method for the mKdV equation with variable coefficients. Phys. Lett. A 2008, 372, 2254–2257. [Google Scholar] [CrossRef]
- Ekici, M.; Ünal, M. Application of the rational (G′/G)-expansion method for solving some coupled and combined wave equations. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2022, 71, 116–132. [Google Scholar] [CrossRef]
- Ünal, M.; Ekici, M. The Double (G′/G, 1/G)-Expansion Method and Its Applications for Some Nonlinear Partial Differential Equations. J. Inst. Sci. Technol. 2021, 11, 599–608. [Google Scholar]
- Kudryashov, N.A. Exact solutions of the generalized Kuramoto-Sivashinsky equation. Phys. Lett. A 1990, 147, 287–291. [Google Scholar] [CrossRef]
- Liu, S.; Fu, Z.; Liu, S.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar] [CrossRef]
- Zhang, J.L.; Wang, M.L.; Li, X.Z. The subsidiary ordinary differential equations and the exact solutions of the higher order dispersive nonlinear Schrödinger equation. Phys. Lett. A 2006, 357, 188–195. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Zhang, J. Various exact solutions of nonlinear Schrödinger equation with two nonlinear terms. Chaos Solitons Fractals 2007, 31, 594–601. [Google Scholar] [CrossRef]
- Arafa, A.A.M.; Rida, S.Z.; Mohamed, H. Homotopy analysis method for solving biological population model. Commun. Theor. Phys. 2011, 56, 797. [Google Scholar] [CrossRef]
- Fan, E. Extended tanh-function method and its applications to nonlinear equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Yang, X.; Wu, L.; Zhang, H. A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 457, 128192. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Ekici, M.; Ünal, M. Application of the exponential rational function method to some fractional soliton equations. In Emerging Applications of Differential Equations and Game Theory; IGI Global: Hershey, PA, USA, 2020; pp. 13–32. [Google Scholar]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A.; Akbulut, A. A generalized Kudryashov method to some nonlinear evolution equations in mathematical physics. Nonlinear Dyn. 2016, 85, 2843–2850. [Google Scholar] [CrossRef]
- Date, E.; Jimbo, M.; Kashiwara, M.; Miwa, T. KP hierarchies of orthogonal and symplectic type–Transformation groups for soliton equations VI. J. Phys. Soc. Jpn. 1981, 50, 3813–3818. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Wang, W.; Zhang, H. A Predictor–Corrector Compact Difference Scheme for a Nonlinear Fractional Differential Equation. Fractal Fract. 2023, 7, 521. [Google Scholar] [CrossRef]
- Geng, X.; He, G.; Wu, L. Riemann theta function solutions of the Caudrey–Dodd–Gibbon–Sawada–Kotera hierarchy. J. Geom. Phys. 2019, 140, 85–103. [Google Scholar] [CrossRef]
- Koonprasert, S.; Sirisubtawee, S.; Ampun, S. More explicit solitary solutions of the space-time fractional fifth order nonlinear Sawada-Kotera equation via the improved generalized Riccati equation mapping method. Comput. Math. Appl. 2017, 13, 2629–2658. [Google Scholar]
- Naher, H.; Abdullah, F.A.; Akbar, M.A.; Mohyud-Din, S. Some new solutions of the higher-order Sawada-Kotera equation via the exp-function method. Middle-East J. Sci. Res. 2012, 11, 1659–1667. [Google Scholar]
- Zayed, E.M.E.; Alurrfi, K.A.E. The modified Kudryashov method for solving some seventh order nonlinear PDEs in mathematical physics. World J. Model. Simul. 2015, 11, 308–319. [Google Scholar]
- Guner, O. New exact solutions for the seventh-order time fractional Sawada–Kotera–Ito equation via various methods. Waves Random Complex Media 2020, 30, 441–457. [Google Scholar] [CrossRef]
- Feng, J. New traveling wave solutions to the seventh-order Sawada-Kotera equation. J. Appl. Math. Inform. 2010, 28, 1431–1437. [Google Scholar]
- Jena, R.M.; Chakraverty, S.; Jena, S.K.; Sedighi, H.M. On the wave solutions of time-fractional Sawada-Kotera-Ito equation arising in shallow water. Math. Methods Appl. Sci. 2021, 44, 583–592. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Tuluce Demiray, S.; Pandir, Y.; Bulut, H. Generalized Kudryashov method for time-fractional differential equations. In Abstract and Applied Analysis; Hindawi: London, UK, 2014; Volume 2014. [Google Scholar]
- Sawada, K.; Kotera, T. A method for finding N-soliton solutions of the KdV equation and KdV-like equation. Prog. Theor. Phys. 1974, 51, 1355–1367. [Google Scholar] [CrossRef]
- Caudrey, P.J.; Dodd, R.K.; Gibbon, J.D. A new hierarchy of Korteweg–de Vries equations. Proc. R. Soc. Lond. A Math. Phys. Sci. 1976, 351, 407–422. [Google Scholar]
- Dodd, R.K.; Gibbon, J.D. The prolongation structure of a higher order Korteweg-de Vries equation. Proc. R. Soc. Lond. A Math. Phys. Sci. 1978, 358, 287–296. [Google Scholar]
- Pomeau, Y.; Ramani, A.; Grammaticos, B. Structural stability of the Korteweg-de Vries solitons under a singular perturbation. Phys. D 1988, 31, 127–134. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ekici, M. Exact Solutions to Some Nonlinear Time-Fractional Evolution Equations Using the Generalized Kudryashov Method in Mathematical Physics. Symmetry 2023, 15, 1961. https://doi.org/10.3390/sym15101961
Ekici M. Exact Solutions to Some Nonlinear Time-Fractional Evolution Equations Using the Generalized Kudryashov Method in Mathematical Physics. Symmetry. 2023; 15(10):1961. https://doi.org/10.3390/sym15101961
Chicago/Turabian StyleEkici, Mustafa. 2023. "Exact Solutions to Some Nonlinear Time-Fractional Evolution Equations Using the Generalized Kudryashov Method in Mathematical Physics" Symmetry 15, no. 10: 1961. https://doi.org/10.3390/sym15101961
APA StyleEkici, M. (2023). Exact Solutions to Some Nonlinear Time-Fractional Evolution Equations Using the Generalized Kudryashov Method in Mathematical Physics. Symmetry, 15(10), 1961. https://doi.org/10.3390/sym15101961






