Symmetry and Asymmetry of Chaotic Motion in a Crank Arm and Connecting Rod Due to the Movement of the Follower
Abstract
:1. Introduction
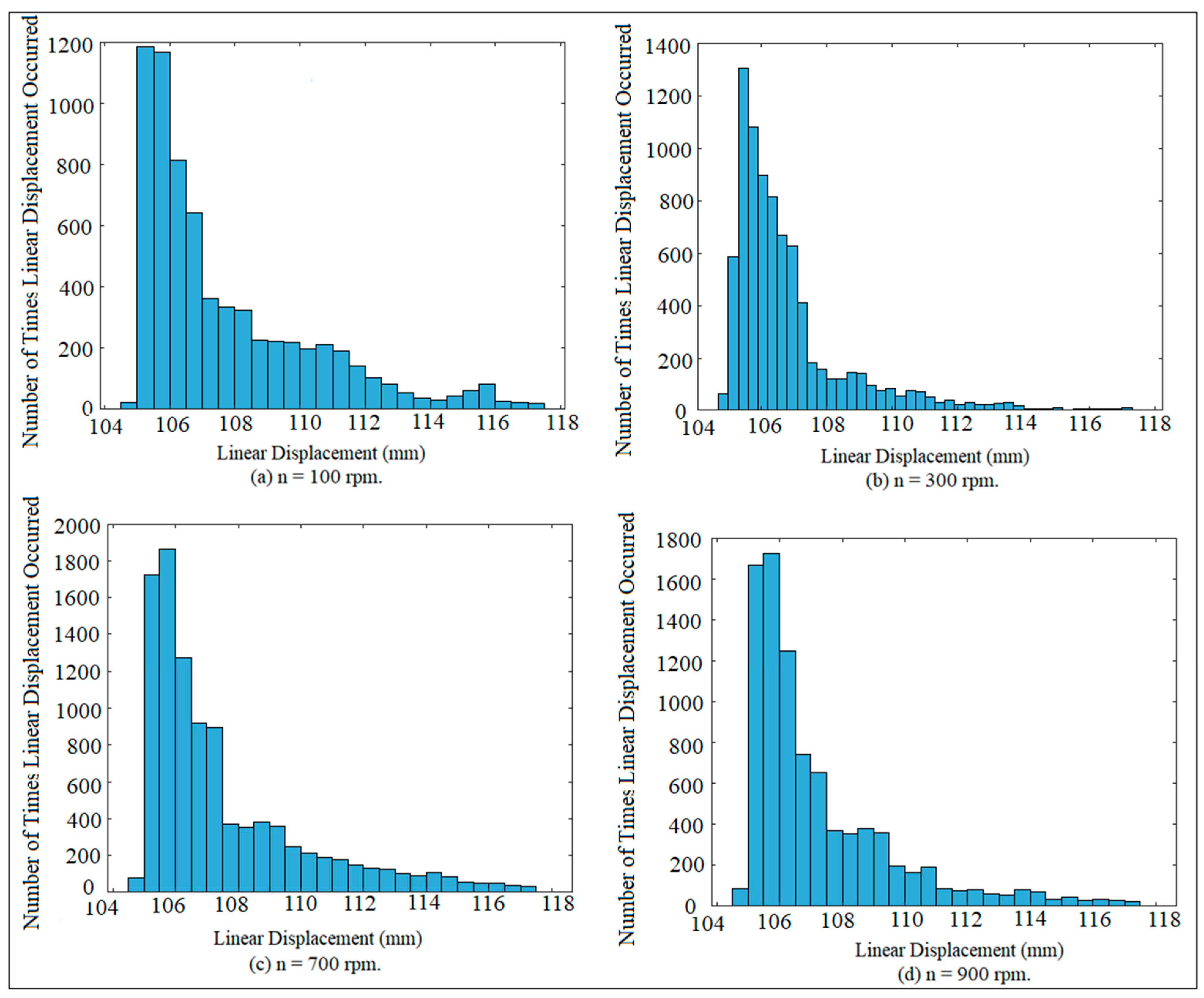
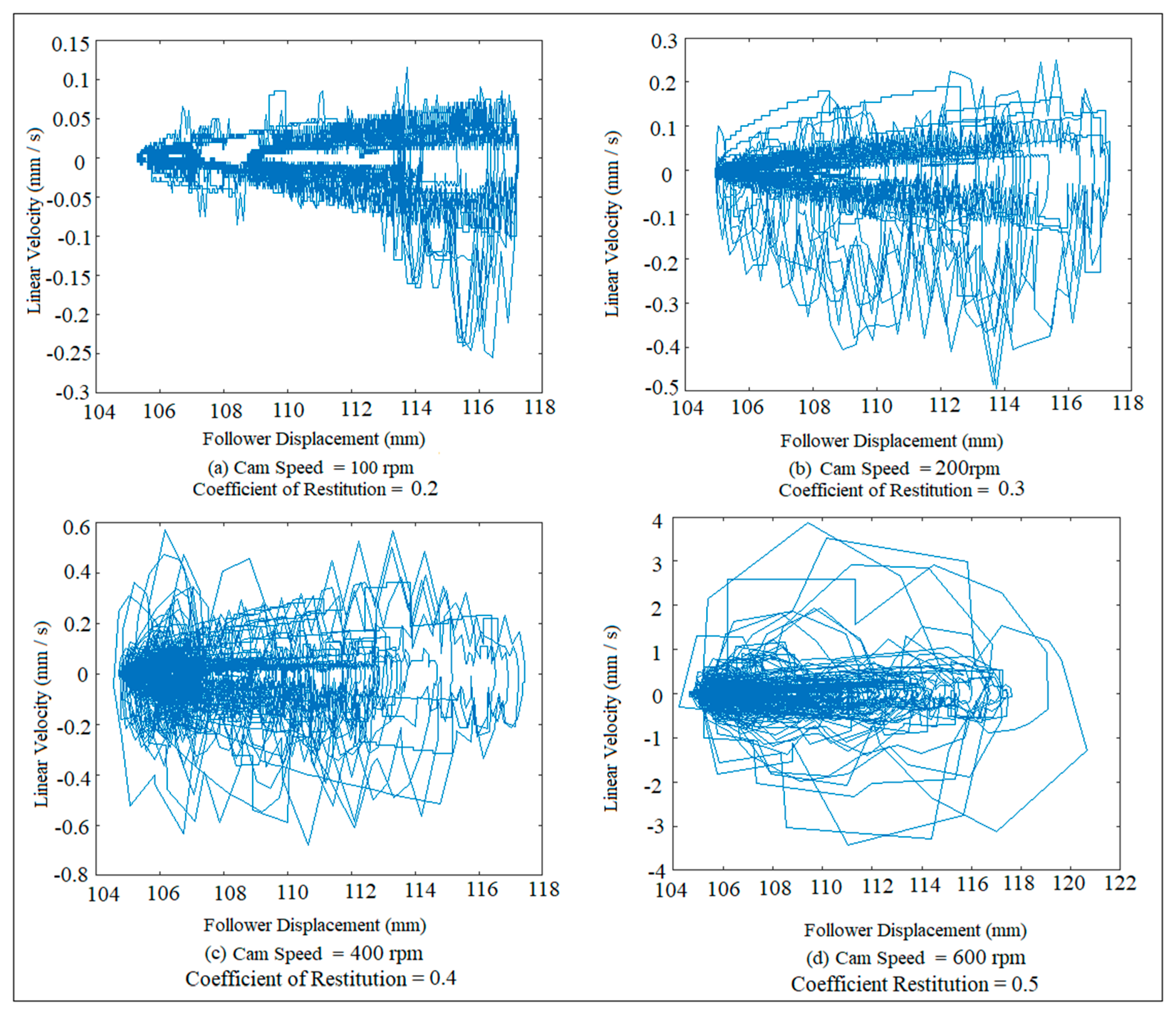
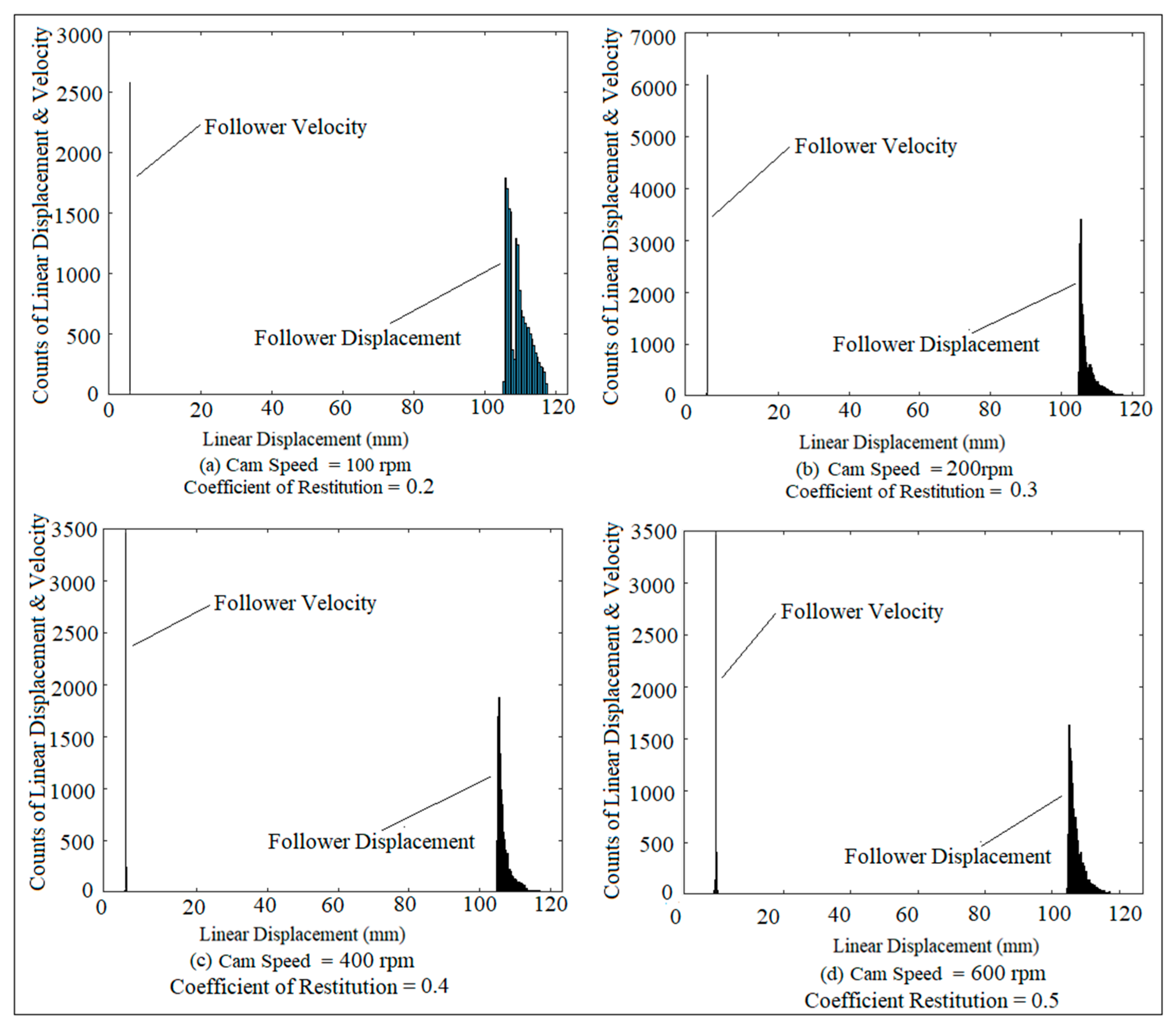
2. Chaotic Phenomenon Detection Using Linear Displacement
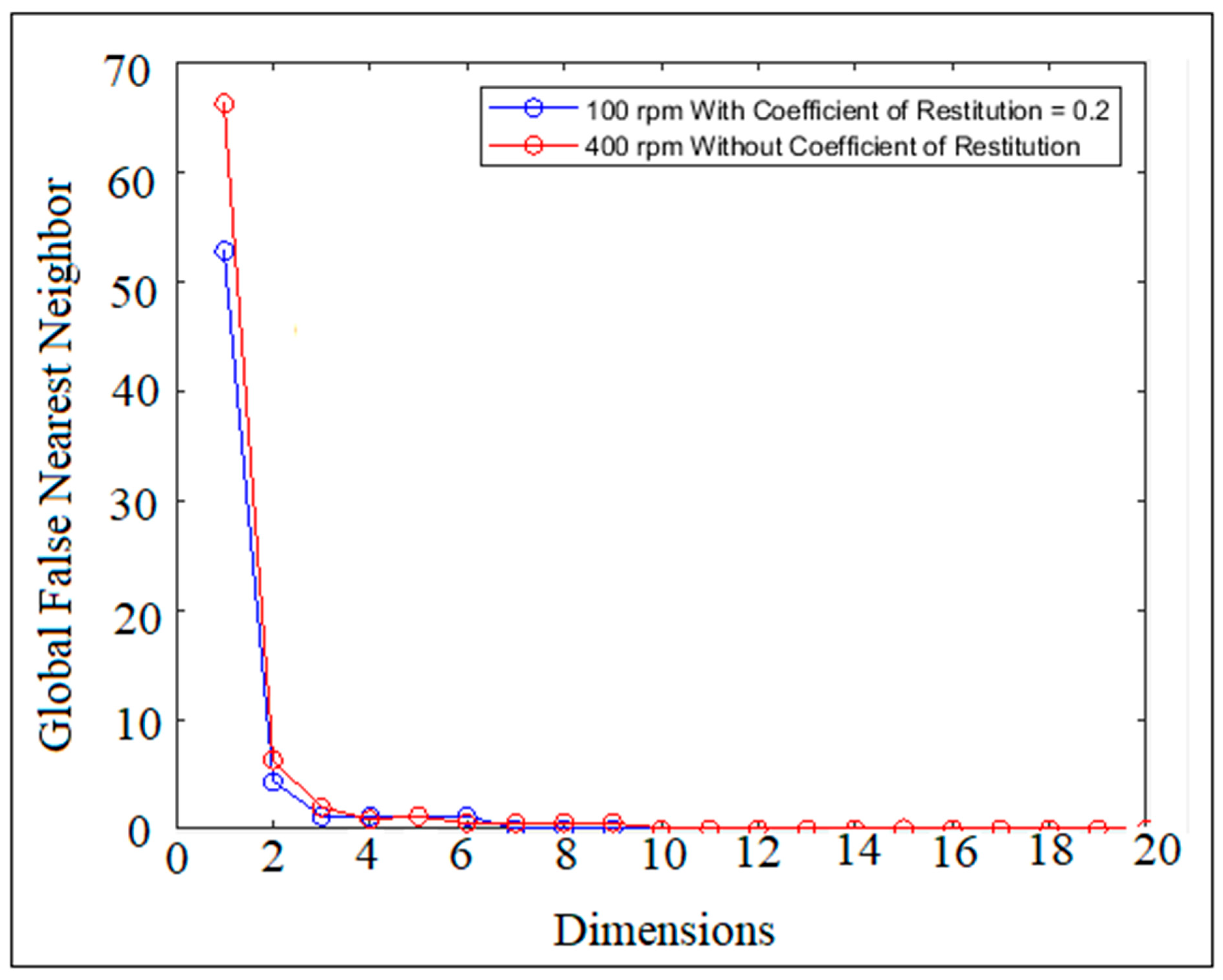
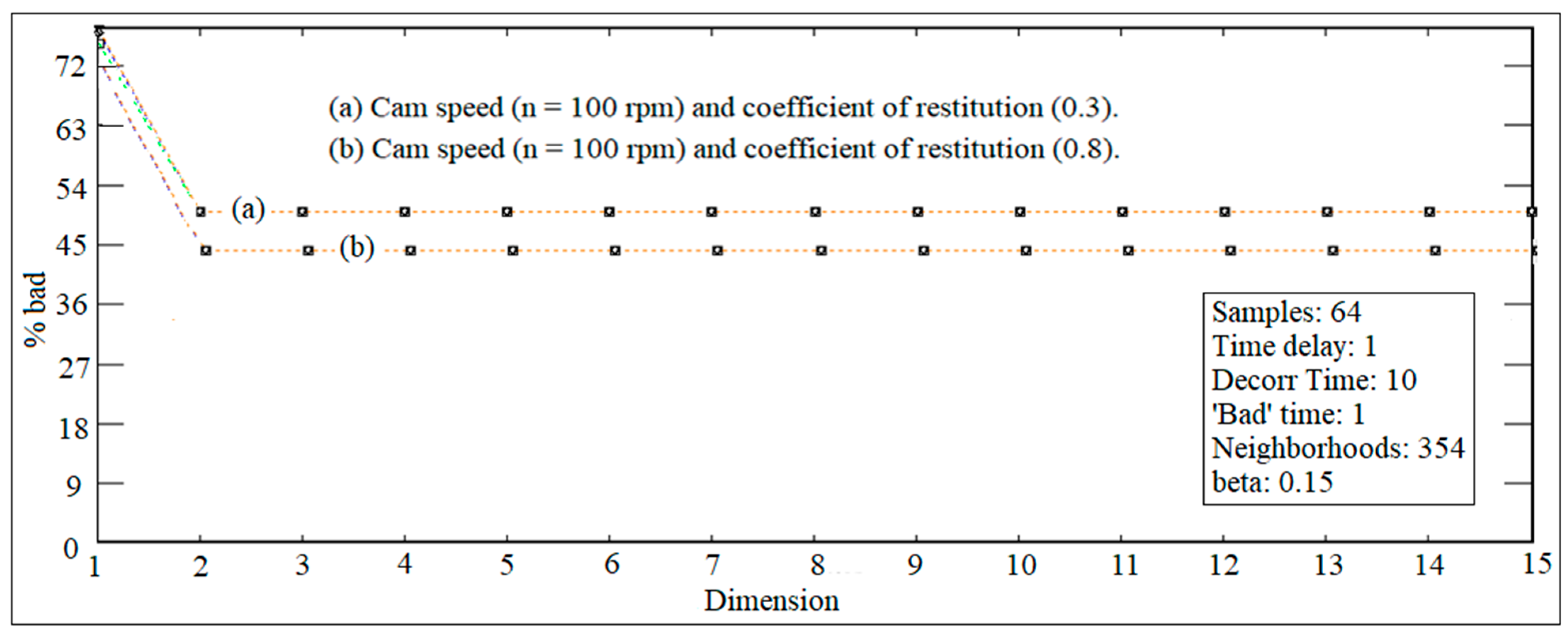
3. Global Dimensions of Chaotic Level
4. Local Dimensions of Chaotic Level
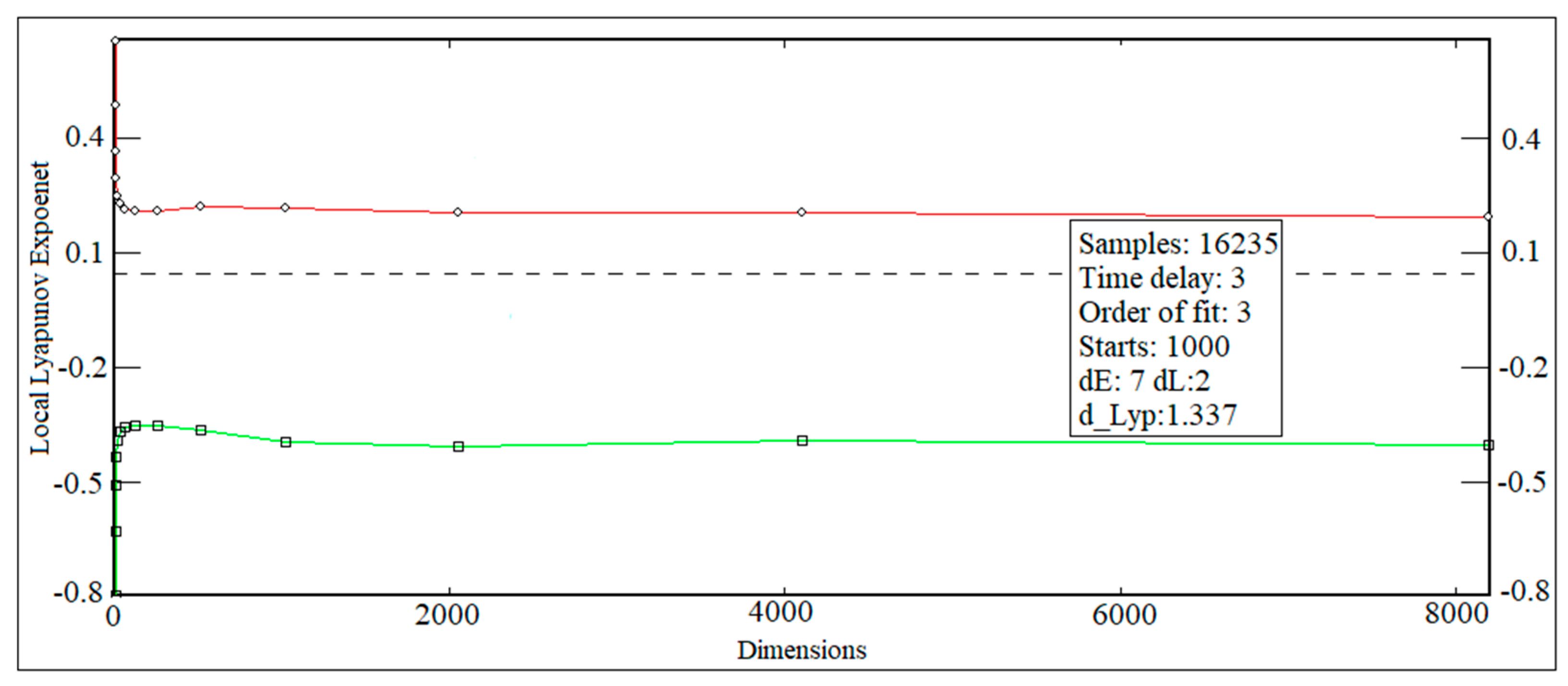
5. Chaotic Detection Using Local Lyapunov Exponent
6. Fast Fourier Transform (FFT)
7. Results and Discussion
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, H.S.; Tsai, W.J. A variable-speed approach for preventing cam-follower separation. J. Adv. Mech. Des. Syst. Manuf. 2008, 2, 12–23. [Google Scholar] [CrossRef]
- Osorio, G.; di Bernardo, M.; Santini, S. Corner-impact bifurcations: A novel class of discontinuity-induced bifurcations in cam-follower systems. SIAM J. Appl. Dyn. Syst. 2008, 7, 18–38. [Google Scholar] [CrossRef]
- Hongbin, Y.; Qingyuan, G.; Honghuan, Y.; Junquang, P. Analysis of the Influence of Machining Errors on the Dynamic Characteristics of the Dobby Modulator. J. Text. Eng. 2021, 67, 77–84. [Google Scholar]
- Nguyen, T.T.N.; Duong, T.X.; Nguyen, V.-S. Design general Cam profiles based on finite element method. Appl. Sci. 2021, 11, 6052. [Google Scholar] [CrossRef]
- Marghitu, D.B.; Zhao, J. Impact of a multiple pendulum with a non-linear contact force. Math. J. 2020, 8, 1202. [Google Scholar] [CrossRef]
- De Groote, W.; Hoecke, S.V.; Crevecoeur, G. Physics-based neural network models for prediction of cam-follower dynamics beyond nominal operations. IEEE/ASME Trans. Mechatron. 2021, 27, 2345–2355. [Google Scholar] [CrossRef]
- De Groote, W.; Kikken, E.; Hostens, E.; Van Hoecke, S.; Crevecoeur, G. Neural network augmented physics models for systems with partially unknown dynamics: Application to slider–crank mechanism. IEEE/ASME Trans. Mechatron. 2021, 27, 103–114. [Google Scholar] [CrossRef]
- Cheng, Y.; Sun, Y.; Song, P.; Liu, L. Spatial-temporal motion control via composite cam-follower mechanisms. ACM Trans. Graph. 2021, 40, 1–15. [Google Scholar] [CrossRef]
- Chang, X.; Pan, H.; Xu, J.; Wang, T. Study of Fault Identification of Clearance in Cam Mechanism. Appl. Sci. 2022, 12, 7420. [Google Scholar] [CrossRef]
- Khajiyeva, L.A.; Kudaibergenov, A.K.; Abdraimova, G.A.; Sabirova, R.F. Modeling of Nonlinear Dynamics of Planar Mechanisms with Elastic and Flexible Pre-Stressed Elements; Advances in Mechanism Design III: Proceedings of TMM 2020 13; Springer: Cham, Switzerland, 2021; pp. 94–103. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, X. Test study and nonlinear dynamic analysis of planar multi-link mechanism with compound clearances. Eur. J. Mech. A/Solids 2021, 88, 104260. [Google Scholar] [CrossRef]
- Alzate, R.; Piiroinen, P.T.; di Bernardo, M. From complete to incomplete chattering: A novel rout to chaos in impacting cam-follower systems. Appl. Sci. 2012, 22, 1250102. [Google Scholar] [CrossRef]
- Wangqun, D.; Haibo, F.; Jianjun, W.; Yongfeng, Y. Effect of surface morphology on dynamic characteristics of cam-follower oblique impact system. J. Shock Vib. 2019, 2019, 3956169. [Google Scholar]
- Planchard, D. SolidWorks 2016 Reference Guide: A Comprehensive Reference Guide with over 250 Standalone Tutorials; Sdc Publications: Mission, KS, USA, 2015. [Google Scholar]
- Qiau, M.; Liang, Y.; Tavares, A.; Shi, X. Multilayer perceptron optimization for chaotic time series modeling. J. Entropy. 2023, 25, 973. [Google Scholar] [CrossRef] [PubMed]
- Ott, E.; Antonsen, T.M. Low dimensional behavior of large systems of globally coupled oscillators. Chaos Interdiscip. J. Nonlinear Sci. 2008, 18, 037113. [Google Scholar] [CrossRef] [PubMed]
- Ispolatov, I.; Madhok, V.; Allende, S.; Doebeli, M. Chaos in high-dimensional dissipative dynamical systems. J. Sci. Rep. 2015, 5, 12506. [Google Scholar] [CrossRef] [PubMed]
- Parlitz, U. Estimating Lyapunov exponents from time series. In Chaos Detection and Predictability; Skokos, C., Gottwald, G.A., Laskar, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–34. [Google Scholar]
- Terrier, P.; Fabienne, R. Maximum Lyapunov exponent revisited: Long-term attractor divergence of gait dynamics is highly sensitive to the noise structure of stride intervals. J. Gait Posture 2018, 66, 236–241. [Google Scholar] [CrossRef] [PubMed]

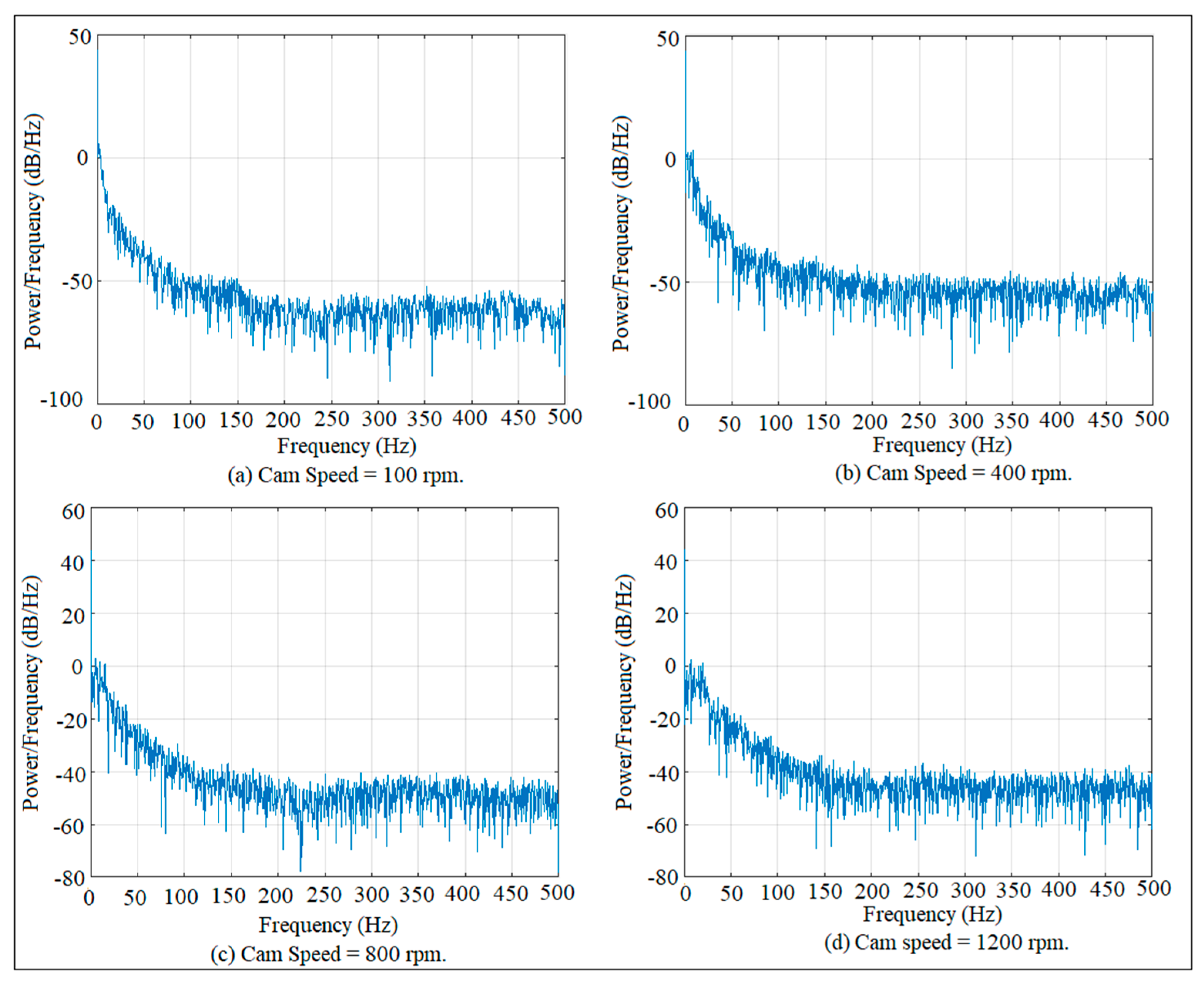


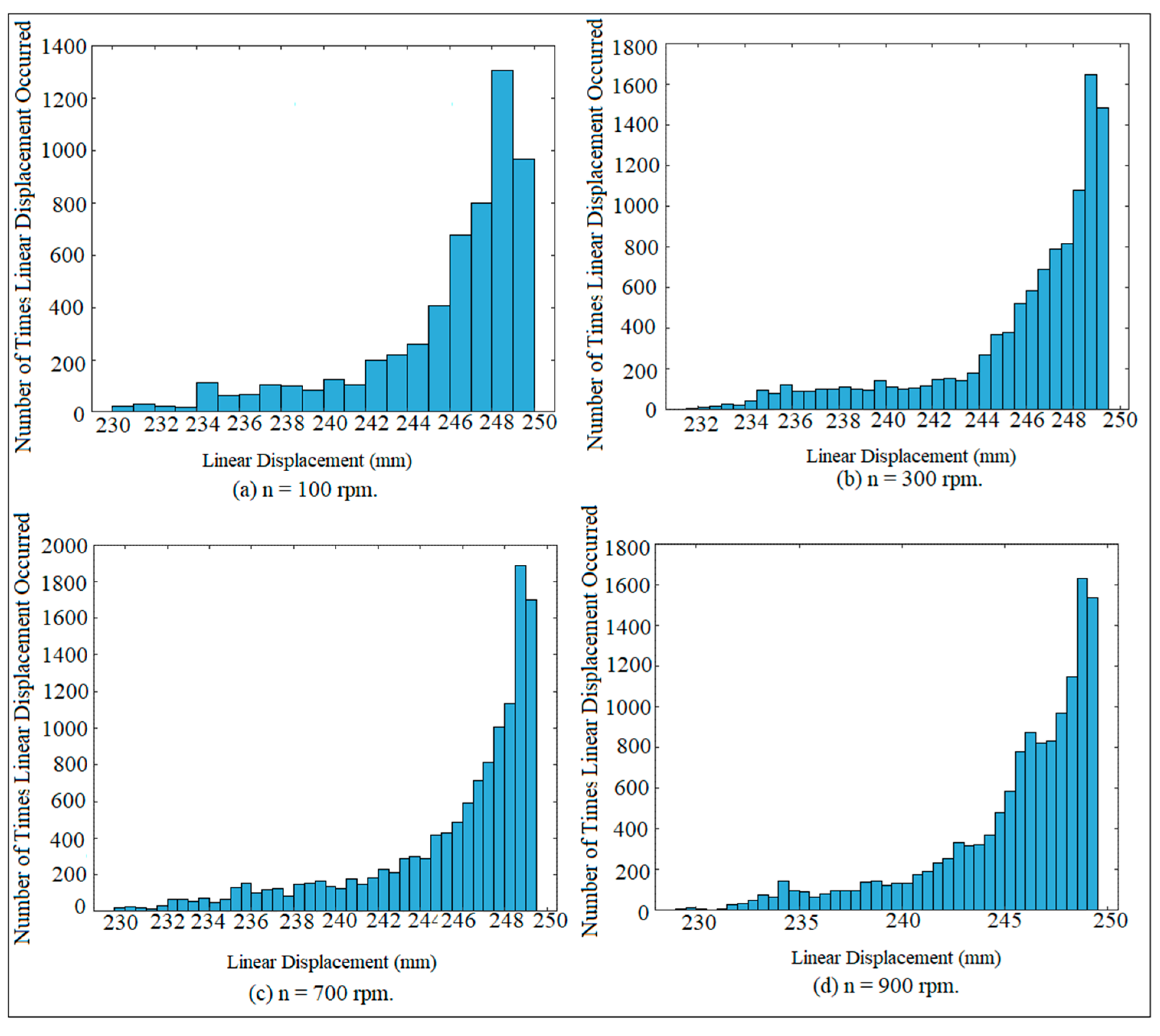
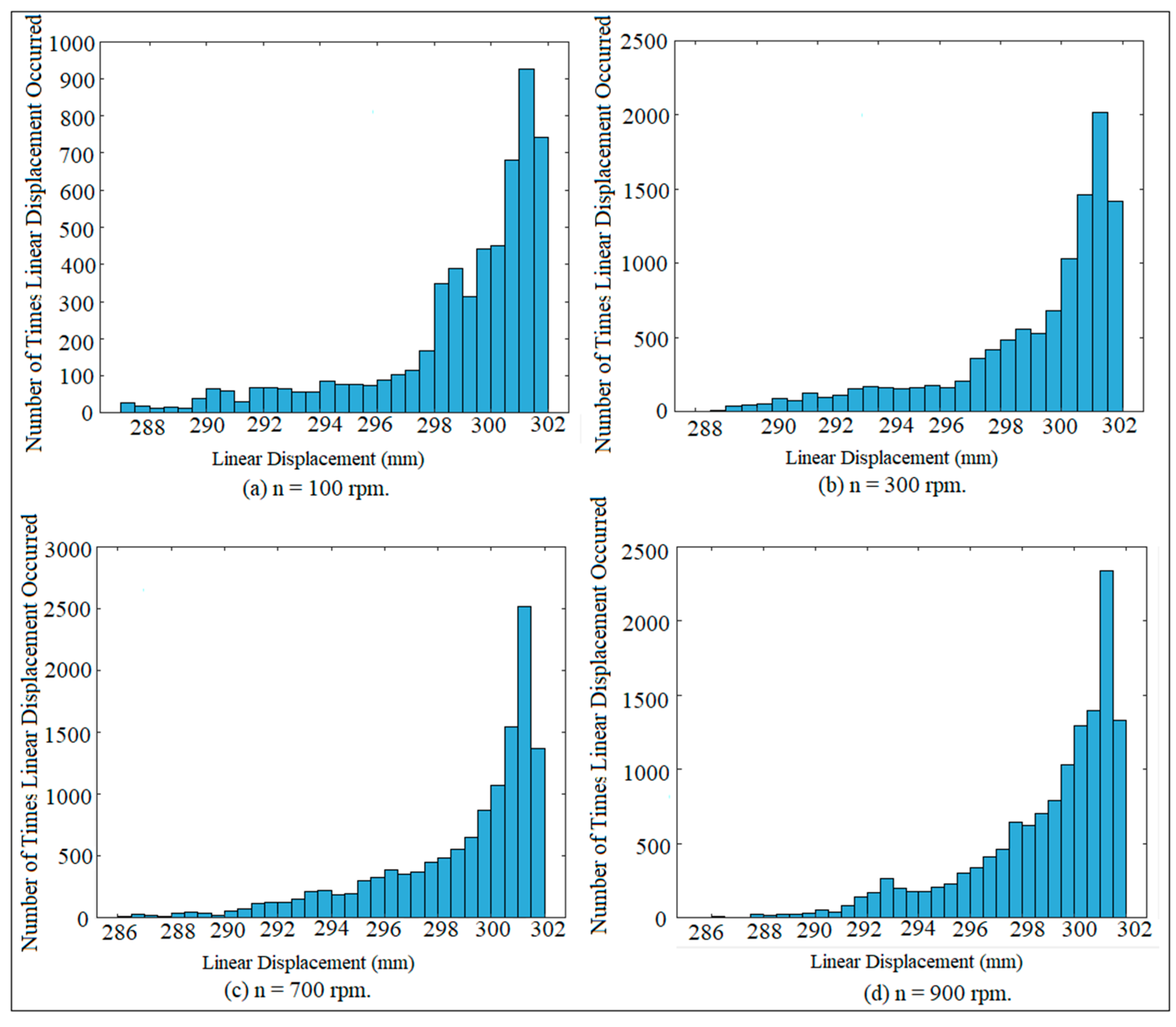

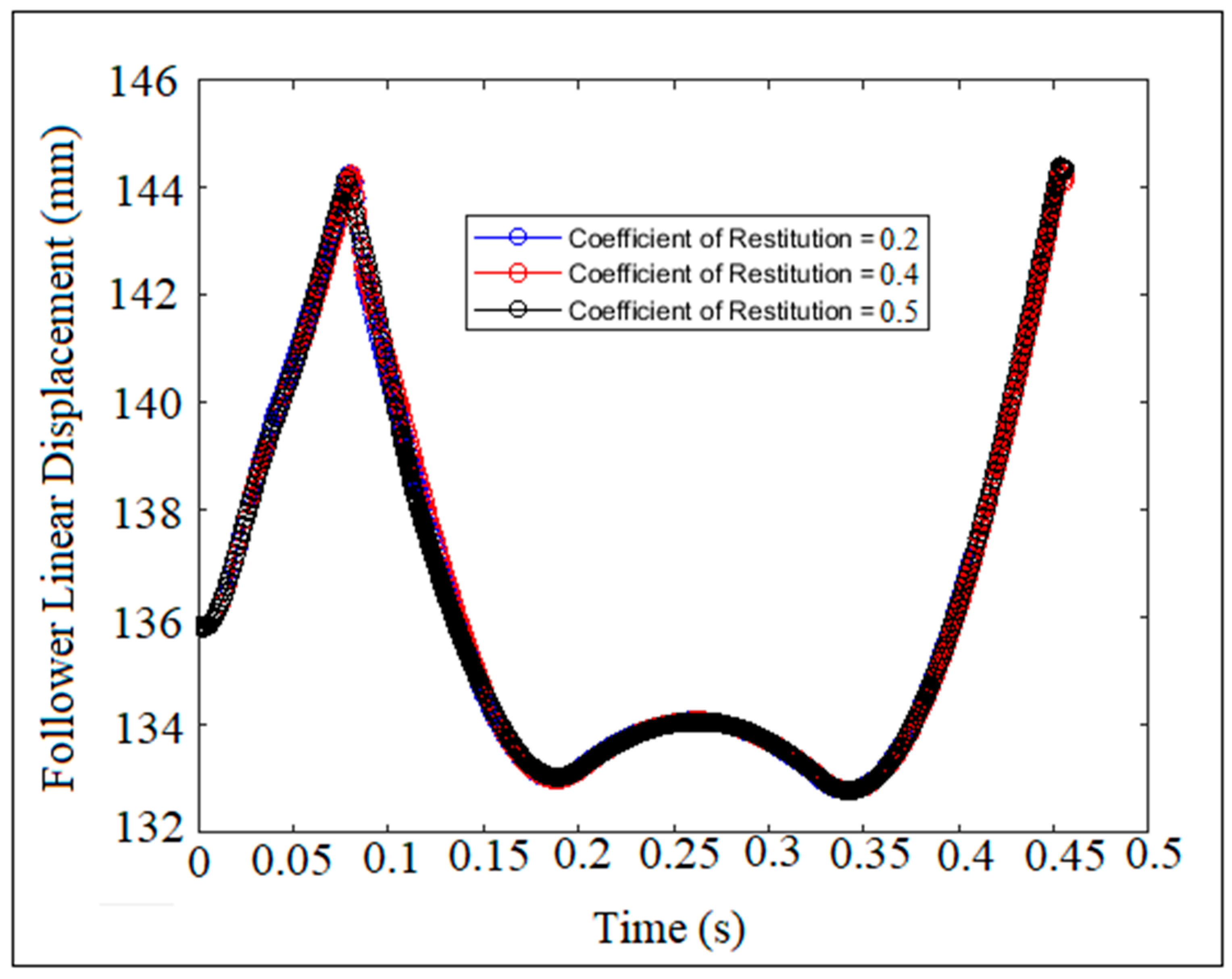






| Cam Speeds | 700 rpm | 900 rpm | 1200 rpm | 1500 rpm | 1800 rpm | 2000 rpm |
|---|---|---|---|---|---|---|
| Guide Distance = 17 mm | 1.701 | 1.386 | 1.392 | 1.912 | 1.337 | 1.432 |
| Guide Distance = 19 mm | 1.710 | 1.661 | 1.513 | 1.308 | 1.368 | 1.652 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousuf, L.S. Symmetry and Asymmetry of Chaotic Motion in a Crank Arm and Connecting Rod Due to the Movement of the Follower. Symmetry 2023, 15, 2148. https://doi.org/10.3390/sym15122148
Yousuf LS. Symmetry and Asymmetry of Chaotic Motion in a Crank Arm and Connecting Rod Due to the Movement of the Follower. Symmetry. 2023; 15(12):2148. https://doi.org/10.3390/sym15122148
Chicago/Turabian StyleYousuf, Louay S. 2023. "Symmetry and Asymmetry of Chaotic Motion in a Crank Arm and Connecting Rod Due to the Movement of the Follower" Symmetry 15, no. 12: 2148. https://doi.org/10.3390/sym15122148
APA StyleYousuf, L. S. (2023). Symmetry and Asymmetry of Chaotic Motion in a Crank Arm and Connecting Rod Due to the Movement of the Follower. Symmetry, 15(12), 2148. https://doi.org/10.3390/sym15122148





