On the Polarization Dependence of Two-Photon Processes including X-ray Scattering
Abstract
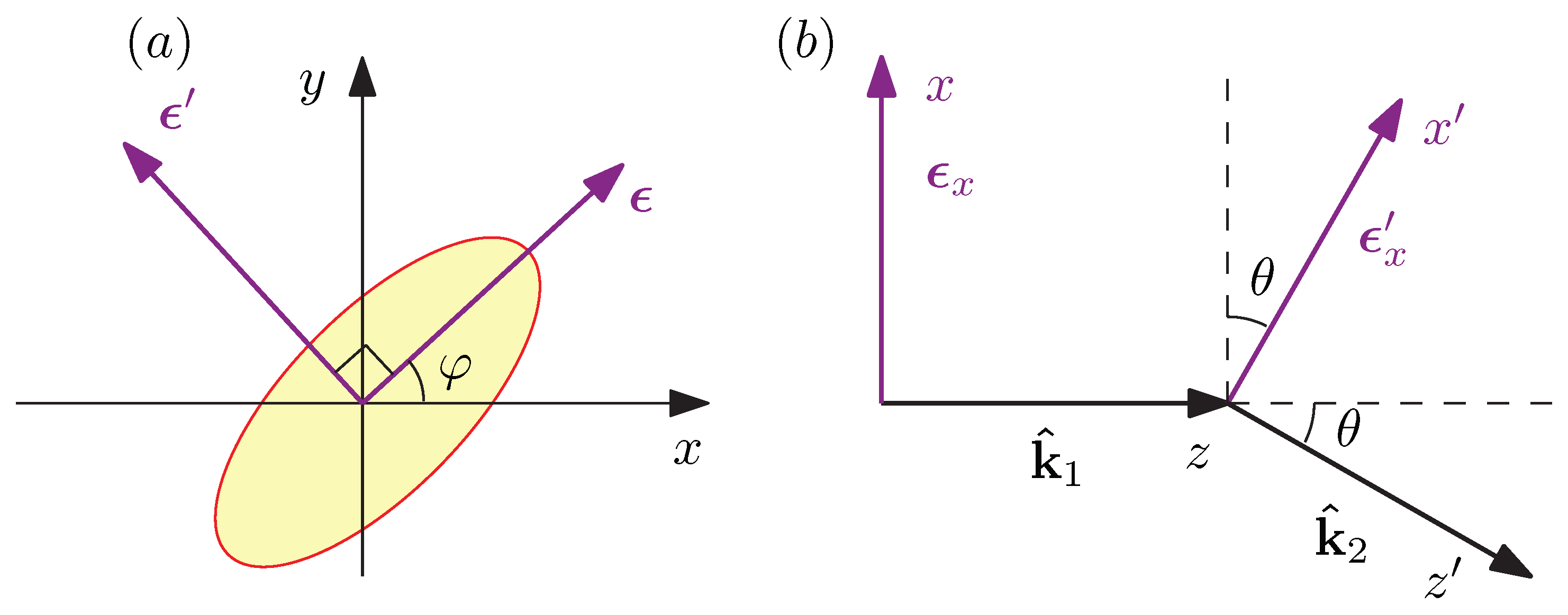
:1. Introduction
2. Tensor Representations of the Photon Density Matrix
3. Polarization Dependence of the Cross Section of X-ray Scattering
3.1. Cross Section in the Vector Form
3.2. Cross Section in Terms of Stokes Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CD | Circular dichroism |
| CP | Circular polarization |
| LP | Linear polarization |
References
- Singh, G.; Upmanyu, A.; Singh, P.; Kainth, H.; Shahi, J.; Singh, R.; Kumar, S. Rayleigh scattering of 66Dy-K X-rays in elements with 22 ≤ Z ≤90. Radiat. Phys. Chem. 2017, 141, 257–263. [Google Scholar] [CrossRef]
- Kane, P.; Kissel, L.; Pratt, R.; Roy, S. Elastic scattering of γ-rays and X-rays by atoms. Phys. Rep. 1986, 140, 75–159. [Google Scholar] [CrossRef]
- Kissel, L. RTAB: The Rayleigh scattering database. Radiat. Phys. Chem. 2000, 59, 185–200. [Google Scholar] [CrossRef]
- Kissel, L.; Zhou, B.; Roy, S.C.; Sen Gupta, S.K.; Pratt, R.H. The validity of form-factor, modified-form-factor and anomalous-scattering-factor approximations in elastic scattering calculations. Acta Crystallogr. Sect. A 1995, 51, 271–288. [Google Scholar] [CrossRef]
- Olukayode, S.; Froese Fischer, C.; Volkov, A. Revisited relativistic Dirac–Hartree–Fock X-ray scattering factors. I. Neutral atoms with Z = 2–118. Acta Crystallogr. Sect. A 2023, 79, 59–79. [Google Scholar] [CrossRef]
- Volotka, A.; Samoilenko, D.; Fritzsche, S.; Serbo, V.G.; Surzhykov, A. Polarization of Photons Scattered by Ultra-Relativistic Ion Beams. Ann. Phys. 2022, 534, 2100252. [Google Scholar] [CrossRef]
- Strnat, S.; Yerokhin, V.A.; Volotka, A.V.; Weber, G.; Fritzsche, S.; Müller, R.A.; Surzhykov, A. Polarization studies on Rayleigh scattering of hard X rays by closed-shell atoms. Phys. Rev. A 2021, 103, 012801. [Google Scholar] [CrossRef]
- Volotka, A.V.; Surzhykov, A.; Fritzsche, S. Rayleigh scattering of linearly polarized light: Scenario of the complete experiment. Phys. Rev. A 2020, 102, 042814. [Google Scholar] [CrossRef]
- Strnat, S.; Sommerfeldt, J.; Yerokhin, V.; Middents, W.; Stöhlker, T.; Surzhykov, A. Circular Polarimetry of Hard X-rays with Rayleigh Scattering. Atoms 2022, 10, 140. [Google Scholar] [CrossRef]
- Tiedtke, K.; Feldhaus, J.; Hahn, U.; Jastrow, U.; Nunez, T.; Tschentscher, T.; Bobashev, S.V.; Sorokin, A.A.; Hastings, J.B.; Möller, S.; et al. Gas detectors for X-ray lasers. J. Appl. Phys. 2008, 103, 094511. [Google Scholar] [CrossRef] [Green Version]
- Chernov, V.E.; Dorofeev, D.L.; Elfimov, S.V.; Zon, B.A.; Gavrilov, G.E.; Naryshkin, Y.G. Pseudopotential calculations of photoionization of atoms in the X-ray photon energy range and FEL beam monitor development. Laser Phys. Lett. 2015, 12, 036002. [Google Scholar] [CrossRef]
- Middents, W.; Weber, G.; Spillmann, U.; Krings, T.; Vockert, M.; Volotka, A.; Surzhykov, A.; Stöhlker, T. Possible Polarization Measurements in Elastic Scattering at the Gamma Factory Utilizing a 2D Sensitive Strip Detector as Dedicated Compton Polarimeter. Ann. Phys. 2022, 534, 2100285. [Google Scholar] [CrossRef]
- Manakov, N.L.; Meremianin, A.V.; Carney, J.P.J.; Pratt, R.H. Circular dichroism effects in atomic X-ray scattering. Phys. Rev. A 2000, 61, 032711. [Google Scholar] [CrossRef]
- Manakov, N.L.; Meremianin, A.V.; Maquet, A.; Carney, J.P.J. Photon-polarization effects and their angular dependence in relativistic two-photon bound–bound transitions. J. Phys. B 2000, 33, 4425–4446. [Google Scholar] [CrossRef]
- Knyazeva, V.A.; Lyashchenko, K.N.; Zhang, M.; Yu, D.; Andreev, O.Y. Investigation of two-photon 2s → 1s decay in one-electron and one-muon ions. Phys. Rev. A 2022, 106, 012809. [Google Scholar] [CrossRef]
- Manakov, N.L. Polarization anomalies caused by dissipation processes in the scattering of light by gases. JETP 1994, 79, 696–706. [Google Scholar]
- Manakov, N.L.; Frolov, M.V.; Borca, B.; Starace, A.F. Multiphoton detachment of a negative ion by an elliptically polarized, monochromatic laser field. J. Phys. B 2003, 36, R49. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. The Classical Theory of Fields; Course of Theoretical Physics; Elsevier Science: Hoboken, NJ, USA, 2000; Volume 2. [Google Scholar]
- Berestetskii, V.; Lifshitz, E.; Pitaevskii, L. Quantum Electrodynamics; Course of Theoretical Physics; Pergamon Press: Oxford, UK, 1982; Volume 4. [Google Scholar]
- Carney, J.P.J.; Pratt, R.H.; Manakov, N.L.; Meremianin, A.V. Dependence of photon-atom scattering on energy resolution and target angular momentum. Phys. Rev. A 2000, 61, 042704. [Google Scholar] [CrossRef]
- Roy, S.C.; Sarkar, B.; Kissel, L.D.; Pratt, R.H. Polarization effects in elastic photon-atom scattering. Phys. Rev. A 1986, 34, 1178–1187. [Google Scholar] [CrossRef]
- Istomin, A.Y.; Pronin, E.A.; Manakov, N.L.; Marmo, S.I.; Starace, A.F. Elliptic and Circular Dichroism Effects in Two-Photon Double Ionization of Atoms. Phys. Rev. Lett 2006, 97, 123002. [Google Scholar] [CrossRef]
- Nabekawa, Y.; Hasegawa, H.; Takahashi, E.J.; Midorikawa, K. Production of Doubly Charged Helium Ions by Two-Photon Absorption of an Intense Sub-10-fs Soft X-ray Pulse at 42 eV Photon Energy. Phys. Rev. Lett 2005, 94, 043001. [Google Scholar] [CrossRef] [Green Version]
- Orfanos, I.; Skantzakis, E.; Nayak, A.; Dumergue, M.; Kühn, S.; Sansone, G.; Kling, M.F.; Schröder, H.; Bergues, B.; Csontos, J.; et al. Two-XUV-photon double ionization of neon. Phys. Rev. A 2022, 106, 043117. [Google Scholar] [CrossRef]
- Jiang, W.C.; Shan, J.Y.; Gong, Q.; Peng, L.Y. Virtual Sequential Picture for Nonsequential Two-Photon Double Ionization of Helium. Phys. Rev. Lett 2015, 115, 153002. [Google Scholar] [CrossRef]
- Nikolopoulos, L.A.A.; Lambropoulos, P. Helium double ionization signals under soft-x-ray coherent radiation. J. Phys. B 2006, 39, 883. [Google Scholar] [CrossRef]
- Kheifets, A.S.; Ivanov, I.A. Convergent close-coupling calculations of two-photon double ionization of helium. J. Phys. B 2006, 39, 1731. [Google Scholar] [CrossRef] [Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manakov, N.L.; Meremianin, A.V. On the Polarization Dependence of Two-Photon Processes including X-ray Scattering. Symmetry 2023, 15, 422. https://doi.org/10.3390/sym15020422
Manakov NL, Meremianin AV. On the Polarization Dependence of Two-Photon Processes including X-ray Scattering. Symmetry. 2023; 15(2):422. https://doi.org/10.3390/sym15020422
Chicago/Turabian StyleManakov, Nikolai L., and Alexei V. Meremianin. 2023. "On the Polarization Dependence of Two-Photon Processes including X-ray Scattering" Symmetry 15, no. 2: 422. https://doi.org/10.3390/sym15020422




