The Hyperbolic Ptolemy’s Theorem in the Poincaré Ball Model of Analytic Hyperbolic Geometry
Abstract
:1. Introduction
- (1)
- The vector addition admits scalar multiplication, giving rise to vector spaces which, in turn, form the algebraic setting for analytic Euclidean geometry. In full analogy,
- (2)
- The Einstein addition, which pertains to relativistically admissible velocities, also permits scalar multiplication, giving rise to Einstein gyrovector spaces, which, in turn, form the algebraic setting for the Klein ball model of analytic hyperbolic geometry [1,2,3,4,5]. Accordingly, the Klein model of hyperbolic geometry is also known as the relativistic model of hyperbolic geometry [6,7]. Furthermore, in full analogy,
- (3)
- (1)
- In [6], we presented the well-known proof of Ptolemy’s theorem in terms of the standard trigonometry of analytic Euclidean plane geometry. In particular, the associated law of cosines was employed.
- (2)
- In full analogy, in [6], we discovered the hyperbolic Ptolemy’s theorem in the Klein (relativistic) model of analytic hyperbolic plane geometry. The proof of the resulting hyperbolic Ptolemy’s theorem is obtained by means of the gyrotrigonometry that the Klein model of analytic hyperbolic geometry admits. In particular, the associated law of gyrocosines was employed.
- (3)
- In full analogy, in this article, we discover the hyperbolic Ptolemy’s theorem in the Poincaré ball model of analytic hyperbolic plane geometry. The proof of the resulting hyperbolic Ptolemy’s theorem is obtained by means of the gyrotrigonometry that the Poincaré model of analytic hyperbolic geometry admits. In particular, the associated law of gyrocosines is employed.
2. Möbius Addition and Scalar Multiplication
3. Gyrotrigonometry in Möbius Gyrovector Planes and Its Law of Gyrocosines
4. Ptolemy’s theorem in the Poincaré Ball Model of Hyperbolic Geometry
5. Gyrodiametric Gyrotriangles
Funding
Data Availability Statement
Conflicts of Interest
References
- Ungar, A.A. A Gyrovector Space Approach to Hyperbolic Geometry; Morgan & Claypool Pub.: San Rafael, CA, USA, 2009. [Google Scholar]
- Ungar, A.A. Analytic Hyperbolic Geometry: Mathematical Foundations And Applications; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2005. [Google Scholar]
- Ungar, A.A. Analytic Hyperbolic Geometry and Albert Einstein’s Special Theory of Relativity, 2nd ed.; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2022. [Google Scholar]
- Ungar, A.A. Gyrovector spaces and their differential geometry. Nonlinear Funct. Anal. Appl. 2005, 10, 791–834. [Google Scholar]
- Ungar, A.A. Hyperbolic Triangle Centers: The Special Relativistic Approach; Springer: New York, NY, USA, 2010. [Google Scholar]
- Ungar, A.A. Ptolemy’s theorem in the relativistic model of analytic hyperbolic geometry. Symmetry 2023, 15, 649. [Google Scholar] [CrossRef]
- Ungar, A.A. Hyperbolic trigonometry in the Einstein relativistic velocity model of hyperbolic geometry. Comput. Math. Appl. 2000, 40, 313–332. [Google Scholar]
- Ungar, A.A. From Möbius to gyrogroups. Amer. Math. Mon. 2008, 115, 138–144. [Google Scholar] [CrossRef]
- Suksumran, T. The algebra of gyrogroups: Cayley’s theorem, Lagrange’s theorem and isomorphism theorems. In Essays in Mathematics and Its Applications: In Honor of Vladimir Arnold; Rassias, T.M., Pardalos, P.M., Eds.; Springer: New York, NY, USA, 2016; pp. 369–437. [Google Scholar]
- Ferreira, M. Factorizations of Möbius gyrogroups. Adv. Appl. Clifford Algebr. 2009, 19, 303–323. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, M.; Ren, G. Möbius gyrogroups: A Clifford algebra approach. J. Algebra 2011, 328, 230–253. [Google Scholar]
- Ferreira, M. Gyrogroups in projective hyperbolic Clifford analysis. In Hypercomplex Analysis and Applications; Trends Math.; Birkhäuser/Springer: Basel, Switzerland, 2011; pp. 61–80. [Google Scholar]
- Ferreira, M. Harmonic analysis on the Einstein gyrogroup. J. Geom. Symmetry Phys. 2014, 35, 21–60. [Google Scholar]
- Ferreira, M. Harmonic Analysis on the Möbius Gyrogroup. J. Fourier Anal. Appl. 2015, 21, 281–317. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, M. Harmonic analysis on the proper velocity gyrogroup. Banach J. Math. Anal. 2017, 11, 21–49. [Google Scholar]
- Ferreira, M.; Suksumran, T. Orthogonal gyrodecompositions of real inner product gyrogroups. Symmetry 2020, 12, 941. [Google Scholar]
- Ferreira, M. Gyroharmonic analysis on relativistic gyrogroups. Math. Interdiscip. Res. 2016, 1, 69–109. [Google Scholar]
- Honma, T.; Hatori, O. A gyrogeometric mean in the einstein gyrogroup. Symmetry 2020, 12, 1333. [Google Scholar]
- Wattanapan, J.; Atiponrat, W.; Suksumran, T. Embedding of strongly topological gyrogroups in path-connected and locally path-connected gyrogroups. Symmetry 2020, 12, 1817. [Google Scholar]
- Suksumran, T. On metric structures of normed gyrogroups. In Mathematical Analysis and Applications; Springer: Cham, Switzerland, 2019; Volume 154, pp. 529–542. [Google Scholar]
- Suksumran, T. Two theorems on direct products of gyrogroups. AIMS Math. 2023, 8, 6278–6287. [Google Scholar]
- Suksumran, T. On Schreier graphs of gyrogroup actions. J. Pure Appl. Algebra 2022, 226, 107134. [Google Scholar]
- Mahdavi, S.; Ashrafi, A.R.; Salahshour, M.A. Normal subgyrogroups of certain gyrogroups. Quasigroups Relat. Syst. 2022, 30, 115–122. [Google Scholar]
- Li, P.; Shen, R. On topological gyrogroups. Filomat 2023, 37, 5087–5093. [Google Scholar]
- Zhang, J.; Liang, Q. Extensions of some topological properties in topological gyrogroups. Topol. Appl. 2022, 322, 108328. [Google Scholar]
- Lal, R.; Kakkar, V. Gyrogroups associated with groups. Comm. Algebra 2022, 50, 524–537. [Google Scholar]
- Bao, M.; Lin, F. Feathered gyrogroups and gyrogroups with countable pseudocharacter. Filomat 2019, 33, 5113–5124. [Google Scholar]
- Bao, M.; Lin, F. Submetrizability of strongly topological gyrogroups. Houst. J. Math. 2021, 47, 427–443. [Google Scholar]
- Kim, S. Ordered gyrovector spaces. Symmetry 2020, 12, 1041. [Google Scholar] [CrossRef]
- Kim, S. Distributivity on the gyrovector spaces. Kyungpook Math. J. 2015, 55, 13–20. [Google Scholar] [CrossRef] [Green Version]
- Kim, S. Gyrovector spaces on the open convex cone of positive definite matrices. Math. Interdisc. Res. 2016, 1, 173–185. [Google Scholar]
- Watanabe, K. A confirmation by hand calculation that the Möbius ball is a gyrovector space. Nihonkai Math. J. 2016, 27, 99–115. [Google Scholar]
- Watanabe, K. Orthogonal gyroexpansion in Möbius gyrovector spaces. J. Funct. Spaces 2017, 13, 1518254. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, K. Continuous quasi gyrolinear functionals on möbius gyrovector spaces. J. Funct. Spaces 2020, 2020, 1950727. [Google Scholar] [CrossRef]
- Watanabe, K. On quasi gyrolinear maps between möbius gyrovector spaces induced from finite matrices. Symmetry 2021, 13, 76. [Google Scholar] [CrossRef]
- Abe, T.; Watanabe, K. Finitely generated gyrovector subspaces and orthogonal gyrodecomposition in the Möbius gyrovector space. J. Math. Anal. Appl. 2017, 449, 77–90. [Google Scholar] [CrossRef]
- Abe, T.; Hatori, O. Generalized gyrovector spaces and a Mazur-Ulam theorem. Publ. Math. Debr. 2015, 87, 393–413. [Google Scholar] [CrossRef]
- Hatori, O. Extension of isometries in generalized gyrovector spaces of the positive cones. In Problems and Recent Methods in Operator Theory; American Mathematical Society: Providence, RI, USA, 2017; Volume 687, pp. 145–156. [Google Scholar]
- Hatori, O. Examples and applications of generalized gyrovector spaces. Results Math. 2017, 71, 295–317. [Google Scholar]
- Demirel, O. The first sharp gyrotriangle inequality in Möbius gyrovector space (D,⊕,⊗). Forum Geom. 2017, 17, 439–447. [Google Scholar]
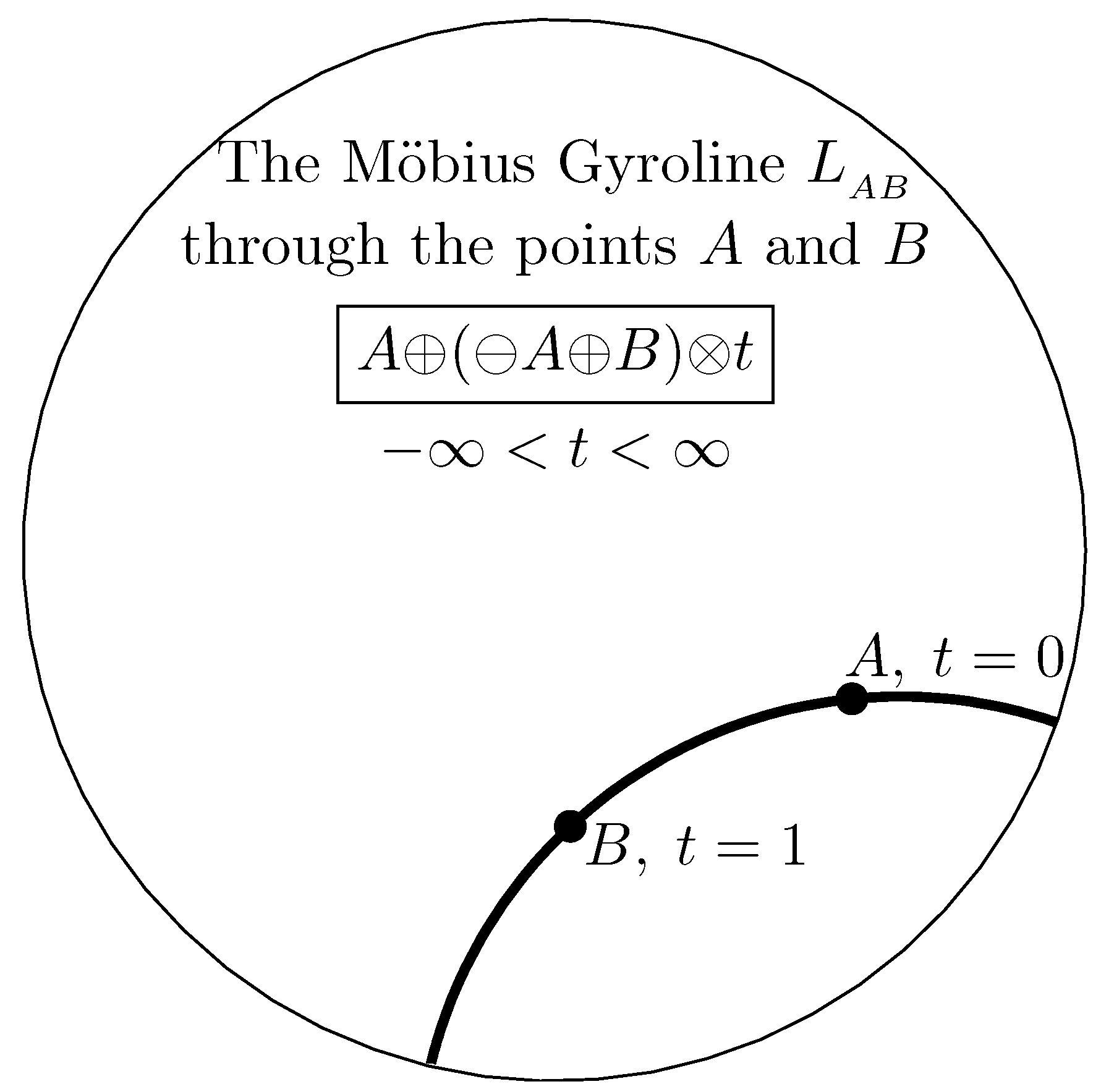
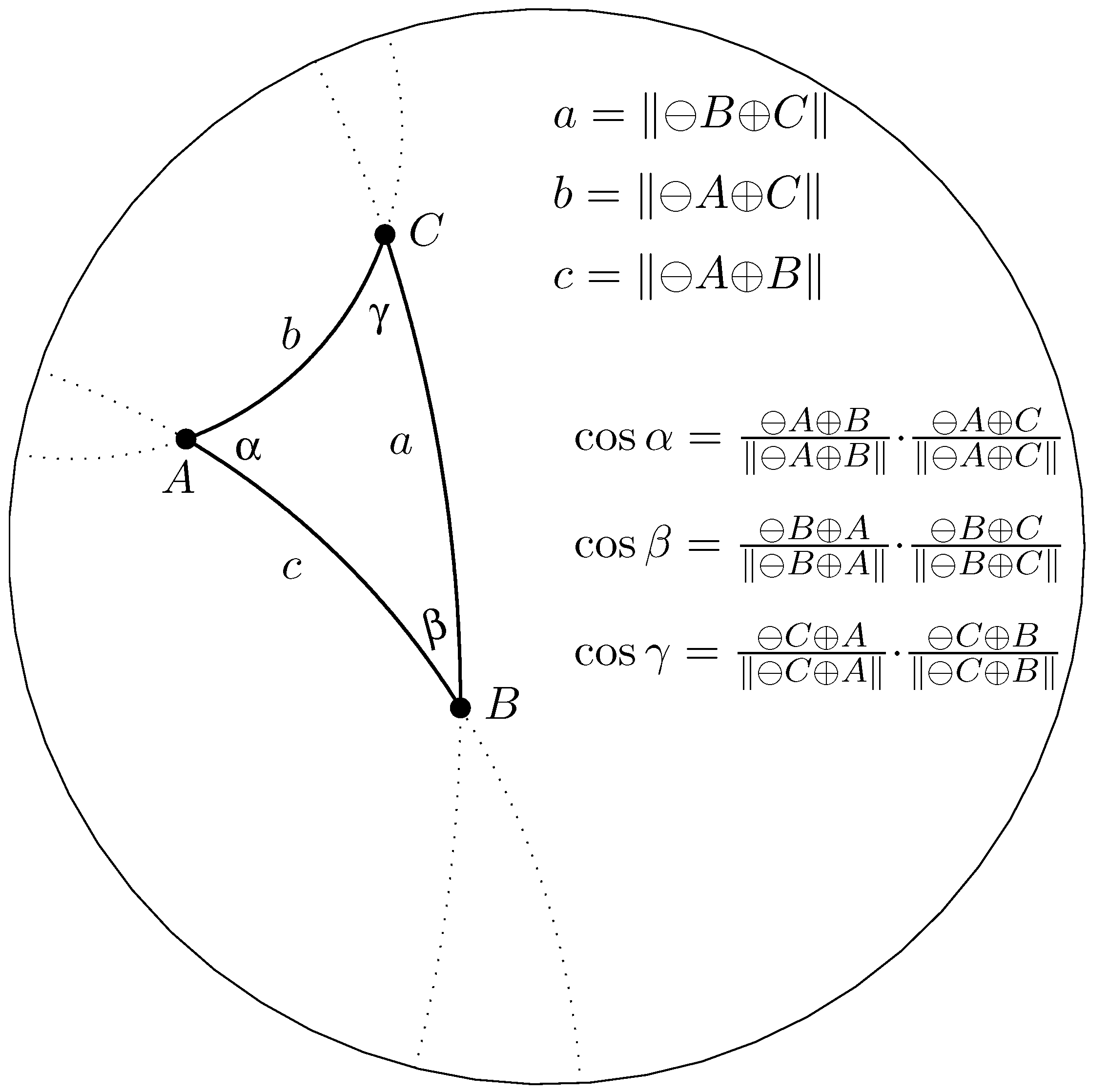
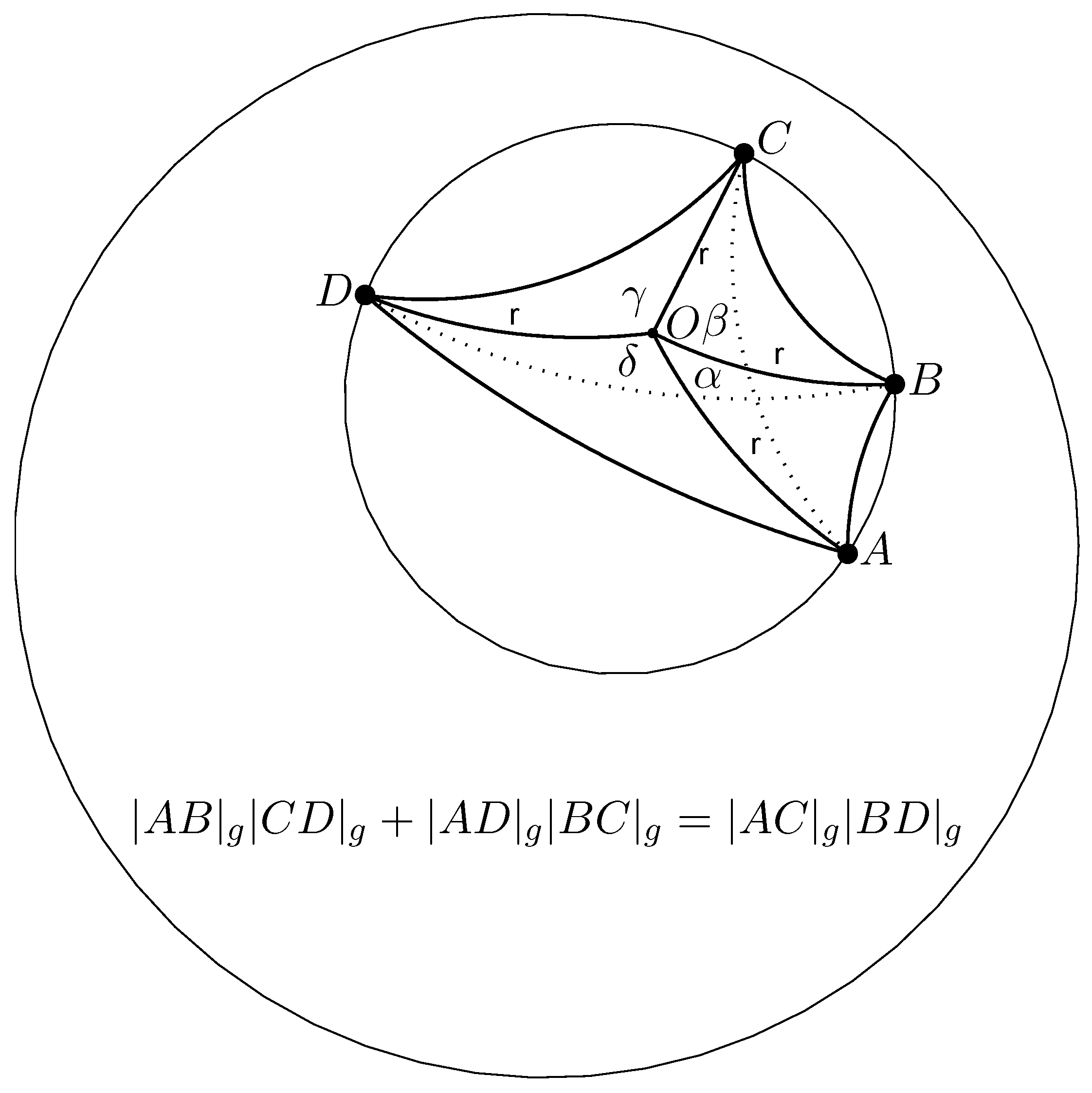

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ungar, A.A. The Hyperbolic Ptolemy’s Theorem in the Poincaré Ball Model of Analytic Hyperbolic Geometry. Symmetry 2023, 15, 1487. https://doi.org/10.3390/sym15081487
Ungar AA. The Hyperbolic Ptolemy’s Theorem in the Poincaré Ball Model of Analytic Hyperbolic Geometry. Symmetry. 2023; 15(8):1487. https://doi.org/10.3390/sym15081487
Chicago/Turabian StyleUngar, Abraham A. 2023. "The Hyperbolic Ptolemy’s Theorem in the Poincaré Ball Model of Analytic Hyperbolic Geometry" Symmetry 15, no. 8: 1487. https://doi.org/10.3390/sym15081487
APA StyleUngar, A. A. (2023). The Hyperbolic Ptolemy’s Theorem in the Poincaré Ball Model of Analytic Hyperbolic Geometry. Symmetry, 15(8), 1487. https://doi.org/10.3390/sym15081487





