Dynamics in a Competitive Nicholson’s Blowflies Model with Continuous Time Delays
Abstract
:1. Introduction
- (1)
- If , then ;
- (2)
- If , then .
2. Main Results
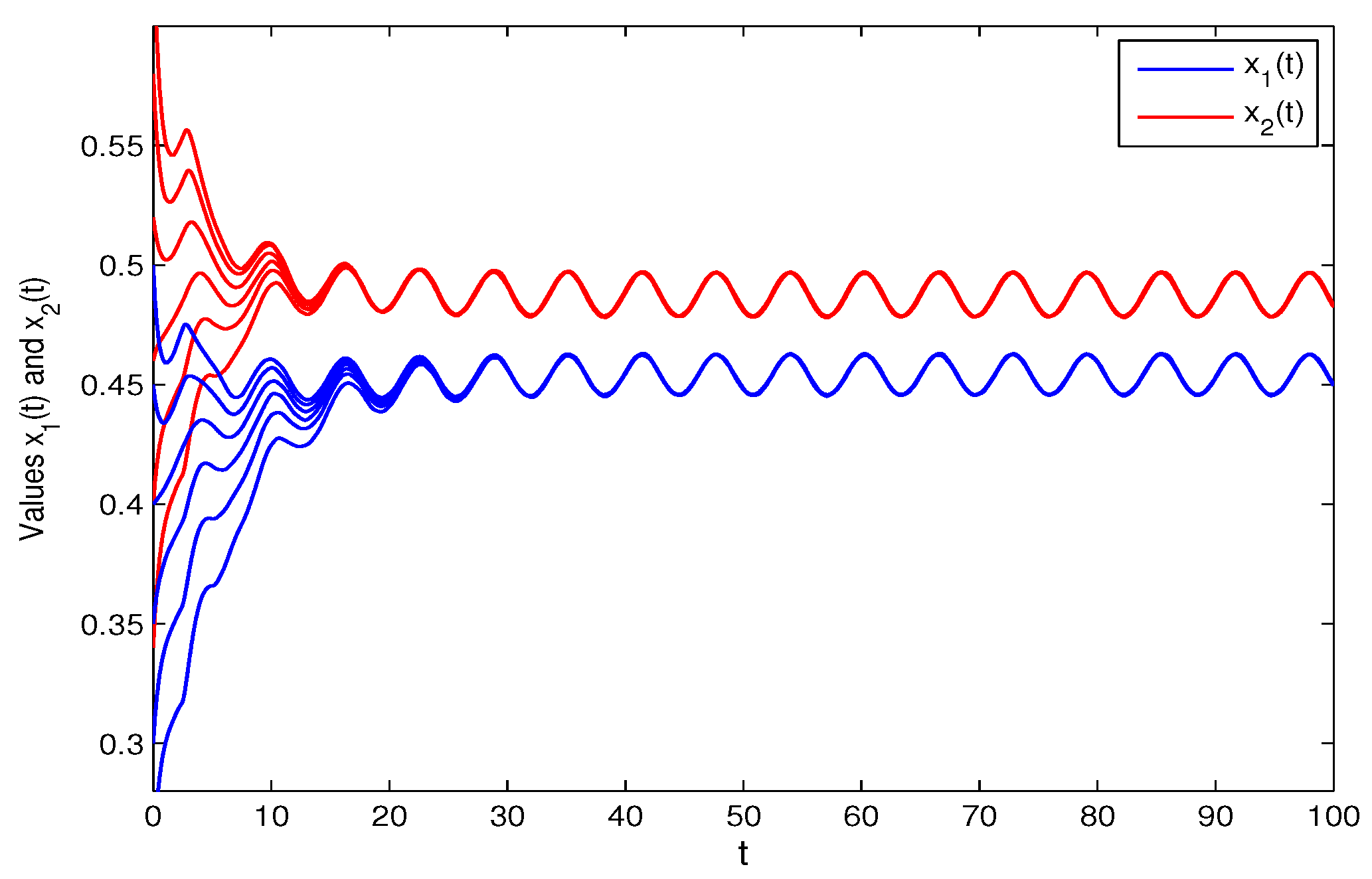
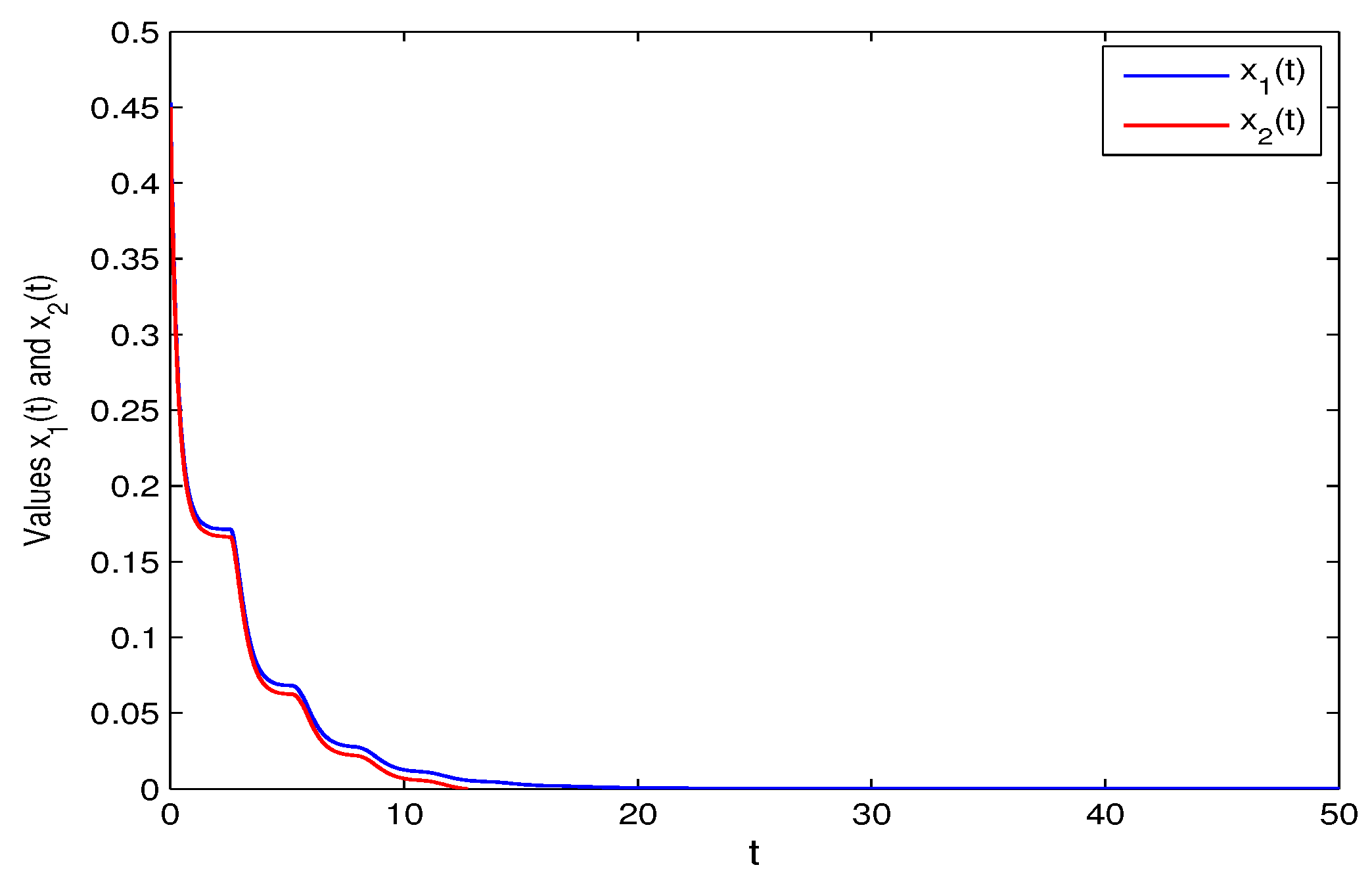
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gurney, W.S.C.; Blythe, S.P.; Nisbet, R.M. Nicholson’s blowflies revisited. Nature 1980, 287, 17–21. [Google Scholar] [CrossRef]
- Saker, S.H.; Agarwal, S. Oscillation and global attractivity in a periodic Nicholson’s blowflies model. Math. Comput. Model. 2002, 35, 719–731. [Google Scholar] [CrossRef]
- Berezansky, L.; Braverman, E.; Idels, L. Nicholson’s blowflies differential equations revisited: Main results and open problems. Appl. Math. Model. 2010, 34, 1405–1417. [Google Scholar] [CrossRef]
- Berezansky, L.; Idels, L.; Troib, L. Global dynamics of Nicholson-type delay systems with applications. Nonlinear Anal. Real World Appl. 2011, 12, 436–445. [Google Scholar] [CrossRef]
- Zhou, Q. The positive periodic solution for Nicholson-type delay system with linear harvesting terms. Appl. Math. Model. 2013, 37, 5581–5590. [Google Scholar] [CrossRef]
- Jiang, J. Dynamic Properties of Competitive Nicholson’s Blowflies Model. Master’s Thesis, Hunan University, Changsha, China, 2011. [Google Scholar]
- Muhammadhaji, A.; Halik, A. Dynamics in a nonautonomous Nicholson-type delay system. J. Math. 2021, 2021, 6696453. [Google Scholar] [CrossRef]
- Ezekiel, I.D.; Iyase, S.A.; Anake, T.A. Stability analysis of a nontrivial solution for delayed Nicholson blowflies’ model with linear harvesting function. J. Phys. Conf. Ser. 2022, 2199, 012034. [Google Scholar] [CrossRef]
- Wu, R.; Xu, Z. Spreading dynamics of a discrete Nicholson’s blowflies equation with distributed delay. Proc. R. Soc. Edinburgh Sect. A Math. 2023, 2023, 1–23. [Google Scholar] [CrossRef]
- Mu, X.; Jiang, D.; Hayat, T.; Alsaedi, A.; Ahmad, B. Dynamical behavior of a stochastic Nicholson’s blowflies model with distributed delay and degenerate diffusion. Nonlinear Dyn. 2021, 103, 2081–2096. [Google Scholar] [CrossRef]
- Long, X.; Gong, S. New results on stability of Nicholson’s blowflies equation with multiple pairs of time-varying delays. Appl. Math. Lett. 2020, 100, 106027. [Google Scholar] [CrossRef]
- Li, D.; Wu, X.; Yan, S. Periodic traveling wave solutions of the Nicholson’s blowflies model with delay and advection. Electron. Res. Arch. 2023, 31, 2568–2579. [Google Scholar] [CrossRef]
- Ding, X. Global asymptotic stability of a scalar delay Nicholson’s blowflies equation in periodic environment. Electron. J. Qual. Theory Differ. Equ. 2022, 2022, 14. [Google Scholar] [CrossRef]
- Fan, W.; Zhang, J. Novel results on persistence and attractivity of delayed Nicholson’s blowflies system with patch structure. Taiwan. J. Math. 2023, 27, 141–167. [Google Scholar] [CrossRef]
- Belmabrouk, N.; Damak, M.; Miraoui, M. Stochastic Nicholson’s blowflies model with delays. Int. J. Biomath. 2023, 16, 2250065. [Google Scholar] [CrossRef]
- Muhammadhaji, A.; Halik, A. Dynamic analysis of a model for Spruce Budworm populations with delay. J. Funct. Spaces 2021, 2021, 1091716. [Google Scholar] [CrossRef]
- Moujahid, A.; Vadillo, F. Impact of delay on stochastic predator-prey models. Symmetry 2023, 15, 1244. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Muhammadhaji, A. Dynamics in a Competitive Nicholson’s Blowflies Model with Continuous Time Delays. Symmetry 2023, 15, 1495. https://doi.org/10.3390/sym15081495
Wu Z, Muhammadhaji A. Dynamics in a Competitive Nicholson’s Blowflies Model with Continuous Time Delays. Symmetry. 2023; 15(8):1495. https://doi.org/10.3390/sym15081495
Chicago/Turabian StyleWu, Zhiqiao, and Ahmadjan Muhammadhaji. 2023. "Dynamics in a Competitive Nicholson’s Blowflies Model with Continuous Time Delays" Symmetry 15, no. 8: 1495. https://doi.org/10.3390/sym15081495




