Asymmetric Right-Skewed Size-Biased Bilal Distribution with Mathematical Properties, Reliability Analysis, Inference and Applications
Abstract
1. Introduction
2. Structure of the SBBD
3. Special Cases of the SBBD
3.1. Moments and Related Measure
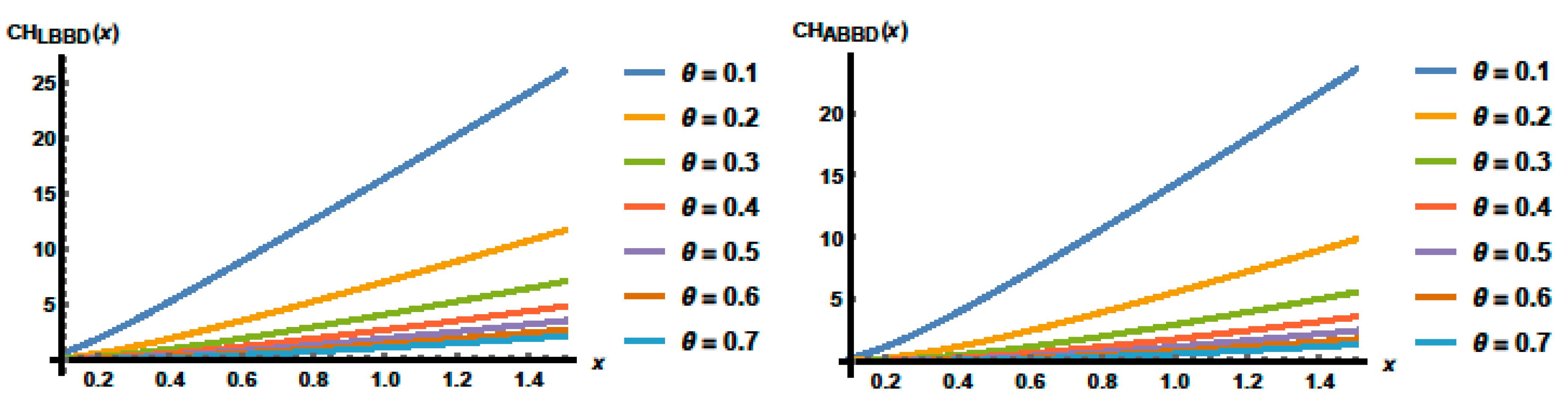
3.2. Reliability Functions
3.3. Parameters Estimation
3.4. Fisher’s Information and Entropies
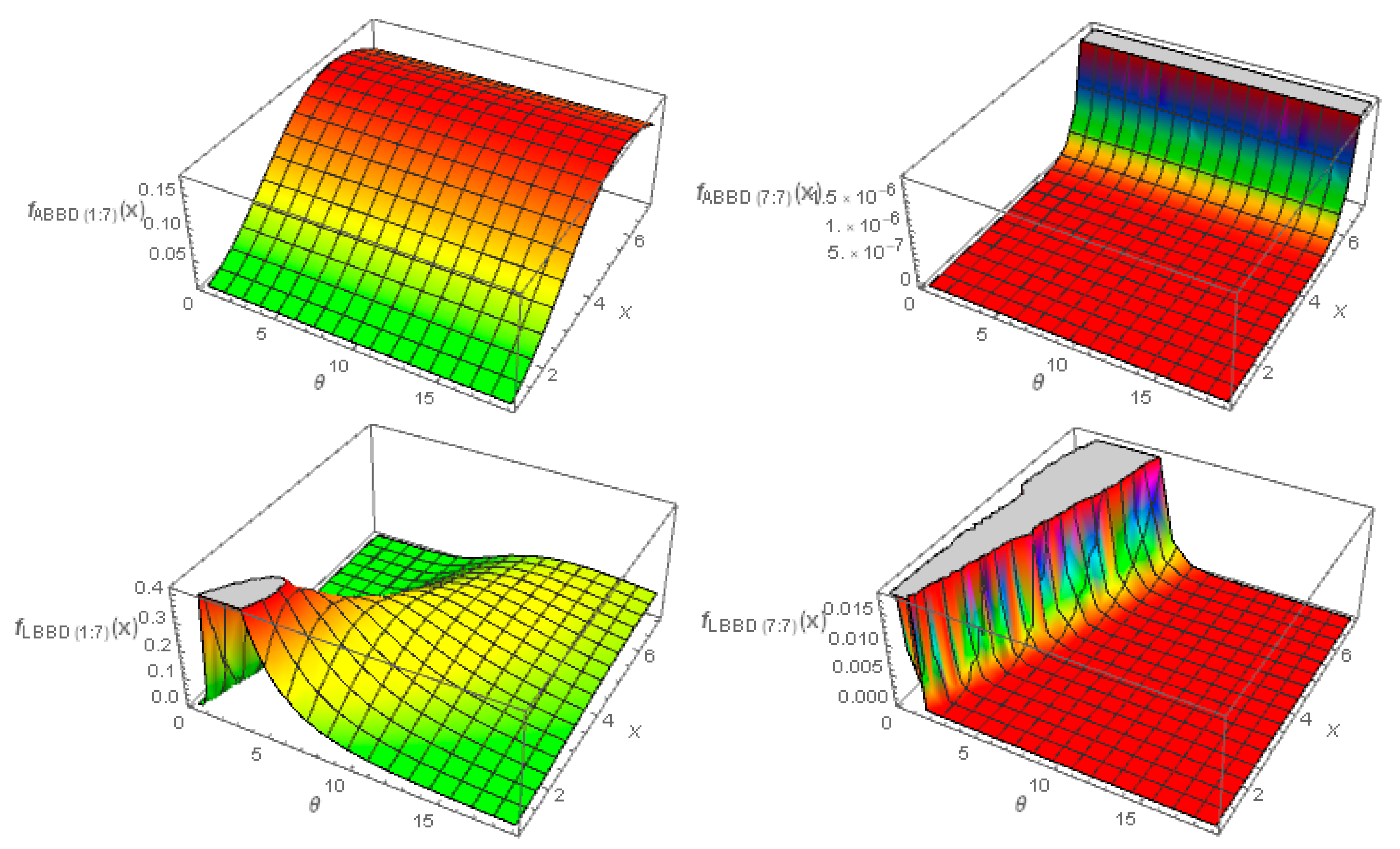
3.5. Order Statistics
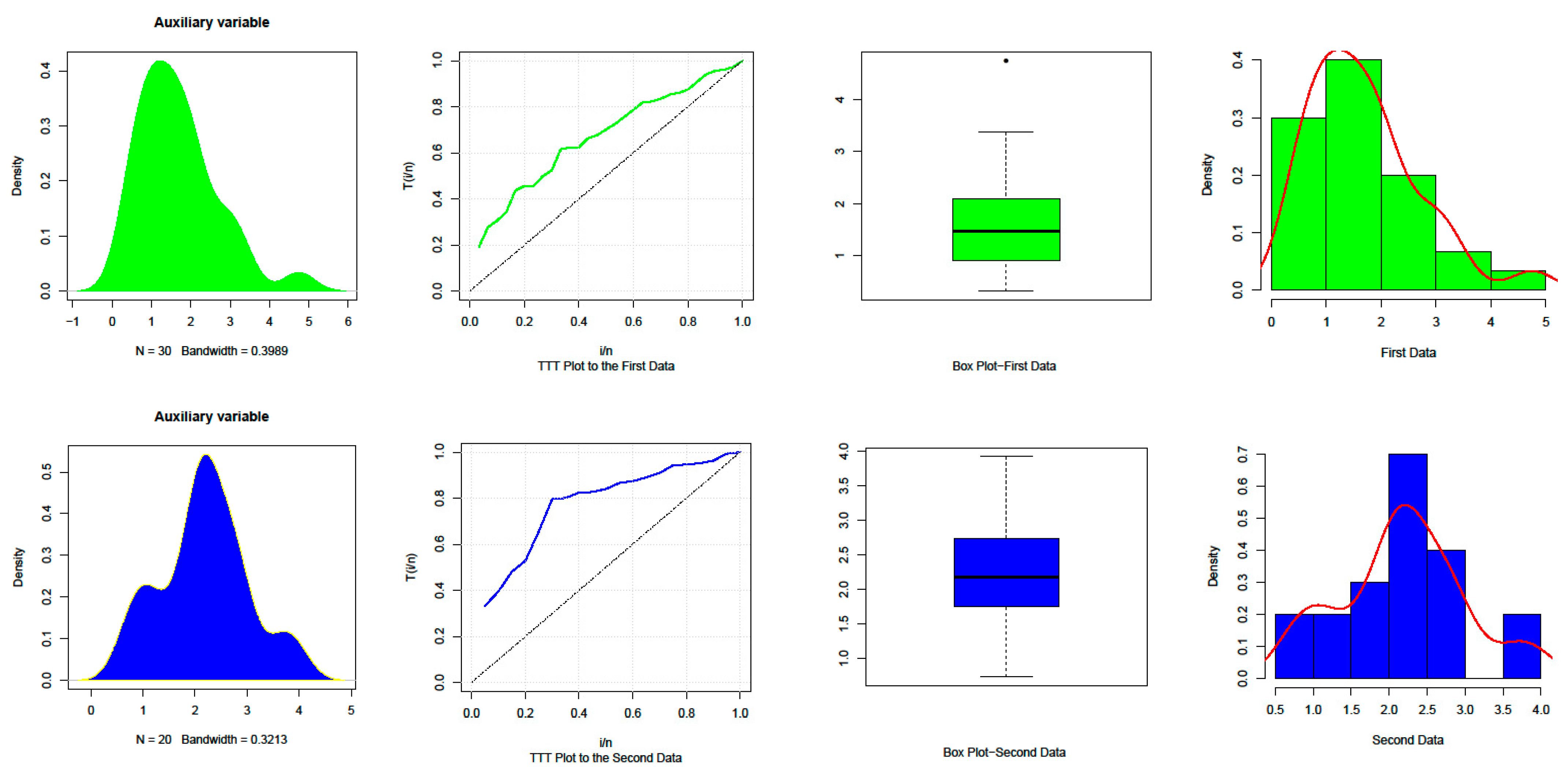
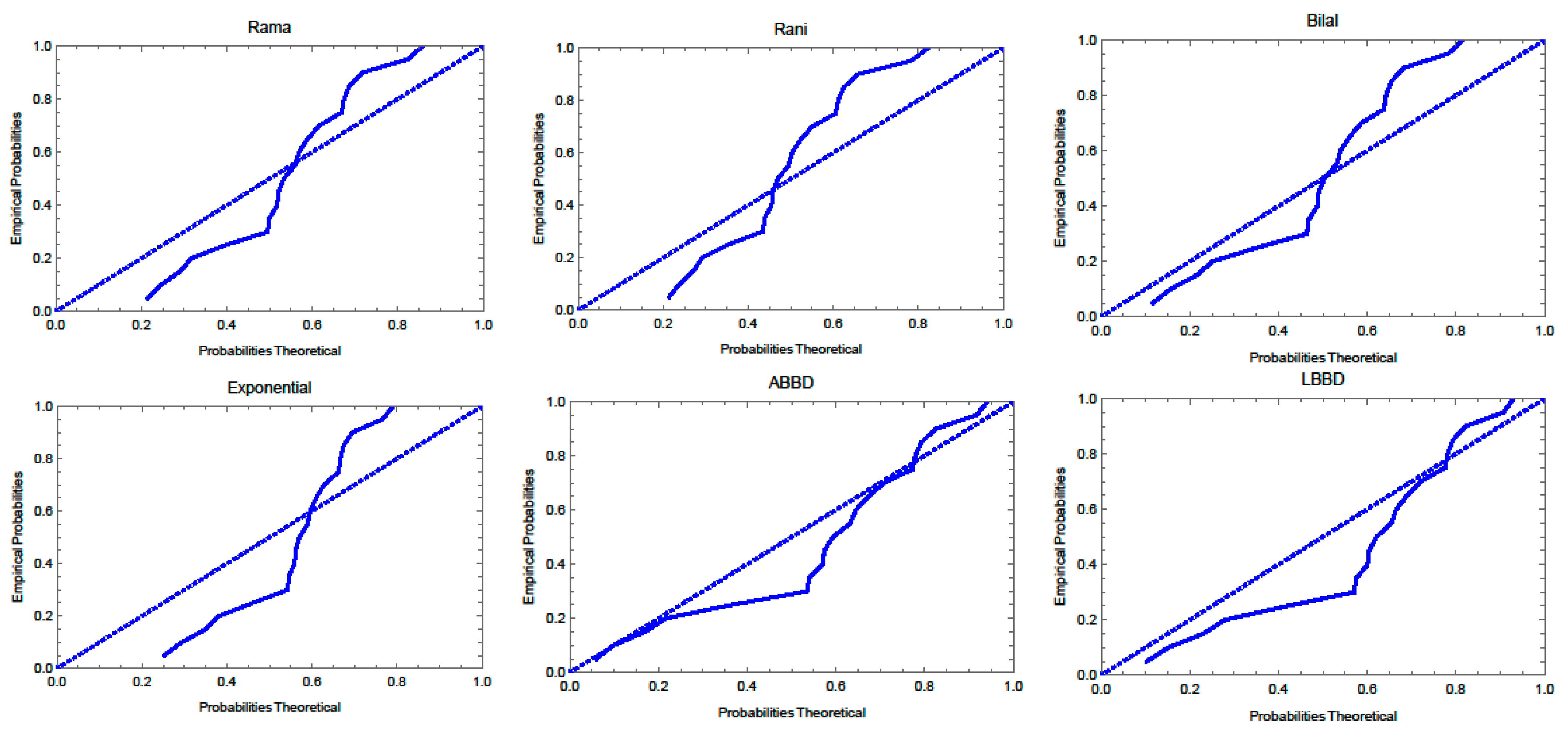
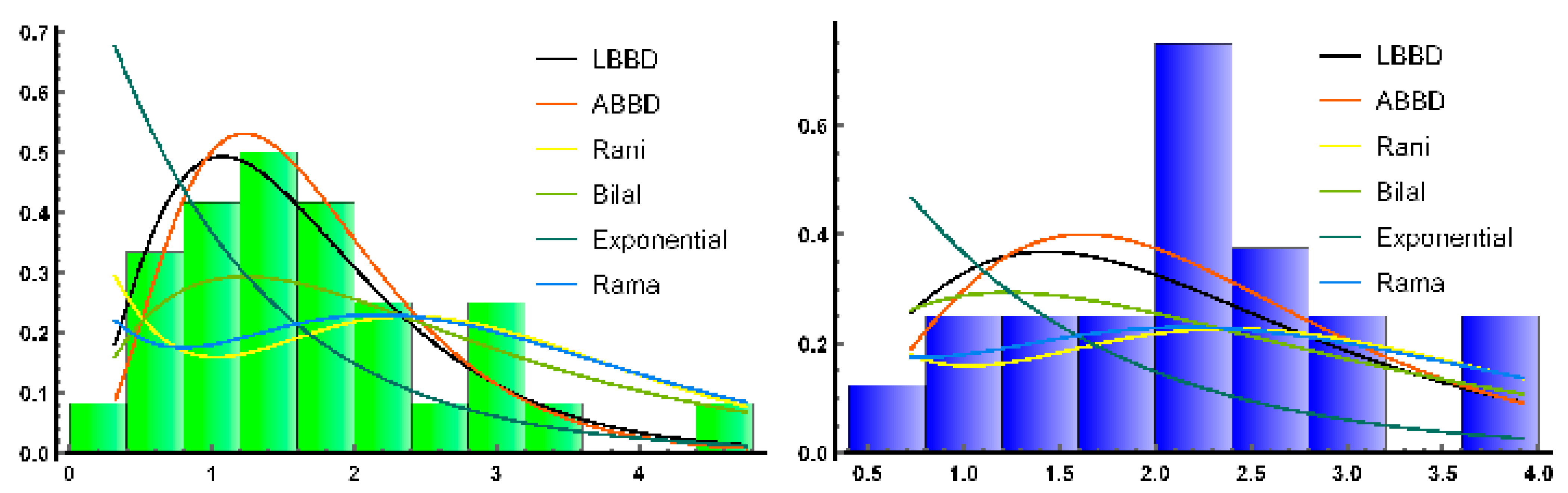
4. Applications to Real Data
- o
- o
- o
- o
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fisher, R.A. The effect of methods of ascertainment upon the estimation of frequencies. Ann. Eugen. 1934, 6, 13–25. [Google Scholar] [CrossRef]
- Cox, D.R. Renewal Theory; Metrheun’s Monograph; Barnes and Noble, Inc.: New York, NY, USA, 1962. [Google Scholar]
- Rao, C.R. On discrete distributions arising out of methods of ascertainment. Sankhya Indian J. Stat. Ser. A 1965, 27, 311–324. [Google Scholar]
- Patil, G.P.; Rao, C.R. Weighted distributions and size-biased sampling with applications to wildlife populations and human families. Biometrics 1978, 34, 179–189. [Google Scholar] [CrossRef]
- Gupta, R.C.; Keating, J.P. Relations for reliability measures under length biased sampling. Scand. J. Stat. 1986, 13, 49–56. [Google Scholar]
- Arnold, B.C.; Nagaraja, H.N. On some properties of bivariate weighted distributions. Commun. Stat.-Theory Methods 1991, 20, 1853–1860. [Google Scholar] [CrossRef]
- Modi, K.; Gill, V. Length-biased weighted Maxwell distribution. Pak. J. Stat. Oper. Res. 2015, 2015, 465–472. [Google Scholar] [CrossRef][Green Version]
- Mobarak, M.A.; Nofal, Z.; Mahdy, M. On size-biased weighted transmuted Weibull distribution. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2017, 7, 317–325. [Google Scholar] [CrossRef]
- Sharma, V.K.; Dey, S.; Singh, S.K.; Manzoor, U. On length and area-biased Maxwell distributions. Commun. Stat.-Simul. Comput. 2018, 47, 1506–1528. [Google Scholar] [CrossRef]
- Al-Omari, A.I.; Al-Nasser, A.D.; Ciavolino, E. A size-biased Ishita distribution and application to real data. Qual. Quant. 2019, 53, 493–512. [Google Scholar] [CrossRef]
- Hassan, A.S.; Almetwally, E.M.; Khaleel, M.A.; Nagy, H.F. Weighted power Lomax distribution and its length biased version: Properties and estimation based on censored samples. Pak. J. Stat. Oper. Res. 2021, 17, 343–356. [Google Scholar] [CrossRef]
- Maina, C.B.; Weke, P.G.; Ogutu, C.A.; Ottieno, J.A. A Normal weighted inverse Gaussian distribution for skewed and heavy-tailed data. Appl. Math. 2022, 13, 163–177. [Google Scholar] [CrossRef]
- Benchiha, S.; Al-Omari, A.I.; Alotaibi, N.; Shrahili, M. Weighted generalized Quasi Lindley distribution: Different methods of estimation, applications for COVID-19 and engineering data. AIMS Math 2021, 6, 11850–11878. [Google Scholar] [CrossRef]
- Abbas, S.; Zaniab, S.; Mehmood, O.; Ozal, G.; Shahbaz, M.Q. A new generalized weighted exponential distribution: Properties and applications. Thail. Stat. 2022, 20, 271–283. [Google Scholar]
- Dar, A.A.; Ahmed, A.; Reshi, J.A. Weighted Gamma-Pareto distribution and its application. Pak. J. Stat. 2020, 36, 287–304. [Google Scholar]
- Sahmran, M.A. Modified weighted Pareto distribution type I (MWPDTI). Baghdad Sci. J. 2020, 17, 0869. [Google Scholar] [CrossRef]
- Abd-Elrahman, A.M. Utilizing ordered statistics in lifetime distributions production: A new lifetime distribution and applications. J. Probab. Stat. Sci. 2013, 11, 153–164. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; The Regents of the University of California: Oakland, CA, USA, 1961. [Google Scholar]
- Lorenz, M. Methods of measuring the concentration of wealth. Publ. Am. Stat. Assoc. 1905, 9, 209–219. [Google Scholar]
- Bonferroni, C. Elementi di Statistica Generale; Libreria Seeber: Firenze, Italy, 1930. [Google Scholar]
- Hinkley, D. On quick choice of power transformation. J. R. Stat. Soc. Ser. C 1977, 26, 67–69. [Google Scholar] [CrossRef]
- Jamal, F.; Arslan Nasir, M.; Ozel, G.; Elgarhy, M.; Mamode Khan, N. Generalized inverted Kumaraswamy generated family of distributions: Theory and applications. J. Appl. Stat. 2019, 46, 2927–2944. [Google Scholar] [CrossRef]
- Afify, A.Z.; Nofal, Z.M.; Butt, N.S. Transmuted complementary Weibull geometric distribution. Pak. J. Stat. Oper. Res. 2014, 10, 435–454. [Google Scholar] [CrossRef]
- Shanker, R. Rani distribution and its application. Biom. Biostat. Int. J. 2017, 6, 1–14. [Google Scholar] [CrossRef][Green Version]
- Shanker, R. Rama distribution and its application. Int. J. Stat. Appl. 2017, 7, 26–35. [Google Scholar]
- Al-Omari, A.I.; Bouza, C.N. Review of ranked set sampling: Modifications and applications. Rev. Investig. Oper. 2014, 35, 215–240. [Google Scholar]




| 0.1 | 0.1711 | 0.0881 | 0.1267 | 0.0750 |
| 0.2 | 0.3421 | 0.1762 | 0.2533 | 0.1500 |
| 0.3 | 0.5132 | 0.2643 | 0.3800 | 0.2249 |
| 0.4 | 0.6842 | 0.3523 | 0.5067 | 0.2999 |
| 0.5 | 0.8553 | 0.4404 | 0.6333 | 0.3749 |
| 0.6 | 1.0263 | 0.5285 | 0.7600 | 0.4499 |
| 0.7 | 1.1974 | 0.6166 | 0.8867 | 0.5249 |
| 0.8 | 1.3684 | 0.7047 | 1.0133 | 0.5999 |
| 0.9 | 1.5395 | 0.7927 | 1.1400 | 0.6748 |
| 1 | 1.7105 | 0.8808 | 1.2667 | 0.7498 |
| 1.1 | 1.8816 | 0.9689 | 1.3933 | 0.8248 |
| 1.2 | 2.0526 | 1.0570 | 1.5200 | 0.8998 |
| 1.3 | 2.2237 | 1.1451 | 1.6467 | 0.9748 |
| 1.4 | 2.3947 | 1.2332 | 1.7733 | 1.0497 |
| 1.5 | 2.5658 | 1.3212 | 1.9000 | 1.1247 |
| 1.6 | 2.7368 | 1.4093 | 2.0267 | 1.1997 |
| 1.7 | 2.9079 | 1.4974 | 2.1533 | 1.2747 |
| 1.8 | 3.0790 | 1.5855 | 2.2800 | 1.3497 |
| 1.9 | 3.2500 | 1.6736 | 2.4067 | 1.4247 |
| 2 | 3.4211 | 1.7617 | 2.5333 | 1.4996 |
| 2.1 | 3.5921 | 1.8497 | 2.6600 | 1.5746 |
| 2.2 | 3.7632 | 1.9378 | 2.7867 | 1.6496 |
| 2.3 | 3.9342 | 2.0259 | 2.9133 | 1.7246 |
| 2.4 | 4.1053 | 2.1140 | 3.0400 | 1.7996 |
| 2.5 | 4.2763 | 2.2021 | 3.1667 | 1.8745 |
| n | |||||
|---|---|---|---|---|---|
| 2 | 2.0002 | 0.1628 | 2.0003 | 0.1871 | |
| 3 | 3.0003 | 0.2442 | 3.0005 | 0.2807 | |
| 40 | 5 | 5.0005 | 0.4069 | 5.0008 | 0.4678 |
| 7 | 7.0007 | 0.5697 | 7.0011 | 0.6549 | |
| 10 | 10.0010 | 0.8141 | 10.0016 | 0.9356 | |
| 2 | 2.0023 | 0.1152 | 2.0027 | 0.1325 | |
| 3 | 3.0034 | 0.1728 | 3.0040 | 0.1987 | |
| 80 | 5 | 5.0057 | 0.2881 | 5.0066 | 0.3312 |
| 7 | 7.0080 | 0.4033 | 7.0093 | 0.4637 | |
| 10 | 10.0114 | 0.5762 | 10.0133 | 0.6624 | |
| 2 | 2.0010 | 0.0940 | 2.0011 | 0.1081 | |
| 3 | 3.0014 | 0.1410 | 3.0017 | 0.1621 | |
| 120 | 5 | 5.0024 | 0.2350 | 5.0029 | 0.2702 |
| 7 | 7.0033 | 0.3291 | 7.0040 | 0.3783 | |
| 10 | 10.0048 | 0.4700 | 10.0057 | 0.5405 | |
| 2 | 2.0004 | 0.0814 | 2.0005 | 0.0936 | |
| 3 | 3.0006 | 0.1221 | 3.0008 | 0.1404 | |
| 160 | 5 | 5.0010 | 0.2035 | 5.0013 | 0.2339 |
| 7 | 7.0014 | 0.2849 | 7.0018 | 0.3275 | |
| 10 | 10.0020 | 0.4070 | 10.0026 | 0.4680 | |
| 2 | 1.9996 | 0.0728 | 1.9997 | 0.0837 | |
| 3 | 2.9995 | 0.1092 | 2.9995 | 0.1255 | |
| 200 | 5 | 4.9991 | 0.1819 | 4.9991 | 0.2092 |
| 7 | 6.9988 | 0.2547 | 6.9988 | 0.2928 | |
| 10 | 9.9982 | 0.3640 | 9.9983 | 0.4183 | |
| 2 | 1.9997 | 0.0664 | 1.9997 | 0.0764 | |
| 3 | 2.9995 | 0.0997 | 2.9995 | 0.1146 | |
| 240 | 5 | 4.9992 | 0.1661 | 4.9992 | 0.1909 |
| 7 | 6.9989 | 0.2325 | 6.9989 | 0.2673 | |
| 10 | 9.9984 | 0.3322 | 9.9985 | 0.3819 | |
| 2 | 1.9995 | 0.0460 | 1.9994 | 0.0529 | |
| 3 | 2.9992 | 0.0690 | 2.9992 | 0.0794 | |
| 500 | 5 | 4.9987 | 0.1151 | 4.9986 | 0.1323 |
| 7 | 6.9982 | 0.1611 | 6.9980 | 0.1852 | |
| 10 | 9.9974 | 0.2301 | 9.9972 | 0.2645 |
| 1 | 3.77457 | 2.85636 | 12 | 0.02621 | 0.01984 |
| 2 | 0.94364 | 0.71409 | 13 | 0.02234 | 0.01690 |
| 3 | 0.41940 | 0.31737 | 14 | 0.01926 | 0.01457 |
| 4 | 0.23591 | 0.17852 | 15 | 0.01678 | 0.01270 |
| 5 | 0.15098 | 0.11425 | 16 | 0.01474 | 0.01116 |
| 6 | 0.10485 | 0.07934 | 17 | 0.01306 | 0.00988 |
| 7 | 0.07703 | 0.05829 | 18 | 0.01165 | 0.00882 |
| 8 | 0.05898 | 0.04463 | 19 | 0.01046 | 0.00791 |
| 9 | 0.04660 | 0.03526 | 20 | 0.00944 | 0.00714 |
| 10 | 0.03775 | 0.02856 | 21 | 0.00856 | 0.00648 |
| 11 | 0.03120 | 0.02361 | 22 | 0.00780 | 0.00590 |
| LBBD | ABBD | LBBD | ABBD | |
|---|---|---|---|---|
| 2 | 1.91705 | 2.1183 | 2.89788 | 3.09913 |
| 3 | 1.83624 | 2.03994 | 2.81706 | 3.02077 |
| 4 | 1.78815 | 1.99309 | 2.76898 | 2.97392 |
| 5 | 1.75559 | 1.96127 | 2.73642 | 2.94210 |
| 6 | 1.73178 | 1.93796 | 2.71261 | 2.91879 |
| 7 | 1.71348 | 1.92001 | 2.69431 | 2.90083 |
| 8 | 1.69888 | 1.90568 | 2.67971 | 2.88651 |
| 9 | 1.68693 | 1.89392 | 2.66776 | 2.87475 |
| 10 | 1.67692 | 1.88408 | 2.65775 | 2.86491 |
| 11 | 1.66840 | 1.87570 | 2.64923 | 2.85653 |
| 12 | 1.66104 | 1.86845 | 2.64187 | 2.84928 |
| 13 | 1.65462 | 1.86212 | 2.63545 | 2.84295 |
| 14 | 1.64895 | 1.85654 | 2.62978 | 2.83737 |
| 15 | 1.64390 | 1.85156 | 2.62473 | 2.83239 |
| 16 | 1.63938 | 1.84710 | 2.62021 | 2.82793 |
| 17 | 1.63530 | 1.84308 | 2.61613 | 2.82390 |
| 18 | 1.63160 | 1.83942 | 2.61243 | 2.82025 |
| 19 | 1.62822 | 1.83608 | 2.60905 | 2.81691 |
| 20 | 1.62512 | 1.83302 | 2.60595 | 2.81385 |
| 21 | 1.62227 | 1.83021 | 2.60310 | 2.81104 |
| Data | n | Mean | SD | Median | Min | Max | Range | Skew | Kurtosis | SE |
|---|---|---|---|---|---|---|---|---|---|---|
| Set 1 | 30 | 1.68 | 1 | 1.47 | 0.32 | 4.75 | 4.43 | 1.03 | 0.93 | 0.18 |
| Set 2 | 20 | 2.18 | 0.84 | 2.17 | 0.73 | 3.92 | 3.19 | 0.11 | −0.57 | 0.19 |
| Data | Measures | Model | |||||
|---|---|---|---|---|---|---|---|
| ABBD | LBBD | Rama | Exp | Rani | Bilal | ||
| Data Set 1 | AIC | 79.361 | 78.183 | 90.880 | 92.949 | 96.997 | 80.734 |
| CAIC | 79.504 | 78.326 | 91.023 | 93.092 | 97.140 | 80.877 | |
| BIC | 80.762 | 79.584 | 92.281 | 94.350 | 98.398 | 82.136 | |
| HQIC | 79.810 | 78.632 | 91.328 | 93.397 | 97.445 | 81.183 | |
| Erro | 0.092 | 0.143 | 0.134 | 0.109 | 0.111 | 0.265 | |
| MML | 38.681 | 38.091 | 44.440 | 45.474 | 47.499 | 39.367 | |
| MLE | 0.976 | 1.322 | 1.634 | 0.597 | 1.833 | 2.019 | |
| Data Set 2 | AIC | 53.648 | 56.329 | 64.411 | 73.248 | 66.567 | 61.55 |
| CAIC | 53.870 | 56.552 | 64.633 | 73.470 | 66.789 | 61.774 | |
| BIC | 54.644 | 57.325 | 65.407 | 74.244 | 67.562 | 62.548 | |
| HQIC | 53.842 | 56.524 | 64.605 | 73.443 | 66.761 | 61.746 | |
| Erro | 0.148 | 0.229 | 0.140 | 0.102 | 0.122 | 0.4247 | |
| MML | 25.824 | 27.165 | 31.206 | 35.624 | 32.283 | 29.776 | |
| MLE | 1.283 | 1.737 | 1.403 | 0.458 | 1.630 | 2.645 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Omari, A.I.; Alsultan, R.; Alomani, G. Asymmetric Right-Skewed Size-Biased Bilal Distribution with Mathematical Properties, Reliability Analysis, Inference and Applications. Symmetry 2023, 15, 1578. https://doi.org/10.3390/sym15081578
Al-Omari AI, Alsultan R, Alomani G. Asymmetric Right-Skewed Size-Biased Bilal Distribution with Mathematical Properties, Reliability Analysis, Inference and Applications. Symmetry. 2023; 15(8):1578. https://doi.org/10.3390/sym15081578
Chicago/Turabian StyleAl-Omari, Amer Ibrahim, Rehab Alsultan, and Ghadah Alomani. 2023. "Asymmetric Right-Skewed Size-Biased Bilal Distribution with Mathematical Properties, Reliability Analysis, Inference and Applications" Symmetry 15, no. 8: 1578. https://doi.org/10.3390/sym15081578
APA StyleAl-Omari, A. I., Alsultan, R., & Alomani, G. (2023). Asymmetric Right-Skewed Size-Biased Bilal Distribution with Mathematical Properties, Reliability Analysis, Inference and Applications. Symmetry, 15(8), 1578. https://doi.org/10.3390/sym15081578








