New Results Regarding Positive Periodic Solutions of Generalized Leslie–Gower-Type Population Models

Abstract

In this paper, we focus on the existence of positive periodic solutions of generalized Leslie–Gower-type population models. Using the topological degree, we provide sufficient conditions to demonstrate the existence of positive periodic solutions to the considered models. It is interesting that the positive periodic solutions in this paper are general positive functions, not e exponential functions, which generalizes and improves the existing results. We note that due to the symmetrical property of periodic solutions, the results of this paper provide a deeper understanding of the periodic behavior of biological populations. Two numerical examples show the effectiveness of our main results.

1. Introduction

In 1948, Leslie [1] firstly introduced the Leslie predator–prey model:

$$\begin{array}{cc}\hfill x^{\prime }\left(t\right)& =x(a-bx)-f\left(x\right)y,\hfill \\ \hfill y^{\prime }\left(t\right)& =y\left(c-d{\displaystyle \frac{y}{x}}\right),\hfill \end{array}$$

where $x\left(t\right)$ and $y\left(t\right)$ denote the population densities at time t, and $f\left(x\right)$ represents the functional response to the prey x. After this, Leslie and Gower [2] systematically studied the biological behavior of this model and established the Leslie–Gower-type population model. In recent years, more and more scholars are paying attention to research on the Leslie–Gower-type population model and its generalizations. Wu and Xie [3] considered a piecewise-smooth Leslie–Gower model with a weak Allee effect and Holling type I functional response and showed that the predator’s food quality and Allee effect have significant impacts and lead to complicated dynamical phenomena. Zhang, Cai and Shen [4] studied a fast–slow Leslie-type predator–prey system with a piecewise-linear functional response by using the canard theory and the singular perturbation theory. In [5], Gao and Yang investigated the extinction and persistence of a generalized Leslie–Gower Holling type II model with Lévy jumps. For more results from studies about Leslie–Gower models, see [6,7,8,9,10,11,12] and related references.

In 2011, Zhu and Wang [13] studied a generalized Leslie–Gower-type population model with Holling type IIschemes:

$$\begin{array}{cc}\hfill x_1^{\prime }\left(t\right)& =x_1\left(t\right)\left[a_1\left(t\right)-b\left(t\right)x_1\left(t\right)-{\displaystyle \frac{c_1\left(t\right)x_2\left(t\right)}{x_1\left(t\right)+k_1}}\right]\hfill \\ \hfill x_2^{\prime }\left(t\right)& =x_2\left(t\right)\left[a_2\left(t\right)-{\displaystyle \frac{c_2\left(t\right)x_2\left(t\right)}{x_1\left(t\right)+k_2}}\right],\hfill \end{array}$$

(1)

where $x_1\left(t\right)$ and $x_2\left(t\right)$ indicate the population densities at time t; $a_1$ is the growth rate of the prey $x_1\left(t\right)$; $a_2$ is the growth rate of the predator $x_2\left(t\right)$; $b\left(t\right)$ denotes the strength of competition in individuals of species $x_1\left(t\right)$; $c_1\left(t\right)$ and $c_2\left(t\right)$ indicate the maximum value of the per capita reduction rate of the prey and predator, respectively; and $k_1$ and $k_2$ represent the extent to which the environment provides protection to the prey and predator, respectively. To obtain the positive periodic solutions of system (1), let $x_1\left(t\right)=e^{y_1\left(t\right)}$ and $x_2\left(t\right)=e^{y_2\left(t\right)}$; then, system (1) can be rewritten as

$$\begin{array}{cc}\hfill y_1^{\prime }\left(t\right)& =a_1\left(t\right)-b\left(t\right)e^{y_1\left(t\right)}-{\displaystyle \frac{c_1\left(t\right)e^{y_2\left(t\right)}}{e^{y_1\left(t\right)}+k_1}}\hfill \\ \hfill y_2^{\prime }\left(t\right)& =a_2\left(t\right)-{\displaystyle \frac{c_2\left(t\right)e^{y_2\left(t\right)}}{e^{y_1\left(t\right)}+k_2}}.\hfill \end{array}$$

(2)

Obviously, if system (2) has a periodic solution ${(y_1\left(t\right),y_2\left(t\right))}^T$, then system (1) has a positive periodic solution $\left(\exp \right(y_1\left(t\right),\exp {\left(y_2\left(t\right)\right)}^T$. However, the positive periodic solution to system (1) involves e exponential functions, not general positive functions. In this paper, we will use the topological degree to obtain a general form of positive periodic solution for system (1).

In 2002, Aziz-Alaoui [14] studied a Leslie–Gower-type tritrophic population model

$$\begin{array}{cc}\hfill x_1^{\prime }\left(t\right)& =a_0\left(t\right)x_1\left(t\right)-b_0\left(t\right)x_1^2\left(t\right)-{\displaystyle \frac{v_0\left(t\right)x_1\left(t\right)x_2\left(t\right)}{d_0\left(t\right)+x_1\left(t\right)}}\hfill \\ \hfill x_2^{\prime }\left(t\right)& =-a_1\left(t\right)x_2\left(t\right)+{\displaystyle \frac{v_1\left(t\right)x_1\left(t\right)x_2\left(t\right)}{d_1\left(t\right)+x_1\left(t\right)}}-{\displaystyle \frac{v_2\left(t\right)x_2\left(t\right)x_3\left(t\right)}{d_2\left(t\right)+x_2\left(t\right)}}\hfill \\ \hfill x_3^{\prime }\left(t\right)& =c_3\left(t\right)x_3^2\left(t\right)-{\displaystyle \frac{v_3\left(t\right)x_3^2\left(t\right)}{d_2\left(t\right)+x_2\left(t\right)}}.\hfill \end{array}$$

(3)

When all coefficients in system (3) are positive constants, Aziz-Alaoui proved some theorems on the existence of an attracting set, boundedness of the system, and the existence and global or local stability of equilibria. In system (3), $x_1\left(t\right),x_2\left(t\right)$ and $x_3\left(t\right)$ represent the population densities at time t; $a_0\left(t\right)$ is the growth rate of the prey $x_1$; $b_0\left(t\right)$ estimates the strength of competition among individuals; $d_0\left(t\right)$ estimates the extent to which the environment provides protection to the prey; $a_1\left(t\right)$ denotes the rate at which $x_2$ will die out when $x_1$ does not exist; $v_0\left(t\right)$ is the maximum value which per capita reduction rate of $x_1$ can achieve; the meanings of $v_1\left(t\right)$ and $d_1\left(t\right)$ are same as those of $v_0\left(t\right)$ and $d_0\left(t\right)$; the meanings of $v_2\left(t\right)$ and $v_3\left(t\right)$ are same as those of $v_0\left(t\right)$ and $v_1\left(t\right)$; $d_2\left(t\right)$ is the value of $x_2$ at the per capita removal rate; and $d_3\left(t\right)$ represents the residual loss in species $x_3$. In the present paper, we suppose that all coefficients in system (3) are positive $\omega -$periodic solutions. We will use the topological degree and mathematical analysis techniques to determine the existence of a positive $\omega -$periodic solution to system (3).

The main contributions of this paper are as follows:

(1)

We study two classes of population models by using topological degree theory and obtain the existence results of positive periodic solutions which are general positive functions and different from existing ones.

(2)

We develop the topological degree theory for investigating the existence of positive periodic solutions of population models.

(3)

To find some a priori bounds of positive periodic solutions, the suitable conditions for the coefficients of the considered population models are given.

The structure of the remainder of this paper is as follows: Section 2 gives the results of the existence of a positive periodic solutions to system (1). Section 3 gives the results of the existence of a positive periodic solution to system (3). Section 4 contains two examples verifying our results. Finally, we provide our conclusions.

2. Positive Periodic Solutions to System (1)

Let $\Omega$ be a subset of the topological space. $\partial \Omega$ and $\overline{\Omega }$ be the boundary and the closure of $\Omega$. Let

$$C_{\omega }=\{x\left(t\right)={(x_1\left(t\right),x_2\left(t\right))}^T\in C(\mathbb{R},{\mathbb{R}}^2):x(t+\omega )=x\left(t\right)\mathrm{for}\mathrm{all}t\in \mathbb{R}\}$$

with the norm $\left|\right|x\left|\right|={\max }_{t\in [0,\omega ]}\left\{\sup \right|x_1\left(t\right)|,\sup |x_2\left(t\right)\left|\right\}$. Obviously, $C_{\omega }$ is a two dimensional Banach space.

The existence of positive periodic solutions to system (1) will be proven by using the topological degree (see Theorem 6.3 in [15]) in the present case. Consider thefollowing lemma:

Lemma 1. 

Suppose there is a bounded open subset $\Xi \subset C_{\omega }$ such that the following are true:

(1) 

The system

$$x^{\prime }\left(t\right)=\lambda F(t,x\left(t\right))$$

(4)

does not have solutions to $\partial \Xi \cap {\mathbb{R}}^2$ for $\lambda \in (0,1)$, where

$$x\left(t\right)={(x_1\left(t\right),x_2\left(t\right))}^T,F(t,x\left(t\right))={(F_1(t,x\left(t\right)),F_2(t,x\left(t\right)))}^T,$$

$$\begin{array}{cc}\hfill F_1(t,x\left(t\right))& =x_1\left(t\right)\left[a_1\left(t\right)-b\left(t\right)x_1\left(t\right)-{\displaystyle \frac{c_1\left(t\right)x_2\left(t\right)}{x_1\left(t\right)+k_1}}\right],\hfill \\ \hfill F_2(t,x\left(t\right))& =x_2\left(t\right)\left[a_2\left(t\right)-{\displaystyle \frac{c_2\left(t\right)x_2\left(t\right)}{x_1\left(t\right)+k_2}}\right].\hfill \end{array}$$

(2) 

$g\left(x\right)\ne \mathbf{0}={(0,0)}^T$ for $x\in \partial \Xi \cap {\mathbb{R}}^2$, where $g\left(x\right)={(g_1\left(x\right),g_2\left(x\right))}^T:{\mathbb{R}}^2\to {\mathbb{R}}^2$,

$$\begin{array}{cc}\hfill g_1\left(x\right)& ={\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{x}_1\left(t\right)\left[a_1\left(t\right)-b\left(t\right)x_1\left(t\right)-{\displaystyle \frac{c_1\left(t\right)x_2\left(t\right)}{x_1\left(t\right)+k_1}}\right]dt,\hfill \\ \hfill g_2\left(x\right)& ={\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{x}_2\left(t\right)\left[a_2\left(t\right)-{\displaystyle \frac{c_2\left(t\right)x_2\left(t\right)}{x_1\left(t\right)+k_2}}\right]dt.\hfill \end{array}$$

(5)

(3) 

$de{g}_B(g,\Xi \cap {\mathbb{R}}^2,0)\ne 0.$

Then, system (1) has at least one $\omega -$periodic solution on $\overline{\Xi }$.

To determine the results for the existence of periodic solutions to system (1) by using Lemma 1, consider the following assumptions:

(H₁)

The following inequality is satisfied:

$$\underset{t\in [0,\omega ]}{\min }(c_2\left(t\right)-a_2\left(t\right))>0.$$

(H₂)

The following inequality is satisfied:

$$\underset{t\in [0,\omega ]}{\min }{\displaystyle \frac{1}{b\left(t\right)}}\left(a_1\left(t\right)-{\displaystyle \frac{c_1\left(t\right)R_0}{k_1}}\right)>0,$$

where $R_0$ is defined by Lemma 2.

Lemma 2. 

If assumption ($H_1$) holds, then any non-negative ω-periodic solution to system (4) is bounded above for all $\lambda \in (0,1)$.

Proof. 

Let $x\left(t\right)={(x_1\left(t\right),x_2\left(t\right))}^T$ be the $\omega$-periodic solution to system (4). Let

$$x^{+}=\underset{t\in [0,\omega ]}{\max }\{x_1\left(t\right),x_2\left(t\right)\}=R>0.$$

If there exists a point ${\xi }_1\in [0,\omega ]$ such that $x^{+}=x_1\left({\xi }_1\right)=R$, then $x_1^{\prime }\left({\xi }_1\right)=0$. Using the first equation of system (4), we arrive at

$$0=a_1\left({\xi }_1\right)-b\left({\xi }_1\right)x_1\left({\xi }_1\right)-{\displaystyle \frac{c_1\left({\xi }_1\right)x_2\left({\xi }_1\right)}{x_1\left({\xi }_1\right)+k_1}},$$

i.e.,

$$0=a_1\left({\xi }_1\right)-b\left({\xi }_1\right)R-{\displaystyle \frac{c_1\left({\xi }_1\right)x_2\left({\xi }_1\right)}{R+k_1}},$$

Then,

$$x_2\left({\xi }_1\right)={\displaystyle \frac{(a_1\left({\xi }_1\right)-b\left({\xi }_1\right)R)(R+k_1)}{c_1\left({\xi }_1\right)}}.$$

Since $x_2\left({\xi }_1\right)>0$, we have

$$R<{\displaystyle \frac{a_1\left({\xi }_1\right)}{b\left({\xi }_1\right)}}\le \underset{t\in [0,\omega ]}{\max }{\displaystyle \frac{a_1\left(t\right)}{b\left(t\right)}}:=R_{0,1}.$$

(6)

If there exists ${\xi }_2\in [0,\omega ]$ such that $x^{+}=x_2\left({\xi }_2\right)=R$, then $x_2^{\prime }\left({\xi }_2\right)=0$. Using the second equation of system (4), we arrive at

$$0=a_2\left({\xi }_2\right)-{\displaystyle \frac{c_2\left({\xi }_2\right)x_2\left({\xi }_2\right)}{x_1\left({\xi }_1\right)+k_2}},$$

i.e.,

$$0={\displaystyle \frac{c_2\left({\xi }_2\right)R}{x_1\left({\xi }_2\right)+k_2}}-a_2\left({\xi }_2\right).$$

Then, we obtain

$$0\ge {\displaystyle \frac{c_2\left({\xi }_2\right)R}{R+k_2}}-a_2\left({\xi }_2\right).$$

(7)

Adding and subtracting the term $c_2\left({\xi }_2\right)$ in (7), we can assert that

$$0\ge c_2\left({\xi }_2\right)-a_2\left({\xi }_2\right)-c_2\left({\xi }_2\right)\left(1-{\displaystyle \frac{R}{R+k_2}}\right).$$

Based on assumption (${\mathrm{H}}_1$), we arrive at $R\gg 0$ such that

$$0\ge \underset{{\xi }_2\in [0,\omega ]}{\min }\left[c_2\left({\xi }_2\right)-a_2\left({\xi }_2\right)-c_2\left({\xi }_2\right)\left(1-{\displaystyle \frac{R}{R+k_2}}\right)\right]>0$$

which is contradictory. Hence, there is a positive number $R_{0,2}$ such that

$$x_2\left(t\right)\le R_{0,2}\mathrm{for}\mathrm{all}t\in [0,\omega ].$$

(8)

In view of (6) and (8), we obtain

$$x_i\left(t\right)\le R_0\mathrm{for}\mathrm{all}t\in [0,\omega ],i=1,2,$$

where $R_0=\max \{R_{0,1},R_{0,2}\}$. □

Next, we consider the lower bounds for the solutions of system (4).

Lemma 3. 

If assumptions ($H_1$) and ($H_2$) are satisfied, then every non-negative ω-periodic solution to system (4) is bounded below for all $\lambda \in (0,1)$.

Proof. 

Let $x\left(t\right)={(x_1\left(t\right),x_2\left(t\right))}^T$ be the $\omega$-periodic solution to system (4) and

$$x^{-}=\underset{t\in [0,\omega ]}{\min }\{x_1\left(t\right),x_2\left(t\right)\}=r>0.$$

If there is a point ${\eta }_1\in [0,\omega ]$ such that $x^{-}=x_1\left({\eta }_1\right)=r$, then $x_1^{\prime }\left({\eta }_1\right)=0$. Using the first equation of system (4), we arrive at

$$0=a_1\left({\eta }_1\right)-b\left({\eta }_1\right)x_1\left({\eta }_1\right)-{\displaystyle \frac{c_1\left({\eta }_1\right)x_2\left({\eta }_1\right)}{x_1\left({\eta }_1\right)+k_1}},$$

i.e.,

$$0=a_1\left({\eta }_1\right)-b\left({\eta }_1\right)r-{\displaystyle \frac{c_1\left({\eta }_1\right)x_2\left({\eta }_1\right)}{r+k_1}}.$$

Using Lemma 2 and assumption (H₂), we obtain

$${\displaystyle \frac{c_1\left({\eta }_1\right)R_0}{k_1}}+b\left({\eta }_1\right)r-a_1\left({\eta }_1\right)\ge 0$$

and

$$\begin{array}{cc}\hfill r& >{\displaystyle \frac{1}{b\left({\eta }_1\right)}}\left[a_1\left({\eta }_1\right)-{\displaystyle \frac{c_1\left({\eta }_1\right)R_0}{k_1}}\right]\hfill \\ & \ge \underset{t\in [0,\omega ]}{\min }{\displaystyle \frac{1}{b\left(t\right)}}\left(a_1\left(t\right)-{\displaystyle \frac{c_1\left(t\right)R_0}{k_1}}\right)\hfill \\ & =r_{0,1}.\hfill \end{array}$$

(9)

If there exists ${\eta }_2\in [0,\omega ]$ such that $x^{-}=x_2\left({\eta }_2\right)=r$, then $x_2^{\prime }\left({\eta }_2\right)=0$. Using the second equation of system (4), we obtain

$$0=a_2\left({\eta }_2\right)-{\displaystyle \frac{c_2\left({\eta }_2\right)x_2\left({\eta }_2\right)}{x_1\left({\eta }_2\right)+k_2}},$$

i.e.,

$$0=a_2\left({\eta }_2\right)-{\displaystyle \frac{c_2\left({\eta }_2\right)r}{x_1\left({\eta }_2\right)+k_2}}.$$

Thus,

$$\begin{array}{cc}\hfill r& >{\displaystyle \frac{a_2\left({\eta }_2\right)k_2}{c_2\left({\eta }_2\right)}}\hfill \\ & \ge \underset{t\in [0,\omega ]}{\min }{\displaystyle \frac{a_2\left(t\right)k_2}{c_2\left(t\right)}}\hfill \\ & =r_{0,2}.\hfill \end{array}$$

(10)

From (9) and (10), we have

$$x_i\left(t\right)\ge r_0\mathrm{for}\mathrm{all}t\in [0,\omega ],i=1,2,$$

where $r_0=\min \{r_{0,1},r_{0,2}\}$. □

Theorem 1. 

Assume that assumptions ($H_1$) and ($H_2$) are satisfied. Then, system (1) has at least one positive ω-periodic solution.

Proof. 

Since assumptions (${\mathrm{H}}_1$) and (${\mathrm{H}}_2$) hold, from Lemmas 2 and 3, the positive periodic solutions of system (4) have lower and upper bounds. So, define $\Xi$ by

$$\Xi =\{x\left(t\right)={(x_1\left(t\right),x_2\left(t\right))}^T\in C_{\omega }:r_0<x_i\left(t\right)<R_0,i=1,2\},$$

where $r_0$ and $R_0$ are the lower and upper bounds of system (4), respectively. We easily obtain that system (4) has no solution in $\partial \Xi$ for all $\lambda \in (0,1)$. Thus, condition (1) of Lemma 1 is satisfied. Next, we show that condition (2) of Lemma 1 is satisfied. If $x_1=r_0$, from the first equation of (5) and assumption (${\mathrm{H}}_2$), we have

$$\begin{array}{cc}\hfill g_1\left({\check{x}}_1\right)& ={\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{r}_0\left[a_1\left(t\right)-b\left(t\right)r_0-{\displaystyle \frac{c_1\left(t\right)x_2\left(t\right)}{r_0+k_1}}\right]dt,\hfill \\ & \ge {\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{r}_0\left[a_1\left(t\right)-b\left(t\right)r_0-{\displaystyle \frac{c_1\left(t\right)R_0}{k_1}}\right]dt>0,\hfill \end{array}$$

(11)

where ${\check{x}}_1={(r_0,x_2)}^T$, $r_0$ is sufficiently small. If $x_2=r_0$, using the second equation of (5), we have

$$\begin{array}{cc}\hfill g_2\left({\check{x}}_2\right)& ={\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{r}_0\left[a_2\left(t\right)-{\displaystyle \frac{c_2\left(t\right)r_0}{x_1\left(t\right)+k_2}}\right]dt,\hfill \\ & \ge {\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{r}_0\left[a_2\left(t\right)-{\displaystyle \frac{c_2\left(t\right)r_0}{k_2}}\right]dt>0,\hfill \end{array}$$

(12)

where ${\check{x}}_2={(x_1,r_0)}^T$. Furthermore, if $x_1=R_0$, from the first equation of (5) and assumption (${\mathrm{H}}_2$), we have

$$\begin{array}{cc}\hfill g_1\left({\widehat{x}}_1\right)& ={\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{R}_0\left[a_1\left(t\right)-b\left(t\right)R_0-{\displaystyle \frac{c_1\left(t\right)x_2\left(t\right)}{R_0+k_1}}\right]dt,\hfill \\ & \ge {\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{R}_0\left[a_1\left(t\right)-b\left(t\right)R_0-{\displaystyle \frac{c_1\left(t\right)R_0}{k_1}}\right]dt>0,\hfill \end{array}$$

(13)

where ${\widehat{x}}_1={(R_0,x_2)}^T$. If $x_2=R_0$, using the second equation of (5), we have

$$\begin{array}{cc}\hfill g_2\left({\widehat{x}}_2\right)& ={\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{R}_0\left[a_2\left(t\right)-{\displaystyle \frac{c_2\left(t\right)R_0}{x_1\left(t\right)+k_2}}\right]dt,\hfill \\ & \le {\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{R}_0\left[a_2\left(t\right)-c_2\left(t\right)\right]dt<0,\hfill \end{array}$$

(14)

where ${\widehat{x}}_2={(x_1,R_0)}^T$. From (11)–(14), we determine that condition (2) of Lemma 1 is satisfied. Finally, we show that condition (3) of Lemma 1 holds. Define the map

$$H(x,\mu )={(H_1(x,\mu ),H_2(x,\mu ))}^T:\Xi \to C_{\omega },\mu \in [0,1],$$

where

$$\begin{array}{cc}\hfill H_1(x,\mu )& =\mu x_1+{\displaystyle \frac{1-\mu }{\omega }}{\int }_0^{\omega }{x}_1\left(t\right)\left[a_1\left(t\right)-b\left(t\right)x_1\left(t\right)-{\displaystyle \frac{c_1\left(t\right)x_2\left(t\right)}{x_1\left(t\right)+k_1}}\right]dt,\hfill \\ \hfill H_2(x,\mu )& =\mu x_2+{\displaystyle \frac{1-\mu }{\omega }}{\int }_0^{\omega }{x}_2\left(t\right)\left[a_2\left(t\right)-{\displaystyle \frac{c_2\left(t\right)x_2\left(t\right)}{x_1\left(t\right)+k_2}}\right]dt.\hfill \end{array}$$

Obviously, $H(x,\mu )\ne \mathbf{0}$ for $x\in \partial \Xi$; then, $H(x,\mu )$ is a homotopy. Using the homotopy invariance property of the Brouwer degree, we have

$$\begin{array}{cc}\hfill de{g}_B(g,\Xi \cap {\mathbb{R}}^2,0)& =de{g}_B(H(x,1),\Xi \cap {\mathbb{R}}^2,0)\hfill \\ & =de{g}_B(H(x,0),\Xi \cap {\mathbb{R}}^2,0)\hfill \\ & \ne 0.\hfill \end{array}$$

We use Lemma 1 to conclude that system (1) has at least one positive $\omega$-periodic solution on $\overline{\Xi }$. □

Remark 1. 

In [13], the authors obtained sufficient conditions for the global attractivity of positive periodic solutions to system (1) by using the Lyapunov functional method. Hence, in this paper, we do not consider the asymptotic property of the positive periodic solutions to system (1).

3. Positive Periodic Solutions to System (3)

Let

$$P_{\omega }=\{x\left(t\right)={(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right))}^T\in C(\mathbb{R},{\mathbb{R}}^3):x(t+\omega )=x\left(t\right)\mathrm{for}\mathrm{all}t\in \mathbb{R}\}$$

with the norm $\left|\right|x\left|\right|={\max }_{t\in [0,\omega ]}\left\{\sup \right|x_i\left(t\right)|,i=1,2,3\}$. Obviously, $P_{\omega }$ is a three-dimensional Banach space.

To obtain the results of the existence of positive periodic solutions to system (3), we consider the following lemma:

Lemma 4. 

Assume there is a bounded open subset $\Lambda \subset P_{\omega }$ such that the following are true:

(1) 

The system

$$x^{\prime }\left(t\right)=\lambda \mathcal{F}(t,x\left(t\right))$$

(15)

does not have solutions to $\partial \Lambda \cap {\mathbb{R}}^3$ for $\lambda \in (0,1)$, where $x\left(t\right)={(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right))}^T$,

$$\mathcal{F}(t,x\left(t\right))={({\mathcal{F}}_1(t,x\left(t\right)),{\mathcal{F}}_2(t,x\left(t\right)),{\mathcal{F}}_3(t,x\left(t\right)))}^T,$$

$$\begin{array}{cc}\hfill {\mathcal{F}}_1(t,x\left(t\right))& =a_0\left(t\right)x_1\left(t\right)-b_0\left(t\right)x_1^2\left(t\right)-{\displaystyle \frac{v_0\left(t\right)x_1\left(t\right)x_2\left(t\right)}{d_0\left(t\right)+x_1\left(t\right)}},\hfill \\ \hfill {\mathcal{F}}_2(t,x\left(t\right))& =-a_1\left(t\right)x_2\left(t\right)+{\displaystyle \frac{v_1\left(t\right)x_1\left(t\right)x_2\left(t\right)}{d_1\left(t\right)+x_1\left(t\right)}}-{\displaystyle \frac{v_2\left(t\right)x_2\left(t\right)x_3\left(t\right)}{d_2\left(t\right)+x_2\left(t\right)}},\hfill \\ \hfill {\mathcal{F}}_3(t,x\left(t\right))& =c_3\left(t\right)x_3^2\left(t\right)-{\displaystyle \frac{v_3\left(t\right)x_3^2\left(t\right)}{d_2\left(t\right)+x_2\left(t\right)}}.\hfill \end{array}$$

(2) 

$f\left(x\right)\ne \mathbf{0}={(0,0,0)}^T$ for $x\in \partial \Lambda \cap {\mathbb{R}}^3$, where $f\left(x\right)={(f_1\left(x\right),f_2\left(x\right),f_3\left(x\right))}^T:{\mathbb{R}}^3\to {\mathbb{R}}^3$,

$$\begin{array}{cc}\hfill f_1\left(x\right)& ={\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{x}_1\left(t\right)\left[a_0\left(t\right)-b_0\left(t\right)x_1\left(t\right)-{\displaystyle \frac{v_0\left(t\right)x_2\left(t\right)}{d_0\left(t\right)+x_1\left(t\right)}}\right]dt,\hfill \\ \hfill f_2\left(x\right)& ={\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{x}_2\left(t\right)\left[-a_1\left(t\right)+{\displaystyle \frac{v_1\left(t\right)x_1\left(t\right)}{d_1\left(t\right)+x_1\left(t\right)}}-{\displaystyle \frac{v_2\left(t\right)x_3\left(t\right)}{d_2\left(t\right)+x_2\left(t\right)}}\right]dt,\hfill \\ \hfill f_3\left(x\right)& ={\displaystyle \frac{1}{\omega }}{\int }_0^{\omega }{x}_3\left(t\right)\left[c_3\left(t\right)x_3\left(t\right)-{\displaystyle \frac{v_3\left(t\right)x_3\left(t\right)}{d_2\left(t\right)+x_2\left(t\right)}}\right]dt.\hfill \end{array}$$

(3) 

$de{g}_B(f,\Lambda \cap {\mathbb{R}}^3,0)\ne 0.$

Then, system (3) has at least one ω-periodic solution to $\overline{\Lambda }$.

In this section, we need the following assumptions:

(A₁)

The following inequality is satisfied:

$${\displaystyle \frac{v_3\left(t\right)}{c_3\left(t\right)}}>d_2\left(t\right)+R_{0,2}\mathrm{for}\mathrm{all}t\in [0,\omega ],$$

where $R_{0,2}$ is defined by (18).

(A₂)

The following inequality holds:

$$1-\omega v_1\left(t\right)>0\mathrm{for}\mathrm{all}t\in [0,\omega ].$$

(A₃)

The following inequality holds:

$$v_1\left(t\right)-a_1\left(t\right)>0\mathrm{for}\mathrm{all}t\in [0,\omega ].$$

(A₄)

The following inequality holds:

$$\underset{t\in [0,\omega ]}{\min }{\displaystyle \frac{1}{b_0\left(t\right)}}\left(a_0\left(t\right)-{\displaystyle \frac{v_0\left(t\right)R_0}{d_0\left(t\right)}}\right)>0,$$

where $R_0$ is defined by Lemma 5.

(A₅)

The following inequalities hold:

$$1-\omega a_1\left(t\right)>0\mathrm{for}\mathrm{all}t\in [0,\omega ]$$

and

$${\gamma }_0-\omega v_2^{+}{R}_0>0,$$

where $R_0$ is defined by Lemma 5, and ${\gamma }_0$ is defined by (21).

(A₆)

The following inequality holds:

$${\displaystyle \frac{v_1^{-}{r}_{0,1}}{d_1^{-}+r_{0,1}}}-a_1^{+}>0,$$

where $r_{0,1}$ and $r_{0,2}$ are defined by (20) and (22), respectively.

Lemma 5. 

If assumption ($A_1$) holds, then every non-negative ω-periodic solution to system (15) is bounded above for all $\lambda \in (0,1)$.

Proof. 

Let $x\left(t\right)={(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right))}^T$ be the $\omega$-periodic solution to system (15) and

$$x^{+}=\underset{t\in [0,\omega ]}{\max }\left\{x_i\left(t\right)\right\}=R>0,i=1,2,3.$$

If there is a point ${\xi }_1\in [0,\omega ]$ such that $x^{+}=x_1\left({\xi }_1\right)=R$, then $x_1^{\prime }\left({\xi }_1\right)=0$. Using the first equation of system (15), we have

$$0=a_0\left({\xi }_1\right)-b_0\left({\xi }_1\right)x_1\left({\xi }_1\right)-{\displaystyle \frac{v_0\left({\xi }_1\right)x_2\left({\xi }_1\right)}{x_1\left({\xi }_1\right)+d_0\left({\xi }_1\right)}},$$

i.e.,

$$0=a_0\left({\xi }_1\right)-b_0\left({\xi }_1\right)R-{\displaystyle \frac{v_0\left({\xi }_1\right)x_2\left({\xi }_1\right)}{R+d_0\left({\xi }_1\right)}},$$

Then,

$$x_2\left({\xi }_1\right)={\displaystyle \frac{(a_0\left({\xi }_1\right)-b_0\left({\xi }_1\right)R)(R+d_0\left({\xi }_1\right))}{v_0\left({\xi }_1\right)}}.$$

Since $x_2\left({\xi }_1\right)>0$, we have

$$R<{\displaystyle \frac{a_0\left({\xi }_1\right)}{b_0\left({\xi }_1\right)}}\le \underset{t\in [0,\omega ]}{\max }{\displaystyle \frac{a_0\left(t\right)}{b_0\left(t\right)}}:=R_{0,1}.$$

(16)

If there is a point ${\xi }_3\in [0,\omega ]$ such that $x^{+}=x_3\left({\xi }_3\right)=R$, then $x_3^{\prime }\left({\xi }_3\right)=0$. Using the third equation of system (15), we have

$$0=c_3\left({\xi }_3\right)x_3\left({\xi }_3\right)-{\displaystyle \frac{v_3\left({\xi }_3\right)x_3\left({\xi }_3\right)}{d_2\left({\xi }_3\right)+x_2\left({\xi }_3\right)}},$$

i.e.,

$$0=c_3\left({\xi }_3\right)-{\displaystyle \frac{v_3\left({\xi }_3\right)}{d_2\left({\xi }_3\right)+x_2\left({\xi }_3\right)}}.$$

Thus, according to assumption (${\mathrm{A}}_1$), we have

$$\begin{array}{cc}\hfill x_2\left({\xi }_3\right)& ={\displaystyle \frac{v_3\left({\xi }_3\right)}{c_3\left({\xi }_3\right)}}-d_2\left({\xi }_3\right)\hfill \\ & \le \underset{t\in [0,\omega ]}{\max }\left({\displaystyle \frac{v_3\left(t\right)}{c_3\left(t\right)}}-d_2\left(t\right)\right)\hfill \\ & ={\delta }_0.\hfill \end{array}$$

(17)

From the second equation of system (15) and (17), we arrive at

$$\begin{array}{cc}\hfill x_2\left(t\right)& =x\left({\xi }_3\right)+{\int }_{{\xi }_3}^t{x}_2^{\prime }\left(s\right)ds\hfill \\ & \le {\delta }_0+{\int }_0^{\omega }{\displaystyle \frac{v_1\left(t\right)x_1\left(t\right)x_2\left(t\right)}{d_1\left(t\right)+x_1\left(t\right)}}dt\hfill \\ & \le {\delta }_0+\omega v_1^{+}{x}_2^{+}.\hfill \end{array}$$

Thus, according to assumption (${\mathrm{A}}_2$), we have

$$x_2\left(t\right)\le {\displaystyle \frac{{\delta }_0}{1-\omega v_1^{+}}}:=R_{0,2}\mathrm{for}\mathrm{all}t\in [0,\omega ].$$

(18)

If there is a point ${\xi }_2\in [0,\omega ]$ such that $x^{+}=x_2\left({\xi }_2\right)=R\le R_{0,2}$, then $x_2^{\prime }\left({\xi }_2\right)=0$. Using the second equation of system (15), we arrive at

$$-a_1\left({\xi }_2\right)+{\displaystyle \frac{v_1\left({\xi }_2\right)x_1\left({\xi }_2\right)}{d_1\left({\xi }_2\right)+x_1\left({\xi }_2\right)}}-{\displaystyle \frac{v_2\left({\xi }_2\right)x_3\left({\xi }_2\right)}{d_2\left({\xi }_2\right)+x_2\left({\xi }_2\right)}}=0,$$

i.e.,

$$a_1\left({\xi }_2\right)-{\displaystyle \frac{v_1\left({\xi }_2\right)x_1\left({\xi }_2\right)}{d_1\left({\xi }_2\right)+x_1\left({\xi }_2\right)}}+{\displaystyle \frac{v_2\left({\xi }_2\right)x_3\left({\xi }_2\right)}{d_2\left({\xi }_2\right)+R}}=0,$$

Then,

$$a_1\left({\xi }_2\right)-v_1\left({\xi }_2\right)+{\displaystyle \frac{v_2\left({\xi }_2\right)x_3\left({\xi }_2\right)}{d_2\left({\xi }_2\right)+R_{0,2}}}<0.$$

Thus, according to assumption (${\mathrm{A}}_3$), we have

$$\begin{array}{cc}\hfill x_3\left({\xi }_2\right)& \le {\displaystyle \frac{(v_1\left({\xi }_2\right)-a_1\left({\xi }_2\right))(d_2\left({\xi }_2\right)+R_{0,2})}{v_2\left({\xi }_2\right)}}\hfill \\ & \le \underset{t\in [0,\omega ]}{\max }{\displaystyle \frac{(v_1\left(t\right)-a_1\left(t\right))(d_2\left(t\right)+R_{0,2})}{v_2\left(t\right)}}\hfill \\ & ={\delta }_1.\hfill \end{array}$$

(19)

From the third equation of systems (15) and (19) and assumption (${\mathrm{A}}_1$), we have

$$\begin{array}{cc}\hfill x_3\left(t\right)& =x_3\left({\xi }_2\right)+{\int }_{{\xi }_2}^t{x}_3^{\prime }\left(s\right)ds\hfill \\ & =x_3\left({\xi }_2\right)+\lambda {\int }_{{\xi }_2}^t\left[c_3\left(s\right)x_3^2\left(s\right)-{\displaystyle \frac{v_3\left(s\right)x_3^2\left(s\right)}{d_2\left(s\right)+x_2\left(s\right)}}\right]ds\hfill \\ & \le {\delta }_1+\lambda {\int }_{{\xi }_2}^t{x}_3^2\left(s\right)\left[c_3\left(s\right)-{\displaystyle \frac{v_3\left(s\right)}{d_2\left(s\right)+R_{0,2}}}\right]ds\hfill \\ & \le {\delta }_1:=R_{0,3}.\hfill \end{array}$$

(20)

In view of (16), (18) and (20), we obtain

$$x_i\left(t\right)\le R_0\mathrm{for}\mathrm{all}t\in [0,\omega ],i=1,2,3,$$

where $R_0=\max \{R_{0,1},R_{0,2},R_{0,3}\}$. □

Lemma 6. 

If assumptions ($A_1$)–($A_6$) hold, then every non-negative ω-periodic solution to system (15) is bounded below for all $\lambda \in (0,1)$.

Proof. 

Let $x\left(t\right)={(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right))}^T$ be the $\omega$-periodic solution to system (15) and

$$x^{-}=\underset{t\in [0,\omega ]}{\min }\left\{x_i\left(t\right)\right\}=r>0,i=1,2,3.$$

If there exists ${\eta }_1\in [0,\omega ]$ such that $x^{-}=x_1\left({\eta }_1\right)=r$, then $x_1^{\prime }\left({\eta }_1\right)=0.$ Using the first equation of system (15), we have

$$0=a_0\left({\eta }_1\right)-b_0\left({\eta }_1\right)x_1\left({\eta }_1\right)-{\displaystyle \frac{v_0\left({\eta }_1\right)x_2\left({\eta }_1\right)}{x_1\left({\eta }_1\right)+d_0\left({\eta }_1\right)}},$$

i.e.,

$$0=a_0\left({\eta }_1\right)-b_0\left({\eta }_1\right)r-{\displaystyle \frac{v_0\left({\eta }_1\right)x_2\left({\eta }_1\right)}{r+d_0\left({\eta }_1\right)}}.$$

In view of Lemma 5 and assumption (${\mathrm{A}}_4$), we obtain

$${\displaystyle \frac{c_1\left({\eta }_1\right)R_0}{k_1}}+b_0\left({\eta }_1\right)r-a_1\left({\eta }_1\right)\ge 0$$

and

$$\begin{array}{cc}\hfill r& >{\displaystyle \frac{1}{b_0\left({\eta }_1\right)}}\left[a_0\left({\eta }_1\right)-{\displaystyle \frac{v_0\left({\eta }_1\right)R_0}{d_0\left({\eta }_1\right)}}\right]\hfill \\ & \ge \underset{t\in [0,\omega ]}{\min }{\displaystyle \frac{1}{b_0\left(t\right)}}\left(a_0\left(t\right)-{\displaystyle \frac{v_0\left(t\right)R_0}{d_0\left(t\right)}}\right)\hfill \\ & =r_{0,1}.\hfill \end{array}$$

(21)

If there is a point ${\eta }_3\in [0,\omega ]$ such that $x^{-}=x_3\left({\eta }_3\right)=r$, then $x_3^{\prime }\left({\eta }_3\right)=0$. Using the third equation of system (15), we have

$$0=c_3\left({\eta }_3\right)x_3\left({\eta }_3\right)-{\displaystyle \frac{v_3\left({\eta }_3\right)x_3\left({\eta }_3\right)}{d_2\left({\eta }_3\right)+x_2\left({\eta }_3\right)}},$$

i.e.,

$$0=c_3\left({\eta }_3\right)-{\displaystyle \frac{v_3\left({\eta }_3\right)}{d_2\left({\eta }_3\right)+x_2\left({\eta }_3\right)}}.$$

Thus, according to assumption (${\mathrm{A}}_1$), we have

$$\begin{array}{cc}\hfill x_2\left({\eta }_3\right)& ={\displaystyle \frac{v_3\left({\eta }_3\right)}{c_3\left({\eta }_3\right)}}-d_2\left({\eta }_3\right)\hfill \\ & \ge \underset{t\in [0,\omega ]}{\min }\left({\displaystyle \frac{v_3\left(t\right)}{c_3\left(t\right)}}-d_2\left(t\right)\right)\hfill \\ & ={\gamma }_0.\hfill \end{array}$$

(22)

From the second equation of system (15) and (22), we have

$$\begin{array}{cc}\hfill x_2\left(t\right)& =x_2\left({\xi }_3\right)+{\int }_{{\xi }_3}^t{x}_2^{\prime }\left(s\right)ds\hfill \\ & \ge {\gamma }_0+{\int }_0^{\omega }\left[-a_1\left(t\right)x_2\left(t\right)-{\displaystyle \frac{v_2\left(t\right)x_2\left(t\right)x_3\left(t\right)}{d_2\left(t\right)+x_2\left(t\right)}}\right]dt\hfill \\ & \ge {\gamma }_0-\omega a_1^{+}{x}_2^{+}-\omega v_2^{+}{R}_0.\hfill \end{array}$$

According to assumption (${\mathrm{A}}_5$), we obtain

$$x_2\left(t\right)\ge {\displaystyle \frac{{\gamma }_0-\omega v_2^{+}{R}_0}{1-\omega a_1^{+}}}:=r_{0,2}\mathrm{for}\mathrm{all}t\in [0,\omega ].$$

(23)

If there is a point ${\eta }_2\in [0,\omega ]$ such that $x^{-}=x_2\left({\eta }_2\right)=r\ge r_{0,2}$, then $x_2^{\prime }\left({\eta }_2\right)=0$. Using the second equation of system (15), we arrive at

$$-a_1\left({\eta }_2\right)+{\displaystyle \frac{v_1\left({\eta }_2\right)x_1\left({\eta }_2\right)}{d_1\left({\eta }_2\right)+x_1\left({\eta }_2\right)}}-{\displaystyle \frac{v_2\left({\eta }_2\right)x_3\left({\eta }_2\right)}{d_2\left({\eta }_2\right)+x_2\left({\eta }_2\right)}}=0,$$

i.e.,

$$a_1\left({\eta }_2\right)-{\displaystyle \frac{v_1\left({\eta }_2\right)x_1\left({\eta }_2\right)}{d_1\left({\eta }_2\right)+x_1\left({\eta }_2\right)}}+{\displaystyle \frac{v_2\left({\eta }_2\right)x_3\left({\eta }_2\right)}{d_2\left({\eta }_2\right)+r}}=0,$$

Then,

$$a_1^{+}-{\displaystyle \frac{v_1^{-}{r}_{0,1}}{d_1^{-}+r_{0,1}}}+{\displaystyle \frac{v_2^{+}{x}_3\left({\eta }_2\right)}{d_2^{-}+r_{0,2}}}>0.$$

According to assumption (${\mathrm{A}}_6$), we obtain

$$x_3\left({\eta }_2\right)>{\displaystyle \frac{d_2^{-}+r_{0,2}}{v_2^{+}}}\left({\displaystyle \frac{v_1^{-}{r}_{0,1}}{d_1^{-}+r_{0,1}}}-a_1^{+}\right):={\gamma }_1.$$

(24)

Using the third equation of system (15), assumption (${\mathrm{A}}_1$), and (24), we have

$$\begin{array}{cc}\hfill x_3\left(t\right)& =x_3\left({\eta }_2\right)+{\int }_{{\xi }_2}^t{x}_3^{\prime }\left(s\right)ds\hfill \\ & =x_3\left({\eta }_2\right)+\lambda {\int }_{{\xi }_2}^t\left[c_3\left(s\right)x_3^2\left(s\right)-{\displaystyle \frac{v_3\left(s\right)x_3^2\left(s\right)}{d_2\left(s\right)+x_2\left(s\right)}}\right]ds\hfill \\ & \ge {\gamma }_1-\underset{t\in [0,\omega ]}{\max }\left[c_3\left(t\right)-{\displaystyle \frac{v_3\left(t\right)}{d_2\left(t\right)+R_{0,2}}}\right]{\left(x_3^{+}\right)}^2\left(t\right)\hfill \\ & ={\gamma }_1-\vartheta {\left(x_3^{+}\right)}^2\left(t\right),\hfill \end{array}$$

where $\vartheta ={\max }_{t\in [0,\omega ]}\left[c_3\left(t\right)-{\displaystyle \frac{v_3\left(t\right)}{d_2\left(t\right)+R_{0,2}}}\right].$ Hence, we have

$$x_3\left(t\right)\ge {\displaystyle \frac{1+\sqrt{1+4{\gamma }_1\vartheta }}{2\vartheta }}:=r_{0,3}forallt\in [0,\omega ].$$

(25)

From (20), (22), and (25), we have

$$x_i\left(t\right)\ge r_0\mathrm{for}\mathrm{all}t\in [0,\omega ],i=1,2,3$$

where $r_0=\min \{r_{0,1},r_{0,2},r_{0,3}\}$. □

Theorem 2. 

Assume that assumptions ($A_1$)–($A_6$) are satisfied. Then, system (3) has at least one positive ω-periodic solution.

Proof. 

Since assumptions (${\mathrm{A}}_1$)–(${\mathrm{A}}_6$) hold, from Lemmas 5 and 6, the periodic solutions to system (15) have lower and upper bounds. So, define $\Lambda$ as

$$\Lambda =\{x\left(t\right)={(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right))}^T\in P_{\omega }:r_0<x_i\left(t\right)<R_0,i=1,2,3\},$$

where $r_0$ and $R_0$ are the lower and upper bounds of system (15), respectively. We easily determine that system (15) has no solution in $\partial \Xi$ for all $\lambda \in (0,1)$. Thus, condition (1) of Lemma 4 is satisfied. We also determine that conditions (2) and (3) of Lemma 4 hold. Since the proof is similar to the corresponding proof of Theorem 1, we omit it. Therefore, we use Lemma 4 to conclude that system (3) has at least one positive $\omega$-periodic solution on $\overline{\Lambda }$. □

Remark 2. 

There have been numerous achievements regarding the dynamic properties of three-population models (see [1,2,14]). This is especially true in in [14], where the authors provided a detailed discussion on the dynamic behavior of the equilibrium point of system (3). Therefore, this article will not discuss the above-mentioned issues.

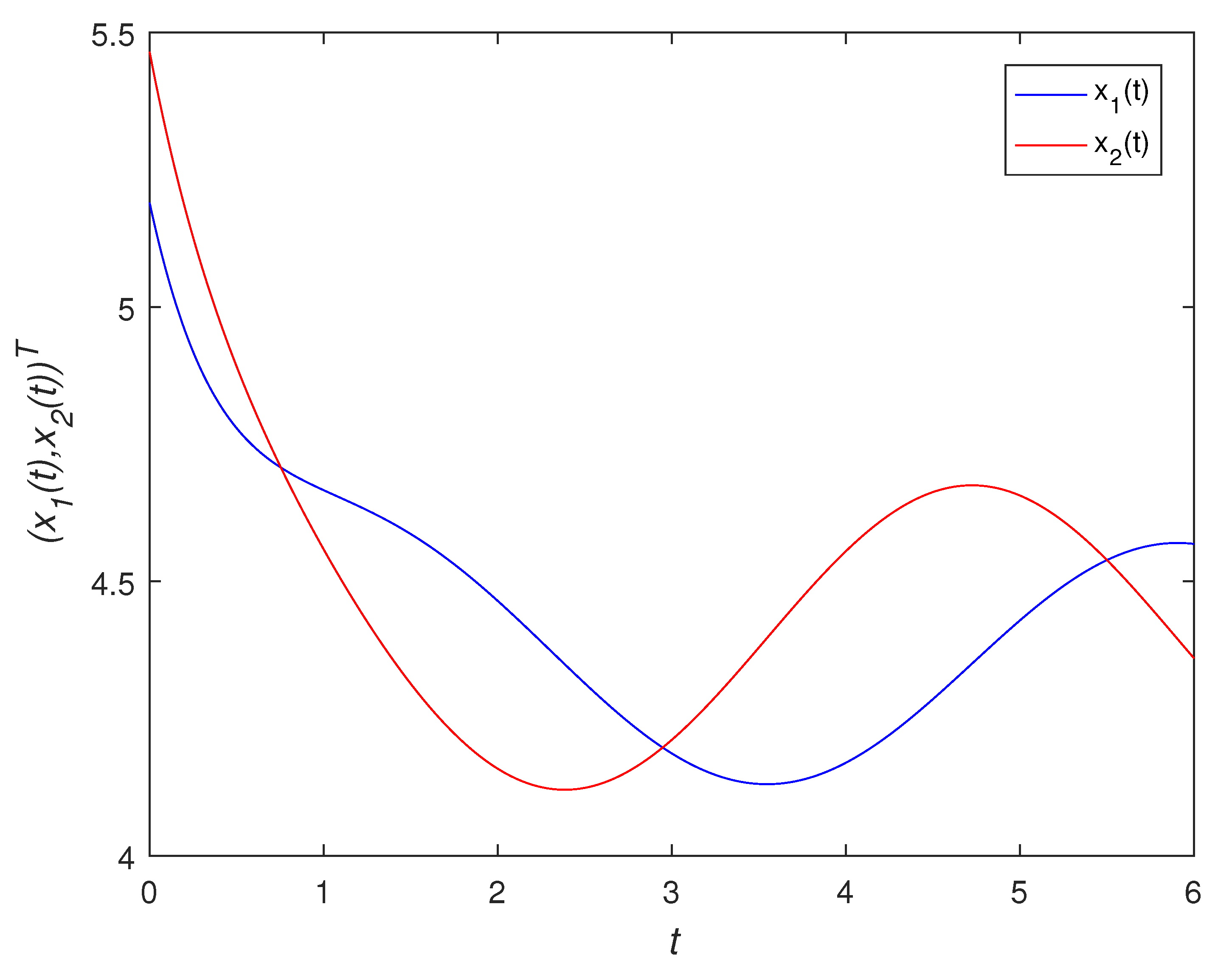
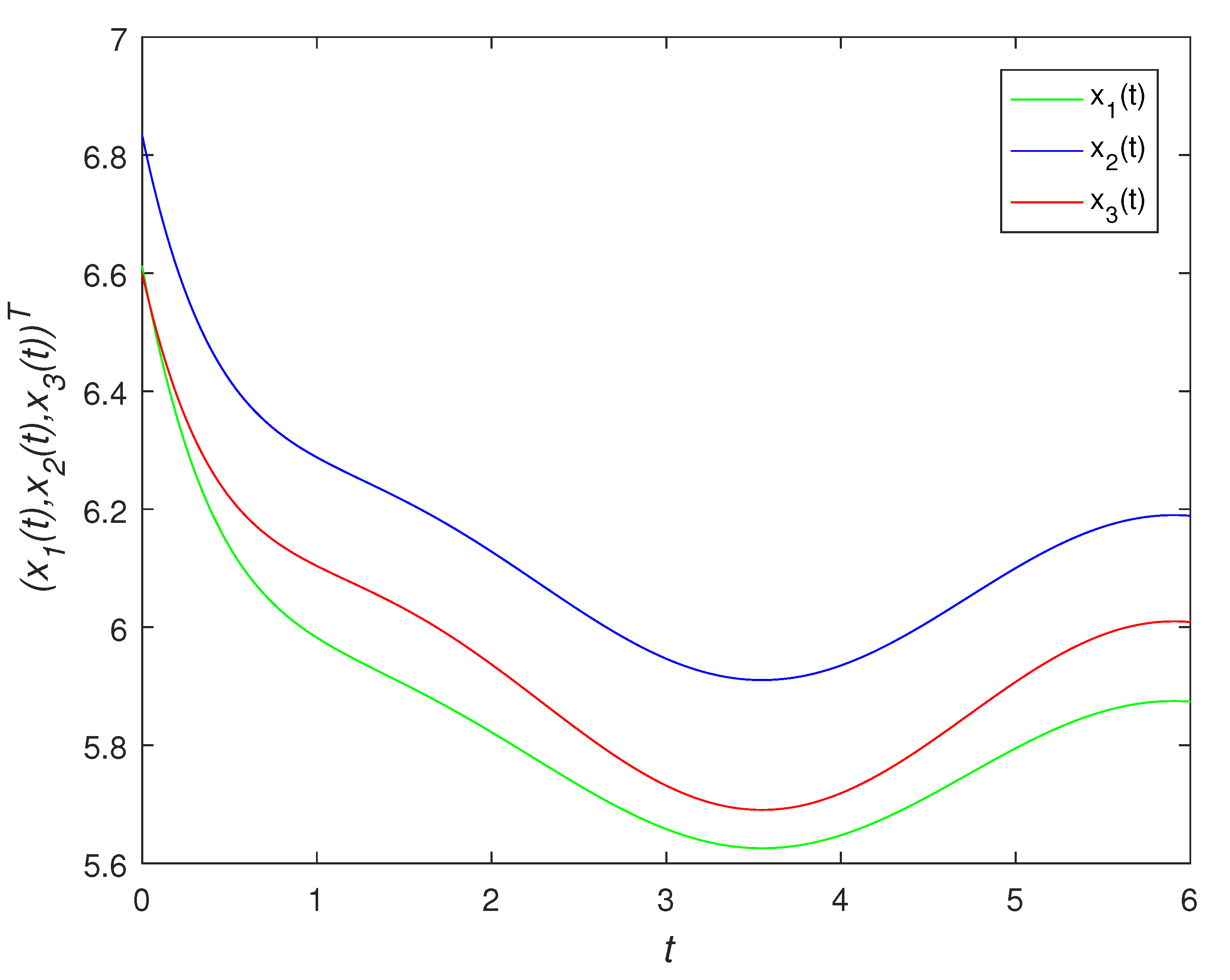
4. Numerical Examples

This section presents two examples that demonstrate the validity of our results.

Example 1. 

Consider the following equation:

$$\begin{array}{cc}\hfill x_1^{\prime }\left(t\right)& =x_1\left(t\right)\left[a_1\left(t\right)-b\left(t\right)x_1\left(t\right)-{\displaystyle \frac{c_1\left(t\right)x_2\left(t\right)}{x_1\left(t\right)+k_1}}\right]\hfill \\ \hfill x_2^{\prime }\left(t\right)& =x_2\left(t\right)\left[a_2\left(t\right)-{\displaystyle \frac{c_2\left(t\right)x_2\left(t\right)}{x_1\left(t\right)+k_2}}\right],\hfill \end{array}$$

(26)

where

$$a_1\left(t\right)=4.8+\sin {\displaystyle \frac{4}{3}}t>0,b\left(t\right)=2-\cos {\displaystyle \frac{4}{3}}t>0,c_1\left(t\right)=0.4+0.1\sin {\displaystyle \frac{4}{3}}t>0,k_1=20,$$

$$a_2\left(t\right)=0.5+0.1\cos {\displaystyle \frac{4}{3}}t>0,c_2\left(t\right)=6-\sin {\displaystyle \frac{4}{3}}t>0,k_2=5.$$

Choosing $R_0=100$, after a simple calculation, we have $\omega =1.5\pi$,

$$\underset{t\in [0,\omega ]}{\min }(c_2\left(t\right)-a_2\left(t\right))=4.4>0,$$

$$\underset{t\in [0,\omega ]}{\min }{\displaystyle \frac{1}{b\left(t\right)}}\left(a_1\left(t\right)-{\displaystyle \frac{c_1\left(t\right)R_0}{k_1}}\right)\approx 0.47>0.$$

Hence, all conditions of Theorem 1 hold, and we determine that system (26) has a positive $1.5\pi$-periodic solution. Figure 1 shows the positive periodic solution to system (26).

Example 2. 

Consider the following equation:

$$\begin{array}{cc}\hfill x_1^{\prime }\left(t\right)& =a_0\left(t\right)x_1\left(t\right)-b_0\left(t\right)x_1^2\left(t\right)-{\displaystyle \frac{v_0\left(t\right)x_1\left(t\right)x_2\left(t\right)}{d_0\left(t\right)+x_1\left(t\right)}}\hfill \\ \hfill x_2^{\prime }\left(t\right)& =-a_1\left(t\right)x_2\left(t\right)+{\displaystyle \frac{v_1\left(t\right)x_1\left(t\right)x_2\left(t\right)}{d_1\left(t\right)+x_1\left(t\right)}}-{\displaystyle \frac{v_2\left(t\right)x_2\left(t\right)x_3\left(t\right)}{d_2\left(t\right)+x_2\left(t\right)}}\hfill \\ \hfill x_3^{\prime }\left(t\right)& =c_3\left(t\right)x_3^2\left(t\right)-{\displaystyle \frac{v_3\left(t\right)x_3^2\left(t\right)}{d_2\left(t\right)+x_2\left(t\right)}},\hfill \end{array}$$

(27)

where

$$a_0\left(t\right)=6.5+\sin {\displaystyle \frac{4}{3}}t>0,b_0\left(t\right)=1.5-\cos {\displaystyle \frac{4}{3}}t>0,v_0\left(t\right)=0.2+0.1\sin {\displaystyle \frac{4}{3}}t>0,$$

$$d_0\left(t\right)=11+\sin {\displaystyle \frac{4}{3}}t>0,d_1\left(t\right)=0.2+0.1\cos {\displaystyle \frac{4}{3}}t>0,a_1\left(t\right)=0.03+0.01\cos {\displaystyle \frac{4}{3}}t>0,$$

$$v_1\left(t\right)=0.1-0.01\sin {\displaystyle \frac{4}{3}}t>0,v_2\left(t\right)=0.0003-0.0001\sin {\displaystyle \frac{4}{3}}t>0,v_3\left(t\right)=10-\sin {\displaystyle \frac{4}{3}}t>0,$$

$$d_2\left(t\right)=2-\cos {\displaystyle \frac{4}{3}}t>0,c_3\left(t\right)=0.004-0.002\sin {\displaystyle \frac{4}{3}}t>0,$$

Choosing $R_0=100,R_{0,2}=50,r_{0,1}=0.1,{\gamma }_0=0.5$, after a simple calculation, we have

$$\omega =1.5\pi ,v_2^{+}=0.3,v_1^{-}=0.09,d_1^{-}=0.1,a_1^{+}=0.04,$$

$${\displaystyle \frac{v_3\left(t\right)}{c_3\left(t\right)}}\ge 150>d_2\left(t\right)+R_{0,2},$$

$$1-\omega v_1\left(t\right)\approx 0.48>0,$$

$$v_1\left(t\right)-a_1\left(t\right)\ge 0.05>0,$$

$$\underset{t\in [0,\omega ]}{\min }{\displaystyle \frac{1}{b_0\left(t\right)}}\left(a_0\left(t\right)-{\displaystyle \frac{v_0\left(t\right)R_0}{d_0\left(t\right)}}\right)=1>0,$$

$$1-\omega a_1\left(t\right)\approx 0.72>0,$$

$${\gamma }_0-\omega v_2^{+}{R}_0\approx 0.36>0,$$

$${\displaystyle \frac{v_1^{-}{r}_{0,1}}{d_1^{-}+r_{0,1}}}-a_1^{+}=0.005>0.$$

Hence, all conditions of Theorem 2 hold, and we determine that system (27) has a positive $1.5\pi$-periodic solution. Figure 2 shows the positive periodic solution to system (27).

5. Conclusions

The existence of periodic solutions in population models has always been a hot research topic. In the present paper, we investigate the existence of positive periodic solutions for two types of population models. We obtain results indicating the existence of positive periodic solutions using topological degree theory. It should be pointed out that the positive periodic solutions obtained in the past were mostly exponential functions. However, positive periodic solutions are general positive functions. Hence, the research in this paper extends the existing research results. In the next paper, we will explore the existence of positive periodic solutions for neutral-type population models, and we will also consider the existence of positive periodic solutions for population models on different time scales.