On Nilpotent Elements, Weak Symmetry and Related Properties of Skew Generalized Power Series Rings

Abstract

The skew generalized power series ring $R\left[\right[S,\omega \left]\right]$ is a ring construction involving a ring R, a strictly ordered monoid $(S,\le )$, and a monoid homomorphism $\omega :S\to End\left(R\right)$. The ring $R\left[\right[S,\omega \left]\right]$ is a common generalization of ring extensions such as (skew) polynomial rings, (skew) Laurent polynomial rings, (skew) power series rings, (skew) Laurent series rings, (skew) Mal’cev–Neumann series rings, and (skew) monoid rings. In this paper, we study the nilpotent elements of skew generalized power series rings and the relationships between the properties of the rings R and $R\left[\right[S,\omega \left]\right]$ expressed in terms of annihilators, such as weak symmetry, weak zip, and the nil-Armendariz and McCoy properties. We obtain results on transferring the weak symmetry and weak zip properties between the rings R and $R\left[\right[S,\omega \left]\right]$, as well as sufficient and necessary conditions for a ring R to be $(S,\omega )$-nil-Armendariz or linearly $(S,\omega )$-McCoy.

1. Introduction

In this paper, rings are associative and have unity, but are not necessarily commutative. The set of nilpotent elements of a ring R is denoted by $nil\left(R\right)$. We say that $nil\left(R\right)$ is a subring of R if $nil\left(R\right)$ satisfies all the conditions required to be a subring, except for containing the unity of R. By Šter’s theorem [1] (Theorem 2.1), $nil\left(R\right)$ is a subring of R if and only if the set $nil\left(R\right)$ is closed under addition. If R is a ring and X is a nonempty subset of R, then the right (resp., left) annihilator of X in R is denoted by $r_R\left(X\right)$ (resp., $l_R\left(X\right)$).

The structure of the set $nil\left(R\right)$ can provide information about the properties of the ring R and conversely, the properties of a ring R can determine the structure of the set $nil\left(R\right)$. For example, if a ring R is reduced, meaning that $nil\left(R\right)=0$, then R is symmetric, which means that $abc=0$ implies $acb=0$ for any $a,b,c\in R$ (see [2]). Additionally, by [3] (Lemma 1), if a ring R is reduced, then R is an Armendariz ring, i.e., for any two polynomials $f\left(x\right)=a_0+\cdots +a_m{x}^m,g\left(x\right)=b_0+\cdots +b_n{x}^n\in R\left[x\right]$,

$$f\left(x\right)g\left(x\right)=0\mathrm{implies}{a}_i{b}_j=0\mathrm{for}\mathrm{all}i\mathrm{and}j(\mathit{the}\mathit{Armendariz}\mathit{condition}).$$

(1)

On the other hand, according to [4] (Corollary 3.3), if R is an Armendariz ring, then $nil\left(R\right)$ forms a subring of R.

The important role that Armendariz rings play in ring theory arises from the fact that they are precisely rings R for which the mapping $A\mapsto A\left[x\right]$ is a bijection between the right annihilator ideals of the ring R and the polynomial ring $R\left[x\right]$ ([5] (Proposition 3.1)). For an Armendariz ring R this feature allows for the transfer of certain ring properties related to annihilators between the rings R and $R\left[x\right]$. In particular, this applies to the zip property. Recall that a ring R is said to be right zip if, whenever $r_R\left(X\right)=0$ for a subset X of R, there is a finite subset Y of X with $r_R\left(Y\right)=0$. According to [6] (Theorem 11), an Armendariz ring R is right zip if and only if $R\left[x\right]$ is also right zip.

A wider class than Armendariz rings is formed by McCoy rings. A ring R is called right McCoy (resp., left McCoy) if, for any two nonzero polynomials $f\left(x\right),g\left(x\right)\in R\left[x\right]$,

$$f\left(x\right)g\left(x\right)=0\mathrm{implies}f\left(x\right)r(\mathrm{resp}.,rg\left(x\right)=0)\mathrm{for}\mathrm{some}\mathrm{nonzero}r\in R.$$

(2)

A ring is said to be McCoy if it is both left and right McCoy. If condition (2) holds for any two nonzero linear polynomials $f\left(x\right)=a_0+a_{1}x,g\left(x\right)=b_0+b_{1}x\in R\left[x\right]$, then R is said to be right (resp., left) linearly McCoy. By [7] (Theorem 2), all symmetric rings are McCoy and, thus, also linearly McCoy.

All classes of rings mentioned above are important in ring theory and are intensively studied. They are defined either by referring to the vanishing of certain products in the ring R and the polynomial ring $R\left[x\right]$, or by properties of annihilators. Since the study of these classes has proven fruitful, various generalizations began to be considered. These generalizations arise in two ways. One approach involves replacing zero in the definitions of the classes with the set $nil\left(R\right)$ of nilpotent elements of R. The other approach involves replacing $R\left[x\right]$ with other extensions of R, such as the power series ring $R\left[\right[x\left]\right]$, the Laurent polynomial ring $R[x,x^{-1}]$, the Laurent series ring $R\left[[x,x^{-1}]\right]$, the monoid ring $R\left[S\right]$, as well as the skew versions of these. For example, a ring R is said to be:

-

weak symmetric if for any $a,b,c\in R$, $abc\in nil\left(R\right)$ implies $acb\in nil\left(R\right)$ ([8] (Definition 1));

-

power series-wise Armendariz if for any two power series $f\left(x\right)={\sum }_{i=0}^{\infty }{a}_i{x}^i$ and $g\left(x\right)={\sum }_{i=0}^{\infty }{b}_j{x}^j$ in $R\left[\right[x\left]\right]$, if $f\left(x\right)g\left(x\right)=0$, then $a_i{b}_j=0$ for all i and j [9];

-

nil-Armendariz if for any two polynomials $f\left(x\right)={\sum }_{i=0}^m{a}_i{x}^i$ and $g\left(x\right)={\sum }_{i=0}^n{b}_j{x}^j$ in $R\left[x\right]$, if $f\left(x\right)g\left(x\right)\in nil\left(R\right)\left[x\right]$, then $a_i{b}_j\in nil\left(R\right)$ for all i and j ([4] (Definition 2.3)).

Although new classes of Armendariz-like rings were introduced by generalizing or analogizing the Armendariz condition (1), the theory for each class was developed independently, resulting in many papers with similar outcomes. To address the issue of fragmentation and the resulting parallel results, a unified approach to all Armendariz-like ring classes was proposed in [10]. The core idea was to study the Armendariz condition within the framework of the skew generalized power series ring $R\left[\right[S,\omega \left]\right]$ (the construction of $R\left[\right[S,\omega \left]\right]$ will be recalled in Section 2). Since (skew) polynomial rings, (skew) power series rings, (skew) Laurent polynomial rings, (skew) Laurent series rings, and (skew) monoid rings are all special cases of the $R\left[\right[S,\omega \left]\right]$ construction, the classes of Armendariz-like rings are natural subclasses of the broader class of $(S,\omega )$-Armendariz rings (see the definition in Section 2). Therefore, any general result about $(S,\omega )$-Armendariz rings automatically applies to each of these subclasses, with the corresponding results following directly from a unified argument. A similar approach was later used to unify results on nil-Armendariz-like rings, right McCoy-like rings, right linearly McCoy-like rings (see Section 2), and other classes of rings.

In this paper, we study the nilpotent elements of skew generalized power series rings and the relationships between the properties of the base ring R and the skew generalized power series ring $R\left[\right[S,\omega \left]\right]$ expressed in terms of annihilators. We investigate under what assumptions regarding the ring R, the strictly ordered monoid $(S,\le )$, and the monoid homomorphism $\omega :S\to End\left(R\right)$, such relationships hold. Some results of this paper generalize existing results on skew generalized power series rings (and some correct a couple of them).

The structure of this paper is as follows. Section 2 provides a review of the construction of skew generalized power series rings and demonstrates that the important ring extensions listed in the Abstract are indeed particular instances of this general construction. All of these extensions are well-studied, and their skew variants are well-known tools in algebra, often used to illustrate the asymmetry between left-sided and right-sided versions of various ring concepts. In Section 2, we also recall the definitions of the counterparts of Armendariz rings, nil Armendariz rings, McCoy rings, and linearly McCoy rings, all formulated within the framework of skew generalized power series rings.

In Section 3, we study the nilpotent elements of the skew generalized power series ring $R\left[\right[S,\omega \left]\right]$, focusing on connections between the structure of the nilpotent elements in R and $R\left[\right[S,\omega \left]\right]$, as well as the properties of $(S,\omega )$-nil-Armendariz rings (see Section 2 for their definition). For example, in Theorem 3, we prove that under suitable assumptions, a ring R is $(S,\omega )$-nil-Armendariz if and only if $nil\left(R\right)$ is an ideal of R.

In Section 4, we study weak symmetric rings, weak zip rings, McCoy rings, and linearly McCoy rings in the framework of skew generalized power series rings. In particular, in Proposition 7 (resp., Theorem 5), we prove that, under some assumptions, a ring R is weak symmetric (resp., weak zip) if and only if the skew generalized power series ring $R\left[\right[S,\omega \left]\right]$ is weak symmetric (resp., weak zip).

In this paper, the monoid operation is written multiplicatively, except in specific examples where additive notation is more appropriate. We denote by $End\left(R\right)$ the monoid of endomorphisms of a ring R, and by $Aut\left(R\right)$ the group of automorphisms of R. When an order ≤ is considered on a set S, the term “order” refers to “partial order”, unless explicitly stated otherwise. An order ≤ on S is called trivial (resp., total) if every pair of distinct elements of S is incomparable (resp., comparable) with respect to ≤. We use $\mathbb{Z}$ to denote the set of integers, ${\mathbb{N}}_0$ for the set of non-negative integers, and $\mathbb{N}$ for the set of positive integers.

2. Skew Generalized Power Series Rings

The notion of the skew generalized power series ring was introduced by the author and M. Ziembowski in [11]. This construction includes, as special cases, many other ring constructions, such as skew polynomial rings, skew power series rings, skew Laurent polynomial rings, skew Laurent series rings, skew monoid rings, skew group rings, skew Mal’cev–Neumann series rings, as well as their non-skewed versions and generalized power series rings. Consequently, every result regarding skew generalized power series rings has a counterpart for each of these specific constructions, and these counterparts can be derived from a single common proof. This approach not only yields new results for multiple ring constructions at once but also unifies existing theorems. Such a methodology has been applied, for example, in [10,12,13,14,15,16,17,18,19,20].

In this section, we will recall the construction of the skew generalized power series ring and demonstrate how the aforementioned ring extensions can be viewed as special cases of this construction. To achieve this, we first need to establish some definitions.

An ordered set $(S,\le )$ is said to be artinian if any strictly decreasing chain of elements in S is finite. The ordered set $(S,\le )$ is called narrow if S does not contain an infinite number of pairwise order-incomparable elements. An ordered monoid is a pair $(S,\le )$, where S is a monoid and ≤ is an order on S such that for all $a,b,c\in S$, if $a\le b$, then both $ac\le bc$ and $ca\le cb$. An ordered monoid $(S,\le )$ is called strictly ordered if, for all $a,b,c\in S$, the strict inequality $a<b$ implies the strict inequalities $ac<bc$ and $ca<cb$.

For a ring R and a strictly ordered monoid $(S,\le )$, Ribenboim defined the ring of generalized power series $R\left[\right[S\left]\right]$ in the 1990s. The ring $R\left[\right[S\left]\right]$ consists of all functions from S to R whose support is both artinian and narrow, equipped with pointwise addition and convolution multiplication (see [21]). This construction provides interesting examples of rings and has been the subject of extensive study (e.g., in [21,22,23,24,25]).

In [11], the skew generalized power series ring construction was introduced, as a “skewed” version of the Ribenboim power series ring $R\left[\right[S\left]\right]$. The construction involves a ring R, a strictly ordered monoid $(S,\le )$, and a monoid homomorphism $\omega :S\to End\left(R\right)$, and proceeds as follows: for each $s\in S$, let ${\omega }_s$ denote the image of s under $\omega$, i.e., ${\omega }_s=\omega \left(s\right)$. Define A as the set of all functions $f:S\to R$ whose support $supp\left(f\right)=\{s\in S\mid f(s)\ne 0\}$ is both artinian and narrow. For any $s\in S$ and $f,g\in A$, the set

$$X_s(f,g)=\{(u,v)\in supp\left(f\right)\times supp\left(g\right)\mid s=uv\}$$

is finite. This allows us to define the product $fg:S\to R$ of $f,g\in A$ by the following formula:

$$\left(fg\right)\left(s\right)=\sum _{(u,v)\in X_s(f,g)}f\left(u\right){\omega }_u\left(g\left(v\right)\right)\mathrm{for}\mathrm{any}s\in S,$$

where the sum over the empty set is conventionally taken to be 0. Equipped with pointwise addition and multiplication as defined above, A forms a ring, which is referred to as the ring of skew generalized power series with coefficients in R and exponents in S, denoted by $R\left[\right[S,\omega \left]\right]$. An element $f\in R\left[\right[S,\omega \left]\right]$ is sometimes written as a sum $f=r_1{s}_1+\cdots +r_n{s}_n$, where $s_i\in S$ and $r_i=f\left(s_i\right)\in R$, provided that $\mathrm{supp}\left(f\right)$ is finite. In this case, we will say that we are using the monoid ring notation. We will also denote the identity element in the monoid S, the ring R, and the ring $R\left[\right[S,\omega \left]\right]$ by the same symbol 1. If I is a nonempty subset of R, then $I\left[\right[S,\omega \left]\right]$ denotes the set of all $f\in R\left[\right[S,\omega \left]\right]$ with $supp\left(f\right)\subseteq I$, that is,

$$I\left[\right[S,\omega \left]\right]=\{f\in R[[S,\omega ]]\mid f(s)\in I\cup \{0\}\mathrm{for}\mathrm{all}s\in S\}.$$

To each $r\in R$ and $s\in S$, we associate the elements ${\mathsf{c}}_r,{\mathsf{e}}_s$ of $R\left[\right[S,\omega \left]\right]$, which are defined as follows:

$${\mathsf{c}}_r\left(x\right)=\left\{\begin{array}{cc}r\hfill & \mathrm{if}x=1,\hfill \\ 0\hfill & \mathrm{if}x\in S\setminus \left\{1\right\}\hfill \end{array}\right.\mathrm{and}{\mathsf{e}}_s\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}x=s,\hfill \\ 0\hfill & \mathrm{if}x\in S\setminus \left\{s\right\}.\hfill \end{array}\right.$$

In monoid ring notation, this means that ${\mathsf{c}}_r$ and ${\mathsf{e}}_s$ correspond to the power series ${\mathsf{c}}_r=r1$ and ${\mathsf{e}}_s=1s$, respectively. It is clear that the map $r\mapsto {\mathsf{c}}_r$ defines a ring embedding of R into $R\left[\right[S,\omega \left]\right]$, while $s\mapsto {\mathsf{e}}_s$ defines a monoid embedding of S into the multiplicative monoid of the ring $R\left[\right[S,\omega \left]\right]$. Moreover, we have the equality ${\mathsf{e}}_s{\mathsf{c}}_r={\mathsf{c}}_{{\omega }_s\left(r\right)}{\mathsf{e}}_s$.

Following up on our earlier statement, we now explain why the classical constructions referenced in the Abstract and the opening paragraph of this section are special cases of the construction of skew generalized power series rings.

Let R be a ring, and let $\alpha$ be an endomorphism of R. Consider the additive monoid $S={\mathbb{N}}_0=\mathbb{N}\cup \left\{0\right\}$, the set of non-negative integers under addition. Then the map $\omega :S\to End\left(R\right)$, defined by the following:

$$\omega \left(n\right)={\alpha }^n\mathrm{for}\mathrm{all}n\in S,$$

(3)

is obviously a homomorphism of monoids. If, in addition, $\alpha$ is an automorphism of R, then the formula (3) defines a monoid homomorphism $\omega :S\to Aut\left(R\right)$, where in this case, $S=\mathbb{Z}$ is the additive monoid of integers. For the additive monoids ${\mathbb{N}}_0$ and $\mathbb{Z}$, we can consider two distinct orderings ≤, namely the trivial order and the standard total order. Under both orderings, these monoids are strictly ordered, which allows us to construct the ring $R\left[\right[S,\omega \left]\right]$ of skew generalized power series in each case. The specific construction of the skew generalized power series ring $R\left[\right[S,\omega \left]\right]$ depends on two factors: whether $\alpha$ is an endomorphism or an automorphism, and whether the ordering ≤ is trivial or total. By choosing the appropriate additive monoid—either ${\mathbb{N}}_0$ or $\mathbb{Z}$—we obtain, as special cases, the following four classical “skew” extensions of the ring R, listed in the last column of Table 1.

Table 1. Four classical “skew” ring extensions as special cases of skew generalized power series rings.

Map $\mathit{\alpha }$	Monoid S	Ordering ≤	Ring $\mathit{R}\left[\right[\mathit{S},\mathit{\omega }\left]\right]$
endomorphism	${\mathbb{N}}_0$	trivial	skew polynomial ring $R[x,\alpha ]$
endomorphism	${\mathbb{N}}_0$	total	skew power series ring $R\left[\right[x,\alpha \left]\right]$
automorphism	$\mathbb{Z}$	trivial	skew Laurent polynomial ring $R[x,x^{-1};\alpha ]$
automorphism	$\mathbb{Z}$	total	skew Laurent series ring $R\left[[x,x^{-1};\alpha ]\right]$

An obvious endomorphism of a ring R is the identity map $i{d}_R$ of R, which is also an automorphism of R. Hence, we can consider the four “skew” ring extensions of R presented in Table 1, assuming that $\alpha =i{d}_R$, and as a result obtaining their classical “unskewed” versions. These versions are listed in the last column of Table 2, which can be considered a continuation of Table 1.

Table 2. Four classical “non-skew” ring extensions as special cases of skew generalized power series rings.

Map $\mathit{\alpha }$	Monoid S	Ordering ≤	Ring $\mathit{R}\left[\right[\mathit{S},\mathit{\omega }\left]\right]$
$i{d}_R$	${\mathbb{N}}_0$	trivial	polynomial ring $R\left[x\right]$
$i{d}_R$	${\mathbb{N}}_0$	total	power series ring $R\left[\right[x\left]\right]$
$i{d}_R$	$\mathbb{Z}$	trivial	Laurent polynomial ring $R[x,x^{-1}]$
$i{d}_R$	$\mathbb{Z}$	total	Laurent series ring $R\left[[x,x^{-1}]\right]$

Moreover, any monoid S can be regarded as a strictly ordered monoid with respect to the trivial order on S. Consequently, if R is a ring, S is a monoid, and $\omega :S\to End\left(R\right)$ is a homomorphism of monoids, we can pair the monoid S with the trivial order ≤ on S and form the ring $R\left[\right[S,\omega \left]\right]$ of skew generalized power series, which is denoted by $R[S,\omega ]$ in this case. It is obvious that the ring $R[S,\omega ]$ coincides with the classical skew monoid ring constructed from the ring R and the monoid S, involving the action $\omega$ of S on R. When the homomorphism $\omega$ is trivial (meaning that $\omega$ sends each element of S to the identity endomorphism $i{d}_R$ of R), we write $R\left[S\right]$ instead of $R[S,\omega ]$. Clearly, the ring $R\left[S\right]$ coincides with the ordinary monoid ring of S over R. In particular, if G is a group, then $R\left[G\right]$ is the group ring of G over R, and if furthermore $\omega :G\to Aut\left(R\right)$ is a group homomorphism, then $R[G,\omega ]$ is the skew group ring.

Note that if $(T,\le )$ is a totally ordered set and A is a subset of T, then A is artinian and narrow if and only if A is well-ordered. Therefore, if $(G,\le )$ is a totally ordered group, then the generalized power series ring $R\left[\right[G\left]\right]$ is identical to the Mal’cev–Neumann series ring $R\left(\right(G\left)\right)$. Moreover, if $\omega :G\to Aut\left(R\right)$ is a homomorphism of groups, then the skew generalized power series ring $R\left[\right[G,\omega \left]\right]$ is the same as the skew Mal’cev–Neumann series ring $R\left(\right(G,\omega \left)\right)$ (see [26] (§14)).

Figure 1 illustrates how many classical extensions of a ring R are special cases of the construction of the skew generalized power series ring.

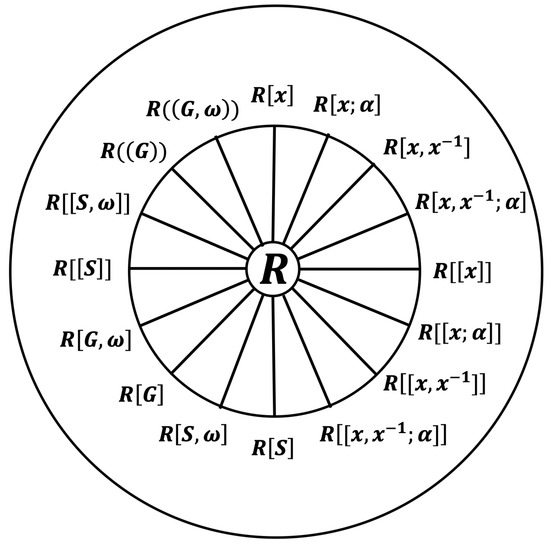
Figure 1. Particular cases of the skew generalized power series ring construction.

Below, we present the definitions of the counterparts of Armendariz rings, nil-Armendariz rings, McCoy rings, and linearly McCoy rings, all formulated in the framework of skew generalized power series rings. The defined classes of rings will be the focus of our studies throughout the remainder of this paper.

Assume that R is a ring, $(S,\le )$ is a strictly ordered monoid, and $\omega :S\to \mathrm{End}\left(R\right)$ is a monoid homomorphism. We say that the ring R is:

-

$(S,\omega )$-Armendariz if whenever $fg=0$ for $f,g\in R\left[\right[S,\omega \left]\right]$, we have $f\left(s\right){\omega }_s\left(g\left(t\right)\right)=0$ for all $s,t\in S$ ([10] (Definition 2.1));

-

$(S,\omega )$-nil-Armendariz if whenever $fg\in nil\left(R\right)\left[\right[S,\omega \left]\right]$ for $f,g\in R\left[\right[S,\omega \left]\right]$, we have $f\left(s\right){\omega }_s\left(g\left(t\right)\right)\in nil\left(R\right)$ for all $s,t\in S$ ([27] (Definition 3.1));

-

right $(S,\omega )$-McCoy if whenever $fg=0$ for nonzero elements $f,g\in R\left[\right[S,\omega \left]\right]$, there exists a nonzero element $r\in R$ such that in $R\left[\right[S,\omega \left]\right]$ we have $f{\mathsf{c}}_r=0$, or equivalently, in R we have $f\left(s\right){\omega }_s\left(r\right)=0$ for any $s\in S$ ([28] (p. 3), [29] (Definition 2.18));

-

right (resp., left) linearly $(S,\omega )$-McCoy if for all $a_0,a_1,b_0,b_1\in R$ and $s\in S\setminus \left\{1\right\}$, whenever the elements ${\mathsf{c}}_{a_0}+{\mathsf{c}}_{a_1}{\mathsf{e}}_s$ and ${\mathsf{c}}_{b_0}+{\mathsf{c}}_{b_1}{\mathsf{e}}_s$ of $R\left[\right[S,\omega \left]\right]$ are both nonzero and satisfy $({\mathsf{c}}_{a_0}+{\mathsf{c}}_{a_1}{\mathsf{e}}_s)({\mathsf{c}}_{b_0}+{\mathsf{c}}_{b_1}{\mathsf{e}}_s)=0$, then there exists a nonzero element $r\in R$ such that $({\mathsf{c}}_{a_0}+{\mathsf{c}}_{a_1}{\mathsf{e}}_s){\mathsf{c}}_r=0$ (resp., ${\mathsf{c}}_r({\mathsf{c}}_{b_0}+{\mathsf{c}}_{b_1}{\mathsf{e}}_s)=0$), i.e., $a_{0}r=a_1{\omega }_s\left(r\right)=0$ (resp. $r{b}_0=r{b}_1=0$) ([28] (Definition 3.1)).

3. Nilpotent Elements of Skew Generalized Power Series Rings

Let R be a ring and $\alpha$ an endomorphism of R. In this section we will need the following notions, introduced in [30] (Definition 2.1) and [31]:

-

$\alpha$ is called compatible, and R is said to be α-compatible, if for all $a,b\in R$, $ab=0$ if and only if $a\alpha \left(b\right)=0$;

-

$\alpha$ is called rigid, and R is said to be α-rigid, if for all $a\in R$, $a\alpha \left(a\right)=0$ implies $a=0$.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. As in [10] (Definition 2.4), the ring R is said to be $(S,\omega )$-compatible (resp., $(S,\omega )$-rigid) if ${\omega }_s$ is compatible (resp., rigid) for all $s\in S$.

In [10] (p. 366), it is demonstrated how compatibility naturally occurs in the context of $(S,\omega )$-Armendariz rings. Compatibility has the following properties, which will be frequently used later on. Note that a ring R is $(S,\omega )$-compatible if and only if S coincides with the set $C\left(S\right)$ defined in the lemma below.

Lemma 1.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Define $C\left(S\right)$ to be the set of all $s\in S$ such that ${\omega }_s$ is compatible. Then $C\left(S\right)$ is a submonoid of S; furthermore, for any elements $a_1,a_2,\dots ,a_n\in R$ and $s_1,s_2,\dots ,s_n\in C\left(S\right)$, we have

$$a_1{a}_2\cdots a_n\in nil\left(R\right)\mathit{if} \mathit{and} \mathit{only} \mathit{if}{\omega }_{s_1}\left(a_1\right){\omega }_{s_2}\left(a_2\right)\cdots {\omega }_{s_n}\left(a_n\right)\in nil\left(R\right).$$

Proof. 

Let $s,t\in C\left(S\right)$. Then for all $a,b\in R$ we have

$$a{\omega }_{st}\left(b\right)=0\iff a{\omega }_s\left({\omega }_t\left(b\right)\right)=0\iff a{\omega }_t\left(b\right)=0\iff ab=0.$$

Hence $st\in C\left(S\right)$, proving that $C\left(S\right)$ is multiplicatively closed. Since the identity endomorphism $i{d}_R$ of R belongs to $C\left(S\right)$, it follows that $C\left(S\right)$ is a submonoid of S. To prove the remaining part of the lemma, it suffices to repeat the arguments from the proof of [29] (Lemma 2.2) (or, alternatively, from the proof of [13] (Lemma 2.6)). □

Recall that a unique product monoid (or a u.p. monoid) is a monoid S with the property that for any two nonempty finite subsets $A,B\subseteq S$, there exist elements $a_0\in A$ and $b_0\in B$ such that $a_0{b}_0\ne ab$ for every pair $(a,b)\in A\times B\setminus \left\{(a_0,b_0)\right\}$. The element $a_0{b}_0$ is referred to as a u.p. element of the set $AB=\{ab\mid a\in A,b\in B\}$. Unique product monoids and groups are of considerable importance in the theory of monoid and group rings. The class of u.p. monoids includes both left and right totally ordered monoids, submonoids of free groups, and torsion-free nilpotent groups.

In the context of skew generalized power series rings, a more stringent condition on ordered monoids is required. Namely, according to [32] (Definition, p. 211), an ordered monoid $(S,\le )$ is said to be an artinian narrow unique product monoid (or an a.n.u.p. monoid) if for every pair of artinian and narrow nonempty subsets A and B of S, the product $AB$ contains a u.p. element. It is worth noting that every finite subset of an ordered set is both artinian and narrow, which implies that all a.n.u.p. monoids are, in fact, u.p. monoids.

We have the following result for skew generalized power series rings with exponents in a strictly ordered a.n.u.p. monoid.

Proposition 1.

Let R be a ring, $(S,\le )$ be a strictly ordered a.n.u.p. monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Let I be an ideal of R, satisfying the following two conditions:

(a)

${\omega }_s\left(I\right)\subseteq I$ for any $s\in S$;

(b)

$a{\omega }_s\left(a\right)\in I$ implies $a\in I$ for any $a\in R$ and $s\in S$.

Let $f,g\in R\left[\right[S,\omega \left]\right]$ be such that $fg\in I\left[\right[S,\omega \left]\right]$. Then $f\left(s\right){\omega }_s\left(g\left(t\right)\right)\in I$ for any $s,t\in S$.

Proof. 

Denote $\overline{R}=R/I$. By condition (a), the map $\overline{\omega }:S\to End\left(\overline{R}\right)$, given by ${\overline{\omega }}_s(x+I)={\omega }_s\left(x\right)+I$, is well-defined. By condition (b), the ring $\overline{R}$ is $(S,\overline{\omega })$-rigid. Hence, [10] (Theorem 4.12) implies that $\overline{R}$ is $(S,\overline{\omega })$-Armendariz. Let $\Phi :R\left[[S,\omega ]\right]\to \overline{R}\left[[S,\overline{\omega }]\right]$ be defined by $\Phi \left(h\right)\left(u\right)=h\left(u\right)+I$ for any $h\in R\left[\right[S,\omega \left]\right]$ and $u\in S$. Then, by [10] (Lemma 2.6), $\Phi$ is a ring homomorphism with $ker(\Phi )=I\left[\right[S,\omega \left]\right]$. Therefore, if $f,g\in R\left[\right[S,\omega \left]\right]$ are such that $fg\in I\left[\right[S,\omega \left]\right]$, then $\Phi \left(f\right)\Phi \left(g\right)=\Phi \left(fg\right)=0$. Since $\overline{R}$ is $(S,\overline{\omega })$-Armendariz, for any $s,t\in S$ we have $\Phi \left(f\right)\left(s\right)·{\overline{\omega }}_s(\Phi \left(g\right)\left(t\right))=0$, which means $(f\left(s\right)+I)·({\omega }_s\left(g\left(t\right)\right)+I)=0+I$. Hence $f\left(s\right){\omega }_s\left(g\left(t\right)\right)\in I$. □

As a consequence of Proposition 1, we can derive the following corollary:

Corollary 1

([27] (Proposition 3.6)). Let R be a ring, $(S,\le )$ be a strictly ordered a.n.u.p. monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. If R is $(S,\omega )$-compatible and $nil\left(R\right)$ is an ideal of R, then R is $(S,\omega )$-nil-Armendariz.

Proof. 

Obviously, ${\omega }_s\left(nil\left(R\right)\right)\subseteq nil\left(R\right)$ for any element $s\in S$. Furthermore, by Lemma 1, $a{\omega }_s\left(a\right)\in nil\left(R\right)$ implies $a\in nil\left(R\right)$ for any $a\in R$ and $s\in S$. Therefore, applying Proposition 1 with $I=nil\left(R\right)$ completes the proof. □

Below, we note two more corollaries of Proposition 1 that pertain to Ribenboim’s generalized power series rings $R\left[\right[S\left]\right]$.

Recall that an ideal I of a ring R is said to be completely prime (resp., completely semiprime), if the factor ring $R/I$ is a domain (resp., a reduced ring), i.e., if $ab\in I$ (resp., $a^2\in I$) implies $a\in I$ or $b\in I$ (resp., $a\in I$).

Corollary 2.

Let R be a ring, $(S,\le )$ be a strictly ordered a.n.u.p. monoid, and I be a completely semiprime ideal of R. Let $f,g\in R\left[\right[S\left]\right]$ be such that $fg\in I\left[\right[S\left]\right]$. Then $f\left(s\right)g\left(t\right)\in I$ for any $s,t\in S$.

The intersection of all completely prime ideals of a ring R is called the generalized nil-radical of R and is denoted by $N_g\left(R\right)$ ([33] (§ 7.8)). The generalized nil-radical $N_g\left(R\right)$ is the smallest ideal I of R with the property that the factor ring $R/I$ is reduced; in particular, the ideal $N_g\left(R\right)$ is completely semiprime.

Corollary 3.

Let R be a ring, and $(S,\le )$ be a strictly ordered a.n.u.p. monoid. If $f,g\in R\left[\right[S\left]\right]$ are such that $fg\in N_g\left(R\right)\left[\left[S\right]\right]$, then $f\left(s\right)g\left(t\right)\in N_g\left(R\right)$ for any $s,t\in S$.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. The following result provides a sufficient condition for $nil\left(R\right)$ to be a subring of R within the context of the skew generalized power series ring $R\left[\right[S,\omega \left]\right]$.

Before stating the result, we recall that for a monoid S and an element $s\in S$, $⟨s⟩$ denotes the submonoid of S generated by s, i.e., $⟨s⟩=\{s^n\mid s\in \mathbb{N}\cup \left\{0\right\}\}$. Thus $⟨s⟩$ consists of all powers of s, including the identity element $s^0=1$ of S.

Proposition 2.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume there exists an element $s\in S\setminus \left\{1\right\}$ such that the following two conditions hold:

(a)

${\omega }_s$ is compatible;

(b)

for any $f,g\in R\left[\right[S,\omega \left]\right]$ with $supp\left(f\right)\cup supp\left(g\right)\subseteq ⟨s⟩$, if $fg\in nil\left(R\right)\left[\right[S,\omega \left]\right]$, then $f\left(s^k\right)g\left(1\right)\in nil\left(R\right)$ for all non-negative integers k.

Then $nil\left(R\right)$ is a subring of R.

Proof. 

We will use monoid ring notation in the proof. By assumption, there exists an element $s\in S\setminus \left\{1\right\}$ that satisfies both conditions (a) and (b). We first show that the sequence $1,s,s^2,s^3,\dots$ consists of pairwise distinct elements of S. For the sake of contradiction, suppose that there exist non-negative integers k and m with $k<m$ such that $s^k=s^m$. We can assume that m is the smallest positive integer for which this holds. Then the elements $1,s,\dots ,s^{m-1}$ are distinct, and for the elements $f=s^k+s^{k+1}+\cdots +s^{m-1}$ and $g=1-s$ of $R\left[\right[S,\omega \left]\right]$, we have $supp\left(f\right)\cup supp\left(g\right)\subseteq ⟨s⟩$ and

$$fg=(s^k+s^{k+1}+\cdots +s^{m-1})(1-s)=s^k-s^m=0\in nil\left(R\right)\left[[S,\omega ]\right].$$

Hence, condition (b) yields $f\left(s^k\right)g\left(1\right)=1·1=1\in nil\left(R\right)$, which is a contradiction. Therefore, indeed the elements of the sequence $1,s,s^2,s^3,\dots$ are distinct. (Note that under somewhat stronger assumptions this fact is also established in [27] (Proposition 3.31(2))).

To complete the proof, we apply ideas from the proof of [4] (Lemma 3.1), adapting them to the context of skew generalized power series rings. We begin with showing that for any $a,b,c\in nil\left(R\right)$ the following hold:

(1)

$ab\in nil\left(R\right)$;

(2)

$a(b+c)\in nil\left(R\right)$;

(3)

$a+bc\in nil\left(R\right)$.

Since $a,b,c\in nil\left(R\right)$, for some $n\in \mathbb{N}$ we have $b^n=c^n=0$. We define two pairs of elements of $R\left[\right[S,\omega \left]\right]$ as follows:

$$f_1=1-bs,f_2=1+bs+b{\omega }_s\left(b\right)s^2+\cdots +b{\omega }_s\left(b\right){\omega }_{s^2}\left(b\right)\cdots {\omega }_{s^{n-2}}\left(b\right)s^{n-1},$$

$$g_1=1-cs,g_2=1+cs+c{\omega }_s\left(c\right)s^2+\cdots +c{\omega }_s\left(c\right){\omega }_{s^2}\left(c\right)\cdots {\omega }_{s^{n-2}}\left(c\right)s^{n-1}.$$

By applying (a), we conclude that

$$f_1{f}_2=1\mathrm{and}{g}_1{g}_2=1.$$

(4)

Therefore in $R\left[\right[S,\omega \left]\right]$ we have that $\left(a{f}_1\right)f_2=a\left(f_1{f}_2\right)=a\in nil\left(R\right)\left[[S,\omega ]\right]$. Since $supp\left(a{f}_1\right)\cup supp\left(f_2\right)\subseteq ⟨s⟩$, by condition (b) we obtain $\left(a{f}_1\right)\left(s\right)·f_2\left(1\right)=-ab·1=-ab\in nil\left(R\right)$, which proves (1). By (4), we also have that $\left(a{f}_1{g}_1\right)\left(g_2{f}_2\right)=a\in nil\left(R\right)\left[[S,\omega ]\right]$. Using (b) again, we obtain $\left(a{f}_1{g}_1\right)\left(s\right)·\left(g_2{f}_2\right)\left(1\right)=a(-b-c)·1=-a(b+c)\in nil\left(R\right)$, which proves (2). To prove (3), note that by (1), $bc\in nil\left(R\right)$ and thus, by (2), $c(a+bc)\in nil\left(R\right)$. Therefore, $(a+bc)c\in nil\left(R\right)$ as well, and since ${\omega }_s$ is compatible, Lemma 1 implies that $(a+bc){\omega }_s\left(c\right)\in nil\left(R\right)$. Consequently, in $R\left[\right[S,\omega \left]\right]$ we have

$$(b+(a+bc)s)(1-cs)=b+as-(a+bc){\omega }_s\left(c\right)s^2\in nil\left(R\right)\left[[S,\omega ]\right],$$

and condition (b) yields $(b+(a+bc\left)s\right)\left(s\right)·(1-cs)\left(1\right)=(a+bc)·1=a+bc\in nil\left(R\right)$, proving (3).

Having shown (3), we complete the proof by applying (3) repeatedly as follows. If $a,b\in nil\left(R\right)$, then $a^2+ab\in nil\left(R\right)$. Hence $(a^2+ab)+ba\in nil\left(R\right)$ and, consequently, $((a^2+ab)+ba)+b^2={(a+b)}^2\in nil\left(R\right)$. Thus $a+b\in nil\left(R\right)$, which shows that $nil\left(R\right)$ is additively closed. Since, by (a), $nil\left(R\right)$ is multiplicatively closed as well, it follows that $nil\left(R\right)$ is a subring of R. □

Note that if the endomorphism ${\omega }_s$ is compatible for some $s\ne 1$, then by Lemma 1, condition (b) in Proposition 2 is automatically satisfied when R is $(S,\omega )$-nil-Armendariz. Therefore, it follows from Proposition 2 that if ${\omega }_s$ is compatible for some $s\ne 1$, then the condition that $nil\left(R\right)$ is a subring of R is necessary for R to be $(S,\omega )$-nil-Armendariz. This result was established in [13] (Proposition 2.11(i)).

Furthermore, if the monoid $(S,\le )$ is nontrivial and the ring R is both $(S,\omega )$-compatible and $(S,\omega )$-nil-Armendariz, then all assumptions of Proposition 2 are satisfied. Therefore, the following conclusion follows from Proposition 2 (as well as from [13] (Proposition 2.11(i))).

Theorem 1.

Let R be a ring, $(S,\le )$ be a strictly ordered nontrivial monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. If R is $(S,\omega )$-compatible and $(S,\omega )$-nil-Armendariz, then $nil\left(R\right)$ is a subring of R.

As a direct consequence of Theorem 1, we obtain the following well-known result on nil-Armendariz rings:

Corollary 4

([4] (Theorem 3.2)). If R is a nil-Armendariz ring, then $nil\left(R\right)$ is a subring of R.

We now show that if at least one nontrivial element s of a strictly ordered monoid $(S,\le )$ generates an artinian and narrow submonoid, then the nilpotent elements of any $(S,\omega )$-nil-Armendariz ring form a multiplicative ideal of R. From [11] (Lemma 1.4), recall that the submonoid $⟨s⟩$ of S generated by s is artinian and narrow if and only if $s^m\le s^n$ for some positive integers m and n such that $m<n$.

Lemma 2.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. If R is $(S,\omega )$-nil-Armendariz and $⟨s⟩$ is artinian and narrow for some $s\in S\setminus \left\{1\right\}$, then $\{qa,aq\}\subseteq nil\left(R\right)$ for any $q\in nil\left(R\right)$ and $a\in R$.

Proof. 

We appropriately modify the proof of [34] (Lemma 4). Let $s\in S\setminus \left\{1\right\}$ be such that $⟨s⟩$ is artinian and narrow, and let $q\in nil\left(R\right)$ and $a\in R$. As in the first part of the proof of Proposition 2, one can show that the elements of the sequence $1,s,s^2,s^3,\dots$ are pairwise distinct. Furthermore, since the set $⟨s⟩$ is artinian and narrow, so is the support of the function $f:S\to R$, given by

$$f=1+as+a{\omega }_s\left(a\right)s^2+a{\omega }_s\left(a\right){\omega }_{s^2}\left(a\right)s^3+\cdots .$$

Hence f is an element of $R\left[\right[S,\omega \left]\right]$. Since $(1-as)f=1$, we obtain that $(q-(qa\left)s\right)f=q(1-as)f=q·1=q\in nil\left(R\right)\left[\right[S,\omega \left]\right]$. By hypothesis R is $(S,\omega )$-nil-Armendariz, which implies that

$$(q-\left(qa\right)s)\left(s\right)·{\omega }_s\left(f\left(1\right)\right)=\left(qa\right)·{\omega }_s\left(1\right)=\left(qa\right)·1=qa\in nil\left(R\right).$$

Since $qa\in nil\left(R\right)$, it follows that $aq\in nil\left(R\right)$ as well. □

By combining Proposition 2 and Lemma 2, we obtain the following result:

Theorem 2.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. If R is $(S,\omega )$-nil-Armendariz and for some $s,t\in S\setminus \left\{1\right\}$, $⟨s⟩$ is artinian and narrow, and ${\omega }_t$ is compatible, then $nil\left(R\right)$ is an ideal of R.

Proof. 

By Proposition 2, $nil\left(R\right)$ is a subring of R. Now Lemma 2 completes the proof. □

Observe that in Theorem 2, the assumption that $⟨s⟩$ is artinian and narrow for some $s\in S\setminus \left\{1\right\}$, is not superfluous. Otherwise, by considering $\omega$ as trivial, we conclude that $nil\left(R\right)$ is an ideal in every nil-Armendariz ring R, and hence in every Armendariz ring R. However, this is not the case. Indeed, by [10] (Corollary 6.3), all right chain rings (i.e., rings whose right ideals are totally ordered by inclusion) are Armendariz, but there exist right chain rings R such that $nil\left(R\right)$ is not an ideal of R (see [35] (p. 431)). Therefore, Theorem 2.14 and Lemma 2.13 in [13] are somewhat imprecise in this regard.

Note that by combining Theorem 2 and [11] (Lemma 1.4), one obtains [27] (Proposition 3.32).

The following theorem provides us with a characterization of when nilpotent elements of a ring form an ideal, in relation to the $(S,\omega )$-nil-Armendariz property.

Theorem 3.

Let R be a ring, $(S,\le )$ be a strictly ordered a.n.u.p. monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that R is $(S,\omega )$-compatible, and $⟨s⟩$ is artinian and narrow for some $s\in S\setminus \left\{1\right\}$. Then R is $(S,\omega )$-nil-Armendariz if and only if $nil\left(R\right)$ is an ideal of R.

Proof. 

The result follows by combining Corollary 1 and Theorem 2. □

According to [34] (Definition 3), a ring R is said to be nil power series-wise Armendariz if whenever $f\left(x\right)g\left(x\right)\in nil\left(R\right)\left[\right[x\left]\right]$ for $f\left(x\right)={\sum }_{i=0}^{\infty }{a}_i{x}^i,g\left(x\right)={\sum }_{j=0}^{\infty }{b}_j{x}^j\in R\left[\left[x\right]\right]$, then $a_i{b}_j\in nil\left(R\right)$ for all i and j. The following characterization of nil power series-wise Armendariz rings is an immediate consequence of Theorem 3.

Corollary 5

([34] (Theorem 1)). A ring R is nil power series-wise Armendariz if and only if $nil\left(R\right)$ is an ideal of R.

In the remainder of this section, we will focus on the relationships between the sets $nil\left(R\right[[S,\omega ]\left]\right)$ and $nil\left(R\right)\left[\right[S,\omega \left]\right]$.

Lemma 3.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that R is $(S,\omega )$-compatible, and for power series $f_1,f_2,\dots ,f_n\in R\left[[S,\omega ]\right]$ consider the following two conditions:

(i)

$f_1{f}_2\cdots f_n\in nil\left(R\right)\left[[S,\omega ]\right]$;

(ii)

$f_1\left(s_1\right)f_2\left(s_2\right)\cdots f_n\left(s_n\right)\in nil\left(R\right)$ for any $s_1,s_2,\dots ,s_n\in S$.

Then we have the following:

(a)

([27] (Proposition 3.10)) If R is $(S,\omega )$-nil-Armendariz, then (i) implies (ii).

(b)

If $nil\left(R\right)$ is a subring of R, then (ii) implies (i).

Proof. (a) is proved in [27] (Proposition 3.10).

(b): Assume that $nil\left(R\right)$ is a subring of R and (ii) holds. Since R is $(S,\omega )$-compatible, Lemma 1 implies that for any $s_1,s_2,\dots ,s_n\in S$ we have

$$f_1\left(s_1\right){\omega }_{s_1}\left(f\left(s_2\right)\right){\omega }_{s_1{s}_2}\left(f\left(s_3\right)\right)\cdots {\omega }_{s_1{s}_2\cdots s_{n-1}}\left(f_n\left(s_n\right)\right)\in nil\left(R\right).$$

(5)

Let $s\in S$ and

$$X_s(f_1,\dots ,f_n)=\{(s_1,\dots ,s_n)\in supp\left(f_1\right)\times \cdots \times supp\left(f_n\right)\mid s_1\cdots s_n=s\}.$$

Then we have the following:

$$(f_1{f}_2\cdots f_n)\left(s\right)=\sum _{(s_1,\dots ,s_n)\in X_s(f_1,\dots ,f_n)}{f}_1\left(s_1\right){\omega }_{s_1}\left(f\left(s_2\right)\right)\cdots {\omega }_{s_1{s}_2\cdots s_{n-1}}\left(f_n\left(s_n\right)\right).$$

Since $nil\left(R\right)$ is a subring of R, it follows from (5) that $(f_1{f}_2\cdots f_n)\left(s\right)\in nil\left(R\right)$, and thus (i) holds. □

The following corollary generalizes [27] (Proposition 3.10).

Corollary 6.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. If R is $(S,\omega )$-compatible and $(S,\omega )$-nil-Armendariz, then for any power series $f_1,f_2,\dots ,f_n\in R\left[[S,\omega ]\right]$ the following conditions are equivalent:

(i)

$f_1{f}_2\cdots f_n\in nil\left(R\right)\left[[S,\omega ]\right]$;

(ii)

$f_1\left(s_1\right)f_2\left(s_2\right)\cdots f_n\left(s_n\right)\in nil\left(R\right)$ for any $s_1,s_2,\dots ,s_n\in S$.

Proof. 

The implication (i) ⇒ (ii) follows from Lemma 3(a), while the opposite implication (ii) ⇒ (i) is a consequence of Proposition 2 and Lemma 3(b). □

For a subset X of a ring R, $r_R\left(X\right)$ denotes the right annihilator of X in R, i.e., $r_R\left(X\right)=\{a\in R\mid Xa=0\}$, whereas the set $N{r}_R\left(X\right)=\{a\in R\mid Xa\subseteq nil\left(R\right)\}$ is called the right weak annihilator of X ([36] (p. 526)). Note that if $X=\left\{1\right\}$, then $N{r}_R\left(X\right)=nil\left(R\right)$.

As we will see in Theorem 4, the concept of a right weak annihilator is useful for characterizing $(S,\omega )$-nil-Armendariz rings. In particular, we will apply the property of right weak annihilators stated in Proposition 3 below.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. For a nonempty subset V of $R\left[\right[S,\omega \left]\right]$ we define $C_V=\{g\left(t\right)\mid g\in V,t\in S\}$.

Proposition 3.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that R is $(S,\omega )$-compatible and $(S,\omega )$-nil-Armendariz, and let V be a nonempty subset of $R\left[\right[S,\omega \left]\right]$. Then we have the following:

(a)

$N{r}_{R\left[\right[S,\omega \left]\right]}\left(V\right)\subseteq N{r}_R\left(C_V\right)\left[[S,\omega ]\right]$.

(b)

If $nil\left(R\right)\left[\right[R,\omega \left]\right]\subseteq nil\left(R\right[[S,\omega ]\left]\right)$, then $N{r}_{R\left[\right[S,\omega \left]\right]}\left(V\right)=N{r}_R\left(C_V\right)\left[[S,\omega ]\right]$.

Proof. (a): Let $f\in N{r}_{R\left[\right[S,\omega \left]\right]}\left(V\right)$. Then $Vf\subseteq nil\left(R\right[[S,\omega ]\left]\right)$. Hence for any $g\in V$ there exists a positive integer n such that ${\left(gf\right)}^n=0$. Thus for any $s,t\in S$, by Corollary 6 we have ${\left(g\left(s\right)f\left(t\right)\right)}^n\in nil\left(R\right)$, and $g\left(s\right)f\left(t\right)\in nil\left(R\right)$ follows, which shows that $C_{V}f\left(t\right)\subseteq nil\left(R\right)$. Therefore, $f\left(t\right)\in N{r}_R\left(C_V\right)$ and, consequently, $f\in N{r}_R\left(C_V\right)\left[[S,\omega ]\right]$, which completes the proof of (a).

(b) By (a), to prove (b), it suffices to show that $N{r}_R\left(C_V\right)\left[[S,\omega ]\right]\subseteq N{r}_{R\left[\right[S,\omega \left]\right]}\left(V\right)$. Let $f\in N{r}_R\left(C_V\right)\left[[S,\omega ]\right]$. Then for any $g\in V$ and $s,t\in S$ we have $g\left(s\right)f\left(t\right)\in nil\left(R\right)$ and thus Corollary 6 implies $gf\in nil\left(R\right)\left[\right[S,\omega \left]\right]=nil\left(R\right[[S,\omega ]\left]\right)$. Thus $Vf\subseteq nil\left(R\right[[S,\omega ]\left]\right)$, that is, $f\in N{r}_{R\left[\right[S,\omega \left]\right]}\left(V\right)$, as desired. □

By applying Proposition 3(a) with $V=\left\{{\mathsf{c}}_1\right\}$, we obtain the following corollary:

Corollary 7

([27] (Corollary 3.11)). Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. If R is $(S,\omega )$-compatible and $(S,\omega )$-nil-Armendariz, then $nil\left(R\right[[S,\omega ]\left]\right)\subseteq nil\left(R\right)\left[\right[S,\omega \left]\right]$.

Now, we establish the promised characterization of $(S,\omega )$-nil-Armendariz rings in the language of right weak annihilators.

Theorem 4.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. If R is $(S,\omega )$-compatible, then the following conditions are equivalent:

(i)

R is $(S,\omega )$-nil-Armendariz and $nil\left(R\right)\left[\right[S,\omega \left]\right]\subseteq nil\left(R\right[[S,\omega ]\left]\right)$.

(ii)

$N{r}_{R\left[\right[S,\omega \left]\right]}\left(V\right)=N{r}_R\left(C_V\right)\left[[S,\omega ]\right]$ for any subset V of $R\left[\right[S,\omega \left]\right]$.

Proof. (i) ⇒ (ii): This implication follows from Proposition 3(b).

(ii) ⇒ (i): Assume (ii). By applying (ii) to $V=\left\{{\mathsf{c}}_1\right\}$, we obtain $nil\left(R\right[[S,\omega ]]=nil(R\left)\right[[S,\omega ]]$. To complete the proof, it suffices to show that R is $(S,\omega )$-nil-Armendariz. For this, consider any $f,g\in R\left[\right[S,\omega \left]\right]$ with $fg\in nil\left(R\right)\left[\right[S,\omega \left]\right]$. Then $fg\in nil\left(R\right[[S,\omega ]\left]\right)$, and by applying (ii) we obtain $g\in N{r}_{R\left[\right[S,\omega \left]\right]}\left(\left\{f\right\}\right)=N{r}_R\left(C_{\left\{f\right\}}\right)\left[[S,\omega ]\right]$. Thus for any $t\in S$ we have $C_{\left\{f\right\}}g\left(t\right)\subseteq nil\left(R\right)$ and, consequently, for any $s,t\in S$ we have $f\left(s\right)g\left(t\right)\in nil\left(R\right)$. Since R is $(S,\omega )$-compatible, by Lemma 1 we obtain $f\left(s\right){\omega }_s\left(g\left(t\right)\right)\in nil\left(R\right)$. Therefore, R is $(S,\omega )$-nil-Armendariz. □

In the following result, which generalizes [28] (Proposition 2.13), we present one more property of right weak annihilators in the context of skew generalized power series rings. As in [28] (p. 8), for a ring R, a strictly ordered monoid $(S,\le )$, and a monoid homomorphism $\omega :S\to End\left(R\right)$, we denote

$$NAn{n}_R\left(2^R\right)=\{N{r}_R\left(U\right)\mid U\subseteq R\},\mathrm{and}$$

$$NAn{n}_{R\left[\right[S,\omega \left]\right]}\left(2^{R\left[\right[S,\omega \left]\right]}\right)=\{N{r}_{R\left[\right[S,\omega \left]\right]}\left(V\right)\mid V\subseteq R\left[[S,\omega ]\right]\}.$$

Thus, $NAn{n}_R\left(2^R\right)$ (resp. $NAn{n}_{R\left[\right[S,\omega \left]\right]}(2^{R\left[\right[S,\omega \left]\right]}$) is the set of all right weak annihilators in R (resp. $R\left[\right[S,\omega \left]\right]$).

Proposition 4.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that R is $(S,\omega )$-compatible and $(S,\omega )$-nil-Armendariz, and $nil\left(R\right)\left[\right[R,\omega \left]\right]\subseteq nil\left(R\right[[S,\omega ]\left]\right)$. Then the map

$$\psi :NAn{n}_R\left(2^R\right)\to NAn{n}_{R\left[\right[S,\omega \left]\right]}\left(2^{R\left[\right[S,\omega \left]\right]}\right),$$

defined by $\psi \left(I\right)=I\left[\right[S,\omega \left]\right]$ for any $I\in NAn{n}_R\left(2^R\right)$, is bijective.

Proof. 

If $I\in NAn{n}_R\left(2^R\right)$, then $I=N{r}_R\left(U\right)$ for some $U\subseteq R$. Hence, by Proposition 3(b), we have the following:

$$\psi \left(I\right)=I\left[[S,\omega ]\right]=N{r}_R\left(U\right)\left[[S,\omega ]\right]=N{r}_{R\left[\right[S,\omega \left]\right]}\left(U\right)\in NAn{n}_{R\left[\right[S,\omega \left]\right]}\left(2^{R\left[\right[S,\omega \left]\right]}\right).$$

Thus $\psi$ indeed maps $NAn{n}_R\left(2^R\right)$ to $NAn{n}_{R\left[\right[S,\omega \left]\right]}\left(2^{R\left[\right[S,\omega \left]\right]}\right)$.

To show that $\psi$ is injective, note that if $I_1,I_2\in NAn{n}_R\left(2^R\right)$ are such that $\psi \left(I_1\right)=\psi \left(I_2\right)$, then $I_1\left[[S,\omega ]\right]=I_2\left[[S,\omega ]\right]$ and $I_1=I_2$ follows.

To show that $\psi$ is surjective, consider any element $J\in NAn{n}_{R\left[\right[S,\omega \left]\right]}\left(2^{R\left[\right[S,\omega \left]\right]}\right)$. Then $J=N{r}_{R\left[\right[S,\omega \left]\right]}\left(V\right)$ for some $V\subseteq R\left[\right[S,\omega \left]\right]$. Hence by Proposition 3(b) we have $J=N{r}_R\left(C_V\right)\left[[S,\omega ]\right]=\psi \left(C_V\right)$. □

Let R be a ring and S be a monoid. For an element $f=a_1{s}_1+\dots +a_n{s}_n$ of the monoid ring $R\left[S\right]$ we denote $\epsilon \left(f\right)=a_1+\cdots +a_n$. In the proof of Proposition 5 we will need the fact that the map $\epsilon :R\left[S\right]\to R$, defined in this way and called the augmentation, is a ring homomorphism. For completeness, we provide the proof of this property.

Lemma 4.

Let R be a ring and S be a monoid. Then, for any $f,g\in R\left[S\right]$, we have $\epsilon (f+g)=\epsilon \left(f\right)+\epsilon \left(g\right)$ and $\epsilon \left(fg\right)=\epsilon \left(f\right)\epsilon \left(g\right)$.

Proof. 

It is clear that $\epsilon (f+g)=\epsilon \left(f\right)+\epsilon \left(g\right)$. To prove that $\epsilon \left(fg\right)=\epsilon \left(f\right)\epsilon \left(g\right)$ as well, let $f=a_1{s}_1+\cdots +a_n{s}_n$ and $g=b_1{t}_1+\dots +b_m{t}_m$. We will proceed by induction on n. If $n=1$, then $fg=a_1{s}_1(b_1{t}_1+\cdots +b_m{t}_m)=\left(a_1{b}_1\right)\left(s_1{t}_1\right)+\cdots +\left(a_1{b}_m\right)\left(s_1{t}_m\right)$ and thus $\epsilon \left(fg\right)=a_1{b}_1+\cdots +a_1{b}_m=a_1(b_1+\cdots +b_m)=\epsilon \left(f\right)\epsilon \left(g\right)$. Assume that $n\ge 2$ and $\epsilon \left(f^{\prime }g\right)=\epsilon \left(f^{\prime }\right)\epsilon \left(g\right)$ holds for any $f^{\prime }\in R\left[S\right]$ of length less that n. Let $f^{\prime }=a_1{s}_1+\cdots +a_{n-1}{s}_{n-1}$. Applying the induction hypothesis, we obtain the following: $\epsilon \left(fg\right)=\epsilon \left((f^{\prime }+a_n{s}_n)g\right)=\epsilon (f^{\prime }g+a_n{s}_{n}g)=\epsilon \left(f^{\prime }g\right)+\epsilon \left(a_n{s}_{n}g\right)=\epsilon \left(f^{\prime }\right)\epsilon \left(g\right)+\epsilon \left(a_n{s}_n\right)\epsilon \left(g\right)=\epsilon (f^{\prime }+a_n{s}_n)\epsilon \left(g\right)=\epsilon \left(f\right)\epsilon \left(g\right),$ which completes the proof. □

Using Lemma 4, we derive the following result.

Proposition 5.

Let R be a ring and $(S,\le )$ be a nontrivial strictly ordered monoid such that $nil\left(R\right)\left[\right[S\left]\right]\subseteq nil\left(R\right[\left[S\right]\left]\right)$. Then $nil\left(R\right)$ is a subring of R.

Proof. 

Since S is nontrivial, there exists $s\in S\setminus \left\{1\right\}$. Let $a,b\in nil\left(R\right)$. Then, using monoid ring notation, $a+bs\in nil\left(R\right)\left[\right[S\left]\right]\subseteq nil\left(R\right[\left[S\right]\left]\right)$, and thus ${(a+bs)}^n=0$ for some positive integer n. Since $R\left[S\right]$ is a subring of $R\left[\right[S\left]\right]$ and $a+bs\in R\left[S\right]$, Lemma 4 implies ${(a+b)}^n=0$ and thus $a+b\in nil\left(R\right)$. Hence $nil\left(R\right)$ is additively closed and, consequently, $nil\left(R\right)$ is a subring of R by Šter’s theorem [1] (Theorem 2.1). □

By applying Proposition 5, we can deduce the following corollary.

Corollary 8.

Let R be a ring and S be a nontrivial monoid such that $nil\left(R\right)\left[S\right]\subseteq nil\left(R\right[S\left]\right)$. Then $nil\left(R\right)$ is a subring of R.

From Corollary 8, we immediately obtain the following result:

Corollary 9

([37] (Proposition 2.1)). If a ring R satisfies $nil\left(R\right)\left[x\right]\subseteq nil\left(R\right[x\left]\right)$, then $nil\left(R\right)$ is a subring of R.

4. Weak Symmetry and Some Related Properties of Skew Generalized Power Series Rings

Recall that a ring R is said to be weak symmetric if for any $a,b,c\in R$, $abc\in nil\left(R\right)$ implies $acb\in nil\left(R\right)$ ([8] (Definition 1)). Although the definition allows for swapping the last two elements in the product $abc\in nil\left(R\right)$, we can also swap the first two elements. Specifically, according to [38] (Theorem 1.2), a ring R is weak symmetric if and only if for any $a,b,c\in R$, $abc\in nil\left(R\right)$ implies $bac\in nil\left(R\right)$. Furthermore, we have the following characterization of weak symmetric rings, which in particular shows that the class of weak symmetric rings coincides with the class of nil-semicommutative rings introduced in [39].

Proposition 6

([38] (Proposition 1.1)). A ring R is weak symmetric if and only if whenever $ab\in nil\left(R\right)$ for $a,b\in R$, then $aRb\subseteq nil\left(R\right)$.

The following three results on nilpotent elements of weak symmetric rings are derived by applying Proposition 6.

Corollary 10.

Let R be a ring and $(S,\le )$ be a nontrivial strictly ordered monoid such that $nil\left(R\right)\left[\right[S\left]\right]\subseteq nil\left(R\right[\left[S\right]\left]\right)$. If R is weak symmetric, then $nil\left(R\right)$ is an ideal of R.

Proof. 

By Proposition 5, $nil\left(R\right)$ is a subring of R. To complete the proof, it suffices to apply Proposition 6. □

Corollary 11.

Let R be a ring and S be a nontrivial monoid such that $nil\left(R\right)\left[S\right]\subseteq nil\left(R\right[S\left]\right)$. If R is weak symmetric, then $nil\left(R\right)$ is an ideal of R.

Proof. 

The result follows from Corollary 8, by considering S as a strictly ordered monoid with respect to the trivial order ≤ on S. □

Corollary 12

([38] (Proposition 1.5(2))). If R is a weak symmetric ring and $nil\left(R\right)\left[x\right]\subseteq nil\left(R\right[x\left]\right)$, then $nil\left(R\right)$ is an ideal of R.

Proof. 

The result is an immediate consequence of Corollary 11. □

In the following proposition, we present a characterization of weak symmetric $(S,\omega )$-nil-Armendariz rings.

Proposition 7.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that R is $(S,\omega )$-compatible and $(S,\omega )$-nil-Armendariz, and $nil\left(R\right[[S,\omega ]\left]\right)=nil\left(R\right)\left[\right[R,\omega \left]\right]$. Then R is weak symmetric if and only if $R\left[\right[S,\omega \left]\right]$ is weak symmetric.

Proof. 

We first prove the “only if” part of the result. Assume that the ring R is weak symmetric, and let $f,g,h$ be any elements of $R\left[\right[S,\omega \left]\right]$ such that $fgh\in nil\left(R\right[[S,\omega ]\left]\right)$. Since $nil\left(R\right[[S,\omega ]\left]\right)=nil\left(R\right)\left[\right[R,\omega \left]\right]$, it follows that $fgh\in nil\left(R\right)\left[\right[S,\omega \left]\right]$ and thus, by Corollary 6, for any $a,b,c\in S$ we have $f\left(a\right)g\left(b\right)h\left(c\right)\in nil\left(R\right)$. Hence, by weak symmetry of R, $f\left(a\right)h\left(c\right)g\left(b\right)\in nil\left(R\right)$ follows. Given the arbitrary choice of elements $a,b,c\in R$, by Corollary 6 we have $fhg\in nil\left(R\right)\left[\right[S,\omega \left]\right]=nil\left(R\right[[S,\omega ]]$. Thus $R\left[\right[S,\omega \left]\right]$ is weak symmetric.

To prove the “if” part, it is sufficient to observe that R is a subring of $R\left[\right[S,\omega \left]\right]$ and that a subring of a weak symmetric ring is also weak symmetric. □

Using Proposition 7, we derive the following relationship between the weak symmetry of the rings R and $R\left[\right[S,\omega \left]\right]$:

Corollary 13

([28] (Proposition 2.11)). Let R be a ring, $(S,\le )$ be a strictly ordered a.n.u.p. monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that R is $(S,\omega )$-compatible and $nil\left(R\right)$ is a nilpotent ideal of R. Then R is weak symmetric if and only if $R\left[\right[S,\omega \left]\right]$ is weak symmetric.

Proof. 

By Corollary 1 and [28] (Theorem 2.6), the ring R is $(S,\omega )$-nil-Armendariz, and $nil\left(R\right[[S,\omega ]\left]\right)=nil\left(R\right)\left[\right[R,\omega \left]\right]$. Hence, applying Proposition 7 completes the proof. □

Zip rings are defined in terms of annihilators, as recalled in Section 1, whereas weak zip rings are defined using weak annihilators. Namely, according to [36], a ring R is said to be weak zip if for any subset $X\subseteq R$ such that $N{r}_R\left(X\right)\subseteq nil\left(R\right)$ there exists a finite subset $Y\subseteq X$ such that $N{r}_R\left(Y\right)\subseteq nil\left(R\right)$. The following observation is useful for studying the weak zip condition in the context of skew generalized power series rings.

Lemma 5.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Then we have the following:

(a)

$nil\left(R\right[[S,\omega ]\left]\right)\subseteq nil\left(R\right)\left[\right[S,\omega \left]\right]$ if and only if $N{r}_{R\left[\right[S,\omega \left]\right]}\left(U\right)\subseteq N{r}_R\left(U\right)\left[[S,\omega ]\right]$ for any nonempty subset U of R.

(b)

$nil\left(R\right[[S,\omega ]\left]\right)\supseteq nil\left(R\right)\left[\right[S,\omega \left]\right]$ if and only if $N{r}_{R\left[\right[S,\omega \left]\right]}\left(U\right)\supseteq N{r}_R\left(U\right)\left[[S,\omega ]\right]$ for any nonempty subset U of R.

(c)

$nil\left(R\right[[S,\omega ]\left]\right)=nil\left(R\right)\left[\right[S,\omega \left]\right]$ if and only if $N{r}_{R\left[\right[S,\omega \left]\right]}\left(U\right)=N{r}_R\left(U\right)\left[[S,\omega ]\right]$ for any nonempty subset U of R.

Proof. (a): To prove the “only if” part, assume that $nil\left(R\right[[S,\omega ]\left]\right)\subseteq nil\left(R\right)\left[\right[R,\omega \left]\right]$, and let $f\in N{r}_{R\left[\right[S,\omega \left]\right]}\left(U\right)$. Then, $Uf\subseteq nil\left(R\right[[S,\omega ]\left]\right)\subseteq nil\left(R\right)\left[\right[S,\omega \left]\right]$ and thus, for any $u\in U$ and $s\in S$, we have $u·f\left(s\right)=\left({\mathsf{c}}_{u}f\right)\left(s\right)\in nil\left(R\right)$ and $f\left(s\right)\in N{r}_R\left(U\right)$ follows. Hence $f\in N{r}_R\left(U\right)\left[[S,\omega ]\right]$.

To prove the “if” part, it suffices to consider the set $U=\left\{1\right\}$.

(b): First, we prove the “only if” part. For, let $f\in N{r}_R\left(U\right)\left[[S,\omega ]\right]$. Then for any $s\in S$ we have $f\left(s\right)\in N{r}_R\left(U\right)$, and thus $U·f\left(s\right)\subseteq nil\left(R\right)$. Hence $\left({\mathsf{c}}_{u}f\right)\left(s\right)=u·f\left(s\right)\in nil\left(R\right)$ for any $u\in U$, and thus ${\mathsf{c}}_{u}f\in nil\left(R\right)\left[[S,\omega ]\right]\subseteq nil(R\left[[S,\omega ]\right]$, which implies $Uf\subseteq nil\left(R\right[[S,\omega ]\left]\right)$. Hence $f\in N{r}_{R\left[\right[S,\omega \left]\right]}\left(U\right)$. As in (a), to prove the “if” part, it suffices to consider the set $U=\left\{1\right\}$.

(c) is an immediate consequence of (a) and (b). □

Using Lemma 5, we obtain the following result:

Proposition 8.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that $nil\left(R\right[[S,\omega ]\left]\right)=nil\left(R\right)\left[\right[R,\omega \left]\right]$. If $R\left[\right[S,\omega \left]\right]$ is weak zip, then R is weak zip.

Proof. 

Assume that $R\left[\right[S,\omega \left]\right]$ is weak zip, and let U be a subset of R such that $N{r}_R\left(U\right)\subseteq nil\left(R\right)$. Then, by applying Lemma 5(c), we obtain

$$N{r}_{R\left[\right[S,\omega \left]\right]}\left(U\right)=N{r}_R\left(U\right)\left[[S,\omega ]\right]\subseteq nil\left(R\right)\left[[S,\omega ]\right]=nil(R\left[[S,\omega ]\right].$$

Hence, since $R\left[\right[S,\omega \left]\right]$ is a weak zip ring, there exists a finite subset $U_0$ of U such that $N{r}_{R\left[\right[S,\omega \left]\right]}\left(U_0\right)\subseteq nil\left(R\left[[S,\omega ]\right]\right)$. Using Lemma 5(c) once again, we obtain

$$N{r}_R\left(U_0\right)\left[[S,\omega ]\right]=N{r}_{R\left[\right[S,\omega \left]\right]}\left(U_0\right)\subseteq nil\left(R\left[[S,\omega ]\right]\right)=nil\left(R\right)\left[[S,\omega ]\right],$$

and thus $N{r}_R\left(U_0\right)\subseteq nil\left(R\right)$. Hence the ring R is weak zip. □

Our next result, which generalizes [28] (Theorem 2.14), provides a characterization of when the skew generalized power series ring $R\left[\right[S,\omega \left]\right]$ is weak zip.

Theorem 5.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that R is $(S,\omega )$-compatible and $(S,\omega )$-nil-Armendariz, and $nil\left(R\right)\left[\right[R,\omega \left]\right]\subseteq nil\left(R\right[[S,\omega ]\left]\right)$. Then R is weak zip if and only if $R\left[\right[S,\omega \left]\right]$ is weak zip.

Proof. 

Assume that R is weak zip. Let V be a subset of $R\left[\right[S,\omega \left]\right]$ such that $N{r}_{R\left[\right[S,\omega \left]\right]}\left(V\right)\subseteq nil\left(R\left[[S,\omega ]\right]\right)$. It follows from Proposition 3(b) and Corollary 7 that

$$N{r}_R\left(C_V\right)\left[[S,\omega ]\right]=N{r}_{R\left[\right[S,\omega \left]\right]}\left(V\right)\subseteq nil\left(R\left[[S,\omega ]\right]\right)\subseteq nil\left(R\right)\left[[S,\omega ]\right]$$

and thus $N{r}_R\left(C_V\right)\subseteq nil\left(R\right)$. Since R is weak zip, there exists a finite subset $W=\{w_1,\dots ,w_m\}\subseteq C_V$ such that $N{r}_R\left(W\right)\subseteq nil\left(R\right)$. For any $w_i$, there exists $f_i\in V$ and $s_i\in S$ such that $w_i=f_i\left(s_i\right)$. Let $V_0=\{f_1,\dots ,f_m\}$. Then $V_0$ is a finite subset of V and $W\subseteq C_{V_0}$. Hence $N{r}_R\left(C_{V_0}\right)\subseteq N{r}_R\left(W\right)\subseteq nil\left(R\right)$, and thus, by Proposition 3(b), we obtain

$$N{r}_{R\left[\right[S,\omega \left]\right]}\left(V_0\right)=N{r}_R\left(C_{V_0}\right)\left[[S,\omega ]\right]\subseteq nil\left(R\right)\left[[S,\omega ]\right]\subseteq nil\left(R\left[[S,\omega ]\right]\right).$$

Therefore, $R\left[\right[S.\omega \left]\right]$ is weak zip.

To prove the “if” part, it suffices to combine Corollary 7 and Proposition 8. □

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Recall from [14] (Definition 2.1) that the ring R is said to be $(S,\omega )$-quasi-Armendariz if for any $f,g\in R\left[\right[S,\omega \left]\right]$, $fR\left[\right[S,\omega \left]\right]g=0$ implies $f\left(u\right){\omega }_u\left(R{\omega }_s\left(g\left(v\right)\right)\right)=0$ for all $u,s,v\in S$.

As in [10] (Definition 4.11), an ordered monoid $(S,\le )$ is called quasi-totally ordered if ≤ can be refined to an order ⪯ with respect to which S becomes a strictly totally ordered monoid. The following proposition generalizes the classical result by Hirano [5] (Corollary 3.8), which states that all semiprime rings are quasi-Armendariz, and also generalizes [28] (Proposition 3.2).

Proposition 9.

Let R be a semiprime ring, $(S,\le )$ be a quasi-totally ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism such that ${\omega }_s$ is surjective for all $s\in S$. Then the ring R is $(S,\omega )$-quasi-Armendariz.

Proof. 

To derive a contradiction, suppose that R is not $(S,\omega )$-quasi-Armendariz. Then, there exist $f,g\in R\left[\right[S,\omega \left]\right]$ and $s_0\in S$ such that $fR\left[\right[S,\omega \left]\right]g=0$ and the set

$$T=\{u{s}_{0}v\mid u,v\in S,f\left(u\right){\omega }_u\left(R{\omega }_{s_0}\left(g\left(v\right)\right)\right)\ne 0\}$$

is nonempty. By assumption, the order ≤ can be refined to an order ⪯ on S such that $(S,⪯)$ is a strictly totally ordered monoid. Since $T\subseteq supp\left(f\right)·\left\{s_0\right\}·supp\left(g\right)$, T is artinian and narrow with respect ≤, and thus T is well-ordered with respect to ⪯. Hence there exists the smallest element t of T with respect to ⪯. Let us consider the set

$$W=\{(u,v)\in S\times S\mid u{s}_{0}v\in T,u{s}_{0}v=t\}.$$

Since $W\subseteq supp\left(f\right)\times supp\left(g\right)$ and $supp\left(f\right),supp\left(g\right)$ are artinian and narrow, it follows that W is finite. Let $W=\{(u_1,v_1),\dots ,(u_n,v_n)\}$ with $v_1⪯v_2⪯\dots ⪯v_n$. Note that $v_i=v_j$ implies $u_i{s}_0{v}_j=u_i{s}_0{v}_i=t=u_j{s}_0{v}_j$; hence, $u_i=u_j$ and thus $(u_i,v_i)=(u_j,v_j)$. Therefore, it must be $v_1\prec v_2\prec \dots \prec v_n$.

Since $fR\left[\right[S,\omega \left]\right]g=0$, for any $r\in R$ we have the following:

$$0=f{\mathsf{c}}_r{\mathsf{e}}_{s_0}g\left(t\right)=\sum _{i=1}^{n}f\left(u_i\right){\omega }_{u_i}\left(r{\omega }_{s_0}\left(g\left(v_i\right)\right)\right).$$

(6)

If $n=1$, then $0=f\left(u_1\right){\omega }_{u_1}\left(r{\omega }_{s_0}\left(g\left(v_1\right)\right)\right)$ for any $r\in R$. Hence $u_1{s}_0{v}_1\notin T$ and thus $(u_1,v_1)\notin W$, a contradiction. Therefore, $n>1$. Let $1<i\le n$ be arbitrary. Then $u_i{s}_0{v}_1\prec u_i{s}_0{v}_i=t$, and thus the minimality of t implies that $u_i{s}_0{v}_1\notin T$, which in turn implies that $f\left(u_i\right){\omega }_{u_i}\left(R{\omega }_{s_0}\left(g\left(v_1\right)\right)\right)=0$. Thus, for any elements $a,b\in R$, by setting $r=a{\omega }_{s_0}\left(g\left(v_1\right)\right)b$ in (6), we obtain

$$0=\sum _{i=1}^{n}f\left(u_i\right){\omega }_{u_i}\left(a{\omega }_{s_0}\left(g\left(v_1\right)\right)b{\omega }_{s_0}\left(g\left(v_i\right)\right)\right)=f\left(u_1\right){\omega }_{u_1}\left(a{\omega }_{s_0}\left(g\left(v_1\right)\right)b{\omega }_{s_0}\left(g\left(v_1\right)\right)\right)=$$

$$=f\left(u_1\right){\omega }_{u_1}\left(a\right){\omega }_{u_1}\left({\omega }_{s_0}\left(g\left(v_1\right)\right)\right){\omega }_{u_1}\left(b\right){\omega }_{u_1}\left({\omega }_{s_0}\left(g\left(v_1\right)\right)\right).$$

Since ${\omega }_{u_1}$ is surjective, it follows that $f\left(u_1\right)R{\omega }_{u_1}\left({\omega }_{s_0}\left(g\left(v_1\right)\right)\right)R{\omega }_{u_1}\left({\omega }_{s_0}\left(g\left(v_1\right)\right)\right)=0$. Given that R is semiprime, we conclude that $f\left(u_1\right)R{\omega }_{u_1}\left({\omega }_{s_0}\left(g\left(v_1\right)\right)\right)=0.$ Hence $(u_1,v_1)\notin W$, and this contradiction completes the proof. □

For $(S,\omega )$-quasi-Armendariz rings we also have the following result.

Proposition 10.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. If the ring R is $(S,\omega )$-quasi-Armendariz and I is a right ideal of $R\left[\right[S,\omega \left]\right]$ such that $r_{R\left[\right[S,\omega \left]\right]}\left(I\right)\ne 0$, then $r_R\left(I\right)\ne 0$.

Proof. 

Let $0\ne g\in r_{R\left[\right[S,\omega \left]\right]}\left(I\right)$. Then $Ig=0$, and thus $fR\left[\right[S,\omega \left]\right]g=0$ for any $f\in I$. Since R is $(S,\omega )$-quasi-Armendariz, we have the following:

$$f\left(u\right){\omega }_u\left(g\left(v\right)\right)=0\mathrm{for}\mathrm{all}u,v\in S.$$

(7)

Since g is a nonzero element of $R\left[\right[S,\omega \left]\right]$, $0\ne r=g\left(v\right)\in R$ for some $v\in S$. By (7), for this element r we have $f{\mathsf{c}}_r=fr=0$. Hence $r\in r_R\left(f\right)$ for any $f\in I$, and thus $r_R\left(I\right)\ne 0$. □

By combining Propositions 9 and 10, we obtain the following corollary.

Corollary 14

([28] (Theorem 3.3)). Let R be a semiprime ring, $(S,\le )$ be a quasi-totally ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism such that ${\omega }_s$ is surjective for all $s\in S$. If $r_{R\left[\right[S,\omega \left]\right]}\left(I\right)\ne 0$, then $r_R\left(I\right)\ne 0$ for any right ideal I of $R\left[\right[S,\omega \left]\right]$.

A ring R is said to be semicommutative if $ab=0$ implies $arb=0$ for any $a,b,r\in R$ (semicommutative and symmetric rings without unity are discussed in [40]). The following theorem is a generalization of the well-known result of Camillo and Nielsen [41] (Proposition 5.3) that all semicommutative rings are right linearly McCoy. This theorem generalizes [28] (Theorem 3.17) as well.

Theorem 6.

Let R be a semicommutative ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. If R is $(S,\omega )$-compatible, then the following conditions are equivalent:

(i)

R is right linearly $(S,\omega )$-McCoy.

(ii)

R is left linearly $(S,\omega )$-McCoy.

(iii)

$s^2\notin \{1,s\}$ for any $s\in S\setminus \left\{1\right\}$.

Proof. (i) ⇒ (iii): Assume (i) and suppose that (iii) fails. Then, $s^2=1$ or $s^2=s$ for some $s\in S\setminus \left\{1\right\}$. Note that if $s^2=1$, then $(1-{\mathsf{e}}_s)(1+{\mathsf{e}}_s)=0$, and if $s^2=s$, then $(1-{\mathsf{e}}_s){\mathsf{e}}_s=0$. Hence, by (i), in both cases there exists $0\ne r\in R$ such that $(1-{\mathsf{e}}_s){\mathsf{c}}_r=0$. But the last equality implies $r=0$, a contradiction.

(iii) ⇒ (i): Assume (iii) and let $s\in S\setminus \left\{1\right\}$. Let $f={\mathsf{c}}_{a_0}+{\mathsf{c}}_{a_1}{\mathsf{e}}_s$ and $g={\mathsf{c}}_{b_0}+{\mathsf{c}}_{b_1}{\mathsf{e}}_s$ be elements of $R\left[\right[S,\omega \left]\right]$ such that $f\ne 0$, $g\ne 0$ and $fg=0$. To obtain (i), it suffices to show that $f{\mathsf{c}}_r=0$ for some $r\in R\setminus \left\{0\right\}$. Since $fg=0$ and by (iii) the elements $1,s,s^2$ are distinct, we have the following:

$$a_0{b}_0=0,a_0{b}_1+a_1{\omega }_s\left(b_0\right)=0,a_1{\omega }_s\left(b_1\right)=0.$$

(8)

If $b_1=0$, then we can take $r=b_0$. If $b_1\ne 0$ and $a_0{b}_1=0$, then we can set $r=b_1$. We are left with the case where $a_0{b}_1\ne 0$. Since R is $(S,\omega )$-compatible and semicommutative, it follows from the first equation in (8) that $a_{0}R{\omega }_s\left(b_0\right)=0$, and thus, from the second equation in (8), we obtain $a_0^2{b}_1=0$. Since a consequence of the thirst equation in (8) is $a_{1}R{\omega }_s\left(b_1\right)=0$, then for $r=a_0{b}_1$ we have $f{\mathsf{c}}_r=0$.

We have shown that (i) and (iii) are equivalent. Equivalence (ii) ⇔ (iii) can be proved analogously. □

The following theorem is a generalization of [28] (Theorem 3.22).

Theorem 7.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that R is $(S,\omega )$-compatible and $(S,\omega )$-nil-Armendariz. If $f,g\in R\left[\right[S,\omega \left]\right]$ are such that $fg\in nil\left(R\right)\left[\right[S,\omega \left]\right]$ (in particular, if $fg=0$) and $r_R\left(nil\left(R\right)\right)\ne 0$ (respectively, $l_R\left(nil\left(R\right)\right)\ne 0$), then f or g has a non-zero right (respectively, left) annihilator in R.

Proof. 

Assume that $r_R\left(nil\left(R\right)\right)\ne 0$. Since R is both $(S,\omega )$-nil-Armendariz and $(S,\omega )$-compatible, and $fg\in nil\left(R\right)\left[\right[S,\omega \left]\right]$, it follows from Corollary 6 that $f\left(s\right)g\left(t\right)\in nil\left(R\right)$ for any $s,t\in S$. Given that $r_R\left(nil\left(R\right)\right)\ne 0$, there exists $a\in R\setminus \left\{0\right\}$ such that

$$f\left(s\right)g\left(t\right)a=0\mathrm{for}\mathrm{all}s,t\in S.$$

(9)

If $g\left(t\right)a=0$ for all $t\in S$, then using $(S,\omega )$-compatibility of R we obtain $g{\mathsf{c}}_a=0$, that is, $r_R\left(g\right)\ne 0$. Otherwise $g\left(t_0\right)a\ne 0$ for some $t_0$. In this case, using (9) and $(S,\omega )$-compatibility of R we obtain for $b=g\left(t_0\right)a$ that $f{\mathsf{c}}_b=0$, and thus $r_R\left(f\right)\ne 0$.

The case $l_R\left(nil\left(R\right)\right)\ne 0$ can be proved analogously. □

Recall that a ring R is called von Neumann regular if, for every element $a\in R$, there exists an element $b\in R$ such that $a=aba$.

Proposition 11.

Let R be a ring, $(S,\le )$ be a strictly ordered monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that R is von Neumann regular and ${\omega }_s$ is compatible for some $s\in S\setminus \left\{1\right\}$. If R is right linearly $(S,\omega )$-McCoy, then R is reduced.

Proof. 

Let $s\in S\setminus \left\{1\right\}$ be such that ${\omega }_s$ is compatible. Suppose R is not reduced. Then there exists $a\in R\setminus \left\{0\right\}$ such that $a^2=0$. Since R is von Neumann regular, $a=aba$ for some $b\in R$. Denote $e=1-ab$ and consider elements $f=eb(1-e)+es,g=eba-as$ of $R\left[\right[S,\omega \left]\right]$ (written in monoid ring notation). It is easy to see that if an endomorphism $\alpha$ is compatible, then $\alpha \left(x\right)=x$ for any idempotent $x=x^2$. Hence ${\omega }_s\left(eba\right)={\omega }_s\left(e\right){\omega }_s\left(ba\right)=eba$. Furthermore, since $ea=0$, and ${\omega }_s$ is compatible, $e{\omega }_s\left(a\right)=0$ also holds. Therefore, $fg=0$ with $g\ne 0$, and since R is right linearly $(S,\omega )$-McCoy, $f{c}_r=0$ for some $r\in R\setminus \left\{0\right\}$. This yields $eb(1-e)r=0$ and $e{\omega }_s\left(r\right)=0$, and since R is $(S,\omega )$-compatible, $er=0$ also holds. Thus, using the equality $eb(1-e)r=0$, we obtain $ebr=0$. Therefore, $r=(1-e)r=abr=a(1-e)br=a\left(ab\right)br=a^2{b}^{2}r=0$, a contradiction. □

We close this Section with the following generalization of [28] (Proposition 3.25).

Proposition 12.

Let R be a ring, $(S,\le )$ be a nontrivial strictly ordered a.n.u.p. monoid, and $\omega :S\to End\left(R\right)$ be a monoid homomorphism. Assume that R is von Neumann regular and $(S,\omega )$-compatible. Then the following conditions are equivalent:

(i)

R is right $(S,\omega )$-McCoy.

(ii)

R is right linearly $(S,\omega )$-McCoy.

(iii)

R is $(S,\omega )$-Armendariz.

Proof. 

Implications (i) ⇒ (ii) and (iii) ⇒ (i) are obvious. It remains to prove implication (ii) ⇒ (iii). Assume that (ii) holds. Then, by Proposition 11 we conclude that R is reduced, and thus, by [42] (Lemma 2.2), the ring R is S-rigid. Finally, using [10] (Theorem 4.12), we obtain (iii), as desired. □

5. Conclusions

The construction of the skew generalized power series ring includes, as specific cases, a wide range of classical ring-theoretic extensions, such as polynomial rings, Laurent polynomial rings, power series rings, Laurent series rings, Mal’cev–Neumann series rings, group rings, and the skew versions of all of these. The advantage of studying skew generalized power series rings lies in the fact that any general results about them have counterparts in each of these specific ring extensions. In this paper, such general results are obtained for nilpotent elements and certain ring properties expressed in terms of nilpotent elements and annihilators. Interesting and important directions for future research on skew generalized power series rings include classical radicals and localizations of these rings. The results obtained in this paper, concerning nilpotent elements, may be useful in the study of nil (and related) radicals of skew generalized power series rings.