Early Fault Diagnosis of Bearings Based on Symplectic Geometry Mode Decomposition Guided by Optimal Weight Spectrum Index
Abstract
:1. Introduction
- An SGMD signal reconstruction method guided by the optimal weight spectrum index is proposed to screen out sensitive components reflecting fault characteristics and reduce the influence of noise and interference components.
- Using the information of health and fault signals, the optimal weight spectrum is generated to generate effective fault indicators and provide a robust framework for fault detection.
- Validation of the proposed methodology can be conducted through signal experiments focused on early bearing faults, which substantiates its efficacy in practical applications.
2. Methodological Theory
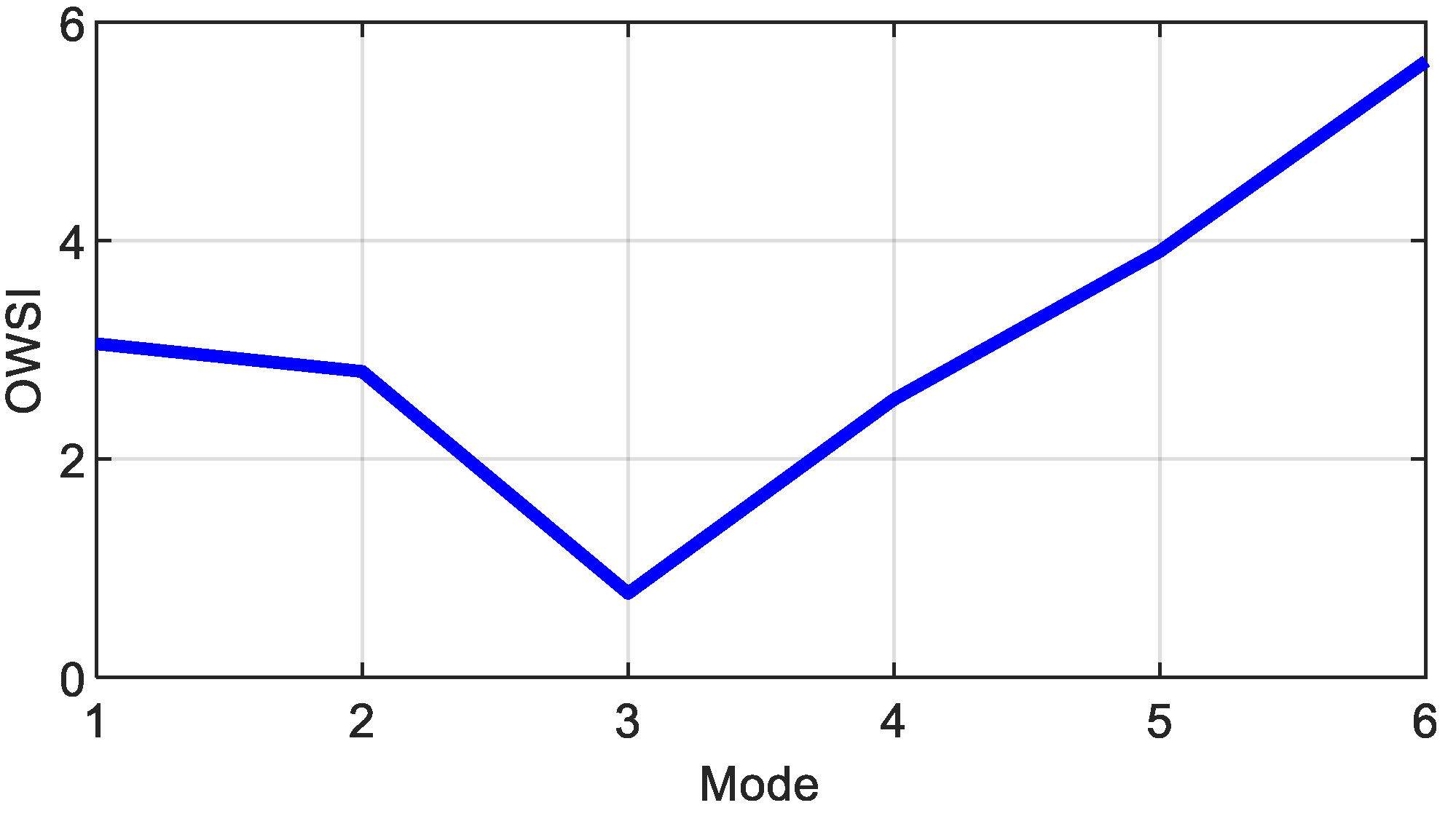
2.1. Optimal Weight Spectrum Theory
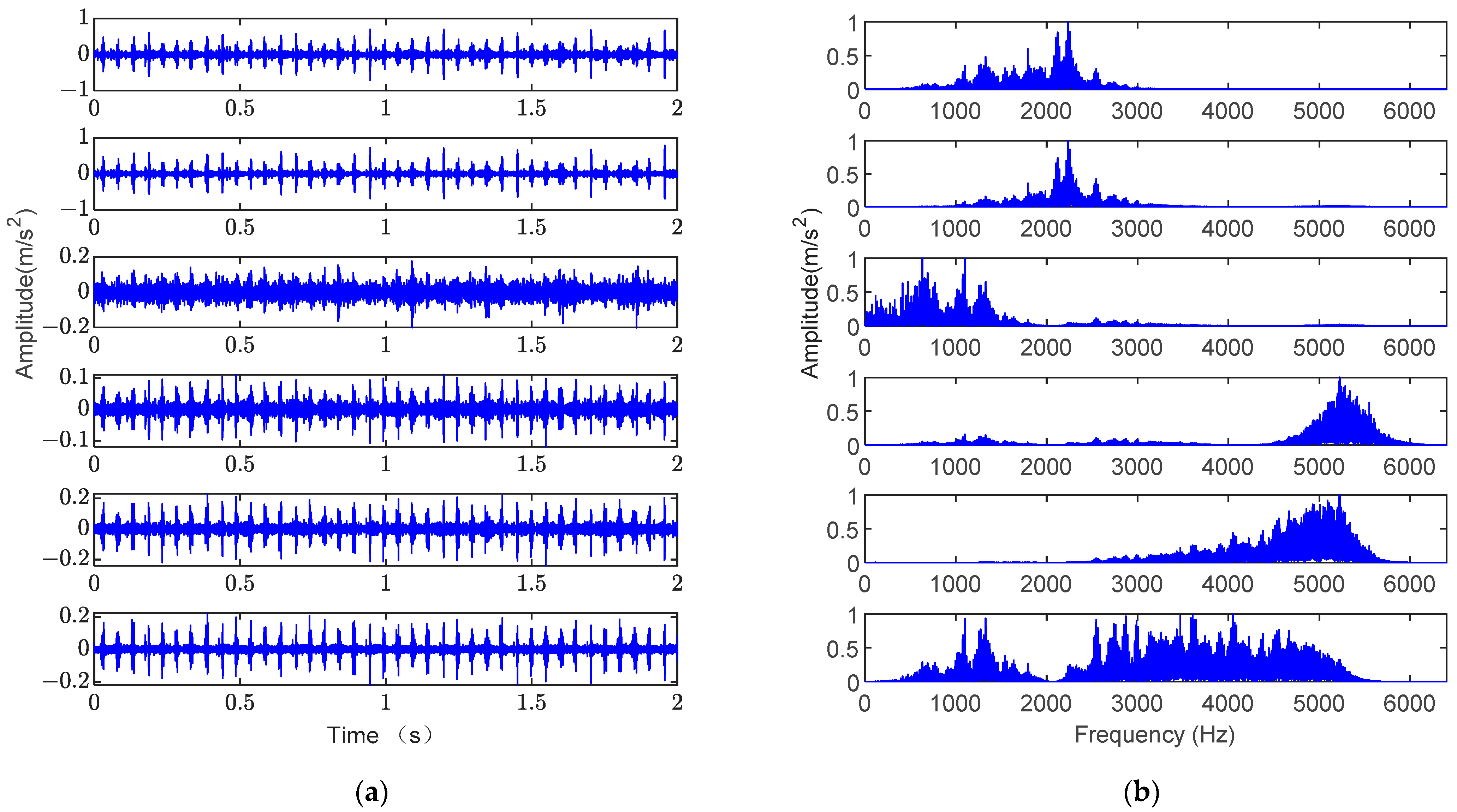
2.2. The Theory of SGMD
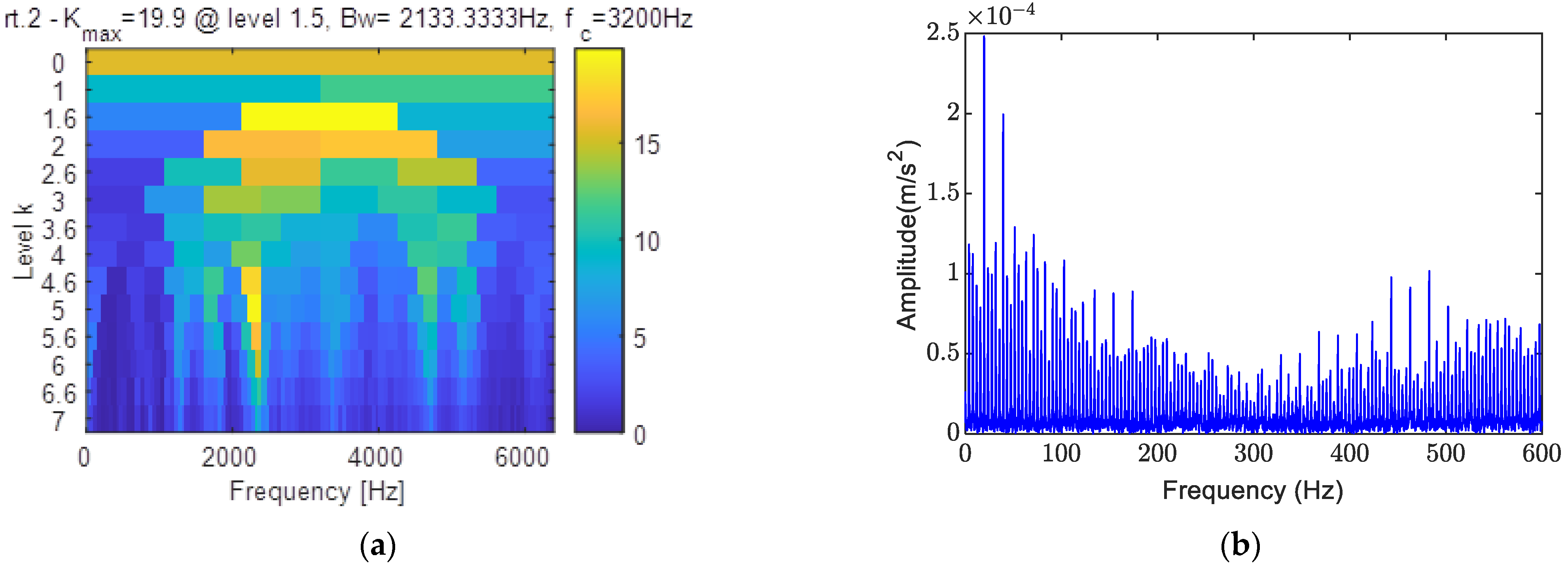
3. The Process of the Proposed Method
4. Experimental Verification and Discussion
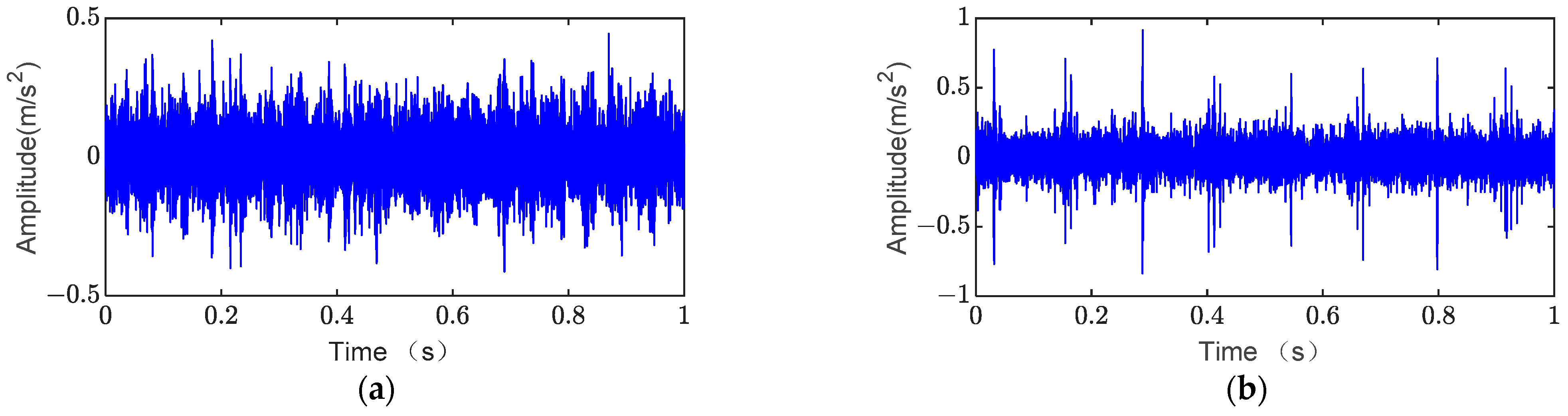
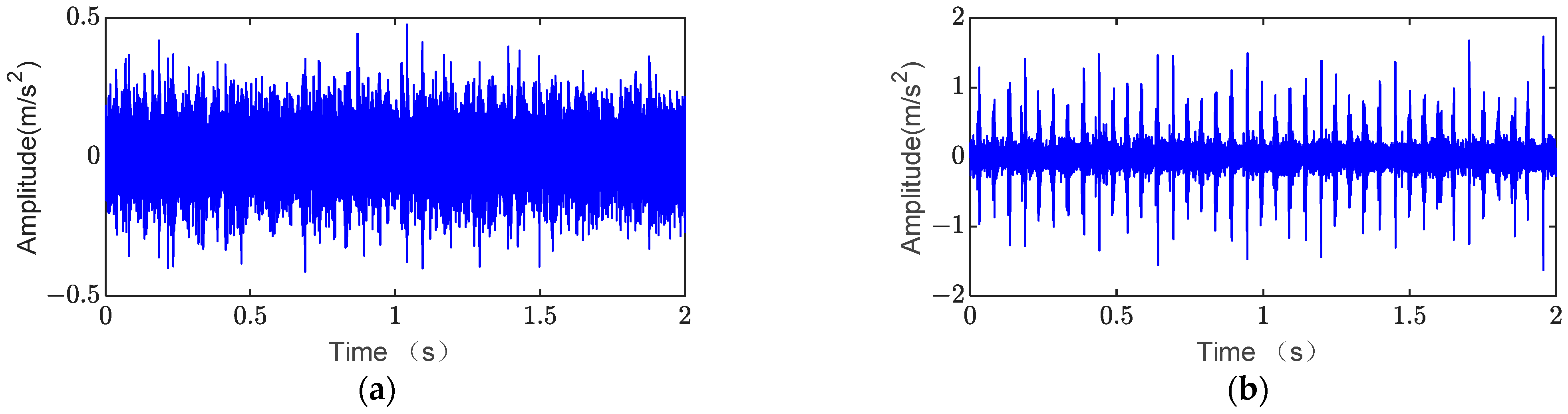
4.1. Experimental Setup
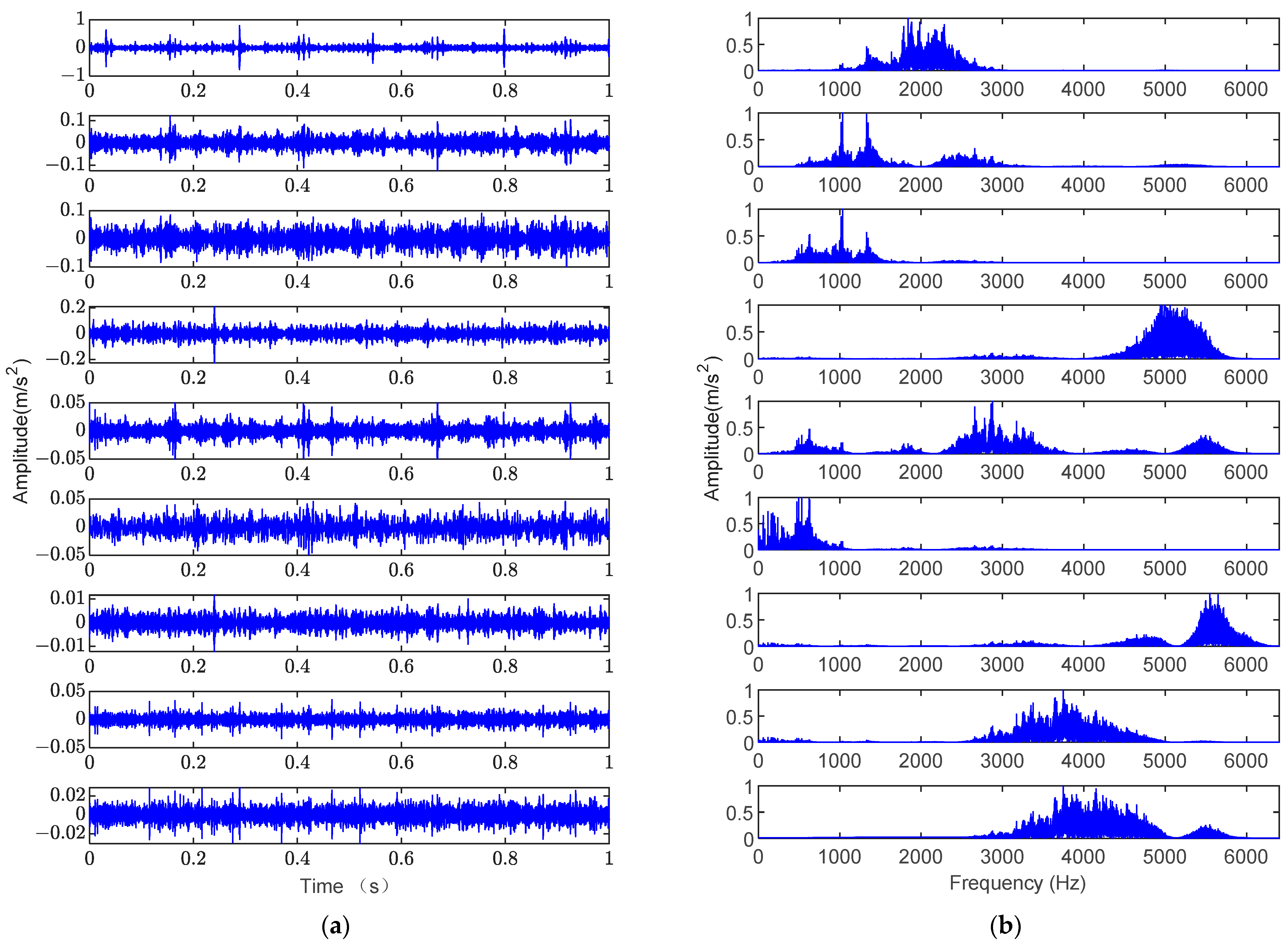
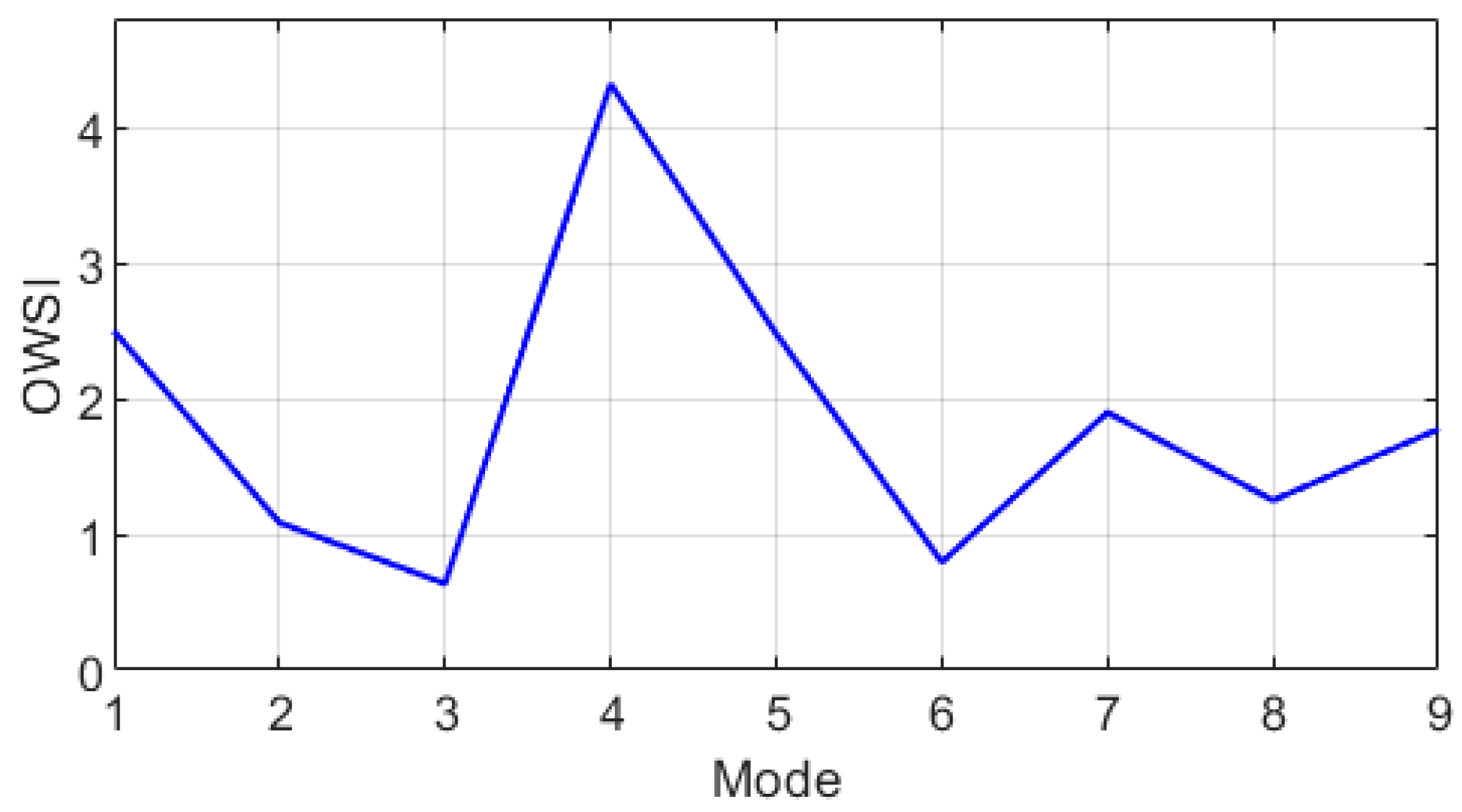
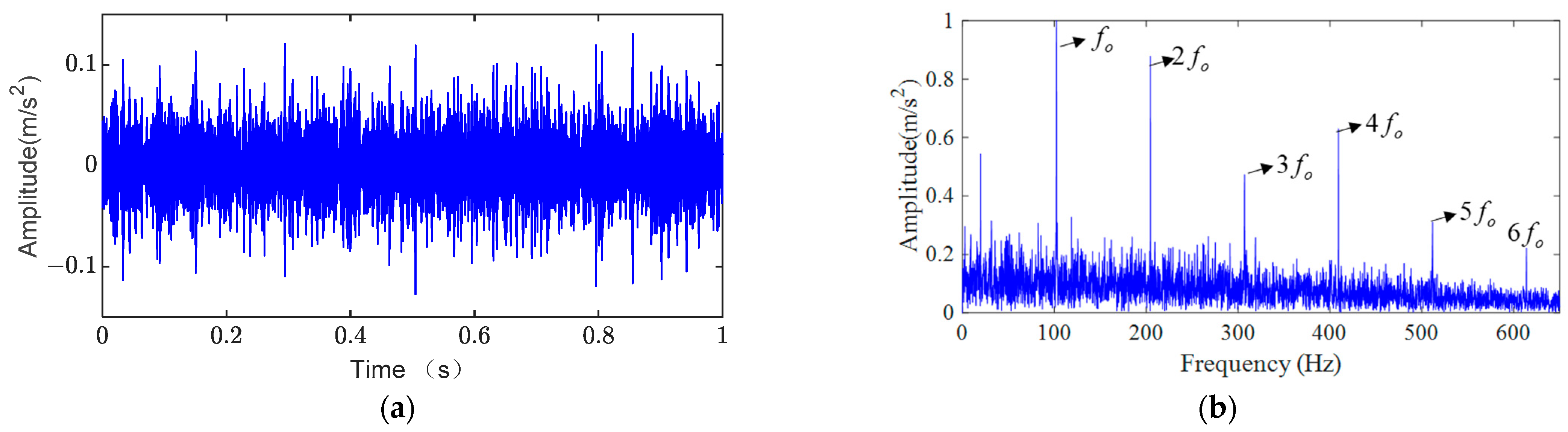
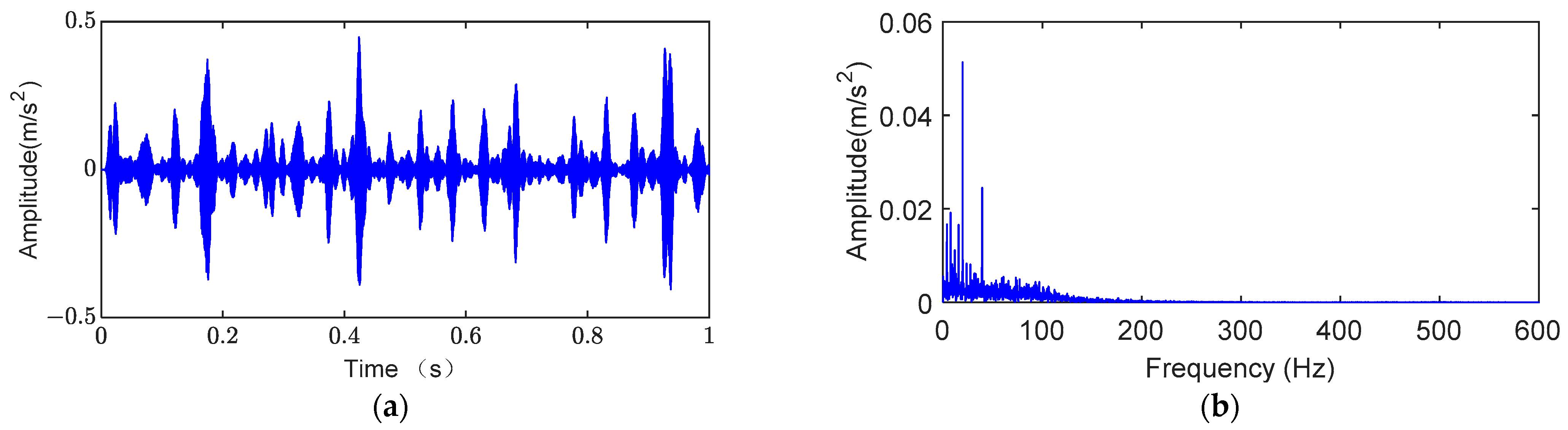
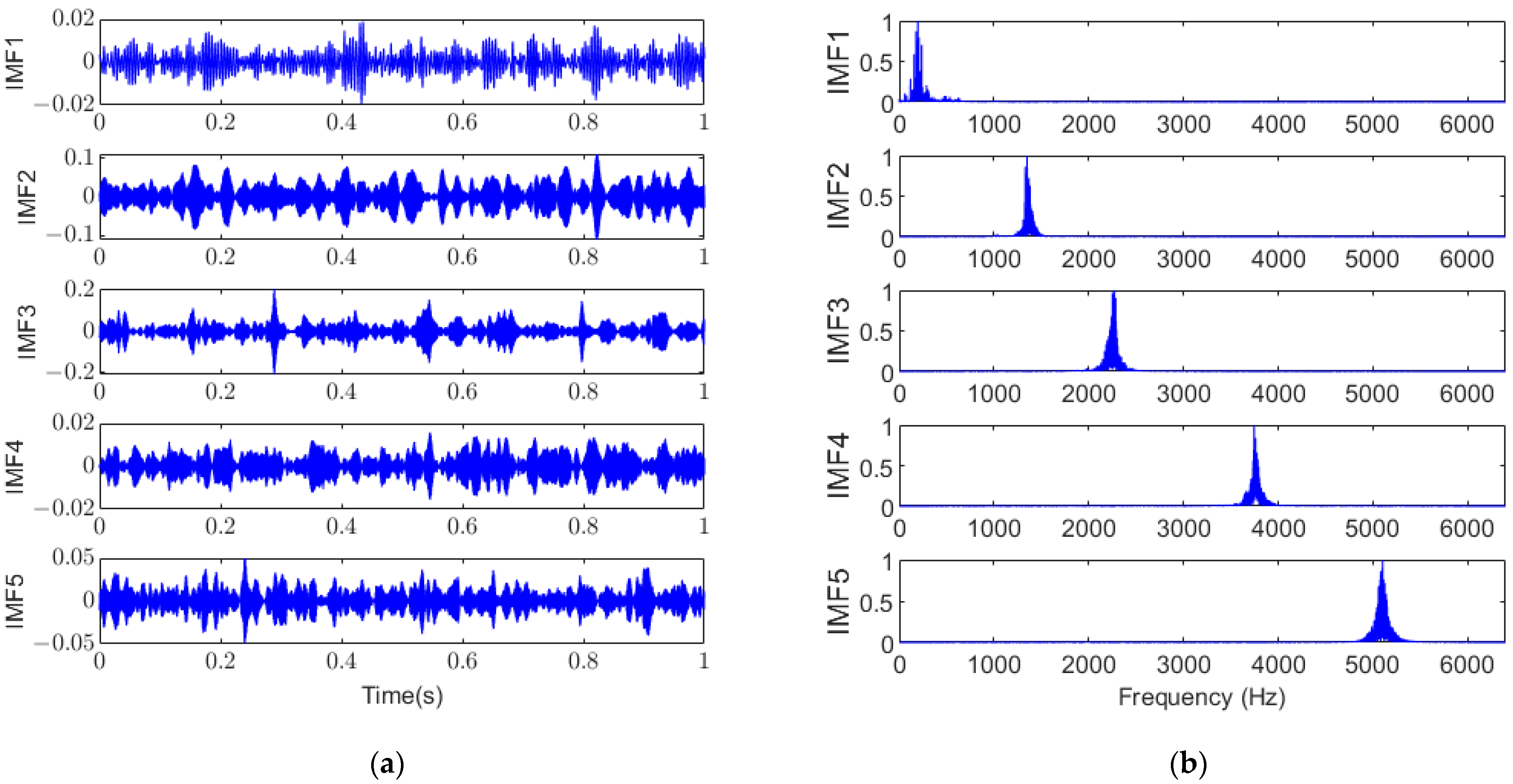
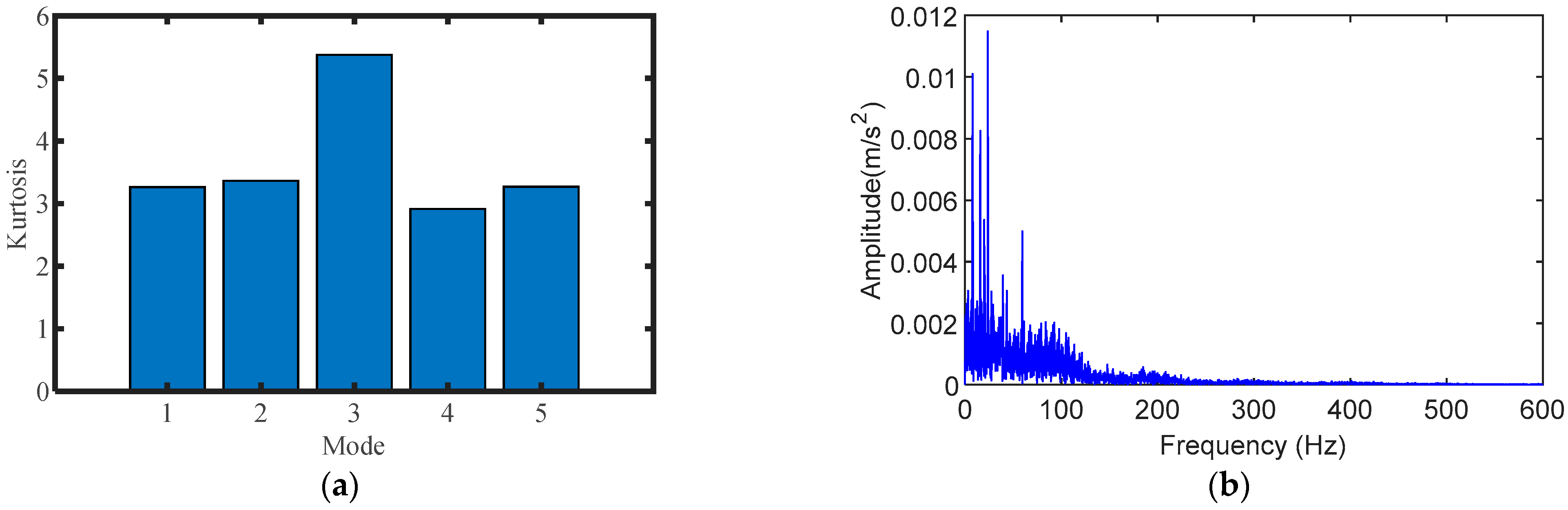
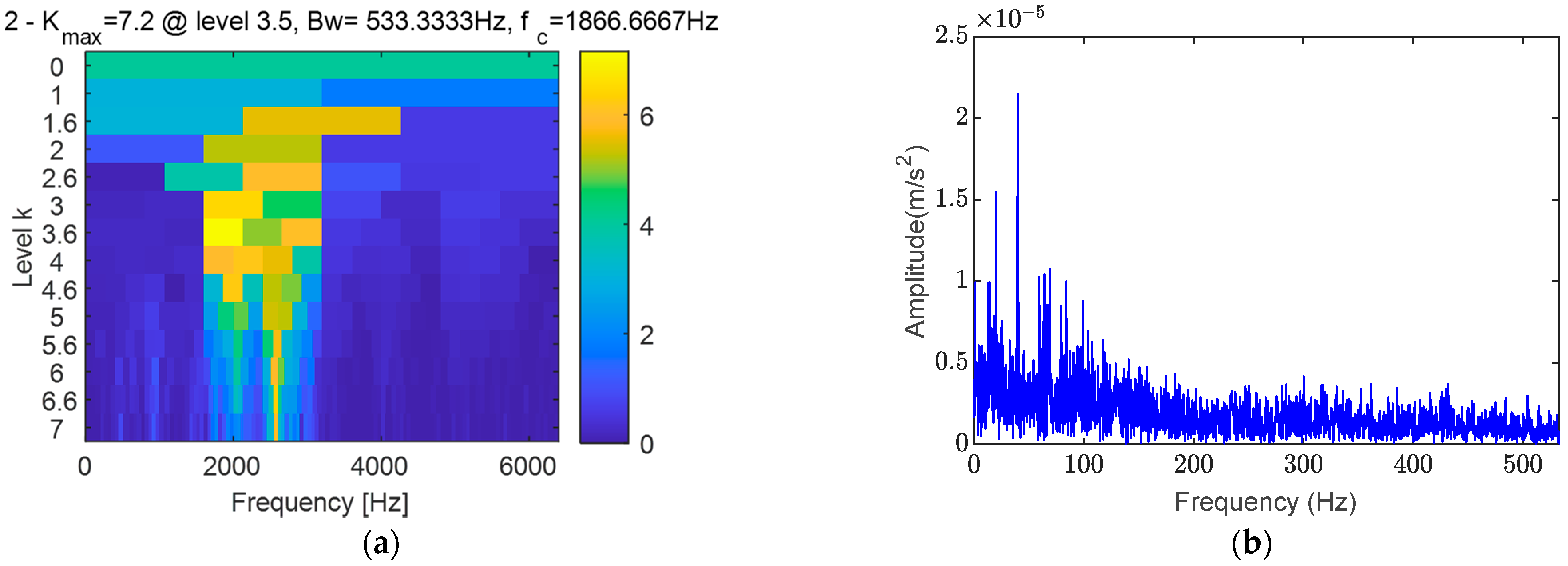
4.2. Outer Ring Fault Analysis
4.3. Inner Ring Failure Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SGMD | Symplectic geometry mode decomposition |
| OWSI | Optimal weight spectrum index |
| SGCs | Symplectic geometric modal components |
| VMD | Variational Mode Decomposition |
| FMD | Feature Mode Decomposition |
| SK | Spectral Kurtosis |
| TFA | Time-frequency analysis |
| EMD | Empirical mode decomposition |
| WT | Wavelet transform |
| SVD | Singular value decomposition |
| TET | Transient-extraction transform |
| DD-ACMD | Data-driven adaptive chirp mode decomposition |
| EEMD | Ensemble Empirical Mode Decomposition |
| MED | Minimum Entropy Deconvolution |
| MCKD | Maximum Correlated Kurtosis Deconvolution |
| SGST | Symplectic Geometric Similar Transform |
| AWSGD | Adaptive Weighted Piezometric Decomposition |
References
- Zhou, P.; Chen, S.; He, Q.; Wang, D.; Peng, Z. Rotating machinery fault-induced vibration signal modulation effects: A review with mechanisms, extraction methods and applications for diagnosis. Mech. Syst. Signal Process. 2023, 200, 110489. [Google Scholar] [CrossRef]
- Kong, X.; Li, X.; Zhou, Q.; Hu, Z.; Shi, C. Attention Recurrent Autoencoder Hybrid Model for Early Fault Diagnosis of Rotating Machinery. IEEE Trans. Instrum. Meas. 2021, 70, 2505110. [Google Scholar] [CrossRef]
- Hong, Y.; Kim, M.; Lee, H.; Park, J.J.; Lee, D. Early Fault Diagnosis and Classification of Ball Bearing Using Enhanced Kurtogram and Gaussian Mixture Model. IEEE Trans. Instrum. Meas. 2019, 68, 4746–4755. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Wang, X.; Liu, B.; Liang, X. Early fault diagnosis of rolling bearings based on hierarchical symbol dynamic entropy and binary tree support vector machine. J. Sound Vib. 2018, 428, 72–86. [Google Scholar] [CrossRef]
- Qin, Y. A New Family of Model-Based Impulsive Wavelets and Their Sparse Representation for Rolling Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 2716–2726. [Google Scholar] [CrossRef]
- Li, Z.; Gao, J.; Li, H.; Zhang, Z.; Liu, N.; Zhu, X. Synchroextracting transform: The theory analysis and comparisons with the synchrosqueezing transform. Signal Process. 2020, 166, 107243. [Google Scholar] [CrossRef]
- Yu, G.; Huang, X.; Lin, T.; Dong, H. A non-linear time–frequency tool for machinery fault diagnosis under varying speed condition. Mech. Syst. Signal Process. 2023, 186, 109849. [Google Scholar] [CrossRef]
- Dong, H.; Yu, G.; Lin, T.; Li, Y. An energy-concentrated wavelet transform for time-frequency analysis of transient signal. Signal Process. 2023, 206, 108934. [Google Scholar] [CrossRef]
- Yu, G. A Concentrated Time-Frequency Analysis Tool for Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2019, 69, 371–381. [Google Scholar] [CrossRef]
- Miao, Y. Automatic instantaneous frequency estimator for multicomponent signals with the variable number of components. Signal Process. 2022, 197, 108541. [Google Scholar] [CrossRef]
- Wang, H.; Chen, S.; Zhai, W. Data-driven adaptive chirp mode decomposition with application to machine fault diagnosis under non-stationary conditions. Mech. Syst. Signal Process. 2023, 188, 109997. [Google Scholar] [CrossRef]
- Zhang, Y.; Xing, K.; Bai, R.; Sun, D.; Meng, Z. An enhanced convolutional neural network for bearing fault diagnosis based on time–frequency image. Measurement 2020, 157, 107667. [Google Scholar] [CrossRef]
- Xia, S.; Zhang, J.; Ye, S.; Xu, B.; Xiang, J.; Tang, H. A mechanical fault detection strategy based on the doubly iterative empirical mode decomposition. Appl. Acoust. 2019, 155, 346–357. [Google Scholar] [CrossRef]
- Lazhari, M.; Sadhu, A. Decentralized modal identification of structures using an adaptive empirical mode decomposition method. J. Sound Vib. 2019, 447, 20–41. [Google Scholar] [CrossRef]
- Zhao, H.W.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adaptive Data Anal. 2009, 1, 1–41. [Google Scholar]
- Lei, Y.; He, Z.; Zi, Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Li, S. Research on test bench bearing fault diagnosis of improved EEMD based on improved adaptive resonance technology. Measurement 2021, 185, 109986. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Pan, J.; Chen, G.; Zi, Y.; Yuan, J.; Chen, B.; He, Z. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2016, 70–71, 1–35. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Rolling element bearing fault diagnosis using wavelet transform. Neurocomputing 2011, 74, 1638–1645. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, N.; Li, N.; Du, W.; Wang, J. A new fault diagnosis method based on adaptive spectrum mode extraction. Struct. Health Monit. 2021, 20, 3354–3370. [Google Scholar] [CrossRef]
- Wang, Z.; Du, W.; Wang, J.; Zhou, J.; Han, X.; Zhang, Z.; Huang, L. Research and application of improved adaptive MOMEDA fault diagnosis method. Measurement 2019, 140, 63–75. [Google Scholar] [CrossRef]
- Sun, Y.; Jian, M.; Zhang, X.; Dong, J.; Shen, L.; Chen, B. Reconstruction of normal and albedo of convex Lambertian objects by solving ambiguity matrices using SVD and optimization method. Neurocomputing 2016, 207, 95–104. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, B.; Liu, Y.; Zhang, H. Fault Feature-Extraction Method of Aviation Bearing Based on Maximum Correlation Re’nyi Entropy and Phase-Space Reconstruction Technology. Entropy 2022, 24, 1459. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Xu, Y.; Zhang, K.; Zhang, X. Singular component decomposition and its application in rolling bearing fault diagnosis. Meas. Sci. Technol. 2024, 35, 015120. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60–61, 243–251. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Lian, J.; Liu, Z.; Wang, H.; Dong, X. Adaptive variational mode decomposition method for signal processing based on mode characteristic. Mech. Syst. Signal Process. 2018, 107, 53–77. [Google Scholar] [CrossRef]
- Li, J.; Yao, X.; Wang, H.; Zhang, J. Periodic impulses extraction based on improved adaptive VMD and sparse code shrinkage denoising and its application in rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2019, 126, 568–589. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Endo, H.; Randall, R.B. Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter. Mech. Syst. Signal Process. 2007, 21, 906–919. [Google Scholar] [CrossRef]
- McDonald, G.L.; Zhao, Q.; Zuo, M.J. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection. Mech. Syst. Signal Process. 2012, 33, 237–255. [Google Scholar] [CrossRef]
- Lyu, X.; Hu, Z.; Zhou, H.; Wang, Q. Application of improved MCKD method based on QGA in planetary gear compound fault diagnosis. Measurement 2019, 139, 236–248. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, B.; Li, C.; Lin, J.; Zhang, D. Feature Mode Decomposition: New Decomposition Theory for Rotating Machinery Fault Diagnosis. IEEE Trans. Ind. Electron. 2023, 70, 1949–1960. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, B.; Lin, J.; Zhao, M.; Liu, H.; Liu, Z.; Li, H. A review on the application of blind deconvolution in machinery fault diagnosis. Mech. Syst. Signal Process. 2022, 163, 108202. [Google Scholar] [CrossRef]
- Lee, J.; Liu, Y.; Yu, L. SGST: An Open Source Semantic Geostreaming Toolkit. In Proceedings of the 2011 ACM SIGSPATIAL International Workshop on GeoStreaming, IWGS 2011, Chicago, IL, USA, 1 November 2011; Volume 1, pp. 17–20. [Google Scholar]
- Cheng, J.; Yang, Y.; Hu, N.; Cheng, Z.; Cheng, J. A noise reduction method based on adaptive weighted symplectic geometry decomposition and its application in early gear fault diagnosis. Mech. Syst. Signal Process. 2021, 149, 107351. [Google Scholar] [CrossRef]
- Pan, H.; Yang, Y.; Li, X.; Zheng, J.; Cheng, J. Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis. Mech. Syst. Signal Process. 2019, 114, 189–211. [Google Scholar] [CrossRef]
- Hou, B.; Wang, D.; Kong, J.; Liu, J.; Peng, Z.; Tsui, K. Understanding importance of positive and negative signs of optimized weights used in the sum of weighted normalized Fourier spectrum/envelope spectrum for machine condition monitoring. Mech. Syst. Signal Process. 2022, 174, 109094. [Google Scholar] [CrossRef]
- Hou, B.; Wang, D.; Peng, Z.; Tsui, K. Adaptive Fault Components Extraction by Using an Optimized Weights Spectrum Based Index for Machinery Fault Diagnosis. IEEE Trans. Ind. Electron. 2024, 71, 985–995. [Google Scholar] [CrossRef]








| Bearing Type | NU205EM/PS |
|---|---|
| Inner race diameter (mm) | 25 |
| Outer race diameter (mm) | 52 |
| Rolling element diameter (mm) | 7.5 |
| Pitch diameter (mm) | 39 |
| Roller number | 13 |
| Contact angle α (°) | 0 |
| Failure Name | Fault Characteristic Frequency Calculation Formula | Failure Frequency |
|---|---|---|
| inner ring failure | 155 Hz | |
| outer ring failure | 105 Hz |
| Methods | Inner Ring Failure | Outer Ring Failure |
|---|---|---|
| Proposed method | √ | √ |
| FMD | × | × |
| VMD | × | × |
| Spectral kurtosis | × | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, C.; Zhou, Y.; Han, B.; Liu, P. Early Fault Diagnosis of Bearings Based on Symplectic Geometry Mode Decomposition Guided by Optimal Weight Spectrum Index. Symmetry 2024, 16, 408. https://doi.org/10.3390/sym16040408
Wei C, Zhou Y, Han B, Liu P. Early Fault Diagnosis of Bearings Based on Symplectic Geometry Mode Decomposition Guided by Optimal Weight Spectrum Index. Symmetry. 2024; 16(4):408. https://doi.org/10.3390/sym16040408
Chicago/Turabian StyleWei, Chenglong, Yiqi Zhou, Bo Han, and Pengchuan Liu. 2024. "Early Fault Diagnosis of Bearings Based on Symplectic Geometry Mode Decomposition Guided by Optimal Weight Spectrum Index" Symmetry 16, no. 4: 408. https://doi.org/10.3390/sym16040408






