Theoretical Investigation and Improvement of Characteristics of InAs/GaAs Quantum Dot Intermediate Band Solar Cells by Optimizing Quantum Dot Dimensions
Abstract
1. Introduction
2. Theoretical Framework
3. Results and Discussion
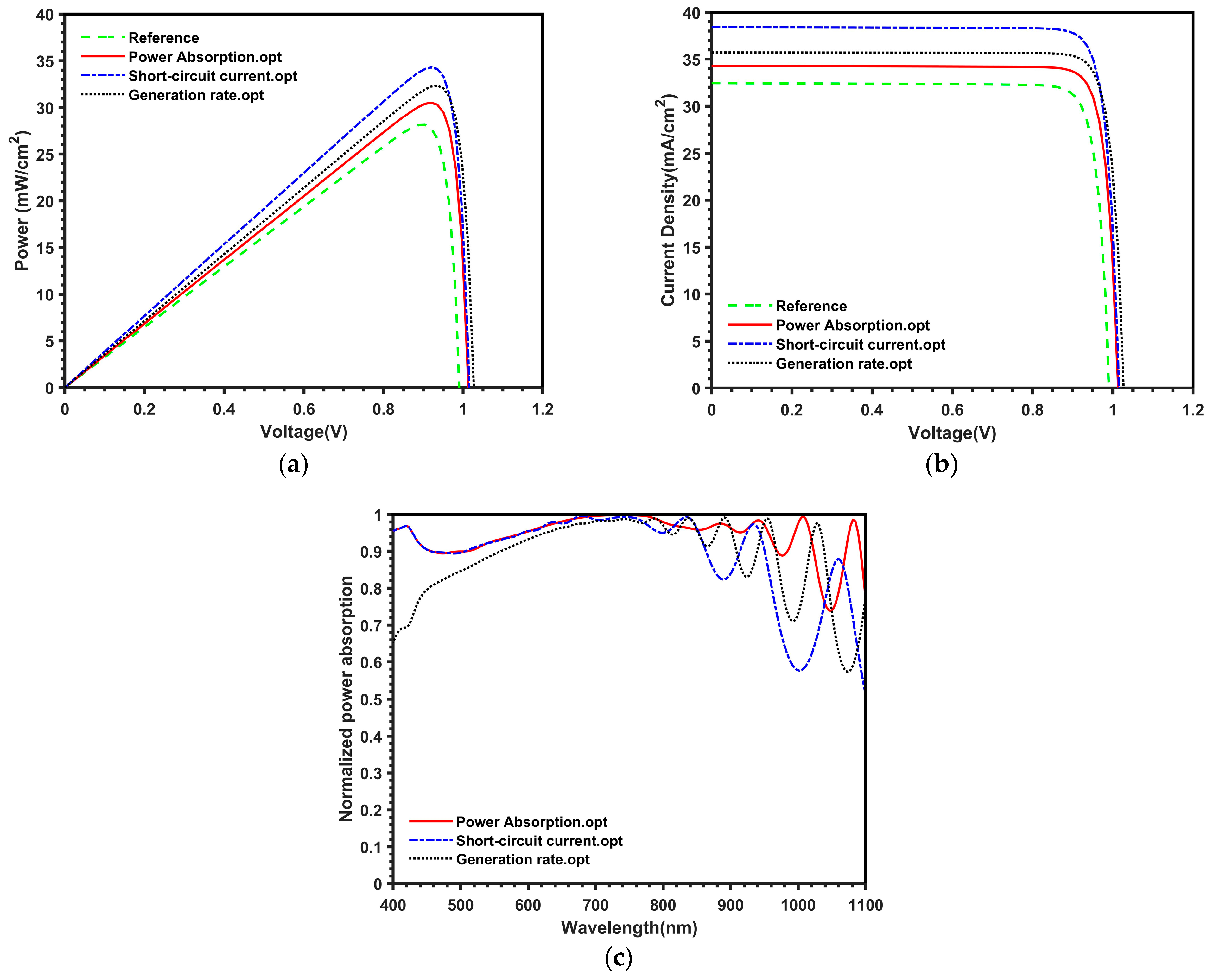
3.1. Improvement Based on Power Absorption Optimization
3.2. Improvement Based on the Short-Circuit Current Density Optimization
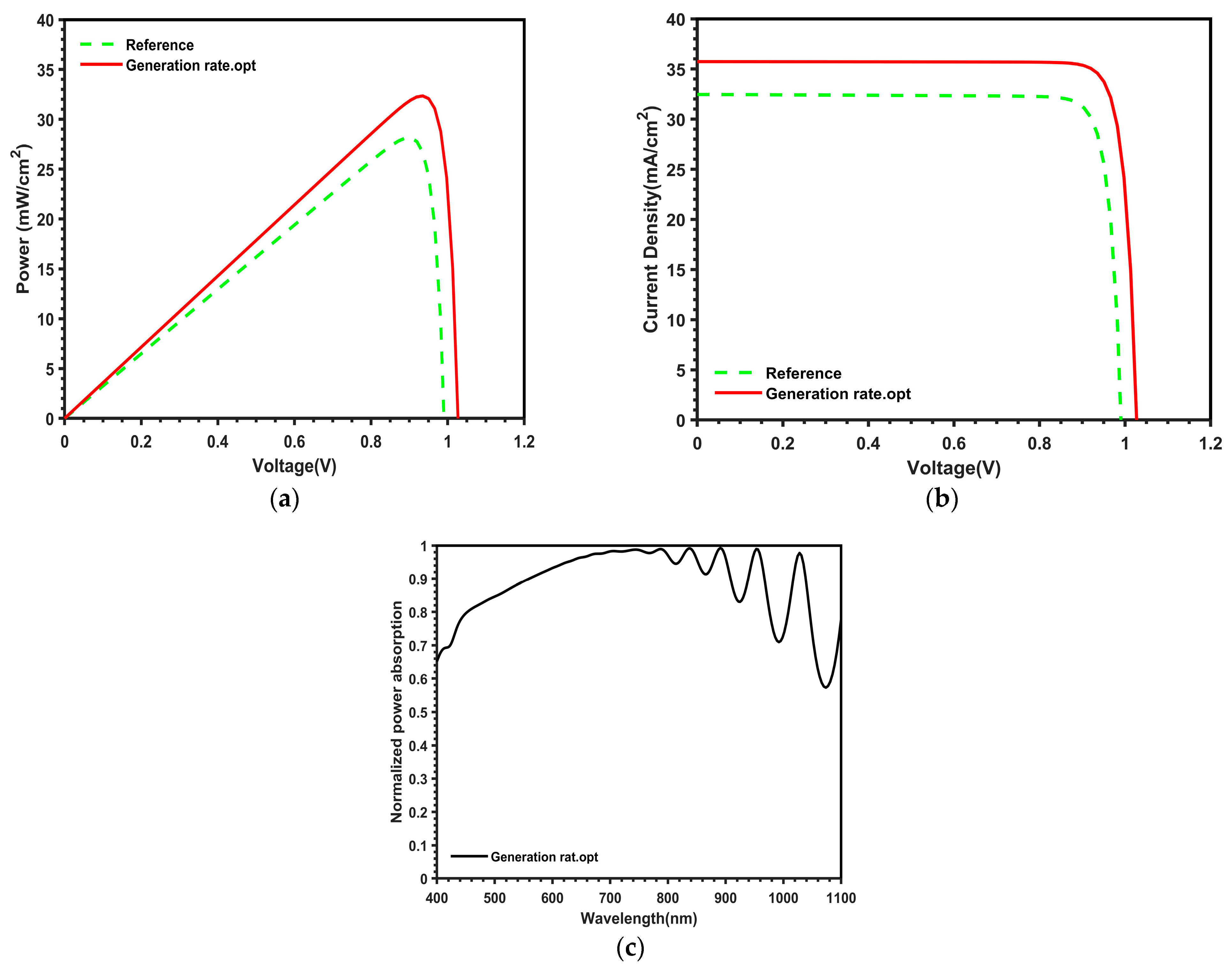
3.3. Improvement Based on the Generation Rate Optimization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dambhare, M.V.; Butey, B.; Moharil, S.V. Solar photovoltaic technology: A review of different types of solar cells and its future trends. J. Phys. Conf. Ser. 2021, 1913, 012053. [Google Scholar] [CrossRef]
- Olyaee, S.; Farhadipour, F.; Ghahremanirad, E. Enhanced photovoltaic properties of InAs/GaAs quantum-dot intermediate-band solar cells by using cylindrical QDs. Dig. J. Nanomater. Biostruct. 2018, 13, 271–277. [Google Scholar]
- Hossain, M.K.; Haque, M.D.; Sarker, S.; Arshad, M. Performance Analysis of Intermediate Band Solar Cell (IBSC). J. Mater. Sci. Eng. 2015, 4, 2169-0022. [Google Scholar]
- Amine, A.; Wakif, A.; Kinani, M.A.; Mir, Y.; Oukerroum, A.; Zazoui, M. Physical insights into the effects of QDssize and temperature on efficiency of InAs/GaAs QDsintermediate band solar cell. Phys. A Stat. Mech. Its Appl. 2020, 547, 123786. [Google Scholar] [CrossRef]
- Yang, G.; Liu, W.; Bao, Y.; Chen, X.; Ji, C.; Wei, B.; Yang, F.; Wang, X. Performance optimization of In (Ga) As QD intermediate band solar cells. Discov. Nano 2023, 18, 67. [Google Scholar] [CrossRef] [PubMed]
- Sikder, U.; Haque, A. Optimization of idealized QD intermediate band solar cells considering spatial variation of generation rates. IEEE Access 2013, 1, 363–370. [Google Scholar] [CrossRef]
- Olyaee, S.; Farhadipour, F. Investigation of hybrid Ge QDs/Si nanowires solar cell with improvement in cell efficiency. Opt. Appl. 2018, 48, 633–645. [Google Scholar]
- Behaghel, B.; Tamaki, R.; Chen, H.-L.; Rale, P.; Lombez, L.; Shoji, Y.; Delamarre, A.; Cattoni, A.; Collin, S.; Okada, Y.; et al. A hot-carrier assisted InAs/AlGaAs quantum-dot intermediate-band solar cell. Semicond. Sci. Technol. 2019, 34, 084001. [Google Scholar] [CrossRef]
- Blakers, A.; Zin, N.; McIntosh, K.R.; Fong, K. High efficiency silicon solar cells. Energy Procedia 2013, 33, 1–10. [Google Scholar] [CrossRef]
- Nayak, P.K.; Mahesh, S.; Snaith, H.J.; Cahen, D. Photovoltaic solar cell technologies: Analysing the condition of the art. Nat. Rev. Mater. 2019, 4, 269–285. [Google Scholar] [CrossRef]
- Green, M.A.; Dunlop, E.D.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Hao, X. Solar cell efficiency tables (version 56). Prog. Photovolt. Res. Appl. 2020, 28, 629–638. [Google Scholar] [CrossRef]
- Soonmin, H.; Hardani; Nandi, P.; Mwankemwa, B.S.; Malevu, T.D.; Malik, M.I. Overview on Different Types of Solar Cells: An Update. Appl. Sci. 2023, 13, 2051. [Google Scholar] [CrossRef]
- Starowicz, A.; Rusanowska, P.; Zieliński, M. Photovoltaic cell–the history of invention–review. Polityka Energetyczna-Energy Policy J. 2023, 26, 169–180. [Google Scholar] [CrossRef]
- Deshpande, R.A. Advances in solar cell technology: An overview. J. Sci. Res. 2021, 65, 72–75. [Google Scholar] [CrossRef]
- Hedayati, M.; Olyaee, S. High-efficiency p-n homojunction perovskite and CIGS tandem solar cell. Crystals 2022, 12, 703. [Google Scholar] [CrossRef]
- Hedayati, M.; Olyaee, S. Proposal of CIGS dual-junction solar cell and investigation of different metal grids effect. Opt. Quantum Electron. 2020, 52, 347. [Google Scholar] [CrossRef]
- Lee, T.D.; Ebong, A.U. A review of thin film solar cell technologies and challenges. Renew. Sustain. Energy Rev. 2017, 70, 1286–1297. [Google Scholar] [CrossRef]
- Lee, T.D.; Ebong, A. Thin film solar technologies: A review. In Proceedings of the 2015 12th International Conference on High-Capacity Optical Networks and Enabling/Emerging Technologies (HONET), Islamabad, Pakistan, 21–23 December 2015. [Google Scholar]
- Kim, S.; Chung, J.-W.; Lee, H.; Park, J.; Heo, Y.; Lee, H.-M. Remarkable progress in thin-film silicon solar cells using high-efficiency triple-junction technology. Sol. Energy Mater. Sol. Cells 2013, 119, 26–35. [Google Scholar] [CrossRef]
- Ghahremanirad, E.; Olyaee, S.; Hedayati, M. The influence of embedded plasmonic nanostructures on optical absorption of perovskite solar cells. Photonics 2019, 6, 37. [Google Scholar] [CrossRef]
- Ghahremanirad, E.; Olyaee, S.; Nejand, B.A.; Nazari, P.; Ahmadi, V.; Abedi, K. Improving the performance of perovskite solar cells using kesterite mesostructure and plasmonic network. Sol. Energy 2018, 169, 498–504. [Google Scholar] [CrossRef]
- Ghahremanirad, E.; Olyaee, S.; Nejand, B.A.; Ahmadi, V.; Abedi, K. Hexagonal array of mesoscopic HTM based perovskite solar cell with embedded plasmonic nanoparticles. Phys. Status Solidi B Basic Solid State Phys. 2018, 255, 1700291. [Google Scholar] [CrossRef]
- Chopra, K.L.; Paulson, P.D.; Dutta, V. Thin-film solar cells: An overview. Prog. Photovolt. Res. Appl. 2004, 12, 69–92. [Google Scholar] [CrossRef]
- Vodapally, S.N.; Ali, M.H. A Comprehensive Review of Solar Photovoltaic (PV) Technologies, Architecture, and Its Applications to Improved Efficiency. Energies 2023, 16, 319. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A. Increasing the efficiency of ideal solar cells by photon induced transitions at intermediate levels. Phys. Rev. Lett. 1997, 78, 5014. [Google Scholar] [CrossRef]
- Kunrugsa, M. Optical absorption spectra of GaSb/GaAs quantum-ring-with-dot structures and their potential for intermediate band solar cells. J. Phys. D Appl. Phys. 2023, 56, 435103. [Google Scholar] [CrossRef]
- Perez, L.M.; Aouami, A.E.; Feddi, K.; Tasco, V.; Abdellah, A.B.; Dujardin, F.; Courel, M.; Riquelme, J.A.; Laroze, D.; Feddi, E.M. Parameters Optimization of Intermediate Band Solar Cells: Cases of PbTe/CdTe, PbSe/ZnTe and InN/GaN QDs. Crystals 2022, 12, 1002. [Google Scholar] [CrossRef]
- Nozawa, T.; Takagi, H.; Watanabe, K.; Arakawa, Y. Direct observation of two-step photon absorption in an InAs/GaAs single QD for the operation of intermediate-band solar cells. Nano Lett. 2015, 15, 4483–4487. [Google Scholar] [CrossRef]
- Tomić, S.; Sogabe, T.; Okada, Y. In-plane coupling effect on absorption coefficients of InAs/GaAs QDsarrays for intermediate band solar cell. Prog. Photovolt. Res. Appl. 2015, 23, 546–558. [Google Scholar] [CrossRef]
- Tamaki, R.; Shoji, Y.; Okada, Y.; Miyano, K. Spectrally resolved interband and intraband transitions by two-step photon absorption in InGaAs/GaAs QD solar cells. IEEE J. Photovolt. 2014, 5, 229–233. [Google Scholar] [CrossRef]
- Gatissa, T.A.; Debela, T.S.; Ali, B.M. Dependence of QD solar cell parameters on the number of QD layers. AIP Adv. 2023, 13, 075215. [Google Scholar] [CrossRef]
- Jing, Q.; Meng, X.; Wang, C.; Zhao, H. Exciton Dynamic in Pyramidal InP/ZnSe QDsfor Luminescent Solar Concentrators. ACS Appl. Nano Mater. 2023, 6, 4449–4454. [Google Scholar] [CrossRef]
- Mantashian, G.A.; Mantashyan, P.A.; Hayrapetyan, D.B. Modeling of QDswith the Finite Element Method. Computation 2023, 11, 5. [Google Scholar] [CrossRef]
- Heidarzadeh, H.; Rostami, A.; Dolatyari, M. Excellent properties of cylindrical QDs for the design of hot-carrier assisted IBSCs with appropriate ESCs. Opt. Quantum Electron. 2022, 54, 489. [Google Scholar] [CrossRef]
- Yu, L.; Li, Z. Synthesis of ZnxCd1−xSe@ ZnO hollow spheres in different sizes for QDssensitized solar cells application. Nanomaterials 2019, 9, 132. [Google Scholar] [CrossRef]
- Li, Z.; Yu, L.; Wang, H.; Yang, H.; Ma, H. TiO2 passivation layer on ZnO hollow microspheres for QDs sensitized solar cells with improved light harvesting and electron collection. Nanomaterials 2020, 10, 631. [Google Scholar] [CrossRef] [PubMed]
- Welser, R.E.; Polly, S.J.; Kacharia, M.; Fedorenko, A.; Sood, A.K.; Hubbard, S.M. Design and demonstration of high-efficiency quantum well solar cells employing thin strained superlattices. Sci. Rep. 2019, 9, 13955. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.; Rao, H.; Mora-Seró, I.; Bisquert, J.; Zhong, X. Quantum dot-sensitized solar cells. Chem. Soc. Rev. 2018, 47, 7659–7702. [Google Scholar] [CrossRef] [PubMed]
- Grieve, K.; Mulvaney, P.; Grieser, F. Synthesis and electronic properties of semiconductor nanoparticles/QDs. Curr. Opin. Colloid Interface Sci. 2000, 5, 168–172. [Google Scholar] [CrossRef]
- Nozik, A.J. Multiple exciton generation in semiconductor QDs. Chem. Phys. Lett. 2008, 457, 3–11. [Google Scholar] [CrossRef]
- Ramiro, I.; Martí, A. Intermediate band solar cells: Present and future. Prog. Photovolt. Res. Appl. 2021, 29, 705–713. [Google Scholar] [CrossRef]
- Tavakoli, M.M.; Tavakoli, R.; Hasanzadeh, S.; Mirfasih, M.H. Interface engineering of perovskite solar cell using a reduced-graphene scaffold. J. Phys. Chem. C 2016, 120, 19531–19536. [Google Scholar] [CrossRef]
- Buonomenna, M.G. Inorganic thin-film solar cells: Challenges at the terawatt-scale. Symmetry 2023, 15, 1718. [Google Scholar] [CrossRef]
- Mantashyan, P.; Mantashian, G.; Hayrapetyan, D. Talbot effect in InAs/GaAs coupled cylindrical quantum dots ensemble. Phys. E Low-Dimens. Syst. Nanostruct. 2023, 148, 115662. [Google Scholar] [CrossRef]
- Lima, R.P.A.; Amado, M. Electronic conditions of on-and off-center donors in quantum rings of finite width. J. Lumin. 2008, 128, 858–861. [Google Scholar] [CrossRef]
- Brus, L.E. Electron–electron and electron-hole interactions in small semiconductor crystallites: The size dependence of the lowest excited electronic condition. J. Chem. Phys. 1984, 80, 4403–4409. [Google Scholar] [CrossRef]
- Aroutiounian, V.; Petrosyan, S.; Khachatryan, A.; Touryan, K.J. Quantum dot solar cells. J. Appl. Phys. 2001, 89, 2268–2271. [Google Scholar] [CrossRef]
- Luque, A.; Linares, P.G.; Antolin, E.; Ramiro, I. Understanding the operation of QD intermediate band solar cells. J. Appl. Phys. 2012, 111, 044502. [Google Scholar] [CrossRef]
- Luque, A.; Hegedus, S. (Eds.) Handbook of Photovoltaic Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Soga, T. (Ed.) Nanostructured Materials for Solar Energy Conversion; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Bahrami, A.; Mohammadnejad, S.; Soleimaninezhad, S. Photovoltaic cells technology: Principles and recent developments. Opt. Quantum Electron. 2013, 45, 161–197. [Google Scholar] [CrossRef]
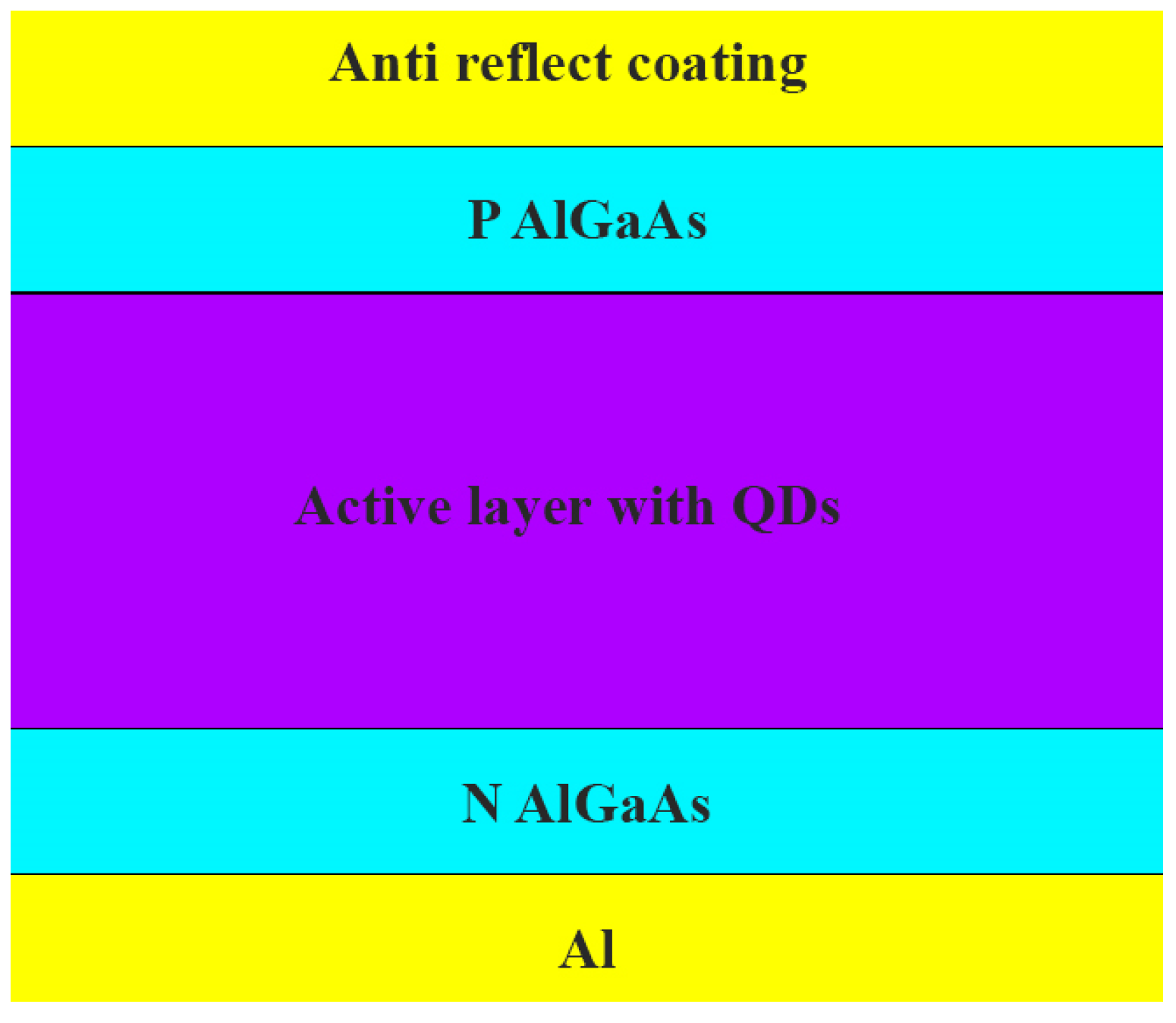
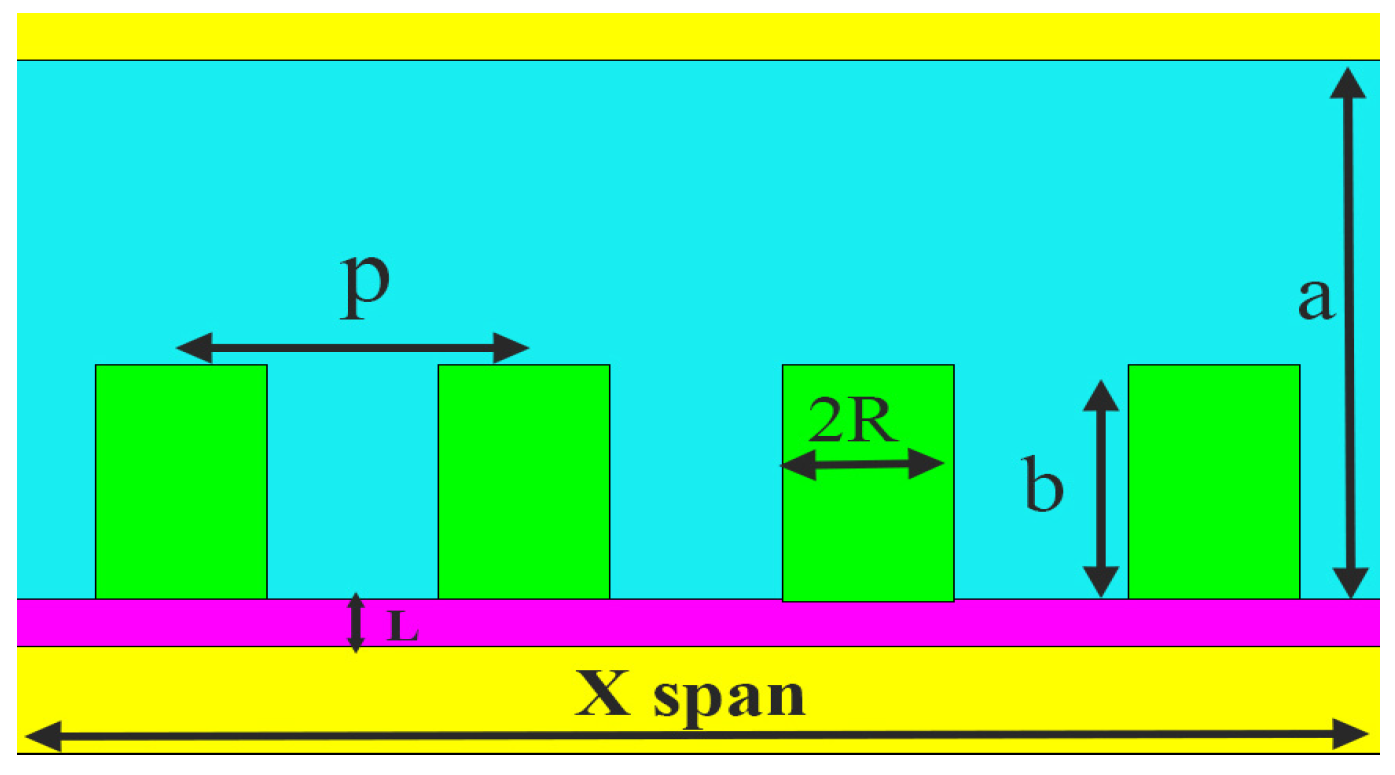



| Material | Thickness |
|---|---|
| Base-aluminium (Al) | 200 nm |
| Emitter-Al | 200 nm |
| Al0.2Ga0.8As | 20 nm |
| GaAs | 200 nm |
| Symmetric array of InAs cylindrical QDs | R = 10 nm, a = 10 nm |
| 10 layer | p = 30 nm |
| GaAs | 200 nm |
| Strain GaP | 10 nm |
| Al0.8Ga0.2As | 30 nm |
| Anti-reflect coating (n = 1.7) | 100 nm |
| X Span (nm) | R (nm) | P (nm) | b (nm) | a (nm) | L (nm) | Efficiency | FF |
|---|---|---|---|---|---|---|---|
| 320 | 25 | 62.86 | 80 | 111.1 | 10.29 | 30.52% | 87% |
| X Span (nm) | R (nm) | P (nm) | b (nm) | a (nm) | L (nm) | Efficiency | FF |
|---|---|---|---|---|---|---|---|
| 351.11 | 25 | 71.2 | 80 | 96.36 | 10.07 | 34.30% | 88% |
| X Span (nm) | R (nm) | P (nm) | b (nm) | a (nm) | L (nm) | Efficiency | FF |
|---|---|---|---|---|---|---|---|
| 350 | 10 | 30 | 28.52 | 40 | 6.51 | 32.34% | 88% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhadipour, F.; Olyaee, S.; Kosarian, A. Theoretical Investigation and Improvement of Characteristics of InAs/GaAs Quantum Dot Intermediate Band Solar Cells by Optimizing Quantum Dot Dimensions. Symmetry 2024, 16, 435. https://doi.org/10.3390/sym16040435
Farhadipour F, Olyaee S, Kosarian A. Theoretical Investigation and Improvement of Characteristics of InAs/GaAs Quantum Dot Intermediate Band Solar Cells by Optimizing Quantum Dot Dimensions. Symmetry. 2024; 16(4):435. https://doi.org/10.3390/sym16040435
Chicago/Turabian StyleFarhadipour, Farzad, Saeed Olyaee, and Abdolnabi Kosarian. 2024. "Theoretical Investigation and Improvement of Characteristics of InAs/GaAs Quantum Dot Intermediate Band Solar Cells by Optimizing Quantum Dot Dimensions" Symmetry 16, no. 4: 435. https://doi.org/10.3390/sym16040435
APA StyleFarhadipour, F., Olyaee, S., & Kosarian, A. (2024). Theoretical Investigation and Improvement of Characteristics of InAs/GaAs Quantum Dot Intermediate Band Solar Cells by Optimizing Quantum Dot Dimensions. Symmetry, 16(4), 435. https://doi.org/10.3390/sym16040435






