Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method
Abstract
:1. Introduction
2. Governing Equation and Cubic B-Spline Collocation Method
3. Linear Stability Analysis
4. Numerical Examples and Results
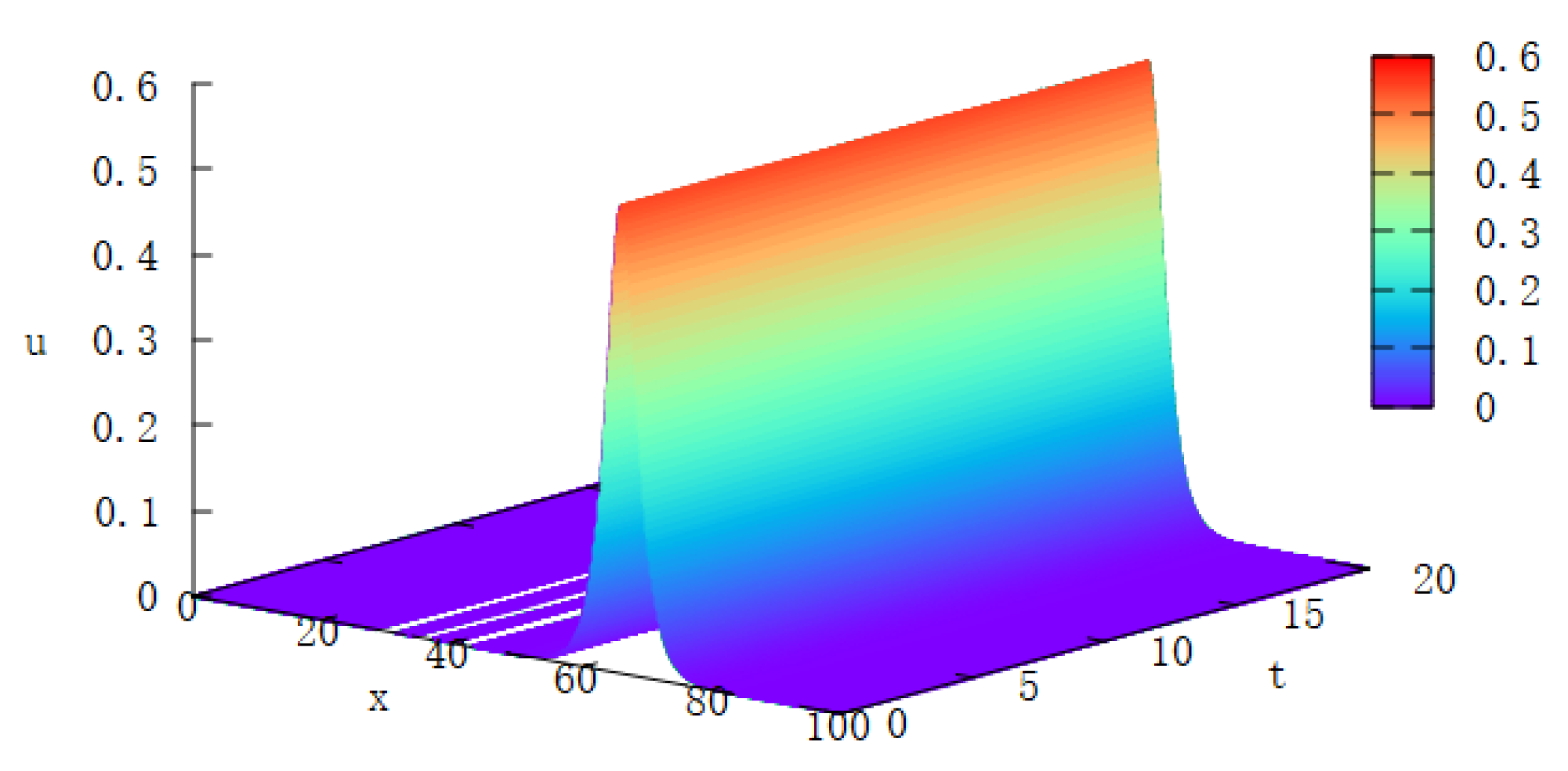
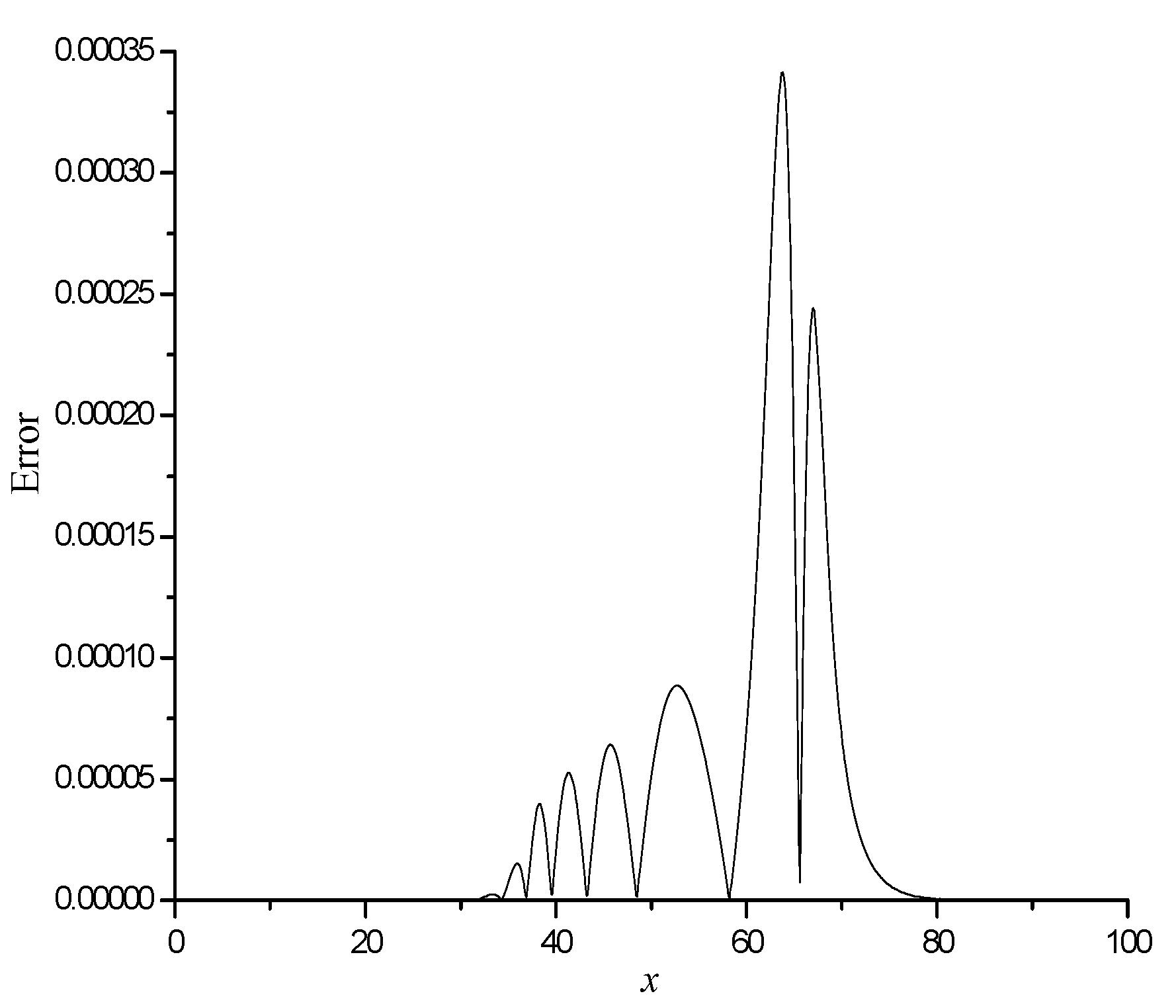
4.1. Single Solitary Waves
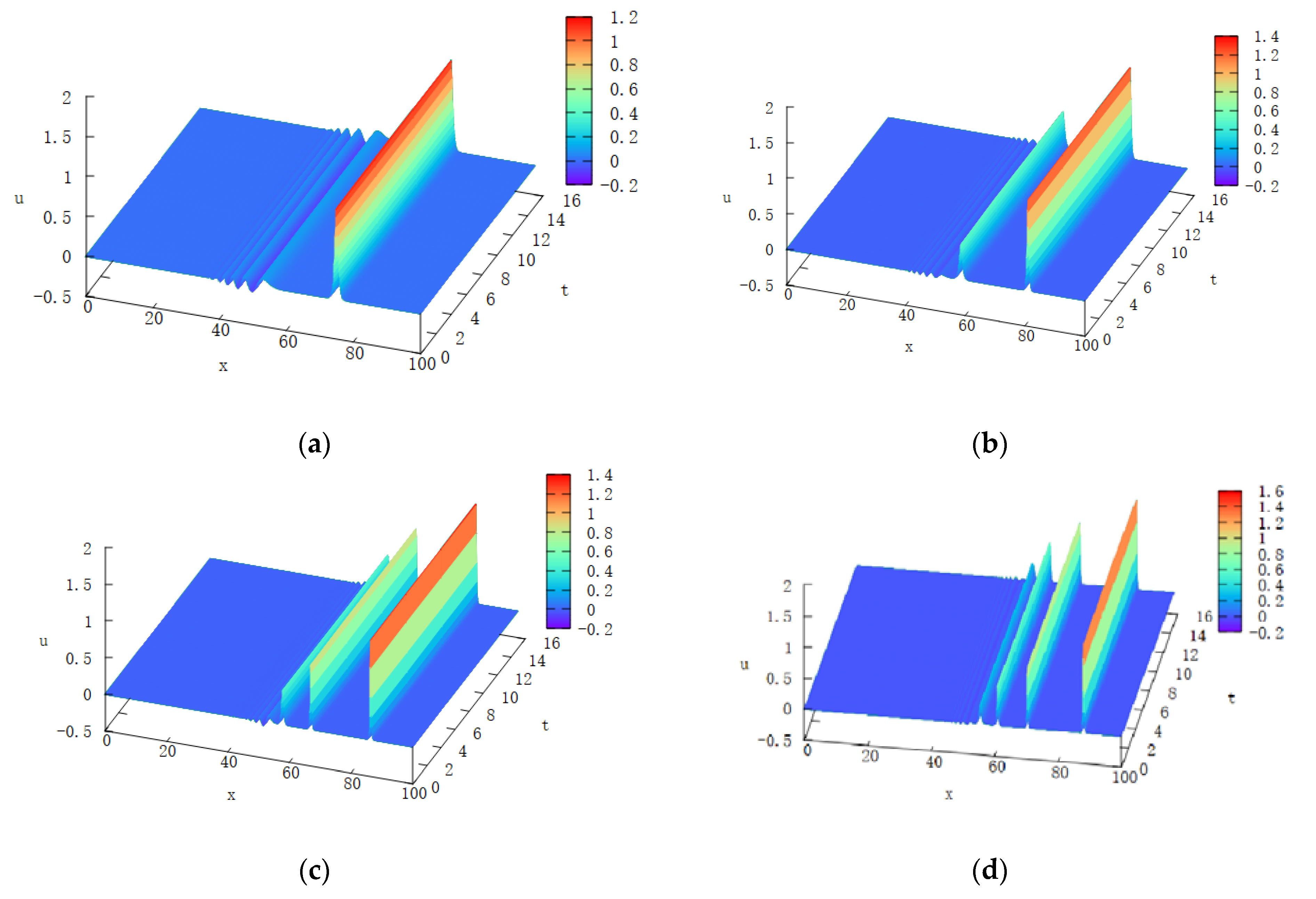
4.2. Interaction of Two Solitary Waves
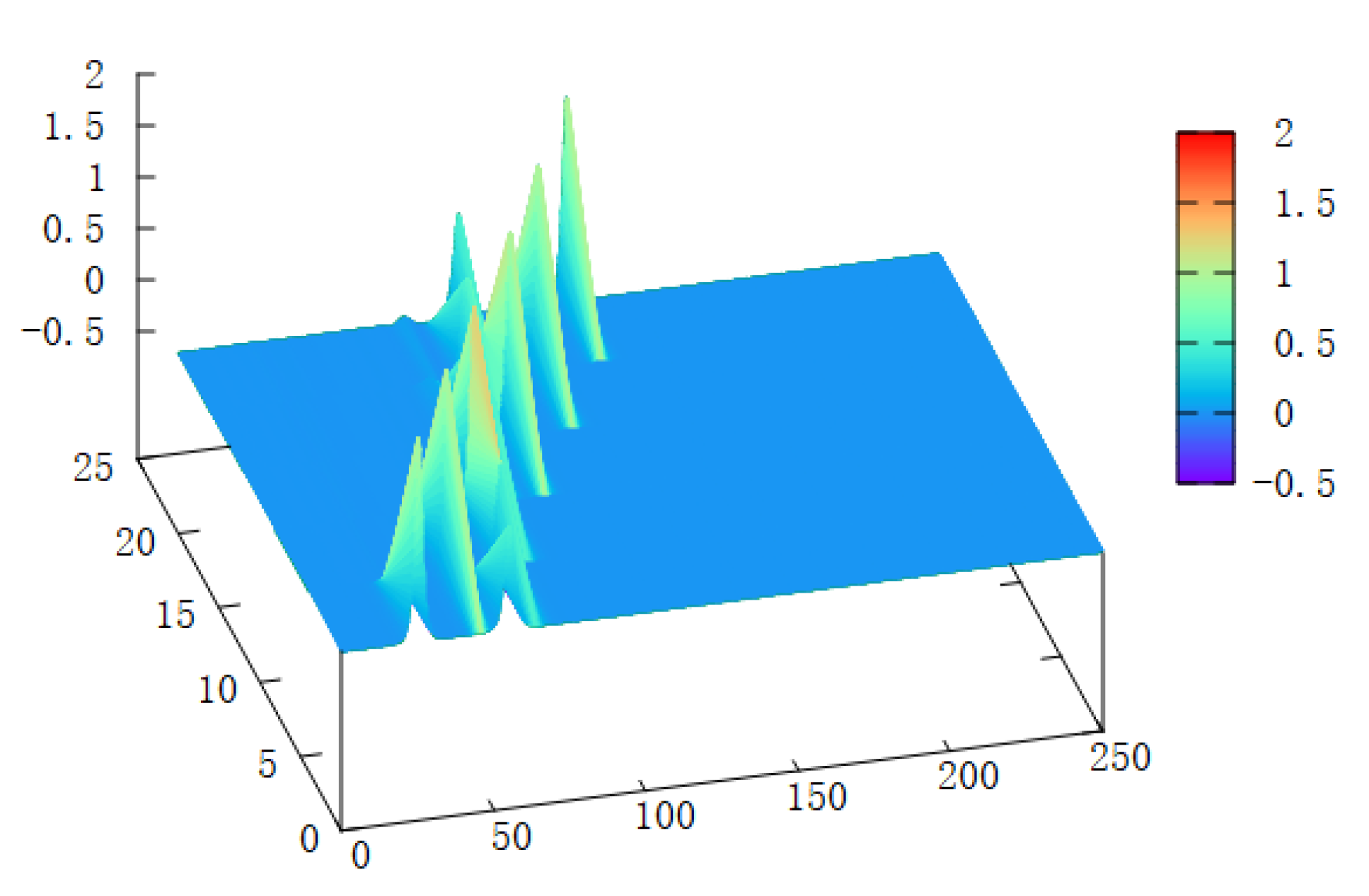
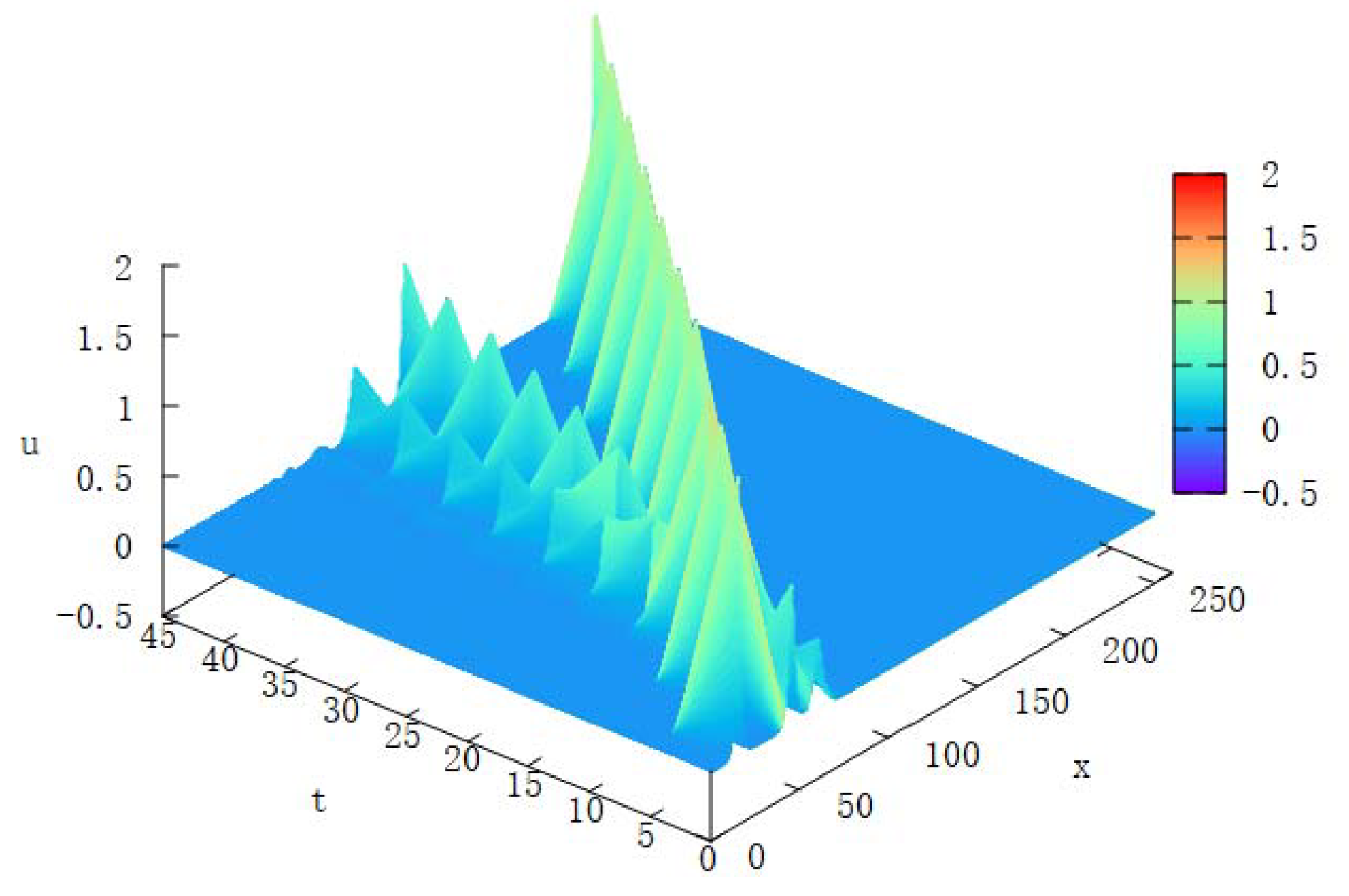
4.3. Interaction of Three Solitary Waves
4.4. The Maxwellian Initial Condition
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peregrine, D.H. Calculations of the development of an undular bore. J. Fluid Mech. 1966, 25, 321–330. [Google Scholar] [CrossRef]
- Bona, J.L.; Pyrant, P.J. A mathematical model for long wave generated by wave makers in nonlinear dispersive systems. Proc. Comp. Philos. Soc. 1973, 37, 91. [Google Scholar]
- Bona, J.L.; Pritchard, W.G.; Scott, L.R. Numerical scheme for a model of nonlinear dispersive waves. J. Comput. Phys. 1985, 60, 167–176. [Google Scholar] [CrossRef]
- Eilbeck, J.C.; McGuire, G.R. Numerical study of regularized long wave equation I: Numerical methods. J. Comput. Phys. 1975, 19, 43–57. [Google Scholar] [CrossRef]
- Alexander, M.E.; Morris, J.H. Galerkin method for some model equation for nonlinear dispersive waves. J. Comput. Phys. 1979, 30, 428–451. [Google Scholar] [CrossRef]
- Evans, D.J.; Raslan, K.R. The Tanh function method for solving some important nonlinear partial differential equations. Int. J. comput. Math. 2005, 82, 897–905. [Google Scholar] [CrossRef]
- Jain, P.C.; Shankar, R.; Single, T.V. Numerical solutions of RLW equation. Commun. Numer. Meth. Eng. 1993, 9, 587–594. [Google Scholar] [CrossRef]
- Bhardwaj, D.; Shankar, R. A computational method for regularized long wave equation. Comput. Math. Appl. 2000, 40, 1397–1404. [Google Scholar] [CrossRef]
- Zaki, S.I. Solitary waves of the spitted RLW equation. Comput. Phys. Commun. 2001, 138, 80–91. [Google Scholar] [CrossRef]
- Gardner, L.R.T.; Gardner, G.A.; Dogan, A. A least squares finite element scheme for the RLW equation. Commun. Numer. Meth. Eng. 1996, 12, 795–804. [Google Scholar] [CrossRef]
- Dag, I. Least squares quadratic B-splines finite element method for the regularized long wave equation. Comput. Meth. Appl. Mech. Eng. 2000, 182, 205–215. [Google Scholar] [CrossRef]
- Soliman, A.A.; Raslan, K.R. Collocation method using quadratic B-spline for the RLW equation. Int. J. Comput. Math. 2001, 78, 399–412. [Google Scholar] [CrossRef]
- Dag, I.; Saka, B.; Irk, D. Application of cubic B-splins for numerical solution of the RLW equation. Appl. Math Comput. 2004, 195, 373–389. [Google Scholar]
- Raslan, K.R. A computational method for the regularized long wave (RLW) equation. Appl. Math. Comput. 2005, 176, 1101–1118. [Google Scholar] [CrossRef]
- Soliman, A.A.; Hussien, M.H. Collocation solution for RLW equation with septic splines. Appl. Math. Comput. 2005, 161, 623–636. [Google Scholar] [CrossRef]
- Zhang, L. A finite difference scheme for generalized long wave equation. Appl. Math. Comput. 2005, 168, 962–972. [Google Scholar] [CrossRef]
- Kaya, D. A numerical simulation of solitary wave solutions of the generalized regularized long wave equation. Appl. Math. Comput. 2004, 149, 833–841. [Google Scholar] [CrossRef]
- Khalifa, A.K.; Raslan, K.R.; Alzubaidi, H.M. A finite difference scheme for the MRLW and solitary wave interactions. Appl. Math. Comput. 2007, 189, 346–354. [Google Scholar] [CrossRef]
- Gardner, L.R.T.; Gardner, G.A.; Ayoub, F.A.; Amin, N.K. Approximations of solitary waves of the MRLW equation by B-spline finite element. Arab. J. Sci. Eng. 1997, 22, 183–193. [Google Scholar]
- Tirmizi, I.A. A numerical technique for solution of the MRLW equation using quartic B-splines. Appl. Math. Model. 2010, 34, 4151–4160. [Google Scholar]
- Khalifa, A.K.; Raslan, K.R.; Alzubaidi, H.M. A collocation method with B-splines for solving the MRLW equation. J. Comput. Appl. Math. 2008, 212, 406–418. [Google Scholar] [CrossRef]
- Iqbal, A.; Abd Hamid, N.N.; Md. Ismail, A.I. Soliton solution of Schrödinger equation using cubic B-spline Galerkin method. Fluids 2019, 4, 108. [Google Scholar] [CrossRef]
- Iqbal, A.; Abd Hamid, N.N.; Ismail, A.I.M. Cubic B-spline Galerkin method for numerical solution of the coupled nonlinear Schrödinger equation. Math. Comput. Simulat. 2020, 174, 32–44. [Google Scholar] [CrossRef]
- Zaki, S.I. A quintic B-spline finite elements scheme for the KdVB equation. Comput. Methods Appl. Mech. Engrg. 2000, 188, 121–134. [Google Scholar] [CrossRef]
- Karakoç, S.B.G.; Uçar, Y.; Yağmurlu, N.M. Numerical solutions of the MRLW equation by cubic B-spline Galerkin finite elements method. Kuwait J. Sci. 2015, 42, 141–159. [Google Scholar]
- Lu, C.; Huang, W.; Qiu, J. An Adaptive moving mesh finite element solution of the Regularized Long Wave Equation. J. Sci. Comput. 2018, 74, 122–144. [Google Scholar] [CrossRef]
- Parvizi, M.; Khodadadian, A.; Eslahchi, M.R. Analysis of Ciarlet–Raviart mixed finite element methods for solving damped Boussinesq equation. J. Comput. Appl. Math. 2020, 379, 112818. [Google Scholar] [CrossRef]
- Parvizi, M.; Khodadadian, A.; Eslahchi, M.R. A mixed finite element method for solving coupled wave equation of Kirchhoff type with nonlinear boundary damping and memory term. Math. Methods Appl. Sci. 2021, 44, 12500–12521. [Google Scholar] [CrossRef]
| Time | |||||
|---|---|---|---|---|---|
| 0 | 3.58197 | 1.34508 | 0.153723 | 0 | 0 |
| 2 | 3.58197 | 1.34508 | 0.153723 | 1.67168 | 1.13519 |
| 4 | 3.58197 | 1.34508 | 0.153723 | 2.77610 | 1.63633 |
| 6 | 3.58197 | 1.34508 | 0.153723 | 3.52219 | 1.90878 |
| 8 | 3.58197 | 1.34508 | 0.153723 | 4.12108 | 2.13960 |
| 10 | 3.58197 | 1.34508 | 0.153723 | 4.65688 | 2.35813 |
| 12 | 3.58197 | 1.34508 | 0.153723 | 5.16261 | 2.57283 |
| 14 | 3.58197 | 1.34508 | 0.153723 | 5.65426 | 2.78427 |
| 16 | 3.58197 | 1.34508 | 0.153723 | 6.13872 | 2.99420 |
| 18 | 3.58197 | 1.34508 | 0.153723 | 6.62082 | 3.20474 |
| 20 | 3.58197 | 1.34508 | 0.153723 | 7.10258 | 3.41575 |
| Schemes | Analytical | Our Scheme | Cubic B-Splin Coll-CN [20] | |
|---|---|---|---|---|
| c = 0.3 t = 20 | 3.58197 | 3.58197 | 3.58197 | |
| 1.34508 | 1.34508 | 1.34508 | ||
| 0.153723 | 0.153723 | 0.153723 | ||
| 0 | 7.10258 | 6.06885 | ||
| 0 | 3.41575 | 2.96650 | ||
| Time | ||||||
|---|---|---|---|---|---|---|
| Our Scheme | Cubic B-Splin Coll-CN [20] | Our Scheme | Cubic B-Splin Coll-CN [20] | Our Scheme | CubicB-Splin Coll-CN [20] | |
| 0 | 11.4677 | 11.4677 | 14.6291 | 14.6291 | 22.8806 | 22.8806 |
| 2 | 11.4677 | 11.4677 | 14.6297 | 14.6292 | 22.8805 | 22.8807 |
| 4 | 11.4677 | 11.4677 | 14.6294 | 14.6292 | 22.8803 | 22.8807 |
| 6 | 11.4677 | 11.4677 | 14.6296 | 14.6295 | 22.8806 | 22.8806 |
| 8 | 11.4677 | 11.4677 | 14.6336 | 14.6451 | 22.8850 | 22.8454 |
| 10 | 11.4677 | 11.4677 | 14.6337 | 14.5963 | 22.8878 | 22.8913 |
| 12 | 11.4677 | 11.4677 | 14.6293 | 14.6287 | 22.8808 | 22.8814 |
| 14 | 11.4677 | 11.4677 | 14.6295 | 14.6295 | 22.8805 | 22.8807 |
| 16 | 11.4677 | 11.4677 | 14.6296 | 14.6294 | 22.8804 | 22.8808 |
| 18 | 11.4677 | 11.4677 | 14.6296 | 14.6293 | 22.8804 | 22.8809 |
| 20 | 11.4677 | 11.4677 | 14.6294 | 14.6292 | 22.8803 | 22.8809 |
| Analytical | 11.467698 | 14.629243 | 22.880466 | |||
| Time | ||||||
|---|---|---|---|---|---|---|
| Our Scheme | Cubic B-Splin Coll-CN [20] | Our Scheme | Cubic B-Splin Coll-CN [20] | Our Scheme | Cubic B-Splin Coll-CN [20] | |
| 0 | 14.9801 | 13.6891 | 15.8374 | 15.4549 | 23.0083 | 22.8816 |
| 5 | 14.9801 | 13.6891 | 15.8381 | 15.3109 | 23.0081 | 22.6939 |
| 10 | 14.9801 | 13.6891 | 15.8516 | 15.6514 | 23.0202 | 22.8388 |
| 15 | 14.9801 | 13.6891 | 15.8392 | 15.6548 | 23.0077 | 22.9347 |
| 20 | 14.9802 | 13.6891 | 15.8382 | 15.6557 | 23.0083 | 22.9330 |
| 25 | 14.9802 | 13.6892 | 15.8379 | 15.6559 | 23.0084 | 22.9336 |
| 30 | 14.9802 | 13.6894 | 15.8379 | 15.6559 | 23.0084 | 22.9348 |
| 35 | 14.9802 | 13.6913 | 15.8379 | 15.6564 | 23.0084 | 22.9343 |
| 40 | 14.9802 | 13.7015 | 15.8379 | 15.6566 | 23.0084 | 22.9335 |
| 45 | 14.9441 | 13.7043 | 15.8379 | 15.6563 | 23.0055 | 22.9303 |
| Analytical | 14.9801 | 15.8218 | 22.9923 | |||
| Time | ||||
|---|---|---|---|---|
| 0.1 | 3 | 1.77247 | 1.37737 | 0.76204 |
| 6 | 1.77247 | 1.37737 | 0.76204 | |
| 9 | 1.77247 | 1.37737 | 0.76204 | |
| 12 | 1.77247 | 1.37737 | 0.76204 | |
| 15 | 1.77247 | 1.37737 | 0.76204 | |
| 0.04 | 3 | 1.77254 | 1.29950 | 0.83975 |
| 6 | 1.77254 | 1.29951 | 0.83974 | |
| 9 | 1.77254 | 1.29952 | 0.83973 | |
| 12 | 1.77254 | 1.29952 | 0.83973 | |
| 15 | 1.77254 | 1.29952 | 0.83973 | |
| 0.015 | 3 | 1.77302 | 1.26345 | 0.88107 |
| 6 | 1.77302 | 1.26344 | 0.88109 | |
| 9 | 1.77302 | 1.26343 | 0.88100 | |
| 12 | 1.77302 | 1.26341 | 0.88090 | |
| 15 | 1.77302 | 1.26341 | 0.88087 | |
| 0.01 | 3 | 1.77364 | 1.25554 | 0.89927 |
| 6 | 1.77363 | 1.25548 | 0.89905 | |
| 9 | 1.77361 | 1.25525 | 0.89763 | |
| 12 | 1.77361 | 1.25528 | 0.89778 | |
| 15 | 1.77363 | 1.25551 | 0.89920 |
| Computed Examples | ||||||||
|---|---|---|---|---|---|---|---|---|
| Our Scheme | Cubic B-Splin Coll-CN [20] | Our Scheme | Cubic B-Splin Coll-CN [20] | Our Scheme | Cubic B-Splin Coll-CN [20] | |||
| Single solitary waves | c = 1 (t = 10) | 0 | 0 | 0.00001 | 0.00003 | 0.00001 | 0.00005 | |
| c = 0.3 (t = 20) | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Two solitary waves (t = 20) | 0 | 0 | 0.0046 | 0.032 | 0.0075 | 0.0459 | ||
| Three solitary waves (t = 45) | 0.0361 | 0.0102 | 0.0142 | 0.3 | 0.0147 | 0.241 | ||
| The Maxwellian initial condition (t = 15) | = 0.1 | 0 | 0 | 0 | 0.00005 | 0 | 0.000063 | |
| = 0.04 | 0 | 0.00001 | 0.00002 | 0.00002 | 0.00002 | 0.000028 | ||
| = 0.015 | 0 | 0.00001 | 0.00004 | 0.00004 | 0.00012 | 0.000248 | ||
| = 0.01 | 0.00003 | 0.00004 | 0.00026 | 0.0004 | 0.00164 | 0.001722 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, L.; Sun, J. Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method. Symmetry 2024, 16, 438. https://doi.org/10.3390/sym16040438
Liu X, Zhang L, Sun J. Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method. Symmetry. 2024; 16(4):438. https://doi.org/10.3390/sym16040438
Chicago/Turabian StyleLiu, Xingxia, Lijun Zhang, and Jianan Sun. 2024. "Numerical Analysis of the Discrete MRLW Equation for a Nonlinear System Using the Cubic B-Spline Collocation Method" Symmetry 16, no. 4: 438. https://doi.org/10.3390/sym16040438




