Symmetrical Modeling of Physical Properties of Flexible Structure of Silicone Materials for Control of Pneumatic Soft Actuators
Abstract
:1. Introduction
- (1)
- In theory, the soft robot has unlimited degrees of freedom, so its own structure is simple, and it is easy to design customized functions;
- (2)
- Because the soft robot has good compliance, it can adapt to unknown or complex working environments and facilitate smooth progress of detection;
- (3)
- When in contact with objects, the soft robot can reduce damage to objects and reduce the risk of damage to objects due to improper contact, and it can operate objects of different shapes and sizes;
- (4)
- In addition, the structural design of the soft robot itself is not complicated, the manufacturing and processing process is relatively simple, the preparation time is short, and the production cost is small.
- (1)
- How to design bionic structures and select intelligent materials to quickly and efficiently process soft robots that meet expected needs [12].
- (2)
- (3)
- A soft robot is made of flexible materials, and its material properties are non-linearly transformed. Therefore, the traditional rigid robot D-H law does not apply to soft robots. This poses a serious challenge to the theoretical analysis of soft robots, and the establishment of a new modeling method of soft robots has become an urgent difficulty to overcome.
- (1)
- The gas drive system has a high-power density, can provide relatively large force and speed, and is suitable for some application scenarios that require a high power output.
- (2)
- As a driving medium, gas is widely present in nature, such as air, nitrogen, etc., so gas driving has good availability and accessibility. Compared with other driving methods, such as liquids or chemical compounds, gases are easier to obtain and process.
- (3)
- Gas drives often use compressed gas or fluid as the driving medium. Compared with liquids or chemical compounds, gases are safer when leaking or released and have a smaller impact on the environment. In addition, gas drive usually does not produce harmful substances and meets environmental protection requirements.
- (4)
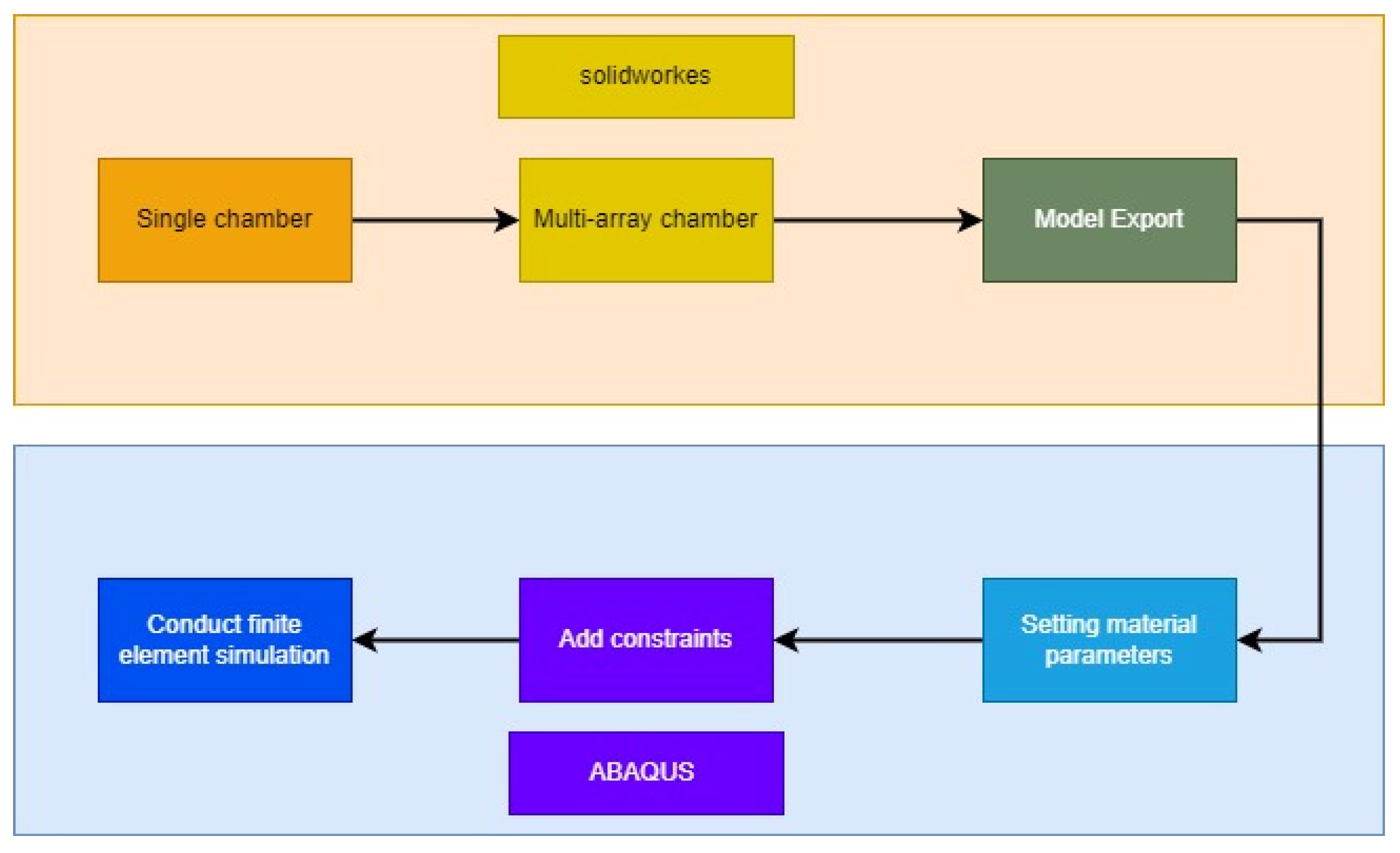
2. Materials and Methods
- Structural design:
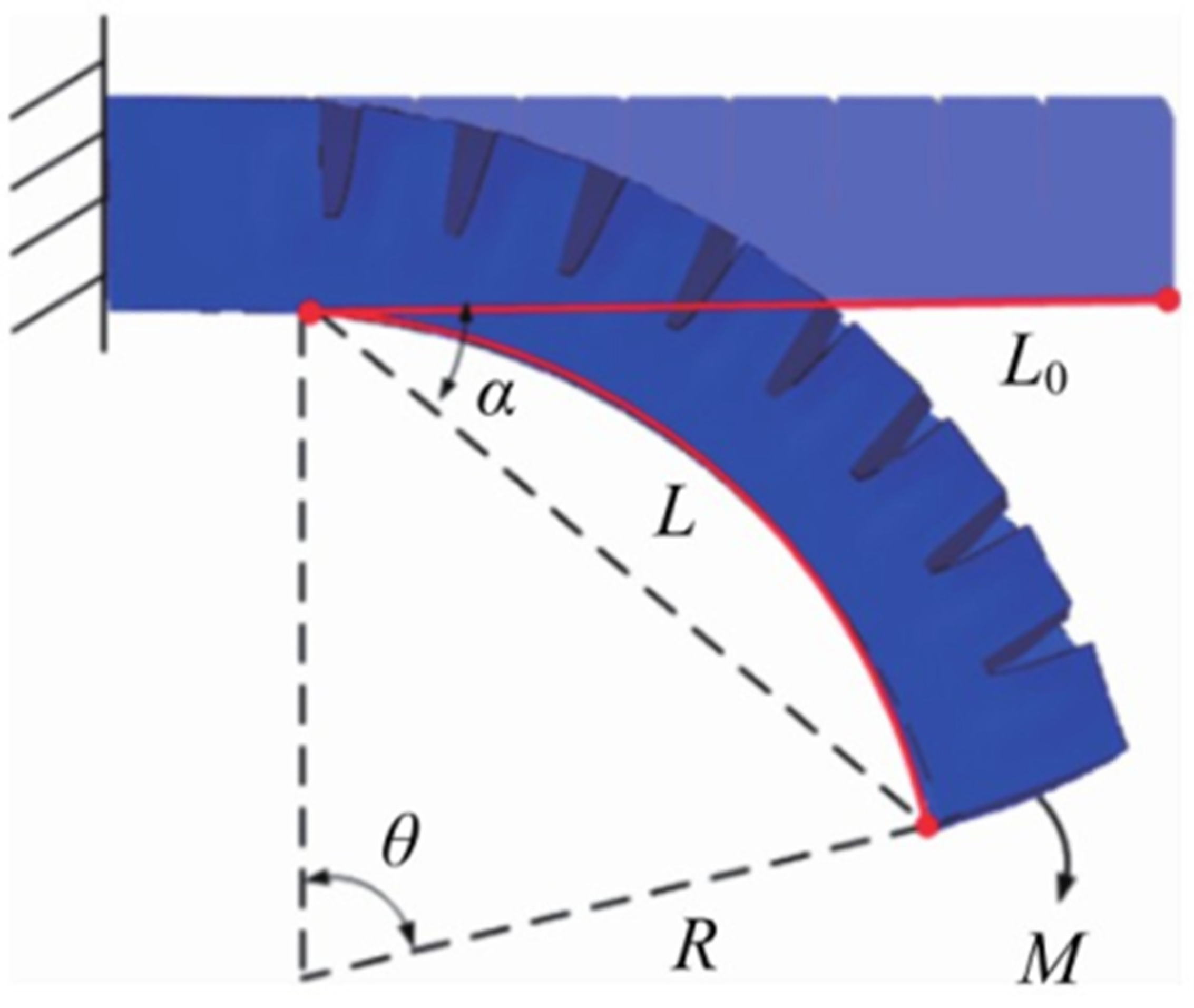
- Mathematical modeling:
- Parameter determination:
- (1)
- Softness: With a Shore A hardness of 30 A, Dragon Skin 30 Silicone is very soft, similar to human skin.
- (2)
- High Stretchability: It has extremely high stretchability and can be stretched to many times its original size without breaking, making it ideal for applications that require high elasticity.
- (3)
- High Strength: Despite its softness, Dragon Skin 30 Silicone also has excellent physical strength and can withstand large pressures and deformations.
- (4)
- Durability: This silicone has excellent durability and anti-aging properties and can maintain its properties for a long time without degradation.
- (5)
- Non-Toxic and Odorless: Dragon Skin 30 Silicone material is non-toxic and odorless, making it suitable for applications that come into contact with the human body.
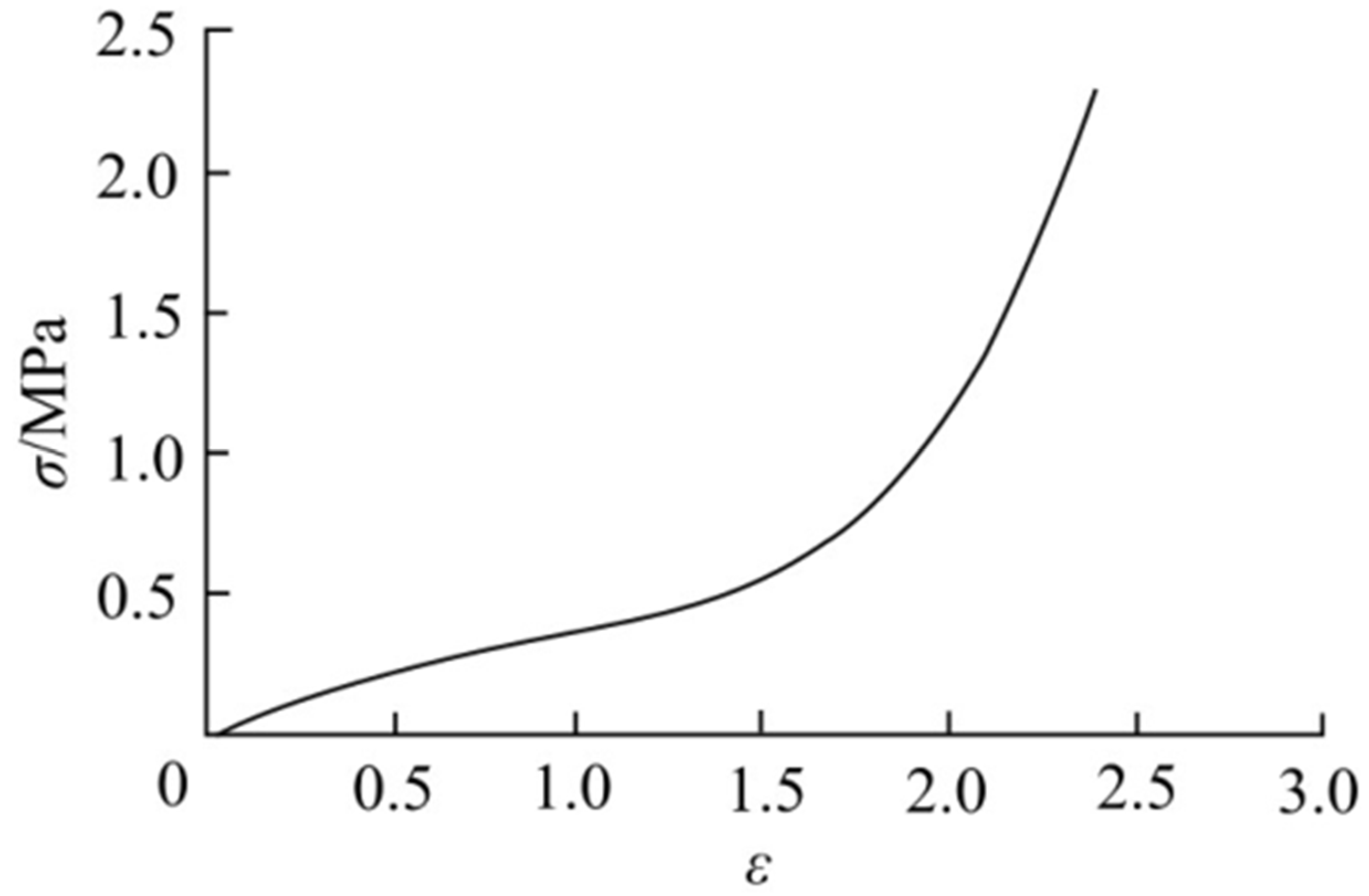
- Simulation optimization of the combination of different factors and parameters:
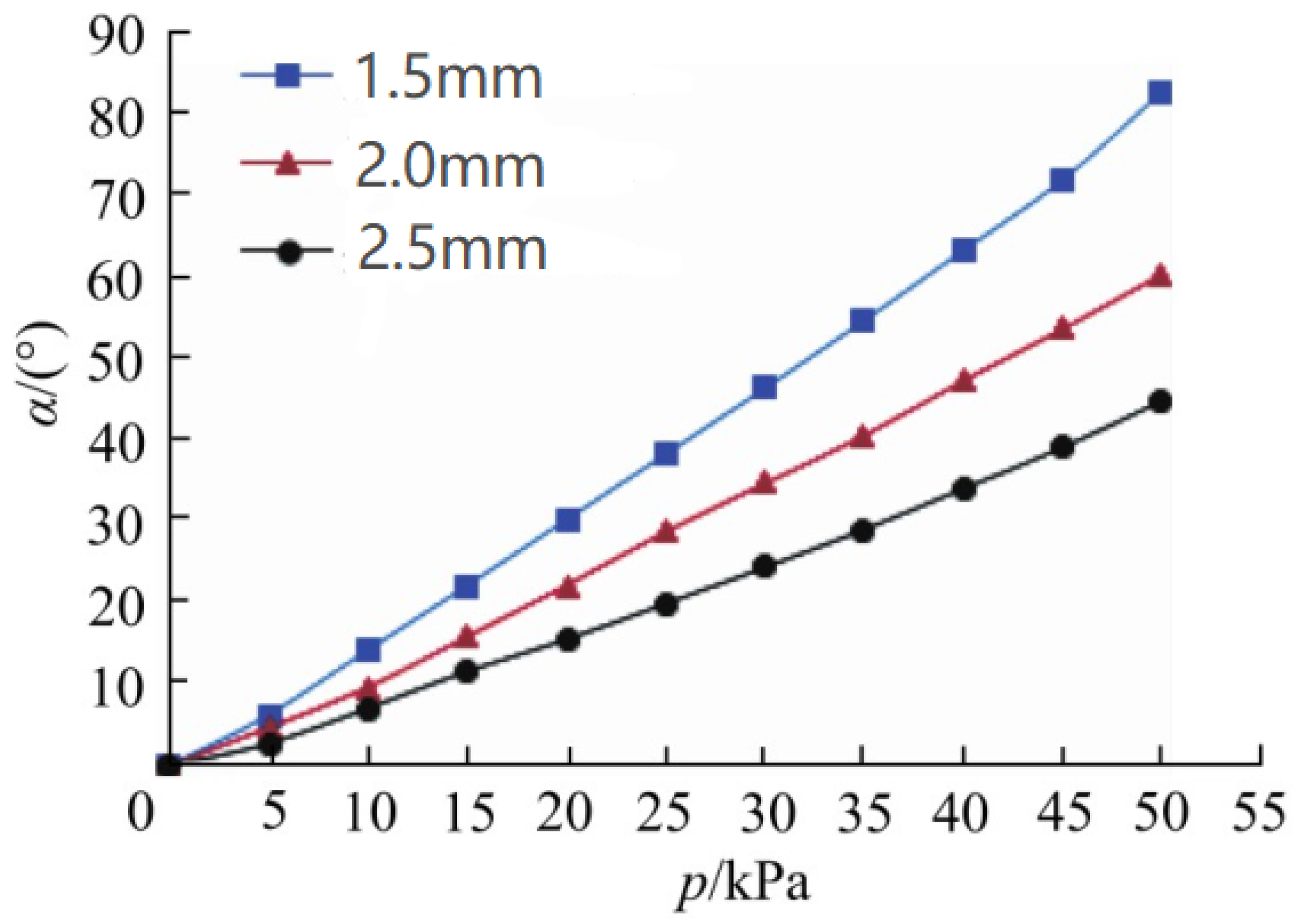
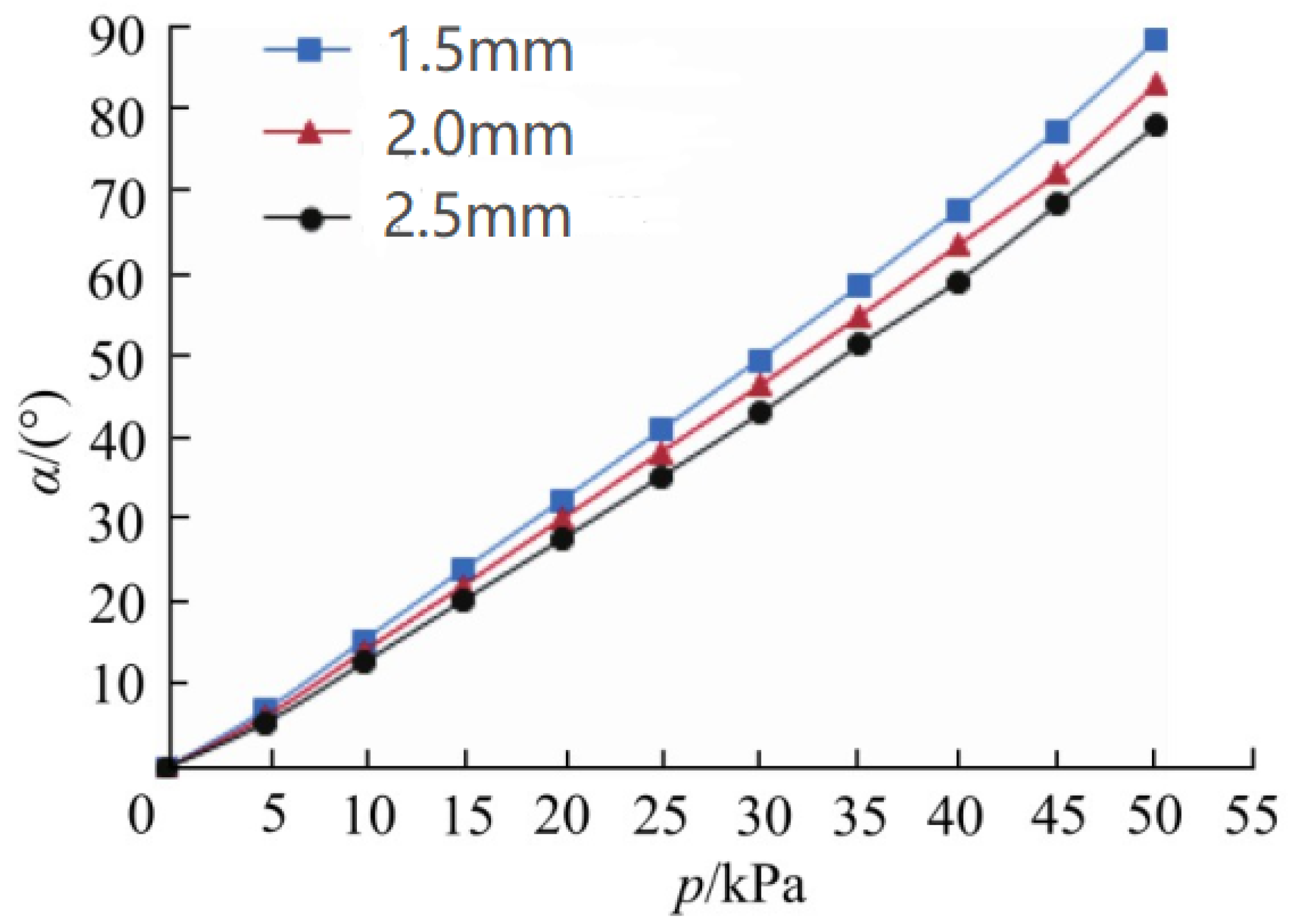
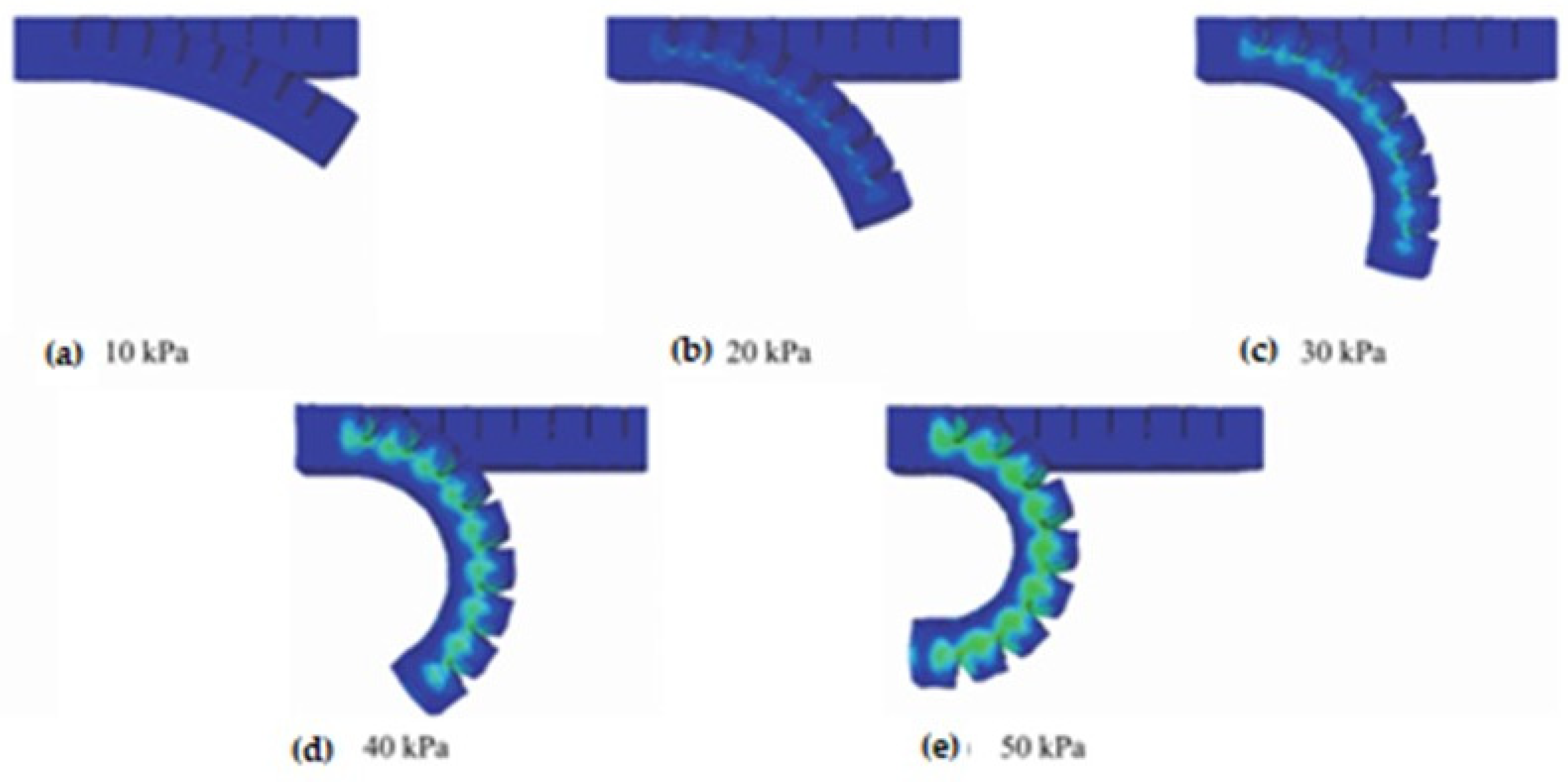
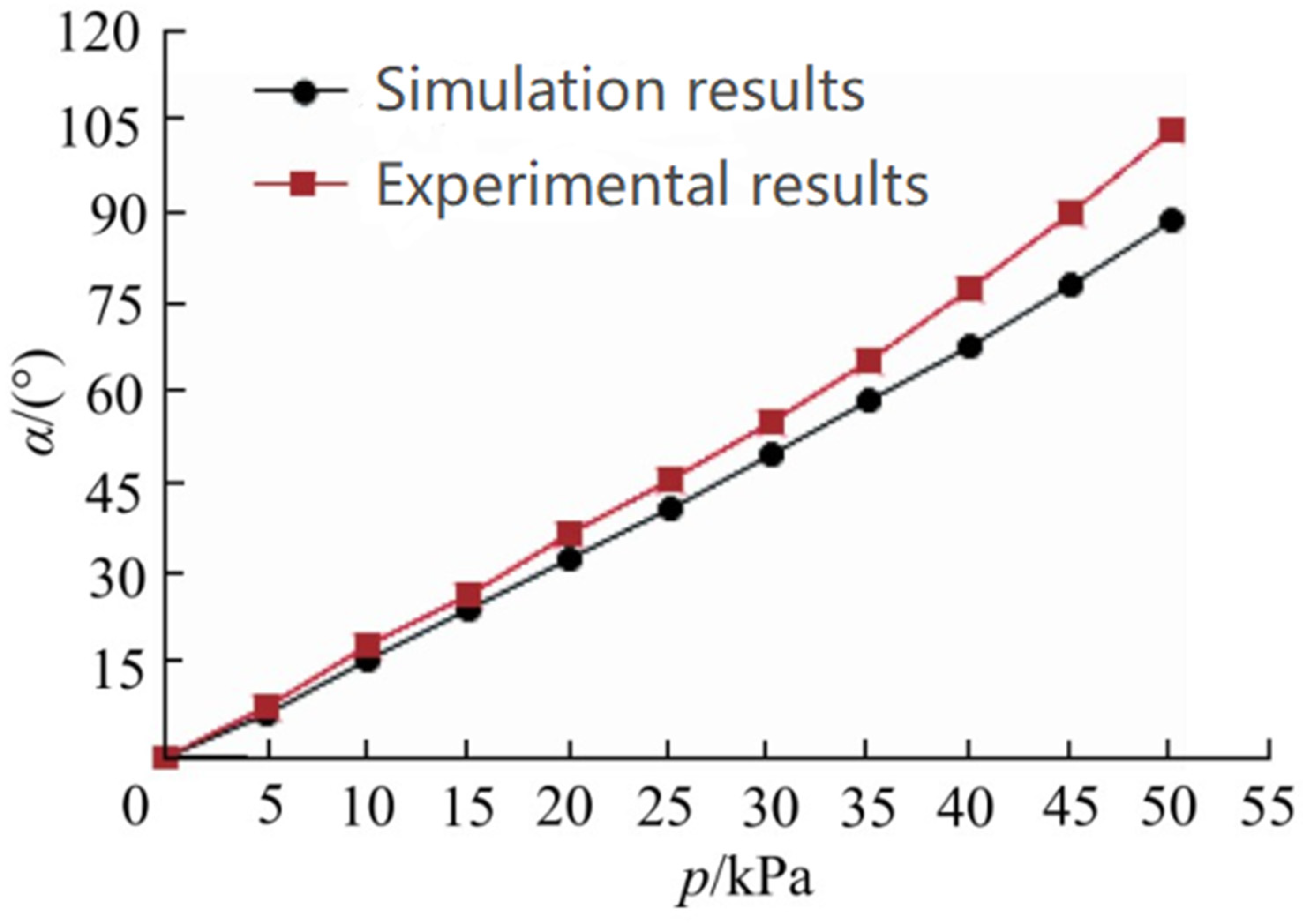
3. Results and Tests
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rothemund, P.; Kim, Y.; Heisser, R.H.; Zhao, X.; Shepherd, R.F.; Keplinger, C. Shaping the future of robotics through materials innovation. Nat. Mater. 2021, 20, 1582–1587. [Google Scholar] [CrossRef] [PubMed]
- Rich, S.I.; Wood, R.J.; Majidi, C. Untethered soft robotics. Nat. Electron. 2018, 1, 102–112. [Google Scholar] [CrossRef]
- Wehner, M.; Truby, R.L.; Fitzgerald, D.J.; Mosadegh, B.; Whitesides, G.M.; Lewis, J.A.; Wood, R.J. An integrated design and fabrication strategy for entirely soft autonomous robots. Nature 2016, 536, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Ying, C.; Zhang, K.; Xie, H.; E, S. An effective nonlinear dynamic formulation to analyze grasping capability of soft pneumatic robotic gripper. Int. J. Smart Nano Mater. 2024, 1–27, ahead-of-print. [Google Scholar] [CrossRef]
- Majidi, C. Soft-matter engineering for soft robotics. Adv. Mater. Technol. 2019, 4, 1800477. [Google Scholar] [CrossRef]
- Branyan, C.; Fleming, C.; Remaley, J.; Kothari, A.; Tumer, K.; Hatton, R.L.; Mengüç, Y. Soft snake robots: Mechanical design and geometric gait implementation. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 282–289. [Google Scholar]
- Cortes-Gonzalez, J.G.; Sandoval-castro, X.Y.; Torres, M.F.R.; Castillo-Castaneda, E. Bio-inspired Design of a Soft Bending Actuator for Flexion of a Human Index Finger: A Case Study. Adv. Mech. Mach. Sci. 2023, 148, 620. [Google Scholar]
- Sokolov, O.; Hošovský, A.; Trojanová, M. Design, Modelling, and Control of Continuum Arms with Pneumatic Artificial Muscles: A Review. Machines 2023, 11, 936. [Google Scholar] [CrossRef]
- Niu, H.; Feng, R.; Xie, Y.; Jiang, B.; Sheng, Y.; Yu, Y.; Baoyin, H.; Zeng, X. MagWorm: A Biomimetic Magnet Embedded Worm-Like Soft Robot. Soft Robot. 2021, 8, 507–518. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.; Shi, H.; Pinto, T.; Tan, X. A novel pneumatic soft snake robot using traveling-wave locomotion in constrained environments. IEEE Robot. Autom. Lett. 2020, 5, 1610–1617. [Google Scholar] [CrossRef]
- Zakharov, L.A.; Martyushev, D.A.; Ponomareva, I.N. Predicting dynamic formation pressure using artificial intelligence methods. J. Min. Inst. 2022, 253, 23–32. [Google Scholar] [CrossRef]
- Leonidovich, Z.Y.; Kovalchuk, M.S.; Batueva, D.E.; Senchilo, N.D. Development of an algorithm for regulating the load schedule of educational institutions based on the forecast of electric consumption within the framework of application of the demand response. Sustainability 2021, 13, 13801. [Google Scholar] [CrossRef]
- Calderón, A.A.; Ugalde, J.C.; Zagal, J.C.; Pérez-Arancibia, N.O. Design fabrication and control of a multi-material-multi-actuator soft robot inspired by burrowing worms. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 31–38. [Google Scholar]
- Xavier, M.S.; Fleming, A.J.; Yong, Y.K. Image-guided locomotion of a pneumatic-driven peristaltic soft robot. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 2269–2274. [Google Scholar]
- Hou, T.; Yang, X.; Su, H.; Chen, L.; Wang, T.; Liang, J.; Zhang, S. Design fabrication and morphing mechanism of soft fins and arms of a squid-like aquatic-aerial vehicle with morphology tradeoff. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 1020–1026. [Google Scholar]
- Zemenkova, M.Y.; Chizhevskaya, E.L.; Zemenkov, Y.D. Intelligent monitoring of the condition of hydrocarbon pipeline transport facilities using neural network technologies. J. Min. Inst. 2022, 258, 933–944. [Google Scholar] [CrossRef]
- Shamil, I.R.; Grigoriev ABeloglazov, I.I.; Savchenkov, S.A.; Gudmestad, O.T. Research risk factors in monitoring well drilling—A case study using machine learning methods. Symmerty 2021, 13, 1293. [Google Scholar]
- Chen, A.; Yin, R.; Cao, L.; Yuan, C.; Ding, H.; Zhang, W. Soft robotics: Definition and research issues. In Proceedings of the 24th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Auckland, New Zealand, 21–23 November 2017; pp. 366–370. [Google Scholar]
- Filippov, E.V.; Zakharov, L.A.; Martyushev, D.A.; Ponomareva, I.N. Reproduction of reservoir pressure by machine learning methods and study of its influence on the cracks formation process in hydraulic fracturing. J. Min. Inst. 2022, 258, 924–932. [Google Scholar] [CrossRef]
- Yang, J.; Wang, F.; Lu, Y. Design of a Bistable Artificial Venus Flytrap Actuated by Low Pressure with Larger Capture Range and Faster Responsiveness. Biomimetics 2023, 8, 181. [Google Scholar] [CrossRef] [PubMed]
- Mészáros, A.; Sárosi, J. Increasing the Force Exertion of a Soft Actuator Using Externally Attachable Inter-Chamber Plates. Actuators 2023, 12, 222. [Google Scholar] [CrossRef]
- van Vlerken, C.; Ballen-Moreno, F.; Roels, E.; Ferrentino, P.; Langlois, K.; Vanderborght, B.; Verstraten, T. Development of an Active Physical Interface for Physical Human-Robot Interaction: Investigation of Soft Pneumatic Actuator Straps for Automatic Enclosure System. Actuators 2023, 12, 241. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.L.; Koshenkova, A.A.; Vorobieva, V.A.; Raspunin, D.L. Assessment of the Impact of Technological Development and Scenario Forecasting of the Sustainable Development of the Fuel and Energy Complex. Energies 2023, 16, 3185. [Google Scholar] [CrossRef]
- Hu, W.; Alici, G. Bioinspired three-dimensional-printed helical soft pneumatic actuators and their characterization. Soft Robot 2020, 7, 267–282. [Google Scholar] [CrossRef]
- Beloglazov, I.I.; Plaschinsky, V.A. Development MPC for the Grinding Process in SAG Mills Using DEM Investigations on Liner Wear. Materials 2024, 17, 795. [Google Scholar] [CrossRef]
- Romashev, A.O.; Nikolaeva, N.V.; Gatiatullin, B.L. Adaptive approach formation using machine vision technology to determine the parameters of enrichment products deposition. J. Min. Inst. 2022, 256, 677–685. [Google Scholar] [CrossRef]
- Gorissen, B.; Reynaerts, D.; Konishi, S.; Yoshida, K.; Kim, J.-W.; De Volder, M. Elastic inflatable actuators for soft robotic applications. Adv. Mater. 2017, 29, 1604977. [Google Scholar] [CrossRef] [PubMed]
- Polygerinos, P.; Correll, N.; Morin, S.A.; Mosadegh, B.; Onal, C.D.; Petersen, K.; Cianchetti, M.; Tolley, M.T.; Shepherd, R.F. Soft robotics: Review of fluid-driven intrinsically soft devices; manufacturing sensing control and applications in human-robot interaction. Adv. Eng. Mater. 2017, 19, 1700016. [Google Scholar] [CrossRef]
- Kozhubaev, Y.N.; Ovchinnikova, E.N.; Ivanov, V.Y.; Krotova, S.Y. Incremental Machine Learning for Soft Pneumatic Actuators with Symmetrical Chambers. Symmetry 2023, 15, 1206. [Google Scholar] [CrossRef]
- Mayer, A.; Müller, D.; Raisch, A.; Hildebrandt, A.; Sawodny, O. Demonstration-based Programming of Multi-Point Trajectories for Collaborative Continuum Robots. IFAC-PaperOnLine 2019, 52, 513–518. [Google Scholar] [CrossRef]
- Zhang, Z.; Long, Y.; Chen, G.; Wu, Q.; Wang, H.; Jiang, H. Soft and lightweight fabric enables powerful and high-range pneumatic actuation. Sci. Adv. 2023, 9, eadg1203. [Google Scholar] [CrossRef] [PubMed]
- Drotman, D.; Jadhav, S.; Sharp, D.; Chan, C.; Tolley, M.T. Electronics-free pneumatic circuits for controlling soft-legged robots. Sci. Robot. 2021, 6, eaay2627. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Song, Z.; Chen, S.; Gu, G.; Zhu, X. Morphological Design for Pneumatic Soft Actuators and Robots with Desired Deformation Behavior. Trans. Robot. 2023, 39, 4408–4428. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, K.; Tang, W.; Qin, K.; Liu, Y.S.Y.; Zou, J. Design and analysis of flexible bending actuator driven by electrohydrodynamic pumps. J. Eng. Des. 2023, 30, 467–475. [Google Scholar] [CrossRef]
- Makhovikov, A.; Kryltsov, S.B.; Matrokhina, K.V.; Trofimets, V.Y. Secure corporate communication system for a metallurgical enterprise Non-ferrous metal. Non-Ferr. Met. 2023, 4, 5–13. [Google Scholar] [CrossRef]
- Matrokhina, K.V.; Trofimets, V.Y.; Mazakov, E.B.; Makhovikov, A.B.; Khaykin, M.M. Development of methodology for scenario analysis of investment projects of enterprises of the mineral resource complex. J. Min. Inst. 2023, 259, 112–124. [Google Scholar] [CrossRef]

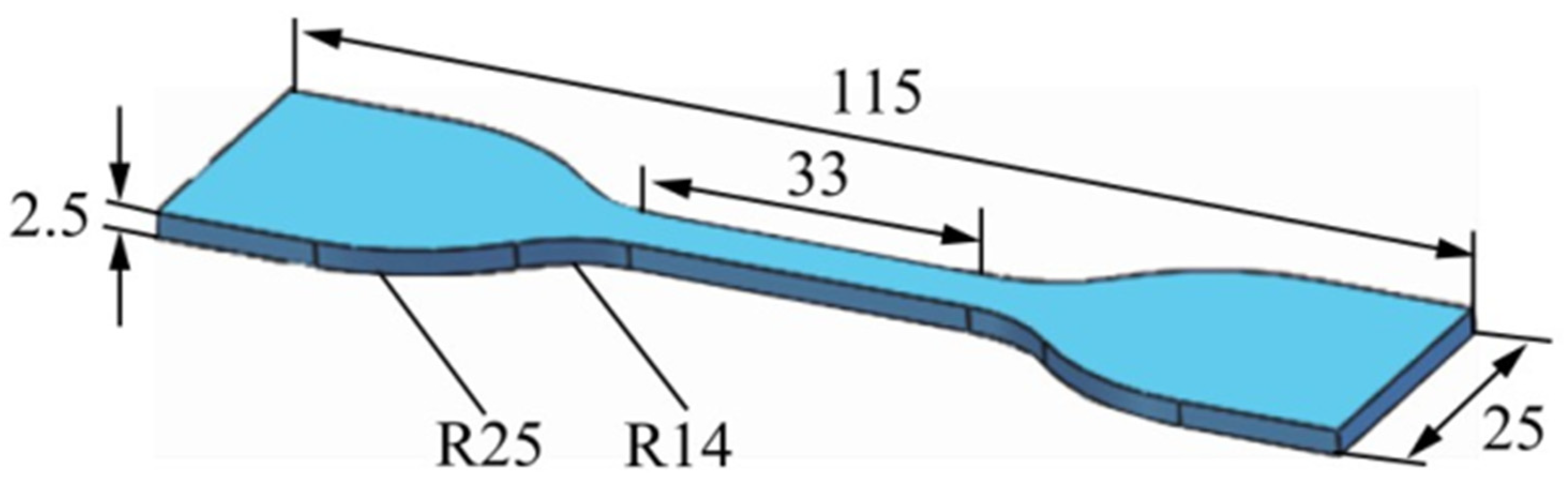


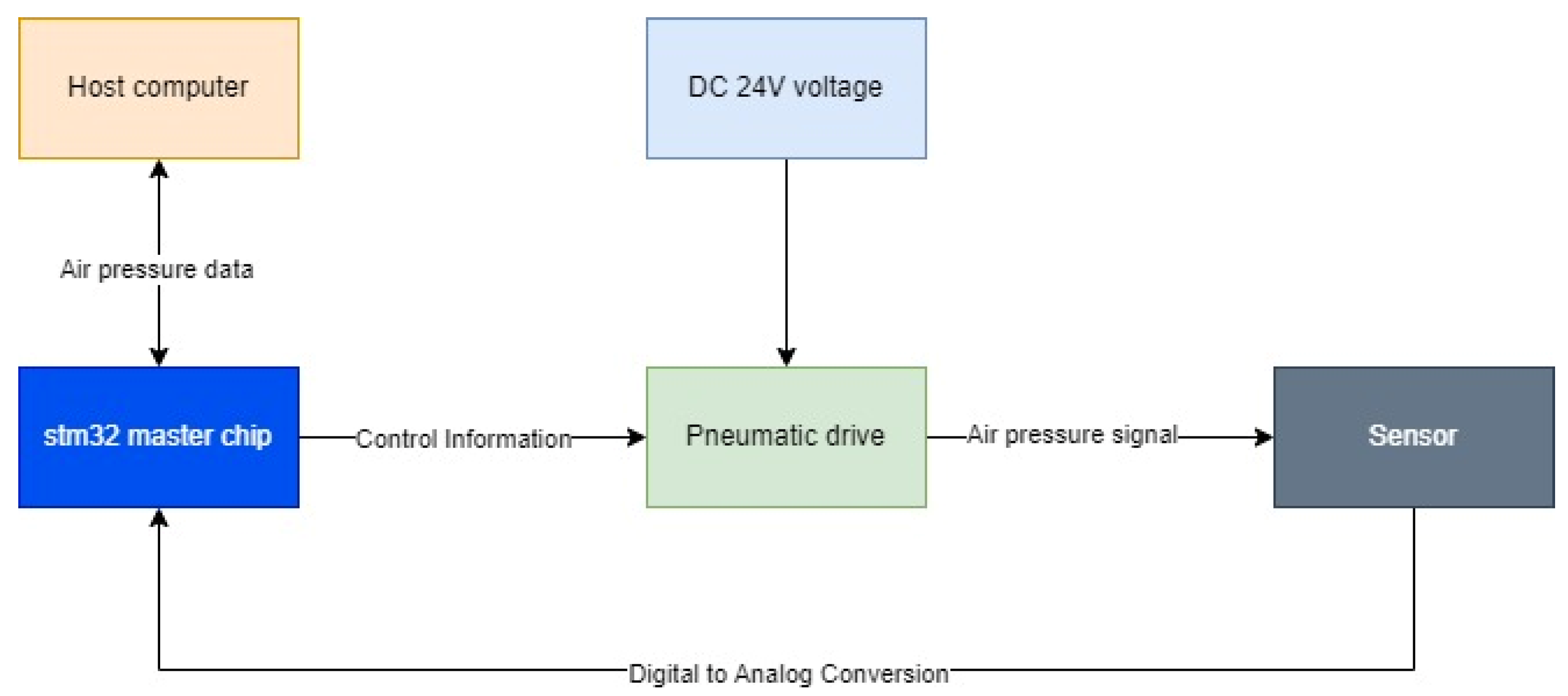

| Parameter | Values (mm) |
|---|---|
| length | 125 |
| width | 20 |
| height | 22 |
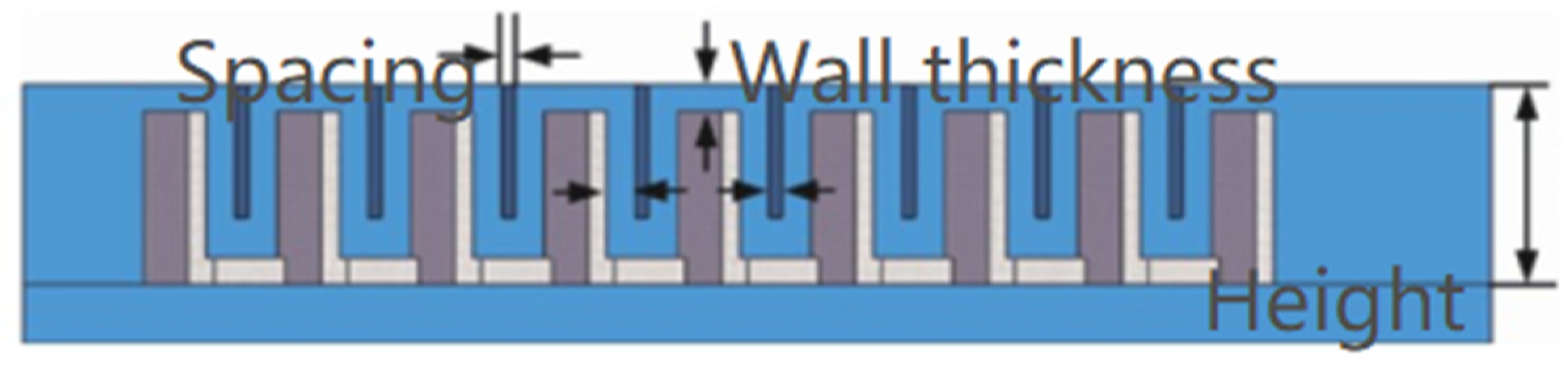
| Factor | Parameter (mm) | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Air cavity wall thickness | 1.5 | 2.0 | 2.5 |
| Air cavity inquiry distance | 1.5 | 2.0 | 2.5 |
| Air cavity height | 10 | 11.0 | 12.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muratbakeev, E.; Kozhubaev, Y.; Yiming, Y.; Umar, S. Symmetrical Modeling of Physical Properties of Flexible Structure of Silicone Materials for Control of Pneumatic Soft Actuators. Symmetry 2024, 16, 750. https://doi.org/10.3390/sym16060750
Muratbakeev E, Kozhubaev Y, Yiming Y, Umar S. Symmetrical Modeling of Physical Properties of Flexible Structure of Silicone Materials for Control of Pneumatic Soft Actuators. Symmetry. 2024; 16(6):750. https://doi.org/10.3390/sym16060750
Chicago/Turabian StyleMuratbakeev, Eduard, Yuriy Kozhubaev, Yao Yiming, and Shehzad Umar. 2024. "Symmetrical Modeling of Physical Properties of Flexible Structure of Silicone Materials for Control of Pneumatic Soft Actuators" Symmetry 16, no. 6: 750. https://doi.org/10.3390/sym16060750





