Enumeration of n-Dimensional Hypercubes, Icosahedra, Rubik’s Cube Dice, Colorings, Chirality, and Encryptions Based on Their Symmetries

Abstract

The whimsical Las Vegas/Monte Carlo cubic dice are generalized to construct the combinatorial problem of enumerating all n-dimensional hypercube dice and dice of other shapes that exhibit cubic, icosahedral, and higher symmetries. By utilizing powerful generating function techniques for various irreducible representations, we derive the combinatorial enumerations of all possible dice in n-dimensional space with hyperoctahedral symmetries. Likewise, a number of shapes that exhibit icosahedral symmetries such as a truncated dodecahedron and a truncated icosahedron are considered for the combinatorial problem of dice enumerations with the corresponding shapes. We consider several dice with cubic symmetries such as the truncated octahedron, dodecahedron, and Rubik’s cube shapes. It is shown that all enumerated dice are chiral, and we provide the counts of chiral pairs of dice in the n-dimensional space. During the combinatorial enumeration, it was discovered that two different shapes of dice exist with the same chiral pair count culminating to the novel concept of isochiral polyhedra. The combinatorial problem of dice enumeration is generalized to multi-coloring partitions. Applications to chirality in n-dimension, molecular clusters, zeolites, mesoporous materials, cryptography, and biology are also pointed out. Applications to the nonlinear n-dimensional hypercube and other dicey encryptions are exemplified with romantic, clandestine messages: “I love U” and “V Elope at 2”.

1. Introduction

The Monte Carlo/Las Vegas dice are special cases of face colorings of a cube with six different numbers/colors under the cubic rotational symmetry action stipulating that the sum of the numbers on the opposite sides of the cube shall be 7. There are exactly 30 possible dice or 15 chiral pairs without any such constraints, and yet only one die is chosen for gambling. Even though a chiral pair of dice exists with the stipulation that the sum of opposite sides shall be 7, only the right-handed die is the favorite of the Las Vegas world of gambling. Yet stimulated by several applications, there are scholarly reasons to consider all possible dice enumerations not only in the 3D space but also regarding the dice and coloring enumerations in n-dimensions. Furthermore, consideration of other shapes of dice such as a truncated octahedron, truncated icosahedron, and so forth could have several applications in chemistry, chirality, material science, and biology, including molecular structures arising from face cappings of such three-dimensional molecular structures to genetic regulatory networks [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. The generalization of these combinatorial enumeration problems to n-dimensional hypercubes, polycubes, polytopes, molecular bodies, and databases [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33] and the related combinatorics of hyperoctahedral or wreath product groups can have profound ramifications in several fields [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. A phenomenal exemplification of such applications is to the cynosure of wreath product objects, namely the celebrated Rubik’s cube, which, in general symmetry terms, is a quintessential element of dynamic symmetry and coloring under the wreath product symmetry action.

The n-dimensional hypercubes are ubiquitous in varied fields such as artificial intelligence, pattern recognition, visual image processing, electrical circuit theory, and information science, including Boolean logic, where the 2ⁿ possible Boolean strings become the vertices of an n-dimensional hypercube [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. Furthermore, hypercubes find applications in biology, chemistry, isomerization reactions, finite automata, enumeration of isomers, genetics, computer graphics, dynamic or transient chirality, protein–protein interactions, intrinsically disordered proteins and their moonlighting functions, computational psychiatry, partitioning of big data, and parallel computing [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. The recursive nature of symmetries of hypercubes can be molded into hyperoctahedral wreath products [1]. These recursive symmetries find numerous applications in isomerization reactions, enumerative combinatorics, nuclear spin statistics, water clusters, nonrigid molecules, proteomics, and spontaneous generation of chirality, a phenomenon made possible by dynamic chiral reaction pathways in isomerization graphs [1,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. The nd-Boolean hypercubes find their ways into novel representations of time measures, the periodic table of elements, quantum similarity measures [4,5,6,7,8,9], biochemical and multi-dimensional imaging [11], big data, Quantitative Shape-Activity Relations (QShAR), and so forth [12,13,14,15].

Combinatorial enumeration of face colorings of n-dimensional hypercubes has a direct bearing to the subject matter of this study, although the vertex-coloring of n-dimensional hypercubes has been the subject matter of numerous studies over the years. Pólya [22,23] alluded to the errors propagated in earlier works on the enumeration of colorings of vertices of nD-hypercubes. The topic has attracted numerous researchers for decades culminating in a plethora of publications owing to their interest in multiple fields [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. In the present study, we apply the face colorings of hypercubes not only to the problem of dice enumerations in n-dimension but also to point out several other applications with multiple color partitions. Furthermore, several chemical and spectroscopic applications require generalized combinatorial/group theory enumeration techniques that include all the irreducible representations of the groups whereas Pólya’s theorem reduces to a special case, namely the one for the totally symmetric representation. In the present study, we consider the enumeration of dice and face colorings of not only objects of cubic symmetries but also of icosahedral symmetries such as a truncated icosahedron and so on, which find applications in the representation of the celebrated buckminsterfullerene. Pólya’s method has been used earlier to enumerate the various cappings and excisings of triangulated polyhedra to yield systems containing from four to twelve vertices [59] while graph theoretical aspects of chemically interesting polyhedra with up to eight vertices have been considered in the context of dynamical isomerizations [60]. Experimental studies on fullerene analogs of gold clusters reveal that the Au₁₃ core with the highest icosahedral (I_h) symmetry is inherent in these structures [61]. Moreover, the first coordination-saturated buckyball encased in an icosidodecahedral Cu₃₀, that is, C₆₀@Cu₃₀@Cl₃₆N₁₂, has been successfully synthesized [62]. Experimental synthetic organic chemical studies have been focused on the chirality of icosahedron-based molecules [63,64,65,66]. Stimulated by such experimental and theoretical studies, we develop combinatorial techniques in the present study that would find natural applications to fullerene derivatives, inorganic polyhedral clusters, mesoporous materials, zeolites, dynamic polyhedral stereochemistry, and large highly symmetric fullerene cages, including the golden fullerenes and nanospheres. Furthermore, the enumeration of n-dimensional dice and colorings could have profound implications in cryptography in encrypting and decrypting messages through face-labeled packets of nD-hypercubes and icosahedral structures.

2. Combinatorial and Group Theoretical Techniques

The symmetry group of an nD-hypercube is an hyperoctahedral group that can be cast into the wreath product form S_n[S₂] where S_n is the full permutation group of n objects with n! permutations. Consequently, the cardinality of the nD-hypercube group is 2ⁿ × n!. For example, the symmetry group of a 10-cube contains 2¹⁰ × 10! permutations spanning 481 conjugacy classes, and hence 481 irreducible representations. Moreover, there are 10 hyperplanes for a 10-cube, and hence enumerating colorings of different hyperplanes of an nD-hypercube for all irreducible representations can be a combinatorially complex and daunting problem, which provides a perfect platform for artificial intelligence. Coxeter [67] has carried out groundbreaking work on the characterization of hypercubes and several other regular polytopes. An nD-hypercube contains (n-q)-hyperplanes where q goes from 0 to n. The largest value of q = n represents the vertices, q = n − 1 represents the edges, q = n − 2 represents the faces, and so on. In the present study, we focus on the face colorings and their combinatorial enumerations. The induced permutations arising from the action of the symmetry group of the nD-hypercube on each of these hyperplanes require complex mathematical techniques involving polynomial generators and Möbius inversion techniques, both of which have been discussed extensively in previous studies. Hence, we will not repeat these details and restrict ourselves to face colorings. Moreover, we consider the enumerations that involve all irreducible representations that require the cycle types of each conjugacy class, which are constructed from matrices of the conjugacy classes of wreath product groups.

Consider a 7D-hypercube, briefly denoted as a 7-cube. The geometrical structure of a 7-cube is characterized by a 7 × 7 configuration matrix in Coxeter’s notation [67] exemplified here where the rows are q values in reverse order, (from 7 to 1) as they represent (n-q)-hyperplanes of the n-cube.

$$\left(\begin{array}{c}\begin{array}{ccccccc}128& 7& 21& 35& 35& 21& 7\\ 2& 448& 6& 15& 20& 15& 6\\ 4& 4& 672& 5& 10& 10& 5\\ 8& 12& 6& 560& 4& 6& 6\\ 16& 32& 24& 8& 280& 3& 3\\ 32& 80& 80& 40& 10& 84& 2\\ 64& 192& 240& 160& 60& 12& 14\end{array}\end{array}\right)$$

The number of (n-q)-hyperplanes for an n-hypercube is obtained as

$$N_q=\left(\begin{array}{c}n\\ q\end{array}\right)2^q$$

In particular, the number of faces for an n-cube is obtained as

$$N_{n-2}=\left(\begin{array}{c}n\\ n-2\end{array}\right)2^{n-2}=\left(\begin{array}{c}n\\ 2\end{array}\right)2^{n-2}=n\left(n-1\right)2^{n-3}$$

When the above formula is applied to the 7D-hypercube we obtain the number of faces as

$$\left(\begin{array}{c}7\\ 2\end{array}\right)2^5=672,$$

which is the diagonal element of the third row in the above configuration matrix.

In order to enumerate the n-cube dice or in general face colorings of the n-cube with a chosen color partition, we consider a set D of faces of the n-cube with a set R as the various colors such as blue, red, green, white, violet, and so on. A face coloring is then a map from the set D to the set R, and the combinatorial enumeration of the face colorings is identical to one of enumerating the equivalence classes of such maps under the action of the symmetry cube of n-cube, which is the wreath product S_n[S₂]. For example, the symmetry group of the 7-cube is isomorphic to the S₇[S₂] wreath product group that contains 2⁷ × 7! permutations. These permutations generate different orbit structures for each set of hyperplanes of the n-cube. In particular, for the faces of the n-cube, the orbit length of the permutation acting on the faces is n(n − 1)x2ⁿ⁻³, and hence the cycle types of the permutations would all be different from the corresponding cycle types and orbit structures for 2ⁿ vertices of the n-cube. We have previously demonstrated the Möbius inversion technique for the construction of cycle types and orbit structures for the various hyperplanes of the n-cube [1,3]. In summary, the Möbius inversion technique yields the orbit structure of every set of hyperplanes for an n-cube. The orbit structure is required in order to construct the generating functions for the colorings of the various hyperplanes of the n-cube.

We briefly discuss this with an illustration of the permutational cycle type of the S₇[S₂] group for the faces, which is obtained by using the Möbius inversion method. As a first step, the 2 × 7 cycle-type matrices for each of the 110 conjugacy classes of the 7D-hypercube should be obtained. These also represent the permutations of the cycle types of the hexeracts (q = 1) of the 7D-hypercube, which is shown in Figure 1. The cycle index used in Pólya’s technique can be generalized for all irreducible representations of the n-cube’s group. Consequently, one needs the cycle types for each conjugacy class of the S_n[S₂] group and for each of the hyperplanes (q = 1,n) of the n-cube. This requires the construction of the cycle types of q = 1 or hexeracts of the 7D-hypercube shown in Figure 1, for example. This is accomplished through matrix generator functions yielding the 2 × n matrices for the n-cube for all conjugacy classes. Subsequently, we invoke the Möbius generating function method, which is used to enumerate all cycle types for q = 2 through n, as demonstrated in previous works for the 7-cube and 8-cube [1,39,40]. Hence, the cycle types of faces of the n-cube are generated by substituting q = n − 2 in this algorithm for generating the cycle types of the hyperplanes of the n-cube.

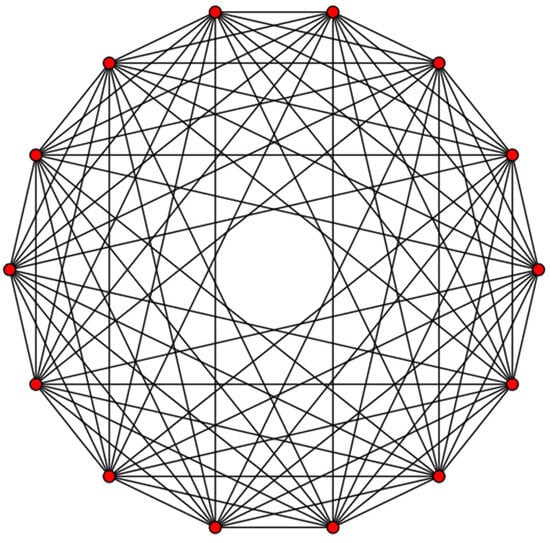
Figure 1. A dual representation of the 7D-hypercube in which 14 hexeracts of the 7D-hypercube are the vertices and edges representing their neighborhood connectivity. The vertices of the graph can also represent the fourteen protons of the nonrigid water heptamer, (H₂O)₇ in its fully nonrigid limit. (Reproduced from Ref. [68]).

The character table of the hyperoctahedral group containing all irreducible representations is required to construct the GCCIs of the irreducible representation Γ with character χ of the group. Let the set D of the faces of the hypercube have cardinality l. In general, the GCCI for the character χ of a group G′ is defined as

$$P_{G^{\prime }}^{\chi }={\displaystyle \frac{1}{\left|G^{\prime }\right|}}{\displaystyle \sum _{g\epsilon G^{\prime }}\chi (g)s_1^{b_1}}{s}_2^{b_2}......s_m^{bm},$$

where the sum is, over all permutation representations of g ∈ G′ that generate b₁ cycles of length 1, b₂ cycles of length 2, ….., b_m cycles of length m upon its action on the set D of the faces of the hypercube. The generalized Pólya substitution in the GCCIs for each representation of S_n[S₂] has a multinomial expansion for coloring the faces of the hypercube with say r colors. Let [l] be an ordered partition, also called the composition of l into p parts such that n₁ ≥ 0, n₂ ≥ 0, …, n_p ≥ 0, ${\sum }_{i=1}^p{n}_i=l$. A multinomial generating function in λs is obtained as

$${\left({\lambda }_1+{\lambda }_2+\dots ..+{\lambda }_p\right)}^l=$$

$${\sum }_{\left[r\right]}^p\begin{array}{c}\left(\begin{array}{c}\\ n_1\end{array}\begin{array}{c}\\ n_2\end{array}l\begin{array}{c}\\ .\end{array}\begin{array}{c}\\ n_p\end{array}\right)\\ \end{array}{{\lambda }_1}^{n_1}{{\lambda }_2}^{n_2}{{\dots \dots ..\lambda }_{p-1}}^{n_{p-1}}{{\lambda }_p}^{n_p},$$

where $\left(\begin{array}{c}\\ n_1\end{array}\begin{array}{c}\\ n_2\end{array}\begin{array}{c}l\\ .\end{array}\begin{array}{c}\\ .\end{array}\begin{array}{c}\\ n_p\end{array}\right)$ are multinomials given by

$$\left(\begin{array}{c}\\ n_1\end{array}\begin{array}{c}\\ n_2\end{array}\begin{array}{c}l\\ .\end{array}\begin{array}{c}\\ .\end{array}\begin{array}{c}\\ n_p\end{array}\right)={\displaystyle \frac{l!}{n_1!n_2!\dots \dots n_{p-1}!n_p!}}.$$

Let the set R, which contains r different types of colors (for example, yellow, blue, green, red, and white…) be the colors that can be used to color the faces of the n-cube. Let w_i be the weight of each color r in R. Consequently, the weight of a function f from D to R is defined as

$$W\left(f\right)={\prod }_{i=1}^{\left|R\right|}w\left(f\left(d_i\right)\right)$$

The generating function for each irreducible representation of the nD-hyperoctahedral group is obtained by the substitution as

$${GF}^{\chi }\left({\lambda }_1,{\lambda }_2\dots ..{\lambda }_p\right)=P_G^{\chi }\{s_k\to \left({{\lambda }_1}^k+{{\lambda }_2}^k+\dots .+{\lambda }_{p-1}^k+{\lambda }_p^k\right)\}$$

The above GFs are computed for each irreducible representation of the n-cube hyperoctahedral group. The coefficient of each term $\left({{\lambda }_1}^{n_1}{{\lambda }_2}^{n_2}\dots ..{{\lambda }_p}^{n_p}\right)$ generates the number of functions in the set R^D that transform in accord with the irreducible representation Γ with character χ. For the totally symmetric irreducible representation A₁, the GF reduces to the celebrated Pólya theorem, or the enumerative GF for the number of equivalence classes of colorings. Likewise, the GF for a chiral representation, which would have a character value of +1 for proper rotations and −1 for improper rotations, would enumerate the number of chiral face colorings for a given color partition in the GF.

As these GFs become combinatorially complex with numerous terms and a large number of irreducible representations in the n-cube, computations become quite intensive. Consequently, we have automated the iterative process with Fortran ‘95 codes that compute the cycle types for all hyperplanes using the Möbius inversion method, the character tables, and then finally the generating functions for the face colorings of the n-cube. We note that the same codes could be used for other hyperplanes of the n-cube such as vertices, edges, cells, tesseracts, and so forth. All of the computations were carried out in quadruple precision (Real*16) arithmetic with an accuracy of up to 32 digits. We note that the needed multinomials for the colorings were computed recursively prior to constructing the GFs and stored in memory for subsequent computations of the GFs of each IR of the n-cube.

3. Results and Discussions

3.1. n-Cube Dice and Chirality

We start with the 4-cube, or tesseract, to illustrate the dice enumeration in the fourth dimension and their chirality. The number of faces of the 4-cube and the order of the 4-cube hyperoctahedral group are 24 and 384, respectively. The generating functions can be derived from the cycle indices for the totally symmetric and chiral representations of the 4-cube, which are shown below:

$$\begin{gathered} {{\mathrm{P}}_{\mathrm{S}4\left[\mathrm{S}2\right]}}^{\mathrm{A}1}={\displaystyle \frac{1}{384}}\{s_1^{24}+4s_1^{12}{s}_2^6+6s_1^4{s}_2^{10}+12s_1^6{s}_2^9+12s_1^4{s}_4^5+4s_2^{12}+24s_1^2{s}_2^{11}+24s_2^2{s}_4^5+32s_3^8+32s_6^4+ \\ {s}_2^{12}+12s_1^2{s}_2^{11}+12s_2^2{s}_4^5+32s_3^4{s}_6^2+32s_6^4+12s_1^4{s}_2^{10}+24{s_1^{2}s}_2{s}_4^5+12s_4^6+48s_2^2{s}_4^5+48s_8^3\} \end{gathered}$$

$$\begin{gathered} {{\mathrm{P}}_{\mathrm{S}4\left[\mathrm{S}2\right]}}^{\mathrm{A}3}={\displaystyle \frac{1}{384}}\{s_1^{24}-4s_1^{12}{s}_2^6+6s_1^4{s}_2^{10}+12s_1^6{s}_2^9-12s_1^4{s}_4^5-4s_2^{12}-24s_1^2{s}_2^{11}+24s_2^2{s}_4^5+32s_3^8-32s_6^4+s_2^{12}+ \\ 12s_1^2{s}_2^{11}-12s_2^2{s}_4^5-32s_3^4{s}_6^2+32s_6^4+12s_1^4{s}_2^{10}-24{s_1^{2}s}_2{s}_4^5+12s_4^6+48s_2^2{s}_4^5-48s_8^3\} \end{gathered}$$

As the maximum of different colors that can be used to color the faces of the 4-cube is 24, the generating functions for the totally symmetric and chiral representations are obtained by replacing every s_k by

$$\left({{\lambda }_1}^k+{{\lambda }_2}^k+\dots +{\lambda }_{23}^k+{\lambda }_{24}^k\right)$$

Thus, the GF contains all possible color distributions for coloring the faces of the 4-cube such that the coefficient of a typical term $\left({{\lambda }_1}^{n_1}{{\lambda }_2}^{n_2}\dots ..{{\lambda }_p}^{n_p}\right)$ in the GF gives the number of irreducible representations that occur in the set of colorings with n₁ colors of type 1, n₂ colors of type 2, and so forth. In particular, as every face of the 4-cube needs to be colored with a different color for the dice enumeration, the coefficient of $\left({\lambda }_1{\lambda }_2\dots ..{\lambda }_{24}\right)$ in the GF enumerates the number of colorings that transform in accord with the irreducible representation. It can be seen for the 4-cube that these numbers for the A₁ and A₃ IRs are given by

$$\mathrm{N}{\mathrm{A}}_1=\mathrm{N}{\mathrm{A}}_3=\{{\displaystyle \frac{1}{384}}\times {\displaystyle \frac{24!}{1!1!\dots .1!}}\}=1.61575104618031104\times {10}^{21}$$

suggesting that all 4-cube dice are chiral, and there are $1.61575104618031104\times {10}^{21}$ pairs with the total number of 4-cube dice enumerated as 3.23150209236062208 $\times {10}^{21}$.

Table 1 shows the number of dice for an n-cube for n up to 12. As seen from Table 1, there are only 30 possible dice for the ordinary cube in the 3-dimension, all of which are chiral, or equivalently, there are 15 chiral pairs of cubic dice. These numbers increase in astronomical proportions as a function of n, as seen from Table 1. The number of dice in the fourth dimension already reaches 3.23150209236062208 × 10²¹ in comparison to the molecular Avogadro number of 6.0221408 × 10²³. The number of dice reaches 2.8214838544319294796427515741969896 × 10¹⁶⁰⁴ in the seventh dimension, beyond which even in REAL*16 arithmetic precision the numbers become too large to be exactly listed, although the mathematical expression for the number of chiral pairs of dice for any n-cube is derived from the GF of the n-cube as

Table 1. Number of possible dice in n-dimensions for n-cubes with all different numbers placed on the faces of the n-cube for n = 3 to 12.

n	Faces	No. of Dice	No. of Chiral Pairs of Dice
3	6	30	15
4	24	3.23150209236062208 × 1021	1.61575104618031104 × 1021
5	80	3.7275758878262397028547673814159646 × 10115	1.8637879439131198514273836907079823 × 10115
6	240	1.7655752446384800870197812159231254 × 10464	8.827876223192400435098906079615627 × 10463
7	672	2.8214838544319294796427515741969896 × 101604	1.4107419272159647398213757870984948 × 101604
8	1792	1.7505019389666 × 105048	8.7525096948331 × 105047
9	4608	9.0935733829966 × 1014876	4.5467866914983 × 1014876
10	11,520	6.0441657269501 × 1041781	3.0220828634751 × 1041781
11	28,160	5.4587584881263 × 10113069	5.4587584881263 × 10113068
12	67,584	1.3084169531614 × 10297066	6.5420847658072 × 10297065

$$N_c={\displaystyle \frac{\left\{n\left(n-1\right)2^{n-3}\right\}!}{n!2^n}}$$

As this number grows astronomically, the natural log of the above number can be computed exactly or by using Stirling’s approximation as

$$\ln \left(N_c\right)\approx n\left(n-1\right)2^{\left(n-3\right)}\left\{\ln \left(\mathrm{n}\right)+\ln \left(\mathrm{n}-1\right)+\left(\mathrm{n}-3\right)\ln \left(2\right)\right\}-\mathrm{n}\left(\mathrm{n}-1\right)2^{\left(n-3\right)}-nln\left(n\right)+n-nln\left(2\right)$$

An exact expression for ln (N_C) can be programmed using the following exact expression:

Recall that for an n-cube, the number of faces (N_f) is given by N_f = $n\left(n-1\right)2^{\left(n-3\right)}$.

Then it can be readily shown that

$$\ln \left(N_c\right)={\sum }_{k=1}^{N_f}\mathrm{l}\mathrm{n}\left(k\right)-\ln \left(n!\right)-nln\left(2\right)$$

The above exact equation was programmed to compute the natural log of the number of chiral pairs of dice for large dimensions 8 to 12. Subsequently, the resultant natural log values were converted to base 10 to compute the original values expressed in scientific notations. The numbers thus computed for dice of hypercubes with dimensions 8 to 12 are also shown in Table 1. The largest value among the hypercubes considered here is for the 12-cube, which can be seen to be 6.5420847658072 × 10²⁹⁷⁰⁶⁵ chiral pairs of dice from Table 1. Hence, the corresponding total number of dice for the 12-cube is 1.3084169531614 × 10²⁹⁷⁰⁶⁶.

Given the large number of possible dice even in the fourth dimension (~1.616 × 10²¹ chiral pairs of dice), the n-cube dice offer a very good platform for cryptographic applications where, for example, 24 faces of the 4-cube can be used to label different fragments of messages or alphabets. Moreover, several such 4-cube packets can be generated to encrypt and decrypt messages using artificial intelligence techniques, as we discuss in a subsequent section. For several chemical and biological applications, the natural logarithm of the enumerated numbers is relevant, and these numbers are still under control for the larger n-cubes. For example, entropies and information content based on dice enumerations would be measured using natural logarithms of the combinatorial numbers enumerated above.

Figure 2 shows a plot of log₁₀ (number of chiral pairs) of nD-dimensional hypercubes as a function of n derived from the data obtained in Table 1 for the number of chiral pairs. As these numbers grow astronomically, we computed the log₁₀ of the number of chiral pairs. As can be seen from Figure 2, the resulting plot reveals a J-type curve as a function of n. Given that the number of chiral pairs has already been scaled to a logarithmic scale, indeed, the J-curve for the combinatorial numbers of dice is quite astonishing.

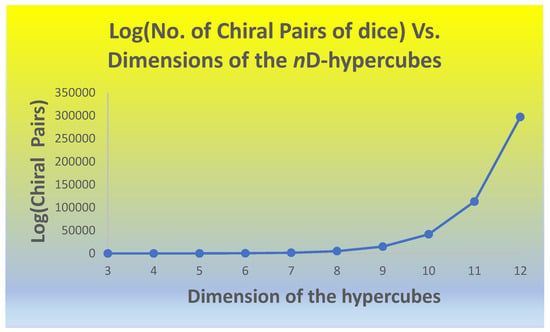
Figure 2. Plot of log₁₀ (number of chiral pairs of dice) as a function of the dimension of the hypercube reveals a J-type curve even for log₁₀ of chiral counts.

3.2. n-Cube Four-Color Problem: Dice Enumeration with Four Colors for the n-Cube and Their Chirality

We consider the special case of a four-color die as the four-color problem in combinatorics and topology is quite significant. For this special case, we take an n-cube die with four different colors, say, green, red, violet, and blue. For such a case, the combinatorics results in a generating function involving partitions with four parts. This is exemplified in Table 2 for a 4-cube with 24 faces and four-color problem for both achiral and chiral combinatorial enumerations.

Table 2. The four-color problem of n-cube: enumerations for the face-colorings of the 4-cube with 4 different colors. The color partition n₁ n₂ n₃ n₄ represents a coloring in which n₁ red, n₂ blue, n₃ green, and n₄ yellow colors are used to color 24 faces of the 4-cube.

Color Partition	No. of A1 Colorings a	No. of A3 Colorings a
24 0 0 0	1	0
23 1 0 0	1	0
22 2 0 0	5	1
21 3 0 0	16	6
20 4 0 0	57	27
19 5 0 0	169	105
18 6 0 0	475	335
17 7 0 0	1099	866
16 8 0 0	2234	1849
15 9 0 0	3843	3307
14 10 0 0	5669	4967
13 11 0 0	7132	6336
12 12 0 0	7725	6871
22 1 1 0	5	1
21 2 1 0	32	13
20 3 1 0	158	97
19 4 1 0	688	503
18 5 1 0	2396	1973
17 6 1 0	6893	6025
16 7 1 0	16,303	14,810
15 8 1 0	32,156	29,818
14 9 1 0	53,118	49,918
13 10 1 0	74,020	70,054
12 11 1 0	87,278	82,892
20 2 2 0	244	145
19 3 2 0	1331	1021
18 4 2 0	5871	4986
17 5 2 0	20,208	18,285
16 6 2 0	56,090	52,312
15 7 2 0	126,548	120,340
14 8 2 0	235,721	226,411
13 9 2 0	365,096	353,006
12 10 2 0	473,741	459,377
11 11 2 0	516,370	501,374
18 3 3 0	7674	6682
17 4 3 0	33,276	30,591
16 5 3 0	110,825	105,097
15 6 3 0	292,629	281,871
14 7 3 0	623,256	606,096
13 8 3 0	1,087,220	1,062,760
12 9 3 0	1,567,505	1,536,897
11 10 3 0	1,879,494	1,845,178
16 4 4 0	138,453	131,493
15 5 4 0	437,694	423,510
14 6 4 0	1,087,993	1,062,443
13 7 4 0	2,168,246	2,129,446
12 8 4 0	3,517,231	3,464,261
11 9 4 0	4,684,708	4,622,058
10 10 4 0	5,152,084	5,085,022
14 5 5 0	1,303,756	1,275,752
13 6 5 0	3,031,508	2,983,480
12 7 5 0	5,618,270	5,548,102
11 8 5 0	8,418,614	8,328,046
10 9 5 0	10,284,396	10,182,022
12 6 6 0	6,553,122	6,474,210
11 7 6 0	11,217,872	11,108,824
10 8 6 0	15,415,306	15,281,078
9 9 6 0	17,123,720	16,981,820
10 7 7 0	17,611,556	17,467,588
9 8 7 0	22,006,070	21,840,340
8 8 8 0	24,753,462	24,573,093
21 1 1 1	51	22
20 2 1 1	425	281
19 3 1 1	2510	2015
18 4 1 1	11,325	9945
17 5 1 1	39,621	36,528
16 6 1 1	110,649	104,649
15 7 1 1	250,736	240,748
14 8 1 1	467,930	453,070
13 9 1 1	725,780	706,350
12 10 1 1	942,226	919,270
11 11 1 1	1,027,332	1,003,242
19 2 2 1	3756	3061
18 3 2 1	22,360	20,105
17 4 2 1	98,101	92,141
16 5 2 1	329,008	316,265
15 6 2 1	871,348	847,760
14 7 2 1	1,859,676	1,822,056
13 8 2 1	3,247,280	3,194,050
12 9 2 1	4,684,626	4,618,066
11 10 2 1	5,618,508	5,544,042
17 3 3 1	130,170	123,075
16 4 3 1	546,260	528,355
15 5 3 1	1,736,268	1,699,440
14 6 3 1	4,325,880	4,260,540
13 7 3 1	8,634,420	8,534,760
12 8 3 1	14,016,130	13,881,320
11 9 3 1	18,677,240	18,517,190
10 10 3 1	20,541,952	20,371,606
15 4 4 1	2,169,038	2,125,858
14 5 4 1	6,481,828	6,396,668
13 6 4 1	15,094,180	14,950,100
12 7 4 1	28,000,166	27,789,946
11 8 4 1	41,975,340	41,705,670
10 9 4 1	51,289,438	50,984,818
13 5 5 1	18,105,486	17,944,878
12 6 5 1	39,180,892	38,920,964
11 7 5 1	67,120,260	66,760,032
10 8 5 1	92,260,524	91,821,066
9 9 5 1	102,499,670	102,032,840
11 6 6 1	78,296,512	77,897,372
10 7 6 1	122,981,972	122,455,864
9 8 6 1	153,698,290	153,094,910
9 7 7 1	175,633,880	174,981,580
8 8 7 1	197,572,890	196,868,820
18 2 2 2	33,487	30,322
17 3 2 2	194,912	185,257
16 4 2 2	818,481	794,136
15 5 2 2	2,602,172	2,552,704
14 6 2 2	6,484,766	6,397,066
13 7 2 2	12,945,012	12,811,992
12 8 2 2	21,015,167	20,835,247
11 9 2 2	28,004,836	27,791,786
10 10 2 2	30,801,270	30,574,296
16 3 3 2	1,088,655	1,059,945
15 4 3 2	4,328,656	4,259,696
14 5 3 2	12,944,976	12,809,676
13 6 3 2	30,156,640	29,928,140
12 7 3 2	55,953,912	55,621,272
11 8 3 2	83,891,030	83,464,690
10 9 3 2	102,511,416	102,030,166
14 4 4 2	16,176,465	16,017,675
13 5 4 2	45,209,956	44,913,056
12 6 4 2	97,864,801	97,385,171
11 7 4 2	167,678,736	167,016,576
10 8 4 2	230,502,306	229,694,856
9 9 4 2	256,090,630	255,234,030
12 5 5 2	117,411,604	116,879,096
11 6 5 2	234,687,752	233,871,724
10 7 5 2	368,679,660	367,606,632
9 8 5 2	460,789,280	459,559,450
10 6 6 2	430,095,214	428,905,586
9 7 6 2	614,294,660	612,823,960
8 8 6 2	691,047,030	689,459,130
8 7 7 2	789,709,860	787,996,500
15 3 3 3	5,765,010	5,682,726
14 4 3 3	21,553,380	21,364,620
13 5 3 3	60,252,960	59,898,540
12 6 3 3	130,442,733	129,871,167
11 7 3 3	223,512,780	222,722,100
10 8 3 3	307,264,170	306,301,230
9 9 3 3	341,378,584	340,355,686
13 4 4 3	75,302,150	74,889,430
12 5 4 3	195,601,766	194,861,566
11 6 4 3	391,016,740	389,884,220
10 7 4 3	614,296,776	612,807,816
9 8 4 3	767,787,880	766,082,150
11 5 5 3	469,162,776	467,900,988
10 6 5 3	859,878,528	858,043,860
9 7 5 3	1,228,207,740	1,225,936,680
8 8 5 3	1,381,679,430	1,379,231,310
9 6 6 3	1,432,840,398	1,430,330,262
8 7 6 3	1,842,059,400	1,839,135,600
7 7 7 3	2,105,109,000	2,101,948,920
12 4 4 4	244,472,700	243,610,770
11 5 4 4	586,400,958	584,936,118
10 6 4 4	1,074,771,633	1,072,641,603
9 7 4 4	1,535,163,270	1,532,530,170
8 8 4 4	1,726,995,915	1,724,156,055
10 5 5 4	1,289,616,636	1,287,246,912
9 6 5 4	2,148,984,460	2,145,744,020
8 7 5 4	2,762,767,590	2,758,994,670
8 6 6 4	3,223,114,485	3,218,943,735
7 7 6 4	3,683,411,640	3,678,907,800
9 5 5 5	2,578,619,766	2,575,009,806
8 6 5 5	3,867,527,364	3,862,884,864
7 7 5 5	4,419,870,336	4,414,853,016
7 6 6 5	5,156,360,952	5,150,820,912
6 6 6 6	6,015,584,844	6,009,464,868

^a N(A₁) + N(A₃) yields the total number of colorings among which N(A₃) enumerates the chiral pairs. N(A₁) − N(A₃) yields the number of achiral colorings for the 4-color problem.

3.3. Chessboard-Type Black and White Dice Enumerations in n-Dimension and Their Chirality

In this section, we consider a black-and-white dice combinatorics akin to that of a chessboard. For this purpose, we take a 6-cube, such as that shown in Figure 3. The generating functions were computed for both totally symmetric and chiral representations for the binomial distribution. The results were computed in quadruple precision and are shown in Table 3 for coloring 240 faces of the 6-cube with black and white colors. We have restricted listing the computed results only for the totally symmetric A₁ irreducible representation. It is pointed out that almost all colorings become chiral when the colorings are evenly distributed, culminating to a maximum of 120 black and 120 white colors for coloring 240 faces of a 6-cube.

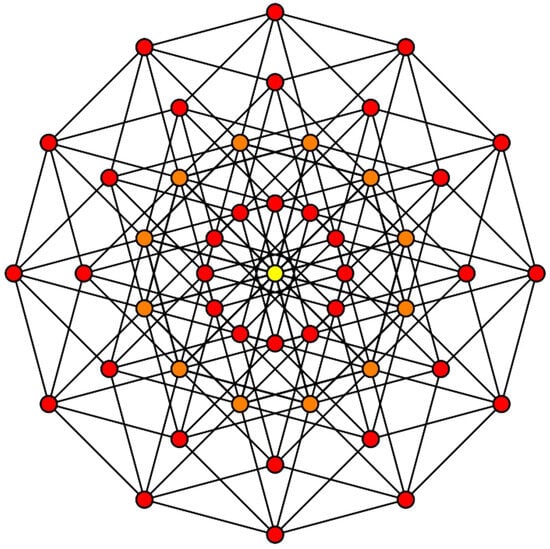
Figure 3. Graphical representation of hexeract or a 6-cube. Table 3 enumerates black and white face colorings of the 6-cube with varied numbers of black and white colors. Figure reproduced from [68].

Table 3. Black-and-white dice of hypercube in the 6th dimension with 240 faces; n_b stands for the number of black colors with 240-n_b being the number of white colors.

nb	N(A1)
0	1
1	1
2	11
3	139
4	4176
5	152635
6	5580266
7	182586993
8	5283117184
9	135891832431
10	3136801139463
11	65570741043751
12	1251192201334018
13	21943233858075034
14	355789263949855043
15	5360531557936453701
16	75382327861202736302
17	993272251366379046339
18	12305535660981459650639
19	143780450498062303705832
20	1588773890867771345864514
21	16644297515678879808798297
22	165686414507591622101552686
23	1570419052306115065132618723
24	14199205570066871577428871140
25	122681136017010754158309432703
26	1014478624347489084027884140426
27	8040682428518284564435181330429
28	61166619897340434689394786752894
29	447149083369066948751292268832796
30	3144948552967196406093283337735784
31	21304490197316629654279247580024508
32	139144951600574592746649080159671056
33	877034846450078628652128896100267264
34	5339594506322238375552079147434465280
35	31427327665763904958336467271605932032
36	178961171429990835258310915317808332800
37	986704837073310196335657862006172680192
38	5271081103312257287838648872443980546048
39	27301496996641809668910837171761665015808
40	137190022408121978237796878411228575170560
41	669219621503025866250112350741134231732224
42	3170826301883363428193286508672704248283136
43	14600549017974504078101835470726548970012672
44	65370639921385716211126737122035700519141376
45	284725453879813021523275240995846178515976192
46	1206988337099206608564703950062943154911313920
47	4982036965898851012606659737835556794489896960
48	20031940300384959298052361807805291335079952384
49	78492500768855341303876241965943810733935427584
50	299841352937027382765902773445578163675698561024
51	1117056020745788242590376169881100544777740353536
52	4060068998479884089705015623755515419238105874432
53	14401754183287135804246166953385408335748576313344
54	49872741338420266137322529195039577022891227611136
55	168660543435384899112410284701246690287995790032896
56	557182152420467968422421922547752056414106468483072
57	1798623088515194841712775021084035912510703835021312
58	5674965951694494062205410635512839112833661296181248
59	17505827173023693533563297554260934909613741294223360
60	52809245305288142132272869107153182169520534320054272
61	155830559917243698043653761141737793516691944388952064
62	449897906857848741029976049141268839915375321375834112
63	1271140117788842474479687792473475435071770769766744064
64	3515496888259767468163216556014840184143394537746726912
65	9518883882057216528608998367914143748380503439084355584
66	25239464838788074127879708050806830413286976339971145728
67	65547266894763058181097740456058221177846743153120378880
68	166759958423441309781250299599634334821117425640231927808
69	415691490562781235971341064888171821804599513259251335168
70	1015474926946222733578581339228367257143428701318056771584
71	2431418839167012178976836276667886688093053146703593472000
72	5707080330822570253408677742000332960960832242019794419712
73	13134102679153312363971846877730573818996158520436289699840
74	29640474965116258983498939796906579169557606545381706956800
75	65604251256123986550051347634863006077799034966669772455936
76	142430282332374444483519754796895120849199732824551463059456
77	303358003928693622016625857618977262242204533973550601601024
78	633940444107398210111331355025827016639517714599813255790592
79	1299979138549348228329063291451252319874543714414110345003008
80	2616208016330563309511496917583731993831663122674685994598400
81	5167818303862841105206809240136218974660614845481150429790208
82	10020525735538923606436025159797456261476584970542687191040000
83	19075217665242770238755496178613251023787049655038318777204736
84	35652490160037082470051758173077553030081498177735400332722176
85	65432805470185704297972943306063050464253178396461240116314112
86	117931219161381211234712613738006405558219054813035950984134656
87	208751813228192029082126716097532138898293814638576077423771648
88	362943493453561141472322840478800602327652562685480290771533824
89	619858550617317904536986031056340852095924421733185407357550592
90	1039984901591277817612034918976099698126465664356715106718973952
91	1714260826798809589470361996501267583138843705609748724712472576
92	2776357208619811182946532139254981696976848855712642666273439744
93	4418288891136903818022397130640910763680489058711583357765943296
94	6909451776565158098396675870686568083843531086171523326916165632
95	10618736414510664024904301130552081477721498205603021838987821056
96	16038716459417148787615793261697627570544461777441421000234237952
97	23810053300578035313573866471631103862233086767820943288313053184
98	34743241040639378059602569562006314113107754712353068755277840384
99	49833739674452441257207592441071504972429917631360631482888486912
100	70265572940977942172662549542368590308742746503025565569864695808
101	97397823878583286179928107075659666820641201605644990708709326848
102	132728407050226242931470451731079405476392486433062572665908232192
103	177830292941079820626630085054867470806112050016763218951307001856
104	234257212816614763710079762418248667308011746087552551552313982976
105	303418866124377217757817320211010493225990120075604352544075153408
106	386429687988593626389672704093941308509024324478124575046739427328
107	483939983088519120899215967419979205493870806825180030389467480064
108	595963127321972621107367481426572082532281766779222667980204670976
109	721716814738535651249288720668083207973311214195686476972126371840
110	859499115734074275578698042830041010298057135266173370496370868224
111	1006620585994861764191267638613753417255640297161311448121542180864
112	1159411210654796139113156147343784043908458958128856461986303574016
113	1313315353662069962889238509921566661821965008467180176968339423232
114	1463079385220025309534502263293078969347233893342480581579761516544
115	1603026109023679904359541354461619193561740429737992388679403831296
116	1727398824378965414180540034621696361312587920268799182661767659520
117	1830747471991382148362281571140508950236269928271495714066772525056
118	1908321517414745798716615408358714803655391352966327587613939073024
119	1956430463231924264230479584872704778184154074936145924234846142464
120	1972734050425523633099066888879877060171554196485690791403223777280

3.4. Rubik’s Cube Enumerations and Colorings

Rubik’s cube [69] is an interesting case of hypercube and hyperoctahedral symmetry, as it has been a cynosure of puzzles and games over four decades. The symmetry operations of a Rubik’s cube can be rationalized by dividing the cubes to corner cubes and edge cubes. As seen from Figure 4, which shows a typical Rubik’s cube, the eight corner cubes carry three faces while the twelve edge cubes carry two faces each. The dynamics of Rubik’s cube facilitates three-fold rotations of each corner cube independent of other cubes while providing two-fold flipping motions of the edge cubes. The eight corners of the overall cube can be permuted in all possible ways with each cube within each corner undergoing a three-fold rotation during various dynamical operations of Rubik’s cube. Likewise, the twelve edge cubes can be permuted in all possible ways with each cube within the edge exhibiting a two-fold flip. This results in the direct product of two hyperoctahedral groups, namely, the corner cubes generate the S₈[C₃] wreath product while the edge cubes give rise to the wreath product S₁₂[S₂]. Consequently, the overall group of Rubik’s cube is the direct product of S₈[C₃] × S₁₂[S₂]. The cubes within Rubik’s cube are partitioned into three classes, 8 corner cubes, 12 edge cubes, and 6 center cubes. Consequently, the 54 faces of Rubik’s cube are partitioned into 24 corner square faces, 24 edge square faces, and 6 central square faces. The overall order of Rubik’s cube group is obtained by multiplying the orders of the comprising wreath product groups, yielding 5.19024039293878272 × 10²⁰ symmetry operations in Rubik’s cube.

Figure 4. Rubik’s cube: there are 5.34018574959804633194496 × 10²⁹ possible dice for Rubik’s cube; see text for details of enumeration. Figure reproduced from [70].

Hence, we arrive at the result for the number of dice that can be obtained by using distinct numbers for each of the corner faces, edge faces, and central faces, that is, treating the sets of faces in the three partitions as independent of each other as

$$N_c={\displaystyle \frac{24!24!6!}{12!x8!x{3}^{8}x{2}^{12}}}=5.34018574959804633194496\times {10}^{29}$$

In the above enumeration, analogous to previous enumerations considered in this study, we treat the faces that are not equivalent separately rather than all faces of the object collectively. This is made possible by the equivalence classes of face partitions generated by the overall group, and consequently, two faces in different classes are never permuted into each other by any of the symmetry operations.

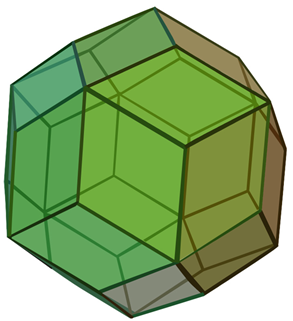
3.5. Dice of Different Shapes with Octahedral/Cubic Symmetries

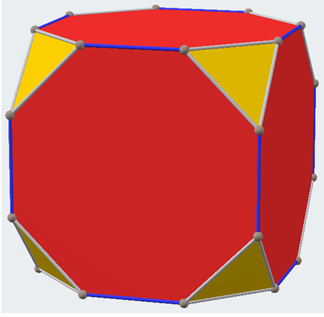
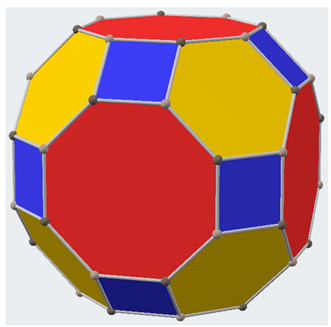
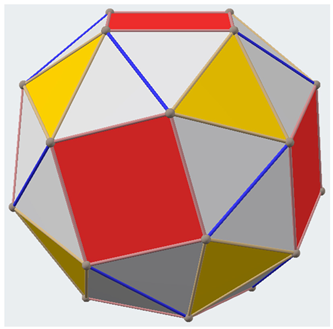
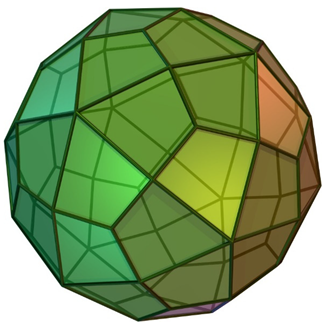
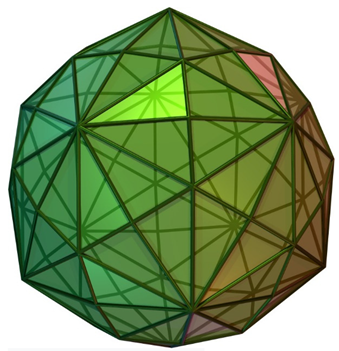
Next, we consider dice that can be constructed with several shapes of octahedral or cubic symmetries and that do not comprise the regular cubes of normal dice. Such dice enumerations not only generalize the normal cubic dice shapes but also pave the way for several applications in a variety of fields. Stimulated by such applications and the mathematically intriguing nature and aesthetics of these shapes, we have shown in Table 4 a collection of dice of varied shapes, a common feature being that their symmetries are all described by the octahedral group O_h containing 48 operations, with the exception of the snub cube, which is chiral with the symmetry group O.

Table 4. Combinatorial enumeration of dice of different shapes with octahedral/cubic symmetries ^a.

Truncated octahedron: 604,800 chiral pairs of dice	Cuboctahedron (isochiral with truncated octahedron): 604,800 chiral pairs of dice
Rhombicdodecahedron: 1,816,214,400 chiral pairs of dice	Deltoidal icositetrahedron: 133,382,785,536,000 chiral pairs of dice
Truncated cube: 6!8!/48 604,800 chiral pairs of dice, isochiral with truncated octahedron	Rhombic cuboctahedron: 6! 12! 8!/48 289,700,167,680,000 chiral pairs of dice
Truncated cuboctahedron: 289,700,167,680,000 chiral pairs of dice, isochiral with rhombic cuboctahedron	Sunb cube (chiral): 7.8939251080108059050165403648 × 1036

^a All images were created by POV-RAY codes and are public domain open-access freely reproduced from Ref. [71].

Table 4 considers several shapes of octahedral or cubic symmetries, many of which are not only mathematically interesting but also have several applications to materials such as zeolites and mesoporous molecular sieves. The combinatorial enumerations considered in Table 4 make use of face partitions. That is, faces of different shapes, for example, squares and hexagons of a truncated octahedron, are treated as different equivalence classes, and thus they are not treated as a single entity in the combinatorial enumeration. This is the case in many practical applications, as a hexagonal face capping is not equivalent to a square face capping in molecular structures. Thus, eight hexagons and six squares are treated as separate equivalence classes in dice enumerations of truncated octahedron dice shown in Table 4.

There are a few interesting findings that emerge from a critical analysis of Table 4. First, all dice enumerated in Table 4 are chiral, and hence we list the number of dice as chiral pairs of dice. We label the faces in different equivalence classes with numbers 1 through |C|, where |C| is the cardinality of the equivalence class C. Although, with the exception of the snub cube, the parent structures shown in Table 4 are not chiral, and the dice originating from every shape are chiral. The snub cube is an interesting case of octahedral symmetry as the structure itself is chiral, as its symmetry group is O rather than O_h. All other structures in Table 4 conform to O_h symmetry.

As can be seen from Table 4, there exist two different structures with the same chiral pairs of dice. For example, the truncated cuboctahedron exhibits the same number of chiral pairs of dice as the rhombic cuboctahedron (see Table 4). We call such structures with different shapes with the same number of chiral pairs of dice as isochiral. In some cases, isochirality arises from mapping the vertices of an octahedron with different shapes of faces while in other cases it is quite interesting in that the number of faces is not the same. For example, the truncated cuboctahedron can be obtained by mapping the red squares of the rhombic cuboctahedron with decagons and triangles with hexagons. Thus, isochirality can be readily explained for such direct topological transforms. On the other hand, the isochirality of a cuboctahedron and truncated octahedron is less obvious from a simple observation. These enumerations and the chirality aspects of the enumerated structures open up a plethora of applications to a number of fields, as we subsequently discuss.

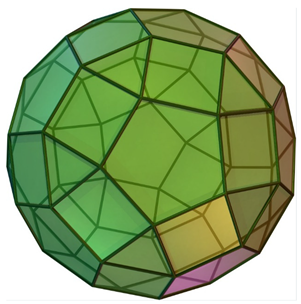
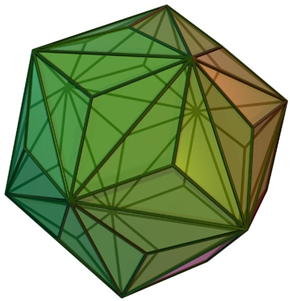
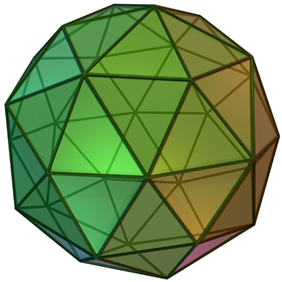
3.6. Enumeration of Dice and Face Colorings of Different Shapes with Icosahedral Symmetries

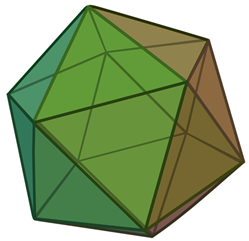
Icosahedral symmetries are quite interesting, as demonstrated earlier [3,72], in that the character values of the three-dimensional irreducible representations of the I_h group are golden ratios or their reciprocals, thus making them interesting candidates for symmetry studies. Furthermore, icosahedral symmetries occur in the molecular structures of boranes, carboranes, and metallacarboranes, as well as in the celebrated buckminsterfullerene, C₆₀, which became the subject matter of the Nobel Prize-winning work of Smalley and coworkers [73,74] and several other studies on related clusters such as Au₆₀⁻ containing icosahedral symmetry [61,62,63,64,65,66,75]. Hence, we devote this subsection to different shapes of icosahedral symmetries.

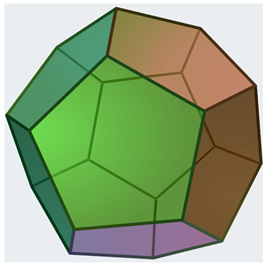
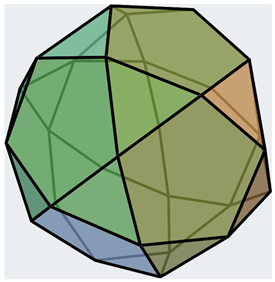
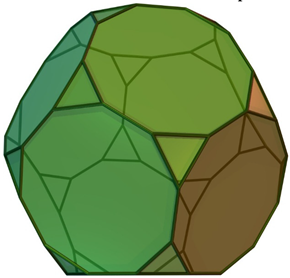
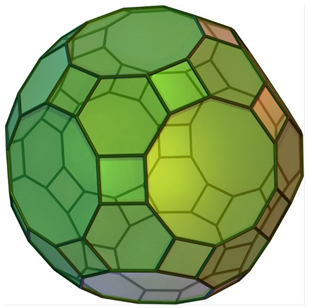
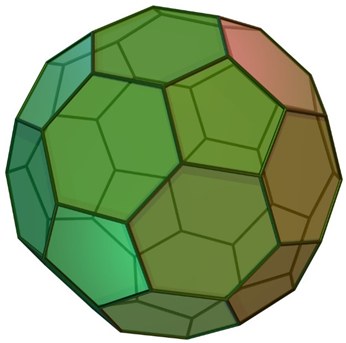
Table 5 shows a number of structures with icosahedral symmetry (I_h) starting with the regular icosahedron itself, which consists of 20 triangles. Many of the structures in Table 5 are Archimedean solids and share the same symmetry group. They differ in number of faces or shapes of faces. While the icosahedron contains 20 triangles, the relative dodecahedron contains 12 pentagons (see Table 5). Consequently, the number of chiral pairs of dice for an icosahedron is considerably larger (20,274,183,401,472,000) compared to 3,991,680 chiral pairs for a dodecahedron. This can be envisaged by mapping the 12 vertices of the icosahedron into pentagons, which generates the dodecahedron. Thus, the dice enumeration of the dodecahedron is equivalent to the vertex coloring problem of the icosahedron with 12 different colors. As can be seen from Table 5, the icosododecahedron and truncated dodecahedron are isochiral as they both generate 9.7113662879985303552 × 10²⁴ chiral pairs of dice. Likewise, there are a number of isochiral pairs of structures, as shown in Table 5. For example, the truncated icosododecahedron and rhombicosidodecahedron are isochiral. The truncated icosododecahedron has also been considered in a molecular context as a candidate for the structure of C₁₂₀, and it has been called an archimedene [76]. The spectra, characteristic polynomials, and other graph theoretical properties of the archimedene and related clusters have been considered [76]. The truncated icosahedron shown in Table 5 is of special interest in the context of fullerenes, which are structures containing 12 pentagons and any number of hexagons. As seen from Table 5, the structure, which is the molecular structure of the C₆₀ buckminsterfullerene, exhibits 9.7113662879985303552 × 10²⁴ chiral pairs of dice.

Table 5. Combinatorial enumeration of dice with different shapes with icosahedral symmetry ^a.

Icosahedron: 20,274,183,401,472,000 chiral pairs of dice	Dodecahedron: 3,991,680 chiral pairs of dice
Icosododecahedron: 9.7113662879985303552 × 1024 chiral pairs of dice	Truncated dodecahedron: 9.7113662879985303552 × 1024 chiral pairs of dice
Truncated icosodedecahedron (archimedene: C120) 2.5759676805753124307695693098745908 × 1057 chiral pairs of dice	Rhombicosidodecahedron: 2.5759676805753124307695693098745908 × 1057 chiral pairs of dice
Rhombic triacontahedron: 2.210440498434925488635904 × 1030 chiral pairs of dice	Triakis icosahedron: 6.93415592728449178689695098601947 × 1079 chiral pairs of dice
Pentakis dodecahedron: 6.93415592728449178689695098601947 × 1079 chiral pairs of dice	Deltoidal hexecontahedron: 6.93415592728449178689695098601947 × 1079 chiral pairs of dice
Disdyakis triacontahedron: 5.574585761207605881323431711741975 × 10196 chiral pairs of dice	Truncated icosahedron: buckminsterfullerene (C60) 9.7113662879985303552 × 1024 chiral pairs of dice
Grand 600-cell/grand polytetrahedron: 4.4102702121446021496460288562760144 × 103171 chiral pairs of dice

^a All images were created by POV-RAY codes and are in the public domain, freely reproduced from Ref. [71].

The last structure, which is shown in Table 5, the grand 600-cell or grand polytetrahedron, requires further discussion as it poses a grand challenge for dice enumeration. First, it contains 1200 triangular faces with a symmetry group that contains 14,400 symmetry elements, which is the square of the order of the icosahedral group. Consequently, the number of chiral pairs of dice for the 600-cell, as seen in Table 5, is given by

N_c = 1200!/14400.

As direct computation of such a large factorial is quite difficult, we invoked Stirling’s approximation for the factorial of large numbers as follows:

$$n!~\sqrt{2\pi n}{({\displaystyle \frac{n}{e}})}^n\{1+{\displaystyle \frac{1}{12n}}+{\displaystyle \frac{1}{288n^2}}-{\displaystyle \frac{139}{51840n^3}}-{\displaystyle \frac{571}{2488320n^4}}\dots \dots \}$$

Using the above approximation for n!, we could compute the number of grand-600 cell dice using Fortran ‘95 compiler with quadruple precision as

1200! ~ 6.350789105488227095490281553037461 × 10³¹⁷⁵

and, thus, the number of grand cell-600 dice as

N_c = 6.350789105488227095490281553037461 × 10³¹⁷⁵/14400 =

4.4102702121446021496460288562760144 × 10³¹⁷¹

On the other hand, an exact expression for ln (N_c) for the grand cell-600 can be obtained using the simplification

$$\mathit{ln}\left(1200!\right)={\sum }_{k=1}^{1200}ln\left(k\right),\mathrm{and}\mathrm{thus}$$

$$\mathit{ln}\left(N_C\right)={\sum }_{k=1}^{1200}ln\left(k\right)-\mathit{ln}\left(14400\right)=7302.981265841281474204826906770904$$

Alternatively,

N_c = e^{7302.98126584128} ~ 10^{3171.644465197693243} = 10^{0.644465197693243} × 10³¹⁷¹

=4.4102701988481145534 × 10³¹⁷¹,

corroborating the approximate result obtained from Stirling’s approximation for the large n!.

The grand 600-cell is certainly a challenging object for the dice enumeration problem.

Among the structures shown in Table 5, the truncated icosahedron or the buckminsterfullerene structure can be studied further, as it poses several interesting questions, and it continues to be a subject of active investigation. Table 6 shows the face colorings of the faces of the buckyball for coloring the hexagons with 6 different colors (vibgyr) and pentagons with 10 different colors (vibgyorblwp). We show the computed combinatorial numbers for the A_g and A_u irreducible representations for 20 hexagons and 12 pentagons, respectively. The sum of A_g and A_u numbers gives the total number of inequivalent face colorings while the A_u numbers correspond to the chiral pairs. The difference between the A_g and A_u numbers yields the number of achiral colorings. As seen from Table 6, as the color partition gets distributed, for example, 4 4 3 3 3 3 for the hexagons, almost every hexagonal face coloring is chiral. The same comment applies to the colorings of pentagons for a distributed color partition (see Table 6).

Table 6. Six-color enumeration for hexagons and ten-color enumeration for pentagons of the buckyball. enumeration of chiral and achiral colorings: for hexagons of the buckyball with 6 types of colors (vibgyr) ^a; for pentagons with 10 types of colors (vibgyorblwp (bl: black, w: white, p: pink)).

Hexagons			Pentagons
Color Partition	Ag	Au	Color Partition	Ag	Au
20 0 0 0 0 0	1	0	12 0 0 0 0 0 0 0 0 0	1	0
19 1 0 0 0 0	1	0	11 1 0 0 0 0 0 0 0 0	1	0
18 2 0 0 0 0	5	1	10 2 0 0 0 0 0 0 0 0	3	0
17 3 0 0 0 0	5	2	9 3 0 0 0 0 0 0 0 0	3	0
16 4 0 0 0 0	15	6	8 4 0 0 0 0 0 0 0 0	5	0
18 1 1 0 0 0	34	23	10 1 1 0 0 0 0 0 0 0	9	2
17 2 1 0 0 0	60	54	9 2 1 0 0 0 0 0 0 0	14	8
16 3 1 0 0 0	58	38	8 3 1 0 0 0 0 0 0 0	10	2
16 2 2 0 0 0	176	151	8 2 2 0 0 0 0 0 0 0	23	10
17 1 1 1 0 0	274	233	9 1 1 1 0 0 0 0 0 0	37	20
16 2 1 1 0 0	498	471	8 2 1 1 0 0 0 0 0 0	57	42
16 1 1 1 1 0	972	966	8 1 1 l 1 1 0 0 0 0 0	102	96
15 5 0 0 0 0	149	113	7 5 0 0 0 0 0 0 0 0	12	2
14 6 0 0 0 0	674	622	6 6 0 0 0 0 0 0 0 0	42	24
15 4 1 0 0 0	1337	1249	7 4 1 0 0 0 0 0 0 0	80	52
14 5 1 0 0 0	2610	2562	6 5 1 0 0 0 0 0 0 0	144	120
15 3 2 0 0 0	3928	3824	7 3 2 0 0 0 0 0 0 0	216	180
14 4 2 0 0 0	7776	7728	6 4 2 0 0 0 0 0 0 0	408	384
14 3 3 0 0 0	15,504	15,504	6 3 3 0 0 0 0 0 0 0	792	792
15 3 1 1 0 0	371	310	7 3 1 1 0 0 0 0 0 0	18	6
14 4 1 1 0 0	1984	1892	6 4 1 1 0 0 0 0 0 0	58	36
15 2 2 1 0 0	4984	4796	7 2 2 1 0 0 0 0 0 0	142	104
14 3 2 1 0 0	9744	9636	6 3 2 1 0 0 0 0 0 0	246	216
14 2 2 2 0 0	6557	6373	6 2 2 2 0 0 0 0 0 0	178	134
15 2 1 1 1 0	19,480	19,280	7 2 1 1 1 0 0 0 0 0	488	436
14 3 1 1 1 0	38,784	38,736	6 3 1 1 1 0 0 0 0 0	936	912
14 2 2 1 1 0	29,352	28,968	6 2 2 1 1 0 0 0 0 0	748	668
14 2 1 1 1 1	58,248	58,032	6 2 1 1 1 1 0 0 0 0	1416	1356
13 7 0 0 0 0	116,304	116,256	5 5 2 0 0 0 0 0 0 0	2784	2760
12 8 0 0 0 0	693	609	5 4 3 0 0 0 0 0 0 0	5544	5544
13 6 1 0 0 0	4597	4457	4 4 4 0 0 0 0 0 0 0	160	118
12 7 1 0 0 0	13,720	13,412	5 5 1 1 0 0 0 0 0 0	296	260
13 5 2 0 0 0	27,216	27,048	5 4 2 1 0 0 0 0 0 0	258	204
12 6 2 0 0 0	22,802	22,438	4 4 3 1 0 0 0 0 0 0	726	660
13 4 3 0 0 0	68,040	67,620	4 4 2 2 0 0 0 0 0 0	1404	1368
12 5 3 0 0 0	135,744	135,576	5 4 1 1 1 0 0 0 0 0	960	888
12 4 4 0 0 0	90,618	90,282	4 4 2 1 1 0 0 0 0 0	1440	1332
13 5 1 1 0 0	136,024	135,296	4 4 1 1 1 1 0 0 0 0	2808	2736
12 6 1 1 0 0	271,488	271,152	5 3 3 1 0 0 0 0 0 0	5544	5544
13 4 2 1 0 0	542,640	542,640	5 3 2 2 0 0 0 0 0 0	4224	4092
12 5 2 1 0 0	407,400	406,560	4 3 3 2 0 0 0 0 0 0	8352	8280
12 4 3 1 0 0	814,128	813,792	5 3 2 1 1 0 0 0 0 0	16,632	16,632
12 4 2 2 0 0	1135	1022	4 3 3 1 1 0 0 0 0 0	33,264	33,264
13 4 1 1 1 0	8501	8305	5 2 2 2 1 0 0 0 0 0	330	270
12 5 1 1 1 0	29,739	29,262	4 3 2 2 1 0 0 0 0 0	1194	1116
12 4 2 1 1 0	58,917	58,665	4 2 2 2 2 0 0 0 0 0	1818	1692
12 4 1 1 1 1	59,085	58,497	5 2 2 1 1 1 0 0 0 0	3510	3420
11 9 0 0 0 0	176,680	176,036	4 3 2 1 1 1 0 0 0 0	6948	6912
10 10 0 0 0 0	352,800	352,632	4 2 2 2 1 1 0 0 0 0	2376	2244
11 8 1 0 0 0	74,014	73,286	4 2 2 1 1 1 1 0 0 0	4656	4584
10 9 1 0 0 0	294,290	293,590	3 3 3 3 0 0 0 0 0 0	7008	6852
11 7 2 0 0 0	441,952	440,468	3 3 3 2 1 0 0 0 0 0	13,896	13,824
10 8 2 0 0 0	882,168	881,412	3 3 2 2 2 0 0 0 0 0	27,720	27,720
11 6 3 0 0 0	1,763,664	1,763,496	3 3 2 2 1 1 0 0 0 0	10,572	10,308
10 7 3 0 0 0	588,509	587,221	3 2 2 2 2 1 0 0 0 0	20,880	20,700
10 6 4 0 0 0	1,175,898	1,175,562	2 2 2 2 2 2 0 0 0 0	41,616	41,544
11 7 1 1 0 0	1,764,280	1,762,880	3 2 2 2 1 1 1 0 0 0	83,160	83,160
10 8 1 1 0 0	3,527,328	3,526,992	2 2 2 2 2 1 1 0 0 0	166,320	166,320
11 6 2 1 0 0	2,647,512	2,644,488	2 2 2 2 1 1 1 1 0 0	3156	3012
10 7 2 1 0 0	5,291,496	5,289,984	2 2 2 2 2 2 0 0 0 0	9312	9168
10 6 3 1 0 0	1466	1340	3 3 3 1 1 1 0 0 0 0	18,480	18,480
10 6 2 2 0 0	12,716	12,478	3 3 2 2 2 0 0 0 0 0	13,992	13,728
11 6 1 1 1 0	50,696	50,080	3 3 2 2 1 1 0 0 0 0	27,792	27,648
10 7 1 1 1 0	100,944	100,608	3 3 2 1 1 1 1 0 0 0	55,440	55,440
10 6 2 1 1 0	118,002	117,162	3 3 1 1 1 1 1 1 0 0	110,880	110,880
10 6 1 1 1 1	353,192	352,240	3 2 2 2 2 1 0 0 0 0	41,736	41,424
9 9 2 0 0 0	705,600	705,264	3 2 2 2 1 1 1 0 0 0	83,232	83,088
9 8 3 0 0 0	176,904	175,812	3 2 2 1 1 1 1 1 0 0	166,320	166,320
8 8 4 0 0 0	705,936	704,928	3 2 1 1 1 1 1 1 1 0	332,640	332,640
9 9 1 1 0 0	1,059,240	1,057,056	3 1 1 1 1 1 1 1 1 1	665,280	665,280
9 8 2 1 0 0	2,116,800	2,115,792	2 2 2 2 2 2 0 0 0 0	62,736	62,184
8 8 3 1 0 0	4,232,592	4,232,592	2 2 2 2 2 1 1 0 0 0	124,920	124,560
8 8 2 2 0 0	882,504	881,076	2 2 2 2 1 1 1 1 0 0	249,552	249,408
9 8 1 1 1 0	1,764,840	1,762,320	2 2 2 1 1 1 1 1 1 0	498,960	498,960
8 8 2 1 1 0	3,527,664	3,526,656	2 2 1 1 1 1 1 1 1 1	997,920	997,920
8 8 1 1 1 1	5,292,168	5,289,312
13 3 3 1 0 0	10,581,984	10,580,976
13 3 2 2 0 0	2,352,468	2,350,452
12 3 3 2 0 0	7,055,328	7,053,312
13 3 2 1 1 0	14,108,640	14,108,640
12 3 3 1 1 0	10,584,000	10,578,960
13 2 2 2 1 0	21,163,968	21,161,952
12 3 2 2 1 0	31,747,296	31,741,584
12 2 2 2 2 0	1648	1510
13 2 2 1 1 1	15,536	15,270
12 3 2 1 1 1	69,812	69,070
12 2 2 2 1 1	138,756	138,378
11 5 4 0 0 0	185,308	184,244
10 5 5 0 0 0	554,856	553,680
11 5 3 1 0 0	1,108,704	1,108,368
11 4 4 1 0 0	324,428	322,888
10 5 4 1 0 0	1,294,012	1,292,612
11 5 2 2 0 0	1,942,136	1,939,000
11 4 3 2 0 0	3,880,632	3,879,120
10 5 3 2 0 0	7,759,920	7,759,584
10 4 4 2 0 0	388,788	387,192
10 4 3 3 0 0	1,940,904	1,938,972
11 5 2 1 1 0	3,881,640	3,878,112
11 4 3 1 1 0	7,760,256	7,759,248
10 5 3 1 1 0	11,641,560	11,637,696
10 4 4 1 1 0	23,279,760	23,278,752
11 4 2 2 1 0	4,853,184	4,848,396
10 5 2 2 1 0	9,700,824	9,698,556
10 4 3 2 1 0	6,468,432	6,464,568
10 4 2 2 2 0	19,401,480	19,397,280
11 4 2 1 1 1	38,799,264	38,798,256
10 5 2 1 1 1	29,105,832	29,096,088
10 4 3 1 1 1	58,200,408	58,195,872
10 4 2 2 1 1	25,866,888	25,864,872
9 7 4 0 0 0	38,802,624	38,794,896
9 6 5 0 0 0	77,598,528	77,596,512
8 7 5 0 0 0	116,400,480	116,392,080
8 6 6 0 0 0	174,608,112	174,588,288
9 7 3 1 0 0	77,370	76,600
9 6 4 1 0 0	154,180	153,760
8 7 4 1 0 0	231,550	230,360
8 6 5 1 0 0	693,500	692,170
9 7 2 2 0 0	1,385,880	1,385,460
9 6 3 2 0 0	462,820	461,000
8 7 3 2 0 0	1,848,420	1,846,740
8 6 4 2 0 0	2,773,160	2,769,520
8 6 3 3 0 0	5,543,520	5,541,840
9 7 2 1 1 0	11,085,360	11,085,360
9 6 3 1 1 0	647,706	645,606
8 7 3 1 1 0	3,234,580	3,231,920
8 6 4 1 1 0	6,468,850	6,464,090
9 6 2 2 1 0	12,933,780	12,932,100
8 7 2 2 1 0	19,402,040	19,396,720
8 6 3 2 1 0	38,799,600	38,797,920
8 6 2 2 2 0	3,881,136	3,878,616
9 6 2 1 1 1	9,702,840	9,696,540
8 7 2 1 1 1	19,400,640	19,398,120
8 6 3 1 1 1	12,935,460	12,930,420
8 6 2 2 1 1	38,801,280	38,796,240
9 5 5 1 0 0	77,597,520	77,597,520
9 5 4 2 0 0	58,204,440	58,191,840
8 5 5 2 0 0	116,398,800	116,393,760
9 4 4 3 0 0	16,169,760	16,162,620
8 5 4 3 0 0	48,502,440	48,494,460
8 4 4 4 0 0	96,998,160	96,995,640
9 5 4 1 1 0	64,667,160	64,662,120
8 5 5 1 1 0	97,004,040	96,989,760
9 4 4 2 1 0	193,996,320	193,991,280
8 5 4 2 1 0	290,998,680	290,982,720
8 4 4 3 1 0	129,334,260	129,324,180
8 4 4 2 2 0	258,658,440	258,658,440
9 4 4 1 1 1	387,992,640	387,982,560
8 5 4 1 1 1	581,995,680	581,967,120
8 4 4 2 1 1	521,000	519,040
7 7 6 0 0 0	2,079,380	2,077,630
7 7 5 1 0 0	3,120,540	3,116,550
7 6 6 1 0 0	6,236,460	6,234,570
7 7 4 2 0 0	12,471,240	12,470,820
7 6 5 2 0 0	832,592	830,212
6 6 6 2 0 0	4,158,480	4,155,540
7 6 4 3 0 0	8,316,680	8,311,360
6 6 5 3 0 0	16,628,880	16,627,200
6 6 4 4 0 0	24,945,000	24,939,120
7 7 4 1 1 0	49,884,960	49,883,280
7 6 5 1 1 0	971,840	969,178
6 6 6 1 1 0	5,821,424	5,818,204
7 6 4 2 1 0	14,555,240	14,546,980
6 6 5 2 1 0	29,100,960	29,097,180
6 6 4 3 1 0	19,402,630	19,396,190
6 6 4 2 2 0	58,201,640	58,194,640
7 6 4 1 1 1	116,397,120	116,395,440
6 6 5 1 1 1	87,308,760	87,291,960
6 6 4 2 1 1	174,598,200	174,590,640
11 3 3 3 0 0	17,463,432	17,455,452
11 3 3 2 1 0	34,920,144	34,917,624
10 3 3 3 1 0	29,103,480	29,094,660
11 3 2 2 2 0	87,302,040	87,292,380
10 3 3 2 2 0	174,595,680	174,593,160
11 3 2 2 1 1	116,398,800	116,393,760
10 3 3 2 1 1	174,603,240	174,585,600
11 2 2 2 2 1	349,191,360	349,186,320
10 3 2 2 2 1	523,792,920	523,773,600
10 2 2 2 2 2	36,382,500	36,369,900
9 5 3 3 0 0	145,500,600	145,490,100
9 5 3 2 1 0	218,260,560	218,234,940
9 4 3 3 1 0	436,491,720	436,480,380
8 5 3 3 1 0	291,000,360	290,981,040
9 5 2 2 2 0	581,983,920	581,978,880
9 4 3 2 2 0	872,982,600	872,961,600
8 5 3 2 2 0	1,309,493,640	1,309,441,560
8 4 3 3 2 0	387,992,700	387,982,620
9 5 2 2 1 1	1,163,967,840	1,163,957,760
9 4 3 2 1 1	1,745,963,520	1,745,924,880
8 5 3 2 1 1	1,109,966	1,107,166
8 4 3 3 1 1	6,652,896	6,649,536
9 4 2 2 2 1	16,632,240	16,623,840
8 5 2 2 2 1	33,257,760	33,254,400
8 4 3 2 2 1	22,174,140	22,167,420
8 4 2 2 2 2	66,515,520	66,508,800
7 7 3 3 0 0	133,024,320	133,024,320
7 7 3 2 1 0	99,776,640	99,759,840
7 6 3 3 1 0	199,539,840	199,533,120
7 7 2 2 2 0	7,761,742	7,757,822
7 6 3 2 2 0	23,284,016	23,274,496
6 6 3 3 2 0	46,560,192	46,556,832
7 7 2 2 1 1	38,804,140	38,793,500
7 6 3 2 1 1	116,402,160	116,390,400
6 6 3 3 1 1	232,794,240	232,790,880
7 6 2 2 2 1	155,198,460	155,191,740
6 6 3 2 2 1	232,803,200	232,781,920
6 6 2 2 2 2	465,588,480	465,581,760
7 5 5 3 0 0	698,389,440	698,365,920
7 5 4 4 0 0	46,563,552	46,553,472
6 5 5 4 0 0	139,680,576	139,670,496
7 5 5 2 1 0	279,351,072	279,351,072
7 5 4 3 1 0	58,205,280	58,191,000
6 5 5 3 1 0	232,797,600	232,787,520
7 4 4 4 1 0	349,203,120	349,174,560
6 5 4 4 1 0	698,382,720	698,372,640
7 5 4 2 2 0	465,595,200	465,575,040
6 5 5 2 2 0	931,170,240	931,170,240
7 4 4 3 2 0	1,396,765,440	1,396,745,280
6 5 4 3 2 0	2,095,161,600	2,095,104,480
6 4 4 4 2 0	290,999,520	290,981,880
6 4 4 3 3 0	581,997,360	581,965,440
7 5 4 2 1 1	1,163,967,840	1,163,957,760
6 5 5 2 1 1	1,745,961,840	1,745,926,560
7 4 4 3 1 1	775,985,400	775,965,240
6 5 4 3 1 1	2,327,935,680	2,327,915,520
6 4 4 4 1 1	3,491,920,320	3,491,856,480
7 4 4 2 2 1	3,103,900,920	3,103,900,920
6 5 4 2 2 1	4,655,871,360	4,655,831,040
6 4 4 3 2 1	27,166,848	27,155,646
6 4 4 2 2 2	54,320,814	54,315,774
5 5 5 5 0 0	54,324,174	54,312,414
5 5 5 4 1 0	162,961,232	162,948,352
5 5 4 4 2 0	325,911,264	325,907,904
5 4 4 4 3 0	67,909,580	67,892,500
4 4 4 4 4 0	271,598,380	271,584,380
5 5 4 4 1 1	407,410,640	407,375,920
5 4 4 4 2 1	814,781,520	814,766,400
4 4 4 4 3 1	543,195,550	543,169,790
4 4 4 4 2 2	1,086,368,700	1,086,361,980
9 3 3 3 2 0	1,629,561,920	1,629,533,920
8 3 3 3 3 0	2,444,369,760	2,444,299,200
9 3 3 2 2 1	81,485,376	81,469,416
8 3 3 3 2 1	325,914,624	325,904,544
9 3 2 2 2 2	488,880,336	488,848,416
8 3 3 2 2 2	977,733,792	977,723,712
7 5 3 3 2 0	407,396,640	407,377,320
7 4 3 3 3 0	814,791,600	814,756,320
6 5 3 3 3 0	1,629,552,960	1,629,542,880
7 5 3 2 2 1	2,444,341,200	2,444,302,560
7 4 3 3 2 1	1,086,375,420	1,086,355,260
6 5 3 3 2 1	3,259,105,920	3,259,085,760
6 4 3 3 3 1	4,888,679,040	4,888,608,480
7 5 2 2 2 2	1,018,503,360	1,018,450,440
7 4 3 2 2 2	2,036,946,240	2,036,923,560
6 5 3 2 2 2	1,357,976,040	1,357,937,400
6 4 3 3 2 2	4,073,890,800	4,073,848,800
5 5 5 3 2 0	6,110,877,360	6,110,769,840
5 5 4 3 3 0	5,431,836,600	5,431,816,440
5 5 5 2 2 1	8,147,778,240	8,147,700,960
5 5 4 3 2 1	10,863,673,020	10,863,632,700
5 4 4 3 3 1	97,780,440	97,765,320
5 5 4 2 2 2	488,871,936	488,856,816
5 4 4 3 2 2	977,743,872	977,713,632
4 4 4 3 3 2	1,955,457,504	1,955,457,504
7 3 3 3 2 2	2,933,201,376	2,933,171,136
6 3 3 3 3 2	1,222,184,880	1,222,137,000
5 5 3 3 2 2	2,444,329,440	2,444,314,320
5 4 3 3 3 2	1,629,563,040	1,629,532,800
4 4 3 3 3 3	4,888,658,880	4,888,628,640
4 4 4 4 2 2	7,333,013,520	7,332,917,760
5 5 3 3 3 1	6,518,191,680	6,518,191,680
5 5 3 3 2 2	9,777,317,760	9,777,257,280
5 4 4 4 3 0	2,036,961,360	2,036,908,440
5 4 4 4 2 1	6,110,833,680	6,110,775,720
5 4 4 3 3 1	8,147,754,720	8,147,724,480
5 4 4 3 2 2	12,221,662,320	12,221,556,480
5 4 3 3 3 2	16,295,509,440	16,295,448,960
5 3 3 3 3 3	21,727,305,720	21,727,305,720
4 4 4 4 4 0	2,546,223,120	2,546,142,480
4 4 4 4 3 1	10,184,706,000	10,184,643,000
4 4 4 4 2 2	15,277,122,000	15,276,958,200
4 4 4 3 3 2	20,369,406,960	20,369,291,040
4 4 3 3 3 3	27,159,162,480	27,159,102,000

^a number of hexagonal face colors: N(A_g) + N(A_u); number of chiral pairs of hexagonal face colors: N(A_u); number of achiral hexagonal face colors: N(A_g) − N(A_u).

4. Applications: Chirality, Zeolites, Mesoporous Materials, Nanomaterials, and Biological Networks

Combinatorial enumerations under symmetry action have several applications to chirality, materials, and biological networks. In the context of chirality, as shown in the previous section, the combinatorial numbers for the totally symmetric A_g representation for any given color partition enumerates the Pólya equivalence classes of face colorings under the full O_h or I_h group. The combinatorial numbers for the chiral A_u IR yield the number of chiral pairs of face colorings while the difference between A_g and A_u numbers yields the number of achiral face colorings. Consequently, the sum of A_g and A_u numbers yields the total number of equivalence classes under the pure rotational operations or in the O or I group, respectively. As it is well known, chirality arises in a face coloring of the geometrical shapes considered here if the mirror image of the face coloring is not superimposable on the original coloring.

Another interesting application of the combinatorial enumeration scheme considered here is to spectroscopy in the context of nuclear spin statistics under symmetry [17,18,57,58]. In this context, the alternating irreducible representation, which is defined with +1 character values for even permutations and −1 for the odd permutations, plays a critical role in the case of fermion statistics. Consequently, the alternating representation is critical to the quantum chemical classification of the rovibronic wavefunctions of fermions, as the total wavefunction for fermions must be antisymmetric as stipulated by the Pauli principle. Consequently, the direct product of the nuclear spin functions of the rovibronic and the IR of the rovibronic level of water clusters in the total nonrigid limit would have to transform according to the alternating representation of the hypercube. Consequently, the combinatorial enumerations considered here are extremely useful in the analysis of experimental spectroscopic properties of a number of weakly bound van der Waals clusters such as (H₂O)_n, (NH₃)_n, and so forth [17,18].

A number of mesoporous materials and zeolite structures are networks of various shapes that we have considered in this study. For example, the structure of the tetragonal zeolite farneseite [76], shown in Figure 5, consists of several truncated octahedra. The combinatorics of a truncated octahedron was considered, as shown in Table 4, among several other structures of octahedral or cubic symmetries. Consequently, when dice enumerations are specialized to the case of a few chosen types of colors, the combinatorics considered reduces to face colorings of complex zeolite types of structures like the one shown in Figure 5. That is, face colorings would correspond to the enumeration of isomeric structures that would arise from face capping of zeolite structures, analogous to the one shown in Figure 5. It is hoped that the present work will stimulate such applications to such novel nanomaterials in the future.

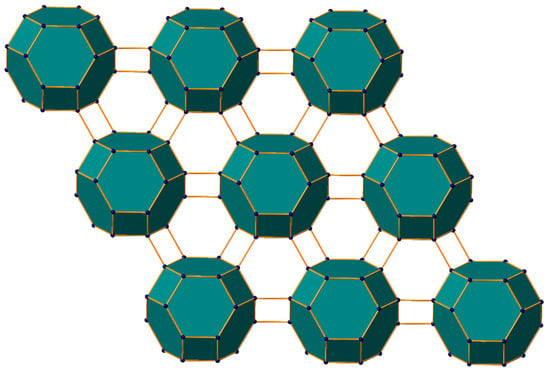
Figure 5. The structure of the tetragonal zeolite farneseite comprising several truncated octahedra. Figure reproduced with permission of authors of Ref. [76]. The enumeration of structures obtained from face capping of such zeolites correspond to face color enumerations considered in the current study.

Cayley trees are recursive symmetry structures that find a number of applications in biological networks such as phylogenetic trees [51]. The symmetry groups of such structures are recursive wreath products, and thus the colorings of vertices or edges of phylogenetic trees follow applications of the techniques considered in this study. These trees also find applications in pandemic trees, as demonstrated in a recent study on COVID-19 [52]. Moreover, in genetics the canalization or control of one genetic trait by another trait in the genetic regulatory networks is well described by the coloring of vertices of the hypercubes. Such genetic regulatory networks play important roles in evolutionary processes [53,54]. In this context, partitioning 2-colorings of the vertices of hypercubes into equivalence classes yields smaller clustering subsets for the statistical analysis of such networks. Consequently, the properties of any representative in an equivalence class contain the same genetic expression as any other function in the same equivalence class. The hypercubes have applications to the representations of DNA bases including DNA unnatural pairs [6].

5. Applications to Cryptography

The combinatorial complexity of various shapes of dice considered here facilitates their applications to cryptography due to the enormous number of configurations rising from the face colorings and number of chiral dice generated from various shapes. As seen from previous tables, the numbers grow in astronomical proportions culminating to 1.3084169531614 × 10²⁹⁷⁰⁶⁶ for a 12-cube or 4.4102702121446021496460288562760144 × 10³¹⁷¹ for the grand cell-600 dice. Such large combinatorial numbers relate to the combinatorial complexity of these shapes. Combinatorial complexity can be measured by the number of dice generated for each shape, as this could be one powerful measure of the complexity. The greater this number is, the more complex the structure. The large combinatorial complexity paves the way for powerful applications in cryptography for encrypting and decrypting messages through labeling the faces of the shapes with words or alphabets contained in a message. Once a mapping of the alphabets or other coded parts of a message to the faces of the shape considered here is made, then the various permutations of the faces would result in an enormous number of configurations allowing complete scrambling of the coded message.

Rubik’s cube is an excellent exemplification of the underlying combinatorial complexity and thus a great candidate for the puzzle that it is known for. As seen from the previous section on Rubik’s cube, there are 5.34018574959804633194496 × 10²⁹ possible dice, suggesting an astronomical number of ways to label the faces of Rubik’s cube. This would indeed enable encryption of messages by labeling the faces of the cube with alphabets or codes. Then the various rotations of the larger faces would scramble the message completely, and there are 5.34018574959804633194496 × 10²⁹ such possibilities in the most general case. Consider two romantic, clandestine messages to illustrate the point using Rubik’s cube, namely “I Love U” and “V Elope at 2”. The first message has six letters and two blank spaces. For example, if say, a corner or edge square of each larger face of Rubik’s cube is chosen to label with six letters in the message, and the cube is scrambled by the various rotations. The receiver then would have to solve Rubik’s cube puzzle to decrypt the message. The complexity of the encryption can be further enhanced by mapping letters to other characters; the simplest would be to map the letters to 26 numbers or other characters including !, @, #, $, %, ^, &, *, and so on to make the message totally look like some sort of gibberish. The other message, “V Elope at 2”, contains 12 characters, 2 repeating es, 3 blanks, and a numeral 2. If these characters are intertwined with other characters or numbers, and one uses, say, a grand cell-600, one would achieve a bit less than the maximum number of 4.4102702121446021496460288562760144 × 10³¹⁷¹ chiral pairs of configurations. The numbers will be reduced by the repeating three blank spaces and two repeating es (assuming upper and lower cases are not differentiated) or roughly by 3!x2! provided all other faces are labeled with other unique numbers or characters, and we would then arrive approximately at 3.67522517678717 × 10³¹⁷⁰ ways to scramble the message “V Elope at 2” using the faces of a grand cell-600 to encrypt the message. Just like the problem of Rubik’s cube, the larger encryption puzzles involving n-dimensional objects can be solved by a series of systematic algorithms. The other nuance that can be introduced in n-dimensional encryption algorithms is to use characters to code a message; for example, a simple message “V Elope at 2” becomes in Wingding font. Note that with the increasing importance of artificial intelligence in the coming years, it is very clear that algorithms with machine learning and AI techniques can be developed to decrypt the messages sent through even such complex pockets of objects, for example, a grand cell-600 or a 12-cube. Indeed n-dimensional hypercubes and other combinatorially complex shapes considered here provide very compelling objects to generate packets of encrypted messages with face, edge, cell, tesseract, or other complex p-dimensional hyperplanes for complex encryption that cannot be easily decrypted without invoking very complex AI algorithms that can unravel puzzles in n-dimensional spaces. Consequently, the present investigation on combinatorics of dice of various shapes in n-dimensions indeed opens up such a plethora of applications in cryptography with potentials for defense and other applications.

6. Conclusions

In the present study, we considered several geometrical forms of dice with octahedral, icosahedral, and higher symmetries including hyperoctahedral symmetries. Combinatorial enumeration of dice for these various shapes as well as the enumeration of dice in n-dimensions were considered. The results not only revealed substantial combinatorial complexities for higher order dice but also the existence of intriguing isochiral dice for some of the geometrical shapes. A number of applications to fullerene cages, icosahedral analogs of fullerenes such as Au₆₀^-, material science, biology, molecular clusters, and cryptography were pointed out. It is clear that these n-dimensional and other complex objects considered here hold considerable promise as candidates for numerous applications going into the future.