The p-Frobenius Number for the Triple of the Generalized Star Numbers

Abstract

In this paper, we give closed-form expressions of the p-Frobenius number for the triple of the generalized star numbers $an(n-1)+1$ for an integer $a\ge 4$. When $a=6$, it is reduced to the famous star number. For the set of given positive integers $\{a_1,a_2,\dots ,a_k\}$, the p-Frobenius number is the largest integer N whose number of non-negative integer representations $N=a_1{x}_1+a_2{x}_2+\cdots +a_k{x}_k$ is at most p. When $p=0$, the 0-Frobenius number is the classical Frobenius number, which is the central topic of the famous linear Diophantine problem of Frobenius.

1. Introduction

For an integer $a\ge 4$, define the generalized star numbers $S_{a,n}$ by

$$S_{a,n}=an(n-1)+1(n=0,1,2,\dots ).$$

(1)

When $a=6$, $S_n:=S_{6,n}$ represents the ordinary star numbers, which are also known as the centered 12-gonal numbers or centered dodecagonal numbers. A star number is a centered figurate number that represents a centered hexagram, similar to the pattern used in Chinese checkers. As can be seen in Figure 1, the star numbers show a nice symmetry. The star numbers are used for a new set of vector-valued Teichmüller modular forms, defined on the Teichmüller space, strictly related to the Mumford forms, which are holomorphic global sections of the vector bundle [1]. The first star numbers are given by the sequence

$$\begin{array}{c}{\left\{S_n\right\}}_{n\ge 0}=1,13,37,73,121,181,253,337,433,541,661,\hfill \\ \hfill 793,937,1093,1261,1441,1633,1837,2053,\dots \end{array}$$

([2] (A.131), [3] (A003154)). Some well-known formulae include:

$$\sum _{n=1}^{\infty }{\displaystyle \frac{1}{S_n}}={\displaystyle \frac{\pi tan(\pi /2\sqrt{3})}{2\sqrt{3}}},\sum _{n=0}^{\infty }{\displaystyle \frac{S_n}{n!}}=7e\mathrm{and}\sum _{n=0}^{\infty }{\displaystyle \frac{S_n}{2^n}}=26.$$

Figure 1. Chinese checkers board.

Geometrically, the n-th generalized star number $S_{a,n}$ is made up of a central point and $2a$ copies of the ($n-1$)-th triangular number, making it numerically equal to the n-th centered ($2a$)-gonal number, but differently arranged. Therefore, $S_{a,n}$ are often called the centered $2a$-gonal numbers. The generalized star numbers satisfy the linear recurrence equation:

$$S_{a,n}=S_{a,n-1}+2a(n-1).$$

When $a=4,5,7,8,9,10,11,12$, the centered $2a$-gonal numbers are listed in [3] (A016754, A062786, A069127, A069129, A069131, A069133, A069173, A069190), respectively.

The p-numerical semigroup $S_p\left(A\right)$ from the set of positive integers $\{a_1,a_2,\dots ,a_k\}$ ($k\ge 2$) is defined as the set of integers that can be expressed in more than p ways as non-negative integral linear combinations of the given positive integers $a_1,a_2,\dots ,a_k$ [4]. Namely,

$$S_p\left(A\right):=\{n\in {\mathbb{N}}_0|d(n;a_1,a_2,\dots ,a_k)>p\},$$

where $d(n;a_1,a_2,\dots ,a_k)$, which is called the denumerant, is the number of non-negative integer representations of n by $a_1,a_2,\dots ,a_k$. The denumerant was investigated by Sylvester [5] and remarked upon by Caley [6]. For some backgrounds on the number of representations, see, for example, [7,8,9]. Recently, the concept of the denumerant has been extensively studied in [10,11,12,13,14]. For a set of non-negative integers, denoted by ${\mathbb{N}}_0$, the set ${\mathbb{N}}_0\setminus S_p$ is finite if and only if $gcd(a_1,a_2,\dots ,a_{\kappa })=1$. Then there exists the largest integer $g_p\left(A\right):=g\left(S_p\right)$ in ${\mathbb{N}}_0\setminus S_p$, which is called the p-Frobenius number. The cardinality of ${\mathbb{N}}_0\setminus S_p$ is called the p-genus (or the p-Sylvester number) and is denoted by $n_p\left(A\right):=n\left(S_p\right)$. This kind of concept is a generalization of the famous Diophantine problem of Frobenius ([15,16]) since $p=0$ is the case when the original Frobenius number $g\left(A\right)=g_0\left(A\right)$ and the genus $n\left(A\right)=n_0\left(A\right)$.

When $k=2$, there exists the explicit closed formula of the p-Frobenius number for any non-negative integer p. However, for $k=3$, the p-Frobenius number cannot be given by any set of closed formulae, which can be reduced to a finite set of certain polynomials ([17]). Since providing a closed explicit formula for any general sequence involving three or more variables is very difficult, many researchers have focused on finding the Frobenius number for special cases (see, for example, [18,19,20]). Though it is even more challenging when $p>0$ (see, for instance, [21,22,23,24]), in [25], the p-Frobenius numbers of the consecutive three triangular numbers were studied.

In this paper, we present the closed-form expressions of the p-Frobenius numbers for the consecutive three star numbers $\{S_{a,n},S_{a,n+1},S_{a,n+2}\}$ (with $a\ge 4$ and $n\ge 2$). Additionally, we provide the explicit formula for their p-Sylvester number.

2. Basic Properties of the Generalized Star Numbers

In this section, we shall show some basic formulae for the generalized star numbers.

Proposition 1.

$$\begin{array}{cc}\hfill & \sum _{n=1}^{\infty }{\displaystyle \frac{1}{S_{a,n}}}={\displaystyle \frac{\pi tan(\pi \sqrt{(a-4)/a}/2)}{\sqrt{a(a-4)}}}(a\ge 5),\sum _{n=0}^{\infty }{\displaystyle \frac{S_{a,n}}{n!}}=(a+1)e,\hfill \\ \hfill & \sum _{n=0}^{\infty }{\displaystyle \frac{{(-1)}^n{S}_{a,n}}{n!}}={\displaystyle \frac{a+1}{e}},\sum _{n=0}^{\infty }{\displaystyle \frac{S_{a,n}}{b^n}}={\displaystyle \frac{2ab}{{(b-1)}^3}}+{\displaystyle \frac{b}{b-1}}(b>1).\hfill \end{array}$$

Proof. 

The second and third identities are trivial from the definition in (1). For the first identity, by referring to [26] (Ch.25), put

$$g\left(z\right):={\displaystyle \frac{1}{az(z-1)+1}}={\displaystyle \frac{1}{a(z-\alpha )(z-\beta )}},$$

where

$$\alpha ={\displaystyle \frac{a+\sqrt{a^2-4a}}{2a}}\mathrm{and}\beta ={\displaystyle \frac{a-\sqrt{a^2-4a}}{2a}}.$$

For $h\left(z\right)=\pi g\left(z\right)cot\pi z$,

$$\begin{array}{cc}\hfill {\mathrm{Res}}_{z=\alpha }h& =\underset{z\to \alpha }{lim}(z-\alpha )\pi g\left(z\right)cot\pi z=\underset{z\to \alpha }{lim}{\displaystyle \frac{\pi cot\pi z}{a(z-\beta )}}={\displaystyle \frac{\pi cot\pi \alpha }{a(\alpha -\beta )}}\hfill \\ \hfill & ={\displaystyle \frac{\pi }{\sqrt{a^2-4a}}}cot\left({\displaystyle \frac{a+\sqrt{a^2-4a}}{2a}}\pi \right)\hfill \\ \hfill & =-{\displaystyle \frac{\pi }{\sqrt{a^2-4a}}}tan\left({\displaystyle \frac{\sqrt{a^2-4a}}{2a}}\pi \right),\hfill \\ \hfill {\mathrm{Res}}_{z=\beta }h& =\underset{z\to \beta }{lim}(z-\beta )\pi g\left(z\right)cot\pi z=\underset{z\to \beta }{lim}{\displaystyle \frac{\pi cot\pi z}{a(z-\alpha )}}={\displaystyle \frac{\pi cot\pi \beta }{a(\beta -\alpha )}}\hfill \\ \hfill & ={\displaystyle \frac{-\pi }{\sqrt{a^2-4a}}}cot\left({\displaystyle \frac{a-\sqrt{a^2-4a}}{2a}}\pi \right)\hfill \\ \hfill & =-{\displaystyle \frac{\pi }{\sqrt{a^2-4a}}}tan\left({\displaystyle \frac{\sqrt{a^2-4a}}{2a}}\pi \right).\hfill \end{array}$$

Hence, we get

$$\begin{array}{cc}\hfill \sum _{n=-\infty }^{\infty }{\displaystyle \frac{1}{an(n-1)+1}}& =\sum _{n=-\infty }^{\infty }g\left(n\right)=-\left({\mathrm{Res}}_{z=\alpha }h+{\mathrm{Res}}_{z=\beta }h\right)\hfill \\ \hfill & ={\displaystyle \frac{2\pi }{\sqrt{a^2-4a}}}tan\left({\displaystyle \frac{\sqrt{a^2-4a}}{2a}}\pi \right).\hfill \end{array}$$

Since

$$\begin{array}{cc}\hfill \sum _{n=-\infty }^{\infty }{\displaystyle \frac{1}{an(n-1)+1}}& =\sum _{n=1}^{\infty }{\displaystyle \frac{1}{an(n-1)+1}}+\sum _{n=0}^{\infty }{\displaystyle \frac{1}{a(-n)(-n-1)+1}}\hfill \\ \hfill & =2\sum _{n=1}^{\infty }{\displaystyle \frac{1}{an(n-1)+1}},\hfill \end{array}$$

we obtain the first identity.

For the fourth identity, consider the function

$$f_b\left(x\right):=\sum _{n=0}^{\infty }{\left({\displaystyle \frac{x}{b}}\right)}^n={\displaystyle \frac{b}{b-x}}(b>1).$$

Since

$$f_b^{\prime \prime }\left(x\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{n(n-1)}{b^n}}{x}^{n-2}={\displaystyle \frac{2b}{{(b-x)}^3}},$$

we have

$$\begin{array}{cc}\hfill \sum _{n=0}^{\infty }{\displaystyle \frac{S_{a,n}}{b^n}}& =a\sum _{n=0}^{\infty }{\displaystyle \frac{n(n-1)}{b^n}}+\sum _{n=0}^{\infty }{\displaystyle \frac{1}{b^n}}\hfill \\ \hfill & ={\displaystyle \frac{2ab}{{(b-1)}^3}}+{\displaystyle \frac{b}{b-1}}\hfill \end{array}$$

□

3. Apéry Set

We introduce the Apéry set [27] to obtain the formulae in this paper.

Let p be a non-negative integer. For a set of positive integers $A=\{a_1,a_2,\dots ,a_k\}$ with $gcd\left(A\right)=1$ and $a_1=min\left(A\right)$, we denote the Apéry set by:

$${\mathrm{Ap}}_p\left(A\right)=\mathrm{Ap}(a_1,a_2,\dots ,a_k)=\{m_0^{\left(p\right)},m_1^{\left(p\right)},\dots ,m_{a_1-1}^{\left(p\right)}\},$$

where each positive integer $m_i^{\left(p\right)}$$(0\le i\le a_1-1)$ satisfies the conditions:

$$\left(\mathrm{i}\right)m_i^{\left(p\right)}\equiv i(mod{a}_1),\left(\mathrm{ii}\right)m_i^{\left(p\right)}\in S_p\left(A\right),\left(\mathrm{iii}\right)m_i^{\left(p\right)}-a_1\notin S_p\left(A\right).$$

Note that $m_0$ is defined to be 0.

It follows that for each p,

$${\mathrm{Ap}}_p\left(A\right)\equiv \{0,1,\dots ,a_1-1\}(mod{a}_1).$$

One of the convenient formulae to obtain the p-Frobenius number is via the elements in the corresponding p-Apéry set ([28]).

Lemma 1.

Let $gcd(a_1,\dots ,a_k)=1$ with $a_1=min\{a_1,\dots ,a_k\}$. Then we have

$$\begin{array}{cc}\hfill g_p(a_1,\dots ,a_k)& =\underset{0\le j\le a_1-1}{max}{m}_j^{\left(p\right)}-a_1,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill n_p(a_1,\dots ,a_k)& ={\displaystyle \frac{1}{a_1}}\sum _{j=0}^{a_1-1}{m}_j^{\left(p\right)}-{\displaystyle \frac{a_1-1}{2}}.\hfill \end{array}$$

(3)

Remark 1.

When $p=0$, the Formulae (2) and (3) are essentially due to Brauer and Shockley [29], and Selmer [30], respectively. More general formulae, including the p-power sum and the p-weighted sum, can be seen in [28,31].

4. Main Result

The p-Frobenius number for three consecutive generalized star numbers can be determined. The general result for a non-negative p is derived from the result for $p=0$, which is stated in the following theorem.

Theorem 1.

When a is even with $a\ge 4$ and $n\ge 2$, we have

$$\begin{array}{cc}\hfill & g_0(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & =\left\{\begin{array}{cc}\left(2n\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}-l\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathit{if}{\displaystyle \frac{3a}{4l}}-{\displaystyle \frac{l-3}{2l}}\le n\le {\displaystyle \frac{3a-2l+2}{2(2l-1)}}\left(l\ge 2\right);\hfill & \\ \left(2ln-{\displaystyle \frac{3a}{2}}+l-3\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}-l+1\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathit{if}{\displaystyle \frac{3a-2l+3}{2(2l-1)}}\le n\le {\displaystyle \frac{3a}{4(l-1)}}-{\displaystyle \frac{l-3}{2(l-1)}}\left(l\ge 2\right);\hfill & \\ \left(2n\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}-1\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathit{if}{\displaystyle \frac{3a}{4}}+1\le n\le {\displaystyle \frac{3a}{2}};\hfill & \\ \left(2n-{\displaystyle \frac{3a}{2}}-2\right)S_{a,n+1}+{\displaystyle \frac{a}{2}}n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathit{if}n\ge {\displaystyle \frac{3a}{2}}+1.\hfill \end{array}\right.\hfill \end{array}$$

When a is odd with $a\ge 5$ and $n\ge 2$, we have

$$\begin{array}{cc}\hfill & g_0(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & =\left\{\begin{array}{cc}\left(2n\right)S_{a,n+1}+{\displaystyle \frac{a-2l+1}{2}}n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathit{if}{\displaystyle \frac{3a-2l+7}{2(2l-1)}}\le n\le {\displaystyle \frac{3a-2l+3}{4(l-1)}}\left(l\ge 2\right);\hfill & \\ \left((2l-1)n-{\displaystyle \frac{3a-2l+7}{2}}\right)S_{a,n+1}+{\displaystyle \frac{a-2l+3}{2}}n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathit{if}{\displaystyle \frac{3a-2l+4}{4(l-1)}}\le n\le {\displaystyle \frac{3a-2l+7}{2(2l-3)}}\left(l\ge 2\right);\hfill & \\ \left(2n\right)S_{a,n+1}+{\displaystyle \frac{a-1}{2}}n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathit{if}n\ge {\displaystyle \frac{3a+5}{2}}.\hfill \end{array}\right.\hfill \end{array}$$

Remark 2.

It is clear that there is no integer between ${\displaystyle \frac{3a}{4l}}-{\displaystyle \frac{l-3}{2l}}$ and ${\displaystyle \frac{3a}{4l}}-{\displaystyle \frac{l-2}{2l}}$ (exclusive), and between ${\displaystyle \frac{3a}{2(2l-1)}}-{\displaystyle \frac{l-1}{2l-1}}$ and ${\displaystyle \frac{3a}{2(2l-1)}}$ (exclusive).

More precisely, for example, when $a=8$ and $a=9$, we have

$$g_0(S_{8,n},S_{8,n+1},S_{8,n+2})=\left\{\begin{array}{cc}4S_{8,n+1}+2S_{8,n+2}-S_{8,n}\hfill & \mathrm{if}n=2;\hfill \\ 6S_{8,n+1}+6S_{8,n+2}-S_{8,n}\hfill & \mathrm{if}n=3;\hfill \\ (4n-13)S_{8,n+1}+3n{S}_{8,n+2}-S_{8,n}\hfill & \mathrm{if}4\le n\le 5;\hfill \\ 2n{S}_{8,n+1}+3n{S}_{8,n+2}-S_{8,n}\hfill & \mathrm{if}7\le n\le 12;\hfill \\ (2n-14)S_{8,n+1}+4n{S}_{8,n+2}-S_{8,n}\hfill & \mathrm{if}n\ge 13\hfill \end{array}\right.$$

and

$$g_0(S_{9,n},S_{9,n+1},S_{9,n+2})=\left\{\begin{array}{cc}{S}_{9,3}+4S_{9,4}-S_{9,2}\hfill & \mathrm{if}n=2;\hfill \\ 6S_{9,4}+6S_{9,5}-S_{9,3}\hfill & \mathrm{if}n=3;\hfill \\ 6S_{9,5}+12S_{9,6}-S_{9,4}\hfill & \mathrm{if}n=4;\hfill \\ 2n{S}_{9,n+1}+3n{S}_{9,n+2}-S_{9,n}\hfill & \mathrm{if}5\le n\le 6;\hfill \\ (3n-15)S_{9,n+1}+4n{S}_{9,n+2}-S_{9,n}\hfill & \mathrm{if}7\le n\le 15;\hfill \\ 2n{S}_{9,n+1}+4n{S}_{9,n+2}-S_{9,n}\hfill & \mathrm{if}n\ge 16,\hfill \end{array}\right.$$

respectively.

4.1. Proof of Theorem 1

4.1.1. Even Case

Let a be even with $a\ge 4$. For a positive integer l, we shall prove that the elements of the 0-Apéry set can be arranged as in Table 1. Here, for simplicity, consider the representation

$$t_{y,z}:=y{S}_{a,n+1}+z{S}_{a,n+2}(y,z\ge 0).$$

First, from the length relationship in the horizontal direction (y value) in Table 1,

$$2ln-{\displaystyle \frac{3}{2}}a+l-3\ge 0\mathrm{and}2ln-{\displaystyle \frac{3}{2}}a+l-3\le 2n,$$

or

$${\displaystyle \frac{3a}{4l}}-{\displaystyle \frac{l-3}{2l}}\le n\le {\displaystyle \frac{3a}{4(l-1)}}-{\displaystyle \frac{l-3}{2(l-1)}}.$$

Since $S_{a,1}=1$, we must assume that $n\ge 2$. Hence,

$${\displaystyle \frac{3a}{4(l-1)}}-{\displaystyle \frac{l-3}{2(l-1)}}\ge 2\mathrm{or}a\ge {\displaystyle \frac{10l-14}{3}}.$$

(4)

Table 1. ${\mathrm{Ap}}_0(S_{a,n},S_{a,n+1},S_{a,n+2})$ when a is even.

$t_{0,0}$	⋯	$t_{2ln-\frac{3}{2}a+l-3,0}$	$t_{2ln-\frac{3}{2}a+l-2,0}$	⋯	⋯	$t_{2n,0}$
⋮		⋮	⋮			⋮
$t_{0,({\displaystyle \frac{a}{2}}-l)n}$	⋯	$t_{2ln-{\displaystyle \frac{3}{2}}a+l-3,({\displaystyle \frac{a}{2}}-l)n}$	$t_{2ln-{\displaystyle \frac{3}{2}}a+l-2,({\displaystyle \frac{a}{2}}-l)n}$	⋯	⋯	$t_{2n,({\displaystyle \frac{a}{2}}-l)n}$
$t_{0,({\displaystyle \frac{a}{2}}-l)n+1}$	⋯	$t_{2ln-{\displaystyle \frac{3}{2}}a+l-3,({\displaystyle \frac{a}{2}}-l)n+1}$
⋮		⋮
⋮		⋮
$t_{0,({\displaystyle \frac{a}{2}}-l+1)n}$	⋯	$t_{2ln-{\displaystyle \frac{3}{2}}a+l-3,({\displaystyle \frac{a}{2}}-l+1)n}$

Since $t_{2n+1,0}-t_{0,n}=(n+1)S_{a,n}$,

$$t_{2n+1,0}\equiv t_{0,n}(mod{S}_{a,n})\mathrm{and}{t}_{2n+1,0}>t_{0,n}.$$

(5)

Since

$$t_{2ln-{\displaystyle \frac{3a}{2}}+l-2,0}+t_{0,({\displaystyle \frac{a}{2}}-l)n+1}={\displaystyle \frac{(a+2l)(n+1)-2}{2}}{S}_{a,n},$$

we have

$$t_{2ln-{\displaystyle \frac{3a}{2}}+l-2,0}\equiv -t_{0,({\displaystyle \frac{a}{2}}-l)n+1}(mod{S}_{a,n}).$$

(6)

We need to verify that the sequence ${\{\ell S_{a,n+1}\}}_{\ell =0}^{S_{a,n}-1}$ encompasses every element of the 0-Apéry set exactly once. After the long subsequence with length $2n+1$

$$t_{0,j},t_{1,j},\dots ,t_{2n,j}(j=0,1,\dots ,({\displaystyle \frac{a}{2}}-l)n),$$

by (5), it is continued to the next subsequence by increasing by n rows:

$$t_{0,j+n},t_{1,j+n},\dots .$$

After the short subsequence with length $2ln-{\displaystyle \frac{3a}{2}}+l-2$

$$t_{0,j},t_{1,j},\dots ,t_{2ln-{\displaystyle \frac{3a}{2}}+l-3,j}(j=({\displaystyle \frac{a}{2}}-l)n+1,({\displaystyle \frac{a}{2}}-l)n+2,\dots ,({\displaystyle \frac{a}{2}}-l+1)n),$$

by (6), it is continued to the long subsequence by decreasing by ($({\displaystyle \frac{a}{2}}-l)n+1$) rows:

$$t_{0,j-({\displaystyle \frac{a}{2}}-l)n-1},t_{1,j-({\displaystyle \frac{a}{2}}-l)n-1},\dots ,t_{2n,j-({\displaystyle \frac{a}{2}}-l)n-1}.$$

Since $gcd(n,({\displaystyle \frac{a}{2}}-l)n+1)=1$, by this process, any element is not overlapped, and all the elements can be counted only once. Since $gcd(S_{a,n},S_{a,n+1})=1$, we have ${\{\ell S_{a,n+1}\}}_{\ell =0}^{S_{a,n}-1}={\{\ell \}}_{\ell =0}^{S_{a,n}-1}$.

In Table 1, there are two candidates to take the largest element of the 0-Apéry set: $t_{2n,({\displaystyle \frac{a}{2}}-l)n}$ or $t_{2ln-{\displaystyle \frac{3}{2}}a+l-3,({\displaystyle \frac{a}{2}}-l+1)n}$. We see that

$$\begin{array}{cc}\hfill & t_{2ln-{\displaystyle \frac{3}{2}}a+l-3,({\displaystyle \frac{a}{2}}-l+1)n}-t_{2n,({\displaystyle \frac{a}{2}}-l)n}:=E(a,n,l)\hfill \\ \hfill & =(2l-1)a{n}^3-\left({\displaystyle \frac{3a^2}{2}}-(3l-2)a\right)n^2-\left({\displaystyle \frac{3a^2}{2}}-(l-1)a-2l+1\right)n\hfill \\ \hfill & -{\displaystyle \frac{3a}{2}}+l-3.\hfill \end{array}$$

Consider the largest root of $E(a,n,l)=0$ on n. Since for $l\ge 2$ and $a\ge {\displaystyle \frac{10l-14}{3}}$ in (4)

$$\begin{array}{cc}\hfill E\left(a,{\displaystyle \frac{3a-2l+3}{2(2l-1)}},l\right)& ={\displaystyle \frac{a(3a+2l+1)(3a-2l+3)}{8{(2l-1)}^2}}-{\displaystyle \frac{3}{2}}\hfill \\ \hfill & \ge {\displaystyle \frac{480l^3-1924l^2+2439l-1019}{12{(2l-1)}^2}}>0,\hfill \\ \hfill E\left(a,{\displaystyle \frac{3a-2l+2}{2(2l-1)}},l\right)& =-2<0,\hfill \end{array}$$

when $n\ge {\displaystyle \frac{3a-2l+3}{2(2l-1)}}$, $t_{2ln-{\displaystyle \frac{3}{2}}a+l-3,({\displaystyle \frac{a}{2}}-l+1)n}$ is the largest, and by Lemma 1 (2), we have

$$\begin{array}{cc}\hfill & g_0(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & =\left(2ln-{\displaystyle \frac{3}{2}}a+l-3\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}-l+1\right)n{S}_{a,n+2}-S_{a,n}.\hfill \end{array}$$

When $n\le {\displaystyle \frac{3a-2l+2}{2(2l-1)}}$, $t_{2n,({\displaystyle \frac{a}{2}}-l)n}$ is the largest, and we have

$$g_0(S_{a,n},S_{a,n+1},S_{a,n+2})=\left(2n\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}-l\right)n{S}_{a,n+2}-S_{a,n}.$$

Since for $l=1$ and $a\ge 2$

$$\begin{array}{cc}\hfill E\left(a,{\displaystyle \frac{3a}{2}}+1,1\right)& ={\displaystyle \frac{9a^3}{4}}+{\displaystyle \frac{9a^2}{2}}+2a-1>0,\hfill \\ \hfill E\left(a,{\displaystyle \frac{3a}{2}},1\right)& =-2<0,\hfill \end{array}$$

when $n\ge {\displaystyle \frac{3a}{2}}+1$, $t_{2n-{\displaystyle \frac{3}{2}}a-2,{\displaystyle \frac{a}{2}}n}$ is the largest, and we have

$$g_0(S_{a,n},S_{a,n+1},S_{a,n+2})=\left(2n-{\displaystyle \frac{3}{2}}a-2\right)S_{a,n+1}+{\displaystyle \frac{a}{2}}n{S}_{a,n+2}-S_{a,n}.$$

When $n\le {\displaystyle \frac{3a}{2}}$, $t_{2n,({\displaystyle \frac{a}{2}}-1)n}$ is the largest, and we have

$$g_0(S_{a,n},S_{a,n+1},S_{a,n+2})=\left(2n\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}-1\right)n{S}_{a,n+2}-S_{a,n}.$$

4.1.2. Odd Case

Let a be odd with $a\ge 5$. We shall prove that when $n\le 3(a+1)/2$, the elements of the 0-Apéry set can be arranged as in Table 2. First, from the length relationship in the horizontal direction (y value) in Table 2,

$$(2l-1)n-{\displaystyle \frac{3a-2l+7}{2}}\ge 0\mathrm{and}(2l-1)n-{\displaystyle \frac{3a-2l+7}{2}}\le 2n,$$

or

$${\displaystyle \frac{3a-2l+7}{2(2l-1)}}\le n\le {\displaystyle \frac{3a-2l+7}{2(2l-3)}}.$$

Since the possible $n\ge 2$, we have

$$n\ge {\displaystyle \frac{3a-2l+7}{2(2l-3)}}\mathrm{or}a\ge {\displaystyle \frac{10l-19}{3}}.$$

(7)

Table 2. ${\mathrm{Ap}}_0(S_{a,n},S_{a,n+1},S_{a,n+2})$ when a is odd.

$t_{0,0}$	⋯	$t_{(2l-1)n-\frac{3a-2l+7}{2}),0}$	$t_{(2l-1)n-\frac{3a-2l+5}{2},0}$	⋯	⋯	$t_{2n,0}$
⋮		⋮	⋮			⋮
$t_{0,{\displaystyle \frac{a-2l+1}{2}}n}$	⋯	$t_{(2l-1)n-{\displaystyle \frac{3a-2l+7}{2}},{\displaystyle \frac{a-2l+1}{2}}n}$	$t_{(2l-1)n-{\displaystyle \frac{3a-2l+5}{2}},{\displaystyle \frac{a-2l+1}{2}}n}$	⋯	⋯	$t_{2n,{\displaystyle \frac{a-2l+1}{2}}n}$
$t_{0,{\displaystyle \frac{a-2l+1}{2}}n+1}$	⋯	$t_{(2l-1)n-{\displaystyle \frac{3a-2l+7}{2}},{\displaystyle \frac{a-2l+1}{2}}n+1}$
⋮		⋮
⋮		⋮
$t_{0,{\displaystyle \frac{a-2l+3}{2}}n}$	⋯	$t_{(2l-1)n-{\displaystyle \frac{3a-2l+7}{2}},{\displaystyle \frac{a-2l+3}{2}}n}$

Since

$$t_{(2l-1)n-{\displaystyle \frac{3a-2l+5}{2}},0}+t_{0,{\displaystyle \frac{a-2l+1}{2}}n+1}={\displaystyle \frac{(a+2l)(n+1)-n-3}{2}}{S}_{a,n},$$

we have

$$t_{(2l-1)n-{\displaystyle \frac{3a-2l+5}{2}},0}\equiv -t_{0,{\displaystyle \frac{a-2l+1}{2}}n+1}(mod{S}_{a,n}).$$

(8)

Now, the sequence ${\{\ell S_{a,n+1}\}}_{\ell =0}^{S_{a,n}-1}$ runs over all elements of 0-Apéry set once. After the long subsequence with length $2n+1$

$$t_{0,j},t_{1,j},\dots ,t_{2n,j}(j=0,1,\dots ,{\displaystyle \frac{a-2l+1}{2}}n),$$

by (5), it is continued to the next subsequence by increasing by n rows:

$$t_{0,j+n},t_{1,j+n},\dots .$$

After the short subsequence with length $(2l-1)n-{\displaystyle \frac{3a-2l+5}{2}}$

$$t_{0,j},t_{1,j},\dots ,t_{(2l-1)n-{\displaystyle \frac{3a-2l+5}{2}},j}(j={\displaystyle \frac{a-2l+1}{2}}n+1,{\displaystyle \frac{a-2l+1}{2}}n+2,\dots ,{\displaystyle \frac{a-2l+3}{2}}n),$$

by (8), it is continued to the long subsequence by decreasing by (${\displaystyle \frac{a-2l+1}{2}}n+1$) rows:

$$t_{0,j-{\displaystyle \frac{a-2l+1}{2}}n-1},t_{1,j-{\displaystyle \frac{a-2l+1}{2}}n-1},\dots ,t_{2n,j-{\displaystyle \frac{a-2l+1}{2}}n-1}.$$

Since $gcd(n,{\displaystyle \frac{a-2l+1}{2}}n+1)=1$, by this process, any element is not overlapped, and all the elements can be counted only once. Since $gcd(S_{a,n},S_{a,n+1})=1$, we have ${\{\ell S_{a,n+1}\}}_{\ell =0}^{S_{a,n}-1}={\{\ell \}}_{\ell =0}^{S_{a,n}-1}$.

In Table 2, there are two candidates to take the largest values: $t_{2n,{\displaystyle \frac{a-2l+1}{2}}n}$ and

$t_{(2l-1)n-{\displaystyle \frac{3a-2l+7}{2}},{\displaystyle \frac{a-2l+3}{2}}n}$. Notice that

$$\begin{array}{cc}\hfill & t_{(2l-1)n-{\displaystyle \frac{3a-2l+7}{2}},{\displaystyle \frac{a-2l+3}{2}}n}-t_{2n,{\displaystyle \frac{a-2l+1}{2}}n}:=O(a,n,l)\hfill \\ \hfill & =2(l-1)a{n}^3-{\displaystyle \frac{a(3a-6l+7)}{2}}{n}^2-{\displaystyle \frac{3a^2-(2l-3)a-4(l-1)}{2}}n\hfill \\ \hfill & -{\displaystyle \frac{3a-2l+7}{2}}.\hfill \end{array}$$

Since for $l\ge 2$ and $a\ge {\displaystyle \frac{10l-19}{3}}$ in (7)

$$\begin{array}{cc}\hfill O\left(a,{\displaystyle \frac{3a-2l+4}{4(l-1)}},l\right)& ={\displaystyle \frac{a(3a+2l)(3a-2l+4)}{32{(l-1)}^2}}-{\displaystyle \frac{3}{2}}\hfill \\ \hfill & \ge {\displaystyle \frac{960l^3-5288l^2+9467l-5559}{96{(l-1)}^2}}>0,\hfill \\ \hfill O\left(a,{\displaystyle \frac{3a-2l+3}{4(l-1)}},l\right)& =-2<0,\hfill \end{array}$$

when $n\le {\displaystyle \frac{3a-2l+3}{4(l-1)}}$, $t_{2n,{\displaystyle \frac{a-2l+1}{2}}n}$ is the largest in the 0-Apéry set. Hence, by Lemma 1 (2), we have

$$g_0(S_{a,n},S_{a,n+1},S_{a,n+2})=\left(2n\right)S_{a,n+1}+{\displaystyle \frac{a-2l+1}{2}}n{S}_{a,n+2}-S_{a,n}.$$

When $n\ge {\displaystyle \frac{3a-2l+4}{4(l-1)}}$, $t_{(2l-1)n-{\displaystyle \frac{3a-2l+7}{2}},{\displaystyle \frac{a-2l+3}{2}}n}$ is the largest, and we have

$$g_0(S_{a,n},S_{a,n+1},S_{a,n+2})=\left((2l-1)n-{\displaystyle \frac{3a-2l+7}{2}}\right)S_{a,n+1}+{\displaystyle \frac{a-2l+3}{2}}n{S}_{a,n+2}-S_{a,n}.$$

For $l=1$, by

$$O(a,n,1)=-{\displaystyle \frac{n(n+1)a(3a+1)}{2}}-{\displaystyle \frac{3a+5}{2}}<0,$$

we can find that $t_{2n,{\displaystyle \frac{a-1}{2}}n}$ is the largest in the 0-Apéry set. Hence, by Lemma 1 (2), we have

$$g_0(S_{a,n},S_{a,n+1},S_{a,n+2})=\left(2n\right)S_{a,n+1}+{\displaystyle \frac{a-1}{2}}n{S}_{a,n+2}-S_{a,n}.$$

5. $\mathit{p}=\mathbf{1}$

The arrangement of the elements of the 1-Apéry set can be determined from those of the 0-Apéry set. As seen in the case where $p=0$, there are four different patterns about the arrangement of the elements of the 0-Apéry set.

Consider the case where a is even with $a\ge 4$. Otherwise, the following argument is not valid. By (5), (6) and $t_{-{\displaystyle \frac{3a}{2}}+2n-1,({\displaystyle \frac{a}{2}}-1)n+1}={\displaystyle \frac{(a+2)n+a}{2}}{S}_{a,n}$, we have the correspondences between the elements of the 0-Apéry set and those of the 1-Apéry set:

$$\begin{array}{cc}\hfill & t_{y,z}\equiv t_{y+2n+1,z-n}(mod{S}_{a,n})(0\le y\le 2n,n\le z\le ({\displaystyle \frac{a}{2}}-l)n;\hfill \\ \hfill & 0\le y\le 2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l)n+1\le z\le ({\displaystyle \frac{a}{2}}-l+1)n),\hfill \\ \hfill & t_{y,z}\equiv t_{y+2ln-{\displaystyle \frac{3a}{2}}+l-2,z+({\displaystyle \frac{a}{2}}-l)n+1}(mod{S}_{a,n})\hfill \\ \hfill & \left(0\le y\le {\displaystyle \frac{3a}{2}}-2(l-1)n-l+2,0\le z\le n-1\right),\hfill \\ \hfill & t_{y,z}\equiv t_{y-{\displaystyle \frac{3a}{2}}+2(l-1)n+l-3,z+({\displaystyle \frac{a}{2}}-l+1)n+1}(mod{S}_n)\hfill \\ \hfill & \left({\displaystyle \frac{3a}{2}}-2(l-1)n-l+3\le y\le 2n,0\le z\le n-1\right),\hfill \end{array}$$

respectively. Namely, in Table 3, the elements in the first n rows are simply moved below the 0-Apéry set to fill in the gap. However, the remaining portion is moved to the lower left. Elements other than the first n rows are shifted to the right side of the 0-Apéry set by shifting up n rows.

Table 3. ${\mathrm{Ap}}_1(S_{a,n},S_{a,n+1},S_{a,n+2})$ when a is even.

$t_{2n+1,0}$

⋯

⋯

$t_{4n+1,0}$

⋮

⋮

⋮

⋮

$t_{2n+1,({\displaystyle \frac{a}{2}}-l-1)n}$

⋯

⋯

$t_{4n+1,({\displaystyle \frac{a}{2}}-l-1)n}$

$t_{2n+1,({\displaystyle \frac{a}{2}}-l-1)n+1}$

⋯

$t_{2(l+1)n-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l-1)n+1}$

⋮

⋮

$t_{2n+1,({\displaystyle \frac{a}{2}}-l)n}$

⋯

$t_{2(l+1)n-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l)n}$

$t_{2ln-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l)n+1}$

⋯

⋯

$t_{2n,({\displaystyle \frac{a}{2}}-l)n+1}$

⋮

⋮

$t_{2ln-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l+1)n}$

⋯

⋯

$t_{2n,({\displaystyle \frac{a}{2}}-1)n}$

$t_{0,({\displaystyle \frac{a}{2}}-1)n+1}$

⋯

$t_{2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l+1)n+1}$

⋮

⋮

$t_{0,({\displaystyle \frac{a}{2}}-l+2)n}$

⋯

$t_{2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l+2)n}$

Set ${\tau }_{x,y,x}:=x{S}_{a,n}+y{S}_{a,n+1}+z{S}_{a,n+2}$. We can show that all the elements of the 1-Apéry set have at least two different representations:

$$\begin{array}{cc}\hfill & {\tau }_{n+1,y,z}={\tau }_{0,y+2n+1,z-n}(0\le y\le 2n,n\le z\le ({\displaystyle \frac{a}{2}}-l)n;\hfill \\ \hfill & 0\le y\le 2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l)n+1\le z\le ({\displaystyle \frac{a}{2}}-l+1)n),\hfill \\ \hfill & {\tau }_{{\displaystyle \frac{(a+2l)(n+1)-2}{2}},y,z}={\tau }_{0,y+2ln-{\displaystyle \frac{3a}{2}}+l-2,z+({\displaystyle \frac{a}{2}}-l)n+1}\hfill \\ \hfill & \left(0\le y\le {\displaystyle \frac{3a}{2}}-2(l-1)n-l+2,0\le z\le n-1\right),\hfill \\ \hfill & {\tau }_{{\displaystyle \frac{(a+2l-2)n+a+2l-4}{2}},y,z}={\tau }_{0,y-{\displaystyle \frac{3a}{2}}+2(l-1)n+l-3,z+({\displaystyle \frac{a}{2}}-l+1)n+1}\hfill \\ \hfill & \left({\displaystyle \frac{3a}{2}}-2(l-1)n-l+3\le y\le 2n,0\le z\le n-1\right).\hfill \end{array}$$

From Table 3, there are four candidates to take the largest value of ${\mathrm{Ap}}_1(S_{a,n},S_{a,n+1},S_{a,n+2})$:

$$t_{2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l+2)n}{t}_{2n,({\displaystyle \frac{a}{2}}-l+1)n},t_{2(l+1)n-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l)n},t_{4n+1,({\displaystyle \frac{a}{2}}-l-1)n}.$$

Since

$$\begin{array}{cc}\hfill & t_{2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l+2)n}-t_{2(l+1)n-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l)n}\hfill \\ \hfill & =t_{2n,({\displaystyle \frac{a}{2}}-l+1)n}-t_{4n+1,({\displaystyle \frac{a}{2}}-l-1)n}=3an(n+1)-1>0,\hfill \end{array}$$

similarly to the case where $p=0$, there are only two possibilities. Namely, when ${\displaystyle \frac{3a}{4l}}-{\displaystyle \frac{l-3}{2l}}\le n\le {\displaystyle \frac{3a-2l+2}{2(2l-1)}}$ ($l\ge 2$) or ${\displaystyle \frac{3a}{4}}+1\le n\le {\displaystyle \frac{3a}{2}}$ ($l=1$), $t_{2n,({\displaystyle \frac{a}{2}}-l+1)n}$ is the largest, so by Lemma 1 (2) we have

$$g_1(S_{a,n},S_{a,n+1},S_{a,n+2})=\left(2n\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}-l+1\right)n{S}_{a,n+2}-S_{a,n}.$$

When ${\displaystyle \frac{3a-2l+3}{2(2l-1)}}\le n\le {\displaystyle \frac{3a}{4(l-1)}}-{\displaystyle \frac{l-3}{2(l-1)}}$ ($l\ge 2$) or $n\ge {\displaystyle \frac{3a}{2}}+1$ ($l=1$), $t_{2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l+2)n}$ is the largest, and we have

$$g_1(S_{a,n},S_{a,n+1},S_{a,n+2})=\left(2ln-{\displaystyle \frac{3a}{2}}+l-3\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}-l+2\right)n{S}_{a,n+2}-S_{a,n}.$$

The case where a is odd is not so similar, but analogous patterns and corresponding congruences and inequalities give the following results. When a is odd with $a\ge 5$ and $n\ge 2$, we have

$$\begin{array}{cc}\hfill & g_1(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & =\left\{\begin{array}{cc}\left(2n\right)S_{a,n+1}+{\displaystyle \frac{a-2l+3}{2}}n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathrm{if}{\displaystyle \frac{3a-2l+7}{2(2l-1)}}\le n\le {\displaystyle \frac{3a-2l+3}{4(l-1)}}\left(l\ge 2\right);\hfill & \\ \left((2l-1)n-{\displaystyle \frac{3a-2l+7}{2}}\right)S_{a,n+1}+{\displaystyle \frac{a-2l+5}{2}}n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathrm{if}{\displaystyle \frac{3a-2+4}{4(l-1)}}\le n\le {\displaystyle \frac{3a-2l+7}{2(2l-3)}}\left(l\ge 2\right);\hfill & \\ \left(2n\right)S_{a,n+1}+{\displaystyle \frac{a+1}{2}}n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathrm{if}n\ge {\displaystyle \frac{3a+5}{2}}.\hfill \end{array}\right.\hfill \end{array}$$

6. $\mathit{p}\ge \mathbf{2}$

The elements of the 2-Apéry set can be determined from those of the 1-Apéry set as follows. See Table 4.

Table 4. ${\mathrm{Ap}}_2(S_{a,n},S_{a,n+1},S_{a,n+2})$.

$t_{4n+2,0}$

⋯

$t_{(2l+4)n-{\displaystyle \frac{3a}{2}}+l-1,0}$

$t_{(2l+4)n-{\displaystyle \frac{3a}{2}}+l,0}$

⋯

⋯

$t_{6n+2,0}$

⋮

⋮

⋮

⋮

$t_{4n+2,({\displaystyle \frac{a}{2}}-l-2)n}$

⋯

$t_{(2l+4)n-{\displaystyle \frac{3a}{2}}+l-1,({\displaystyle \frac{a}{2}}-l-2)n}$

$t_{(2l+4)n-{\displaystyle \frac{3a}{2}}+l,({\displaystyle \frac{a}{2}}-l-2)n}$

⋯

⋯

$t_{6n+2,({\displaystyle \frac{a}{2}}-l-2)n}$

$t_{4n+2,({\displaystyle \frac{a}{2}}-l-2)n+1}$

⋯

$t_{(2l+4)n-{\displaystyle \frac{3a}{2}}+l-1,({\displaystyle \frac{a}{2}}-l-2)n+1}$

⋮

⋮

$t_{4n+2,({\displaystyle \frac{a}{2}}-l-1)n}$

⋯

$t_{(2l+4)n-{\displaystyle \frac{3a}{2}}+l-1,({\displaystyle \frac{a}{2}}-l-1)n}$

$t_{(2l+2)n-{\displaystyle \frac{3a}{2}}+l-1,({\displaystyle \frac{a}{2}}-l-1)n+1}$

⋯

⋯

$t_{4n+1,({\displaystyle \frac{a}{2}}-l-1)n+1}$

⋮

⋮

$t_{(2l+2)n-{\displaystyle \frac{3a}{2}}+l-1,({\displaystyle \frac{a}{2}}-l)n}$

⋯

⋯

$t_{4n+1,({\displaystyle \frac{a}{2}}-l)n}$

$t_{2n+1,({\displaystyle \frac{a}{2}}-l)n+1}$

⋯

$t_{(2l+2)n-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l)n+1}$

⋮

⋮

$t_{2n+1,({\displaystyle \frac{a}{2}}-l+1)n}$

⋯

$t_{(2l+2)n-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l+1)n}$

$t_{2ln-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l+1)n+1}$

⋯

⋯

$t_{2n,({\displaystyle \frac{a}{2}}-l+1)n+1}$

⋮

⋮

$t_{2ln-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l+2)n}$

⋯

⋯

$t_{2n,({\displaystyle \frac{a}{2}}-l+2)n}$

$t_{0,({\displaystyle \frac{a}{2}}-l+2)n+1}$

⋯

$t_{2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l+2)n+1}$

⋮

⋮

$t_{0,({\displaystyle \frac{a}{2}}-l+3)n}$

⋯

$t_{2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l+3)n}$

Similarly to the case where $p=1$, the elements in the first n rows of the main part of the 1-Apéry set are simply moved below the 0-Apéry set to fill the gap. However, the remaining portion is moved to the lower left of the 0-Apéry. Elements beyond the first n rows of the main part are shifted to the right side of the 0-Apéry set by moving them up n rows. The remaining staircase parts are shifted left by $2n+1$ units and up by n units.

In Table 4, by comparing the six candidates

$$\begin{array}{cc}\hfill & t_{2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l+3)n},t_{2n,({\displaystyle \frac{a}{2}}-l+2)n},t_{2(l+1)n-{\displaystyle \frac{3a}{2}}+l-2,({\displaystyle \frac{a}{2}}-l+1)n},\hfill \\ \hfill & t_{4n+1,({\displaystyle \frac{a}{2}}-l)n},t_{2(l+2)n-{\displaystyle \frac{3a}{2}}+l-1,({\displaystyle \frac{a}{2}}-l-1)n},t_{6n+2,({\displaystyle \frac{a}{2}}-l-2)n},\hfill \end{array}$$

we find that $t_{2n,({\displaystyle \frac{a}{2}}-l+2)n}$ is the largest element of the 2-Apéry set when ${\displaystyle \frac{3a}{4l}}-{\displaystyle \frac{l-3}{2l}}\le n\le {\displaystyle \frac{3a-2l+2}{2(2l-1)}}$ ($l\ge 2$) or ${\displaystyle \frac{3a}{4}}+1\le n\le {\displaystyle \frac{3a}{2}}$ ($l=1$); $t_{2ln-{\displaystyle \frac{3a}{2}}+l-3,({\displaystyle \frac{a}{2}}-l+3)n}$ is the largest element of the 2-Apéry set when ${\displaystyle \frac{3a-2l+3}{2(2l-1)}}\le n\le {\displaystyle \frac{3a}{4(l-1)}}-{\displaystyle \frac{l-3}{2(l-1)}}$ ($l\ge 2$) or $n\ge {\displaystyle \frac{3a}{2}}+1$ ($l=1$). Therefore, by Lemma 1 (2) we have

$$\begin{array}{cc}\hfill & g_2(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & =\left\{\begin{array}{cc}\left(2n\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}-l+2\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathrm{if}{\displaystyle \frac{3a}{4l}}-{\displaystyle \frac{l-3}{2l}}\le n\le {\displaystyle \frac{3a-2l+2}{2(2l-1)}}\left(l\ge 2\right);\hfill & \\ \left(2ln-{\displaystyle \frac{3a}{2}}+l-3\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}-l+3\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathrm{if}{\displaystyle \frac{3a-2l+3}{2(2l-1)}}\le n\le {\displaystyle \frac{3a}{4(l-1)}}-{\displaystyle \frac{l-3}{2(l-1)}}\left(l\ge 2\right),\hfill & \\ \left(2n\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}+1\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathrm{if}{\displaystyle \frac{3a}{4}}+1\le n\le {\displaystyle \frac{3a}{2}};\hfill & \\ \left(2n-{\displaystyle \frac{3a}{2}}-2\right)S_{a,n+1}+\left({\displaystyle \frac{a}{2}}+2\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathrm{if}n\ge {\displaystyle \frac{3a}{2}}+1.\hfill \end{array}\right.\hfill \end{array}$$

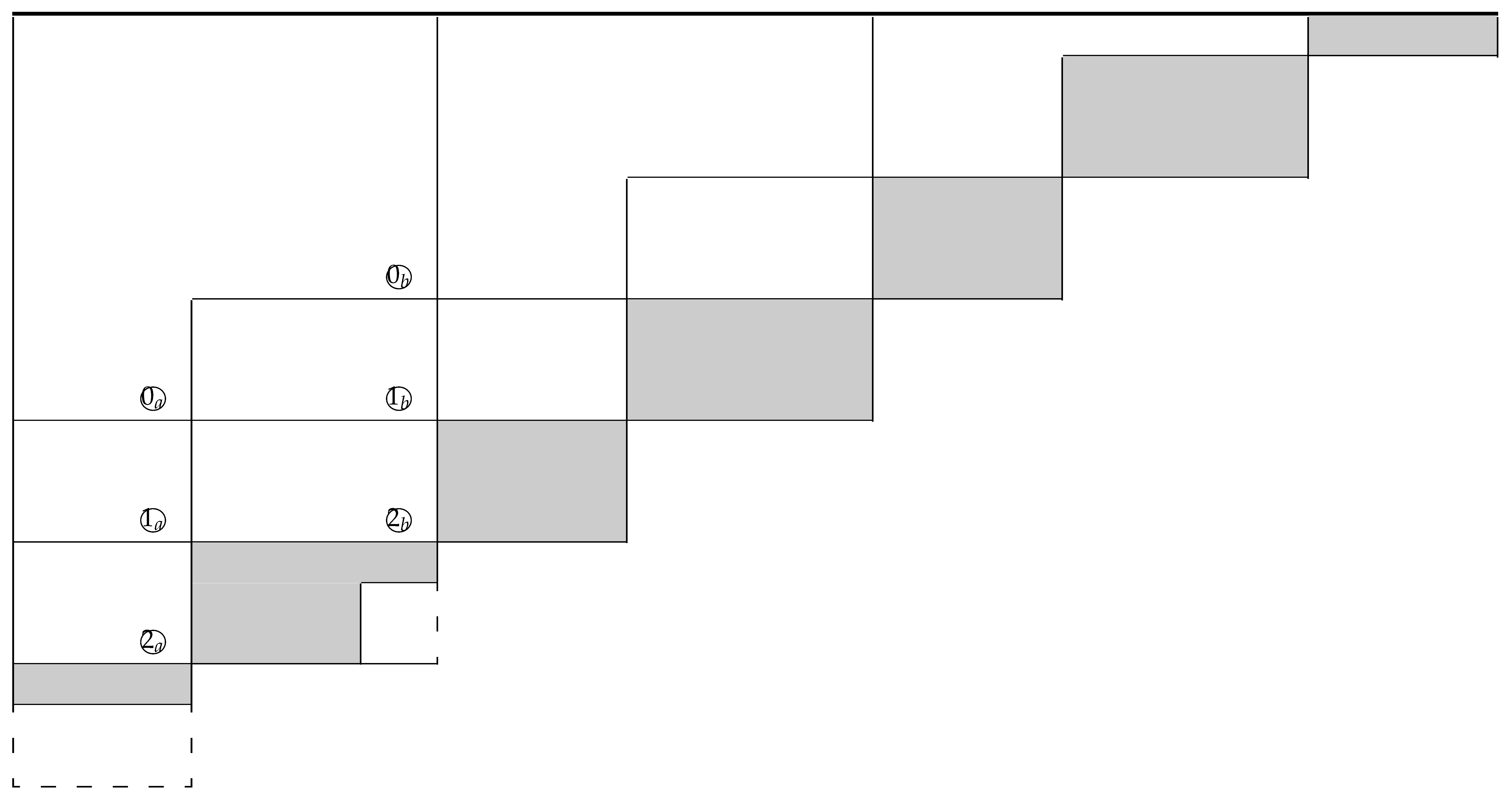
Similarly, for $p=3,4,\dots$, the elements of the p-Apéry set can also be determined from those of the ($p-1$)-Apéry set. However, the same pattern cannot be continued. As seen in Table 5, the situation is changed. $\overline{)0_a}$, $\overline{)1_a}$ and $\overline{)2_a}$ indicate the position of the largest elements of the 0-, 1- and 2-Apéry sets, respectively, when ${\displaystyle \frac{3a-2l+3}{2(2l-1)}}\le n\le {\displaystyle \frac{3a}{4(l-1)}}-{\displaystyle \frac{l-3}{2(l-1)}}$ ($l\ge 2$) or $n\ge {\displaystyle \frac{3a}{2}}+1$ ($l=1$); and $\overline{)0_b}$, $\overline{)1_b}$ and $\overline{)2_b}$ when ${\displaystyle \frac{3a}{4l}}-{\displaystyle \frac{l-3}{2l}}\le n\le {\displaystyle \frac{3a-2l+2}{2(2l-1)}}$ ($l\ge 2$) or ${\displaystyle \frac{3a}{4}}+1\le n\le {\displaystyle \frac{3a}{2}}$ ($l=1$). We can see that no element of the Apéry set can exist at the expected location for the largest value. As can be seen in Table 5, the actual elements of the 3-Apéry set (in this example) are located in the gray area and do not fall in the expected dotted area. Then, in general, for $p\ge {\displaystyle \frac{a}{2}}-l+1$, the same formula cannot be applied, and the situation becomes more and more complicated, though the p-Frobenius numbers should exist.

Table 5. ${\mathrm{Ap}}_3(S_{n,a},S_{n+1,a},S_{n+2,a}).$

Therefore, for a general integer p with $0\le p\le {\displaystyle \frac{a}{2}}-l$, we have the following theorem. Note that while the case where a is odd is not exactly the same, analogous arguments can still be applied.

Theorem 2.

When a is even with $a\ge 6$ and $n\ge 2$, for integers $0\le p\le {\displaystyle \frac{a}{2}}-l$ and $l\ge 2$

$$\begin{array}{cc}\hfill & g_p(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & =\left\{\begin{array}{cc}\left(2n\right)S_{a,n+1}+\left(p+{\displaystyle \frac{a}{2}}-l\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathit{if}{\displaystyle \frac{3a}{4l}}-{\displaystyle \frac{l-3}{2l}}\le n\le {\displaystyle \frac{3a-2l+2}{2(2l-1)}};\hfill & \\ \left(2ln-{\displaystyle \frac{3a}{2}}-1\right)S_{a,n+1}+\left(p+{\displaystyle \frac{a}{2}}-l+1\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathit{if}{\displaystyle \frac{3a-2l+3}{2(2l-1)}}\le n\le {\displaystyle \frac{3a}{4(l-1)}}-{\displaystyle \frac{l-3}{2(l-1)}},\hfill \end{array}\right.\hfill \end{array}$$

for integers $n\ge 2$ and $0\le p\le {\displaystyle \frac{a}{2}}-1$

$$\begin{array}{cc}\hfill & g_p(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & =\left\{\begin{array}{cc}\left(2n\right)S_{a,n+1}+\left(p+{\displaystyle \frac{a}{2}}-1\right)n{S}_{a,n+2}-S_{a,n}\hfill & \mathit{if}{\displaystyle \frac{3a}{4}}+1\le n\le {\displaystyle \frac{3a}{2}};\hfill \\ \left(2n-{\displaystyle \frac{3a}{2}}-2\right)S_{a,n+1}+\left(p+{\displaystyle \frac{a}{2}}\right)n{S}_{a,n+2}-S_{a,n}\hfill & \mathit{if}n\ge {\displaystyle \frac{3a}{2}}+1.\hfill \end{array}\right.\hfill \end{array}$$

When a is odd with $a\ge 5$ and $n\ge 2$, for $0\le p\le {\displaystyle \frac{a-2l+1}{2}}$ with $l\ge 2$

$$\begin{array}{cc}\hfill & g_p(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & =\left\{\begin{array}{cc}\left(2n\right)S_{a,n+1}+\left(p+{\displaystyle \frac{a-2l+1}{2}}\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathit{if}{\displaystyle \frac{3a-2l+7}{2(2l-1)}}\le n\le {\displaystyle \frac{3a-2l+3}{4(l-1)}};\hfill & \\ \left((2l-1)n-{\displaystyle \frac{3a-2l+7}{2}}\right)S_{a,n+1}+\left(p+{\displaystyle \frac{a-2l+3}{2}}\right)n{S}_{a,n+2}-S_{a,n}\hfill & \\ \mathrm{if}{\displaystyle \frac{3a-2l+4}{4(l-1)}}\le n\le {\displaystyle \frac{3a-2l+7}{2(2l-3)}},\hfill \end{array}\right.\hfill \end{array}$$

for integers $n\ge 2$ and $0\le p\le {\displaystyle \frac{a-1}{2}}$

$$\begin{array}{cc}\hfill & g_p(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & =\left(2n\right)S_{a,n+1}+\left(p+{\displaystyle \frac{a-1}{2}}\right)n{S}_{a,n+2}-S_{a,n}\mathit{if}n\ge {\displaystyle \frac{3a+5}{2}}.\hfill \end{array}$$

Remark 3.

When a is even, the first and second conditions in the first identity are equivalent to

$${\displaystyle \frac{3a+6}{4n+2}}\le l\le {\displaystyle \frac{3a+2n+2}{4n+2}}\mathit{and}{\displaystyle \frac{3a+2n+3}{4n+2}}\le l\le {\displaystyle \frac{3a+4n+6}{4n+2}},$$

respectively. When a is odd, the first and second conditions in the third identity are equivalent to

$${\displaystyle \frac{3a+2n+7}{4n+2}}\le l\le {\displaystyle \frac{3a+4n+3}{4n+2}}\mathit{and}{\displaystyle \frac{3a+4n+4}{4n+2}}\le l\le {\displaystyle \frac{3a+6n+7}{4n+2}},$$

respectively.

7. $\mathit{p}$-Genus

Let a be even with $a\ge 4$. Observing Table 1, Table 3 and Table 4, the sum of the elements of the p-Apéry set is made by dividing into three parts: all the left sides of the staircase, all the right sides of the staircase, and the main part. For $0\le p\le {\displaystyle \frac{a}{2}}-l$ with $l\ge 1$ we have

$$\begin{array}{cc}\hfill & \sum _{j=0}^{S_{a,n}-1}{m}_j^{\left(p\right)}\hfill \\ \hfill & =\sum _{\kappa =0}^{p-1}\sum _{y=(2n+1)\kappa }^{(2n+1)\kappa +2ln-{\displaystyle \frac{3a}{2}}+l-3}\sum _{z=(p+{\displaystyle \frac{a}{2}}-2\kappa -l)n+1}^{(p+{\displaystyle \frac{a}{2}}-2\kappa -l+1)n}{t}_{y,z}\hfill \\ \hfill & +\sum _{\kappa =0}^{p-1}\sum _{y=(2n+1)\kappa +2ln-{\displaystyle \frac{3a}{2}}+l-2}^{(2n+1)(\kappa +1)-1}\sum _{z=(p+{\displaystyle \frac{a}{2}}-2\kappa -l-1)n+1}^{(p+{\displaystyle \frac{a}{2}}-2\kappa -l)n}{t}_{y,z}\hfill \\ \hfill & +\sum _{y=p(2n+1)}^{p(2n+1)+2n}\sum _{z=0}^{({\displaystyle \frac{a}{2}}-p-l)n}{t}_{y,z}+\sum _{y=p(2n+1)}^{p(2n+1)+2ln-{\displaystyle \frac{3a}{2}}+l-3}\sum _{z=({\displaystyle \frac{a}{2}}-p-l)n+1}^{({\displaystyle \frac{a}{2}}-p-l+1)n}{t}_{y,z}\hfill \\ \hfill & ={\displaystyle \frac{S_{a,n}}{8}}\left(n\right(2(a^2+4a+4l(l-1))n^2+(3a^2-2(6l-5)a+4(3l-1)(l-2))n\hfill \\ \hfill & +a^2-2(6l-5)a+4(l-2)(l-3))\hfill \\ \hfill & +4(2n+1)\left(2S_{a,n+1}-n(n+1)\right)p-4n(n+1)(2n+1)p^2).\hfill \end{array}$$

By Lemma 1 (3), we have

$$\begin{array}{cc}\hfill & n_p(S_{a,n},S_{a,n+1},S_{a,n+2})={\displaystyle \frac{1}{S_{a,n}}}\sum _{j=0}^{S_{a,n}-1}{m}_j^{\left(p\right)}-{\displaystyle \frac{S_{a,n}-1}{2}}\hfill \\ \hfill & ={\displaystyle \frac{1}{8}}\left(n\right(2(a^2+4a+4l(l-1))n^2+(3a^2-6(2l-1)a+4(3l-1)(l-2))n\hfill \\ \hfill & +a^2-2(6l-7)a+4(l-2)(l-3))\hfill \\ \hfill & +4(2n+1)\left(2S_{a,n+1}-n(n+1)\right)p-4n(n+1)(2n+1)p^2).\hfill \end{array}$$

When a is odd with $a\ge 5$, for $0\le p\le {\displaystyle \frac{a-2l+1}{2}}$ with $l\ge 1$ we have

$$\begin{array}{cc}\hfill & \sum _{j=0}^{S_{a,n}-1}{m}_j^{\left(p\right)}\hfill \\ \hfill & =\sum _{\kappa =0}^{p-1}\sum _{y=(2n+1)\kappa }^{(2n+1)\kappa +(2l-1)n-{\displaystyle \frac{3a-2l+7}{2}}}\sum _{z=(p+{\displaystyle \frac{a-2l+1}{2}}-2\kappa )n+1}^{(p+{\displaystyle \frac{a-2l+3}{2}}-2\kappa )n}{t}_{y,z}\hfill \\ \hfill & +\sum _{\kappa =0}^{p-1}\sum _{y=(2n+1)\kappa +(2l-1)n-{\displaystyle \frac{3a-2l+5}{2}}}^{(2n+1)(\kappa +1)-1}\sum _{z=(p+{\displaystyle \frac{a-2l-1}{2}}-2\kappa )n+1}^{(p+{\displaystyle \frac{a-2l+1}{2}}-2\kappa )n}{t}_{y,z}\hfill \\ \hfill & +\sum _{y=p(2n+1)}^{p(2n+1)+2n}\sum _{z=0}^{({\displaystyle \frac{a-2l+1}{2}}-p)n}{t}_{y,z}+\sum _{y=p(2n+1)}^{p(2n+1)+(2l-1)n-{\displaystyle \frac{3a-2l+7}{2}}}\sum _{z=({\displaystyle \frac{a-2l+1}{2}}-p)n+1}^{({\displaystyle \frac{a-2l+3}{2}}-p)n}{t}_{y,z}\hfill \\ \hfill & ={\displaystyle \frac{S_{a,n}}{8}}\left(n\right(2((a+1)(a+3)+4l(l-2))n^2+(3a^2-4(3l-4)a+(2l-5)(6l-5))n\hfill \\ \hfill & +a^2-4(3l-4)a+(2l-5)(2l-7))\hfill \\ \hfill & +4(2n+1)\left(2S_{a,n+1}-n(n+1)\right)p-4n(n+1)(2n+1)p^2).\hfill \end{array}$$

By Lemma 1 (3), we have

$$\begin{array}{cc}\hfill & n_p(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & ={\displaystyle \frac{1}{8}}\left(n\right(2((a+1)(a+3)+4l(l-2))n^2+(3a^2-12(l-1)a+(2l-5)(6l-5))n\hfill \\ \hfill & +a^2-4(3l-5)a+(2l-5)(2l-7))\hfill \\ \hfill & +4(2n+1)\left(2S_{a,n+1}-n(n+1)\right)p-4n(n+1)(2n+1)p^2).\hfill \end{array}$$

Theorem 3.

When a is even with $a\ge 4$ and $n\ge 2$, for $0\le p\le {\displaystyle \frac{a}{2}}-l$ with $l\ge 1$,

$$\begin{array}{cc}\hfill & n_p(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & ={\displaystyle \frac{1}{8}}\left(n\right(2(a^2+4a+4l(l-1))n^2+(3a^2-6(2l-1)a+4(3l-1)(l-2))n\hfill \\ \hfill & +a^2-2(6l-7)a+4(l-2)(l-3))\hfill \\ \hfill & +4(2n+1)\left(2S_{a,n+1}-n(n+1)\right)p-4n(n+1)(2n+1)p^2).\hfill \end{array}$$

When a is odd with $a\ge 5$ and $n\ge 2$, for $0\le p\le {\displaystyle \frac{a-2l+1}{2}}$ with $l\ge 1$,

$$\begin{array}{cc}\hfill & n_p(S_{a,n},S_{a,n+1},S_{a,n+2})\hfill \\ \hfill & ={\displaystyle \frac{1}{8}}\left(n\right(2((a+1)(a+3)+4l(l-2))n^2+(3a^2-12(l-1)a+(2l-5)(6l-5))n\hfill \\ \hfill & +a^2-4(3l-5)a+(2l-5)(2l-7))\hfill \\ \hfill & +4(2n+1)\left(2S_{a,n+1}-n(n+1)\right)p-4n(n+1)(2n+1)p^2).\hfill \end{array}$$

8. Examples

When $(a,n)=(22,9)$, by our remark of Theorem 2, we see that

$$2\in \left[{\displaystyle \frac{36}{19}},{\displaystyle \frac{43}{19}}\right]$$

and there is no integer in the interval $\left[{\displaystyle \frac{87}{38}},{\displaystyle \frac{54}{19}}\right]$, the first identity of the even case in Theorem 2 is applied with $l=2$. Then, for $0\le p\le 9={\displaystyle \frac{22}{2}}-2$

$$\begin{array}{cc}\hfill & g_p(S_{22,9},S_{22,10},S_{22,11})=g_p(1585,1981,2421)\hfill \\ \hfill & =18S_{22,10}+22(p+9)S_{22,11}-S_{22,10}.\hfill \end{array}$$

The first several terms are

$$\begin{array}{c}{\left\{g_p(S_{22,9},S_{22,10},S_{22,11})\right\}}_{p=0}^9=230174,251963,273752,295541,\hfill \\ \hfill 317330,339119,360908,382697,404486,426275.\end{array}$$

However, when $p=10$, the identity does not give the correct value of 442125 but the wrong value of 448064.

Concerning the p-genus, by the first identity of Theorem 3, we have

$$\begin{array}{c}{\left\{n_p(S_{22,9},S_{22,10},S_{22,11})\right\}}_{p=0}^9=116694,152623,186842,219351,\hfill \\ \hfill 250150,279239,306618,332287,356246,378495.\end{array}$$

When $(a,n)=(13,11)$, by our remark of Theorem 2, we see that there is no integer in the interval $\left[{\displaystyle \frac{34}{23}},{\displaystyle \frac{43}{23}}\right]$ and

$$2\in \left[{\displaystyle \frac{87}{46}},{\displaystyle \frac{56}{23}}\right],$$

the second identity of the odd case in Theorem 2 is applied with $l=2$. Then, for $0\le p\le 5={\displaystyle \frac{13-3}{2}}$ we have

$${\left\{g_p(S_{13,11},S_{13,12},S_{13,13})\right\}}_{p=0}^5=153087,175406,197725,220044,242363,264682.$$

Concerning the p-genus, by the third identity of Theorem 3, we have

$${\left\{n_p(S_{13,11},S_{13,12},S_{13,13})\right\}}_{p=0}^5=79904,116359,149778,180161,207508,231819.$$

9. Final Comments

One should not assume that the results in this paper are quite similar to previous works. Generally, finding explicit formulae for the Frobenius number for sequences or tuples with three or more variables is quite challenging. When $p>0$, the situation becomes even more difficult. For example, triangular numbers are represented by similar quadratic polynomials. Explicit formulae for the p-Frobenius number of consecutive triangular numbers have been successfully provided in [20,25], and the case for squares has also been addressed [32]. However, no explicit formulae have been established for pentagonal, hexagonal, heptagonal, and octagonal numbers, which are given by $n(kn-k+2)/2$ for $k=5,6,7$ and 8, respectively.

For example, triangular numbers are given as a polynomial of similar quadratic polynomials too. The explicit formulae of the p-Frobenius number of consecutive triangular numbers have been successful in being given in [20,25] and the case of squares is also possible [32]. But nothing has been known for pentagonal, hexagonal, heptagonal, octagonal numbers given by $n(kn-k+2)/2$ for $k=5,6,7,8$, respectively.

It would also be interesting to see whether we can derive general explicit formulae for the Frobenius numbers of other well-known polynomials, such as Hermite polynomials, Frobenius–Euler polynomials or Bernoulli–Gegenbauer polynomials (see, for instance, [33,34]).