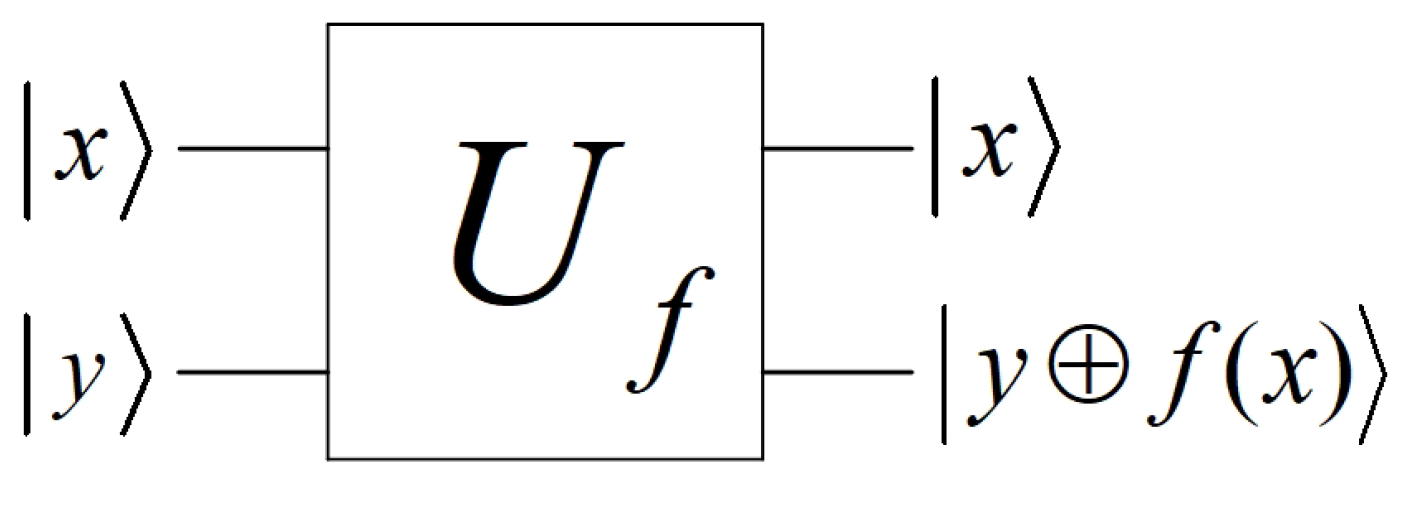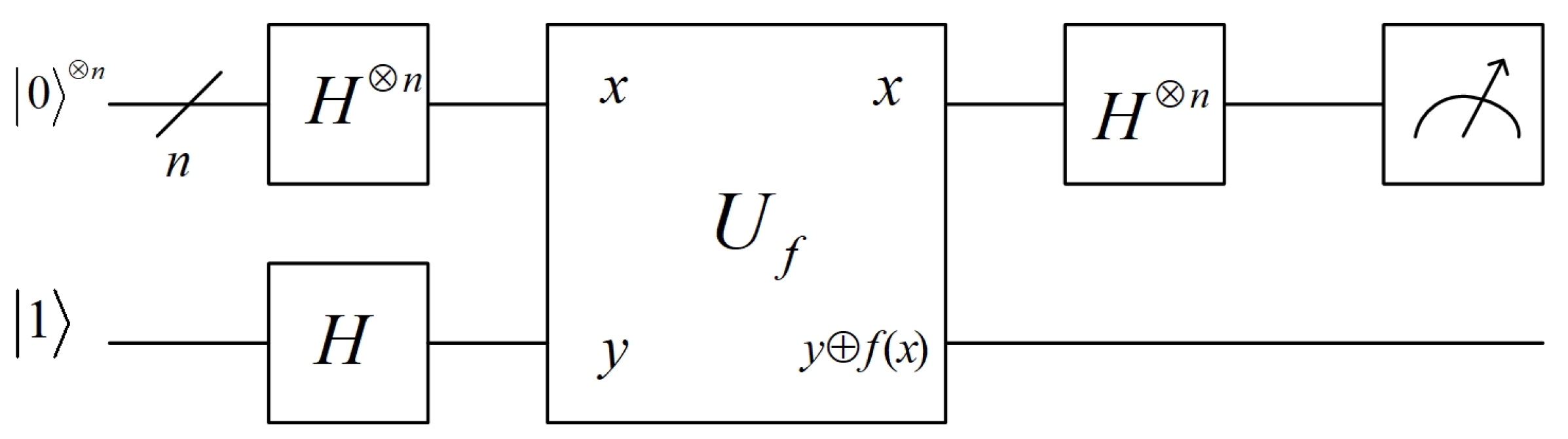Quantum Truncated Differential and Boomerang Attack

Abstract

In order to design quantum-safe block ciphers, it is crucial to investigate the application of quantum algorithms to cryptographic analysis tools. In this study, we use the Bernstein–Vazirani algorithm to enhance truncated differential cryptanalysis and boomerang cryptanalysis. We first propose a quantum algorithm for finding truncated differentials, then rigorously prove that the output truncated differentials must have high differential probability for the vast majority of keys in the key space. Subsequently, based on this algorithm, we design a quantum algorithm for finding boomerang distinguishers. The quantum circuits of the two proposed quantum algorithms contain only polynomial quantum gates and qubits. Compared with classical tools for searching truncated differentials or boomerang distinguishers, the proposed algorithms can maintain the polynomial complexity while fully considering the impact of S-boxes and key scheduling.

1. Introduction

Recently, research on quantum computers has continuously made new progress worldwide. Many scientists, companies and research institutions are committed to utilizing various quantum systems to develop quantum computers. It is foreseen that the successful development of quantum computers will have a profound impact in many fields. Cryptography is one such field.

The two most promising physical implementation schemes for quantum computers are trapped-ion [1] and superconducting circuit [2]. Ion-trap quantum computers have the advantage of great qubit connectivity and small decoherence, while superconducting quantum computers have the advantage of high designability and scalability. In recent years, investigations on ion-trap quantum computers have made great progress [3,4], especially in the improvement of high-fidelity gate [5]. The study of superconducting quantum computers has also made remarkable progress [6,7,8]. Google’s Sycamore quantum computer and IBM’s Eagle quantum computer are both based on superconductivity [9,10]. The power of quantum computers in information processing stems from the novel properties of quantum information that differ from those of classical information. Quantum computers possess the natural feature of parallel computing. When an n-qubit quantum computer processes data, operators actually operate on $2^n$ data states simultaneously. This parallelism may make some problems uncomputable in electronic computers become computable in quantum computers, such as factoring large integers, which is a difficult problem that many public key algorithms are built upon, but may be solved on quantum computers by running Shor’s algorithm [11].

The threats posed by quantum computing to symmetric algorithms have also received considerable attention. The most typical example is Grover’s algorithm [12], which requires only $O\left(\sqrt{M}\right)$ complexity to search an unordered database with M elements, while $O\left(M\right)$ complexity is required in classical computing. Another important algorithm used to attack symmetric schemes is Simon’s algorithm [13]. It was first used for attacking Feistel ciphers  [14,15,16] and EM schemes [14,16]. It was then combined with Grover’s algorithm for extracting the keys of ciphers with FX, Feistel and generalized Feistel structures [17,18,19]. For SPN ciphers, Jaques et al. investigated cryptanalysis of the AES algorithm using Grover’s algorithm [20]. Zhang utilized quantum algorithms to attack generalized Feistel ciphers [21]. Xiang introduced a method for constructing periodic functions and used it to attack LBlock cipher [22]. In addition to the aforementioned quantum algorithms, the Bernstein–Vazirani (BV) algorithm [23] was recently utilized in cryptanalysis [24,25,26,27].

In addition to specific attack strategies, cryptanalytic tools are also crucial for evaluating the security of cryptosystems. In this field, quantum algorithms were first used for differential cryptanalysis [25,28,29] and then for linear cryptanalysis [26,29,30]. Subsequently, quantum collision attacks on hash functions were studied [31,32]. Denisenko analyzed the complexity of quantum differential attack based on the quantum search algorithm [33]. Hosoyamada used quantum algorithms to speed-up classical multidimensional linear attack [34]. Xu et el. applied quantum search algorithm to differential meet-in-the-middle attack [35]. Quantum attacks under this model were also proposed [36,37,38]. Zhang proposed a quantum attack under quantum-related key model against the Sum of Even–Mansour construction [39]. Wu and Feng used BV algorithm to search for related-key differentials and recover key based on quantum counting algorithm [40]. These attacks showcased the superiority of quantum cryptanalytic tools over traditional cryptanalytic tools.

Many quantum attacks on block ciphers are too large in scale to be implemented or even simulated. However, researchers may be able to simulate a small part of the whole quantum attacks. For example, Zhou et al. simulated the quantum circuit of S-boxes instead of the whole cipher when studying the quantum circuit of AES [41]. Qiskit SDK is a powerful open-source tool for the simulations of quantum algorithms. Many small-scale quantum algorithms have been simulated using Qiskit [42,43,44]. LIGHTER-R is another useful tool proposed by Dasu, which can be used to design quantum circuits of Boolean functions [45].

Contributions. In this study, we explore the applications of the Bernstein–Vazirani algorithm to two variants of differential attacks: truncated differential and boomerang attacks. First, we design a quantum algorithm for searching truncated differentials that have a high probability for a large proportion of keys in the key space. Subsequently, based on this algorithm, we construct another quantum algorithm for searching for boomerang distinguishers. We demonstrate the correctness of both quantum algorithms using rigorous proofs. Both quantum algorithms request only polynomial quantum gates and qubits and have the following advantages:

• Quantum adversaries are able to perform the proposed attacks in $Q_1$ model. Namely, there is no need for quantum queries. Compared to many proposed quantum attack algorithms [14,15,16,18,19,46] that require quantum queries, our algorithms are easier to implement.
• Classical cryptanalytic tools for finding truncated differentials with high probability or boomerang distinguishers usually cannot concern all of the details of the involved S-boxes when they are not at a small-scale. The classical tools can only search for truncated differentials or boomerang distinguishers of extremely few rounds when the S-boxes have an 8-bit scale, which is very common in block ciphers. By comparison, our quantum algorithms fully utilize the superiority of quantum computing to improve this issue. They entirely characterized the S-boxes through the accurate implementation of the unitary operator of the block ciphers.
• Classical truncated differential attacks do not involve the key scheduling under the single-key attack model, but our algorithms incorporate the key scheduling into the quantum circuits and thus fully reflect its impact to the differential propagation.

Related works. Paul et al. combined classical boomerang attack with Grover’s algorithm to quantize the traditional boomerang attack [47]. Zhou et al. improved this quantum attack strategy by allowing the retrieval of subkeys from both sides of block ciphers [48]. Boomerang attack includes two stages. The first stage is to find boomerang distinguishers and the second stage is to recover the key using the found distinguishers. The works in [47,48] only focused on the second stage. Both of them studied the use of quantum algorithms for accelerating the retrieval of key. Our work focuses on the first stage and studies the use of quantum algorithms for finding boomerang distinguishers.

2. Preliminaries

The main notations and their definitions are presented in Table 1.

Table 1. Notations.

Notation	Definition
${\mathcal{C}}_{u,v}$	the set containing all Boolean functions mapping u bits to v bits
$\Phi$	the empty set
$S_f(·)$	the Walsh transform of f
$En{c}_k^t$	a t-round block cipher
$En{c}_k^t\left[j\right]$	the j-th component function of $En{c}_k^t$
$S/N$	the ratio of signal to noise
$(\Delta x,\Delta y)$	a differential
$(\overline{\Delta }x,\overline{\Delta }y)$	a truncated differential

2.1. Differential

Throughout this study, $En{c}_k:{\mathbb{F}}_2^n\to {\mathbb{F}}_2^n$ denotes a block cipher, where $k\in {\mathbb{F}}_2^m$ is the master key. $En{c}_k^r=En{c}_{k_r}\circ En{c}_{k_{r-1}}\circ \cdots \circ En{c}_{k_1}$ denotes the r-round iteration of $En{c}_k$. Here $k_1,\cdots$, $k_r$ denote the round keys generated from k according to the key scheduling.

Suppose x and $x^{\prime }$ are two plaintexts, and $En{c}_k^r\left(x\right)=y$, $En{c}_k^r\left(x^{\prime }\right)=y^{\prime }$. We call $\Delta y=y^{\prime }\oplus y$ an output difference and $\Delta x=x^{\prime }\oplus x$ an input difference. $(\Delta x,\Delta y)$ is defined as a differential of $En{c}_k^r$. The probability of differential $(\Delta x,\Delta y)$ is defined as

$$\begin{array}{cc}\hfill \underset{x\leftarrow {\mathbb{F}}_2^n}{Pr}[\Delta x\stackrel{En{c}_k^r}{\to }\Delta y]& =\underset{x\leftarrow {\mathbb{F}}_2^n}{Pr}[En{c}_k^r(x\oplus \Delta x)\oplus En{c}_k^r\left(x\right)=\Delta y]\hfill \\ \hfill & ={\displaystyle \frac{1}{2^n}}\left|\{x\in {\mathbb{F}}_2^n|En{c}_k^r(x\oplus \Delta x)\oplus En{c}_k^r\left(x\right)=\Delta y\}\right|.\hfill \end{array}$$

If this value is equal to p, we call $(\Delta x,\Delta y)$ a p-probability differential of $En{c}_k^r$.

Differential attack was proposed in 1991 and is one of the most commonly used cryptanalysis methods [49]. It utilizes a high-probability differential to break block ciphers. Let $En{c}_k^t=En{c}_{k_t}\circ En{c}_{k_{t-1}}\circ \cdots \circ En{c}_{k_1}$ be the t-round iteration of $En{c}_k$, where $1<t<r$. $En{c}_k^t$ is a reduced cipher of $En{c}_k^r$. In differential attacks the adversaries first search for a differential of $En{c}_k^t$ having high probability, then use this differential to screen out the right subkey involved in the last $r-t$ rounds of $En{c}_k^r$.

Variants of differential cryptanalysis have been proposed, including impossible differential attacks [50], truncated differential attacks [51] and boomerang attacks [52]. These attacks all utilize the no-random statistical properties of the ciphertext differences when specifying the plaintext differences.

Inspired by the concept of differential of block ciphers, we define the differential of Boolean functions. Let ${\mathcal{C}}_{u,v}$ be a set containing all Boolean functions that map u bits to v bits, where $u,v$ are arbitrary positive integers. For any $f\in {\mathcal{C}}_{u,v}$ and $x,x^{\prime }\in {\mathbb{F}}_2^u$, let $f\left(x\right)=y\in {\mathbb{F}}_2^v$ and $f\left(x^{\prime }\right)=y^{\prime }\in {\mathbb{F}}_2^v$. We call $\Delta y=y^{\prime }\oplus y$ an output difference and $\Delta x=x^{\prime }\oplus x$ an input difference. $(\Delta x,\Delta y)$ is defined as a differential of f. The probability of differential $(\Delta x,\Delta y)$ is defined as

$$\begin{array}{cc}\hfill \underset{x\leftarrow {\mathbb{F}}_2^u}{Pr}[\Delta x\stackrel{f}{\to }\Delta y]& =\underset{x\leftarrow {\mathbb{F}}_2^u}{Pr}[f(x\oplus \Delta x)\oplus f\left(x\right)=\Delta y].\hfill \end{array}$$

If this value is equal to p, we call $(\Delta x,\Delta y)$ a p-probability differential of f. Especially, for any function f in ${\mathcal{C}}_{u,1}$, we define two sets

$$\begin{array}{cc}\hfill D_f^0& =\{\Delta x\in {\mathbb{F}}_2^u|f\left(x\right)\oplus f(x\oplus \Delta x)=0,\forall x\in {\mathbb{F}}_2^u\},\hfill \\ \hfill D_f^1& =\{\Delta x\in {\mathbb{F}}_2^u|f\left(x\right)\oplus f(x\oplus \Delta x)=1,\forall x\in {\mathbb{F}}_2^u\}.\hfill \end{array}$$

Let $D_f=D_f^0\cup D_f^1$. The vectors in $D_f$ are called complete differentials of f. For any vector $\Delta x\in D_f^i$ ($i\in \{0,1\}$), $(\Delta x,i)$ is obviously a 1-probability differential. For any $\Delta x\notin D_f^i$, $\Delta x$ cannot form a 1-probability differential of f as an input difference.

2.2. Quantum Computing

In quantum computing theory, information is stored in qubits. A qubit can be realized by any two-level quantum system, such as polarized photons. It is an analogue of a classical bit, but besides the states $|0⟩$ and $|1⟩$, it can also be in a state that is a linear combination of $|0⟩$ and $|1⟩$:

$$|\psi ⟩=\alpha |0⟩+\beta |1⟩,$$

where $\alpha$ and $\beta$ can be any complex numbers that satisfy ${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$. It is usually called a superposition state. Multiple qubits are combined via tensor product. Suppose the first qubit is in the state $|{\psi }_1⟩={\alpha }_1|0⟩+{\beta }_1|1⟩$, the second qubit is in the state $|{\psi }_2⟩={\alpha }_2|0⟩+{\beta }_2|1⟩$, then the system of these two qubits is in the state

$$\begin{array}{cc}\hfill |{\psi }_1⟩\otimes |{\psi }_2⟩& =\left({\alpha }_1\right|0⟩+{\beta }_1|1⟩)\otimes \left({\alpha }_2\right|0⟩+{\beta }_2|1⟩)\hfill \\ & ={\alpha }_1{\alpha }_2|00⟩+{\alpha }_1{\beta }_2|01⟩+{\beta }_1{\alpha }_2|10⟩+{\beta }_1{\beta }_2|11⟩.\hfill \end{array}$$

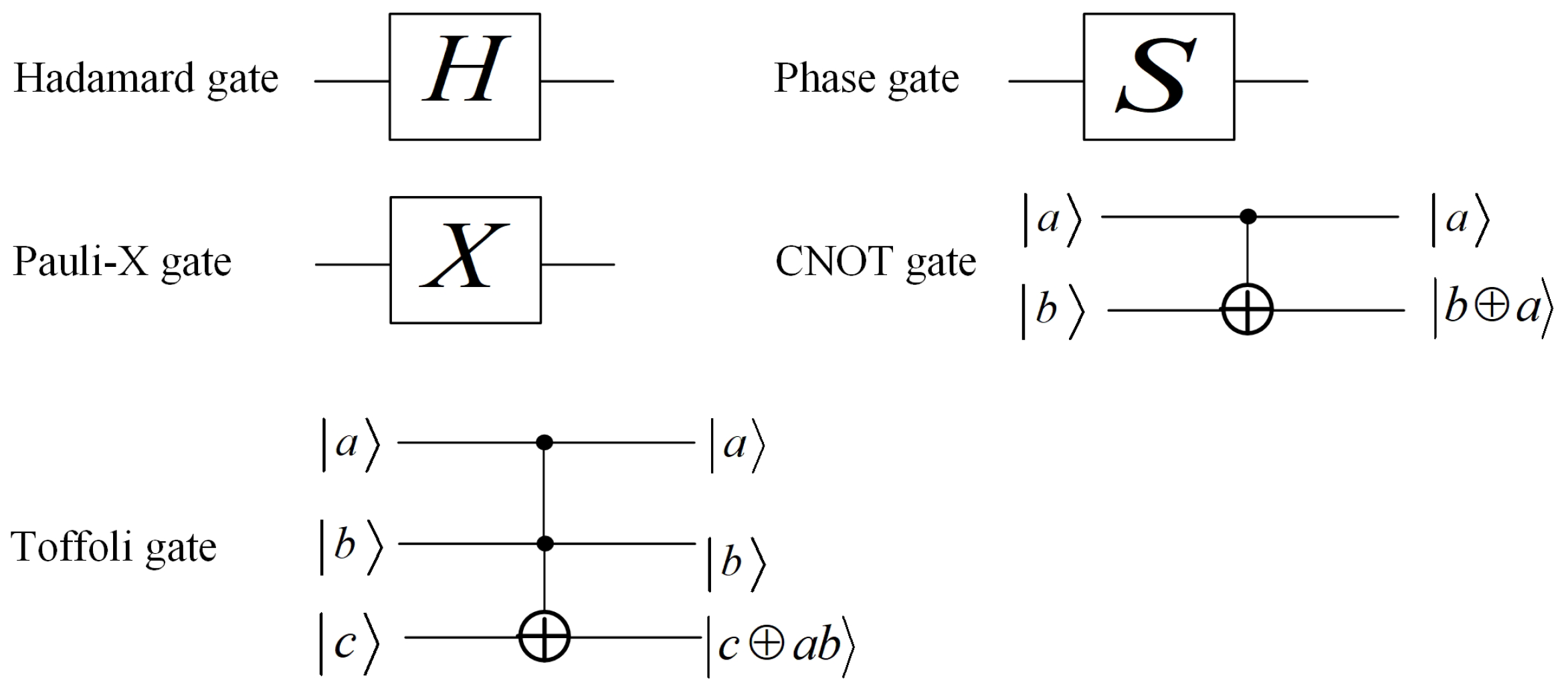
Classical bits can be manipulated by logic gates such as NAND and AND gates. Similarly, qubits are manipulated by quantum gates. Common quantum gates include Pauli-X gate (X gate), Phase gate (S gate), Hadamard gate (H gate), Controlled-NOT gate ($CNOT$ gate) and Toffoli gate. These gates act according to following rules:

$$\begin{array}{cc}\hfill & \begin{array}{cc}X|0⟩=|1⟩,\hfill & X|1⟩=|0⟩,\hfill \\ S|0⟩=|0⟩,\hfill & S|1⟩=e^{i\pi /4}|1⟩,\hfill \\ H|0⟩={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|0⟩+|1⟩),\hfill & H|1⟩={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|0⟩-|1⟩),\hfill \end{array}\hfill \\ \hfill & CNOT|a⟩|b⟩=|a⟩|b\oplus a⟩,\forall a,b\in \{0,1\},\hfill \\ \hfill & Toffoli|a⟩|b⟩|c⟩=|a⟩|b\oplus ⟩|c\oplus ab⟩,\forall a,b,c\in \{0,1\}.\hfill \end{array}$$

These quantum gates are represented in quantum circuits as in Figure 1. A collection of quantum gates interlinked by quantum wires is called a quantum circuit.

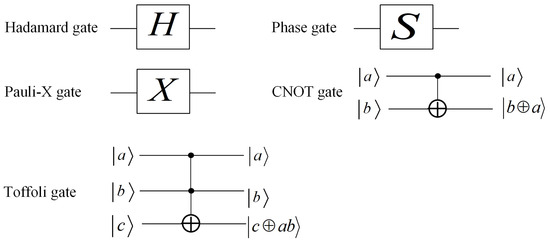
Figure 1. The notation of common quantum gates.

Define $H^{\otimes n}=H\otimes H\otimes \cdots \otimes H$. $H^{\otimes n}$ is the tensor product of n Hadamard gates and

$$H^{\otimes n}{|0⟩}^{\otimes n}={\displaystyle \frac{1}{\sqrt{2^n}}}\left(\right|0⟩+{|1⟩)}^{\otimes n}={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{x\in {\mathbb{F}}_2^n}|x⟩.$$

The $2^n$ states $|00\cdots 00⟩,|00\cdots 01⟩,\cdots$, $|11\cdots 10⟩,|11\cdots 11⟩$ are all called computational basis states. Applying quantum gate $H^{\otimes n}$ on a initial state ${|0⟩}^{\otimes n}$ yields a superposition of all computational basis states.

For any $f\in {\mathcal{C}}_{u,v}$, a quantum circuit realizes f is equivalent to realizing the following operator

$$\begin{array}{c}\hfill U_f:\sum _{x,y}|x⟩|y⟩\to \sum _{x,y}|x⟩|y\oplus f\left(x\right)⟩.\end{array}$$

$U_f$ can be integrated into quantum circuits as presented in Figure 2.

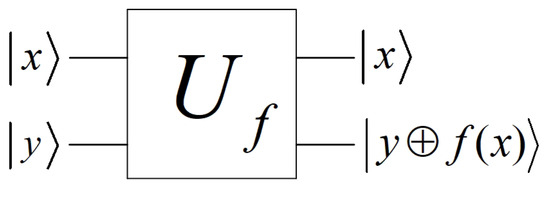
Figure 2. Quantum gate $U_f$.

When quantum state ${\sum }_{x\in {\mathbb{F}}_2^n}{\alpha }_x|x⟩$ is measured on the computational basis states, the probability of outputting x is equal to $|{\alpha }_x{|}^2$. If ${\alpha }_x=0$, the output is definitely not x. Any block cipher $En{c}^r$ can be efficiently realized using a quantum circuit. Namely, there is a quantum circuit with polynomial-complexity taking a state of plaintexts and master keys as input, and outputting the corresponding ciphertexts, realizing the unitary operator

$$U_{En{c}^r}:\sum _{{\displaystyle \genfrac{}{}{0pt}{}{k\in {\mathbb{F}}_2^m}{x,y\in {\mathbb{F}}_2^n}}}|k⟩|x⟩|y⟩\to \sum _{{\displaystyle \genfrac{}{}{0pt}{}{k\in {\mathbb{F}}_2^m}{x,y\in {\mathbb{F}}_2^n}}}|k⟩|x⟩|y\oplus En{c}_k^r\left(x\right)⟩.$$

All quantum circuits can be realized using only the gates in some universal gate set [53], such as $\{{\displaystyle \frac{\pi }{8}},CNOT,Phase,H\}$. Thus, $En{c}^r$ can be realized using a quantum circuit containing only polynomial universal gates. Let the total amount of quantum universal gates in this circuit be $|En{c}^r{|}_Q$. $U_{En{c}^r}$ can be integrated into the quantum circuits as shown in Figure 3.

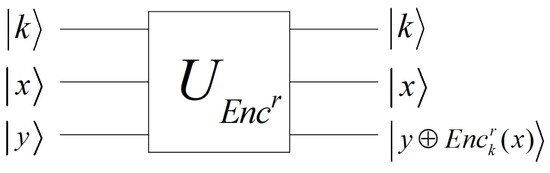
Figure 3. Quantum gate $U_{En{c}^r}$.

Two models have been proposed to describe quantum adversaries: the $Q_1$ and $Q_2$ models [54,55,56]. $Q_1$ adversaries can perform local quantum operations but can merely make queries classically to the cryptography primitives. In addition to classical queries and local quantum operations, $Q_2$ adversaries can also query the quantum oracles of the cryptography primitives. $Q_2$ model is more demanding because it is difficult to achieve the quantum oracles of cryptography primitives in practice.

2.3. Bernstein–Vazirani Algorithm

Bernstein–Vazirani (BV) algorithm [23] was designed to solve the problem: $s\in {\{0,1\}}^n$ being a secret vector, with a quantum circuit of function $f\left(x\right)=s·x$, how to obtain the value of s. BV algorithm runs as follows:

1.

Implement Hadamard transform $H^{(n+1)}$ on $|{\psi }_0{⟩=|0⟩}^{\otimes n}|1⟩$, giving

$$|{\psi }_1⟩=\sum _{x\in {\mathbb{F}}_2^n}{\displaystyle \frac{|x⟩}{\sqrt{2^n}}}·{\displaystyle \frac{|0⟩-|1⟩}{\sqrt{2}}}.$$

2.

Using the quantum circuit of f to get

$$|{\psi }_2⟩=\sum _{x\in {\mathbb{F}}_2^n}{\displaystyle \frac{{(-1)}^{f\left(x\right)}|x⟩}{\sqrt{2^n}}}{\displaystyle \frac{|0⟩-|1⟩}{\sqrt{2}}}.$$

3.

Discarding the unentangled last qubit, perform Hadamard operator $H^{\left(n\right)}$ on the remaining qubits, getting

$$\begin{array}{c}\hfill |{\psi }_3⟩=\sum _{y\in {\mathbb{F}}_2^n}({\displaystyle \frac{1}{2^n}}\sum _{x\in {\mathbb{F}}_2^n}{(-1)}^{f\left(x\right)+y·x})|y⟩.\end{array}$$

(1)

Since $f\left(x\right)=s·x$, we have

$$\begin{array}{cc}\hfill |{\psi }_3⟩& =\sum _{y\in {\mathbb{F}}_2^n}({\displaystyle \frac{1}{2^n}}\sum _{x\in {\mathbb{F}}_2^n}{(-1)}^{(s\oplus y)·x})|y⟩=|s⟩.\hfill \end{array}$$

Therefore, measuring $|{\psi }_3⟩$ gives the value of s.

For any function $f:{\mathbb{F}}_2^n\to {\mathbb{F}}_2$ in ${\mathcal{C}}_{n,1}$, the Walsh transform is defined as the function

$$\begin{array}{cc}\hfill S_f:{\mathbb{F}}_2^n& ⟶{\mathbb{F}}_2\hfill \\ \hfill u& ⟶S_f\left(u\right)={\displaystyle \frac{1}{2^n}}\sum _{x\in {\mathbb{F}}_2^n}{(-1)}^{f\left(x\right)+u·x}.\hfill \end{array}$$

Equation (1) shows that, if BV algorithm is run on a general function $f\in {\mathcal{C}}_{n,1}$, the final quantum state without measured will be

$$\sum _{y\in {\mathbb{F}}_2^n}{S}_f\left(y\right)|y⟩,$$

where $S_f(·)$ is the Walsh transform of f. When this state is measured, the probability of $y\in {\mathbb{F}}_2^n$ being output is $S_f{\left(y\right)}^2$. Thus, BV algorithm running on f must output y such that $S_f\left(y\right)\ne 0$.

Figure 4 shows the circuit of BV algorithm. BV algorithm needs totally $2n+1+{\left|f\right|}_Q$ universal gates. The corresponding quantum circuit requires $n+1$ qubits.

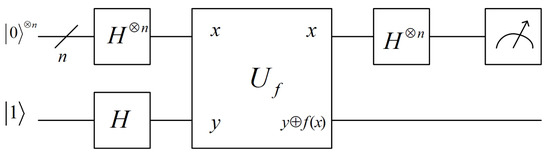
Figure 4. Quantum circuit of BV algorithm.

Utilizing the fact that BV algorithm always outputs the vectors in the support set of the Walsh transform, Li et al. constructed a quantum algorithm used for finding differentials with high probability [57].

For any $f\in {\mathcal{C}}_{n,1}$, let

$$\begin{array}{cc}\hfill {\gamma }_f& ={\displaystyle \frac{1}{2^n}}\underset{\begin{array}{c}\Delta x\in {\mathbb{F}}_2^n\\ \Delta x\notin D_f\end{array}}{max}\underset{i\in \{0,1\}}{max}\left|\{x\in {\mathbb{F}}_2^n|f(x\oplus \Delta x)\oplus f\left(x\right)=i\}\right|\hfill \\ \hfill & =\underset{\begin{array}{c}\Delta x\in {\mathbb{F}}_2^n\\ \Delta x\notin D_f\end{array}}{max}\underset{i\in \{0,1\}}{max}\underset{x\leftarrow {\mathbb{F}}_2^n}{Pr}[\Delta x\stackrel{f}{\to }i].\hfill \end{array}$$

It is easy to verified that ${\gamma }_f<1$. This parameter is the maximum differential probability of f except for the probability-1 differentials. The authors of [25,57] proved the following theorems that illustrate the soundness of the aforementioned algorithm.

Theorem 1 

([57]). If Algorithm 1 outputs two sets $Z^0$ and $Z^1$ when applied to a function $f\in {\mathcal{C}}_{n,1}$, then for any $\Delta x\in Z^i$ ($i=0,1$), any ϵ satisfying $0<ϵ<1$, it holds that

$$\mathrm{Pr}\left[1-{\displaystyle \frac{\left|\right\{x\in {\mathbb{F}}_2^n|f(x\oplus \Delta x)+f\left(x\right)=i\}|}{2^n}}<ϵ\right]>1-e^{-2q\left(n\right){ϵ}^2}.$$

(2)

Algorithm 1 Quantum algorithm for finding high-probability differentials.

Input:$$the quantum circuit realizing $f\in {\mathcal{C}}_{n,1}$, a polynomial $q\left(n\right)$ of n. Output: a differential of function f. 1: Define a set $W:=\Phi$; 2: for $l=1,2,\cdots$, $q\left(n\right)$ do 3:     Apply BV algorithm to f, obtaining an vector u with n bits such that $S_f\left(u\right)\ne 0$; 4:     Let $W=W\cup \left\{u\right\}$; 5: end for 6: Solve the equation $\{x·u=i|u\in W\}$, getting the solution set $Z^i$ for both $i=0,1$; 7: if $Z^0\cup Z^1\subseteq \left\{\overrightarrow{0}\right\}$ then 8:     Output “No”; 9: else 10:     Output $Z^0$ and $Z^1$; 11: end if

Theorem 2 

([25]). Suppose $f\in {\mathcal{C}}_{n,1}$ and there is a constant $a_0$ such that ${\gamma }_f\le a_0<1$. If Algorithm 1 outputs two sets $Z^0$ and $Z^1$ when applied to f with $q\left(n\right)=n$, then for any vector $\Delta x\notin D_f^i$ ($i=0,1$), we have

$$Pr[\Delta x\in Z^i]\le a_0^n.$$

Theorem 1 demonstrates that, for any vector $\Delta x\in Z^i$ ($i=0,1$), the differential probability of $(\Delta x,i)$ to f is greater than $1-ϵ$ with a probability greater $1-e^{-2q\left(n\right){ϵ}^2}$.

3. Quantum Truncated Differential Attack

Knudsen introduced the truncated differential attack in 1994 [51]. This cryptanalytic method has been widely applied to attack symmetric ciphers [58,59]. In the initial version of differential attacks, the adversaries utilize full differences of plaintexts and ciphertexts, whereas in truncated differential attacks the adversaries consider differences partially determined. The adversaries only predict some bits of the differentials rather than the entire differentials.

We still consider the block cipher $En{c}_k^r$ with the key space ${\mathbb{F}}_2^m$. A truncated differential $(\overline{\Delta }x,\overline{\Delta }y)$ of $En{c}_k^r$ is a pair of vectors such that $\overline{\Delta }x,\overline{\Delta }y\in {\{\ast ,0,1\}}^n$, where ∗ denotes an undetermined bit. Let $\overline{\Delta }x=(\overline{\Delta }{x}_1,\cdots$, $\overline{\Delta }{x}_n)$, $\overline{\Delta }y=(\overline{\Delta }{y}_1,\cdots$, $\overline{\Delta }{y}_n)$. then $\overline{\Delta }{x}_i,\overline{\Delta }{y}_i\in \{\ast ,0,1\}$. The bits of $\overline{\Delta }x$ ($\overline{\Delta }y$) that take the value of zero or one are defined as predicted bits, whereas those with a value of ∗ are defined as unpredicted bits.

A truncated difference is equivalent to a set of complete differences. Define

$${\Omega }_{\overline{\Delta }x}=\left\{\Delta x=(\Delta x_1,\cdots ,\Delta x_n)\in {\mathbb{F}}_2^n|\Delta x_i=\overline{\Delta }{x}_i\mathrm{if}\overline{\Delta }{x}_i\ne \ast ,i\in \{1,2,\cdots ,n\}\right\},$$

$${\Omega }_{\overline{\Delta }y}=\left\{\Delta y=(\Delta y_1,\cdots ,\Delta y_n)\in {\mathbb{F}}_2^n|\Delta y_i=\overline{\Delta }{y}_i\mathrm{if}\overline{\Delta }{y}_i\ne \ast ,i\in \{1,2,\cdots ,n\}\right\},$$

then truncated differences $\overline{\Delta }x$ and $\overline{\Delta }y$ are equivalent to ${\Omega }_{\overline{\Delta }x}$ and ${\Omega }_{\overline{\Delta }y}$, respectively. If a complete input difference $\Delta x$ is in ${\Omega }_{\overline{\Delta }x}$, that is, $\Delta x_j=\overline{\Delta }{x}_j$ for all $j\in \{1,\cdots$, $n\}$ such that $\overline{\Delta }{x}_j\ne \ast$, we say that $\Delta x$ matches the truncated difference $\overline{\Delta }x$, and this case is denoted as $\Delta x$∼$\overline{\Delta }x$. Similarly, $\Delta y$∼$\overline{\Delta }y$ implies that $\Delta y$ matches the truncated difference $\overline{\Delta }y$.

Conditional probability

$$\begin{array}{cc}\hfill \underset{x\leftarrow {\mathbb{F}}_2^n}{Pr}\left[\overline{\Delta }x\stackrel{En{c}_k^r}{\to }\overline{\Delta }y\right]& =\underset{x\leftarrow {\mathbb{F}}_2^n}{Pr}[En{c}_k^r(x\oplus \Delta x)\oplus En{c}_k^r\left(x\right)\sim \overline{\Delta }y|\Delta x\sim \overline{\Delta }x]\hfill \\ \hfill & =\underset{x\leftarrow {\mathbb{F}}_2^n}{Pr}[En{c}_k^r(x\oplus \Delta x)\oplus En{c}_k^r\left(x\right)\in {\Omega }_{\overline{\Delta }y}|\Delta x\in {\Omega }_{\overline{\Delta }x}]\hfill \end{array}$$

is defined as the probability of $(\overline{\Delta }x,\overline{\Delta }y)$. If p is equal to the probability of $(\overline{\Delta }x,\overline{\Delta }y)$, we call $(\overline{\Delta }x,\overline{\Delta }y)$ a p-probability truncated differential of $En{c}_k^r$.

Let $En{c}^t$ ($1<t<r$) be a reduced cipher of $En{c}^r$. In a truncated differential attack, the adversaries first search for a truncated differential of $En{c}^t$ that has a high probability and then use this truncated differential, denoted as $(\overline{\Delta }x,\overline{\Delta }y)$, to recover the subkeys involved in the last $r-t$ rounds. In detail, the adversaries fix the plaintext difference $\overline{\Delta }x$ and then use $2M$ pairs of plaintexts, whose differences match $\overline{\Delta }x$, to make encryption queries and obtain $2M$ pairs of corresponding ciphertexts. Subsequently, for each possible candidate subkey of the last $r-t$ rounds, the adversaries use it to decrypt $r-t$ rounds to obtain M output differences of $En{c}_k^t$, in the meantime calculate the amount of the differences that match $\overline{\Delta }y$. Finally, the right subkey is the subkey having the maximum count.

The amount of plaintext pairs required in such a counting scheme and the success probability of obtaining the right key are determined by the ratio of signal to noise [49], and its definition is

$$S/N={\displaystyle \frac{L\times p}{\alpha \times \lambda }},$$

where L denotes the total amount of possible subkeys involved in the last $r-t$ rounds, p denotes the probability of $(\overline{\Delta }x,\overline{\Delta }y)$, $\alpha$ denotes the average count that every plaintext pair contributes and $\lambda$ denotes the proportion of pairs not discarded in the preprocessing procedure. We do not consider any pre-discarding processes, therefore we set $\lambda =1$. A truncated differential attack succeeds only when $S/N>1$. Thus, the adversaries should use a truncated differential that makes the ratio of signal to noise greater than one. The greater $S/N$ is, the easier it is to single out the right subkey.

In the following, we propose a quantum algorithm used for finding truncated differentials. In a classical truncated differential attack, because the adversaries do not know the value of k of the reduced cipher $En{c}_k^t$, they must find a truncated differential whose probability is high regardless of the value of the key k. Therefore, our quantum algorithm is designed to search for truncated differentials that have high probability for a large proportion of keys in ${\mathbb{F}}_2^m$. Specifically, by choosing a polynomial $\tau \left(n\right)$, the adversaries can force our quantum algorithm to output truncated differentials that have a high probability for more than $(1-{\displaystyle \frac{1}{\tau \left(n\right)}})$ proportion of keys in ${\mathbb{F}}_2^m$. We present the algorithm and analyze its effectiveness and complexity.

3.1. Finding Truncated Differentials via BV Algorithm

Given a reduced block cipher $En{c}_k^t$, let $En{c}_k^t\left(x\right)=(En{c}_k^t\left[1\right]\left(x\right),\cdots$, $En{c}_k^t\left[n\right]\left(x\right))$. That is, $En{c}_k^t\left[j\right]$ denotes the j-th component function of $En{c}_k^t$. An intuitive method for finding high-probability truncated differentials is to implement Algorithm 1 on every $En{c}_k^t\left[j\right]$. If Algorithm 1 finds differentials of several component functions that all have high probability and have a common input difference, then we can derive a truncated differential of $En{c}_k^t$ that has high probability. However, running Algorithm 1 on $En{c}_k^t\left[j\right]$ requires quantum queries of $En{c}_k^t$. It is impossible to achieve this even under $Q_2$ model because $En{c}_k^t$ is a reduced cipher instead of the complete cipher $En{c}_k^r$. In the original differential attack, the adversaries are also not able to query the reduced version. They thus analyzed the detailed constructions of the cipher and searched for truncated differentials whose probabilities were high regardless of the value the key took. Inspired by this idea, we consider searching for the truncated differentials with a high probability for most keys.

Since all constructions of the cipher $En{c}_k^t$, except for the private key k, are public, the function

$$\begin{array}{cc}\hfill En{c}^t:{\{0,1\}}^n\times {\{0,1\}}^m& ⟶{\{0,1\}}^n\hfill \\ \hfill (x,k)& ⟶En{c}_k^t\left(x\right)\hfill \end{array}$$

take the key as the input and is known and determined to the adversaries. Thus, the adversaries have access to the quantum circuit of the unitary operator

$$U_{En{c}^t}:|x⟩|k⟩|y⟩\to |x⟩|k⟩|y\oplus En{c}^t(x,k)⟩=|x⟩|k⟩|y\oplus En{c}_k^t\left(x\right)⟩.$$

Let $|En{c}^t{|}_Q$ be the amount of quantum universal gates in this circuit. The adversaries also have the quantum circuit of every component function

$$\begin{array}{cc}\hfill En{c}^t\left[j\right]:{\{0,1\}}^n\times {\{0,1\}}^m& ⟶{\{0,1\}}^n\hfill \\ \hfill (x,k)& ⟶En{c}_k^t\left[j\right]\left(x\right).\hfill \end{array}$$

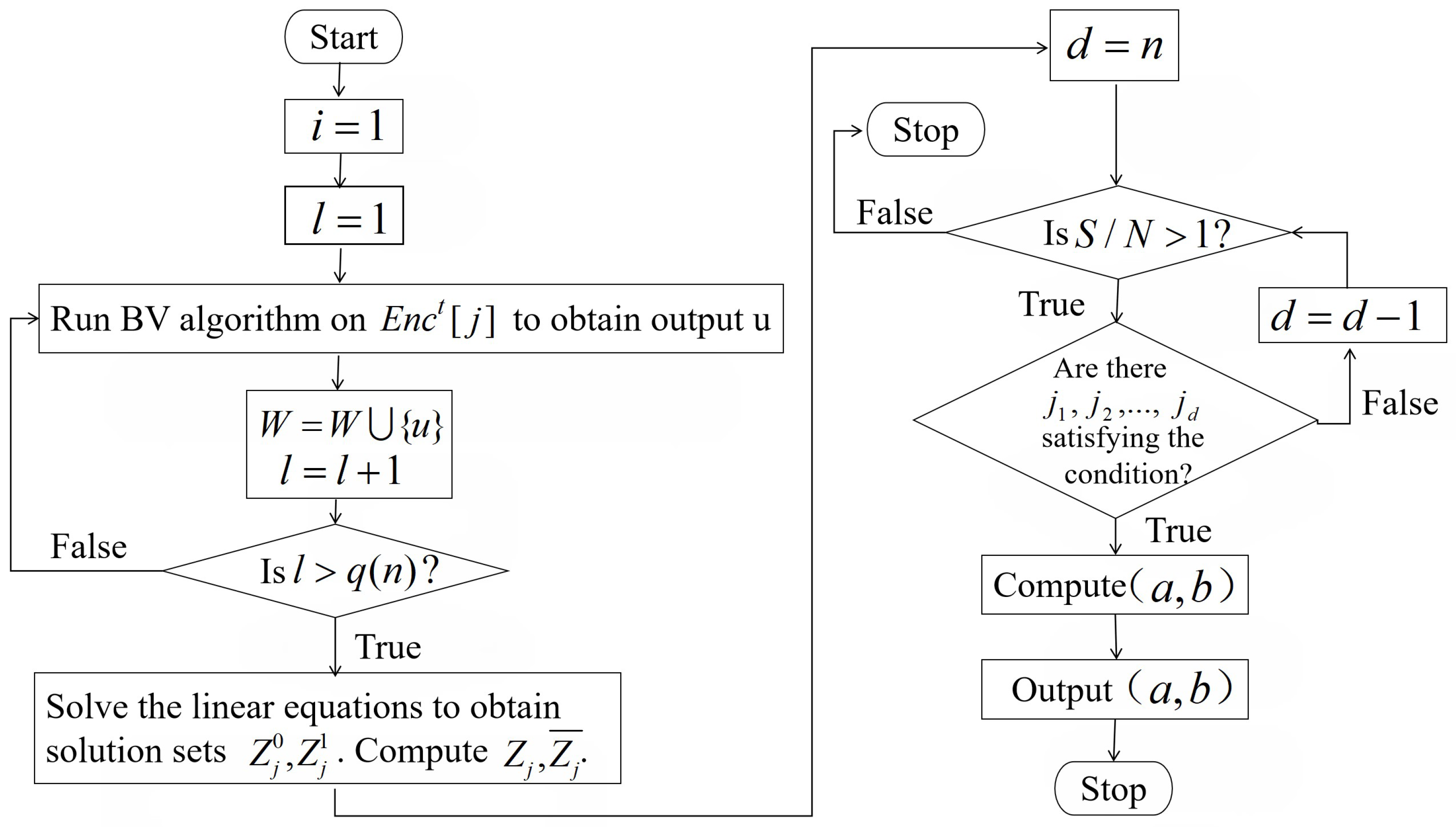
The corresponding amount of gates is $|En{c}^t{\left[j\right]|}_Q$ ($j=1,\cdots$, n). The adversaries have the quantum circuits of $En{c}^t\left[j\right]$’s. Therefore, they can run Algorithm 1 on $En{c}^t\left[j\right]$’s without quantum queries. The adversaries can run Algorithm 1 to obtain the differentials of high probability of every $En{c}^t\left[j\right]$, then by taking a common input difference of part component functions as the input difference, they can obtain a truncated differential having high probability. According to this idea, we propose Algorithm 2 for finding truncated differentials of block ciphers.

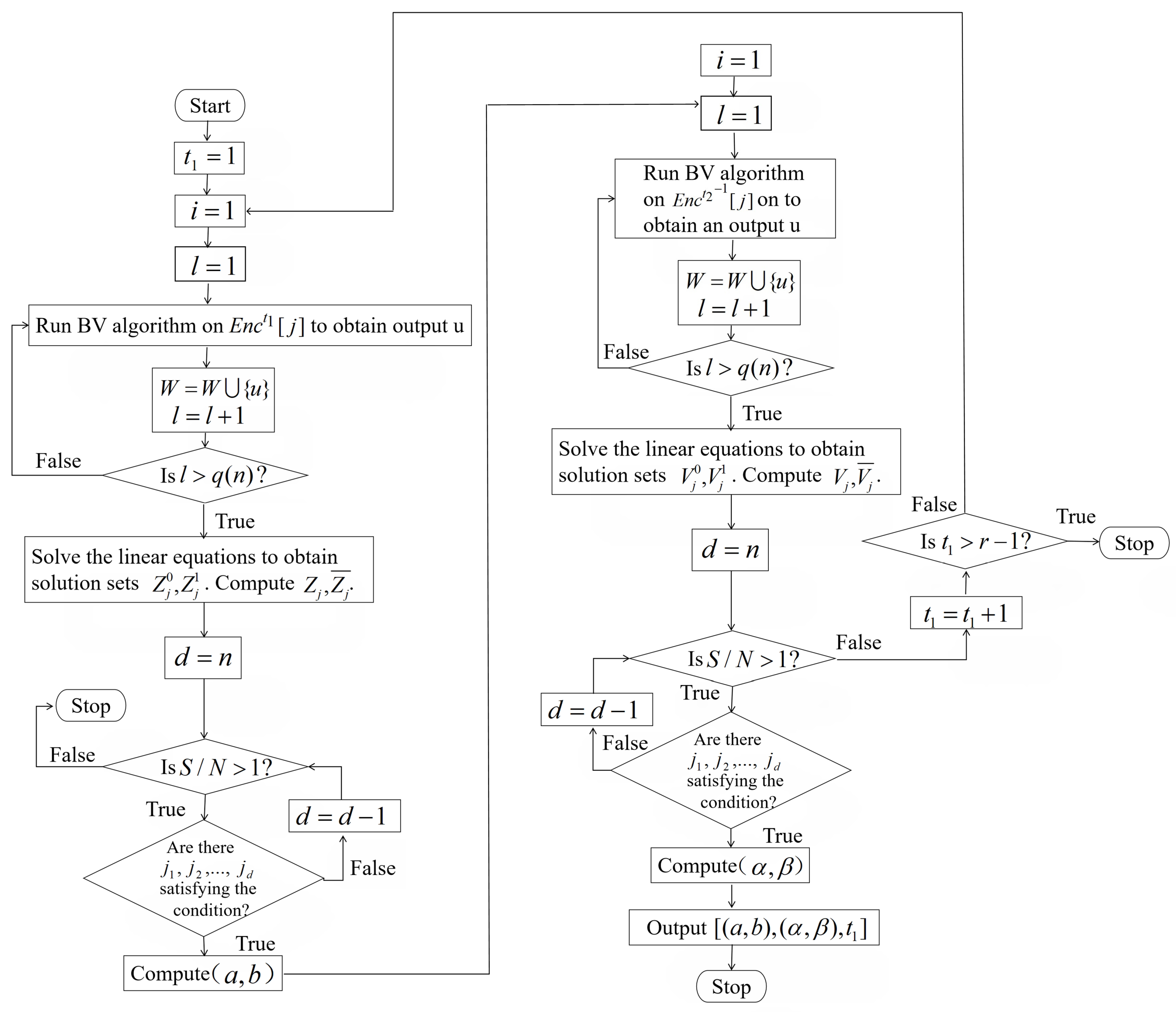
The flowchart of Algorithm 2 is presented in Figure 5. Steps 1–18 of Algorithm 2 are used to determine the high-probability differentials of $En{c}^t\left[j\right]$ for every $j=1,\cdots$, n. The purpose of steps 19–26 is to choose a difference which is a common input difference of as many $En{c}^t\left[j\right]$ as possible. Algorithm 2 outputs a truncated differential $(a,b)$ of $En{c}^t$. The symbol “∗” in b means that the corresponding bits are unpredicted. In a quantum truncated differential attack, the adversaries first choose a polynomial $\tau \left(n\right)$ and a constant $\sigma$ ($0<\sigma <1$), then implement Algorithm 2 to get an output $(a,b)$. According to Theorem 3 which is proven in Section 3.2, the differential probability of $(a,b)$ is greater than $\sigma$ for more than $(1-{\displaystyle \frac{1}{\tau \left(n\right)}})$ proportion of keys in ${\mathbb{F}}_2^m$ with an overwhelming probability.

Algorithm 2 Quantum algorithm for finding high-probability truncated differentials

Input: $$The quantum circuit of $En{c}^t$, a polynomial $\tau \left(n\right)$ and a constant $\sigma$ ($0<\sigma <1$) chosen by the adversaries. Output: a high-probability truncated differential of $En{c}^t$. 1: Let $q\left(n\right)={\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3$; 2: Define a set $W:=\Phi$; 3: for $j=1,2,\cdots$, n do 4:     for $l=1,\cdots$, $q\left(n\right)$ do 5:         Apply BV algorithm to $En{c}^t\left[j\right]$ to get an output $u=(u_1,\cdots$, $u_n,u_{n+1},\cdots$, $u_{n+m})$; 6:         Let $W=W\cup \left\{\right(u_1,\cdots$, $u_n\left)\right\}$; 7:     end for 8:     Solve the linear equation $\{x·u=i_j|u\in W\}$ by Gaussian elimination method, obtaining the solution sets $Z_j^{i_j}$ for $i_j=0,1$, respectively; 9:      Compute the set $Z_j=Z_j^0\cup Z_j^1$; 10:      Let ${\overline{Z}}_j=\Phi$; 11:     for $a\in Z_j^0$ do 12:         Let ${\overline{Z}}_j={\overline{Z}}_j\cup \left\{(a,0)\right\}$; 13:     end for 14:     for $a\in Z_j^1$ do 15:         Let ${\overline{Z}}_j={\overline{Z}}_j\cup \left\{(a,1)\right\}$; 16:     end for 17:     Let $W=\Phi$; 18: end for 19: for $d=n,n-1\cdots$, 1  do 20:     if $S/N=2^d\sigma >1$ then 21:         if there are d different subscripts $j_1,\cdots$, $j_d$ s.t. $Z_{j_1}\cap \cdots \cap Z_{j_d}⊋\left\{\overrightarrow{0}\right\}$ then 22:            Choose at random a vector $a\in Z_{j_1}\cap \cdots \cap Z_{j_d}$, and for $j=1,\cdots$, n, let $$b_j=\left\{\begin{array}{cc}{i}_j,& j\in \{j_1,\cdots ,j_d\}\\ \ast ,& j\notin \{j_1,\cdots ,j_d\},\end{array}\right.$$ where $i_j$ denotes the bit appended to a in the set ${\overline{Z}}_j$, i.e., $(a,i_j)\in {\overline{Z}}_j$; 23:             Let $b=(b_1,\cdots$, $b_n)$ and return $(a,b)$; 24:         end if 25:     end if 26: end for 27: Return “No”;

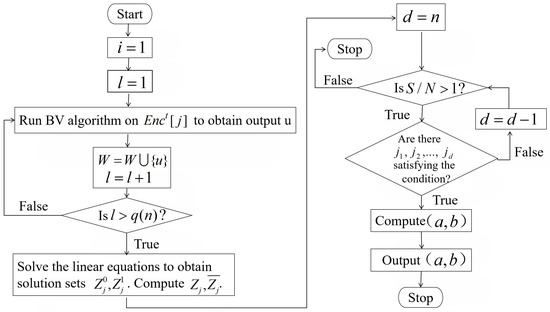
Figure 5. The flowchart of Algorithm 2.

To implement steps 21-22, the adversaries traverse the variables $j_1,j_2,\cdots$, $j_d$ in sequence. For $j_1=1,2,\cdots$, $n-d+1$, $j_2=j_1,j_1+1,\cdots$, $n-d+2$, ⋯, $j_d=j_{d-1},j_{d-1}+1,\cdots$, n, Algorithm 2 needs to compute the intersection of the sets $Z_{j_1},Z_{j_2},\cdots$, $Z_{j_d}$. If the intersection contains nonzero vectors, Algorithm 2 randomly chooses a nonzero vector and outputs it.

In order to demonstrate the feasibility of the output truncated differential $(a,b)$, it is necessary to compute the ratio of signal to noise $S/N$. To this end, we first calculate the parameter $\alpha$, which is equal to the average count that every plaintext pair contributes. There are d bits of the difference b predicted, therefore a total of $2^{n-d}$ output differences matching the truncated difference b. In the counting process, the ciphertexts of a fixed pair of plaintexts are decrypted using L candidate subkeys. The resulting L output differences can be viewed as random vectors. Therefore, every plaintext pair contributes

$$\alpha ={\displaystyle \frac{2^{n-d}}{2^n}}\times L={\displaystyle \frac{L}{2^d}}$$

counts on average. Then

$$N/S\ge {\displaystyle \frac{L\times \sigma }{\frac{L}{2^d}\times 1}}=2^d\sigma >1.$$

This value is greater than one because of the condition $2^d\sigma >1$ in the step 14 of Algorithm 2. After obtaining the output $(a,b)$, the adversaries can utilize it to find the right subkey involved in the last $r-t$ rounds, similar to the traditional truncated differential attack. This attack should work for at least $(1-{\displaystyle \frac{1}{\tau \left(n\right)}})$ proportion of keys in ${\mathbb{F}}_2^m$. Even if “No” is output, the adversaries can adjust the polynomial $\tau \left(n\right)$ and $\sigma$ to increase the success probability.

3.2. Analysis of Algorithm 2

We analyze the correctness and efficiency of Algorithm 2. Theorem 3 indicates the correctness of Algorithm 2.

Theorem 3. 

Suppose Algorithm 2 outputs $(a,b)$, then with an overwhelming probability, there is a subset $S\subseteq {\mathbb{F}}_2^m$ satisfying that $\left|S\right|/|{\mathbb{F}}_2^m|>1-{\displaystyle \frac{1}{\tau \left(n\right)}}$, and for every key $k\in S$,

$${\displaystyle \frac{\left|\right\{x\in {\mathbb{F}}_2^n|En{c}_k^t(x\oplus a)+En{c}_k^t\left(x\right)\sim b\}|}{2^n}}>\sigma .$$

That is, the differential probability of $(a,b)$ is greater than σ for more than $(1-{\displaystyle \frac{1}{\tau \left(n\right)}})$ proportion of keys in ${\mathbb{F}}_2^m$.

Proof. 

b has d predicted bits, whose subscripts are $j_1,\cdots$, $j_d$. Appending m zeros after the vector a gives an $(n+m)$-bit vector $(a\parallel 0,\cdots$, $0)$. Since $a·(u_1,\cdots$, $u_n)=0$, it holds that

$$(a\parallel 0,\cdots ,0)·(u_1,\cdots ,u_n,u_{n+1},\cdots ,u_{n+m})=0.$$

The $(n+m)$-bit vector $(a\parallel 0,\cdots ,0)$ can be viewed as the output of Algorithm 2 when it is applied to $En{c}^t\left[j\right]$ for all $j\in \{j_1,j_2,\cdots ,j_d\}$. From Theorem 1, the probability that

$${\displaystyle \frac{\left|\right\{z\in {\mathbb{F}}_2^{n+m}|En{c}^t\left[j\right](z\oplus (a\parallel 0,\cdots ,0))\oplus En{c}^t\left[j\right]\left(z\right)=b_j)\left\}\right|}{2^{n+m}}}>1-ϵ,\forall j\in \{j_1,j_2,\cdots ,j_d\}$$

holds is greater than ${(1-e^{-2q\left(n\right){ϵ}^2})}^d$. If the above inequality holds, then the number of z that satisfies

$$En{c}^t\left[j\right]\left(z\oplus (a\parallel 0,\cdots ,0)\right)\oplus En{c}^t\left[j\right]\left(z\right)=b_j$$

(3)

for both $j=j_1$ and $j=j_2$ is greater than $2^{n+m}[2(1-ϵ)-1]=2^{n+m}(1-2ϵ)$. Likewise, the number of z satisfying Equation (3) for all $j=j_1,j_2,j_3$ is greater than $2^{n+m}(1-3ϵ)$. By induction, the number of z that satisfies Equation (3) for all $j\in \{j_1,j_2,\cdots ,j_d\}$ is more than $2^{n+m}(1-dϵ)$. Therefore, the probability that

$${\displaystyle \frac{\left|\right\{z\in {\mathbb{F}}_2^{n+m}|En{c}^t(z\oplus (a\parallel 0,\cdots ,0))\oplus En{c}^t\left(z\right)\sim b)\left\}\right|}{2^{n+m}}}>1-dϵ.$$

holds is greater than ${(1-e^{-2q\left(n\right){ϵ}^2})}^d$, which is equivalent to

$${\displaystyle \frac{\left|\right\{(x,k)\in {\mathbb{F}}_2^n\times {\mathbb{F}}_2^m|En{c}_k^t(x\oplus a)\oplus En{c}_k^t\left(x\right)\sim b\}|}{2^{n+m}}}>1-dϵ.$$

(4)

Let

$$Z\left(k\right)={\displaystyle \frac{\left|\right\{x\in {\mathbb{F}}_2^n|En{c}_k^t(x\oplus a)+En{c}_k^t\left(x\right)\sim b\}|}{2^n}}.$$

Equation (4) indicates that ${\mathbb{E}}_k\left[Z\left(k\right)\right]>1-dϵ$. Here ${\mathbb{E}}_k\left[Z\left(k\right)\right]$ is the statistical expectation of $Z\left(k\right)$ and the variable k follows the uniform distribution of ${\mathbb{F}}_2^m$. Therefore, when Equation (4) holds, we have

$${Pr}_k\left[Z\left(k\right)>1-\tau \left(n\right)dϵ\right]>1-{\displaystyle \frac{1}{\tau \left(n\right)}}$$

for any polynomial $\tau \left(n\right)$. This is because, if not, then ${\mathrm{Pr}}_{k\leftarrow {\mathbb{F}}_2^m}[1-Z\left(k\right)\ge \tau \left(n\right)dϵ]\ge {\displaystyle \frac{1}{\tau \left(n\right)}}$, which means

$$\begin{array}{cc}\hfill & {\mathbb{E}}_k\left[Z\left(k\right)\right]\hfill \\ \hfill =& 1-{\mathbb{E}}_k[1-Z\left(k\right)]\hfill \\ \hfill \le & 1-{\displaystyle \frac{1}{\tau \left(n\right)}}·\tau \left(n\right)dϵ\hfill \\ \hfill =& 1-dϵ.\hfill \end{array}$$

This leads to a contradiction. Thus, as long as Equation (4) holds, the proportion of the keys satisfying $Z\left(k\right)>1-\tau \left(n\right)dϵ$ in ${\mathbb{F}}_2^m$ must be greater than $(1-{\displaystyle \frac{1}{\tau \left(n\right)}})$. Let S be a set of all such keys. We have $\left|S\right|/|{\mathbb{F}}_2^m|>1-{\displaystyle \frac{1}{\tau \left(n\right)}}$, and for every $k\in S$,

$$Z\left(k\right)={\displaystyle \frac{\left|\right\{x\in {\mathbb{F}}_2^n|En{c}_k^t(x\oplus a)+En{c}_k^t\left(x\right)\sim b\}|}{2^n}}>1-\tau \left(n\right)dϵ.$$

Let $ϵ={\displaystyle \frac{1-\sigma }{\tau \left(n\right)d}}$. Since $q\left(n\right)={\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3$, the probability that Equation (4) holds is larger than $1-n{e}^{-n}$. Therefore, with an overwhelming probability, there is a subset $S\subseteq {\mathbb{F}}_2^m$ satisfying that $\left|S\right|/|{\mathbb{F}}_2^m|>1-{\displaystyle \frac{1}{\tau \left(n\right)}}$, and for every $k\in S$,

$$\begin{array}{c}\hfill {\displaystyle \frac{\left|\right\{x\in {\mathbb{F}}_2^n|En{c}_k^t(x\oplus a)+En{c}_k^t\left(x\right)\sim b\}|}{2^n}}>1-\tau \left(n\right)dϵ=\sigma ,\end{array}$$

which means that the differential probability of $(a,b)$ is greater than $\sigma$ for more than $(1-{\displaystyle \frac{1}{\tau \left(n\right)}})$ proportion of keys in ${\mathbb{F}}_2^m$    □

When implementing a truncated differential attack, the adversaries first choose a polynomial $\tau \left(n\right)$ and a parameter $\sigma$, then run Algorithm 2 to get $(a,b)$. The polynomial $\tau \left(n\right)$ is used to characterize the expected proportion of keys under which $(a,b)$ has high probability. The parameter $\sigma$ is used characterize the expected differential probability. According to Theorem 3, with an overwhelming probability, for at least $(1-{\displaystyle \frac{1}{\tau \left(n\right)}})$ proportion of keys in ${\mathbb{F}}_2^m$ the probability of $(a,b)$ is greater than $\sigma$. Then the adversaries can use $(a,b)$ to determine the subkey of the last $r-t$ rounds as in a traditional truncated differential attack. This attack works for at least the $(1-{\displaystyle \frac{1}{\tau \left(n\right)}})$ proportion of keys in ${\mathbb{F}}_2^m$. The amount of plaintext pairs required in the counting process is determined by the value of $S/N$. Based on experimental observations, about 20 to 40 appearances of right plaintext pairs are enough [49]. Therefore, about ${\displaystyle \frac{40}{\sigma }}$ plaintext pairs are sufficient.

For analyzing the complexity, we first calculate the amounts of universal gates and qubits required and then estimate the complexity of the classical computing involved.

In Algorithm 2, BV algorithm is performed on each $En{c}^t\left[j\right]$ for $q\left(n\right)$ times ($j\in \{1,2,\cdots$, $n\}$). Every call requires the execution of $2(m+n)+1$ Hadamard gates and one quantum circuit of $En{c}^t\left[j\right]$. Thus, each call requires $2(m+n)+1+|En{c}^t{\left[j\right]|}_Q$ quantum universal gates. The total number of Hadamard gates required for Algorithm 2 is

$$\begin{array}{cc}\hfill & q\left(n\right)\sum _{j=1}^n\left[2(m+n)+1\right]\hfill \\ \hfill =& q\left(n\right)\left[(2m+1)n+2n^2\right]\hfill \\ \hfill =& {\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^4(2n+2m+1).\hfill \end{array}$$

Since it holds that

$$\begin{array}{cc}\hfill & q\left(n\right)\sum _{j=1}^n{\left|En{c}^t\left[j\right]\right|}_Q\hfill \\ \hfill =& q\left(n\right)|En{c}^t{|}_Q\hfill \\ \hfill =& {\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3{\left|En{c}^t\right|}_Q,\hfill \end{array}$$

the total number of times Algorithm 2 needs to execute the quantum circuit of $En{c}^t$ is ${\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3$. In summary, Algorithm 2 requires

$${\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3[2n^2+(2m+1)n+|En{c}^t{|}_Q]$$

(5)

universal gates in total. This number is a polynomial of n and m.

Classical computing part is to solve the linear system $\{x·u=i_j|u\in W\}$ for each $j=1,2,\cdots$, n and $i_j=0,1$. The adversaries need to solve a total of $2n$ systems, and every system has $q\left(n\right)$ equations and n unknowns. Therefore, the classical complexity of this part is $O\left(2q\left(n\right)n^3\right)=O\left({\displaystyle \frac{1}{{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^6\right)$. Applying BV algorithm to every $En{c}^t\left[j\right]$ requires $m+n+1$ qubits. Thus, Algorithm 2 requires

$$q\left(n\right)(n+m+1)={\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3(n+m+1)$$

(6)

qubits in total.

The parameters involved in Algorithm 2 include the constant $\sigma$, polynomial $\tau \left(n\right)$, blocksize n and key length m. For the convenience of parameter analysis, we list the quantum resources required for Algorithm 2 in Table 2, then analyze the influence of these parameters on the complexity of Algorithm 2.

Table 2. Quantum resources required for Algorithm 2.

Hadamard Gate	Quantum Execution of ${\mathit{Enc}}^{\mathit{t}}$	Qubit
${\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^4(2m+2n+1)$	${\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3$	${\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3(m+n+1)$

The parameter $\sigma$ is chosen by the adversary and satisfies $0<\sigma \le 1$. $\sigma$ is the lower bound of the probability of truncated differentials desired by the adversary. Since truncated differentials have at least one predicted bit, the probability of any truncated differential of a random permutation is no more than ${\displaystyle \frac{1}{2}}$. Taking $\sigma ={\displaystyle \frac{1}{2}}$ is sufficient to ensure that the truncated differential output by Algorithm 2 is an effective differential. When more than one bit is predicted, the value of $\sigma$ can take a smaller value. Therefore, the coefficient ${\displaystyle \frac{1}{2{(1-\sigma )}^2}}$ in Table 2 usually can be seen as a small constant.

The parameter $\tau \left(n\right)$ is a polynomial chosen by the adversary. It characterizes the expected proportion of keys under which the output differential has high probability. The larger the value of $\tau \left(n\right)$, the more keys are feasible for the attack, but at the same time, the complexity also increases. The adversary can choose $\tau \left(n\right)$ based on the expected key proportion and acceptable complexity. Especially, $\tau \left(n\right)$ can be chosen as a constant $t_0$, then the number of Hadamard gates is $O\left(n^5\right)$. The number of times $En{c}^t$ needs to be executed quantumly is $O\left(n^3\right)$ and the number of qubits is $O\left(n^4\right)$. Here we omit m because usually $m=O\left(n\right)$.

The values of parameters $n,m$ depend on which block cipher is attacked. For common non-lightweight block ciphers, the value of the blocksize n is generally between 128 and 256, the value of the key length m is generally between 128 and 256. For common lightweight block ciphers, the value of the blocksize n is generally between 32 and 128, the value of the key length m is generally between 64 and 256. We take $\sigma ={\displaystyle \frac{1}{2}}$, $\tau \left(n\right)=2$ as an example and list the values of these parameters of several block ciphers and the corresponding complexity of Algorithm 2 in Table 3.

Table 3. Quantum complexity of Algorithm 2 on specific block ciphers ¹.

Block Cipher	n	m	Hadamard Gate	Quantum Execution of ${\mathit{Enc}}^{\mathit{t}}$	Qubit
LBlock	64	80	$2^{35.2}$	$2^{21.0}$	$2^{28.2}$
PRESENT-80	64	80	$2^{35.2}$	$2^{21.0}$	$2^{28.2}$
SPECK32/64	32	64	$2^{30.6}$	$2^{18.0}$	$2^{24.6}$
Simon-32/64	32	64	$2^{30.6}$	$2^{18.0}$	$2^{24.6}$

¹ Complexity is calculated by taking $\sigma ={\displaystyle \frac{1}{2}}$ and $\tau \left(n\right)=2$.

At present, the largest quantum chip is released by IBM, supporting over 1000-plus qubits [60]. IBM quantum platform supports the quantum circuits of 100-plus qubits. According to Table 3, it is unfeasible to completely implement or simulate Algorithm 2 on a block cipher.

3.3. Simulation

In this subsection, we simulate Algorithm 2 acting on a simple Boolean function. This demonstrates the practicality and correctness of Algorithm 2. Specifically, we choose a Boolean function $F:{\mathbb{F}}_2^4\to {\mathbb{F}}_2^4$, whose truth table in presented in Table 4. Let $F=(F_1,F_2,F_3,F_4)$. To simulate Algorithm 2 with Qiskit, we need to construct the quantum circuit of each component function $F_i$ ($i=1,2,3,4$), then apply BV algorithm on each $F_i$ to find high-probability differentials of $F_i$. Using LIGHTER-R tool or manual deduction it is easy to obtain the construction of quantum circuits of all component functions $F_i^{\prime }s$. The code of the simulation is presented on GitHub [61].

Table 4. Truth table of F.

${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	F	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	F
0	0	0	0	0000	1	0	0	0	1001
0	0	0	1	0010	1	0	0	1	1111
0	0	1	0	0110	1	0	1	0	1111
0	0	1	1	1101	1	0	1	1	0000
0	1	0	0	1111	1	1	0	0	0111
0	1	0	1	1101	1	1	0	1	0001
0	1	1	0	1000	1	1	1	0	0000
0	1	1	1	0011	1	1	1	1	1111

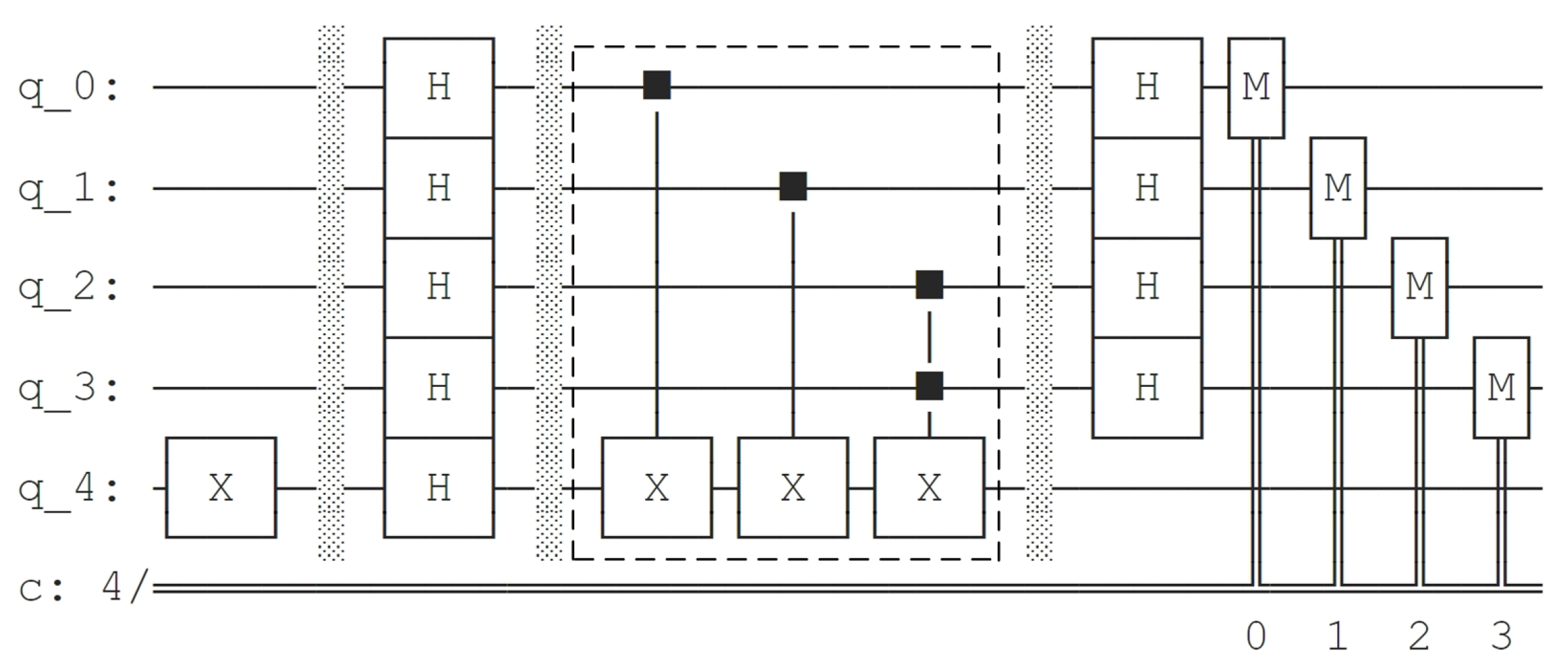
After constructing the quantum circuit of $F_1$ on Qiskit, we use the draw method to generate the quantum circuit diagram of BV algorithm acted on $F_1$. The circuit diagram is shown in Figure 6. The symbol M denotes the measurement on the computational basis states. We add a dotted box to mark the part of quantum circuit implementing $F_1$.

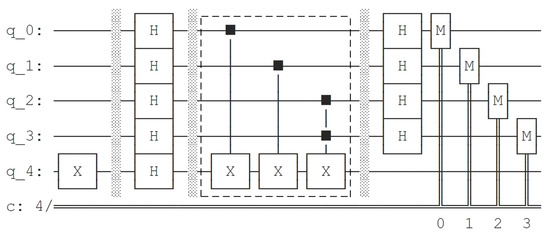
Figure 6. Quantum circuit diagram of BV algorithm acted on $F_1$ generated by Qiskit.

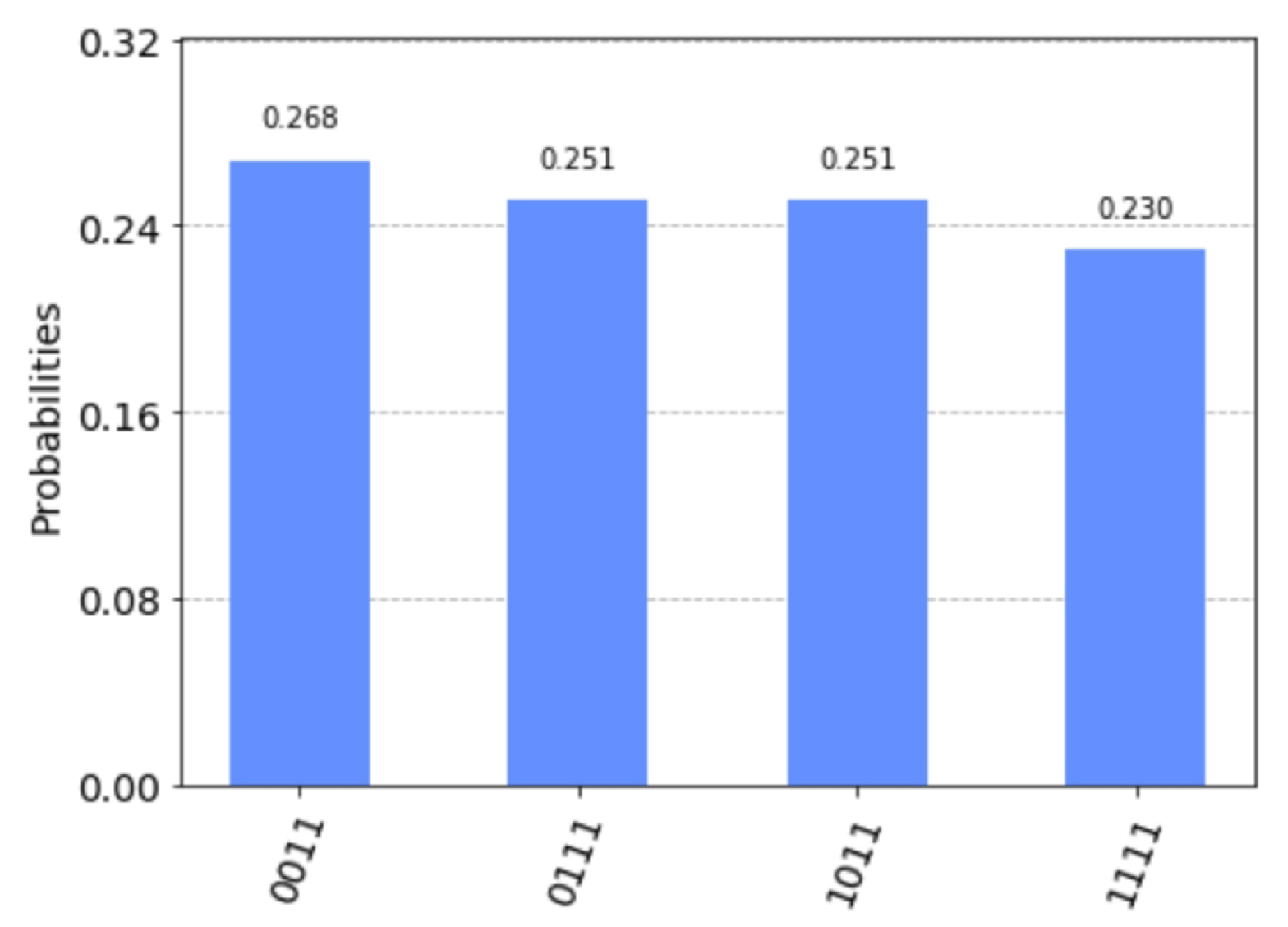
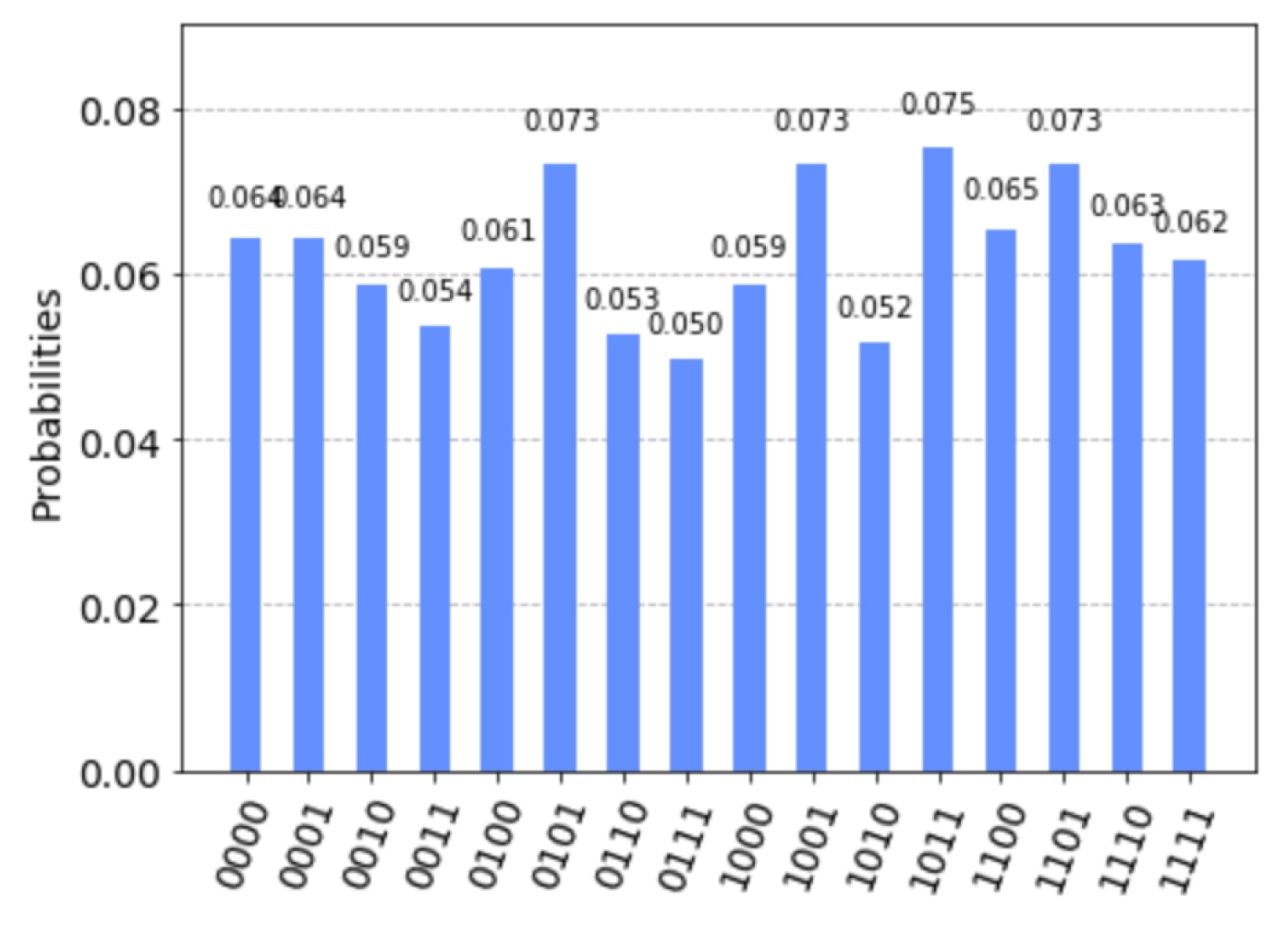
The measurement results simulated by Qiskit are shown in Figure 7. They only take four values: 1100, 1110, 1101 and 1111. Then solving the equation

$$\left\{\begin{array}{c}\left(1100\right)·x=0\hfill \\ \left(1110\right)·x=0\hfill \\ \left(1101\right)·x=0\hfill \\ \left(1111\right)·x=0\hfill \end{array}\right.$$

gives a fundamental solution system: $\left\{\right(1100\left)\right\}$. The solution set of the above equation is $Z_1^0=\left\{\left(1100\right),\left(0000\right)\right\}$. The solution set of the equation

$$\left\{\begin{array}{c}\left(1100\right)·x=1\hfill \\ \left(1110\right)·x=1\hfill \\ \left(1101\right)·x=1\hfill \\ \left(1111\right)·x=1\hfill \end{array}\right.$$

is $Z_1^1=\{\left(1000\right),\left(0100\right)\}$. According to step 9 of Algorithm 2, we let $Z_1=Z_1^0\cup Z_1^1=\{\left(1100\right),\left(0000\right),\left(1000\right),\left(0100\right)\}$.

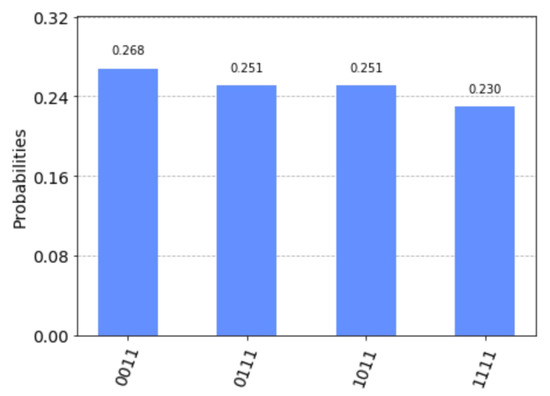
Figure 7. Measurement results on $F_1$ simulated by Qiskit.

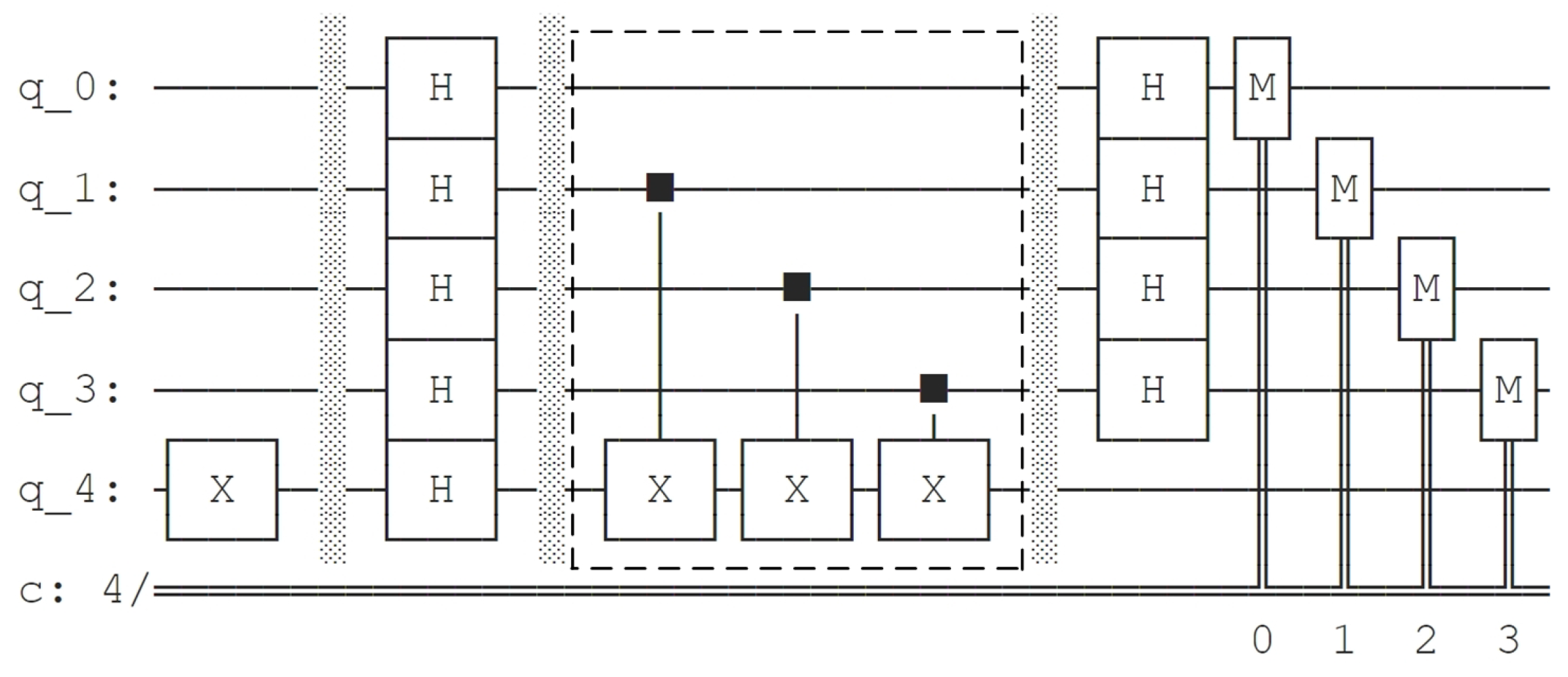
By employing a similar method, we construct the quantum circuit of $F_2$ on Qiskit and use the draw method to generate the quantum circuit diagram of BV algorithm acted on $F_2$. The circuit diagram is shown in Figure 8. We add a dotted box to mark the part of quantum circuit implementing $F_2$.

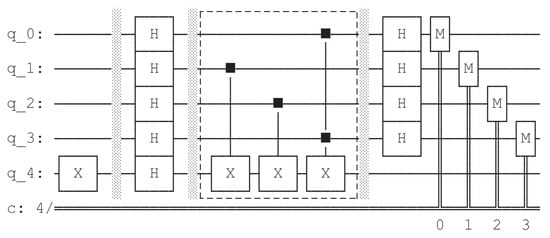
Figure 8. Quantum circuit diagram of BV algorithm acted on $F_2$ generated by Qiskit.

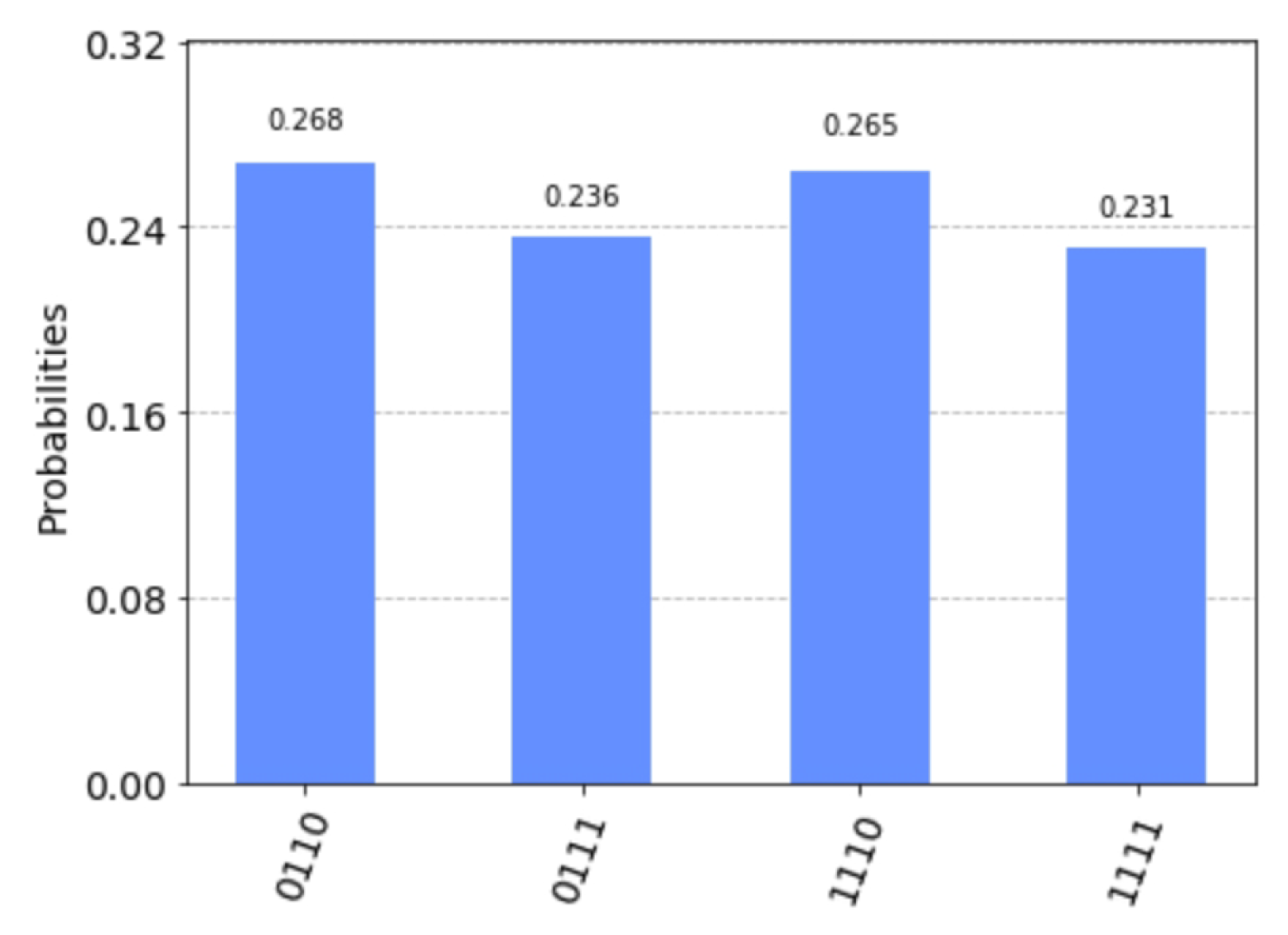
The measurement results simulated by Qiskit are shown in Figure 9. They only take four values: 0110, 1110, 0111 and 1111. Solving the equation

$$\left\{\begin{array}{c}\left(0110\right)·x=0\hfill \\ \left(1110\right)·x=0\hfill \\ \left(0111\right)·x=0\hfill \\ \left(1111\right)·x=0\hfill \end{array}\right.$$

gives a fundamental solution system: $\left\{\right(0110\left)\right\}$. The solution set of the above equation is $Z_2^0=\left\{\left(0110\right),\left(0000\right)\right\}$. The solution set of the equation

$$\left\{\begin{array}{c}\left(0110\right)·x=1\hfill \\ \left(1110\right)·x=1\hfill \\ \left(0111\right)·x=1\hfill \\ \left(1111\right)·x=1\hfill \end{array}\right.$$

is $Z_2^1=\{\left(0100\right),\left(0010\right)\}$. According to step 9 of Algorithm 2, we let $Z_2=Z_2^0\cup Z_2^1=\{\left(0110\right),\left(0000\right),\left(0100\right),\left(0010\right)\}$.

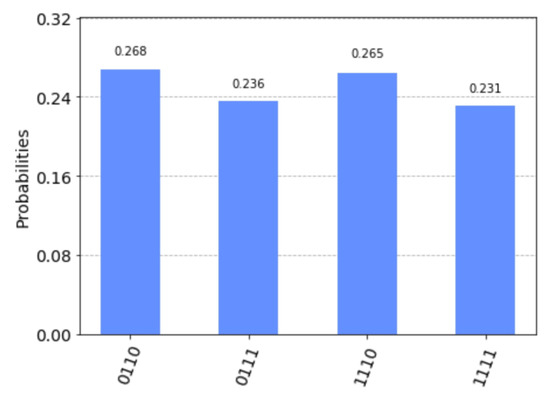
Figure 9. Measurement results on $F_2$ simulated by Qiskit.

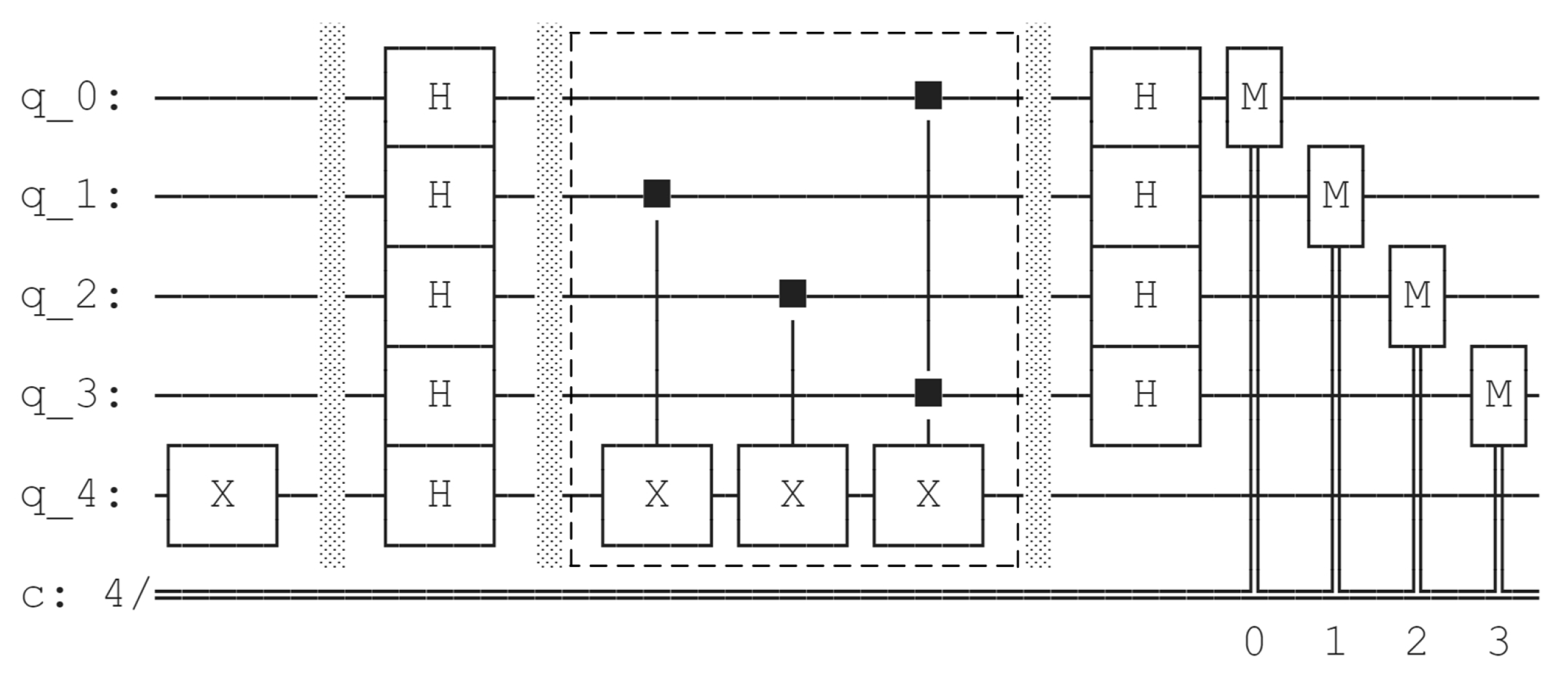
Similarly, we construct the quantum circuit of $F_3$ on Qiskit and use the draw method to generate the quantum circuit diagram of BV algorithm acted on $F_3$. The circuit diagram is shown in Figure 10. We add a dotted box to mark the part of quantum circuit implementing $F_3$.

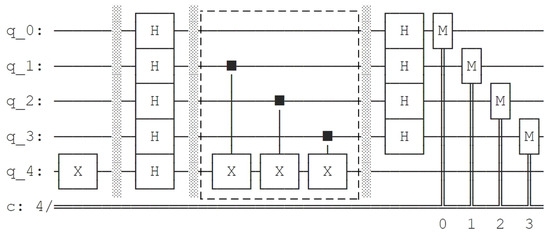
Figure 10. Quantum circuit diagram of BV algorithm acted on $F_3$ generated by Qiskit.

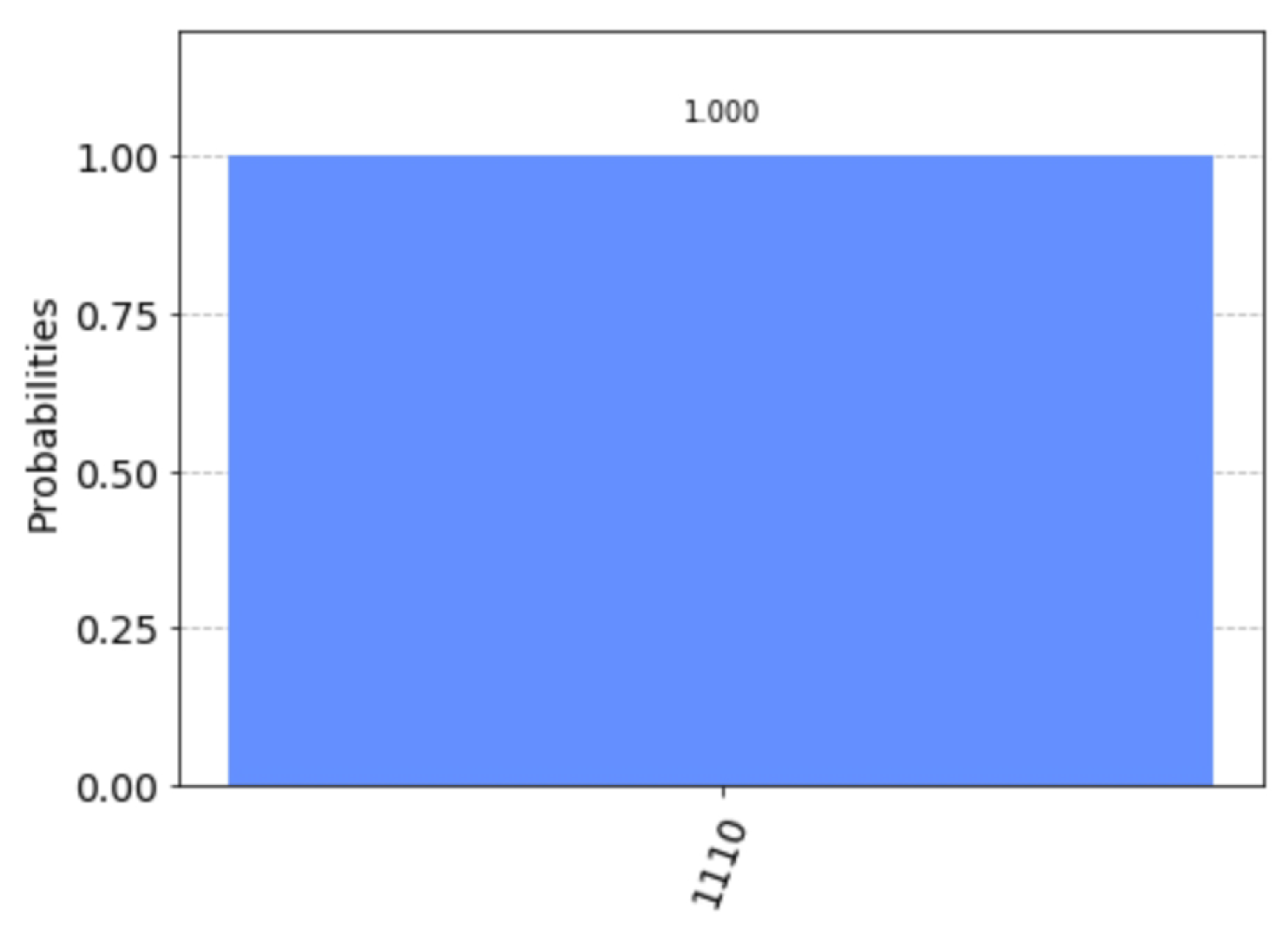
The measurement results simulated by Qiskit are shown in Figure 11. They only take one value: 0111. Solving the equation $\left(0111\right)·x=0$ gives a fundamental solution system: $\left\{\right(1000),(0101),(0011\left)\right\}$. The solution set of this equation is $Z_3^0=\{\left(0000\right),\left(1000\right),\left(0101\right),$$\left(0011\right),\left(1101\right),\left(0110\right),\left(1011\right),\left(1110\right)\}$. The solution set of the equation $\left(0111\right)·x=1$ is $Z_3^1=\left\{\left(0001\right),\left(1001\right),\left(0100\right),\left(0010\right),\left(1100\right),\left(0111\right),\left(1010\right),\left(1111\right)\right\}$. According to step 9 of Algorithm 2, we let

$$\begin{array}{c}\hfill Z_3=Z_3^0\cup Z_3^1=\{\left(0000\right),\left(1000\right),\left(0101\right),\left(0011\right),\left(1101\right),\left(0110\right),\left(1011\right),\left(1110\right),\left(0001\right),\\ \hfill \left(1001\right),\left(0100\right),\left(0010\right),\left(1100\right),\left(0111\right),\left(1010\right),\left(1111\right)\}.\end{array}$$

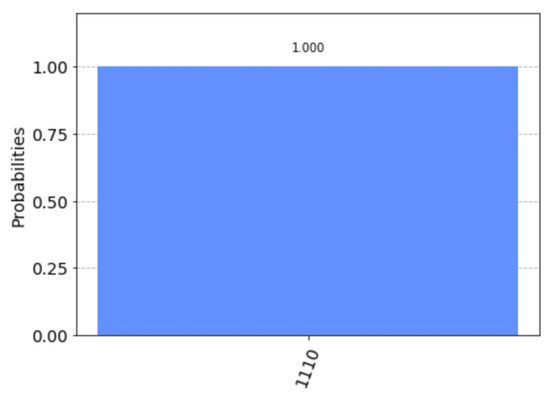
Figure 11. Measurement results on $F_3$ simulated by Qiskit.

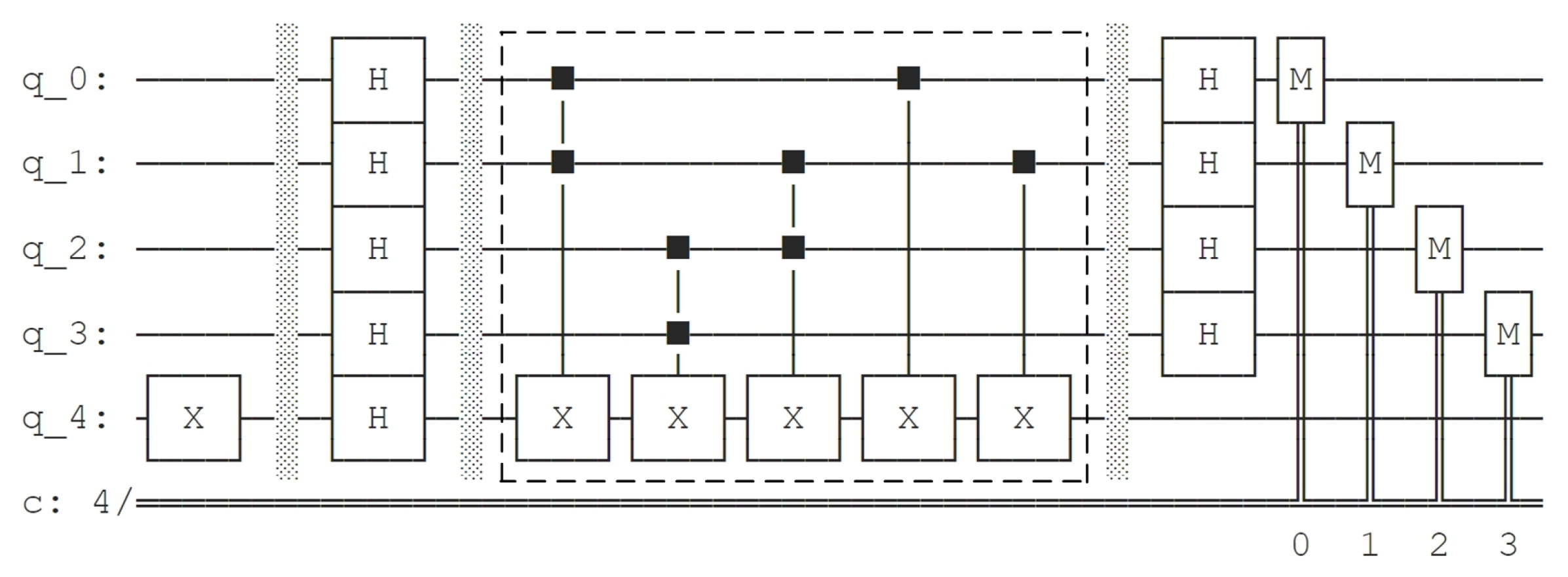
Then we construct the quantum circuit of $F_4$ on Qiskit and use the draw method to generate the quantum circuit diagram of BV algorithm acted on $F_4$. The circuit diagram is shown in Figure 12. We add a dotted box to mark the part of quantum circuit implementing $F_4$.

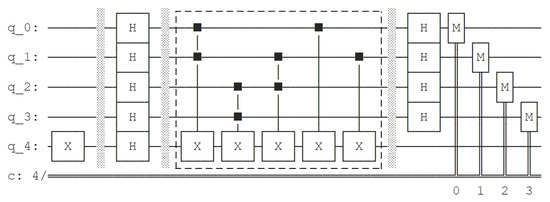
Figure 12. Quantum circuit diagram of BV algorithm acted on $F_4$ generated by Qiskit.

The measurement results simulated by Qiskit are shown in Figure 13. All vectors in ${\mathbb{F}}_2^4$ appear in the measurement results. The system of linear equations $\{u·x=0|u\in {\mathbb{F}}_2^4\}$ has only one solution $Z_4^0=\left\{\left(0000\right)\right\}$. The solution set of the system of linear equations $\{u·x=1|u\in {\mathbb{F}}_2^4\}$ is the empty set, that is, $Z_4^1=\Phi$. According to step 9 of Algorithm 2, we let $Z_4=Z_4^0\cup Z_4^1=\left\{\left(0000\right)\right\}$

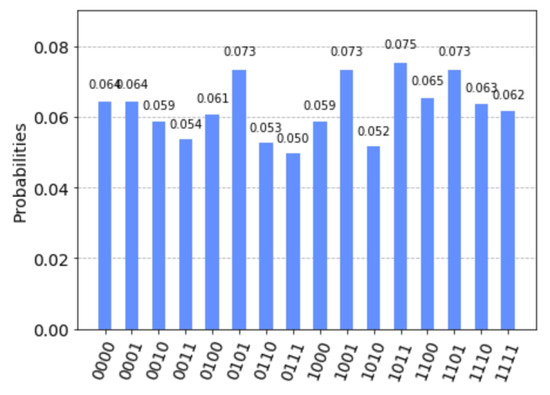
Figure 13. Measurement results on $F_4$ simulated by Qiskit.

Since $Z_1\cap Z_2\cap Z_3\cap Z_4=\left\{\left(0000\right)\right\}$, $Z_1\cap Z_2\cap Z_3=\{\left(0000\right),\left(0100\right)\}$ and $\left(0100\right)\in Z_1^1\cap Z_2^1\cap Z_3^1$, Algorithm 2 chooses $a=\left(0100\right)$ and let $b=(111\ast )$, then output $(a,b)$. It is easy to verify that $F(x\oplus (0100\left)\right)\oplus F\left(x\right)$∼b holds for all $x\in {\mathbb{F}}_2^4$. The probability of the truncated differential $(a,b)$ is one. This indicates that Algorithm 2 can indeed find high-probability truncated differentials.

4. Quantum Boomerang Attack

4.1. Quantum Algorithm for Finding Boomerang Distinguisher

Since its proposal in 1999, the boomerang attack [52] has been widely used as a cryptanalysis method. The principle of boomerang cryptanalysis is to connect two differential paths having a high probability such that the adversaries can attack more rounds. This attack was proposed because, when constructing the differential characteristics of block ciphers, the probability of the differential rapidly decreases as the round number increases. It works in cases where it is difficult to find a $(t_1+t_2)$-round differential characteristic of some block ciphers that has high probability, while it is possible to find $t_1$-round and $t_2$-round differential characteristics having high probability.

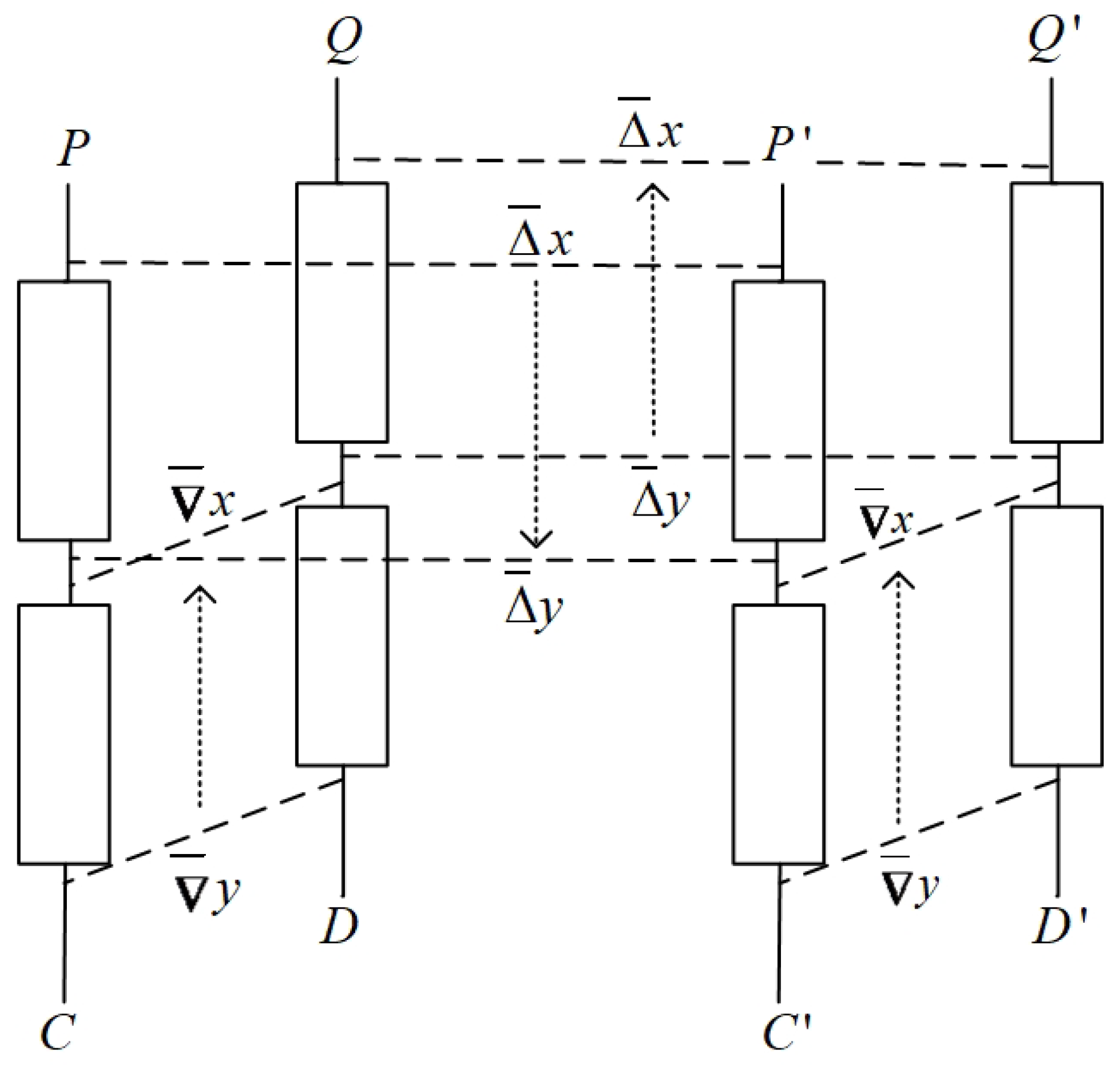
Suppose $En{c}_k^r\left(x\right)=En{c}_k^{t_2}\circ En{c}_k^{t_1}\left(x\right)$, where $t_1+t_2=r$, $En{c}_k^{t_1}$ has a $p_1$-probability truncated differential $(\overline{\Delta }x,\overline{\Delta }y)$ and the inverse function ${En{c}_k^{t_2}}^{-1}$ of $En{c}_k^{t_2}$ has a $p_2$-probability truncated differential $(\overline{\nabla }x,\overline{\nabla }y)$. As shown in Figure 14, $P,P^{\prime },Q,Q^{\prime }$ are four plaintexts and the corresponding ciphertexts under $En{c}_k^r$ are $C,C^{\prime },D,D^{\prime }$, respectively. $P,P^{\prime }$ are said to satisfy the differential $(\overline{\Delta }x,\overline{\Delta }y)$ of $En{c}_k^{t_1}$, if $P\oplus P^{\prime }$∼$\overline{\Delta }x$ and $En{c}_k^{t_1}\left(P\right)\oplus En{c}_k^{t_1}\left(P^{\prime }\right)$∼$\overline{\Delta }y$. If both $P,P^{\prime }$ and $Q,Q^{\prime }$ satisfy the differential $(\overline{\Delta }x,\overline{\Delta }y)$ of $En{c}_k^{t_1}$, and both $C,D$ and $C^{\prime },D^{\prime }$ satisfy the differential $(\overline{\nabla }x,\overline{\nabla }y)$ of ${En{c}_k^{t_2}}^{-1}$, then $(P,P^{\prime },Q,Q^{\prime })$ is called a right quadruple. Such two differentials are called a boomerang distinguisher of $En{c}_k^r$. Quadruples can be generated via the following method:

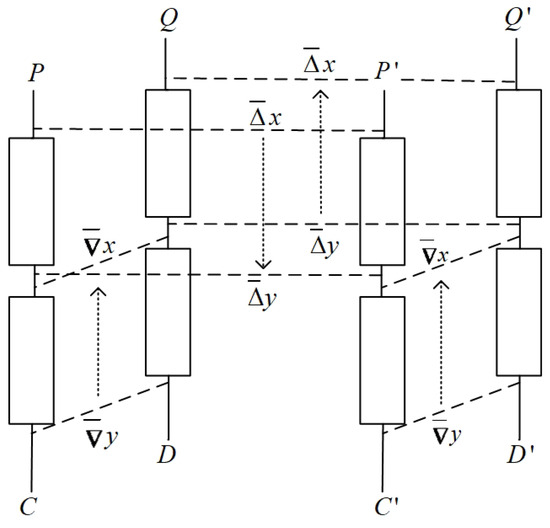
Figure 14. Boomerang attack.

1.

Choose two plaintexts $(P,P^{\prime })$ satisfying $P\oplus P$∼$\overline{\Delta }x$ and denote the corresponding ciphertexts as $(C,C^{\prime })$.

2.

Compute $D=C\oplus \overline{\nabla }y$ and $D^{\prime }=C^{\prime }\oplus \overline{\nabla }y$, and decrypt $D,D^{\prime }$ to obtain the corresponding plaintexts $Q,Q^{\prime }$.

3.

Test whether it holds that $Q\oplus Q^{\prime }$∼$\overline{\Delta }x$.

The probability that $(P,P^{\prime })$ satisfies differential $(\overline{\Delta }x,\overline{\Delta }y)$ is $p_1$. The probability of $(C,D)$ satisfying the differential $(\overline{\nabla }x,\overline{\nabla }y)$ is $p_2$. The probability of $(C^{\prime },D^{\prime })$ satisfying the differential $(\overline{\nabla }x,\overline{\nabla }y)$ is also $p_2$. Under these three conditions, it naturally holds that $En{c}_k^{t_1}\left(Q\right)\oplus En{c}_k^{t_1}\left(Q^{\prime }\right)$∼$\overline{\Delta }y$, so that the probability of $Q\oplus Q^{\prime }$∼$\overline{\Delta }x$ is $p_1$. In summary, the probability of a quadruple generated by the above method being a right quadruple is ${\left(p_1{p}_2\right)}^2$. For a random permutation, this probability is $2^{-d}$, where d is the number of determined bits of $\overline{\Delta }x$. If ${\left(p_1{p}_2\right)}^2>2^{-d}$, then the block cipher can be distinguished from a random permutation through data analysis. A boomerang distinguisher can be used to search for the subkey involved in the last several rounds of the attacked block cipher.

The key to a boomerang attack is to find the boomerang distinguisher, namely, a $t_1$-round truncated differential of $En{c}_k^{t_1}$ and a $t_2$-round truncated differential of ${En{c}_k^{t_2}}^{-1}$ that have a high probability. Thus, the essence of boomerang attack is to find two truncated differentials that have a high probability, which can be achieved using Algorithm 2. According to these analysis, we propose Algorithm 3 for finding boomerang distinguishers.

Steps 4–22 of Algorithm 3 are used to find a truncated differential $(a,b)$ of $En{c}^{t_1}$. The probability of $(a,b)$ is larger than $\sigma$ for at least $1-1/\tau \left(n\right)$ proportion of keys in ${\mathbb{F}}_2^m$. Steps 26–43 are used to find a truncated differential $(\alpha ,\beta )$ of ${En{c}^{t_2}}^{-1}$. The probability of $(\alpha ,\beta )$ is also larger than $\sigma$ for at least $1-1/\tau \left(n\right)$ proportion of keys in ${\mathbb{F}}_2^m$. Steps 23–25 are to determine whether the truncated differential of $En{c}^{t_1}$ has been found. If $\eta =0$, no satisfied truncated differential of $En{c}^{t_1}$ is found, then break out of the current loop and try the next $t_1$. If $(a,b)$ and $(\alpha ,\beta )$ are successfully found, these two differentials form a boomerang distinguisher $\left\{\right(a,b),(\alpha ,\beta \left)\right\}$ of $En{c}_k^r$. The probability of the corresponding quadruple is ${\sigma }^4$ for more than $1-2/\tau \left(n\right)$ proportion of keys in ${\mathbb{F}}_2^m$. The flowchart of Algorithm 3 is presented in Figure 15.

Algorithm 3 Quantum algorithm for finding boomerang distinguishers.

Input: $$The quantum circuit of $En{c}^r$, a polynomial $\tau \left(n\right)$ and a constant $\sigma$ ($0<\sigma <1$) chosen by the adversaries. Output: a boomerang distinguisher of $En{c}^r$. 1: Let $q\left(n\right)={\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3$; 2: Define a set $W:=\Phi$; 3: for$t_1=1,2,\cdots$, $r-1$do 4:     for $j=1,2,\cdots$, n do 5:         for $l=1,\cdots$, $q\left(n\right)$ do 6:            Apply BV algorithm to $En{c}^{t_1}\left[j\right]$ to get an output $u=(u_1,\cdots$, $u_n,\cdots$, $u_{n+m})$; 7:            Let $W=W\cup \left\{\right(u_1,\cdots$, $u_n\left)\right\}$; 8:         end for 9:         Solve the linear equation $\{u·x=i_j|u\in W\}$ to get solution sets $Z_j^{i_j}$ for $i_j=0,1$; 10:          Compute the set $Z_j=Z_j^0\cup Z_j^1$; 11:         Compute the set ${\overline{Z}}_j=\left\{(a,i_j)\right|a\in Z_j^{i_j},i_j=0,1\}$; 12:         Let $W=\Phi$; 13:     end for 14:     Let $\eta =0$; 15:     for $d=n,n-1\cdots$, 1 do 16:         if $S/N=2^d\sigma >1$ then 17:            if there are d different subscripts $j_1,\cdots$, $j_d$ s.t. $Z_{j_1}\cap \cdots \cap Z_{j_d}⊋\left\{\overrightarrow{0}\right\}$ then 18:                Choose at random a vector $a\in Z_{j_1}\cap \cdots \cap Z_{j_d}$, and for $j=1,\cdots$, n, let $$b_j=\left\{\begin{array}{cc}{i}_j,& j\in \{j_1,\cdots ,j_d\}\\ \circledR ,& j\notin \{j_1,\cdots ,j_d\},\end{array}\right.$$ where $i_j$ denotes the bit appended to a in the set ${\overline{Z}}_j$, i.e., $(a,i_j)\in {\overline{Z}}_j$; 19:                 Let $b=(b_1,\cdots$, $b_n)$. Let $\eta =1$ and break out of the current loop; 20:            end if 21:         end if 22:     end for 23:     if $\eta =0$ then 24:         Break out of the current loop; 25:     end if 26:     for $j=1,2,\cdots$, n do 27:         for $l=1,\cdots$, $q\left(n\right)$ do 28:            Apply BV algorithm to ${En{c}^{t_2}}^{-1}\left[j\right]$ to get output $u=(u_1,\cdots$, $u_n,\cdots$, $u_{n+m})$; 29:            Let $W=W\cup \left\{\right(u_1,\cdots$, $u_n\left)\right\}$; 30:         end for 31:         Solve the linear equation $\{u·x=i_j|u\in W\}$, to get solution sets $V_j^{i_j}$ for $i_j=0,1$, respectively; 32:          Compute the set $V_j=V_j^0\cup V_j^1$; 33:         Compute the set ${\overline{V}}_j=\left\{(a,i_j)\right|a\in V_j^{i_j},i_j=0,1\}$; 34:         Let $W=\Phi$; 35:     end for 36:     for $d=n,n-1\cdots$, 1 do 37:         if $S/N=2^d\sigma >1$ then 38:            if there are d different subscripts $j_1,\cdots$, $j_d$ s.t. $V_{j_1}\cap \cdots \cap V_{j_d}⊋\left\{\overrightarrow{0}\right\}$ then 39:                Choose at random a vector $\alpha \in V_{j_1}\cap \cdots \cap V_{j_d}$, and for $j=1,\cdots$, n, let $${\beta }_j=\left\{\begin{array}{cc}{i}_j,& j\in \{j_1,\cdots ,j_d\}\\ \ast ,& j\notin \{j_1,\cdots ,j_d\},\end{array}\right.$$ where $i_j$ denotes the bit appended to $\alpha$ in the set ${\overline{V}}_j$, i.e., $(\alpha ,i_j)\in {\overline{V}}_j$; 40:                 Let $\beta =({\beta }_1,\cdots$, ${\beta }_n)$. Output $[(a,b),(\alpha ,\beta ),t_1]$ and stop; 41:            end if 42:         end if 43:     end for 44: end for 45: Output “No” and stop;

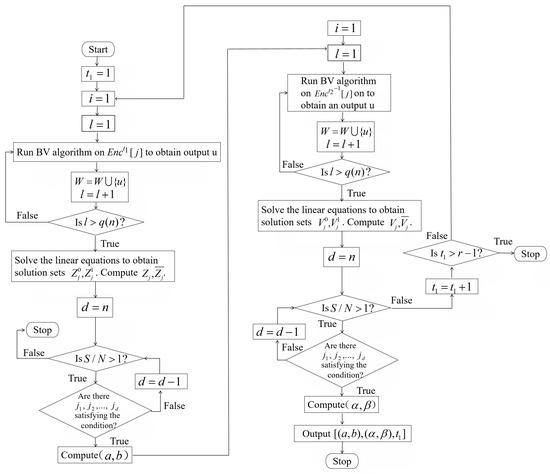
Figure 15. The flowchart of Algorithm 3.

4.2. Analysis of Algorithm 3

The process of Algorithm 3 is actually to call Algorithm 2 on $En{c}^{t_1}$ and ${En{c}^{t_2}}^{-1}$, respectively, for all $t_1=1,2,$⋯, n and $t_2=r-t_1$. Therefore, the total number of Hadamard gates required for Algorithm 3 is

$$\begin{array}{cc}\hfill & \sum _{t_1=1}^{r-1}{\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3\left[4n^2+(4m+2)n\right]\hfill \\ \hfill =& {\displaystyle \frac{r-1}{{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^4(2n+2m+1).\hfill \end{array}$$

Since it holds that

$$\begin{array}{cc}\hfill & \sum _{t_1=1}^{r-1}{\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3(|En{c}^{t_1}{|}_Q+|{En{c}^{t_2}}^{-1}{|}_Q)\hfill \\ \hfill =& \sum _{t_1=1}^{r-1}{\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3\left(\right|En{c}^{t_1}{|}_Q+|En{c}^{t_2}{|}_Q)\hfill \\ \hfill =& \sum _{t_1=1}^{r-1}{\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3{\left|En{c}^r\right|}_Q\hfill \\ \hfill =& {\displaystyle \frac{r-1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3{\left|En{c}^r\right|}_Q,\hfill \end{array}$$

the total number of times Algorithm 3 needs to execute the quantum circuit of $En{c}^r$ is ${\displaystyle \frac{r-1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3$. This number is a polynomial of n and m. In summary, Algorithm 3 requires

$${\displaystyle \frac{r-1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3(4n^2+4mn+2n+|En{c}^r{|}_Q)$$

(7)

universal gates in total.

Algorithm 3 calls Algorithm 2 on $En{c}^{t_1}$ and ${En{c}^{t_2}}^{-1}$, respectively, for all $t_1=1,2,\cdots$, $r-1$ and $t_2=r-t_1$. Thus, Algorithm 3 requires

$${\displaystyle \frac{1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3(m+n+1)\times 2\times (r-1)={\displaystyle \frac{r-1}{{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3(m+n+1)$$

(8)

qubits in total.

The parameters involved in Algorithm 3 include the constant $\sigma$, polynomial $\tau \left(n\right)$, blocksize n, number of rounds r and key length m. For the convenience of parameter analysis, we list the numbers of quantum resources required for Algorithm 3 in Table 5, then analyze the influence of parameters on the complexity of Algorithm 3.

Table 5. Quantum resources required for Algorithm 3.

Hadamard Gate	Quantum Execution of ${\mathit{Enc}}^{\mathit{r}}$	Qubit
${\displaystyle \frac{r-1}{{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^4(2m+2n+1)$	${\displaystyle \frac{r-1}{2{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3$	${\displaystyle \frac{r-1}{{(1-\sigma )}^2}}\tau {\left(n\right)}^2{n}^3(m+n+1)$

Similar to Algorithm 2, the parameters $\sigma$ of Algorithm 3 are chosen by the adversary. ${\sigma }^4$ is the lower bound of the probability of boomerang distinguishers desired by the adversary. Since the probability of any boomerang distinguisher of a random permutation is no more than ${\displaystyle \frac{1}{2^4}}$, taking $\sigma ={\displaystyle \frac{1}{2}}$ is sufficient to ensure that the boomerang distinguisher output by Algorithm 3 is an effective distinguisher.

The parameter $\tau \left(n\right)$ is a polynomial chosen by the adversary. It characterizes the expected proportion of keys under which the output boomerang distinguisher has high probability. Specifically, $\tau \left(n\right)$ can be chosen as a constant $t_0$, then the number of Hadamard gates is $O\left(r{n}^5\right)$, the number of times $En{c}^r$ needs to be executed quantumly is $O\left(r{n}^3\right)$ and the number of qubits is $O\left(r{n}^4\right)$. Here, we omit m because usually $m=O\left(n\right)$.

The values of parameters $n,r,m$ depend on which block cipher is attacked. For common non-lightweight block ciphers, the value of the blocksize n is generally between 128 and 256, the value of the round number r is generally between 10 and 40 and the value of the key length m is generally between 128 and 256. For common lightweight block ciphers, the value of the blocksize n is generally between 32 and 128, the value of the round number r is generally between 32 and 80 and the value of the key length m is generally between 64 and 256. We take $\sigma ={\displaystyle \frac{1}{2}}$, $\tau \left(n\right)=2$ as an example and list the values of these parameters of several common block ciphers and the corresponding complexity of Algorithm 3 in Table 6.

Table 6. Quantum complexity of Algorithm 3 on specific block ciphers ¹.

Block Cipher	n	r	m	Hadamard Gate	Quantum Execution of ${\mathit{Enc}}^{\mathit{r}}$	Qubit
LBlock	64	32	80	$2^{41.1}$	$2^{26.0}$	$2^{34.1}$
PRESENT-80	64	31	80	$2^{41.1}$	$2^{25.9}$	$2^{34.1}$
SPECK32/64	32	22	64	$2^{36.0}$	$2^{22.4}$	$2^{30.0}$
Simon-32/64	32	32	64	$2^{36.5}$	$2^{23.0}$	$2^{30.6}$

¹ Complexity is calculated by taking $\sigma ={\displaystyle \frac{1}{2}}$ and $\tau \left(n\right)=2$.

Since IBM quantum platform only supports operations of 100-plus qubits, according to Table 6, it is unfeasible to completely implement or simulate Algorithm 3 on a block cipher.

5. Results

We apply BV algorithm to truncated differential cryptanalysis and boomerang cryptanalysis and propose two quantum algorithms for finding high-probability truncated differentials and boomerang distinguishers, respectively.

For truncated differential cryptanalysis, we propose Algorithm 2 for finding truncated differentials that have high probability. Given the quantum circuit of a block cipher $En{c}^t$, Algorithm 2 takes the key as a part of the input and repeats running BV algorithm on each component function of $En{c}^t$ to find truncated differentials of each $En{c}^t\left[j\right]$, then obtains a truncated differential of $En{c}^t$ by searching for a common input difference of as many component functions as possible. When executing Algorithm 2, the adversary first chooses parameters $\sigma$ and $\tau \left(n\right)$, Algorithm 2 is then run to obtain a truncated differential. We use quantum information theory and probability theory to rigorously prove that the probability of the truncated differential output by Algorithm 2 must be greater than $\sigma$ for more than $(1-{\displaystyle \frac{1}{\tau \left(n\right)}})$ proportion of keys in ${\mathbb{F}}_2^m$. Algorithm 2 can be run by Q1 quantum adversaries and the complexity is at polynomial level. We take $\sigma ={\displaystyle \frac{1}{2}}$ as an example and list numbers of universal gates and qubits of Algorithm 2 under different values of $\tau \left(n\right)$ in Table 7. The values in Table 7 are obtained according to Equations (5) and (6).

Table 7. Quantum complexity of Algorithm 2 under $\sigma ={\displaystyle \frac{1}{2}}$.

$\mathit{\tau }\left(\mathit{n}\right)$	Universal Gate	Qubit
2	$8n^3(2n^2+2mn+n+|En{c}^t{|}_Q)$	$8n^3(n+m+1)$
$n/2$	${\displaystyle \frac{1}{2}}{n}^5(2n^2+2mn+n+|En{c}^t{|}_Q)$	${\displaystyle \frac{1}{2}}{n}^5(n+m+1)$
n	$2n^5(2n^2+2mn+n+|En{c}^t{|}_Q)$	$2n^5(n+m+1)$

For boomerang cryptanalysis, we propose Algorithm 3 for finding boomerang distinguishers. Given the quantum circuit of a block cipher $En{c}^r$, Algorithm 3 traverses the value of $t_1$ from 1 to $r-1$ and calls Algorithm 2 to find the truncated differentials of $En{c}^{t_1}$ and $En{c}^{t_2}$, respectively, where $t_2=r-t_1$. When executing Algorithm 3, the adversary also needs to choose parameters $\sigma$ and $\tau \left(n\right)$, then runs Algorithm 3 to obtain a boomerang distinguisher of $En{c}^r$. The probability of generating a right quadruple of this boomerang distinguisher is greater than ${\sigma }^4$ for more than $(1-{\displaystyle \frac{2}{\tau \left(n\right)}})$ proportion of keys in ${\mathbb{F}}_2^m$. Algorithm 3 can be run by Q1 quantum adversaries and the complexity is at polynomial level. We take $\sigma ={\displaystyle \frac{1}{2}}$ as an example, and list number of universal gates and qubits of Algorithm 3 under different values of $\tau \left(n\right)$ in Table 8. The values in Table 8 are obtained according to Equations (7) and (8).

Table 8. Quantum complexity of Algorithm 3 under $\sigma ={\displaystyle \frac{1}{2}}$.

$\mathit{\tau }\left(\mathit{n}\right)$	Universal Gate	Qubit
2	$8(r-1)n^3(4n^2+4mn+2n+|En{c}^r{|}_Q)$	$16(r-1)n^3(n+m+1)$
$n/2$	${\displaystyle \frac{1}{2}}(r-1)n^5(4n^2+4mn+2n+|En{c}^r{|}_Q)$	$(r-1)n^5(n+m+1)$
n	$2(r-1)n^5(4n^2+4mn+2n+|En{c}^r{|}_Q)$	$4(r-1)n^5(n+m+1)$

Both Algorithm 2 and Algorithm 3 can be executed in $Q_1$ model. As shown in Table 7 and Table 8, the quantum complexity of both algorithms are at the polynomial level. They show the superiority of quantum computing in cryptanalysis.

6. Conclusions

In this study, we further explored the superior computing power of quantum algorithms when applied to the field of cryptanalysis. We used BV algorithm to enhance two variants of differential cryptanalysis: truncated differential cryptanalysis and boomerang cryptanalysis. We constructed two quantum algorithms that can find truncated differentials and boomerang distinguishers of block ciphers. We prove with an overwhelming probability, that the truncated differentials or boomerang distinguishers found by our algorithms have a high probability for the most keys in the key space.

The complexity of our algorithms is at the polynomial level and adversaries can realize them in Q1 model. Compared to many proposed quantum attack algorithms [14,15,16,18,19,46] which demand quantum queries, our algorithms are more practical for realization. Classical automatic tools for searching truncated differentials with high probability or boomerang distinguishers were unable to consider all the details of S-boxes when the S-boxes were not small-scale. For example, in the case of the widely used 8-bit S-boxes, the classical searching tools can only work for extremely few rounds. In comparison, our algorithms fully utilize the strengths of quantum computing to compensate for this shortcoming. Their quantum circuits strictly compute the S-boxes when performing the operator $U_{En{c}^t}$ and only have polynomial quantum gates. Moreover, classical truncated differential and boomerang attacks are unable to consider the influence of key scheduling in the attack model of single-key, but the proposed algorithms incorporate the key scheduling into the operator $U_{En{c}^t}$ and thus fully consider the impact of the key scheduling. We believe the study of quantum cryptanalysis is crucial for the design of quantum-secure cryptosystems in order to prepare for the arrival of quantum computers.

For further research, reducing the quantum complexity of the proposed algorithms is a meaningful direction. It would also be interesting to explore the possible applications of quantum algorithms in other cryptanalytic tools such as integral and algebraic attacks. Quantum key distribution technique uses quantum systems to generate and distribute keys. The quantum algorithms proposed in this paper are used to attack traditional block ciphers that encrypt classical information. Investigating a combination of the proposed algorithms with quantum key distribution technique may be an interesting research direction.