Trajectory Planning Design for Parallel Parking of Autonomous Ground Vehicles with Improved Safe Travel Corridor
Abstract
:1. Introduction
2. Construction of Parallel Parking Planning Problem
2.1. Vehicle Kinematic Model
2.2. Vehicle Kinematic Constraints
2.3. Initial and Terminal State Constraints
2.4. Path Constraints
2.5. Parking Cost Function
s.t. kinematic constraints (6);
boundary conditions (7);
Path constraint (9) and (10).
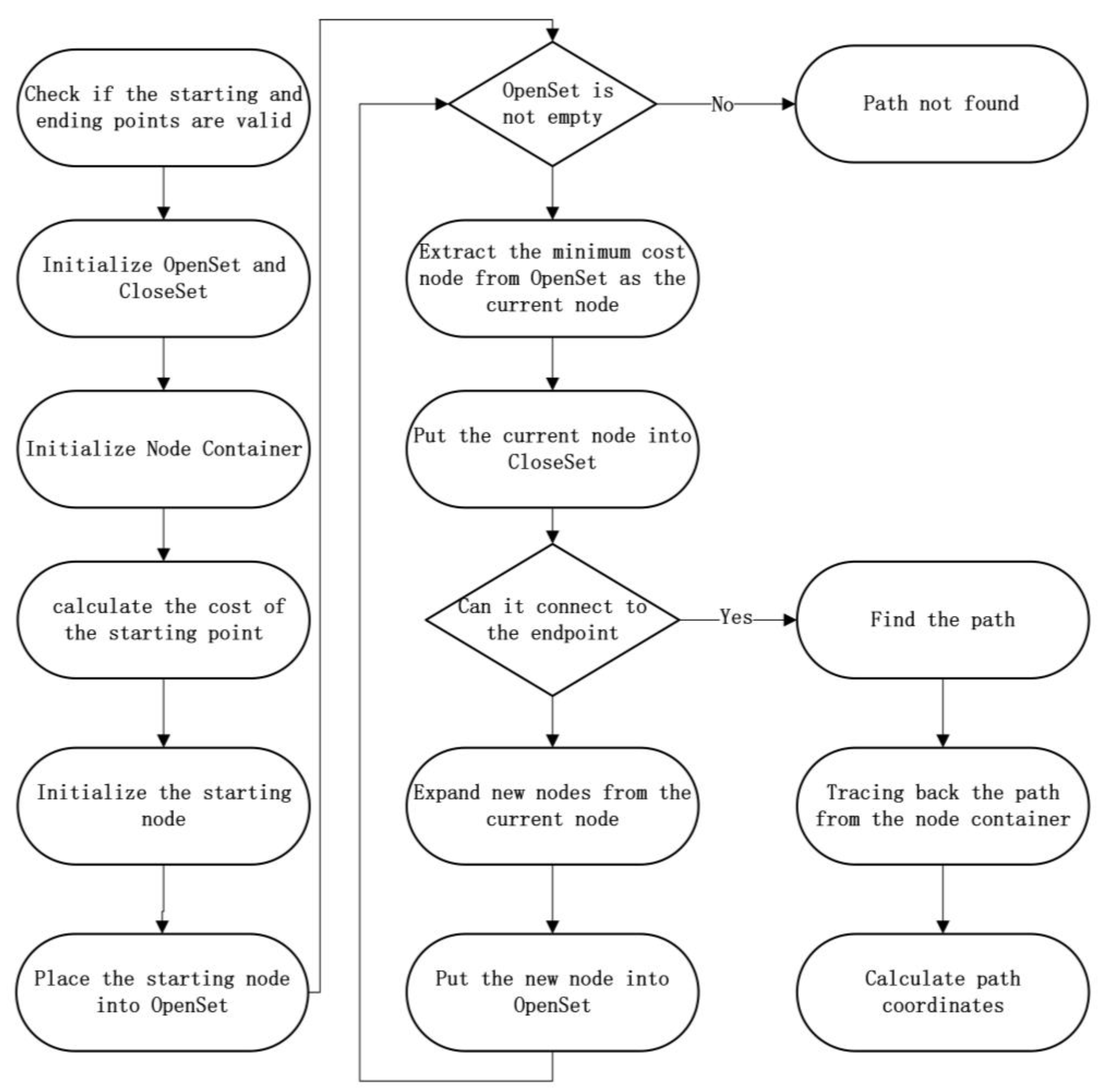
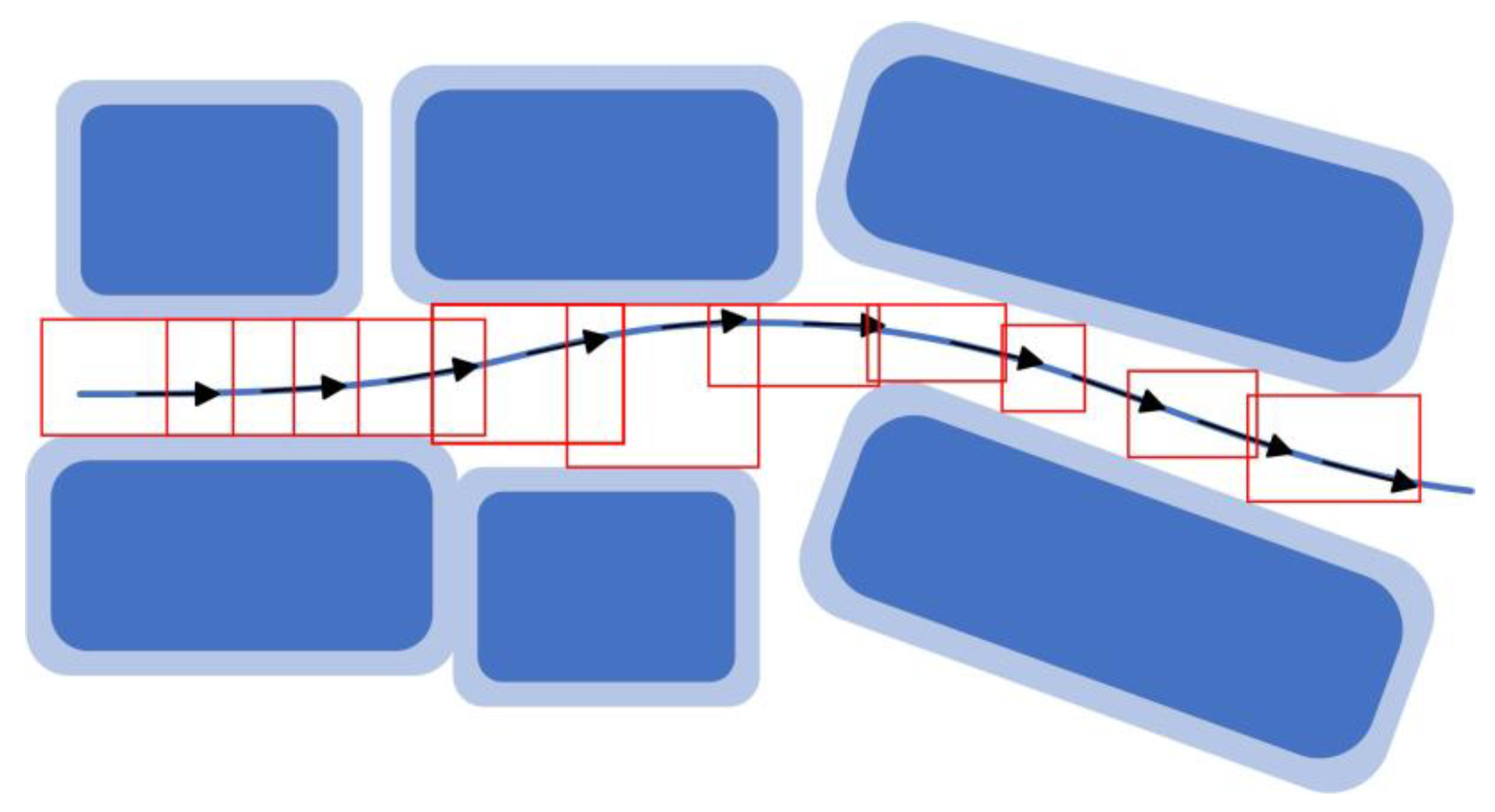
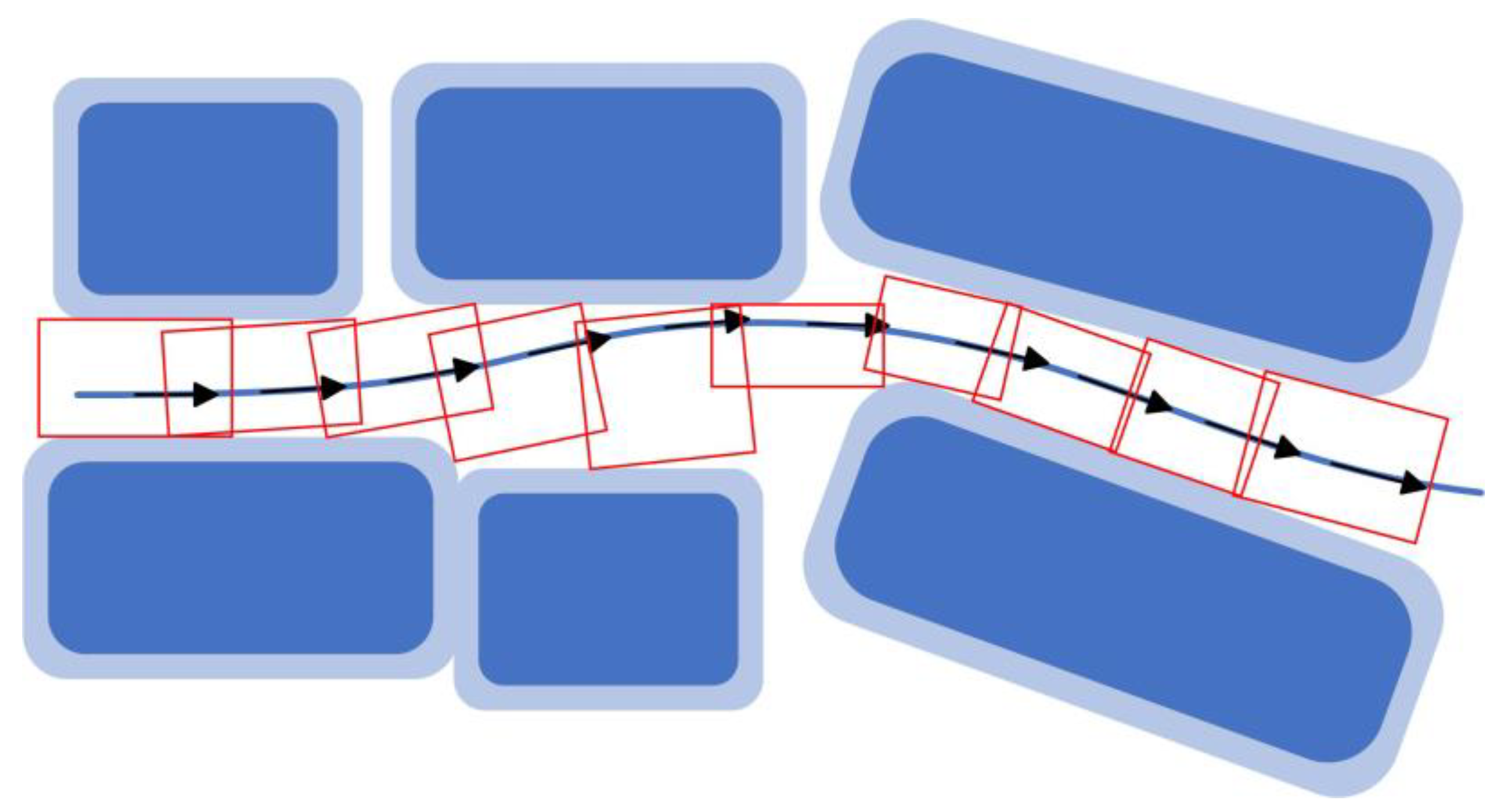
3. Parallel Parking Trajectory Planning Based on I-STC
3.1. Initial Solution of I-STC
- (1)
- Search dimensions
- (2)
- Node expansion method
- (3)
- Cost function of hybrid A*
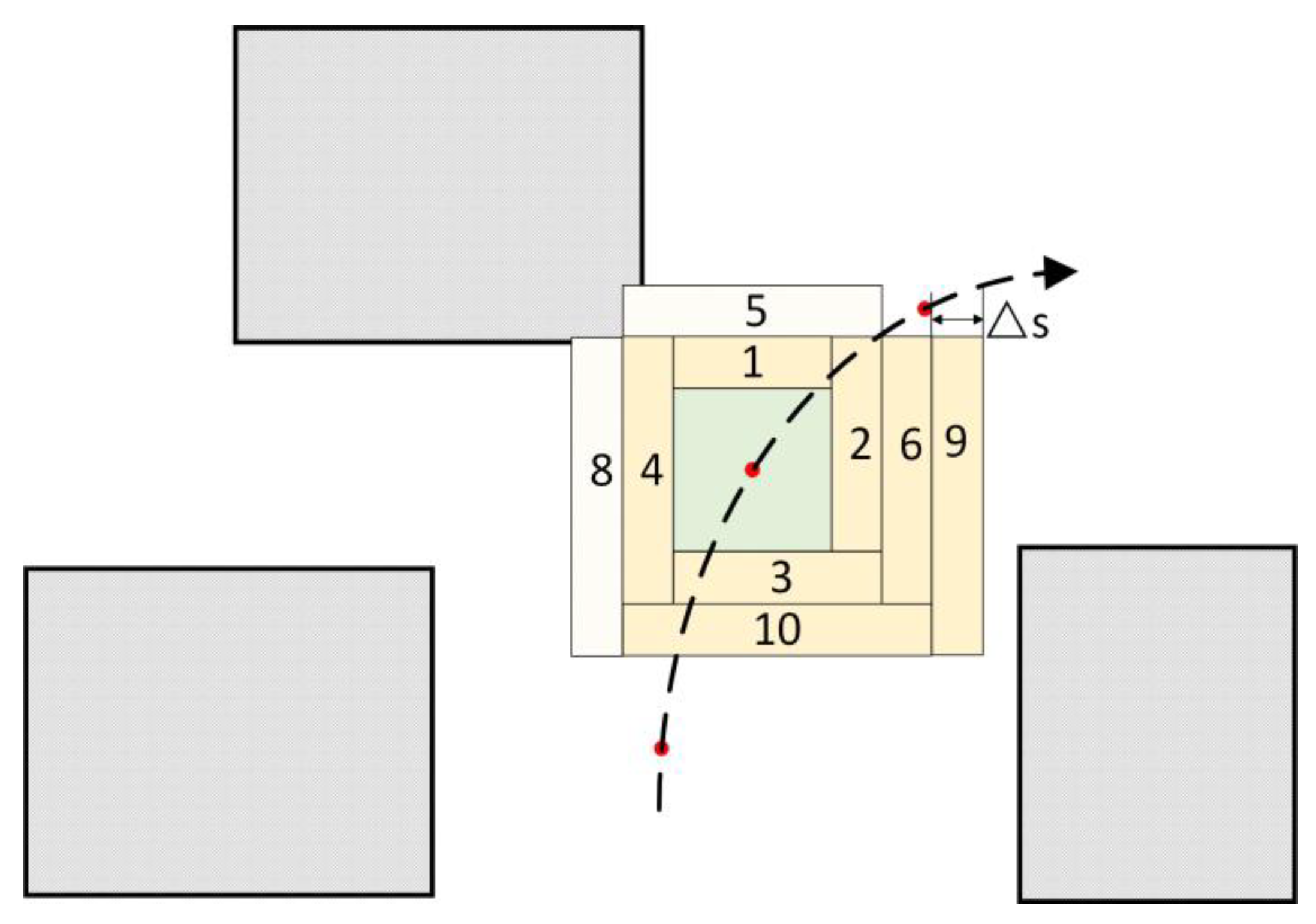
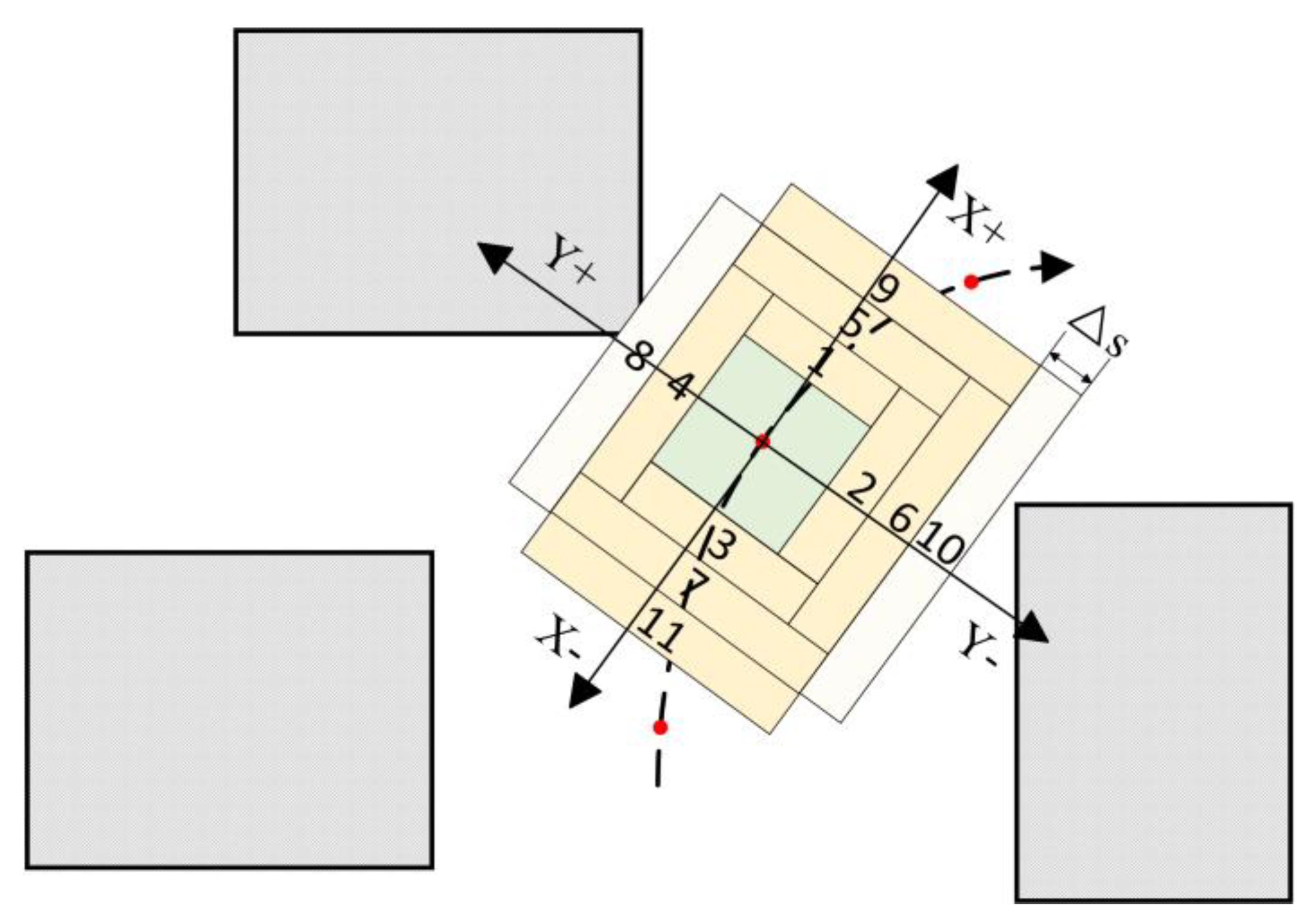
3.2. Construction of I-STC
s.t. kinematic constraints (6);
boundary conditions (7);
Path constraint (10) and (14).
4. Simulation and Results
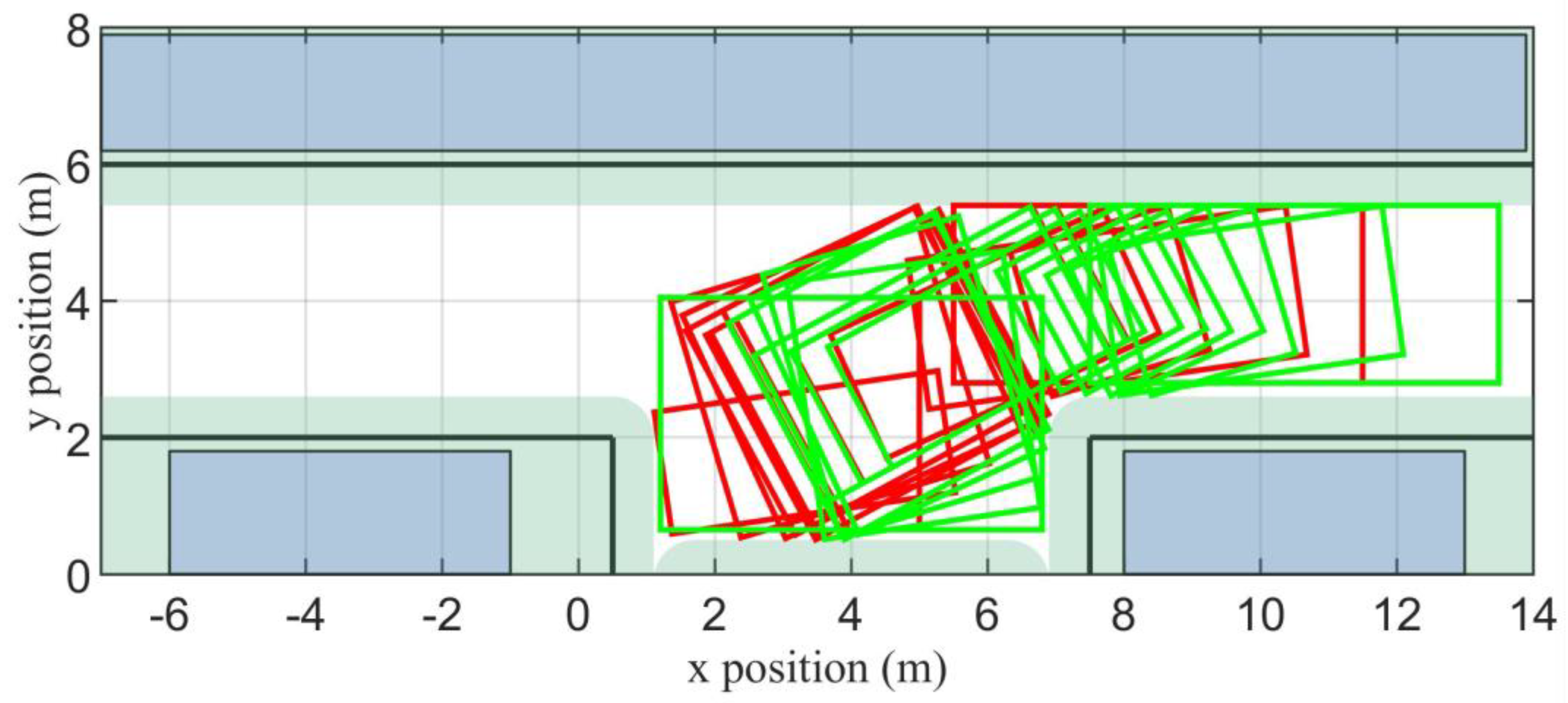
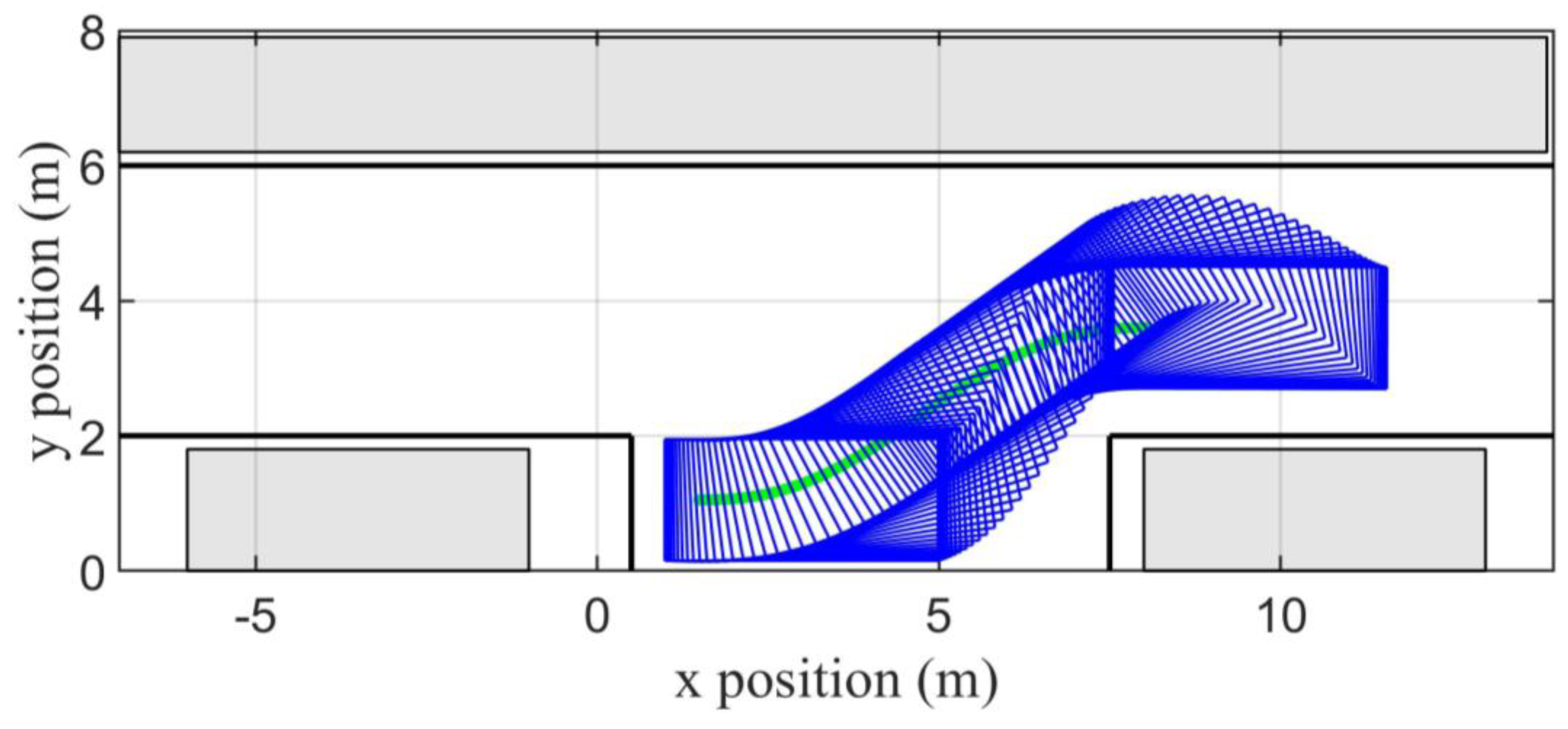
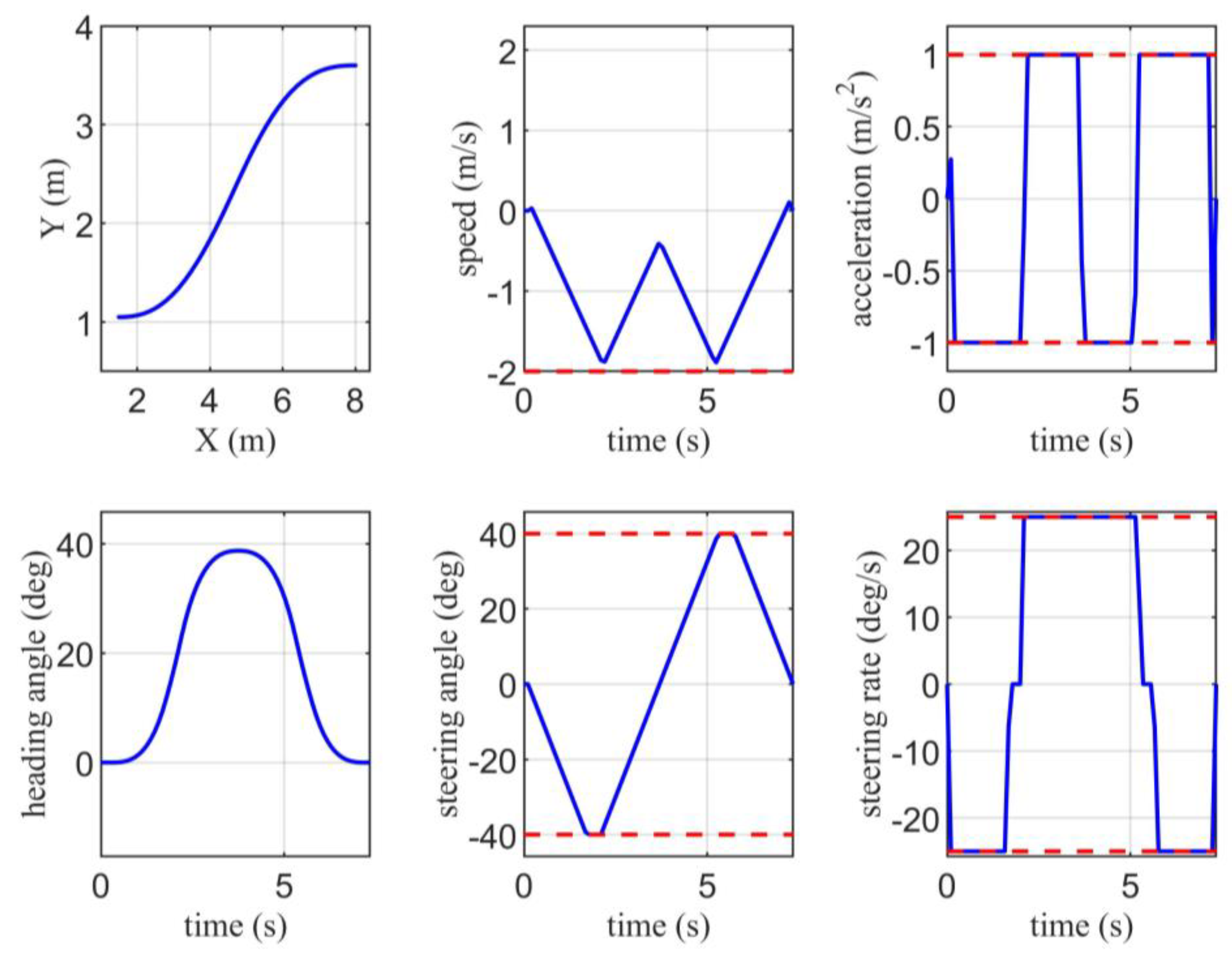
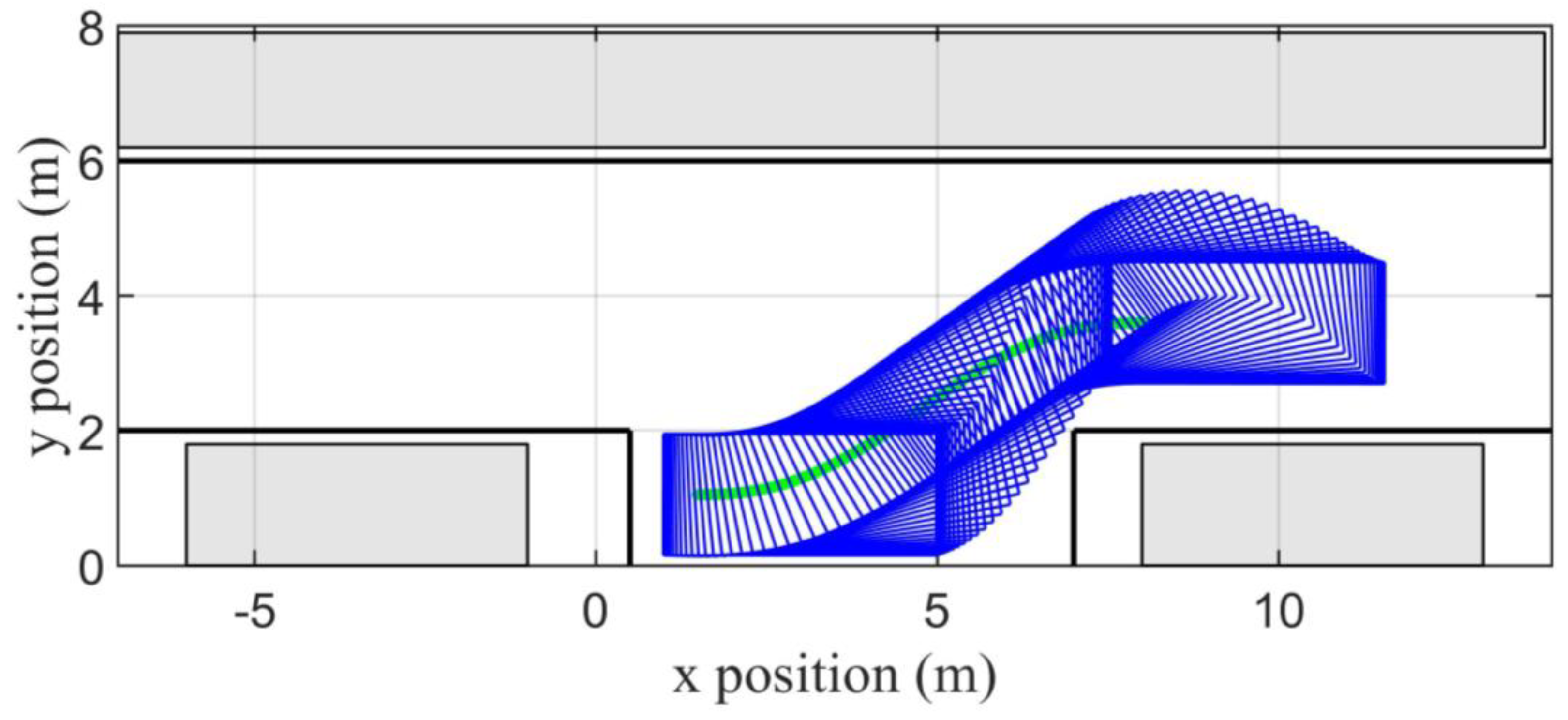
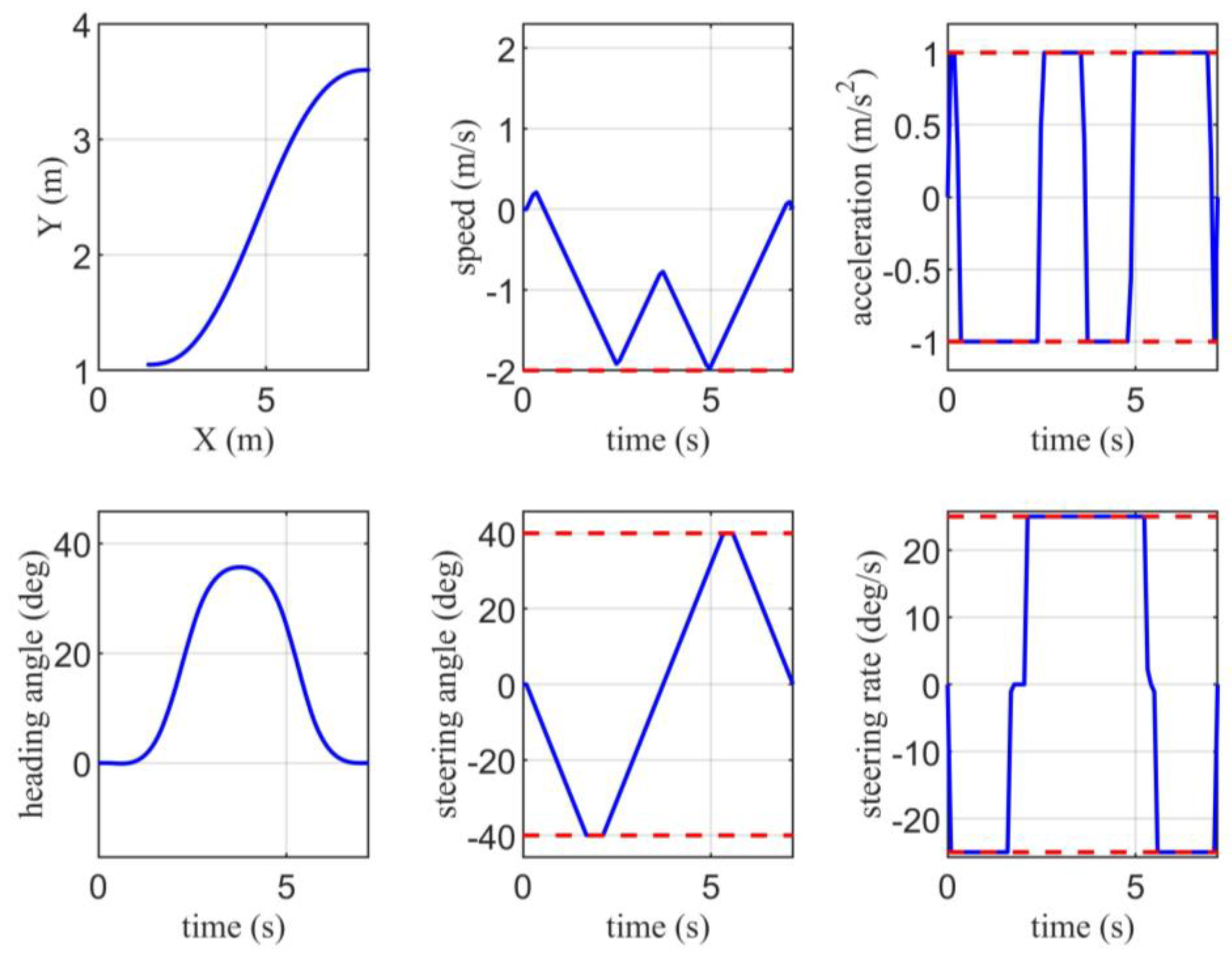
4.1. Scenario 1
4.2. Scenario 2
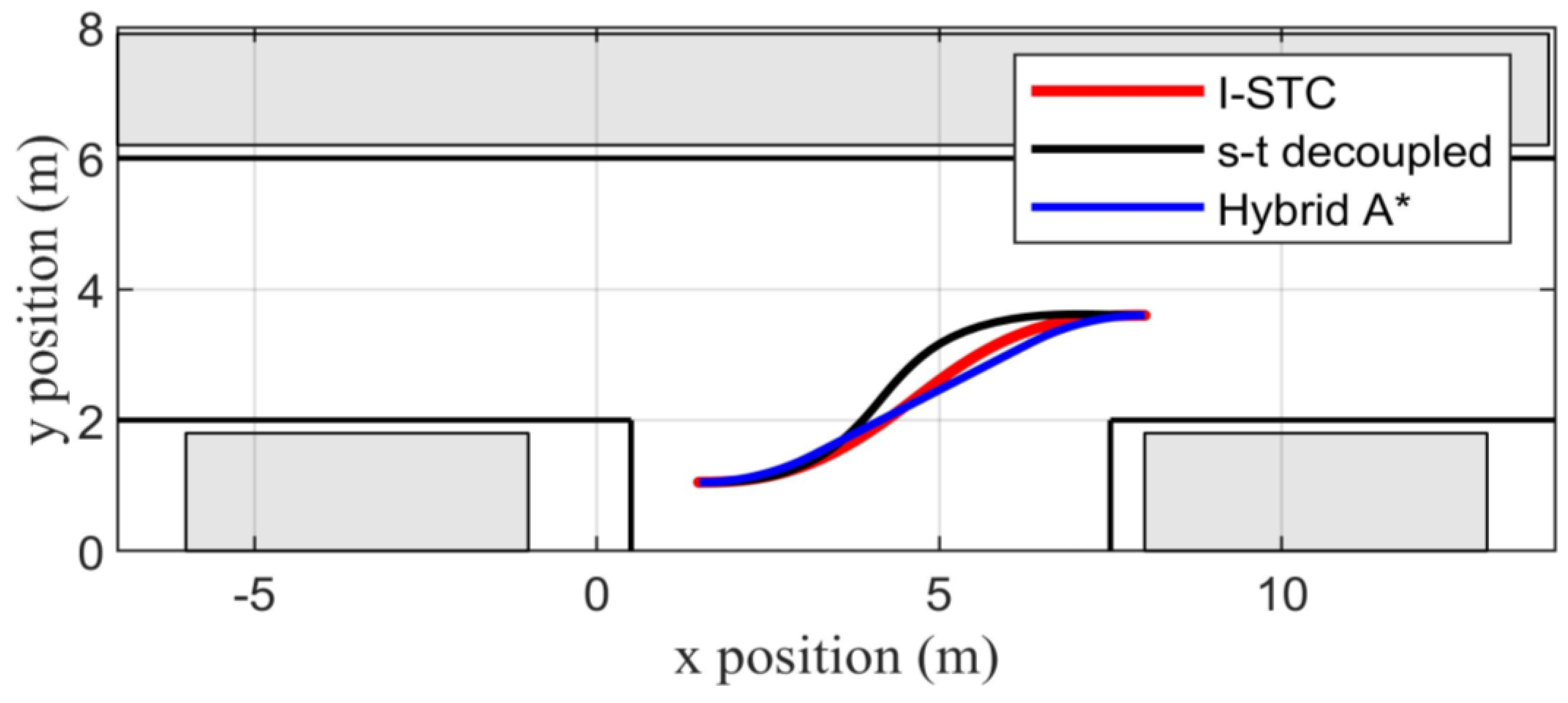
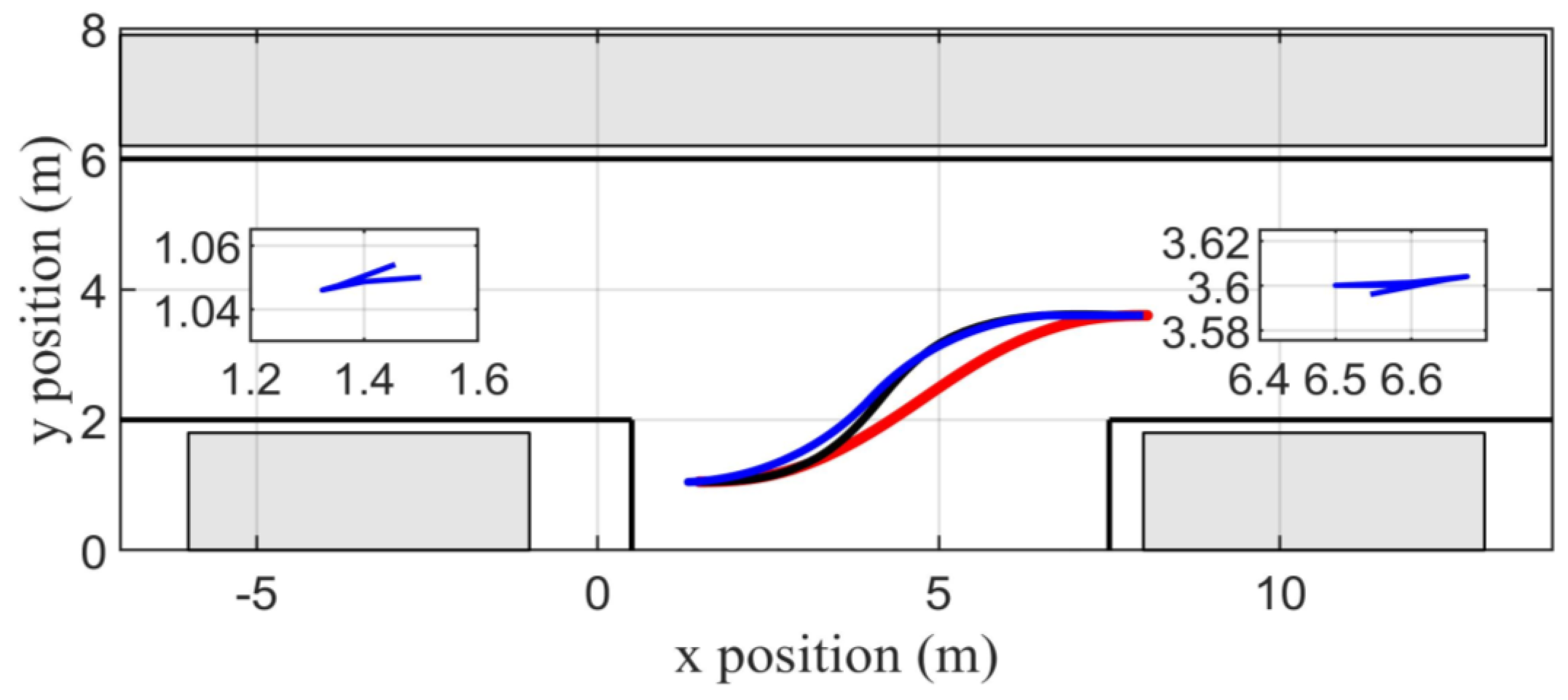
4.3. Comparison against Other Techniques
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rehman, N.U.; Kumar, K. Implementation of an autonomous path planning & obstacle avoidance UGV using SLAM. In Proceedings of the International Conference on Engineering and Emerging Technologies (ICEET), Lahore, Pakistan, 22–23 February 2018; pp. 1–5. [Google Scholar]
- Palanisamy, P.; Mohan, R.E.; Semwal, A.; Jun, M.L.M.; Félix, G.B.; Balakrishnan, S.; Elangovan, K.; Ramalingam, B.; Terntzer, D.N. Drain Structural Defect Detection and Mapping Using AI-Enabled Reconfigurable Robot Raptor and IoRT Framework. Sensors 2021, 21, 7287. [Google Scholar] [CrossRef] [PubMed]
- Claussmann, L.; Revilloud, M.; Gruyer, D.; Glaser, S. A review of motion planning for highway autonomous driving. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1826–1848. [Google Scholar] [CrossRef]
- Zhao, L.; Zheng, G.; Li, J. Automatic parking path optimization based on Bezier curve fitting. In Proceedings of the IEEE International Conference on Automation and Logistics (ICAL), Zhengzhou, China, 15–17 August 2012; pp. 583–587. [Google Scholar]
- Min, K.; Choi, J.; Kim, H.; Myung, H. Design and implementation of path generation algorithm for controlling autonomous driving and parking. In Proceedings of the 12th International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 17–21 October 2012; pp. 956–959. [Google Scholar]
- Li, S.; Wang, J. Parallel Parking Path Planning in Narrow Space Based on a Three-Stage Curve Interpolation Method. IEEE Access 2023, 11, 93841–93851. [Google Scholar] [CrossRef]
- Moon, J.; Bae, I.; Cha, J.; Kim, S. A trajectory planning method based on forward path generation and backward tracking algorithm for automatic parking systems. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 719–724. [Google Scholar]
- Daniali, S.M.; Khosravi, A.; Sarhadi, P.; Tavakkoli, F. An Automatic Parking Algorithm Design Using Multi-Objective Particle Swarm Optimization. IEEE Access 2023, 11, 49611–49624. [Google Scholar] [CrossRef]
- Malfoy, A.; Ajwad, S.A.; Boudkhil, M. Autonomous Parking System for Vehicles: Trajectory Planning and Control. In Proceedings of the IEEE 11th International Conference on Systems and Control (ICSC), Sousse, Tunisia, 18–20 December 2023; pp. 542–547. [Google Scholar]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), St. Louis, MO, USA, 25–28 March 1985; pp. 500–505. [Google Scholar]
- Sudhakara, P.; Ganapathy, V.; Priyadharshini, B.; Sundaran, K. Obstacle Avoidance and Navigation Planning of a Wheeled Mobile Robot using Amended Artificial Potential Field Method. Procedia Comput. Sci. 2018, 133, 998–1004. [Google Scholar] [CrossRef]
- Raja, R.; Dutta, A.; Venkatesh, K.S. New potential field method for rough terrain path planning using genetic algorithm for a 6-wheel rover. Robot. Auton. Syst. 2015, 72, 295–306. [Google Scholar] [CrossRef]
- Wang, D.; Chen, S.; Zhang, Y. Path planning of mobile robot in dynamic environment: Fuzzy artificial potential field and extensible neural network. Artif Life Robot. 2021, 26, 129–139. [Google Scholar] [CrossRef]
- Jhang, J.; Lian, F.L. An Autonomous Parking System of Optimally Integrating Bidirectional Rapidly-Exploring Random Trees and Parking-Oriented Model Predictive Control. IEEE Access 2020, 8, 163502–163523. [Google Scholar] [CrossRef]
- Zheng, K.; Liu, S. RRT based Path Planning for Autonomous Parking of Vehicle. In Proceedings of the IEEE 7th Data Driven Control and Learning Systems Conference (DDCLS), Enshi, China, 25–27 May 2018; pp. 627–632. [Google Scholar]
- Nayak, S.; Otte, M.W. Bidirectional Sampling-Based Motion Planning Without Two-Point Boundary Value Solution. IEEE Trans. Robot. 2022, 38, 3636–3654. [Google Scholar] [CrossRef]
- Xiong, L.; Gao, J.; Fu, Z.; Xiao, K. Path planning for automatic parking based on improved Hybrid A* algorithm. In Proceedings of the 5th CAA International Conference on Vehicular Control and Intelligence (CVCI), Tianjin, China, 29–31 October 2021; pp. 1–5. [Google Scholar]
- Han, L.; Wu, X.; Sun, X. Hybrid path planning algorithm for mobile robot based on A* algorithm fused with DWA. In Proceedings of the IEEE 3rd International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 26–28 May 2023; pp. 1465–1469. [Google Scholar]
- Blackmore, L.; Williams, B. Optimal manipulator path planning with obstacles using disjunctive programming. In Proceedings of the American Control Conference (ACC), Minneapolis, MN, USA, 14–16 June 2006; pp. 3–6. [Google Scholar]
- Poy, Y.L.; Darmaraju, S.; Kwan, B.H. Multi-robot Path Planning using Modified Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Shah Alam, Malaysia, 17 June 2013; pp. 225–230. [Google Scholar]
- Zhang, G.; Chai, S.; Chai, R.; Garcia, M.; Xia, Y. Fuzzy Goal Programming Algorithm for Multi-Objective Trajectory Optimal Parking of Autonomous Vehicles. IEEE Trans. Intell. Vehicle. 2024, 9, 1909–1918. [Google Scholar]
- Liu, P.; Chenv, Z.; Liu, M.; Piao, C.; Wan, K.; Huang, H. Vertical Parking Trajectory Planning with the Combination of Numerical Optimization Method and Gradient Lifting Decision Tree. IEEE Trans. Consum. Electr. 2024, 70, 1845–1856. [Google Scholar] [CrossRef]
- Chai, R.; Tsourdos, A.; Savvaris, A.; Chai, S.; Xia, Y.; Chen, C.L.P. Multiobjective Optimal Parking Maneuver Planning of Autonomous Wheeled Vehicles. IEEE Trans. Ind. Electr. 2020, 67, 10809–10821. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.M.; Shao, Z.J. Spatio-temporal decomposition: A knowledge-based initialization strategy for parallel parking motion optimization. Knowl.-Based Syst. 2016, 107, 179–196. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Man. Cy. S. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Bentes, C.; Saotome, O. Dynamic Swarm Formation with Potential Fields and A* Path Planning in 3D Environment. In Proceedings of the Brazilian Robotics Symposium and Latin American Robotics Symposium (SBR-LARS), Fortaleza, Brazil, 16–19 October 2012; pp. 74–78. [Google Scholar]
- Lian, J.; Ren, W.; Yang, D.; Li, L.; Yu, F. Trajectory Planning for Autonomous Valet Parking in Narrow Environments with Enhanced Hybrid A* Search and Nonlinear Optimization. IEEE Trans. Intell. Veh. 2023, 8, 3723–3734. [Google Scholar] [CrossRef]
- Meng, T.; Yang, T.; Huang, J. Improved Hybrid A-Star Algorithm for Path Planning in Autonomous Parking System Based on Multi-Stage Dynamic Optimization. Int. J. Autom. Technol. 2023, 24, 459–468. [Google Scholar] [CrossRef]
- Hua, Z. Constructing Safe Flight Corridors for Quadrotor Navigation in Cluttered 3-D Environments. In Proceedings of the IEEE 3rd International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 29–31 January 2023; pp. 1625–1628. [Google Scholar]




| Technique | Advantages | Disadvantages | Implemented in | |
|---|---|---|---|---|
| Geometric planning method | Béziers | Low computational cost. Good smoothness | The computational complexity increases with the number of control points | [4,6,7] |
| Polynomials | Low computational cost. Enables curve stitching | Difficult to calculate coefficients and determine equations | [9] | |
| Clothoids | Smooth transition, good curvature continuity | Defining a curve through integration can lead to longer processing times | [8] | |
| Artificial potential field method | Good adaptability and fast computation time | Easy to fall into local minima | [10,11,12,13] | |
| Sampling method | Hybrid A* | Considers the vehicle kinematic model | Not applicable to dynamic environments | [17,18] |
| RRT | Fast speed, strong search ability | Low reliability in complex environments | [14,15,16] | |
| Numerical optimization method | Can effectively consider various constraints | Long computation time | [19,20,21,22,23] | |
| Description | Variable | Description | Variable |
|---|---|---|---|
| Front overhang length | Lf | Heading angle | θ |
| Rear overhang length | Lr | Vehicle wheelbase | Lw |
| Vehicle width | W | Steering angle | Ψ |
| Acceleration of the vehicle | a | Speed of the vehicle | v |
| Angular velocity of the front wheel steering angle | ω | Expansion length of I-STC | l |
| X-coordinate of the center of the rear wheel of the vehicle | x | Y-coordinate of the center of the rear wheel of the vehicle | y |
| State variable of the vehicle | x(t) | Control variable of the vehicle | u(t) |
| Equivalent center points x coordinate for front wheel | xf | Equivalent center points y coordinate for front wheel | yf |
| Equivalent center points x coordinate for rear wheel | xr | Equivalent center points y coordinate for rear wheel | yr |
| Description | Scale | Unit |
|---|---|---|
| Length of parking space | 7, 6.5 | m |
| Width of parking space | 2.2 | m |
| Parking channel width | 4 | m |
| Front overhang length | 0.5 | m |
| Rear overhang length | 0.5 | m |
| Vehicle length | 4 | m |
| Vehicle width | 1.8 | m |
| Vehicle wheelbase | 3 | m |
| Bound of steering angle | 0.68 | rad |
| Bound of acceleration | 1 | m/s2 |
| Bound of velocity | 2 | m/s |
| Bound of steering angular velocity | 0.34 | rad/s |
| Hybrid A* growth step size | 0.3 | m |
| Maximum length of I-STC | 3 | m |
| Expansion step size of I-STC | 0.1 | m |
| Description | Length of Planned Path (m) | Number of Speed Reversals | CPU Time (s) | |
|---|---|---|---|---|
| Scenario 1 | I-STC | 7.1962 | 2 | 1.2384 |
| Spatio-temporal decoupled | 7.3688 | 0 | 14.5823 | |
| Hybrid A* | 7.0708 | 0 | 0.2872 | |
| Scenario 2 | I-STC | 7.2681 | 2 | 2.5726 |
| Spatio-temporal decoupled | 7.3688 | 0 | 28.3473 | |
| Hybrid A* | 7.9354 | 3 | 0.5218 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.; Tao, Y.; Opinat Ikiela, N.V. Trajectory Planning Design for Parallel Parking of Autonomous Ground Vehicles with Improved Safe Travel Corridor. Symmetry 2024, 16, 1129. https://doi.org/10.3390/sym16091129
Jin X, Tao Y, Opinat Ikiela NV. Trajectory Planning Design for Parallel Parking of Autonomous Ground Vehicles with Improved Safe Travel Corridor. Symmetry. 2024; 16(9):1129. https://doi.org/10.3390/sym16091129
Chicago/Turabian StyleJin, Xianjian, Yinchen Tao, and Nonsly Valerienne Opinat Ikiela. 2024. "Trajectory Planning Design for Parallel Parking of Autonomous Ground Vehicles with Improved Safe Travel Corridor" Symmetry 16, no. 9: 1129. https://doi.org/10.3390/sym16091129
APA StyleJin, X., Tao, Y., & Opinat Ikiela, N. V. (2024). Trajectory Planning Design for Parallel Parking of Autonomous Ground Vehicles with Improved Safe Travel Corridor. Symmetry, 16(9), 1129. https://doi.org/10.3390/sym16091129






