The Impact of the Nonlinear Integral Positive Position Feedback (NIPPF) Controller on the Forced and Self-Excited Nonlinear Beam Flutter Phenomenon
Abstract
:1. Introduction
2. Scientific Type
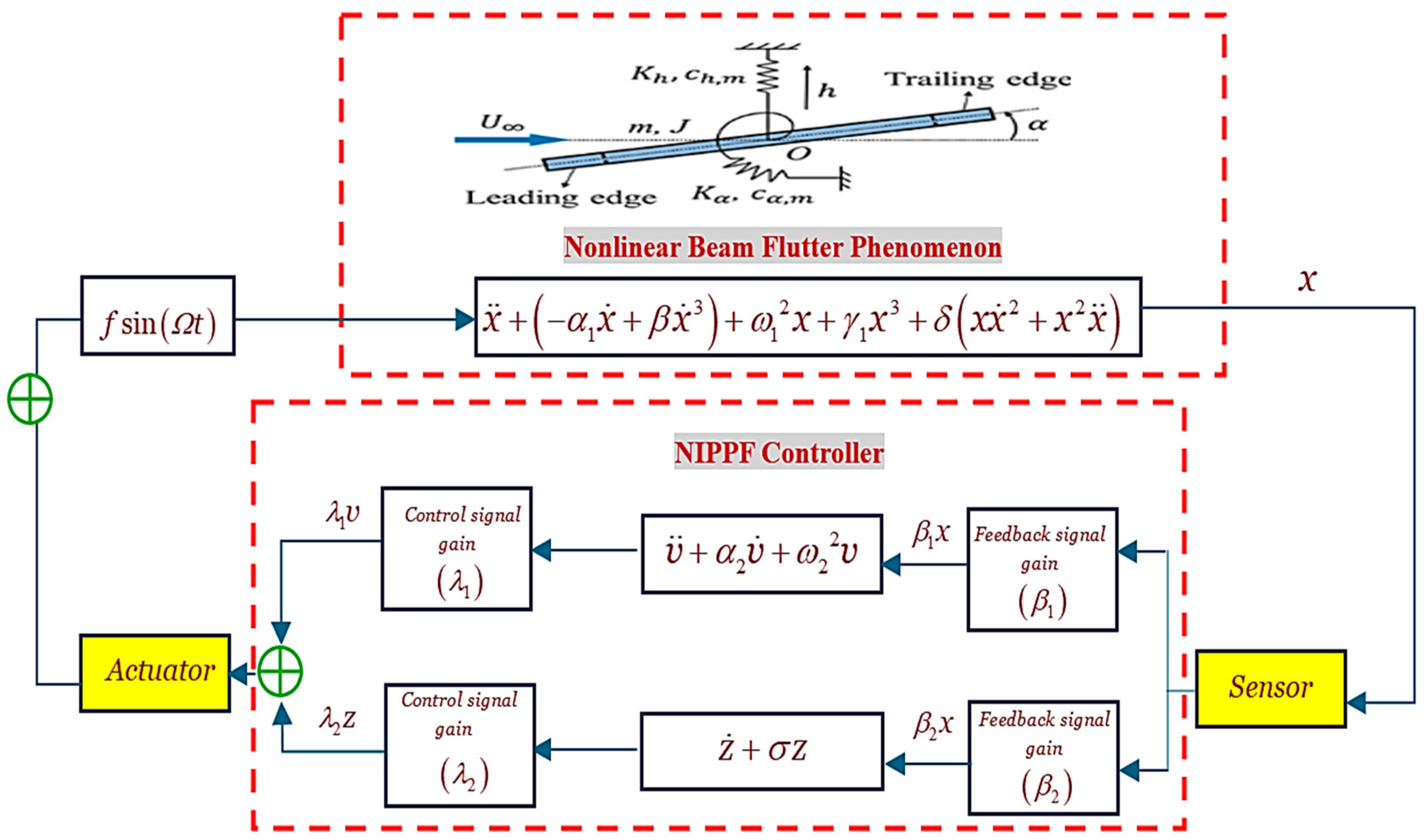
2.1. Uncontrolled System Dynamics
2.2. System Dynamics with NIPPF Control
3. Analytical Investigations
3.1. Perturbation Analysis
- (i)
- PR:
- (ii)
- IR:
3.2. Periodic Solutions
3.3. Fixed-Point Solution
3.4. Determining Stability by Linearizing the System
4. Results and Discussion
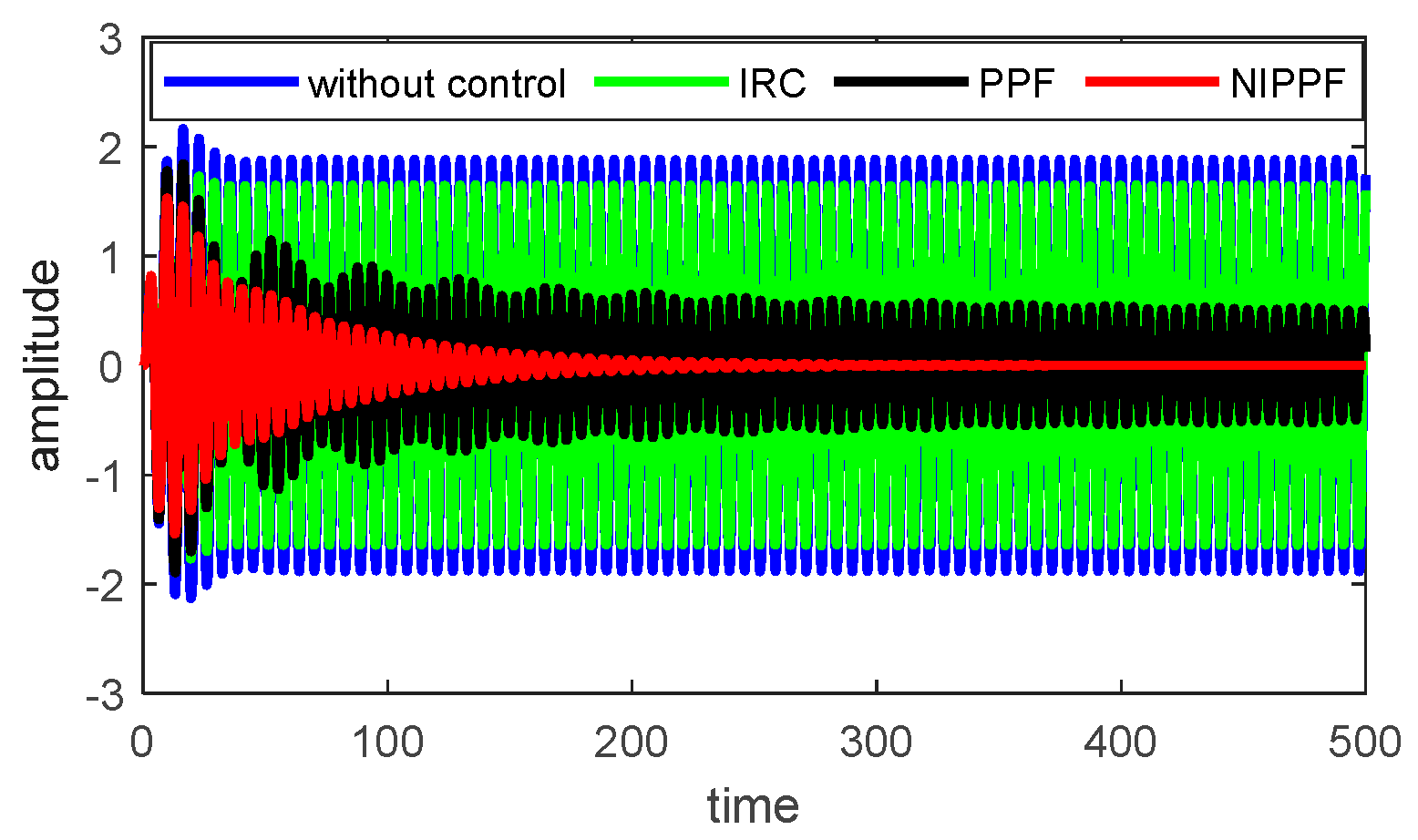
4.1. System Performance with and without NIPPF Control
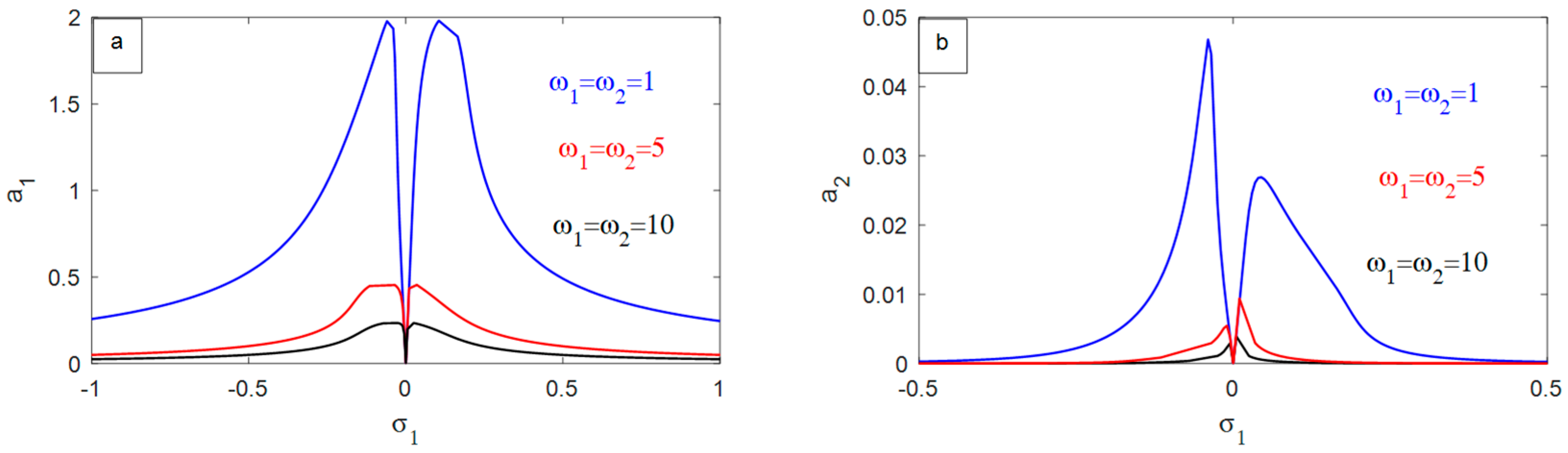
4.2. Occurrence Rejoinder Curvatures (ORC)
5. Comparison
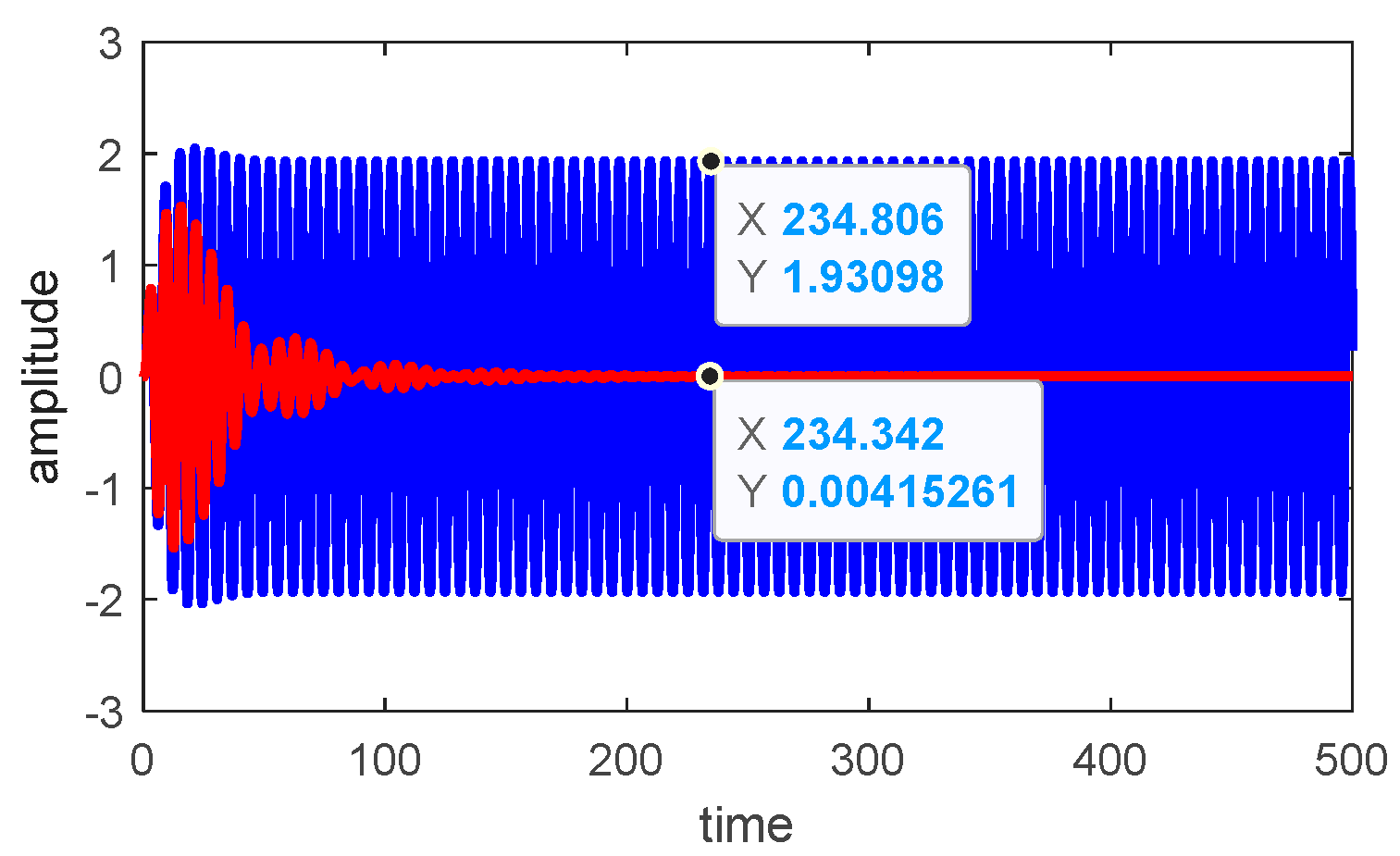
5.1. Comparison between Time History before and after the Controller
5.2. Comparison between Perturbation Solution and Numerical Simulation
5.3. Comparison with Previous Work
6. Conclusions
- The Nonlinear Integral Positive Position Feedback (NIPPF) controller effectively mitigates high-amplitude atmospheres inside nonlinear structures.
- The PR and IR case and is one of the worst vibrating reverberation cases.
- The breadth of the exciting structure declined around 99.8% after employing the NIPPF reaction supervisor associated with its rate deprived of the regulator.
- The efficiency of the NIPPF reaction supervisor, signified as Ea, influences approximately 482.5, showcasing its high effectiveness in supervising the structure’s performance.
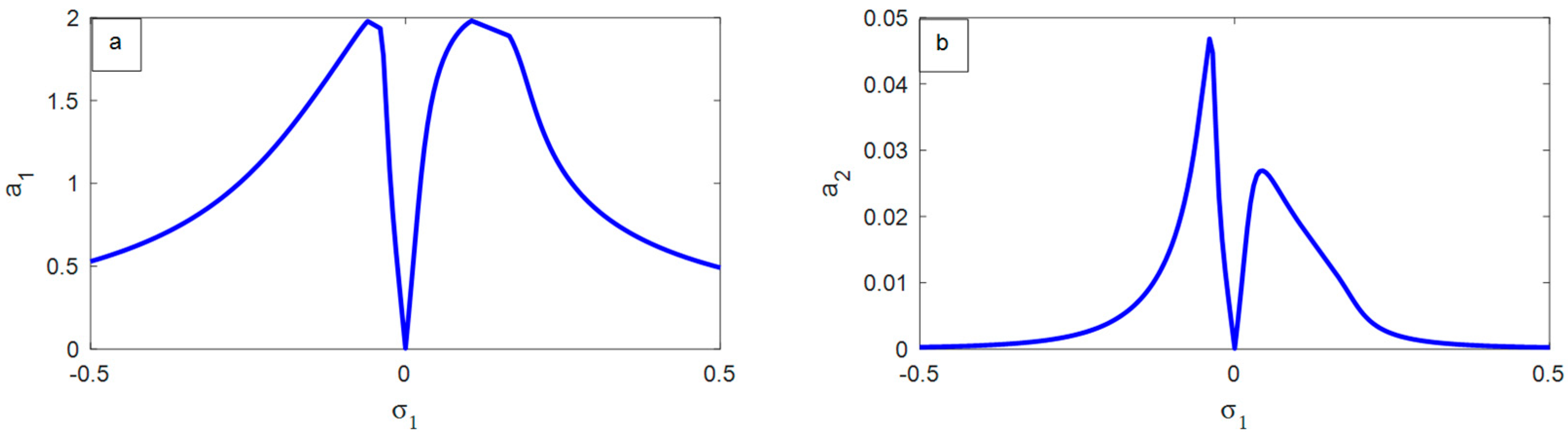
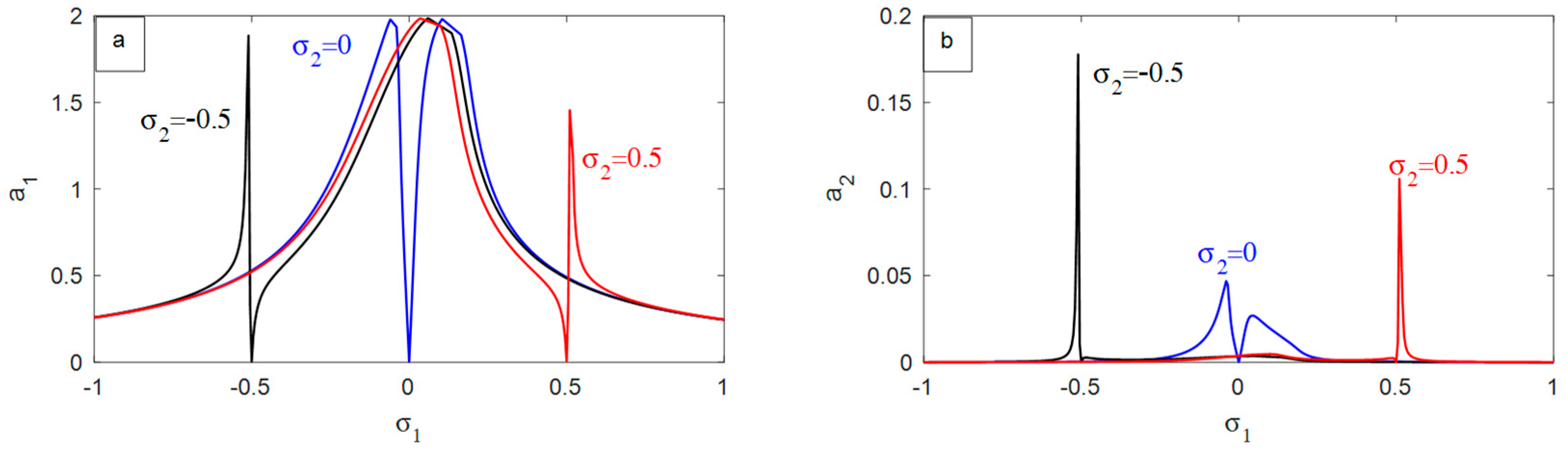
- The comeback or performance of the measured structure deepens with the increase in the peripheral excitement force, .
- The rejoinder of the focal structure diminished with the growth of the natural frequency .
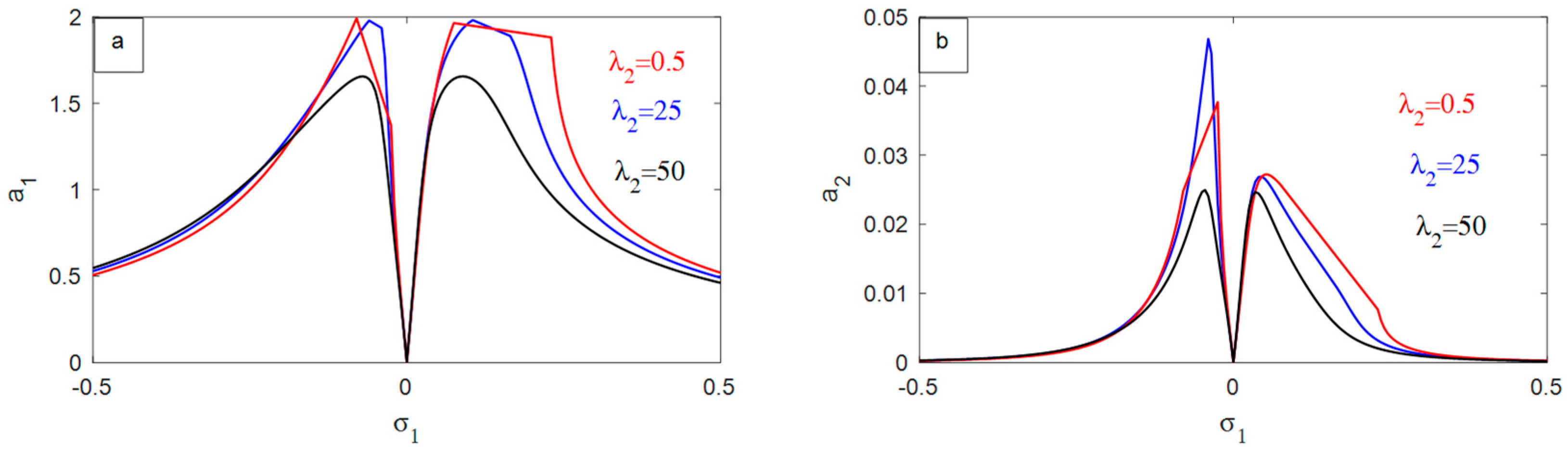
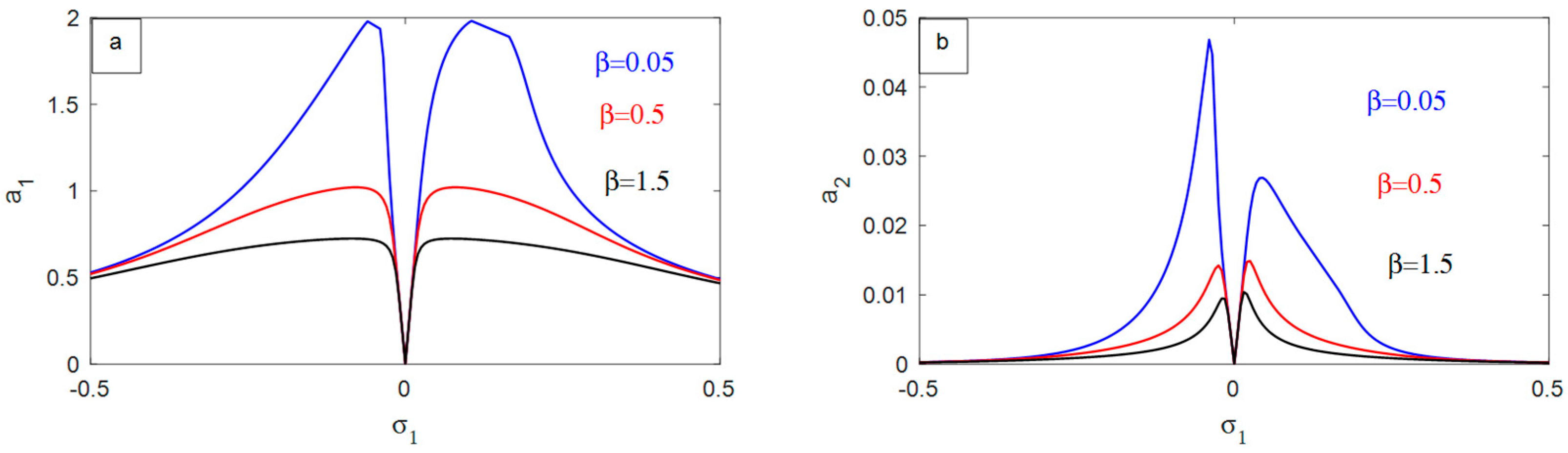
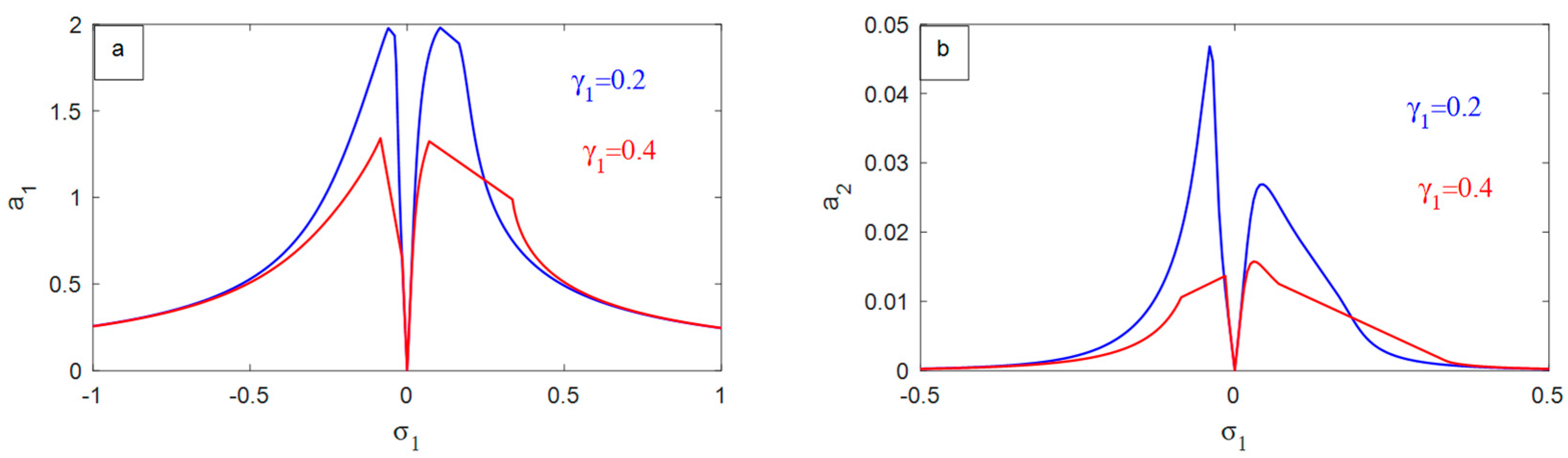
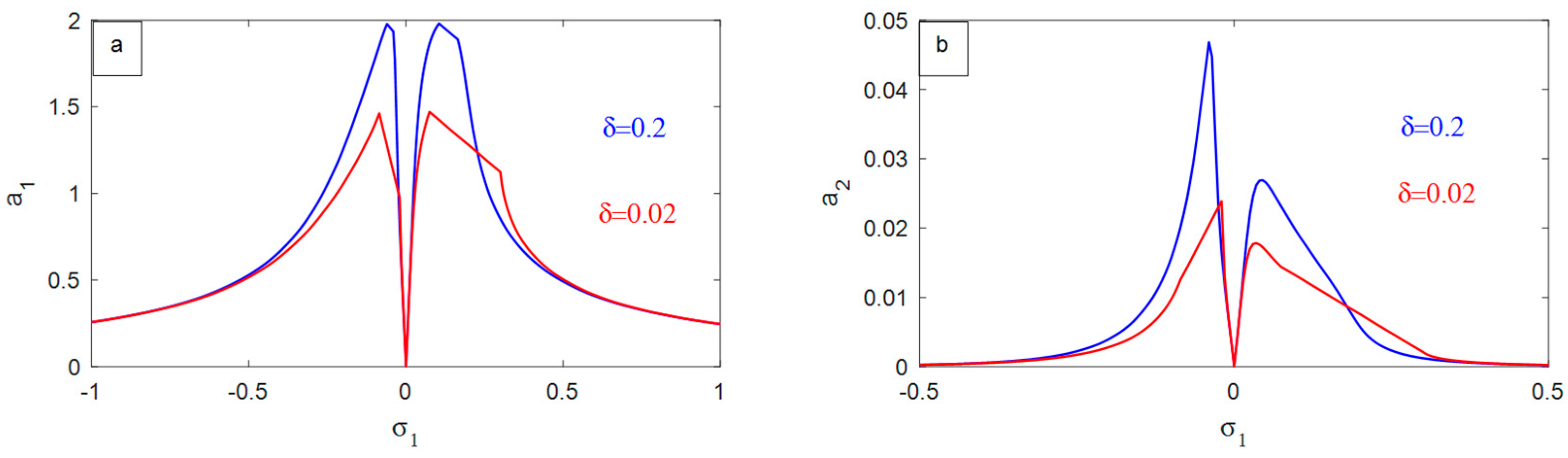
- Increasing the NIPPF parameter shifts the curves to the right, which can improve the performance of the NIPPF controller, particularly in mitigating high-amplitude vibrations within the nonlinear system, which is beneficial to the operation of the NIPPF controller.
- For the NIPPF parameter, the amplitude of the measured system decreases very sluggishly.
- The smallest possible amplitudes of the vibrating suspended cable happen when
- The frequency response curves and the Runge–Kutta fourth-order method yield consistent results, validating the analysis in both the frequency and time domains.
- The closed-loop response of the relative displacement, using the NIPPF controller, exhibits a peak overshoot, which is a characteristic of the system’s transient behavior.
- The modified NIPPF controller effectively controls the relative displacement of the suspension system. This is evident in the improved closed-loop performance, characterized by minimized peak overshoot and settling time.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Dislodgment, speed, and acceleration of the preliminary vein of the system, correspondingly. | |
| Structure rheostat manipulating movement, speed, and acceleration of the controller. | |
| Dimensionless movement, velocity of the controller. | |
| Dimensionless control signal gain. | |
| Dimensionless feedback signal gain. | |
| Dimensionless linear parameter of the controller. | |
| System and control damping coefficients, respectively. | |
| The inherent order and patterns observed in both the system and its control strategy. | |
| The strength and rate of external forces acting on a system. | |
| Nonlinear coefficients of the focal structure. | |
| External excitation frequency. | |
| Detuning parameter. | |
| Slight variation parameter. |
Abbreviations
| MTST | Multiple time scales technique. |
| NIPPF | Nonlinear integral positive position feedback (PPF + IRC). |
| PR | Primary resonance. |
| FREs | Frequency response equations. |
| IR | Internal resonance. |
Appendix A
References
- Warminski, J.; Cartmell, M.P.; Mitura, A.; Bochenski, M. Active vibration control of a nonlinear beam with self-and external excitations. Shock Vib. 2013, 20, 1033–1047. [Google Scholar] [CrossRef]
- Abdelhafez, H.M.; Nasedkin, A.V.; Nassar, M.E. Elimination of the Flutter Phenomenon in a Forced and Self-excited Nonlinear Beam Using an Improved Saturation Controller Algorithm. In Nonlinear Wave Dynamics of Materials and Structures. Advanced Structured Materials; Altenbach, H., Eremeyev, V., Pavlov, I., Porubov, A., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Abadi, A. Nonlinear Dynamics of Self-Excitation in Autoparametric Systems. Ph.D. Thesis, University of Utrecht, Utrecht, The Netherlands, 2003. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Saeed, N.A.; Eissa, M. Nonlinear time delay saturation-based controller for suppression of nonlinear beam vibrations. Appl. Math. Model 2013, 37, 8846–8864. [Google Scholar] [CrossRef]
- Li, W.; Laima, S. Experimental Investigations on Nonlinear Flutter Behaviors of a Bridge Deck with Different Leading and Trailing Edges. Appl. Sci. 2020, 10, 7781. [Google Scholar] [CrossRef]
- An, X.; Li, S.; Wu, T. Modeling Nonlinear Aeroelastic Forces for Bridge Decks with Various Leading Edges Using LSTM Networks. Appl. Sci. 2023, 13, 6005. [Google Scholar] [CrossRef]
- Omidi, E.; Nima Mahmoodi, S. Multimode modified positive position feedback to control a collocated structure. J. Dyn. Syst. Meas. Control 2015, 137, 051003. [Google Scholar] [CrossRef]
- Bauomy, H.S.; El-Sayed, A.T. Outcome of special vibration controller techniques linked to a cracked beam. Appl. Math. Model 2018, 37, 266–287. [Google Scholar]
- Jun, L. Positive position feedback control for high-amplitude vibration of a flexible beam to a principal resonance excitation. Shock Vib. 2010, 17, 187–203. [Google Scholar] [CrossRef]
- Amer, Y.A.; El-Sayed, A.T.; Abdel-Wahab, A.M.; Salman, H.F. Positive position feedback controller for nonlinear beam subject to harmonically excitation. Asian Res. J. Math. 2019, 12, 1–19. [Google Scholar] [CrossRef]
- Zhu, Q.; Yue, J.Z.; Liu, W.Q.; Wang, X.D.; Chen, J.; Hu, G.D. Active vibration control for piezoelectricity cantilever beam: An adaptive feedforward control method. Smart Mater. Struct. 2017, 26, 047003. [Google Scholar] [CrossRef]
- Das, A.S.; Dutt, J.K.; Ray, K. Active control of coupled flexural-torsional vibration in a flexible rotor–bearing system using electromagnetic actuator. Int. J. Non-Linear Mech. 2011, 46, 1093–1109. [Google Scholar] [CrossRef]
- Fuller, C.C.; Elliott, S.; Nelson, P.A. Active Control of Vibration; Academic Press: New York, NY, USA, 1996. [Google Scholar]
- El-Ganaini, W.A.; Saeed, N.A.; Eissa, M. Positive position feedback (PPF) controller for suppression of nonlinear system vibration. Nonlinear Dyn. 2013, 72, 517–537. [Google Scholar] [CrossRef]
- Saeed, N.A.; Awrejcewicz, J.; Elashmawey, R.A.; El-Ganaini, W.A.; Hou, L.; Sharaf, M. On 1/2-DOF active dampers to suppress multistability vibration of a 2-DOF rotor model subjected to simultaneous multiparametric and external harmonic excitations. Nonlinear Dyn. 2024, 112, 12061–12094. [Google Scholar] [CrossRef]
- Fyrillas, M.M.; Szeri, A.J. Control of ultra-and subharmonic resonances. J. Nonlinear Sci. 1998, 8, 131–159. [Google Scholar] [CrossRef]
- Fischer, A.; Eberhard, P. Controlling vibrations of a cutting process using predictive control. Comput. Mech. 2014, 54, 21–31. [Google Scholar] [CrossRef]
- Alluhydan, K.; Moatimid, G.M.; Amer, T.S.; Galal, A.A. Inspection of a Time-Delayed Excited Damping Duffing Oscillator. Axioms 2024, 13, 416. [Google Scholar] [CrossRef]
- Abdelhafez, H.; Nassar, M. Suppression of vibrations of a forced and self-excited nonlinear beam by using positive position feedback controller PPF. Br. J. Math. Comput. Sci. 2016, 17, 1–19. [Google Scholar] [CrossRef]
- Kandil, A.; Hamed, Y.S.; Alsharif, A.M. Rotor active magnetic bearings system control via a tuned nonlinear saturation oscillator. IEEE Access 2021, 9, 133694–133709. [Google Scholar] [CrossRef]
- Bauomy, H. Safety action over oscillations of a beam excited by moving load via a new active vibration controller. Math. Biosci. Eng. 2023, 20, 5135–5158. [Google Scholar] [CrossRef]
- Saeed, N.A.; Awrejcewicz, J.; Hafez, S.T.; Hou, L.; Aboudaif, M.K. Stability, bifurcation, and vibration control of a discontinuous nonlinear rotor model under rub-impact effect. Nonlinear Dyn. 2023, 111, 20661–20697. [Google Scholar] [CrossRef]
- Elashmawey, R.A.; Saeed, N.A.; Elganini, W.A.; Sharaf, M. An asymmetric rotor model under external, parametric, and mixed excitations: Nonlinear bifurcation, active control, and rub-impact effect. J. Low Freq. Noise Vib. Act. Control. 2024. [Google Scholar] [CrossRef]
- Jamshidi, R.; Collette, C. Optimal negative derivative feedback controller design for collocated systems based on H2 and H∞ method. Mech. Syst. Signal Process. 2022, 181, 109497. [Google Scholar] [CrossRef]
- Ren, Y.; Ma, W. Dynamic Analysis and PD Control in a 12-Pole Active Magnetic Bearing System. Mathematics 2024, 12, 2331. [Google Scholar] [CrossRef]
- Amer, Y.A.; Abd EL-Salam, M.N.; EL-Sayed, M.A. Behavior of a Hybrid Rayleigh-Van der Pol-Duffing Oscillator with a PD Controller. J. Appl. Res. Technol. 2022, 20, 58–67. [Google Scholar]
- Hamed, Y.S.; Alotaibi, H.; El-Zahar, E.R. Nonlinear vibrations analysis and dynamic responses of a vertical conveyor system controlled by a proportional derivative controller. IEEE Access 2020, 8, 119082–119093. [Google Scholar] [CrossRef]
- Kevorkian, J.; Cole, J.D. The method of multiple scales for ordinary differential equations. In Applied Mathematical Sciences; Springer: New York, NY, USA, 1996; Volume 114. [Google Scholar]
- Nayfeh, A.H. Perturbation Methods; John Wiley & Sons: New York, NY, USA, 1973. [Google Scholar]
- Dukkipati, R.V. Solving Vibration Analysis Problems Using MATLAB; New Age International Pvt Ltd. Publishers: New Delhi, India, 2007. [Google Scholar]







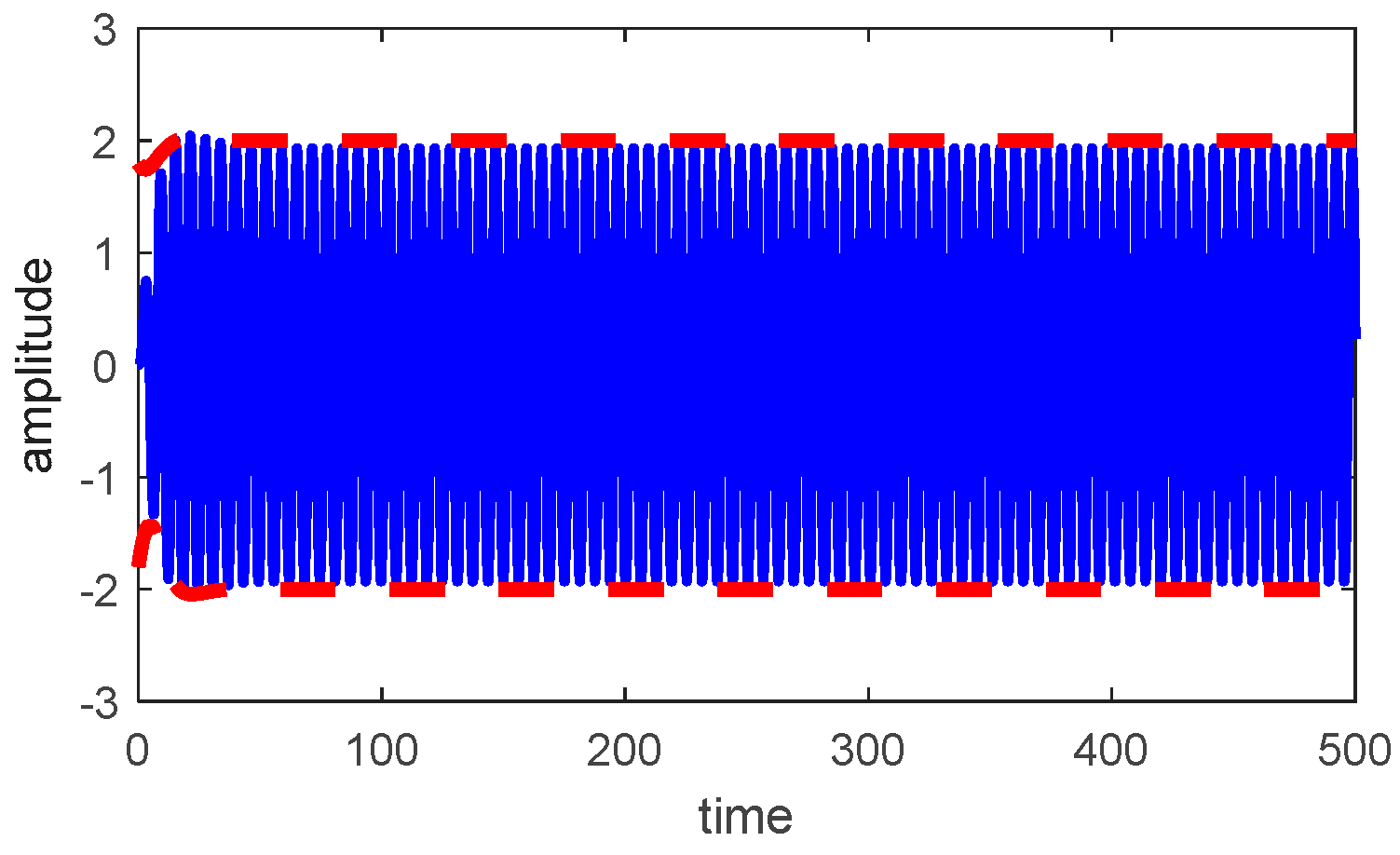

| Time | Approximate Solution beforeNIPPF | Numerical Solution beforeNIPPF |
|---|---|---|
| 62.8 | −1.9 | −1.9 |
| 883.883 | −1.9 | −1.9 |
| 49.6 | 1.9 | 1.9 |
| 833.416 | 1.9 | 1.9 |
| Time | Approximate Solution after NIPPF | Numerical Solution after NIPPF |
| 62.8 | −0.004 | −0.004 |
| 883.883 | −0.004 | −0.004 |
| 49.6 | 0.004 | 0.004 |
| 833.416 | 0.004 | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alluhydan, K.; Amer, Y.A.; EL-Sayed, A.T.; EL-Sayed, M.A. The Impact of the Nonlinear Integral Positive Position Feedback (NIPPF) Controller on the Forced and Self-Excited Nonlinear Beam Flutter Phenomenon. Symmetry 2024, 16, 1143. https://doi.org/10.3390/sym16091143
Alluhydan K, Amer YA, EL-Sayed AT, EL-Sayed MA. The Impact of the Nonlinear Integral Positive Position Feedback (NIPPF) Controller on the Forced and Self-Excited Nonlinear Beam Flutter Phenomenon. Symmetry. 2024; 16(9):1143. https://doi.org/10.3390/sym16091143
Chicago/Turabian StyleAlluhydan, Khalid, Yasser A. Amer, Ashraf Taha EL-Sayed, and Marwa Abdelaziz EL-Sayed. 2024. "The Impact of the Nonlinear Integral Positive Position Feedback (NIPPF) Controller on the Forced and Self-Excited Nonlinear Beam Flutter Phenomenon" Symmetry 16, no. 9: 1143. https://doi.org/10.3390/sym16091143






