Abstract
The aim of this paper is to derive formulae for the generating functions of the Bernstein type polynomials. We give a PDE equation for this generating function. By using this equation, we give recurrence relations for the Bernstein polynomials. Using generating functions, we also derive some identities including a symmetry property for the Bernstein type polynomials. We give some relations among the Bernstein type polynomials, Bernoulli numbers, Stirling numbers, Dahee numbers, the Legendre polynomials, and the coefficients of the classical superoscillatory function associated with the weak measurements. We introduce some integral formulae for these polynomials. By using these integral formulae, we derive some new combinatorial sums involving the Bernoulli numbers and the combinatorial numbers. Moreover, we define Bezier type curves in terms of these polynomials.
1. Introduction
Special functions are one of the most important topics in mathematics, mathematical physics, and other applied sciences. In fact, special functions can be defined with the help of generating functions, infinite series, infinite multipliers, repeated differentiation, integral representations, differentials, differences, integrals, functional equations, trigonometric series, series involving orthogonal functions, etc. Similarly, special polynomials and special numbers are equally important topics in mathematics and other branches of science. Recently, the Bernstein polynomials with their symmetry properties have many applications in various areas involving approximations of functions, statistics, curved surfaces, Computer Aided Geometric Design, etc. By the aid of these polynomials, the Bezier curves and surfaces are constructed. It is well known that the Bezier curves and surfaces have very important geometric applications. In particular, the Bezier curves are used in the construction of many mathematical models in the theory of curves, the theory of splines, etc. The motivation of this article is to not only give new formulae, finite sum formulae, and relations that include the symmetry property by combining Bernstein type polynomials with other special numbers and polynomials, but also investigate some properties of generating functions for these polynomials.
In order to give the main results of this article, the following notations and definitions are needed.
The Bernoulli numbers, , are defined by
It is well known that both the Bernoulli numbers and their generating functions are used in many important subjects, including trigonometric functions, series expansions of hyperbolic functions, the Euler–Maclaurin sum formula, finding the value of the Riemann zeta function at negative integers, Fermat’s Last Theorem, etc. (cf. [1,2]).
The Stirling numbers of the first kind, , are defined by
In both mathematics and combinatorics, the Stirling numbers of the first kind are known to spring up in the problem of finding permutations (cf. [1,2,3]).
The Legendre polynomials are defined by
which gives
The Legendre polynomials are orthogonal polynomials with respect to constant function. These polynomials are widely used in the theory of orthogonal polynomials, in the wave functions of electrons in the orbits of an atom, in the determination of potential functions in the spherically symmetric geometry, etc. (cf. [2,4], (p. 162, Equaation (9) [5])). We give a few values of Legendre polynomials given by Equation (2) as follows:
The Bernstein polynomials arises in the following the Bernstein operator:
where
and , , , and (cf. [6,7,8,9,10,11,12,13,14,15]).
Generating function for the Bernstein polynomials is defined by
(cf. [13,14]; see also [6] and the references cited in each of these earlier works).
The Bernstein polynomials satisfy the following well-known symmetry property:
(cf. [12]). By using (3), a few values of the Berstein polynomials are given as follows:
Although the Bernstein polynomials are very simple and easy to understand and use, it is well known that they provide great convenience in mathematical modeling including real world problems and in fields such as polynomial theory, approximation theory, operator theory, geometry, probability theory, and the construction of curve families (cf. [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]).
Both the Bernstein polynomials and their generating functions are also related to generating functions for the coefficients of the classical superoscillatory function associated with weak measurements, which is given by
where
, , and (cf. [24,25]).
The Daehee numbers of the first kind, , are defined by
(cf. [26]).
The remainder of this article is summarized as follows:
In Section 2, we define a new family of polynomials in terms of Bernstein polynomials and give their generating function. By using this function, we give many formulae involving the Bernstein polynomials, the Legendre polynomials, and the coefficients of the classical superoscillatory function and these polynomials.
In Section 3, by applying the derivative operator to generating function, we derive recurrence relations for the special polynomials in terms of the Bernstein polynomials. We also give some relations involving a symmetry property among the new family of polynomials, and .
In Section 4, by using integral formulae, we derive some combinatorial finite sum formulae.
In Section 5, by using integral formulae, we obtain new formulae involving the new family of polynomials, the Bernoulli numbers, the Stirling numbers of the first kind, the Legendre polynomials, and the Dahehee numbers.
In Section 6, we define Bezier type curves.
Finally, we complete this paper with the conclusion section.
2. Special Polynomials in Terms of Bernstein Polynomials
In this section, we define special polynomials in terms of the Bernstein polynomials with their generating function. We derive some new formulae for these polynomials, the Bernstein polynomials, the Legendre polynomials, and the coefficients of the classical superoscillatory function associated with weak measurements.
We define the following polynomials in terms of the Bernstein polynomials, which are called Bernstein type polynomials:
where and .
Since if , we rewrite (6) as follows:
For and a few values of are given as follows, as shown in Figure 1:
By implementing the computation formula, given by (7), in Mathematica [27] by the Wolfram programming language, we provide Figure 1, which depicts the Bernstein type polynomials .
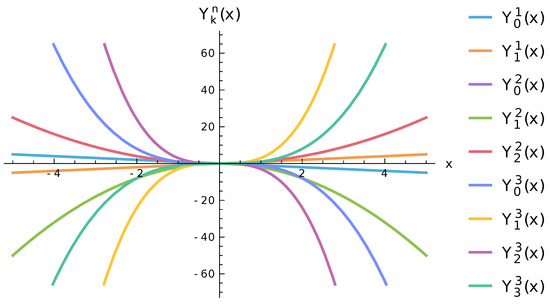
Figure 1.
Depiction of the Bernstein type polynomials in the cases when and .
The generating functions for are inspired by the following subdivision property of the Bernstein polynomials:
(cf. [28]). Therefore, we introduce the following generating functions for .
Theorem 1.
Let and . Then we have
Proof.
In [28], the following equation can be obtained from the subdivision property of the Bernstein basis functions.
Comparing (6) with the (12), we obtain the following formula for :
Remark 1.
Substituting into (6), we obtain , . The above monomial give a base for a class of polynomials.
A relation between the Bernstein polynomials and Bernstein type polynomials is given by the following theorem:
Theorem 2.
Let . Then we have
Proof.
By using Equation (11), we have
Thus,
By using the Cauchy product on the right-hand side of the above equation, we obtain
Comparing coefficient on the both sides of the above equation, we arrive at the desired result. □
3. Recurrence Relation and Derivative Formulae for and
In this section, by applying the derivative operator to , we derive recurrence relations for and partial derivative equation for with the aid of the Bernstein polynomials and their generating function.
The derivative equation of order m for is given by the following theorem.
Theorem 3.
Let . Then we have
Proof.
By applying to Equation (11), we obtain
Applying Leibnitz’s formula to the right-hand side of the above equation, with respect to t, we obtain
Combining the above equation with the following formula (which was proved in Theorem 3.10, [13]):
we obtain
Combining the above equation with (11) yields the desired theorem. □
Theorem 4.
Let . Then we have
Proof.
By substituting into (18), we obtain the following corollary:
Corollary 1.
Let and . Then we have
Theorem 5.
Let . Then we have
Proof.
By using (17), we obtain
By using the Cauchy product on the right-hand side of the above equation, we obtain
By comparing coefficient on both sides of the above equation, we arrive at the desired result. □
Relations Involving the Symmetry Property among , , and
In this subsection, we give some relations among , , and .
A relation between and is given by
(cf. [25]). By using the following symmetry property:
we obtain the symmetry property of as follows:
Since
has no symmetry property.
Therefore,
Remark 2.
From Equation (22), we conclude that polynomials do not form a partition of unity.
4. Combinatorial Finite Sums Formulae
In this section, by using the same method introduced in [28], we derive some combinatorial finite sums formulae.
Theorem 6.
Let with . Then we have
Proof.
If we replace k by n and n by in (25), we find the following relation for integral formulae of the polynomials :
Corollary 2.
Let . Then we have
By using integral of the polynomial , we derive the following new finite combinatorial sums.
Theorem 7.
Let . Then we have
Proof.
Theorem 8.
Let . Then we have
Proof.
From Remark 3.2 in [22], we can write
If we take in the above equation, we obtain
5. Relations among the Integral of the Polynomials and Other Special Numbers
In this section, we give some new formulae involving the integral of the polynomials , the Bernoulli numbers, the Stirling numbers of the first kind, the Legendre polynomials, and the Dahehee numbers.
Theorem 9.
Let . Then we have
Proof.
Combining Equation (25) with the following known formula (cf. [3,26,30]):
after some elementary calculations, we obtain the desired result. □
Theorem 10.
Let Then we have
Theorem 11.
Let Then we have
Proof.
By taking the integral of Equation (24) from 0 to 1, we obtain
Therefore,
Since
we arrive at the desired result. □
6. Bezier Type Curves
Bezier curves are defined by the help of the Bernstein basis functions and control points , , ..., as follows:
By using the same method of the above curve, we define the following Bezier type curves in terms of polynomials and control points , , ..., :
Using (31) and (7), we obtain
Bezier type curves in terms of polynomials of degree n take the following values at and :
Remark 3.
Since polynomials are monomials, the geometric family of the curves which are constructed in terms of Bernstein type polynomials may form a subclass of the Bezier curves.
Here, the applications of the curve are not given theoretically. The curve may be used to manipulate the curve to obtain shape properties. It is possible to investigate implementation for a real world problem such as human facial expression recognition and deformation hands with the help of the curvature of the Bezier type curves, whose machine learning is supported by statistical evaluations on feature vectors using the machine learning algorithm by the same method in [11,12,14,19,20,21].
Investigating the applications of graphs of Bezier type curves and examining the properties and deformation structures of these curves geometrically are outside the scope of this article.
7. Conclusions
We gave a generating function for a new family of polynomials, which are given in terms of Bernstein polynomials. By using this function, we derived some formulae involving the Bernstein polynomials, the Legendre polynomials, and the coefficients of the classical superoscillatory function and these polynomials. By applying the derivative operator to a generating function, we obtained recurrence relations for the new family of polynomials in terms of the Bernstein polynomials. We gave some relations involving a symmetry property among , , and . Using integral formulae for the new family of polynomials, we derived some combinatorial finite sums formulae.
In Section 5, by using integral formulae, we obtained new formulae involving the new family of polynomials, the Bernoulli numbers, the Stirling numbers of the first kind, the Legendre polynomials, and the Dahehee numbers. Finally, we defined the Bezier type curves.
As we mentioned in the introduction and other sections, the results obtained in this article with the newly found results have a high potential to be used in applied sciences, control system theory, neural networks, machine learning, etc. This may provide us with new projects on the research and application of these issues in the future.
Author Contributions
Methodology, A.Y.C. and B.S.; investigation, A.Y.C. and B.S.; writing—original draft preparation, A.Y.C. and B.S.; writing—review and editing, A.Y.C. and B.S.; A.Y.C. and B.S. contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the reviewers for their valuable comments and advices.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Comtet, L. Advanced Combinatorics; D. Reidel Publication Company: Dordrecht, The Netherlands; Boston, MA, USA, 1974. [Google Scholar]
- Srivastava, H.M. Zeta and q-Zeta Functions and Associated Series and Integrals; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Simsek, Y. Explicit formulas for p-adic Integral: Approach to p-adic distributions and some families of special numbers and polynomials. Montes Taurus J. Pure Appl. Math. 2019, 1, 1–76. [Google Scholar]
- Milovanović, M.; Oarcea, A.; Nikolić, S.; Djordjević, A.; Spasić, M. An Approach to Networking a New Type of Artificial Orthogonal Glands within Orthogonal Endocrine Neural Networks. Appl. Sci. 2022, 12, 5372. [Google Scholar] [CrossRef]
- Rainville, E.D. Special Functions; The Macmillan Company: New York, NY, USA, 1960. [Google Scholar]
- Acikgoz, M.; Araci, S. On the generating function for Bernstein polynomials. Am. Inst. Phys. Conf. Proc. 2010, CP1281, 1141–1144. [Google Scholar]
- Bayad, A.; Chikhi, J. Reduction and duality of the generalized Hurwitz-Lerch zetas. Fixed Point Theory Appl. 2013, 82, 82. [Google Scholar] [CrossRef]
- Bernstein, S.N. Demonstration of a theorem of Weierstrass based on the calculus of probabilities. Comm. Kharkov Math. Soc. 1912, 13, 1–2. [Google Scholar]
- Bustamante, J. Bernstein Operators and Their Properties; Birkhauser Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kim, T.; Choi, J.; Kim, Y.H.; Ryoo, C.S. On the Fermionic p-adic integral representation of Bernstein polynomials associated with Euler numbers and polynomials. J. Inequal. Appl. 2010, 2010, 864247. [Google Scholar] [CrossRef][Green Version]
- Kucukoglu, I.; Simsek, B.; Simsek, Y. Multidimensional Bernstein polynomials and Bezier curves: Analysis of machine learning algorithm for facial expression recognition based on curvature. Appl. Math. Comput. 2019, 344–345, 150–162. [Google Scholar] [CrossRef]
- Lorentz, G.G. Bernstein Polynomials; Chelsea Publishing Company: New York, NY, USA, 1986. [Google Scholar]
- Simsek, Y. Functional equations from generating functions: A novel approach to deriving identities for the Bernstein basis functions. Fixed Point Theory Appl. 2013, 2013, 80. [Google Scholar] [CrossRef]
- Simsek, Y. Generating functions for the Bernstein type polynomials: A new approach to deriving identities and applications for the polynomials. Hacet. J. Math. Stat. 2014, 43, 1–14. [Google Scholar]
- Simsek, Y. Construction method for generating functions of special numbers and polynomials arising from analysis of new operators. Math. Methods Appl. Sci. 2018, 41, 6934–6954. [Google Scholar] [CrossRef]
- Fermo, L.; Mezzanotte, D.; Occorsio, D. On the numerical solution of Volterra integral equations on equispaced nodes. Electron. Trans. Numer. Anal. 2023, 59, 9–23. [Google Scholar] [CrossRef]
- Micchelli, C. The saturation class and iterates of the Bernstein polynomials. J. Approx. Theory 1973, 8, 1–18. [Google Scholar] [CrossRef]
- Occorsio, D.; Russo, M.G.; Themistoclakis, W. Some numerical applications of generalized Bernstein operators. Constr. Math. Anal. 2021, 4, 186–214. [Google Scholar] [CrossRef]
- Simsek, B. Formulas derived from moment generating functions and Bernstein polynomials. Appl. Anal. Discret. Math. 2019, 13, 839–848. [Google Scholar] [CrossRef]
- Simsek, B. A note on characteristic function for Bernstein polynomials involving special numbers and polynomials. Filomat 2020, 34, 543–549. [Google Scholar] [CrossRef]
- Simsek, B.; Simsek, B. The computation of expected values and moments of special polynomials via characteristic and generating functions. AIP Conf. Proc. 2017, 1863, 543–549. [Google Scholar]
- Simsek, Y. Combinatorial sums and binomial identities associated with the Beta-type polynomials. Hacet. J. Math. Stat. 2018, 47, 1144–1155. [Google Scholar]
- Venturino, E.; Anit¸a, S.; Mezzanotte, D.; Occorsio, D. A high order numerical scheme for a nonlinear nonlocal reaction–diffusion model arising in population theory. J. Comput. Appl. Math. 2024, 451, 116082. [Google Scholar] [CrossRef]
- Berry, M.V.; Dennis, M.R. Natural superoscillations in monochromatic waves in D dimension. J. Phys. A 2009, 42, 022003. [Google Scholar] [CrossRef]
- Colombo, F.; Krausshar, R.S.; Sabadini, I.; Simsek, Y. On the generating functions and special functions associated with superoscillations. Discrete Appl. Math. 2023, 340, 215–227. [Google Scholar] [CrossRef]
- Kim, D.S.; Kim, T. Daehee Numbers and Polynomials. Appl. Math. Sci. 2013, 1167, 5969–5976. [Google Scholar] [CrossRef]
- Wolfram Research Inc. Mathematica Online (Wolfram Cloud); Wolfram Research Inc.: Champaign, IL, USA, 2021; Available online: https://www.wolframcloud.com (accessed on 1 July 2024).
- Simsek, Y. Analysis of the Bernstein basis functions: An approach to combinatorial sums involving binomial coefficients and Catalan numbers. Math. Meth. Appl. Sci. 2015, 38, 3007–3021. [Google Scholar] [CrossRef]
- Doha, E.; Bhrawy, A.; Saker, M. On the Derivatives of Bernstein Polynomials: An Application for the Solution of High Even-Order Differential Equations. Bound. Value Probl. 2011, 2011, 829543. [Google Scholar] [CrossRef]
- Riordan, J. Introduction to Combinatorial Analysis; Princeton University Press: Princeton, NJ, USA, 1958. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).