Research on Investment and Coordination Strategies for Supply Chain Resilience under Supply Disruption Risk
Abstract
:1. Introduction
2. Literature Review
2.1. Supply Disruption
2.2. Supply Chain Resilience
3. Model Construction and Game Decision Model Analysis
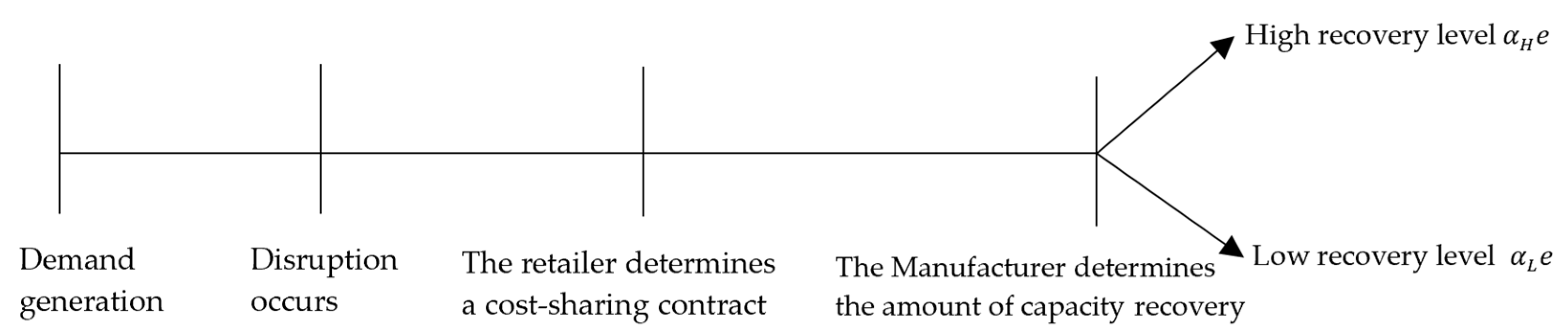
3.1. Problem Description and Modeling Assumptions
3.2. Decentralized Decision Model under the Supply Disruption Risk (Model M)
3.2.1. Manufacturer’s Profit Decision Model
3.2.2. Retailer’s Profit Decision Model
3.3. Centralized Decision Model under the Supply Disruption Risk (Model C)
3.4. Decision Model for Cost-Sharing under the Supply Disruption Risk (Model M-C)
3.4.1. Manufacturer’s Profit Decision Model under the Cost-Sharing Contract
3.4.2. Retailer’s Profit Decision Model under the Cost-Sharing Contract
4. Numerical Simulation
4.1. Supply Chain Members’ Optimal Profit and Resilience Investment Decisions
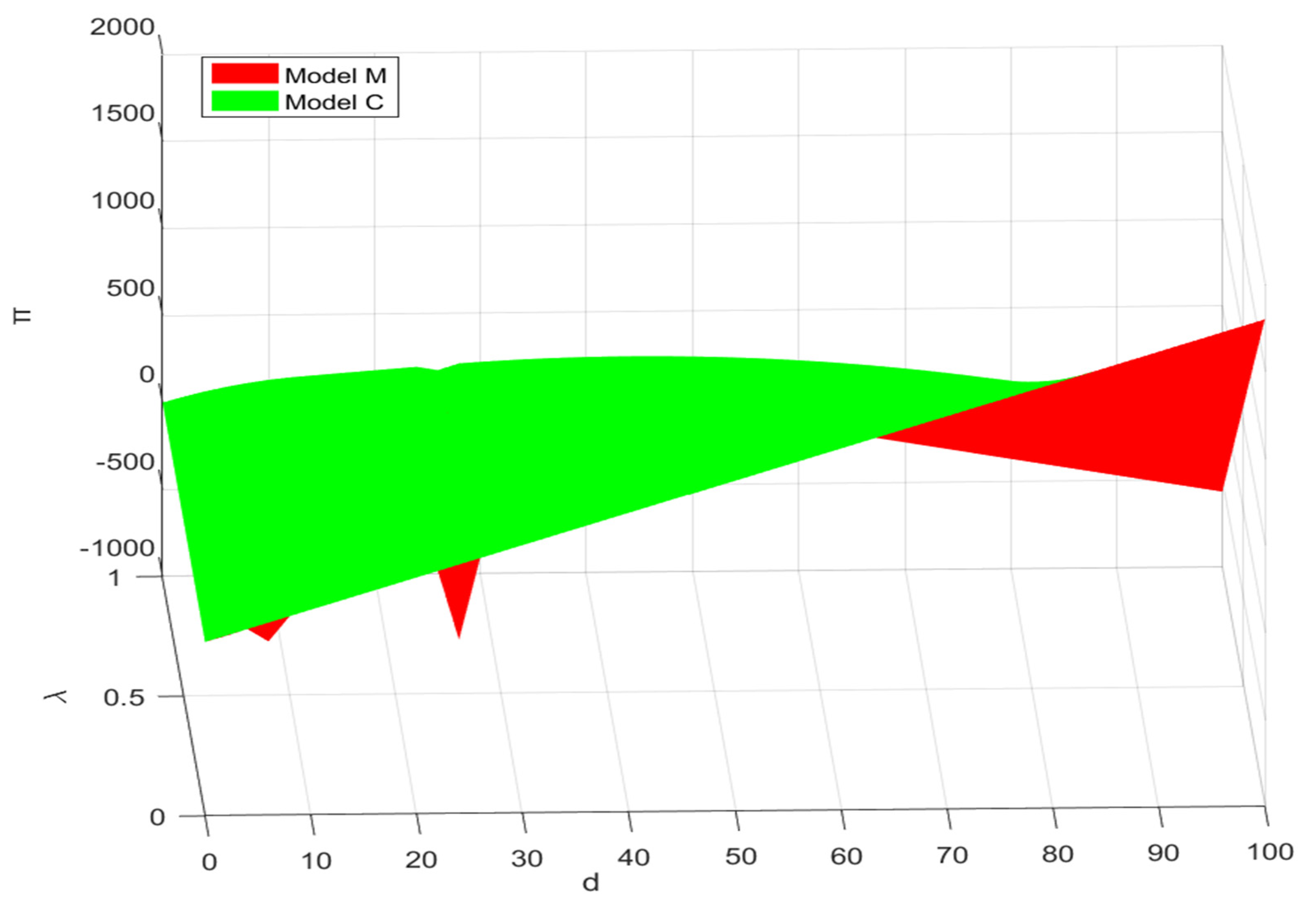
4.1.1. Analysis of Overall Supply Chain Profit
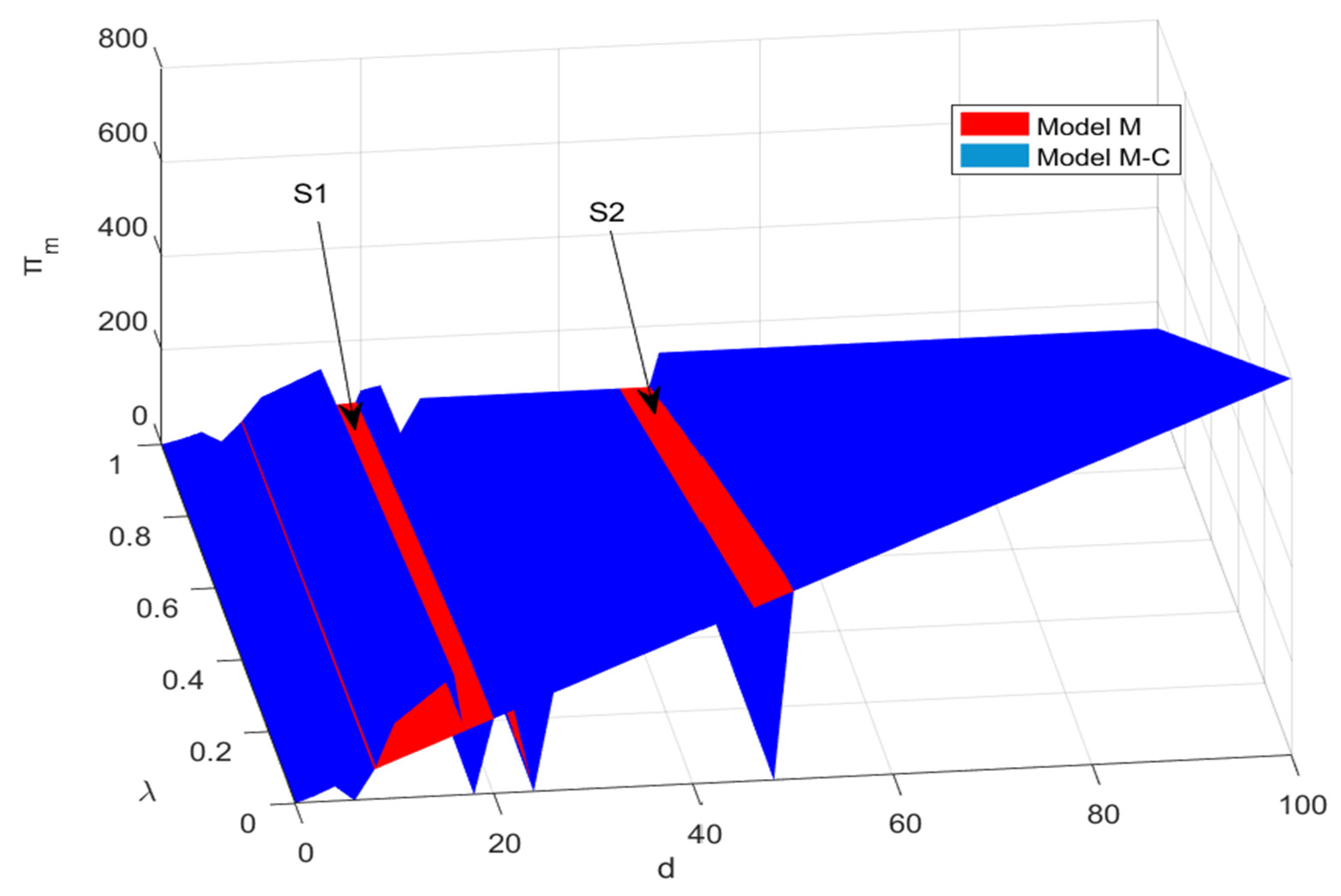
4.1.2. Analysis of Manufacturer’s Profit
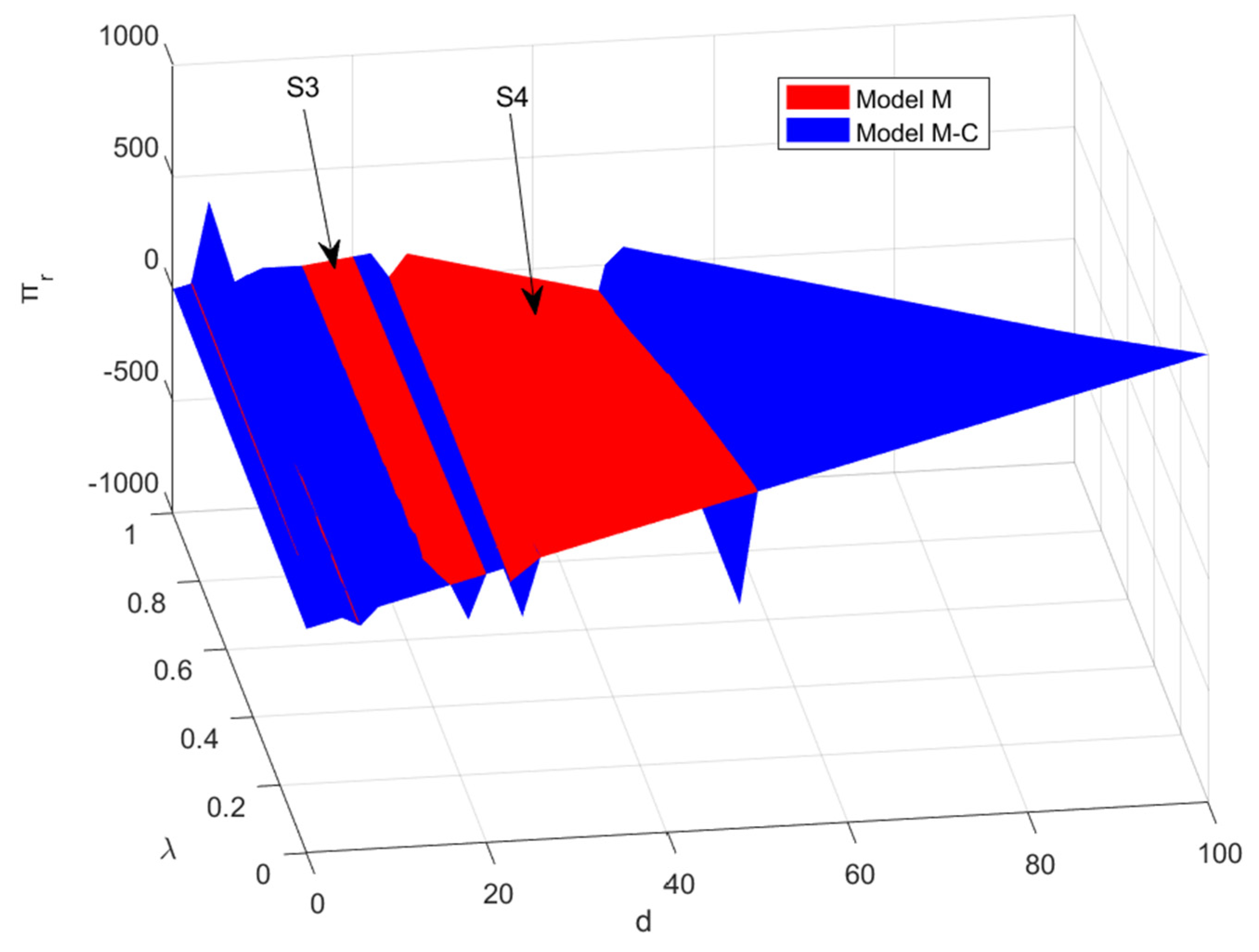
4.1.3. Analysis of Retailer’s Profit
4.1.4. Analysis of Resilience Investment Decision
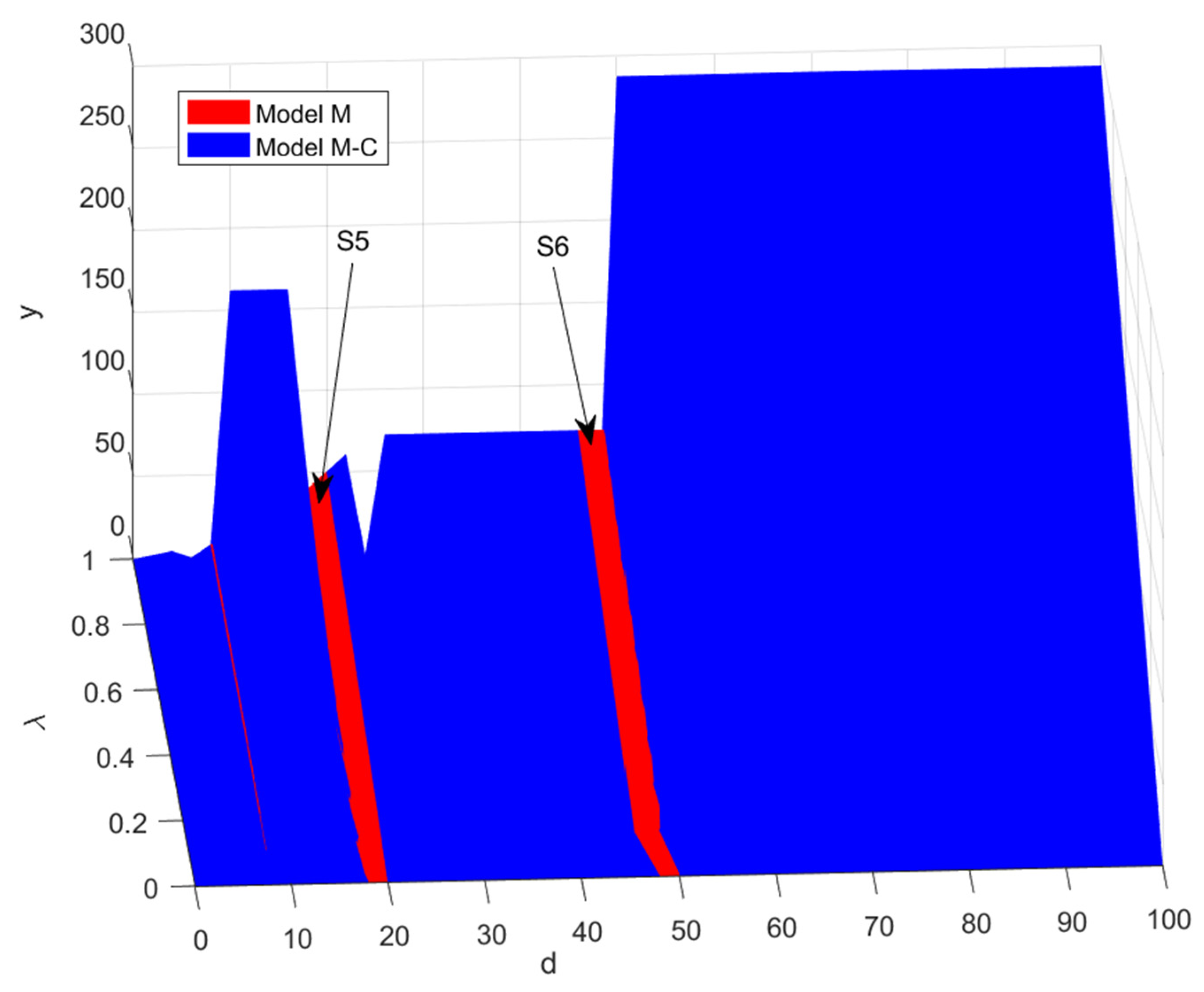
4.2. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, X.; Li, X.; Luo, F.; Wang, M.; Liu, L. How to Promote Mobile Phone Trade-in and the Integration of Green Supply Chain from the Perspective of Multi-Party Game Theory. RAIRO-Oper. Res. 2022, 56, 3117–3135. [Google Scholar] [CrossRef]
- Xu, J.; Bai, Q.; Li, Z.; Zhao, L. Maximizing the Profit of Omnichannel Closed-Loop Supply Chains with Mean–Variance Criteria. Comput. Electr. Eng. 2024, 113, 109030. [Google Scholar] [CrossRef]
- Adobor, H. Supply Chain Resilience: A Multi-Level Framework. Int. J. Logist. Res. Appl. 2019, 22, 533–556. [Google Scholar] [CrossRef]
- Browning, T.; Kumar, M.; Sanders, N.; Sodhi, M.S.; Thürer, M.; Tortorella, G.L. From Supply Chain Risk to System-Wide Disruptions: Research Opportunities in Forecasting, Risk Management and Product Design. Int. J. Oper. Prod. Manag. 2023, 43, 1841–1858. [Google Scholar] [CrossRef]
- Sturm, S.; Hohenstein, N.-O.; Hartmann, E. Linking Entrepreneurial Orientation and Supply Chain Resilience to Strengthen Business Performance: An Empirical Analysis. Int. J. Oper. Prod. Manag. 2023, 43, 1357–1386. [Google Scholar] [CrossRef]
- Huo, B.; Li, D.; Gu, M. The Impact of Supply Chain Resilience on Customer Satisfaction and Financial Performance: A Combination of Contingency and Configuration Approaches. J. Manag. Sci. Eng. 2024, 9, 38–52. [Google Scholar] [CrossRef]
- Ekanayake, E.M.A.C.; Shen, G.Q.P.; Kumaraswamy, M.M. A Fuzzy Synthetic Evaluation of Capabilities for Improving Supply Chain Resilience of Industrialised Construction: A Hong Kong Case Study. Prod. Plan. Control 2023, 34, 623–640. [Google Scholar] [CrossRef]
- Liu, M.; Ding, Y.; Chu, F.; Dolgui, A.; Zheng, F. Robust Actions for Improving Supply Chain Resilience and Viability. Omega 2024, 123, 102972. [Google Scholar] [CrossRef]
- Torshizi, E.; Bozorgi-Amiri, A.; Sabouhi, F. Resilient and Sustainable Global COVID-19 Vaccine Supply Chain Design Considering Reverse Logistics. Appl. Soft Comput. 2024, 151, 111041. [Google Scholar] [CrossRef]
- Lou, G.; Guo, Y.; Lai, Z.; Ma, H.; Tu, X. Optimal Resilience Strategy for Manufacturers to Deal with Supply Disruptions: Investment in Supply Stability versus Dual Sourcing. Comput. Ind. Eng. 2024, 190, 110030. [Google Scholar] [CrossRef]
- Joshi, S.; Luong, H.T. A Two-Stage Capacity Reservation Contract Model with Backup Sourcing Considering Supply Side Disruptions. J. Ind. Prod. Eng. 2024, 41, 60–80. [Google Scholar] [CrossRef]
- Mukherjee, S.; Nagariya, R.; Mathiyazhagan, K.; Scuotto, V. Linking Supply Chain Resilience with Knowledge Management for Achieving Supply Chain Performance. J. Knowl. Manag. 2023, 28, 971–993. [Google Scholar] [CrossRef]
- Gupta, V.; Ivanov, D.; Choi, T.-M. Competitive Pricing of Substitute Products under Supply Disruption. Omega 2021, 101, 102279. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, D.; Dolgui, A.; Sokolov, B.; Ivanova, M. Literature Review on Disruption Recovery in the Supply Chain. Int. J. Prod. Res. 2017, 55, 6158–6174. [Google Scholar] [CrossRef]
- Yoon, J.; Narasimhan, R.; Kim, M.K. Retailer’s Sourcing Strategy under Consumer Stockpiling in Anticipation of Supply Disruptions. Int. J. Prod. Res. 2018, 56, 3615–3635. [Google Scholar] [CrossRef]
- Gultekin, B.; Demir, S.; Gunduz, M.A.; Cura, F.; Ozer, L. The Logistics Service Providers during the COVID-19 Pandemic: The Prominence and the Cause-Effect Structure of Uncertainties and Risks. Comput. Ind. Eng. 2022, 165, 107950. [Google Scholar] [CrossRef]
- Janjua, N.K.; Nawaz, F.; Prior, D.D. A Fuzzy Supply Chain Risk Assessment Approach Using Real-Time Disruption Event Data from Twitter. Enterp. Inf. Syst. 2023, 17, 1959652. [Google Scholar] [CrossRef]
- Shourabizadeh, H.; Kundakcioglu, O.E.; Bozkir, C.D.C.; Tufekci, M.B.; Henry, A.C. Healthcare Inventory Management in the Presence of Supply Disruptions and a Reliable Secondary Supplier. Ann. Oper. Res. 2023, 331, 1149–1206. [Google Scholar] [CrossRef]
- Behl, A.; Gaur, J.; Pereira, V.; Yadav, R.; Laker, B. Role of Big Data Analytics Capabilities to Improve Sustainable Competitive Advantage of MSME Service Firms during COVID-19—A Multi-Theoretical Approach. J. Bus. Res. 2022, 148, 378–389. [Google Scholar] [CrossRef]
- Giri, B.C.; Majhi, J.K.; Chaudhuri, K. Coordination Mechanisms of a Three-Layer Supply Chain under Demand and Supply Risk Uncertainties. RAIRO-Oper. Res. 2021, 55, S2593–S2617. [Google Scholar] [CrossRef]
- Rosales, F.P.; Oprime, P.C.; Royer, A.; Batalha, M.O. Supply Chain Risks: Findings from Brazilian Slaughterhouses. Supply Chain Manag. Int. J. 2020, 25, 343–357. [Google Scholar] [CrossRef]
- Choi, T.-M.; Shi, X. Reducing Supply Risks by Supply Guarantee Deposit Payments in the Fashion Industry in the “New Normal after COVID-19”. Omega 2022, 109, 102605. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, H.; Wang, J. The Coordination Mechanisms of Emergency Inventory Model under Supply Disruptions. Soft Comput. 2018, 22, 5479–5489. [Google Scholar] [CrossRef]
- Fang, X.; Yuan, F. The Coordination and Preference of Supply Chain Contracts Based on Time-Sensitivity Promotional Mechanism. J. Manag. Sci. Eng. 2018, 3, 158–178. [Google Scholar] [CrossRef]
- Saha, S.; Modak, N.M.; Panda, S.; Sana, S.S. Managing a Retailer’s Dual-Channel Supply Chain under Price- and Delivery Time-Sensitive Demand. J. Model. Manag. 2018, 13, 351–374. [Google Scholar] [CrossRef]
- Salam, M.A.; Bajaba, S. The Role of Supply Chain Resilience and Absorptive Capacity in the Relationship between Marketing–Supply Chain Management Alignment and Firm Performance: A Moderated-Mediation Analysis. J. Bus. Ind. Mark. 2022, 38, 1545–1561. [Google Scholar] [CrossRef]
- Li, X.; Ghadami, A.; Drake, J.M.; Rohani, P.; Epureanu, B.I. Mathematical Model of the Feedback between Global Supply Chain Disruption and COVID-19 Dynamics. Sci. Rep. 2021, 11, 15450. [Google Scholar] [CrossRef]
- Liu, H.; Lu, F.; Shi, B.; Hu, Y.; Li, M. Big Data and Supply Chain Resilience: Role of Decision-Making Technology. Manag. Decis. 2023, 61, 2792–2808. [Google Scholar] [CrossRef]
- Munir, M.; Jajja, M.S.S.; Chatha, K.A. Capabilities for Enhancing Supply Chain Resilience and Responsiveness in the COVID-19 Pandemic: Exploring the Role of Improvisation, Anticipation, and Data Analytics Capabilities. Int. J. Oper. Prod. Manag. 2022, 42, 1576–1604. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z. Simulation Analysis of Supply Chain Resilience of Prefabricated Building Projects Based on System Dynamics. Buildings 2023, 13, 2629. [Google Scholar] [CrossRef]
- Adobor, H.; McMullen, R.S. Supply Chain Resilience: A Dynamic and Multidimensional Approach. Int. J. Logist. Manag. 2018, 29, 1451–1471. [Google Scholar] [CrossRef]
- Rajesh, R. Forecasting Supply Chain Resilience Performance Using Grey Prediction. Electron. Commer. Res. Appl. 2016, 20, 42–58. [Google Scholar] [CrossRef]
- Kazancoglu, I.; Ozbiltekin-Pala, M.; Mangla, S.K.; Kazancoglu, Y.; Jabeen, F. Role of Flexibility, Agility and Responsiveness for Sustainable Supply Chain Resilience during COVID-19. J. Clean. Prod. 2022, 362, 132431. [Google Scholar] [CrossRef]
- Al-Hakimi, M.A.; Saleh, M.H.; Borade, D.B. Entrepreneurial Orientation and Supply Chain Resilience of Manufacturing SMEs in Yemen: The Mediating Effects of Absorptive Capacity and Innovation. Heliyon 2021, 7, e08145. [Google Scholar] [CrossRef]
- Siva Kumar, P.; Anbanandam, R. Theory Building on Supply Chain Resilience: A SAP–LAP Analysis. Glob. J. Flex. Syst. Manag. 2020, 21, 113–133. [Google Scholar] [CrossRef]
- Lu, J.; Wang, J.; Song, Y.; Yuan, C.; He, J.; Chen, Z. Influencing Factors Analysis of Supply Chain Resilience of Prefabricated Buildings Based on PF-DEMATEL-ISM. Buildings 2022, 12, 1595. [Google Scholar] [CrossRef]
- Rajesh, R. Technological Capabilities and Supply Chain Resilience of Firms: A Relational Analysis Using Total Interpretive Structural Modeling (TISM). Technol. Forecast. Soc. Chang. 2017, 118, 161–169. [Google Scholar] [CrossRef]
- Lee, S.M.; Rha, J.S. Ambidextrous Supply Chain as a Dynamic Capability: Building a Resilient Supply Chain. Manag. Decis. 2016, 54, 2–23. [Google Scholar] [CrossRef]
- Chowdhury, M.M.H.; Quaddus, M. Supply Chain Resilience: Conceptualization and Scale Development Using Dynamic Capability Theory. Int. J. Prod. Econ. 2017, 188, 185–204. [Google Scholar] [CrossRef]
- Cohen, M.; Cui, S.; Doetsch, S.; Ernst, R.; Huchzermeier, A.; Kouvelis, P.; Lee, H.; Matsuo, H.; Tsay, A.A. Bespoke Supply-Chain Resilience: The Gap between Theory and Practice. J. Oper. Manag. 2022, 68, 515–531. [Google Scholar] [CrossRef]
- Shanker, S.; Barve, A.; Muduli, K.; Kumar, A.; Garza-Reyes, J.A.; Joshi, S. Enhancing Resiliency of Perishable Product Supply Chains in the Context of the COVID-19 Outbreak. Int. J. Logist. Res. Appl. 2022, 25, 1219–1243. [Google Scholar] [CrossRef]
- Pu, G.; Qiao, W.; Feng, Z. Antecedents and Outcomes of Supply Chain Resilience: Integrating Dynamic Capabilities and Relational Perspective. J. Contingencies Crisis Manag. 2023, 31, 706–726. [Google Scholar] [CrossRef]
- Kaviani, M.A.; Tavana, M.; Kowsari, F.; Rezapour, R. Supply Chain Resilience: A Benchmarking Model for Vulnerability and Capability Assessment in the Automotive Industry. Benchmarking Int. J. 2020, 27, 1929–1949. [Google Scholar] [CrossRef]
- Zhang, H.; Jia, F.; You, J.-X. Striking a Balance between Supply Chain Resilience and Supply Chain Vulnerability in the Cross-Border e-Commerce Supply Chain. Int. J. Logist. Res. Appl. 2023, 26, 320–344. [Google Scholar] [CrossRef]
- Shin, N.; Park, S. Evidence-Based Resilience Management for Supply Chain Sustainability: An Interpretive Structural Modelling Approach. Sustainability 2019, 11, 484. [Google Scholar] [CrossRef]
- Wang, Y.; Ren, J.; Zhang, L.; Liu, D. Research on Resilience Evaluation of Green Building Supply Chain Based on ANP-Fuzzy Model. Sustainability 2023, 15, 285. [Google Scholar] [CrossRef]
- Ke, Y.; Lu, L.; Luo, X. Identification and Formation Mechanism of Key Elements of Supply Chain Resilience: Exploration Based on Grounded Theory and Verification of SEM. PLoS ONE 2023, 18, e0293741. [Google Scholar]
- Vimal, K.E.K.; Kumar, A.; Sunil, S.M.; Suresh, G.; Sanjeev, N.; Kandasamy, J. Analysing the Challenges in Building Resilient Net Zero Carbon Supply Chains Using Influential Network Relationship Mapping. J. Clean. Prod. 2022, 379, 134635. [Google Scholar]
- Liu, J.; Gu, B.; Chen, J. Enablers for Maritime Supply Chain Resilience during Pandemic: An Integrated MCDM Approach. Transp. Res. Part Policy Pract. 2023, 175, 103777. [Google Scholar] [CrossRef]
- Ye, F.; Hou, G.; Li, Y.; Fu, S. Managing Bioethanol Supply Chain Resiliency: A Risk-Sharing Model to Mitigate Yield Uncertainty Risk. Ind. Manag. Data Syst. 2018, 118, 1510–1527. [Google Scholar] [CrossRef]
| Author | Main Contributions |
|---|---|
| Beyza et al. (2022) [16] | This article is based on the fuzzy DEMATEL method, where supply chain disruptions and demand changes are two factors caused by the COVID-19 pandemic that can affect financial failure and forecast scope. |
| Khalid et al. (2023) [17] | This article develops a new method for identifying supply chain disruption events in real time using Twitter sources. |
| Hamed et al. (2023) [18] | This article proposes a Markov chain model to analyze inventory management in situations of supply interruption and reliable secondary suppliers. |
| Abhishek et al. (2022) [19] | This article analyzes how small- and medium-sized enterprises lacking research and discussion on big data analysis capabilities can gain sustainable competitive advantages through supply chain coordination, fast trust, and supply chain risk when facing challenges such as supply disruptions. |
| Bibhas et al. (2021) [20] | This article proposes price-only contracts and new revenue-sharing contracts to alleviate the uncertainty of demand and supply in decentralized models, and observes that revenue-sharing contracts can fully coordinate the supply chain. |
| Rosales et al. (2020) [21] | This article aims to identify the risks faced by the supply chain and analyze how these risks affect the coordination level of the supply chain. |
| Ming et al. (2022) [22] | This article explores the common “supply margin payment” plan in the fashion supply chain during supply disruptions. |
| Liu et al. (2018) [23] | This article establishes a collaborative emergency inventory model for responding to supply disruptions and explores the coordination mechanism between both parties in the supply chain. |
| Xingyu et al. (2021) [27] | This article establishes a mathematical model to explore the impact of supply disruptions on global healthcare services. |
| Symbol | Description |
|---|---|
| Production cost per unit of product | |
| Sales price per unit of product | |
| Wholesale price per unit of product | |
| Product order quantity | |
| Supply chain resilience investment level | |
| Supply chain resilience investment cost sensitivity coefficient | |
| Stochastic capacity recovery level, | |
| Capacity recovery coefficient, | |
| Loss per unit of product stockout | |
| Salvage value per unit of product | |
| Probability of supply disruption, | |
| Retailer supply chain resilience cost-sharing ratio, | |
| Supply chain profit | |
| Manufacturer’s profit | |
| Retailer’s profit |
| D | C | D | C | D | C | D | C | D | C | D | C | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 70.3 | 80.51 | 55.75 | 79.13 | 41.20 | 78.65 | 82.00 | 109.94 | 55.00 | 124.84 | 28.00 | 139.75 |
| 0.3 | 71.90 | 75.47 | 59.75 | 68.67 | 47.60 | 61.87 | 86.00 | 97.32 | 65.00 | 93.29 | 44.00 | 89.27 |
| 0.5 | 73.50 | 74.73 | 63.75 | 66.81 | 54.00 | 58.90 | 90.00 | 89.92 | 75.00 | 74.80 | 60.00 | 59.68 |
| 0.7 | 75.10 | 76.73 | 67.75 | 71.81 | 60.40 | 66.90 | 94.00 | 89.47 | 85.00 | 73.67 | 76.00 | 57.88 |
| 0.9 | 76.70 | 80.30 | 71.75 | 80.75 | 66.80 | 81.20 | 98.00 | 96.00 | 95.00 | 90.00 | 92.00 | 84.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Kang, K.; Lu, L.; Ke, Y. Research on Investment and Coordination Strategies for Supply Chain Resilience under Supply Disruption Risk. Symmetry 2024, 16, 1192. https://doi.org/10.3390/sym16091192
Luo X, Kang K, Lu L, Ke Y. Research on Investment and Coordination Strategies for Supply Chain Resilience under Supply Disruption Risk. Symmetry. 2024; 16(9):1192. https://doi.org/10.3390/sym16091192
Chicago/Turabian StyleLuo, Xiaochun, Kai Kang, Lin Lu, and Youan Ke. 2024. "Research on Investment and Coordination Strategies for Supply Chain Resilience under Supply Disruption Risk" Symmetry 16, no. 9: 1192. https://doi.org/10.3390/sym16091192
APA StyleLuo, X., Kang, K., Lu, L., & Ke, Y. (2024). Research on Investment and Coordination Strategies for Supply Chain Resilience under Supply Disruption Risk. Symmetry, 16(9), 1192. https://doi.org/10.3390/sym16091192







