Research on Dynamic Characteristics of Flap Actuation System Considering Joint Clearance and Flexibility
Abstract
1. Introduction
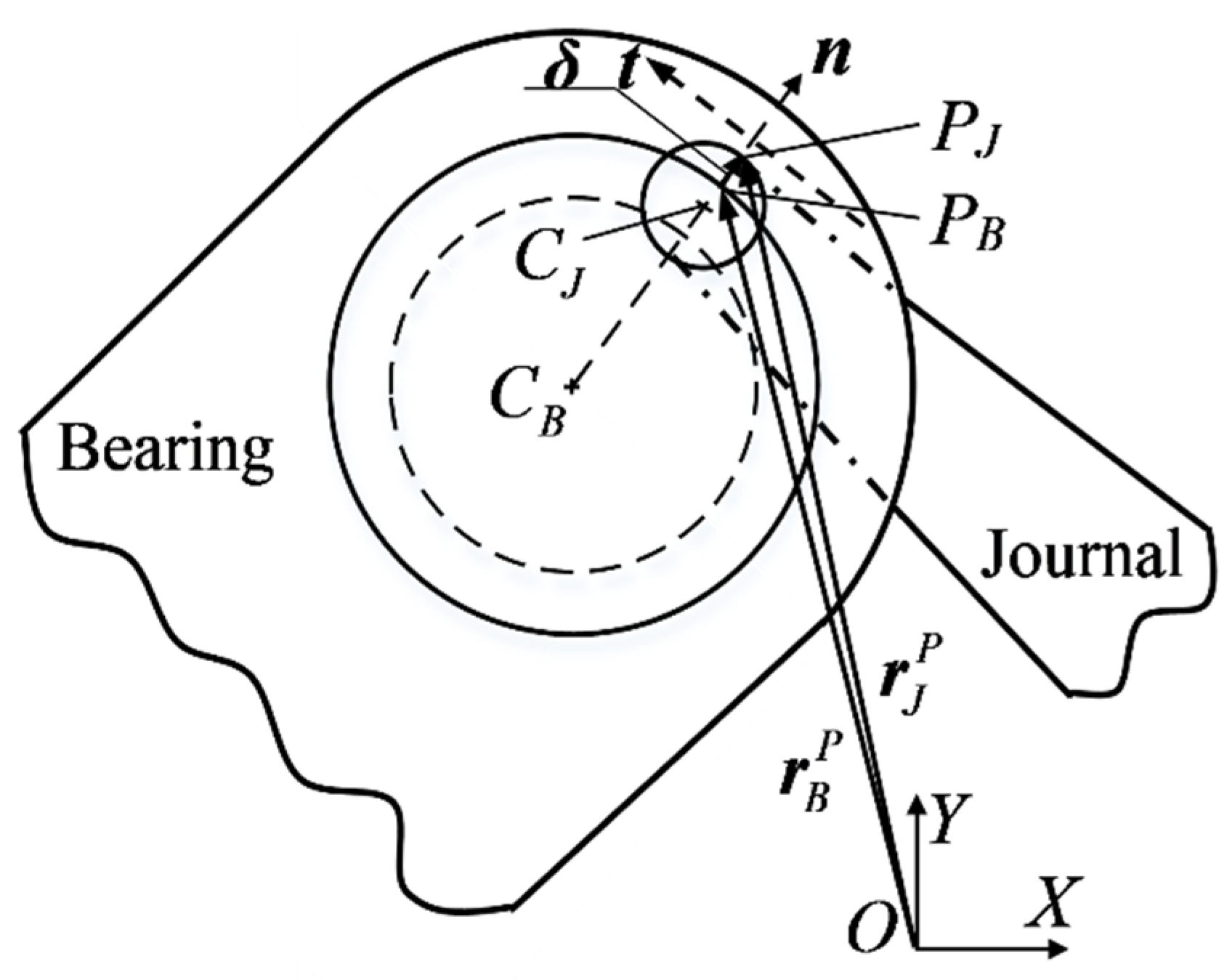
2. Modeling of Clearance Joints
2.1. Mathematical Model
2.2. Modified Normal Contact Force Model
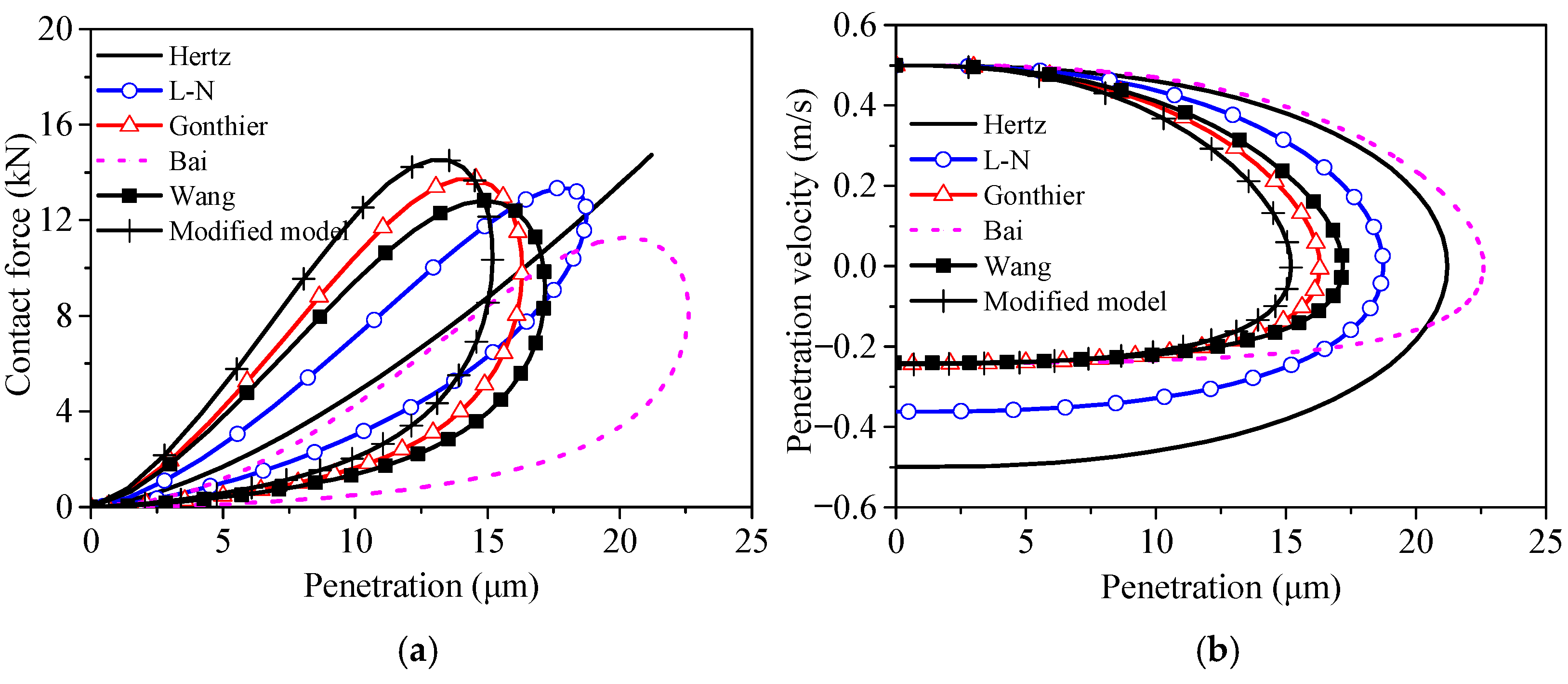
2.2.1. Comparison of Normal Contact Force Models
2.2.2. Embedded Modeling Method
2.2.3. Model Verification
2.3. Tangential Contact Force Model
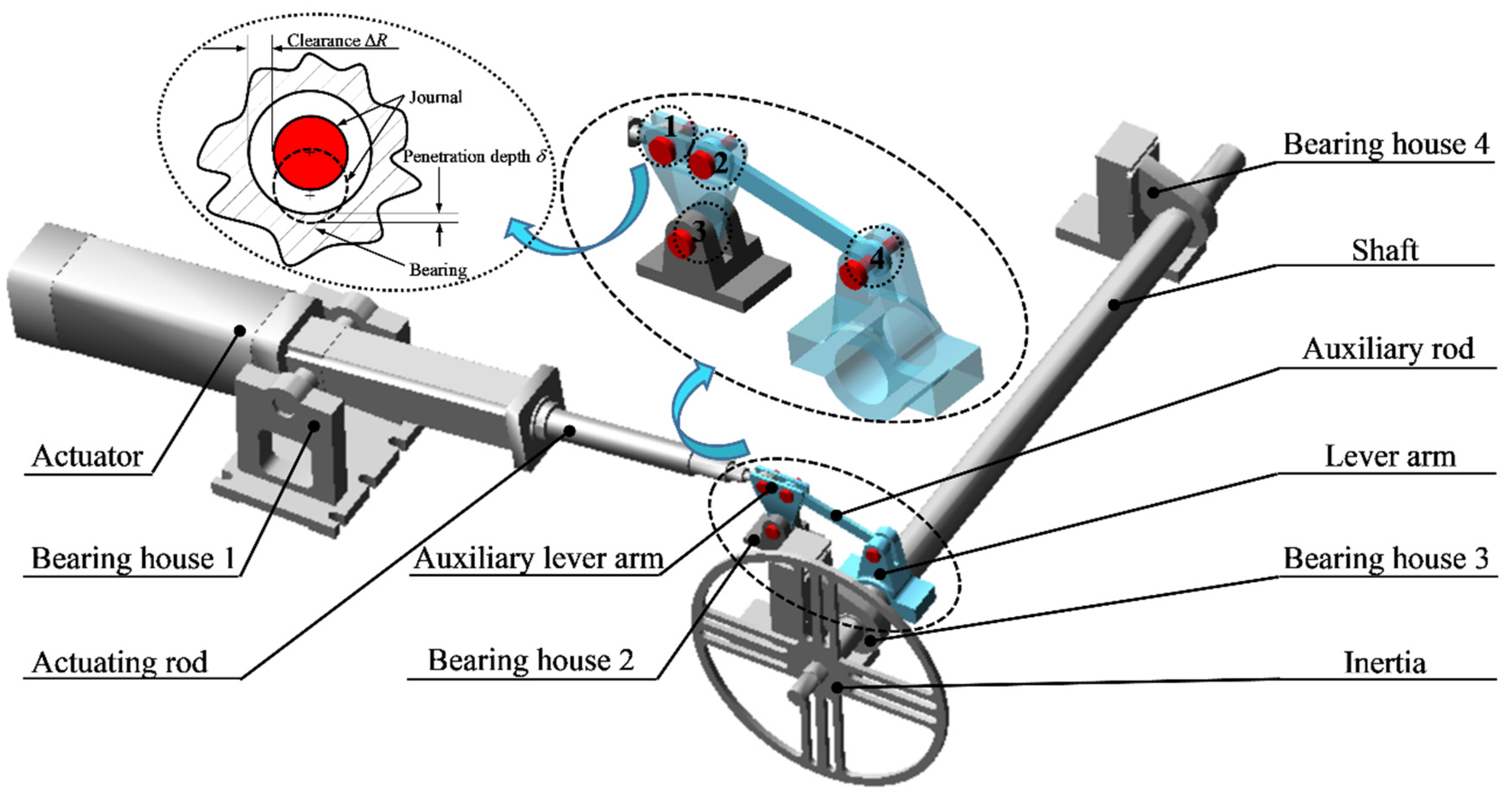
3. Modeling and Simulation of a Rigid Flap Actuation System with Clearance
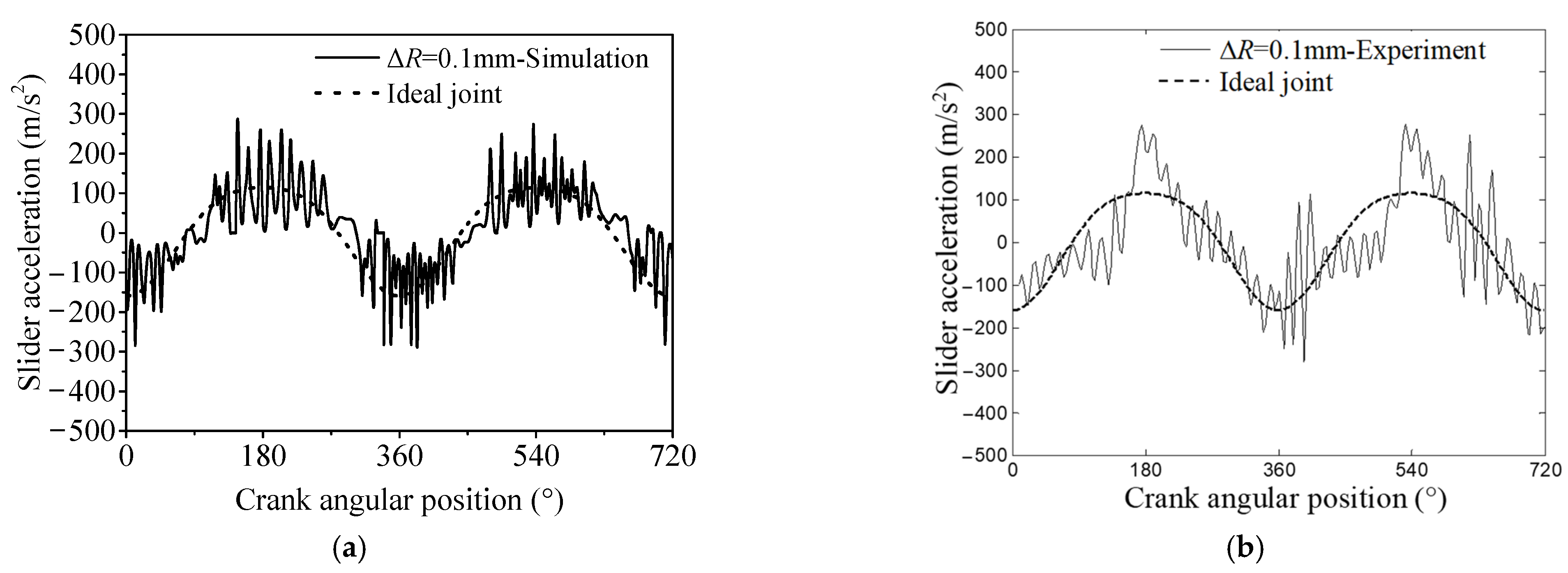
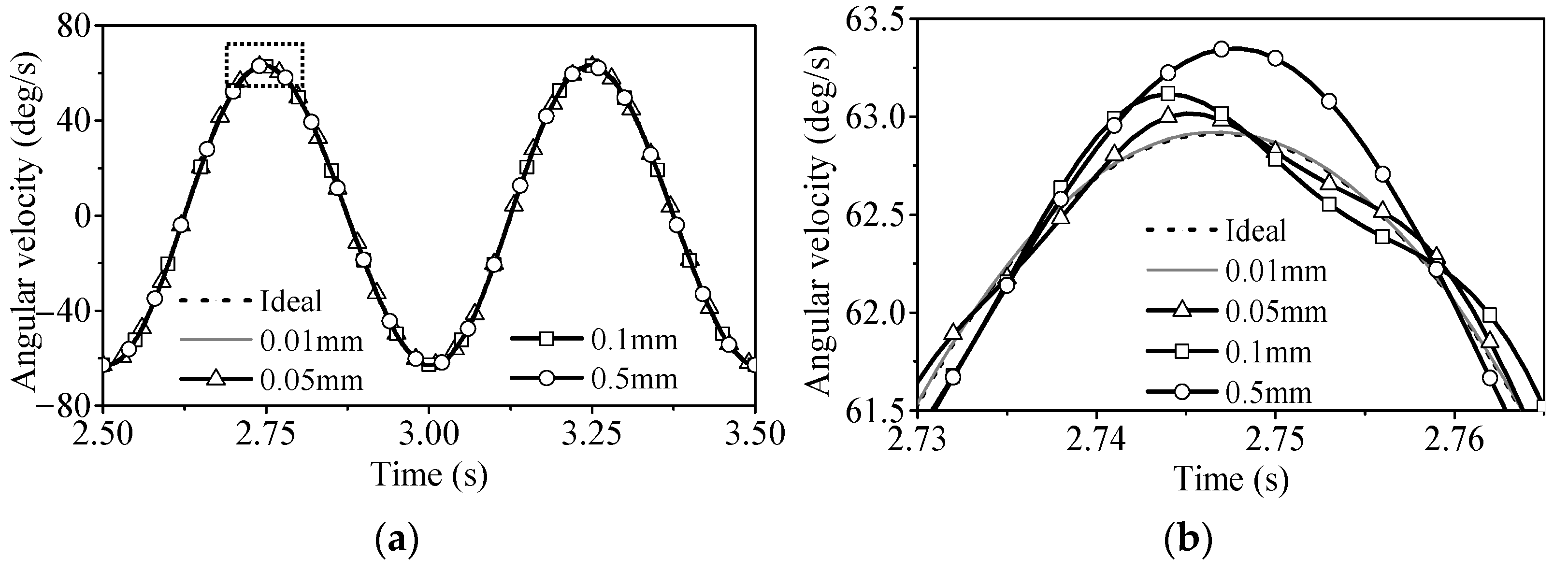
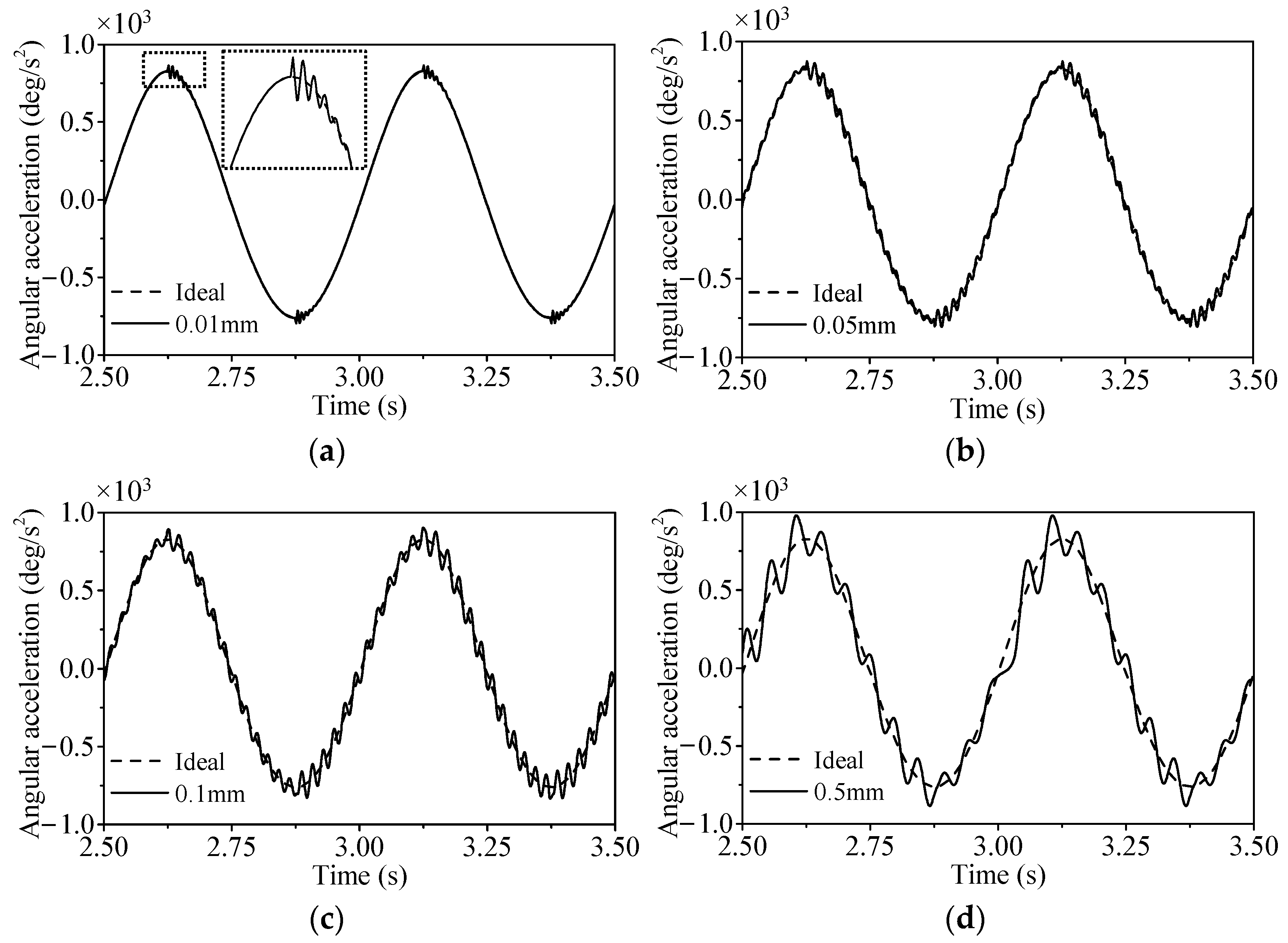
3.1. Influence of Clearance Size
3.2. Influence of Clearance Joint Position
4. Modeling and Simulation of a Rigid-Flexible Flap Actuation System with Clearance
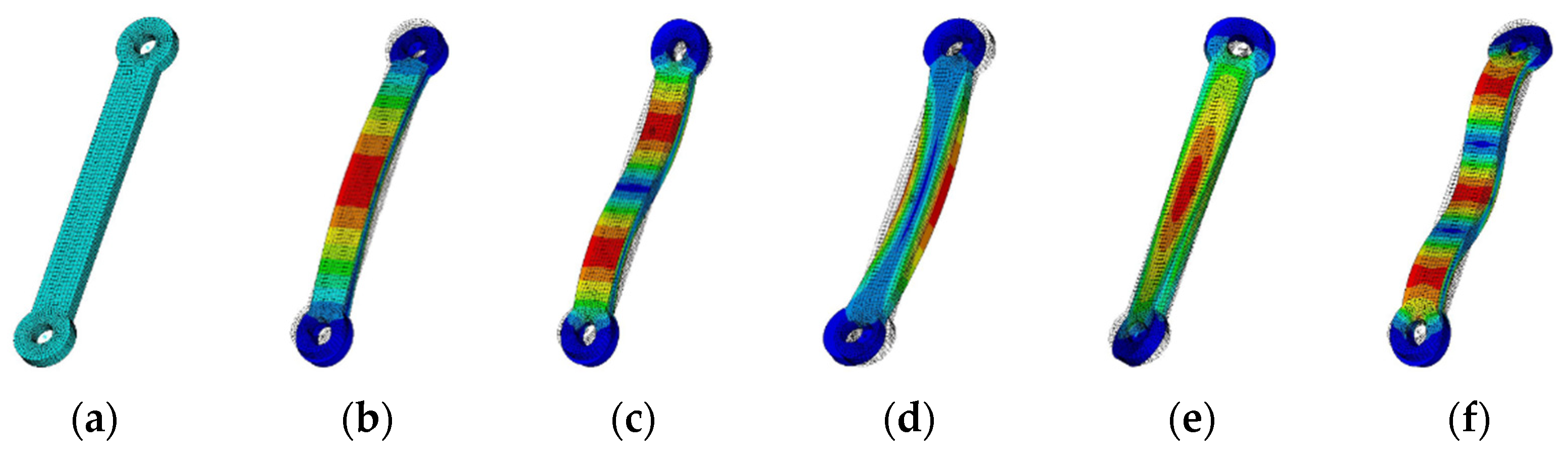
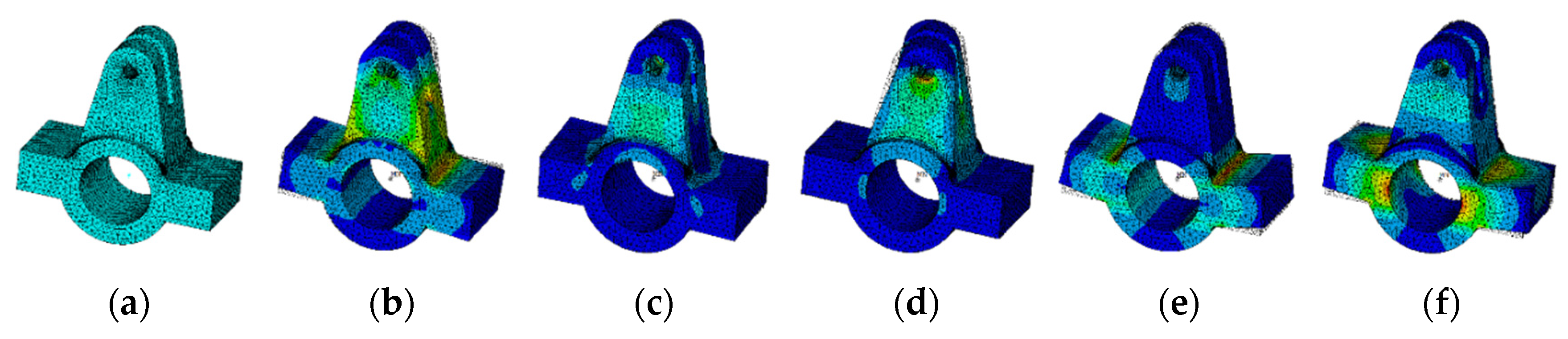
4.1. Modeling of Flexible Parts
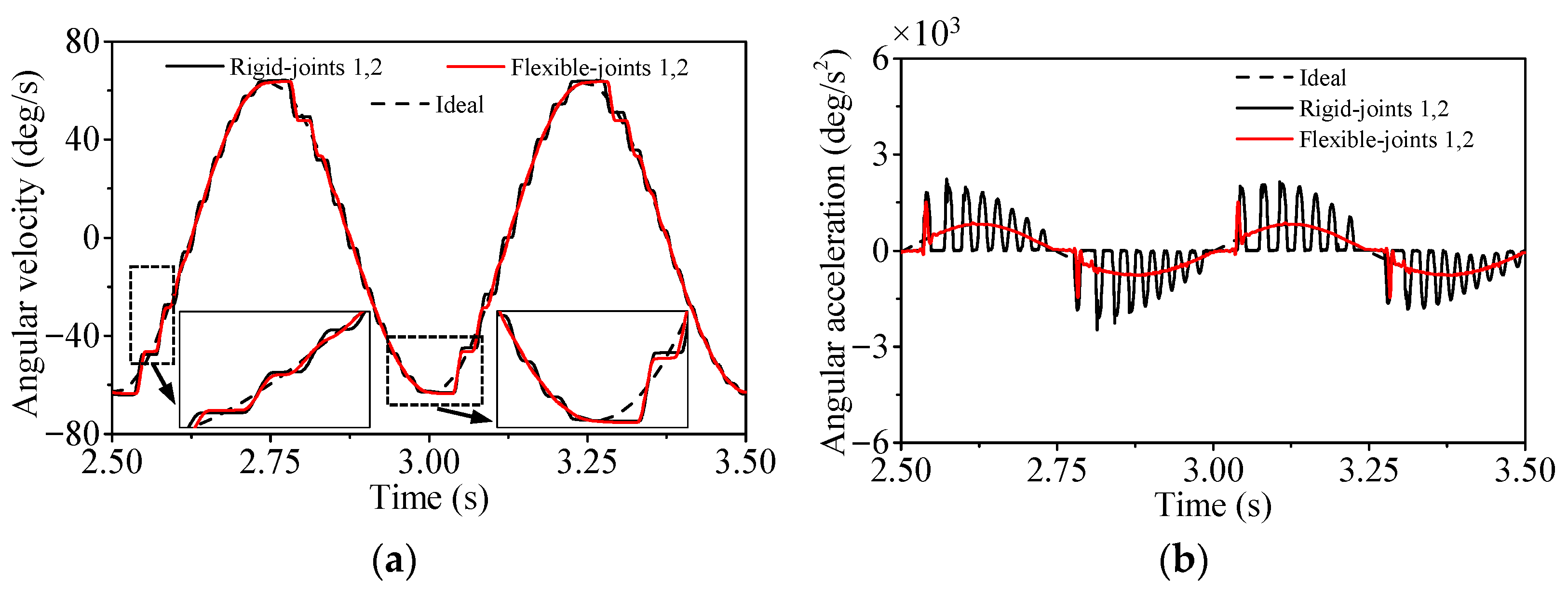
4.2. Influence of Flexible Body Number with Single Clearance Joint
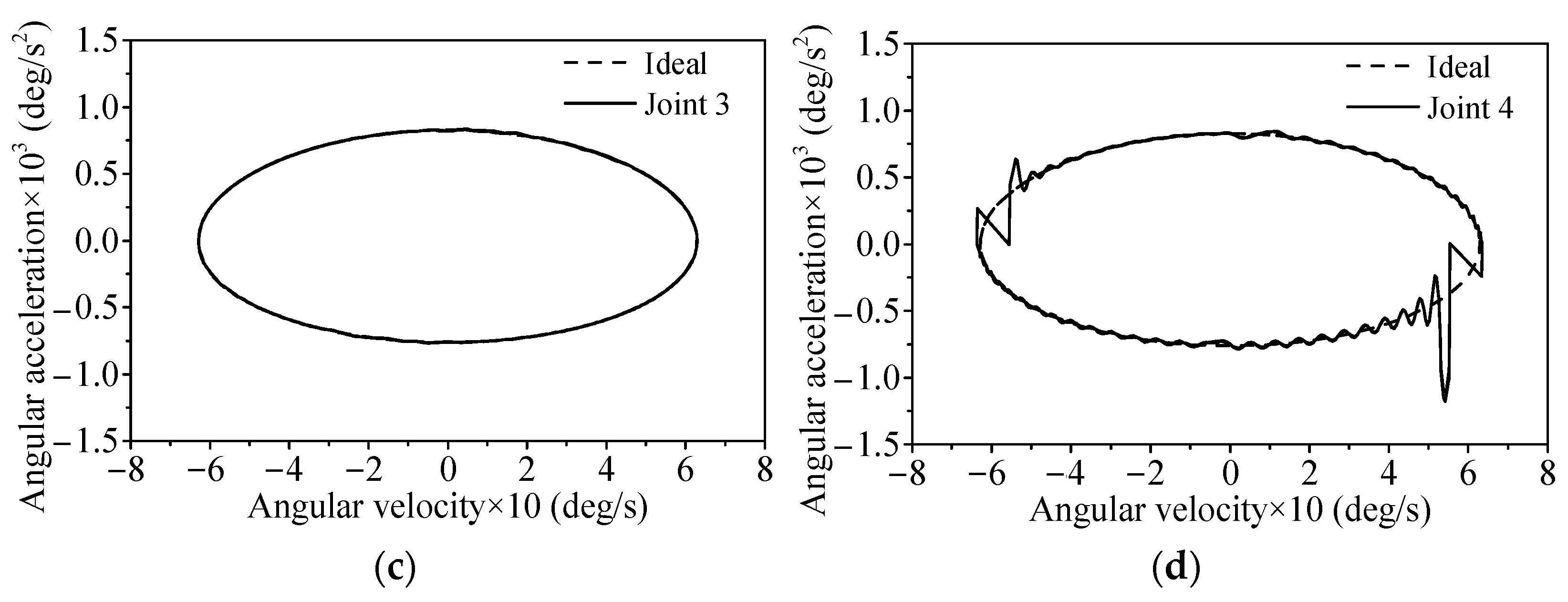
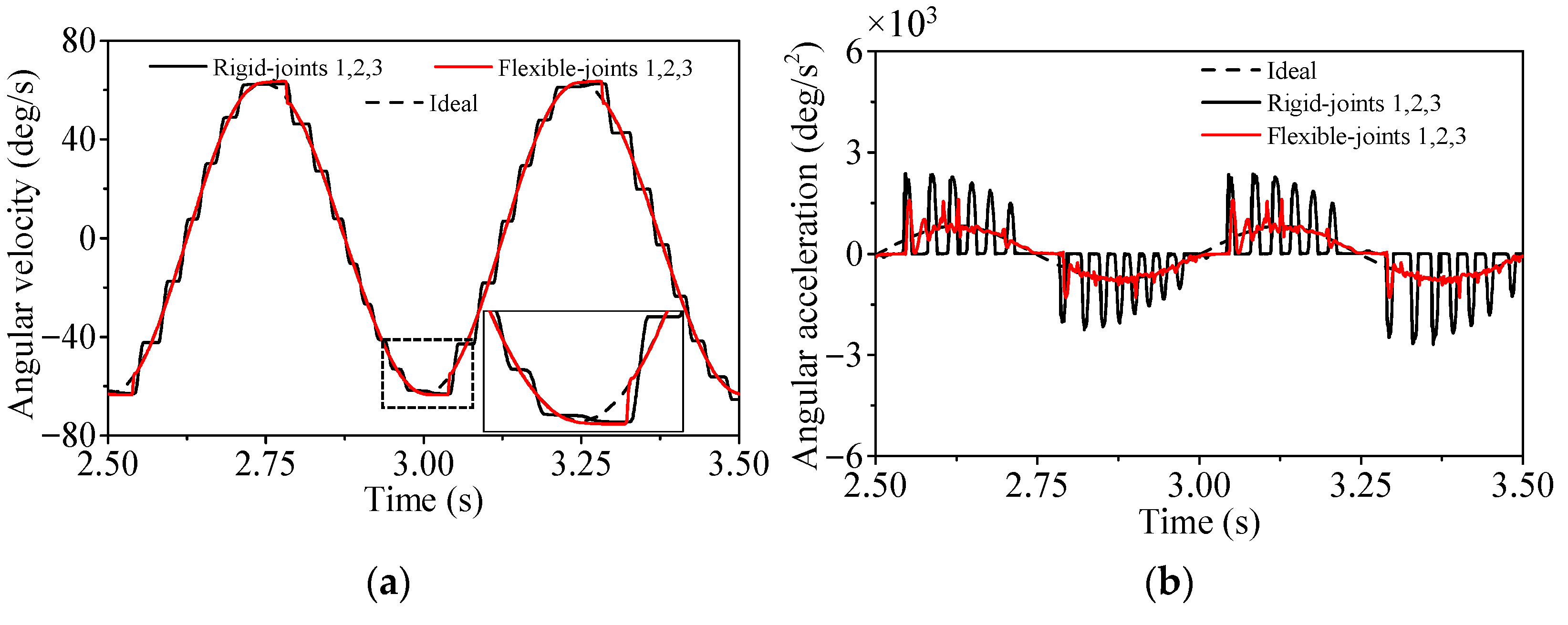
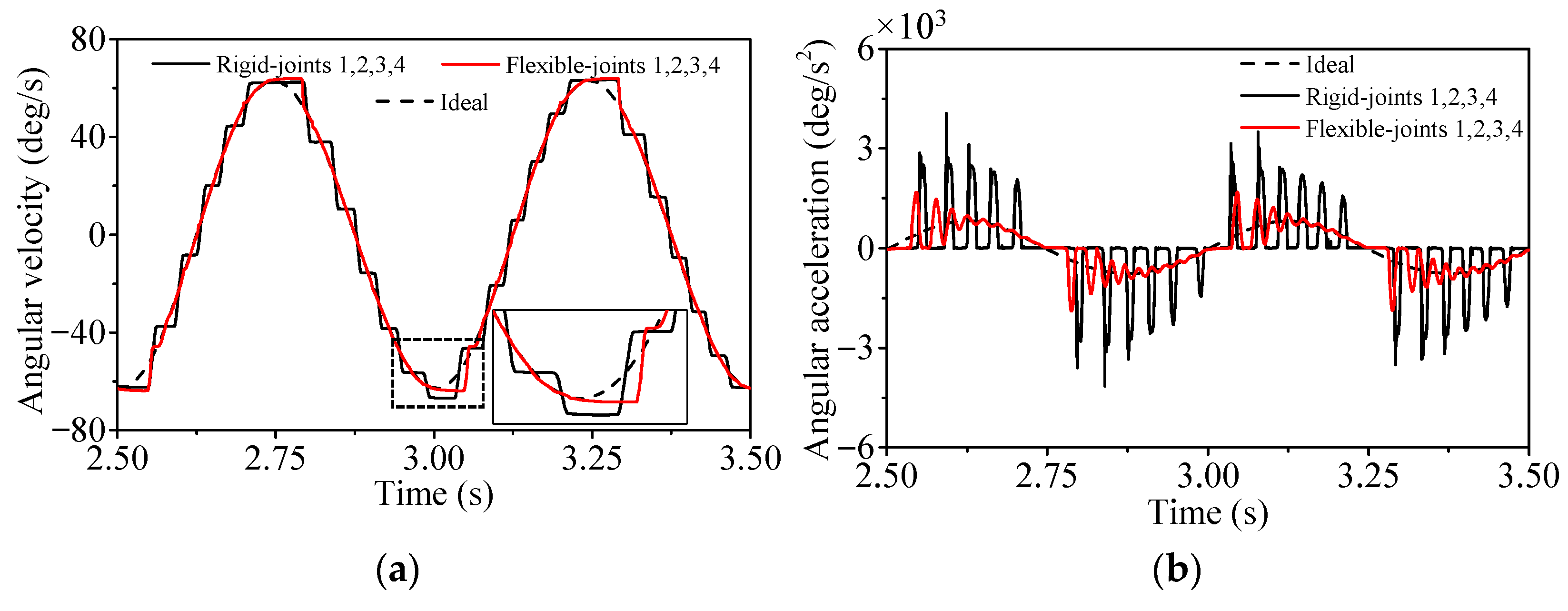
4.3. Influence of Clearance Joint Number with Single Flexible Body
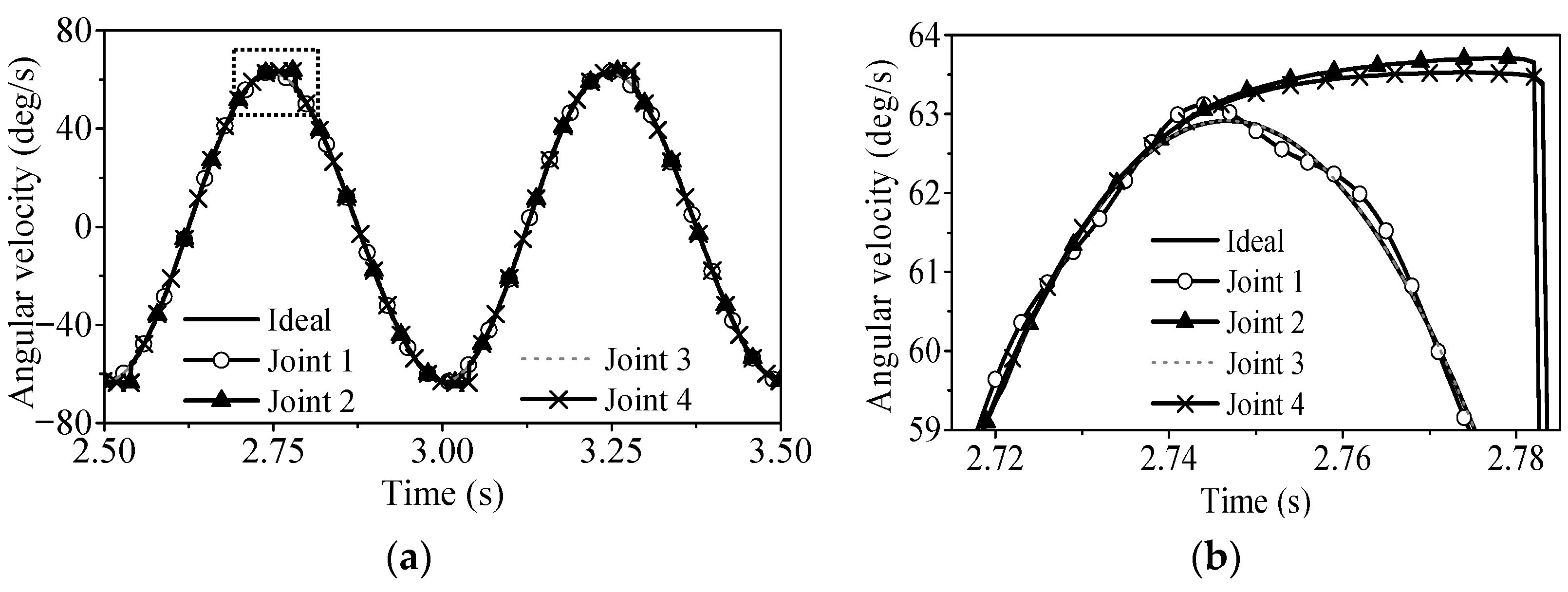
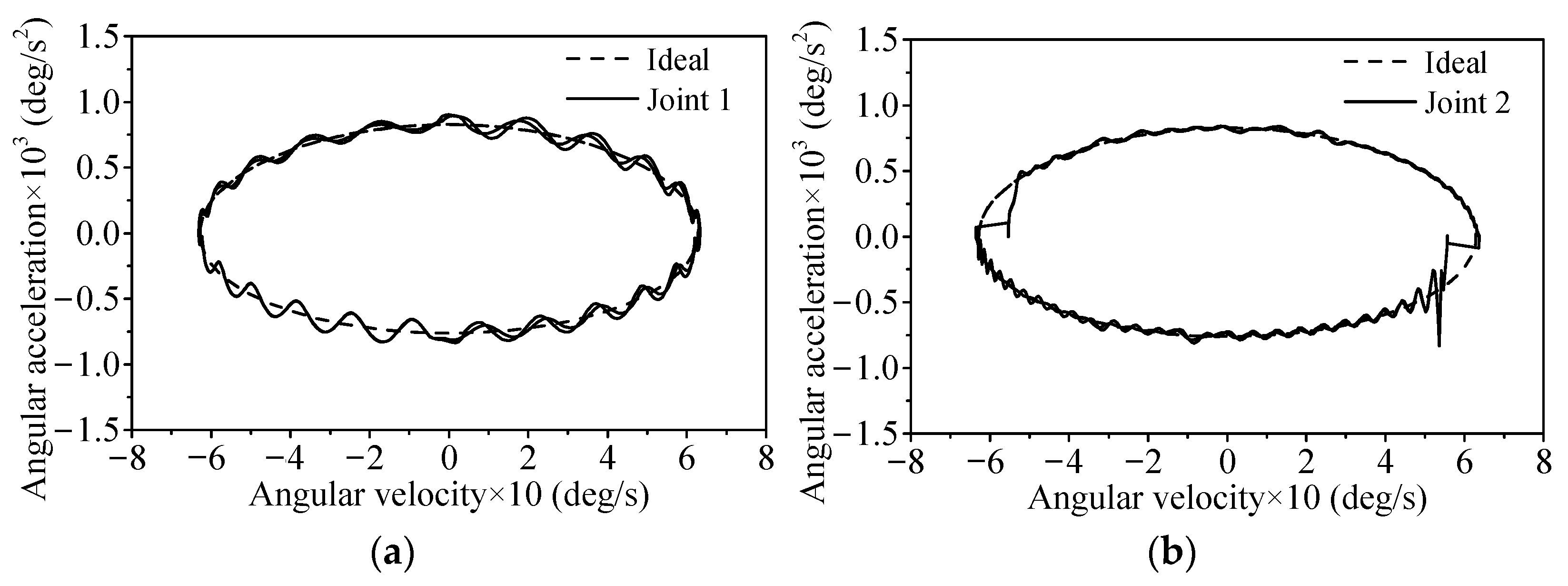
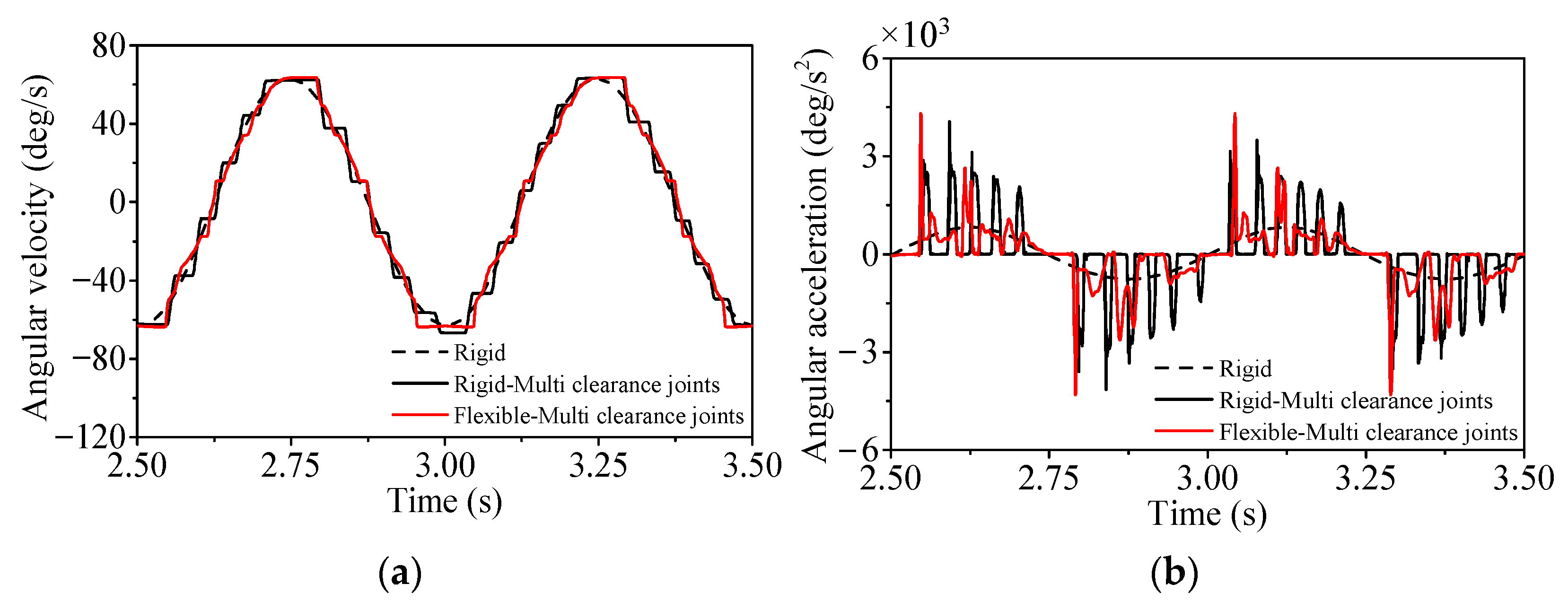
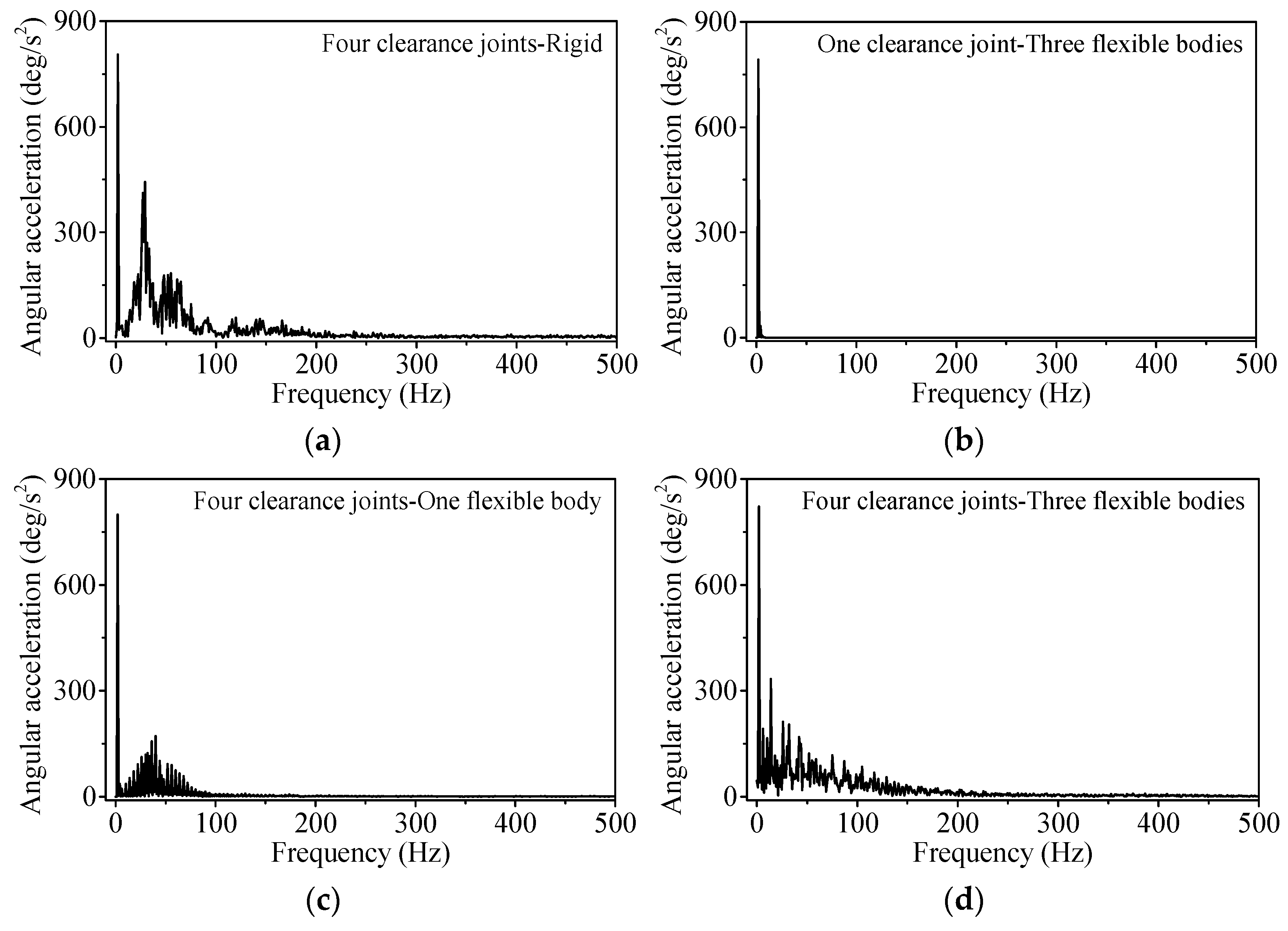
4.4. Coupling Effects of Four Clearance Joints and Three Flexible Bodies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arriola, D.; Thielecke, F. Model-based design and experimental verification of a monitoring concept for an active-active electromechanical aileron actuation system. Mech. Syst. Signal Proc. 2017, 94, 322–345. [Google Scholar] [CrossRef]
- Geng, X.Y.; Wang, X.J.; Wang, L.; Wang, R.X. Non-probabilistic time-dependent kinematic reliability assessment for function generation mechanisms with joint clearances. Mech. Mach. Theory 2016, 104, 202–221. [Google Scholar] [CrossRef]
- Li, Y.Y.; Chen, G.P.; Sun, D.Y.; Gao, Y.; Wang, K. Dynamic analysis and optimization design of a planar slider-crank mechanism with flexible components and two clearance joints. Mech. Mach. Theory 2016, 99, 37–57. [Google Scholar] [CrossRef]
- Marques, F.; Flores, P.; Claro, J.C.P.; Lankarani, H.M. A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 2016, 86, 1407–1443. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, Y.; Chen, C. Dynamic analysis of a planar slider-crank mechanism with clearance for a high speed and heavy load press system. Mech. Mach. Theory 2016, 98, 81–100. [Google Scholar] [CrossRef]
- Daniel, G.B.; Machado, T.H.; Cavalca, K.L. Investigation on the influence of the cavitation boundaries on the dynamic behavior of planar mechanical systems with hydrodynamic bearings. Mech. Mach. Theory 2016, 99, 19–36. [Google Scholar] [CrossRef]
- Li, P.; Chen, W.; Li, D.S.; Yu, R.F.; Zhang, W.J. Wear analysis of two revolute joints with clearance in multibody systems. J. Comput. Nonlinear Dyn. 2016, 11, 011009. [Google Scholar] [CrossRef]
- Cheng, C.; Huang, Q.G. An accurate determination of the Hubble constant from baryon acoustic oscillation datasets. Sci. China-Phys. Mech. Astron. 2015, 58, 599801. [Google Scholar] [CrossRef][Green Version]
- Flores, P.; Ambrósio, J.; Claro, J.C.P.; Lankarani, H.M.; Koshy, C.S. A study on dynamics of mechanical systems including joints with clearance and lubrication. Mech. Mach. Theory 2006, 41, 247–261. [Google Scholar] [CrossRef]
- Zheng, E.L.; Zhu, R.; Zhu, S.H.; Lu, X.J. A study on dynamics of flexible multi-link mechanism including joints with clearance and lubrication for ultra-precision presses. Nonlinear Dyn. 2016, 83, 137–159. [Google Scholar] [CrossRef]
- Dubowsky, S.; Moening, M.F. An experimental and analytical study of impact forces in elastic mechanical systems with clearances. Mech. Mach. Theory 1978, 13, 451–465. [Google Scholar] [CrossRef]
- Erkaya, S.; Doğan, S.; Ulus, S. Effects of joint clearance on the dynamics of a partly compliant mechanism: Numerical and experimental studies. Mech. Mach. Theory 2015, 88, 125–140. [Google Scholar] [CrossRef]
- Schwab, A.L.; Meijaard, J.P.; Meijers, P. A comparison of revolute joint clearance model in the dynamic analysis of rigid and elastic mechanical systems. Mech. Mach. Theory 2002, 37, 895–913. [Google Scholar] [CrossRef]
- Erkaya, S. Experimental investigation of flexible connection and clearance joint effects on the vibration responses of mechanisms. Mech. Mach. Theory 2018, 121, 515–529. [Google Scholar] [CrossRef]
- Erkaya, S.; Doğan, S.; Şefkatlıoğlu, E. Analysis of the joint clearance effects on a compliant spatial mechanism. Mech. Mach. Theory 2016, 104, 255–273. [Google Scholar] [CrossRef]
- Li, Y.Y.; Wang, C.; Huang, W.H. Dynamics analysis of planar rigid-flexible coupling deployable solar array system with multiple revolute clearance joints. Mech. Syst. Signal Proc. 2019, 117, 188–209. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Qian, L.F.; Chen, G.S.; Nie, S.C.; Yin, Q.; Yue, C.C. Dynamics of luffing motion of a hydraulically driven shell manipulator with revolute clearance joints. Def. Technol. 2022, 18, 689–708. [Google Scholar]
- Tan, X.; Chen, G.P.; Shao, H.B. Modeling and analysis of spatial flexible mechanical systems with a spherical clearance joint based on the LuGre friction model. J. Comput. Nonlinear Dyn. 2020, 15, 011005. [Google Scholar] [CrossRef]
- Dong, X.Y.; Sun, Y.; Wu, X.Z.; Wang, R.D. Dynamic modeling and performance analysis of toggle-linkage presses considering mixed clearances and flexibility. Int. J. Non-Linear Mech. 2022, 147, 104243. [Google Scholar] [CrossRef]
- Li, Y.T.; Quan, Q.Q.; Li, H.; Tang, D.W.; Li, Z.H.; Fan, W.Y.; Deng, Z.Q. Air rudder mechanism dynamics considering two elements: Joint clearance and link flexibility. J. Mech. Sci. Technol. 2017, 31, 3189–3197. [Google Scholar] [CrossRef]
- Gonthier, Y.; Mcphee, J.; Lange, C.; Piedboeuf, J.C. A regularized contact model with asymmetric damping and dwell-time dependent friction. Multibody Syst. Dyn. 2004, 11, 209–233. [Google Scholar] [CrossRef]
- Wang, X.P.; Liu, G.; Ma, S.J. Dynamic analysis of planar mechanical systems with clearance joints using a new nonlinear contact force model. J. Mech. Sci. Technol. 2016, 30, 1537–1545. [Google Scholar] [CrossRef]
- Wan, Q.; Liu, G.; Song, C.Y.; Zhou, Y.; Ma, S.J.; Tong, R.T. Study on the dynamic interaction of multiple clearance joints for flap actuation system with a modified contact force model. J. Mech. Sci. Technol. 2020, 34, 2701–2713. [Google Scholar] [CrossRef]
- Hertz, H. Über die berührung fester elasticher körper. J. Reine Angew. Math. 1881, 92, 156–171. [Google Scholar]
- Hunt, K.H.; Crossley, F.R.E. Coefficient of restitution interpreted as damping in vibroimpact. J. Appl. Mech.-Trans. ASME 1975, 42, 440–445. [Google Scholar] [CrossRef]
- Lankarani, H.M.; Nikravesh, P.E. A contact force model with hysteresis damping for impact analysis of multibody systems. J. Mech. Des. 1990, 112, 369–376. [Google Scholar] [CrossRef]
- Flores, P.; Machado, M.; Silva, M.T.; Martins, J.M. On the continuous contact force models for soft materials in multibody dynamics. Multibody Syst. Dyn. 2011, 25, 357–375. [Google Scholar] [CrossRef]
- Bai, Z.F.; Zhao, Y. A hybrid contact force model of revolute joint with clearance for planar mechanical systems. Int. J. Non-Linear Mech. 2013, 48, 15–36. [Google Scholar] [CrossRef]
- Wang, X.P.; Liu, G.; Ma, S.J.; Tong, R.T. Study on dynamic responses of planar multibody systems with dry revolute clearance joint: Numerical and experimental approaches. J. Sound Vibr. 2019, 438, 116–138. [Google Scholar] [CrossRef]
- Ambrósio, J. Impact of rigid and flexible multibody systems: Deformation description and contact models. Virtual Nonlinear Multibody Syst. 2002, 103, 57–81. [Google Scholar]
- Ma, J.; Qian, L.F. Modeling and simulation of planar multibody systems considering multiple revolute clearance joints. Nonlinear Dyn. 2017, 90, 1907–1940. [Google Scholar] [CrossRef]








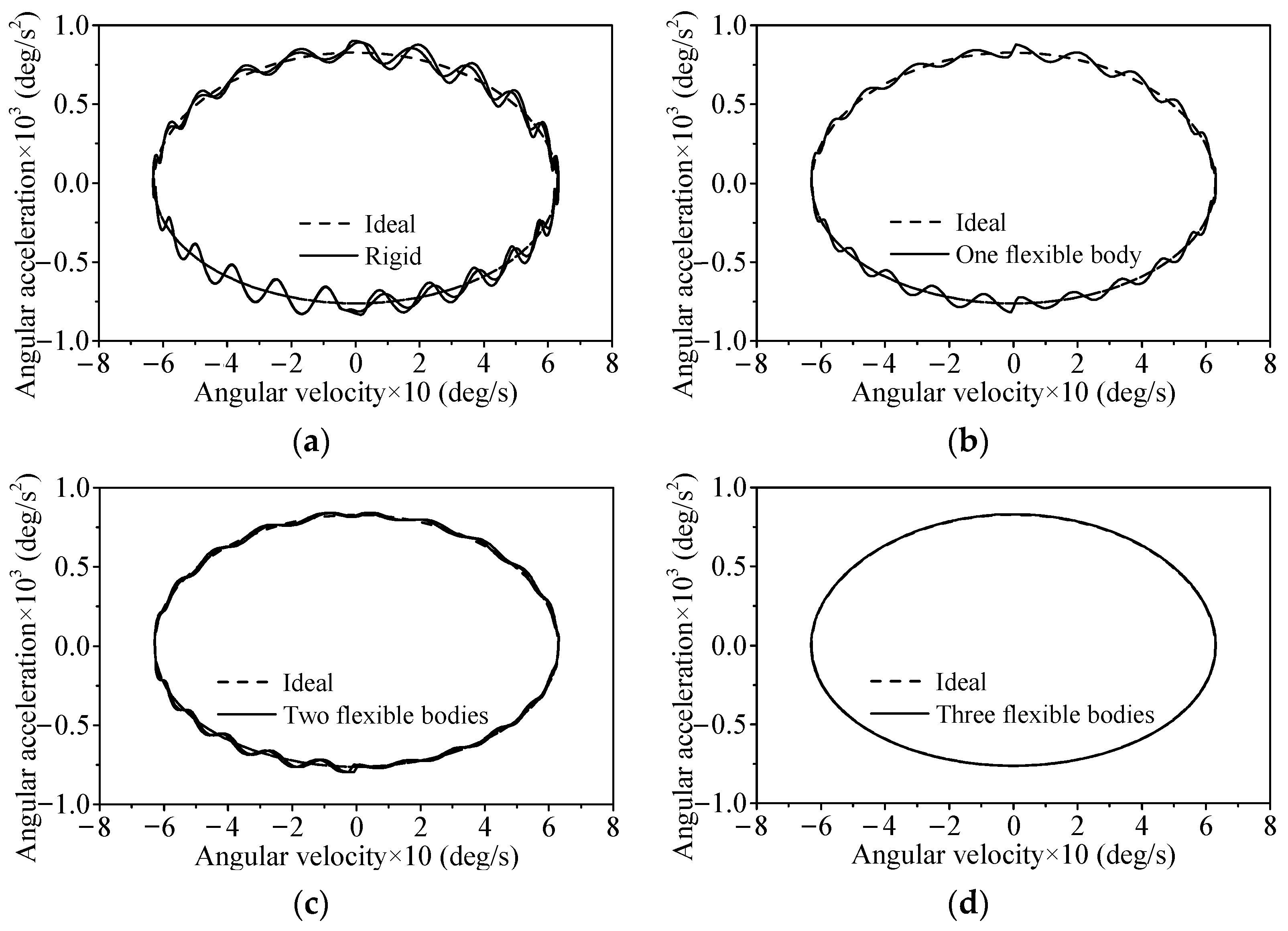

| Model | Radius (mm) | Young’s Modulus (GPa) | Poisson’s Ratio | Mass (kg) | Length (mm) | Initial Velocity (m/s) |
|---|---|---|---|---|---|---|
| Bearing | 10 | 207 | 0.3 | / | 15 | 0 |
| Journal | 9.9 | 207 | 0.3 | 1 | / | 0.5 |
| Hertz [24] | L-N [26] | Gonthier [21] | Bai [28] | Wang [22] | Modified Model [23] | |
|---|---|---|---|---|---|---|
| Actual restitution coefficient | 1 | 0.726 | 0.488 | 0.482 | 0.482 | 0.488 |
| Relative errors | 100% | 45.2% | 2.4% | 3.6% | 3.6% | 2.4% |
| Length (m) | Mass (kg) | Moment of Inertial (kg·m2) | |
|---|---|---|---|
| Crank | 0.05 | 0.343 | 0.000216 |
| Connecting rod | 0.3 | 1.072 | 0.034 |
| Slider | / | 0.347 | 0.000115 |
| Oscillation Peak (m/s2) | Simulation | Experiment | Relative Error | |
|---|---|---|---|---|
| Clearance Size (mm) | ||||
| 0.1 | 283.1 | 268.0 | 5.6% | |
| 0.3 | 318.2 | 297.7 | 6.9% | |
| 0.5 | 371.8 | 345.4 | 7.6% | |
| Parameter | Description | Value | Unit |
|---|---|---|---|
| x | Actuator’s output displacement | 10 | mm |
| f | Actuator’s output frequency | 2 | Hz |
| L | Bearing’s length | 15 | mm |
| cf | Friction coefficient | 0.01 | / |
| cr | Restitution coefficient | 0.46 | / |
| v0 | Given tolerance for the tangential velocity | 0.1 | mm/s |
| v1 | Given tolerance for the tangential velocity | 1 | mm/s |
| Eigenfrequencies | First | Second | Third | Fourth | Fifth | |
|---|---|---|---|---|---|---|
| Parts | ||||||
| Auxiliary lever arm | 3715.8 | 5437.1 | 7921.3 | 7946.1 | 7971.7 | |
| Auxiliary rod | 690.40 | 1648.66 | 1869.88 | 2143.10 | 3588.54 | |
| Lever arm | 5839.3 | 6201.3 | 7240.9 | 7976.3 | 9260.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, Q.; Liu, G.; Liu, Q.; Tong, R.; Ma, S. Research on Dynamic Characteristics of Flap Actuation System Considering Joint Clearance and Flexibility. Machines 2022, 10, 1098. https://doi.org/10.3390/machines10111098
Wan Q, Liu G, Liu Q, Tong R, Ma S. Research on Dynamic Characteristics of Flap Actuation System Considering Joint Clearance and Flexibility. Machines. 2022; 10(11):1098. https://doi.org/10.3390/machines10111098
Chicago/Turabian StyleWan, Qi, Geng Liu, Qi Liu, Ruiting Tong, and Shangjun Ma. 2022. "Research on Dynamic Characteristics of Flap Actuation System Considering Joint Clearance and Flexibility" Machines 10, no. 11: 1098. https://doi.org/10.3390/machines10111098
APA StyleWan, Q., Liu, G., Liu, Q., Tong, R., & Ma, S. (2022). Research on Dynamic Characteristics of Flap Actuation System Considering Joint Clearance and Flexibility. Machines, 10(11), 1098. https://doi.org/10.3390/machines10111098








