Modeling, System Measurements and Controller Investigation of a Small Battery-Powered Fixed-Wing UAV
Abstract
:1. Introduction
2. Mathematical Model of the Fixed Wing UAV
2.1. 6-DOF Equations of Motion
2.2. Aerodynamic Model
3. System Parameters Measurements
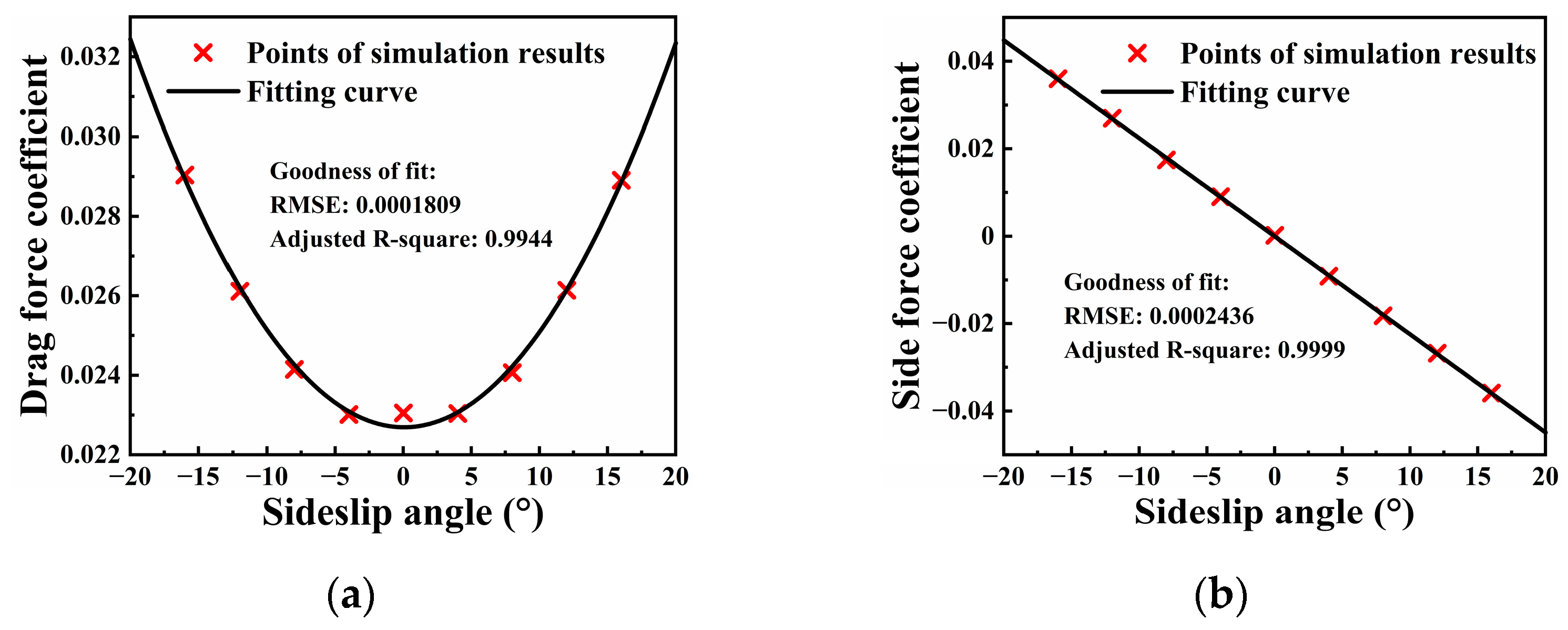
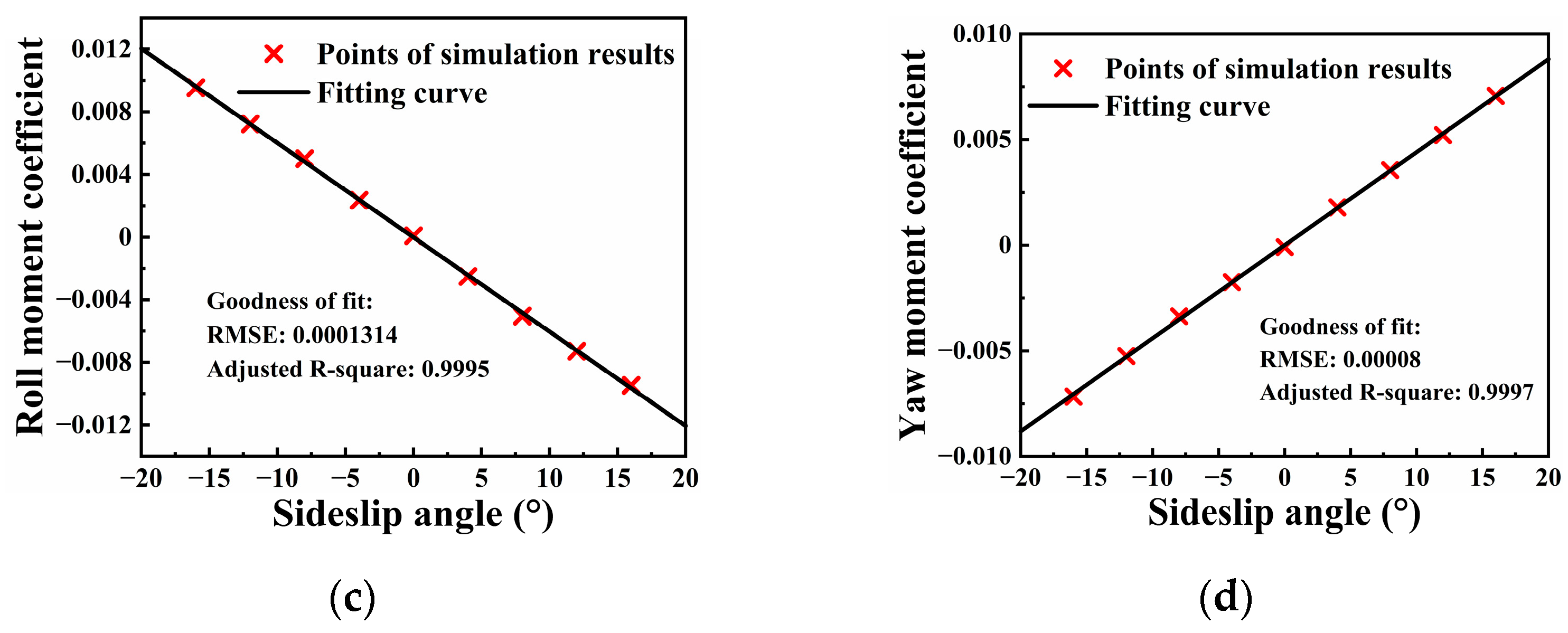
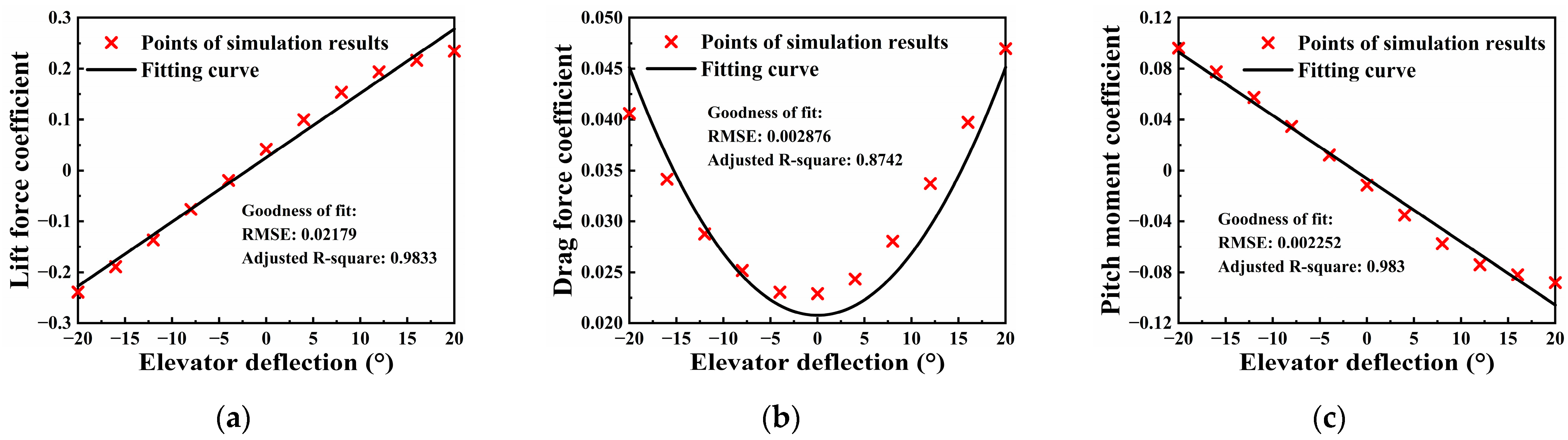
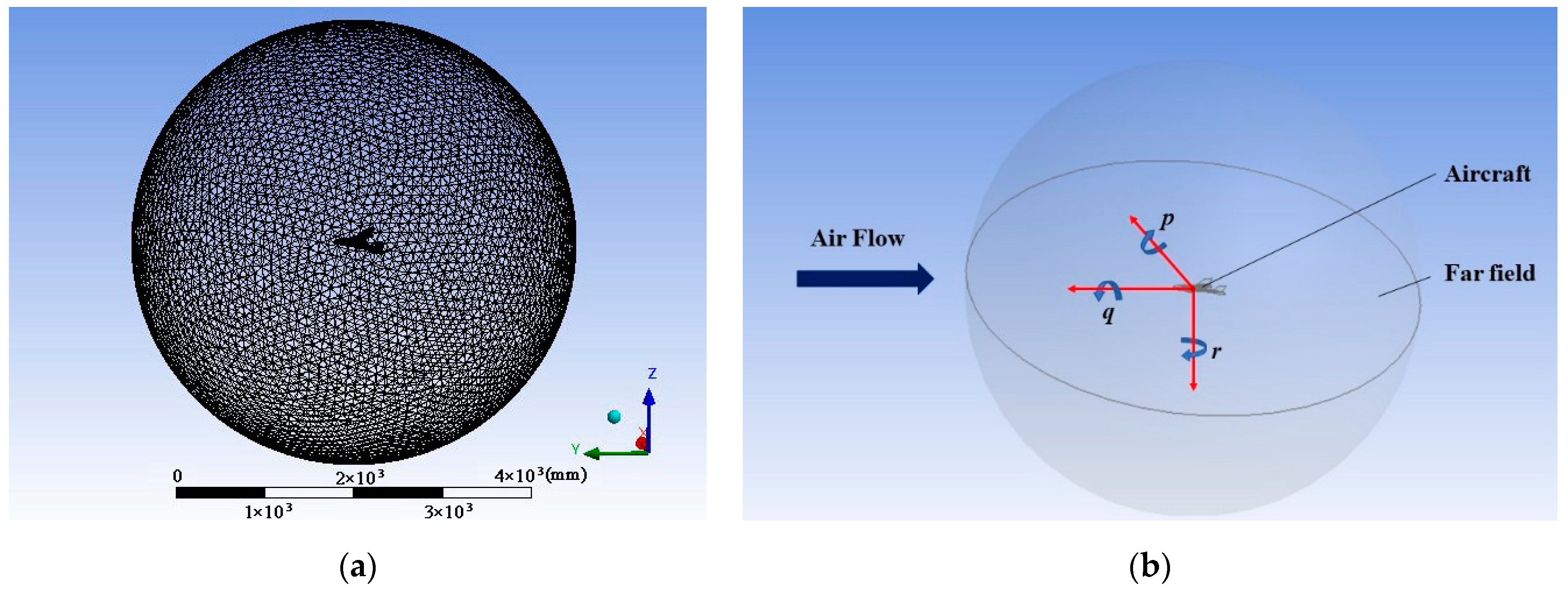
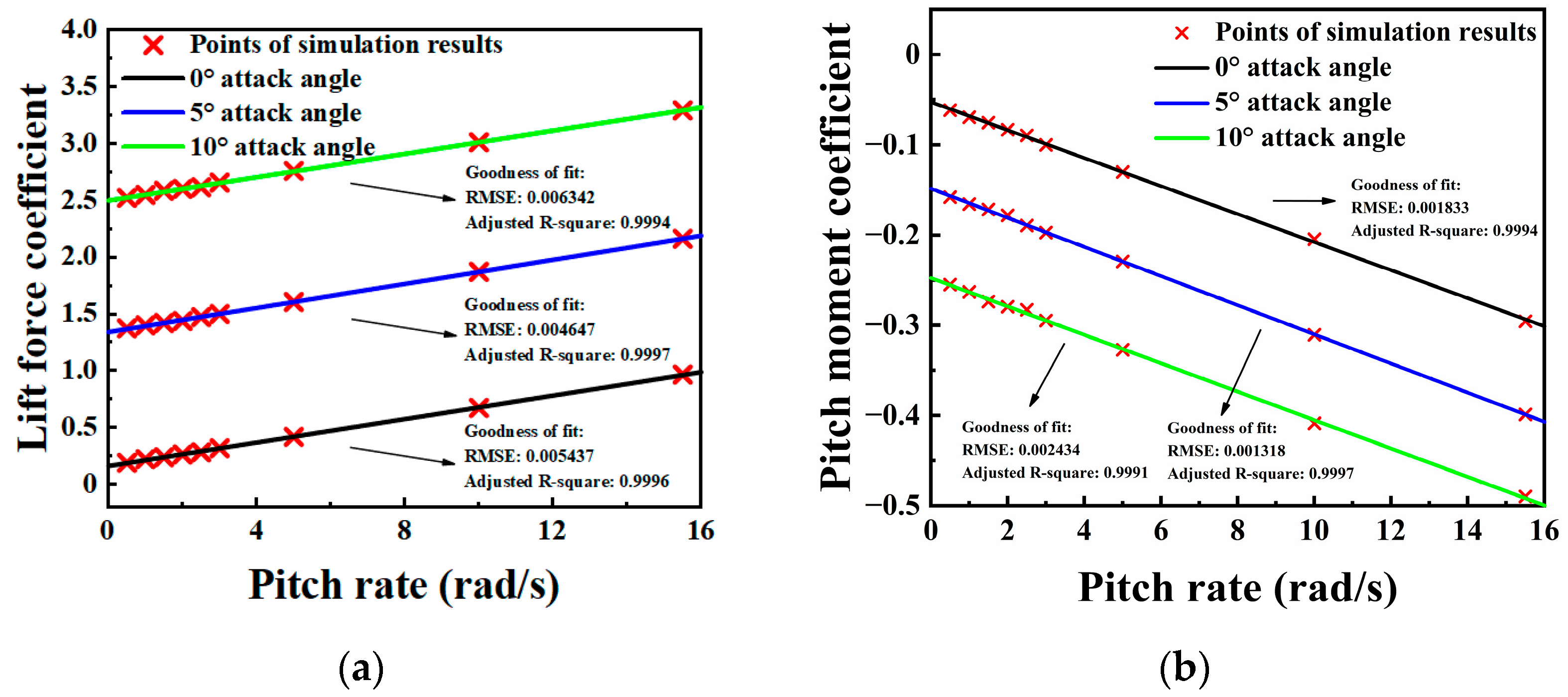
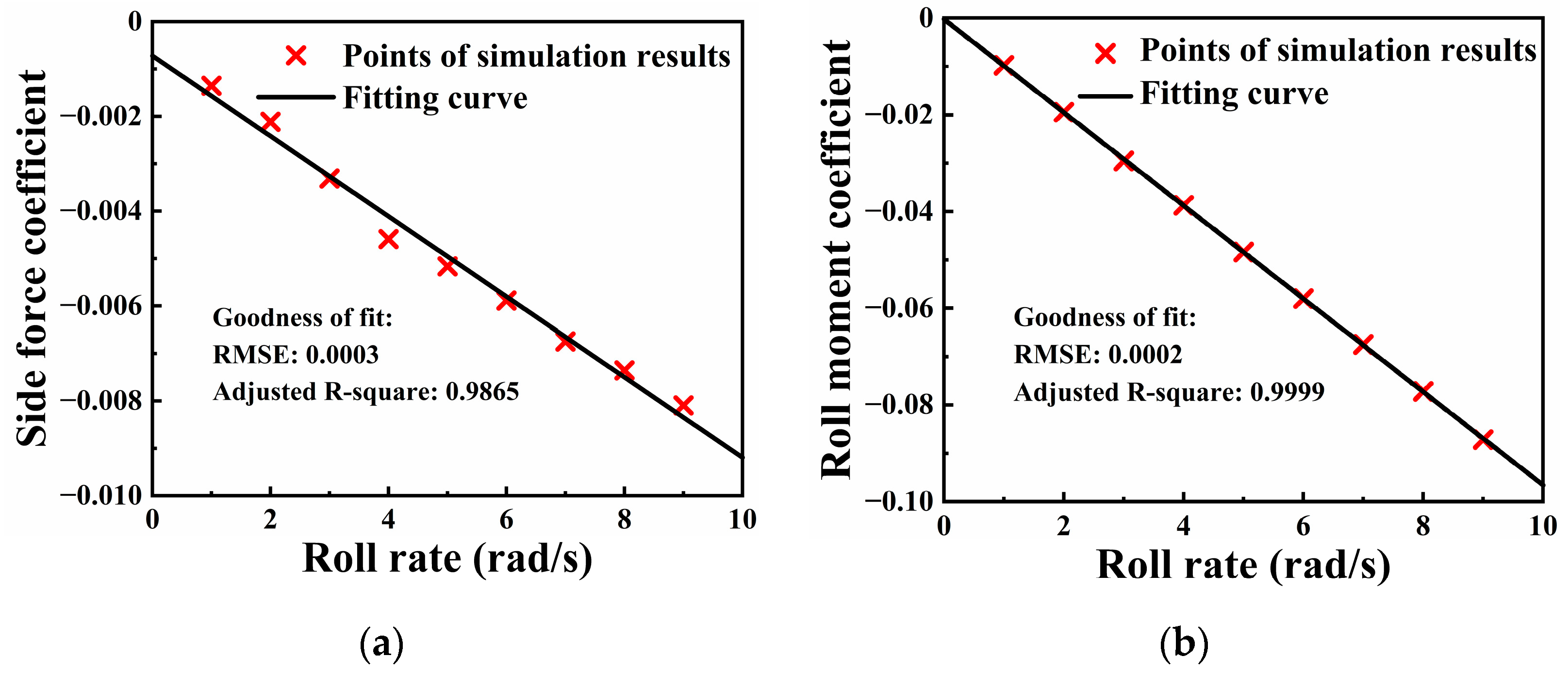
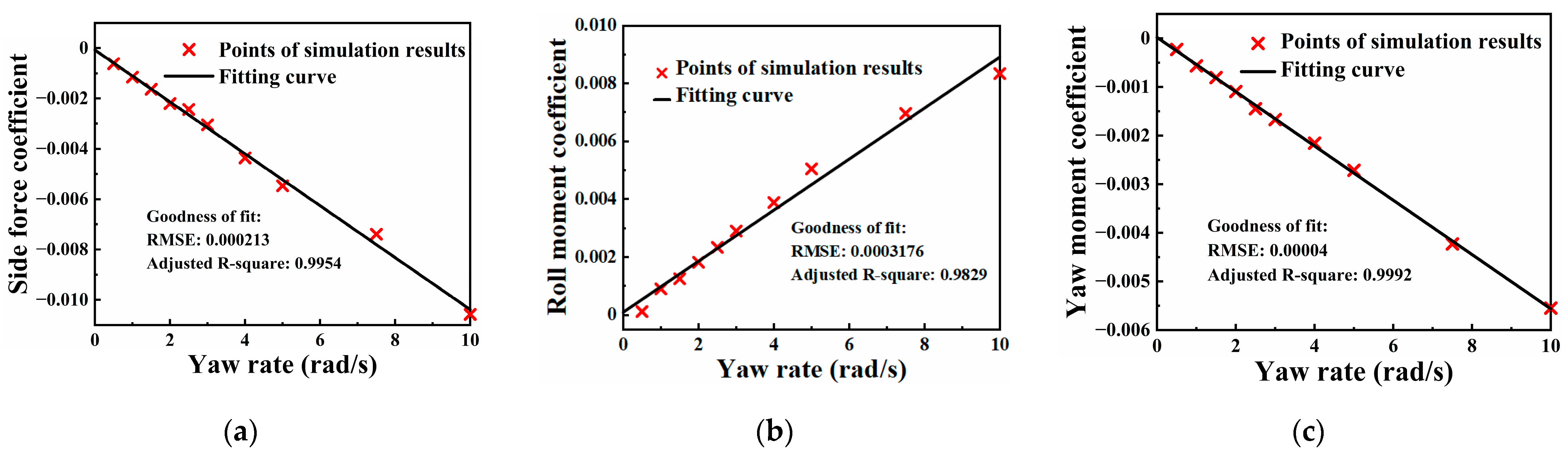
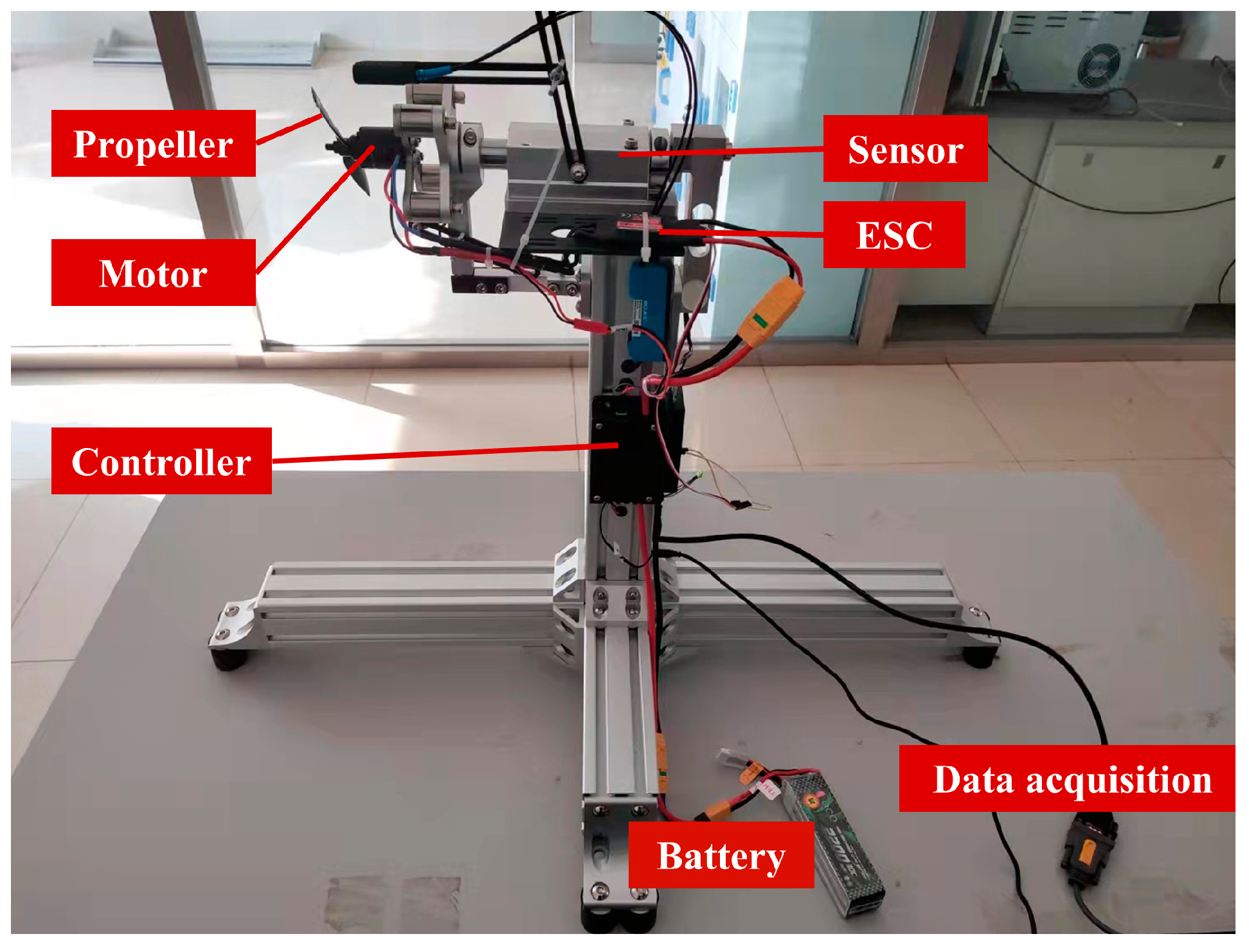
3.1. Aerodynamic Derivatives Measurements
3.1.1. Static Derivatives
3.1.2. Dynamic Derivatives
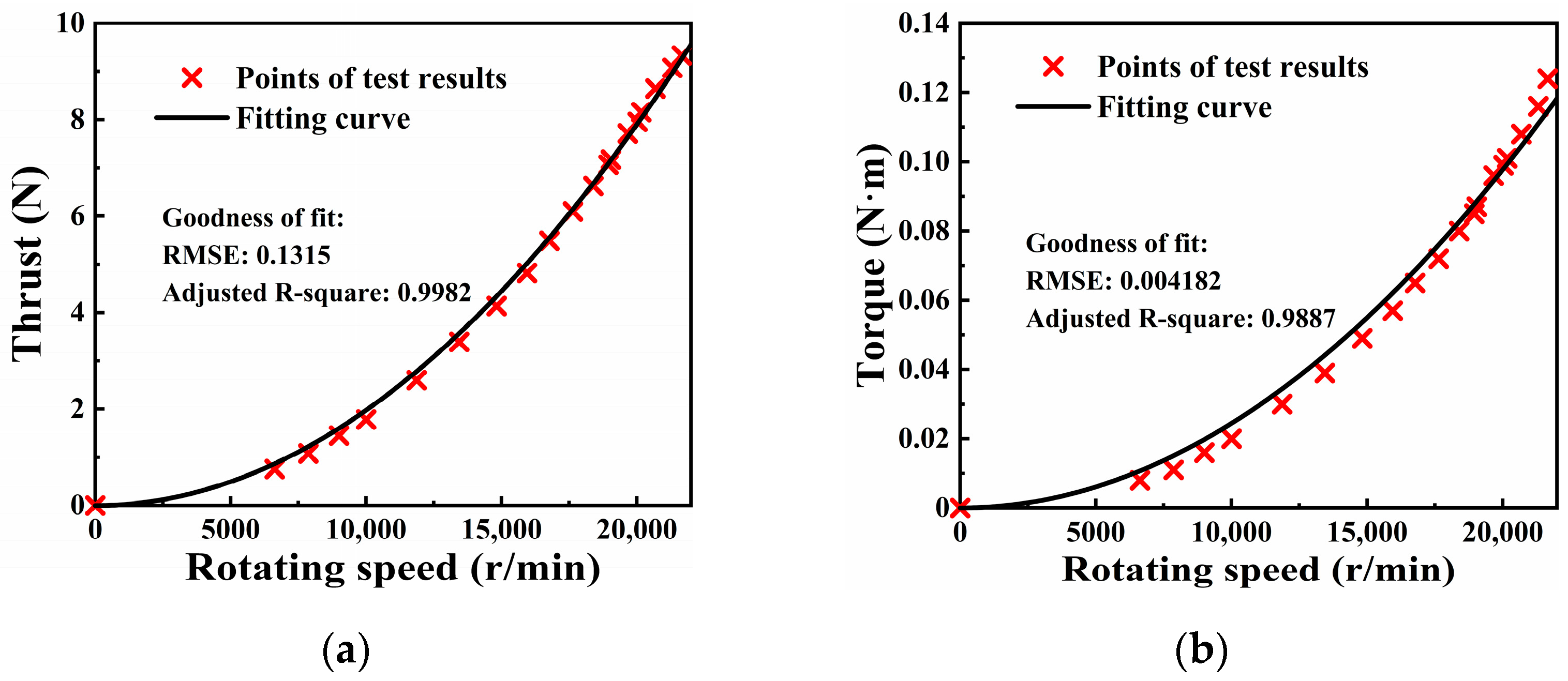
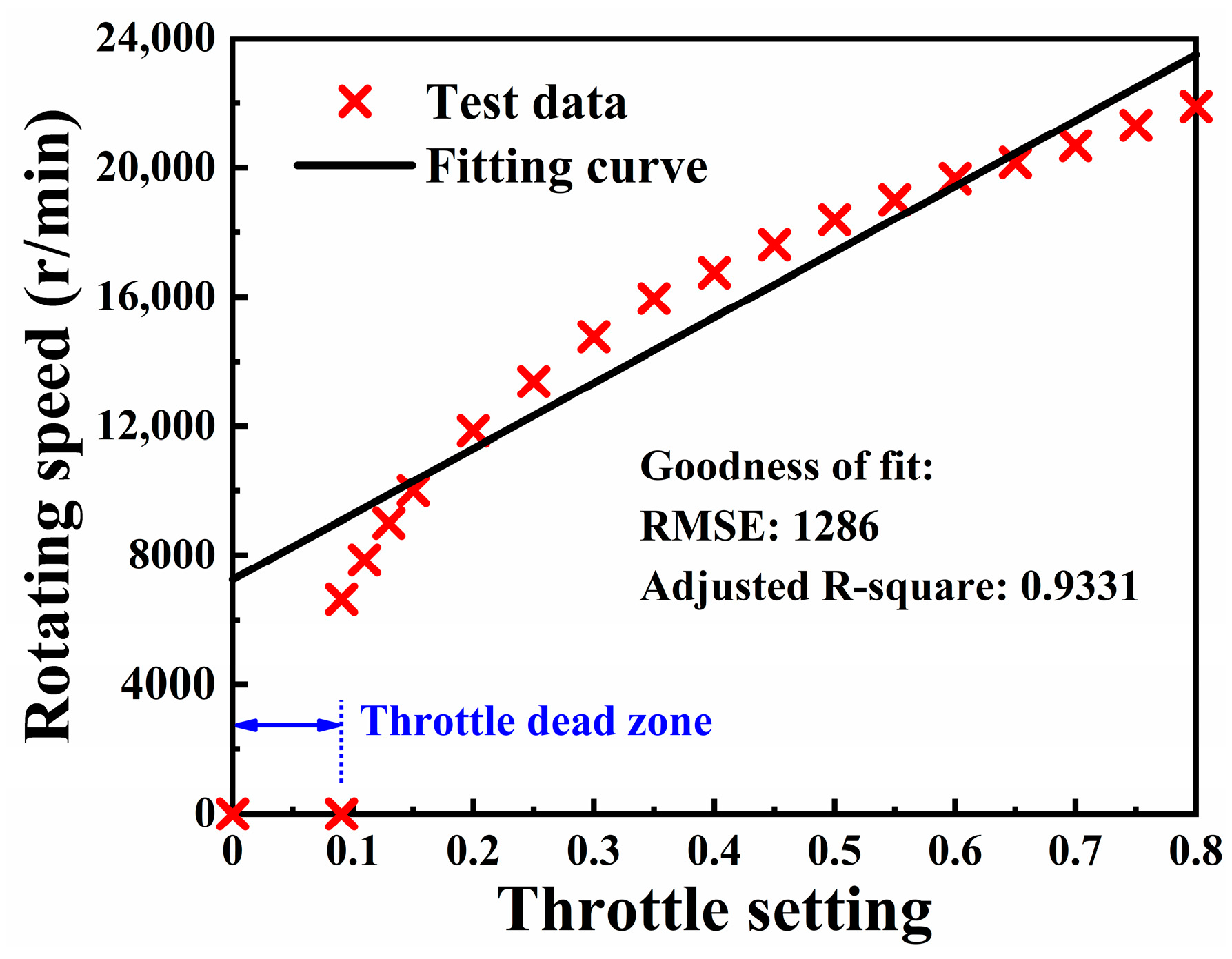
3.2. Propulsion System Measurements
3.2.1. Propeller Model
3.2.2. Motor Model
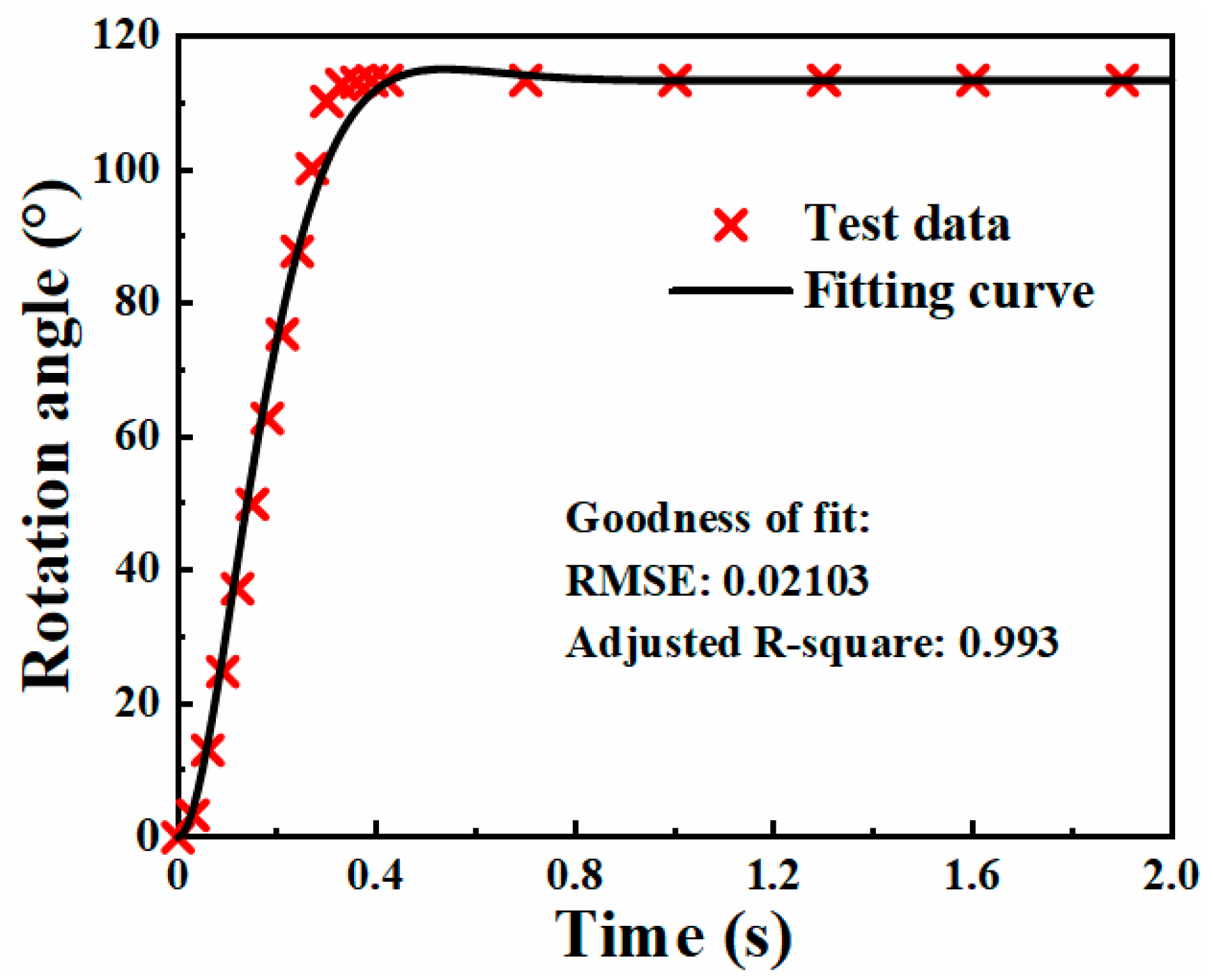
3.2.3. Servo Motor Model
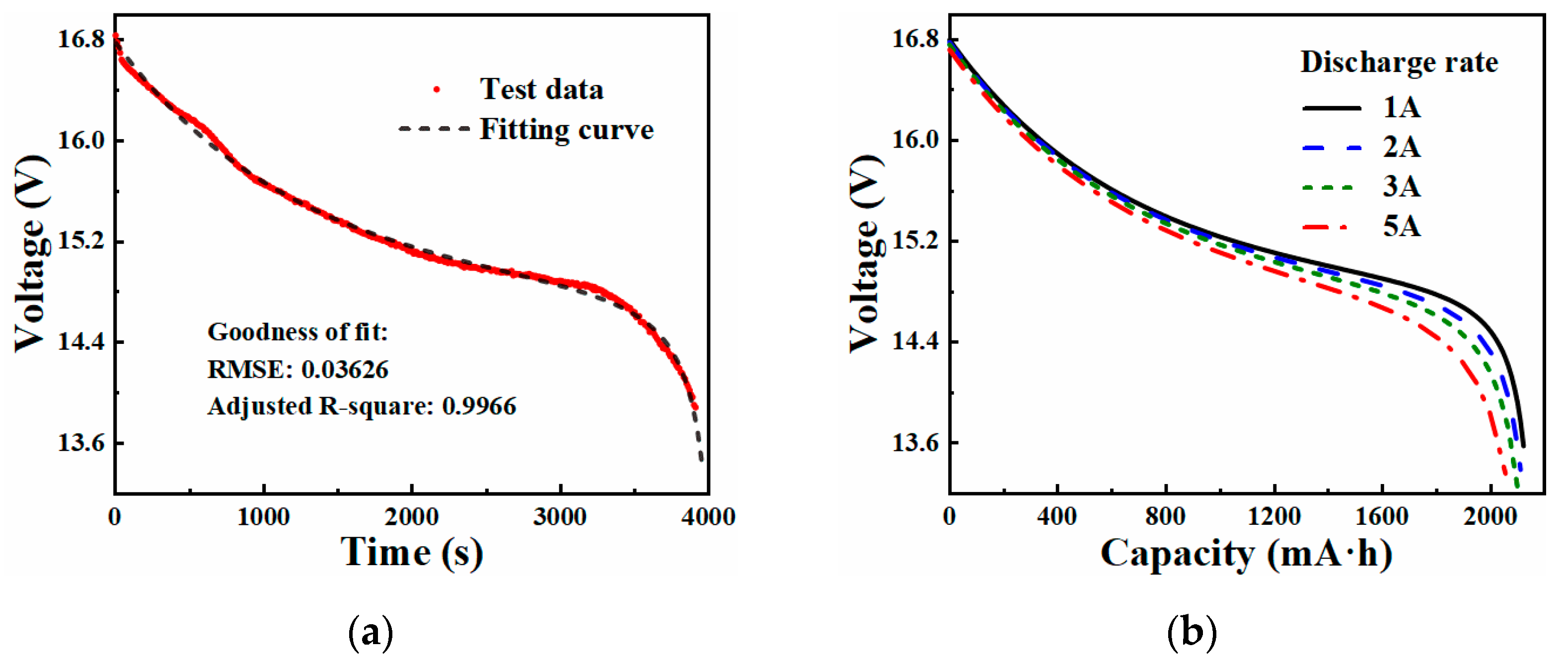
3.2.4. Battery Model
3.3. Mass Moment of Inertia Measurements
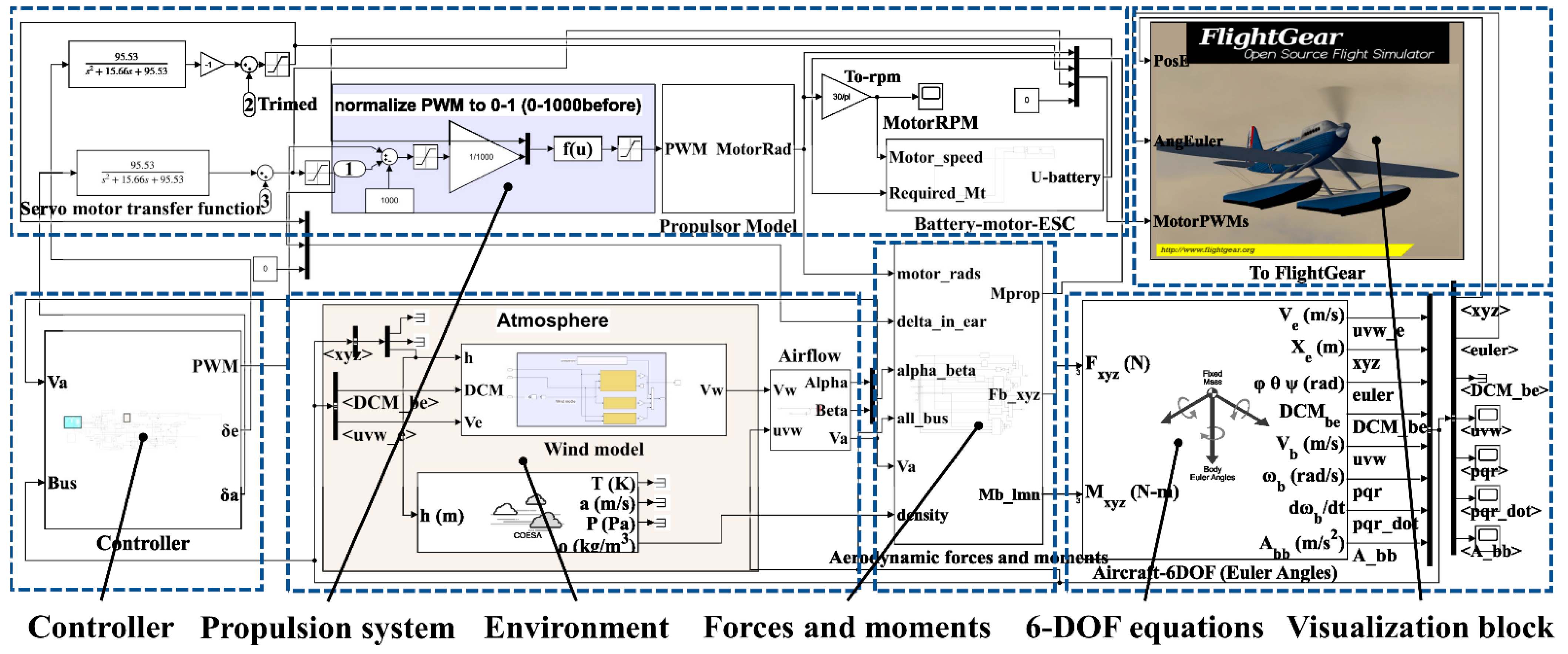
3.4. Simulink Model
4. Control Methods of the Fixed Wing UAV
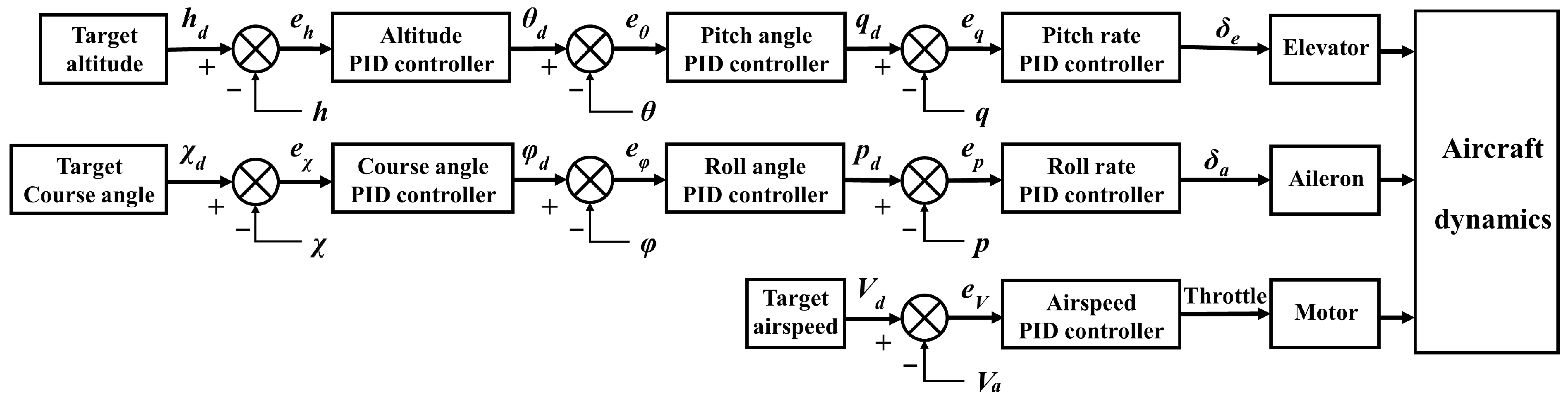
4.1. Stability Controller Design
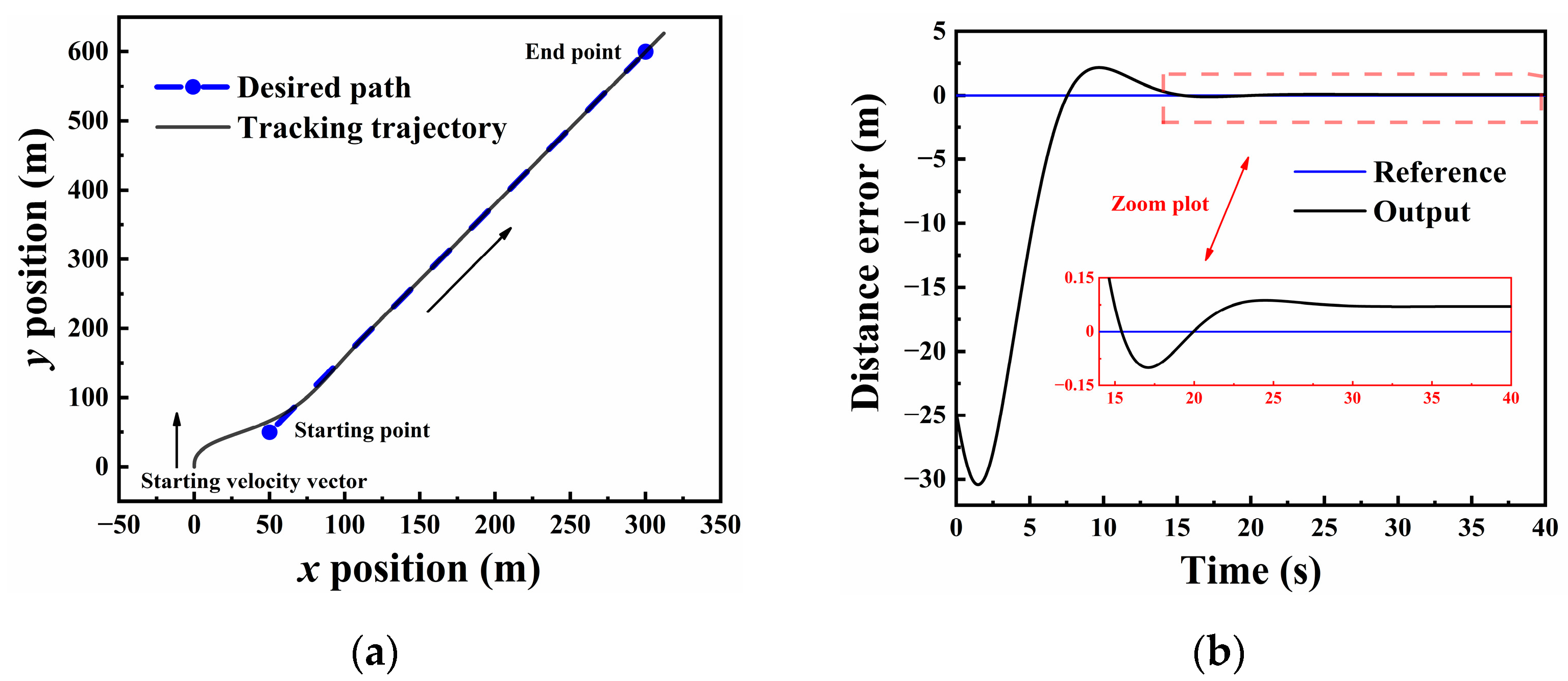
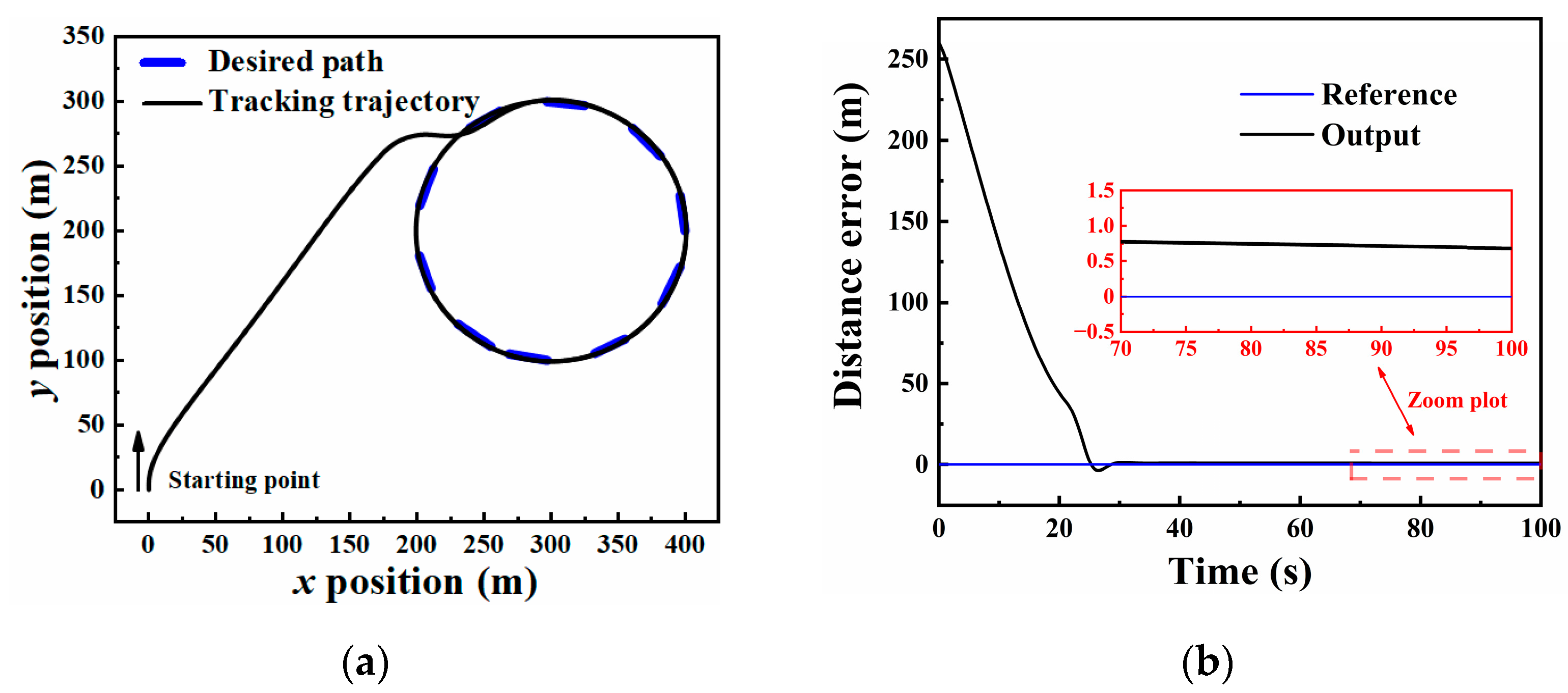
4.2. Path following Controller Design
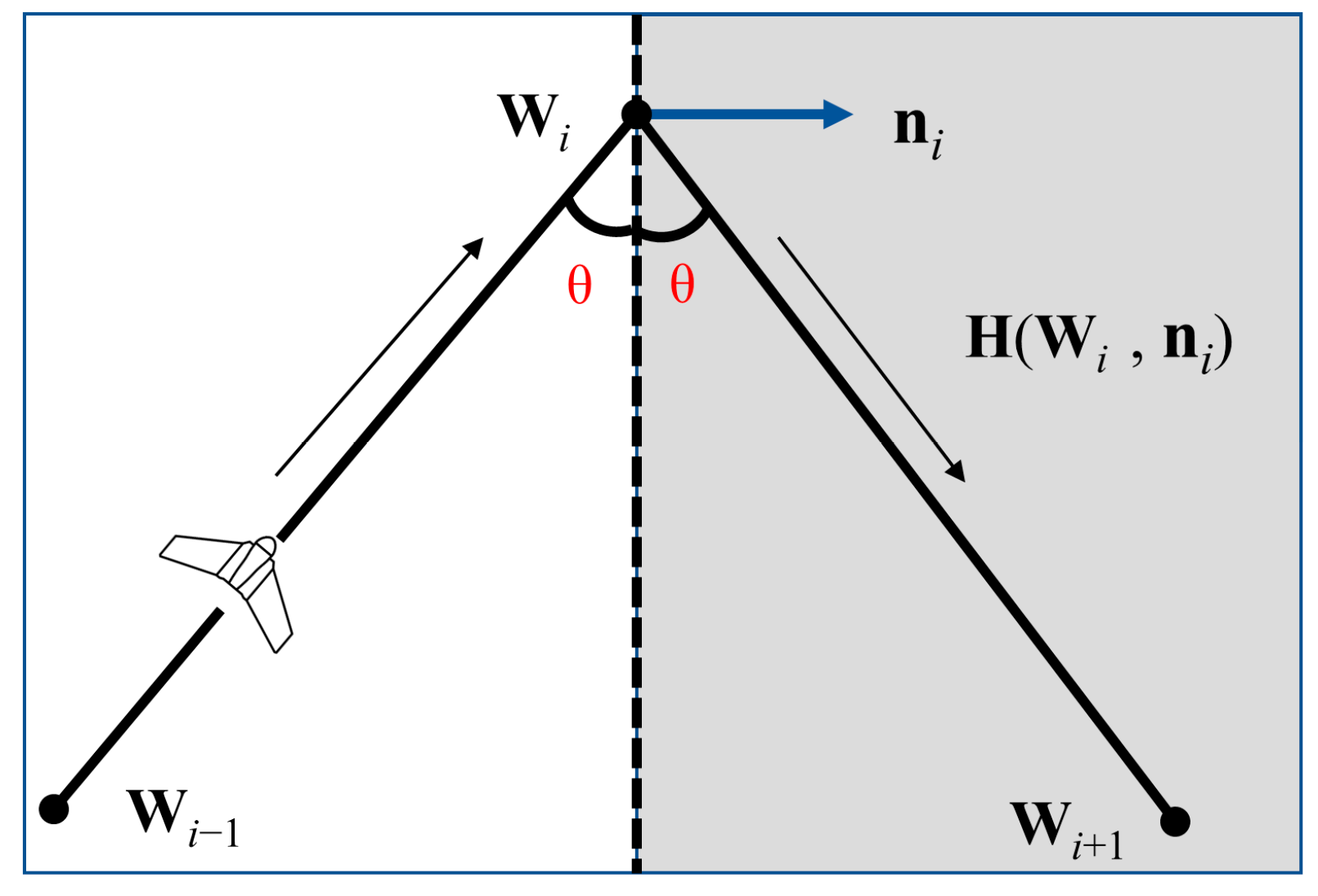
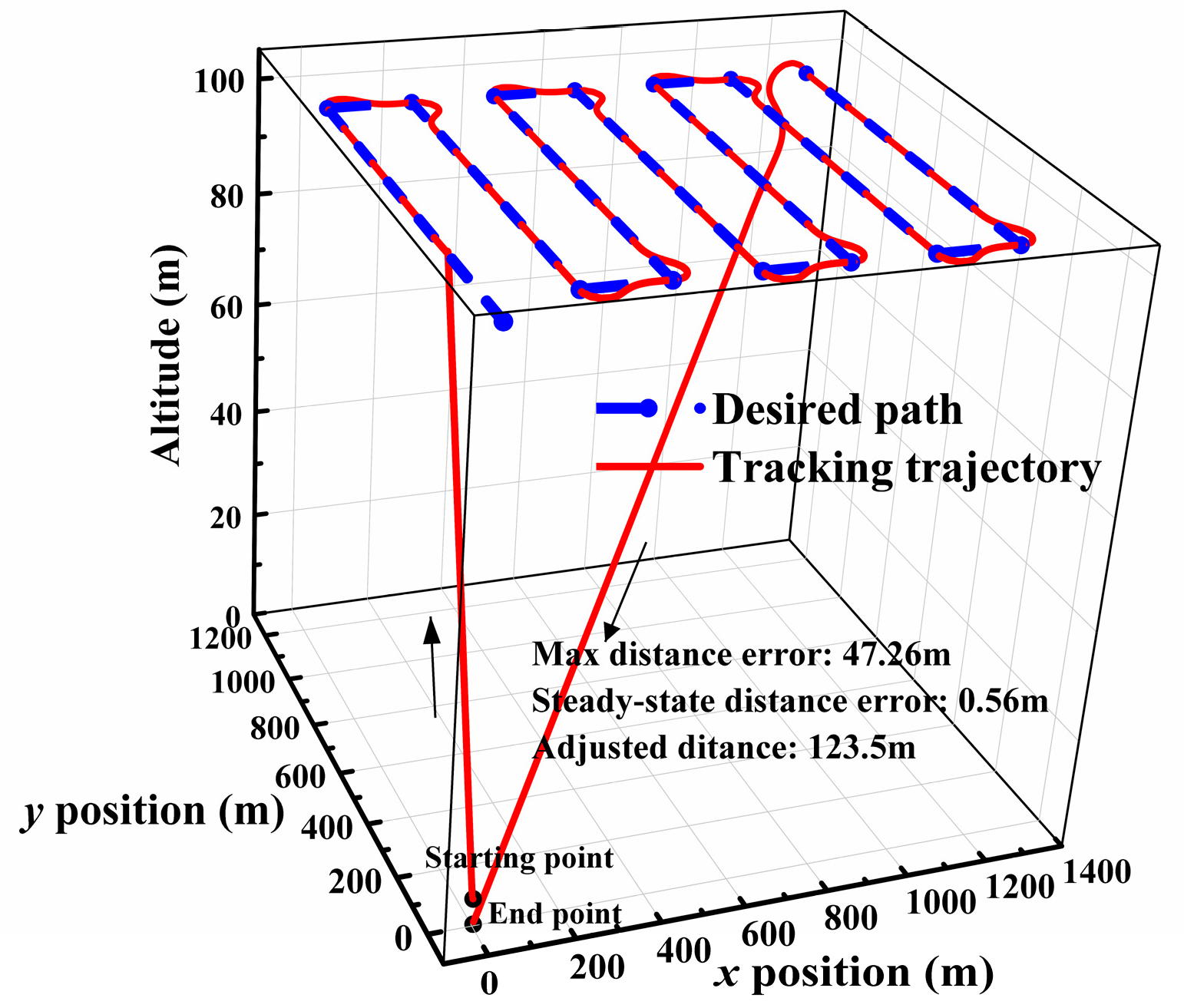
4.3. Path Management Controller Design
5. Discussion
- Some of the aerodynamic coefficient curves obtained by the CFD method in Section 3 were simplified in order to facilitate modeling, which would bring some errors. It is an effective method to verify the CFD simulation results through additional wind tunnel tests to increase the accuracy of the aerodynamic model.
- When obtaining the parameters of the propulsion system and the servo motor through corresponding tests, the layout and performance of the test equipment might affect the test results. For example, the dynamic response of the servo motor would be affected by connecting cables used for data acquisition.
- A simple logic was used in the path management controller to determine whether the drone has reached the waypoint so that the UAV can switch to the next waypoint; however, the aircraft would fly a short distance to adjust the position when it reached the waypoint, which was the shortcoming of the path management controller.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed Transformation Matrices of the UAV’s Mathematical Model
Appendix B. Stability Controller Parameters
| Parameter | Kp | Ki | Kd | |
|---|---|---|---|---|
| Longitudinal | Pitch rate | 0.3889 | 7.5461 | 0.0661 |
| Pitch angle | 8.2978 | 0.2536 | 0.1088 | |
| Altitude | 0.6879 | 0.2373 | 0.1282 | |
| Lateral | Roll rate | 0.2631 | 5.5033 | 0.047 |
| Roll angle | 22.2973 | 0.0329 | 0.7683 | |
| Course angle | 1.02 | 0.0011 | 0 | |
| Throttle | Airspeed | 1.4665 | 0 | 0.2171 |
References
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef] [Green Version]
- Psirofonia, P.; Samaritakis, V.; Eliopoulos, P.; Potamitis, I. Use of Unmanned Aerial Vehicles for agricultural applications with emphasis on crop protection: Three novel case-studies. Int. J. Agric. Sci. 2017, 5, 30–39. [Google Scholar] [CrossRef]
- Triputra, F.R.; Trilaksono, B.R.; Adiono, T.; Sasongko, R.A.; Dahsyat, M. Nonlinear dynamic modeling of a fixed-wing Unmanned Aerial Vehicle: A case study of Wulung. J. Mechatron. Electr. Power Veh. Technol. 2015, 6, 19–30. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wang, L.; Tian, T.; Yin, J. A review of Unmanned Aerial Vehicle Low-Altitude Remote Sensing (UAV-LARS) Use in agricultural monitoring in China. Remote Sens. 2021, 13, 1221. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Malenovský, Z.; King, D.H.; Robinson, S.A. Spatial co-registration of ultra-high resolution visible, multispectral and thermal images acquired with a micro-UAV over Antarctic moss beds. Remote Sens. 2014, 6, 4003–4024. [Google Scholar] [CrossRef] [Green Version]
- Marinello, F.; Pezzuolo, A.; Chiumenti, A.; Sartori, L. Technical analysis of Unmanned Aerial Vehicles (Drones) for agricultural applications. In Proceedings of the 15th International Scientific Conference on Engineering for Rural Development, Jelgava, Latvia, 25–27 May 2016; pp. 870–875. [Google Scholar]
- Boon, M.A.; Drijfhout, A.P.; Tesfamichael, S. Comparison of a fixed-wing and multi-rotor UAV for environmental mapping applications: A case study. In Proceedings of the International Conference on Unmanned Aerial Vehicles in Geomatics, Bonn, Germany, 4–7 September 2017; pp. 47–54. [Google Scholar]
- Panagiotou, P.; Kaparos, P.; Yakinthos, K. Wing let design and optimization for a MALE UAV using CFD. Aerosp. Sci. Technol. 2014, 39, 190–205. [Google Scholar] [CrossRef]
- Tan, B.; Ma, J.; Zhang, Y. Analysis of aerodynamic characteristics for a flying-wing UAV with asymmetric wing damage. In Proceedings of the 2018 33rd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Nanjing, China, 18–20 May 2018; pp. 276–280. [Google Scholar]
- Hassanalian, M.; Abdelkefi, A. Design, manufacturing, and flight testing of a fixed wing Micro Air Vehicle with Zimmerman planform. Meccanica 2017, 52, 1265–1282. [Google Scholar] [CrossRef]
- Chung, P.-H.; Ma, D.-M.; Shiau, J.-K. Design, manufacturing, and flight testing of an experimental flying wing UAV. Appl. Sci. 2019, 9, 3043. [Google Scholar] [CrossRef] [Green Version]
- Aboelezz, A.; Hassanalian, M.; Desoki, A.; Elhadidi, B.; El-Bayoumi, G. Design, experimental investigation, and nonlinear flight dynamics with atmospheric disturbances of a fixed-wing Micro Air Vehicle. Aerosp. Sci. Technol. 2020, 97, 105636. [Google Scholar] [CrossRef]
- Saderla, S.; Rajaram, D.; Ghosh, A.K. Parameter estimation of unmanned flight vehicle using wind tunnel testing and real flight data. J. Aerosp. Eng. 2017, 30, 04016078. [Google Scholar] [CrossRef]
- Priyambodo, T.K.; Majid, A. Modeling and simulation of the UX-6 fixed-wing Unmanned Aerial Vehicle. J. Control Autom. Electr. Syst. 2021, 32, 1344–1355. [Google Scholar] [CrossRef]
- Kandath, H.; Pushpangathan, J.V.; Bera, T.; Dhall, S.; Bhat, M.S. Modeling and closed loop flight testing of a fixed wing Micro Air Vehicle. Micromachines 2018, 9, 111. [Google Scholar] [CrossRef] [Green Version]
- Farhadi, R.M.; Kortunov, V.; Molchanov, A.; Solianyk, T. Estimation of the lateral aerodynamic coefficients for Skywalker X8 flying wing from real flight-test data. Acta Polytech. 2018, 58, 77–91. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.; Chung, J.D. Aerodynamic analysis of tilt-rotor Unmanned Aerial Vehicle with computational fluid dynamics. J. Mech. Sci. Technol. 2006, 20, 561–568. [Google Scholar] [CrossRef]
- Safi’i, I.; Nurohman, C.; Hardy, D.D.A.; Arifianto, O.; Muhammad, H. Thrust modelling for a small UAV. In Proceedings of the 7th Annual International Seminar on Aerospace Science and Technology (ISAST), Jakarta, Indonesia, 24–25 September 2019. [Google Scholar]
- Zhao, A.; Zhang, J.; Li, K.; Wen, D. Design and implementation of an innovative airborne electric propulsion measure system of fixed-wing UAV. Aerosp. Sci. Technol. 2021, 109, 106357. [Google Scholar] [CrossRef]
- Piljek, P.; Kotarski, D.; Krznar, M. Method for characterization of a multirotor UAV electric propulsion system. Appl. Sci. 2020, 10, 8229. [Google Scholar] [CrossRef]
- Virginio, R.; Fuad, F.A.; Jihadil, M.; Ramadhani, M.J.; Rafie, M.; Stevenson, R.; Adiprawita, W. Design and implementation of low cost thrust benchmarking system (TBS) in application for small scale electric UAV propeller characterization. In Proceedings of the 6th International Seminar on Aerospace Science and Technology (ISAST), Jakarta, Indonesia, 25–26 September 2018. [Google Scholar]
- Ulus, S.; Eski, I. Neural network and fuzzy logic-based hybrid attitude controller designs of a fixed-wing UAV. Neural Comput. Appl. 2021, 33, 8821–8843. [Google Scholar] [CrossRef]
- Ulker, H.; Baykara, C.; Ozsoy, C. Design of MPCs for a fixed wing UAV. Aircr. Eng. Aerosp. Technol. 2017, 89, 893–901. [Google Scholar] [CrossRef]
- Melkou, L.; Rezoug, A.; Hamerlain, M. PID-terminal sliding mode control of aircraft UAV. In Proceedings of the 8th UKSim-AMSS European Modelling Symposium on Computer Modelling and Simulation (EMS), Pisa, Italy, 21–23 October 2014; pp. 233–238. [Google Scholar]
- Aboelezz, A.; Mohamady, O.; Hassanalian, M.; Elhadidi, B. Nonlinear flight dynamics and control of a fixed-wing Micro Air Vehicle: Numerical, system identification and experimental investigations. J. Intell. Robot. Syst. 2021, 101, 64. [Google Scholar] [CrossRef]
- Sadraey, M.H. Aircraft Design: A Systems Engineering Approach; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Cinar, G.; Emeneth, M.; Mavris, D.N. A methodology for sizing and analysis of electric propulsion subsystems for Unmanned Aerial Vehicles. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 216. [Google Scholar]
- Avanzini, G.; de Angelis, E.L.; Giulietti, F. Optimal performance and sizing of a battery-powered aircraft. Aerosp. Sci. Technol. 2016, 59, 132–144. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Lan, Y.; Zhang, C.; Li, K. Design and simulation of long-endurance and light agricultural remote sensing fixed-wing UAV. Trans. Chin. Soc. Agric. Mach. 2021, 52, 234–242. (In Chinese) [Google Scholar]
- Etkin, B.; Reid, L.D. Dynamics of Flight; John Wiley & Sons: Hoboken, NJ, USA, 1959. [Google Scholar]
- Pushpangathan, J.V.; Bhat, M.S.; Harikumar, K. Effects of gyroscopic coupling and countertorque in a fixed-wing Nano Air Vehicle. J. Aircr. 2018, 55, 239–250. [Google Scholar] [CrossRef]
- Gryte, K.; Hann, R.; Alam, M.; Rohac, J.; Johansen, T.A.; Fossen, T.I. Aerodynamic modeling of the Skywalker X8 Fixed-Wing Unmanned Aerial Vehicle. In Proceedings of the International Conference on Unmanned Aircraft Systems (Icuas), Dallas, TX, USA, 12–15 June 2018; pp. 826–835. [Google Scholar]
- Su, H.; Bao, X.; Li, J.; Liu, K.; Cen, M.; Song, J. Calculation and analysis on stealth and aerodynamics characteristics of a medium altitude long endurance UAV. Procedia Eng. 2015, 99, 111–115. [Google Scholar]
- Ye, C.; Ma, D. Aircraft dynamic derivatives calculation using CFD techniques. J. Beijing Univ. Aeronaut. Astronaut. 2013, 39, 196–219. (In Chinese) [Google Scholar]
- Jung, D.; Tsiotras, P. Modeling and hardware-in-the-loop simulation for a small unmanned aerial vehicle. In Proceedings of the AIAA Infotech@ Aerospace 2007 Conference and Exhibit, Rohnert Park, CA, USA, 7–10 May 2007; p. 2768. [Google Scholar]
- Moffitt, B.; Bradley, T.; Parekh, D.; Mavris, D. Validation of vortex propeller theory for UAV design with uncertainty analysis. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 406. [Google Scholar]
- Quan, Q. Introduction to Multicopter Design and Control; Springer: Singapore, 2017. [Google Scholar]
- Sufendi; Trilaksono, B.R.; Nasution, S.H.; Purwanto, E.B. Design and implementation of hardware-in-the-loop-simulation for UAV using PID control method. In Proceedings of the 3rd International Conference on Instrumentation, Communications, Information Technology, and Biomedical Engineering (ICICI-BME), Bandung, Indonesia, 7–8 November 2013; pp. 124–130. [Google Scholar]
- Mariga, L.; Silva Tiburcio, I.; Martins, C.A.; Almeida Prado, A.N.; Nascimento Jr, C. Measuring battery discharge characteristics for accurate UAV endurance estimation. Aeronaut. J. 2020, 124, 1099–1113. [Google Scholar] [CrossRef]
- Sun, Y.-H.; Jou, H.-L.; Wu, J.-C. Multilevel Peukert equations based residual capacity estimation method for Lead-Acid battery. In Proceedings of the IEEE International Conference on Sustainable Energy Technologies, Singapore, 24–27 November 2008; pp. 101–105. [Google Scholar]
- McClelland, W.A. Inertia Measurement and Dynamic Stability Analysis of a Radio-Controlled Joined-Wing Aircraft. Master’s Thesis, Air Force Institute of Technology, Greene, OH, USA, 2006. [Google Scholar]
- Wang, B.; Ali, Z.A.; Wang, D. Controller for UAV to oppose different kinds of wind in the environment. J. Control Sci. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Hakim, T.M.I.; Arifianto, O. Implementation of Dryden continuous turbulence model into simulink for LSA-02 flight test simulation. In Proceedings of the 5th International Seminar on Aerospace Science and Technology (ISAST), Medan, Indonesia, 27–29 September 2017. [Google Scholar]
- Lawrence, D.; Frew, E.; Pisano, W. Lyapunov vector fields for autonomous UAV flight control. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; p. 6317. [Google Scholar]
- Park, S.; Deyst, J.; How, J. A new nonlinear guidance logic for trajectory tracking. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; p. 4900. [Google Scholar]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]











| Symbol | Value | Symbol | Value | Symbol | Value |
|---|---|---|---|---|---|
| AR | 3.68 | S | 0.22 m2 | b | 0.9 m |
| c | 0.26 m | ma | 0.9 kg |
| Parameter | Value with 95% Confidence Bounds | Parameter | Value with 95% Confidence Bounds | Parameter | Value with 95% Confidence Bounds |
|---|---|---|---|---|---|
| CL0 | 0.0389 (0.027, 0.0508) | CLα | 3.2684 (3.1721, 3.3641) | CLq | 6.1523 (6.0438, 6.2608) |
| CLδe | 0.7237 (0.6567, 0.7913) | CD0 | 0.0208 (0.0169, 0.0247) | CDα1 | 0.0084 (−0.0237,0.0405) |
| CDα2 | 1.3225 (1.1948, 1.4502) | CDδe | 0.2 (0.1703, 0.2297) | CDβ1 | −0.0001 (−0.001, 0.0007) |
| CDβ2 | 0.0796 (0.0744, 0.0848) | CYβ | −0.1285 (−0.13, −0.1274) | CYp | −0.0292 (−0.032, −0.0263) |
| CYr | −0.0355 (−0.037, −0.0336) | CYδa | 0.0299 (0.0249, 0.0348) | Clβ | −0.0345 (−0.035, −0.0339) |
| Clp | −0.3318 (−0.3338, −0.33) | Clr | 0.0304 (0.0273, 0.0335) | Clδa | 0.182 (0.1477, 0.2163) |
| Cm0 | −0.0112 (−0.0134, −0.009) | Cmα | −0.2625 (−0.28, −0.2444) | Cmq | −1.8522 (−1.888, −1.8155) |
| Cmδe | −0.2845 (−0.311, −0.2565) | Cnβ | 0.0252 (0.0248, 0.0256) | Cnr | −0.0192 (−0.0196, −0.019) |
| Cnδa | −0.0102 (−0.011, −0.0092) |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Speed | 21,428 RPM ± 20 | Thrust | 100 N ± 0.1 |
| Torque | 5 N·m ± 0.005 | Voltage | 65 V ± 0.1 |
| Parameter | Value | Confidence Bounds | Unit |
|---|---|---|---|
| KT | 2.015 × 10−6 | (1.994 × 10−6, 2.036 × 10−6) | Kg·m |
| KM | 2.444 × 10−10 | (2.379 × 10−10, 2.508 × 10−10) | Kg·m2 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| E0 | 14.88 V | K | 0.0138 V/(A·h) | C | 2.191 A·h |
| A | 1.937 V | B | 1.546 A·h−1 | R | 0.006 Ω |
| Symbol | Value [kg·m2] | Symbol | Value [kg·m2] | Symbol | Value [kg·m2] |
|---|---|---|---|---|---|
| Ixx | 0.023 | Ixy | 0 | Iyy | 0.02 |
| Iyz | 0 | Izz | 0.033 | Ixz | 0.006 |
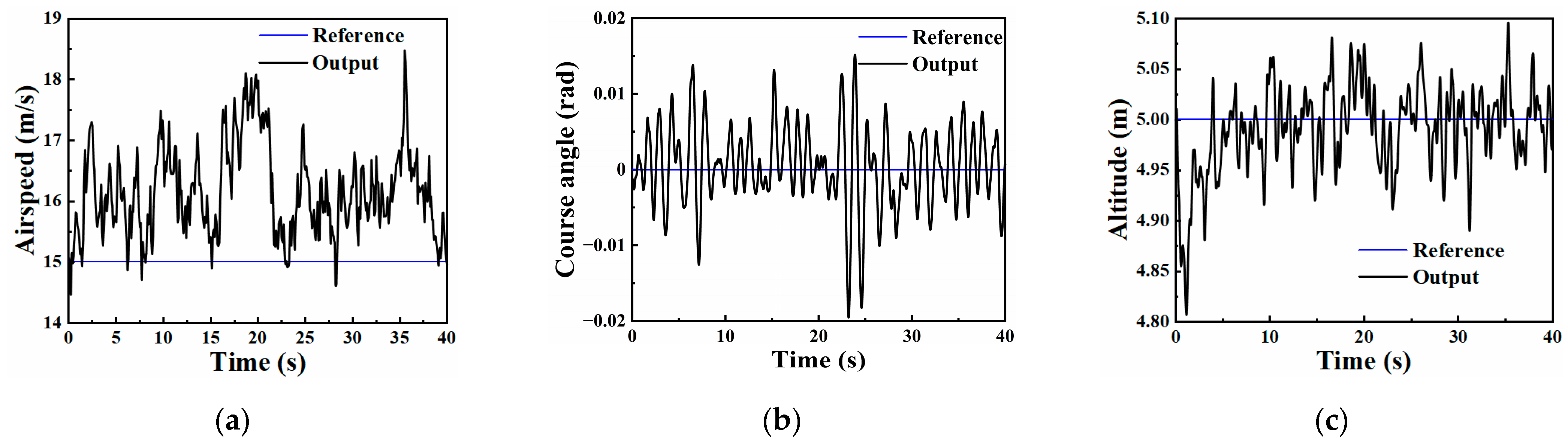
| Control Object | Rise Time [s] | Peak Time [s] | Overshoot [%] | Settling Time [s] | Steady-State Error [%] |
|---|---|---|---|---|---|
| Airspeed | 0.449 | 1.058 | 0 | 0.545 | 0.17 |
| Course angle | 3.983 | 9.091 | 0 | 4.934 | 0.15 |
| Altitude | 0.563 | 0.821 | 28.2 | 3.356 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhu, H.; Zhao, Z.; Zhang, C.; Lan, Y. Modeling, System Measurements and Controller Investigation of a Small Battery-Powered Fixed-Wing UAV. Machines 2021, 9, 333. https://doi.org/10.3390/machines9120333
Wang Y, Zhu H, Zhao Z, Zhang C, Lan Y. Modeling, System Measurements and Controller Investigation of a Small Battery-Powered Fixed-Wing UAV. Machines. 2021; 9(12):333. https://doi.org/10.3390/machines9120333
Chicago/Turabian StyleWang, Yue, Hang Zhu, Zeyang Zhao, Cui Zhang, and Yubin Lan. 2021. "Modeling, System Measurements and Controller Investigation of a Small Battery-Powered Fixed-Wing UAV" Machines 9, no. 12: 333. https://doi.org/10.3390/machines9120333
APA StyleWang, Y., Zhu, H., Zhao, Z., Zhang, C., & Lan, Y. (2021). Modeling, System Measurements and Controller Investigation of a Small Battery-Powered Fixed-Wing UAV. Machines, 9(12), 333. https://doi.org/10.3390/machines9120333






