A Hybrid Multi-Objective Optimization Method Based on NSGA-II Algorithm and Entropy Weighted TOPSIS for Lightweight Design of Dump Truck Carriage

Abstract

The lightweight design of vehicle components is regarded as a complex optimization problem, which usually needs to achieve two or more optimization objectives. It can be firstly solved by a multi-objective optimization algorithm for generating Pareto solutions, before then seeking the optimal design. However, it is difficult to determine the optimal design for lack of engineering knowledge about ideal and nadir values. Therefore, this paper proposes a multi-objective optimization procedure combined with the NSGA-II algorithm with entropy weighted TOPSIS for the lightweight design of the dump truck carriage. The finite element model of the dump truck carriage was firstly developed for modal analysis under unconstrained free state and strength analysis under the full load and lifting conditions. On this basis, the multi-objective lightweight optimization of the dump truck carriage was carried out based on the Kriging surrogate model and the NSGA-II algorithm. Then, the entropy weight TOPSIS method was employed to select the optimal design of the dump truck from Pareto solutions. The results show that the optimized dump truck carriage achieves a remarkable mass reduction of 81 kg, as much as 3.7%, while its first-order natural frequency and strength performance are slightly improved compared with the original model. Accordingly, the proposed procedure provides an effective way for vehicle lightweight design.

1. Introduction

Automobile lightweight design is one effective way to reduce energy consumption and emission and to improve vehicle braking efficiency [1,2,3,4]. It is especially important for the commercial vehicle, since it can also enhance the profits for consumers. The lightweight commercial vehicle structure makes it able to carry much more cargo without increasing its overall weight [5]. High strength steel has been widely used in commercial vehicle structures since it shows an attractive combination of mass reduction potential and material cost saving [6,7,8]. Therefore, optimization design is necessary for the development process of commercial vehicle components to achieve the appropriate distribution of high-strength steel in the structure for avoiding additional cost.

For vehicle lightweight design problems, there are always two or more optimization objectives to be achieved, while these objectives generally conflict with each other. Multi-objective optimization methods are employed to solve this problem in many engineering fields recently. Zhou et al. [9] designed a novel automotive bumper of negative Poisson’s ratio (NPR) structure. Then, a multi-objective robust optimization method based on particle swarm optimization algorithm and six sigma criteria was employed to optimize the NPR structure parameters, for improving its energy absorption capacity. Vo-Duy et al. [10] used the NSGA-II algorithm to solve the multi-objective optimization of a laminated composite beam, for minimizing its weight and maximizing the natural frequency. Liu et al. [11] presented an improved particle swarm optimization algorithm to conduct the lightweight design of auto-body by considering its crashworthiness. Wang et al. [12] conducted the multi-objective parameter optimization of the powertrain and control strategy of a hybrid electric vehicle, which achieved energy and fuel-saving as well as power performance improvement. Xie et al. [13] performed the multi-objective lightweight design of S-rails of cab-in-white of the commercial vehicle to reduce its weight and improve the crashworthiness performances. Jiang et al. [14] performed multi-objective optimization of the control arm and torsion beam. After optimization, the weights of the control arm and torsion beam are reduced by 0.505 kg and 1.189 kg, respectively.

In order to efficiently solve these multi-objective optimization problems, the surrogate models are usually adopted because of their affordable computational cost. Craig et al. [15] used a response surface surrogate model to improve the efficiency of finding lightweight parameters for enhancing automotive crashworthiness, which also reduced the total cost of the optimization. The surrogate model was used by Wang et al. [16] to achieve the lightweight goal of the body in white (BIM), which improved the efficiency of lightweight optimization. The weight is reduced by 4.91 kg, which is as much as 5.70%. Ren et al. [17] performed the multi-objective optimization of the lightweight design of the vehicle frame based on the Kriging surrogate model, which realized the weight reduction of the frame and the improvement of its dynamic performance. Gao et al. [18] used the Kriging surrogate model to optimize the layout of the welded side frame of the intercity electric multiple unit (EMU) bogie frames. After optimization, the weight of the EMU was reduced by 16% with the improvement of fatigue performance.

Normally, the best compromise solution is not easy to select from the Pareto set obtained by multi-objective optimization without enough engineering knowledge. TOPSIS (technique for order preference by similarity to an ideal solution) can convert multiple performance indicators into a single comprehensive index for evaluation and analysis, which is broadly used in many engineering fields. Wang et al. [19] used the improved NSGA-II algorithm and TOPSIS method to perform the multi-objective lightweight design of the car subframe. Pirmohammad et al. [20] studied the effect of length ratio of inner tube to outer tube on crashworthiness of polyurethane foam filled tapered tube, and obtained the best length ratio by the TOPSIS method. On the basis of the analysis of the influence of the damping coefficient and the spring stiffness on suspension performance, Wang et al. [21] improved the lightweight and crashworthiness performance of B-pillar based on the modified particle swarm optimization algorithm and TOPSIS. Ebrahimi-Nejad et al. [21] employed the TOPSIS method to carry out the multi-objective optimization of the suspension system and determined the optimal scheme. In order to improve vehicle ride comfort, Ebrahimi-Nejad et al. [22] adopted the TOPSIS method to seek the best value of the suspension stiffness and damping. Jiang et al. [23] replaced the material of steel bumper anti-collision beam with carbon fiber reinforced plastic (CFRP), and used entropy weighted TOPSIS method to optimize the stacking sequence of CFRP anti-collision beam, so as to achieve the goal of weight reduction under the premise of ensuring the crashworthiness of bumper beam. Ni et al. [24] established a multi-objective optimization model with the minimum energy consumption and optimal machining quality and optimized the cutting parameters and hob parameters by using the improved grey wolf algorithm and TOPSIS method. Accordingly, the TOPSIS method can also be used to determine the best compromise solution to the multi-objective optimization problem.

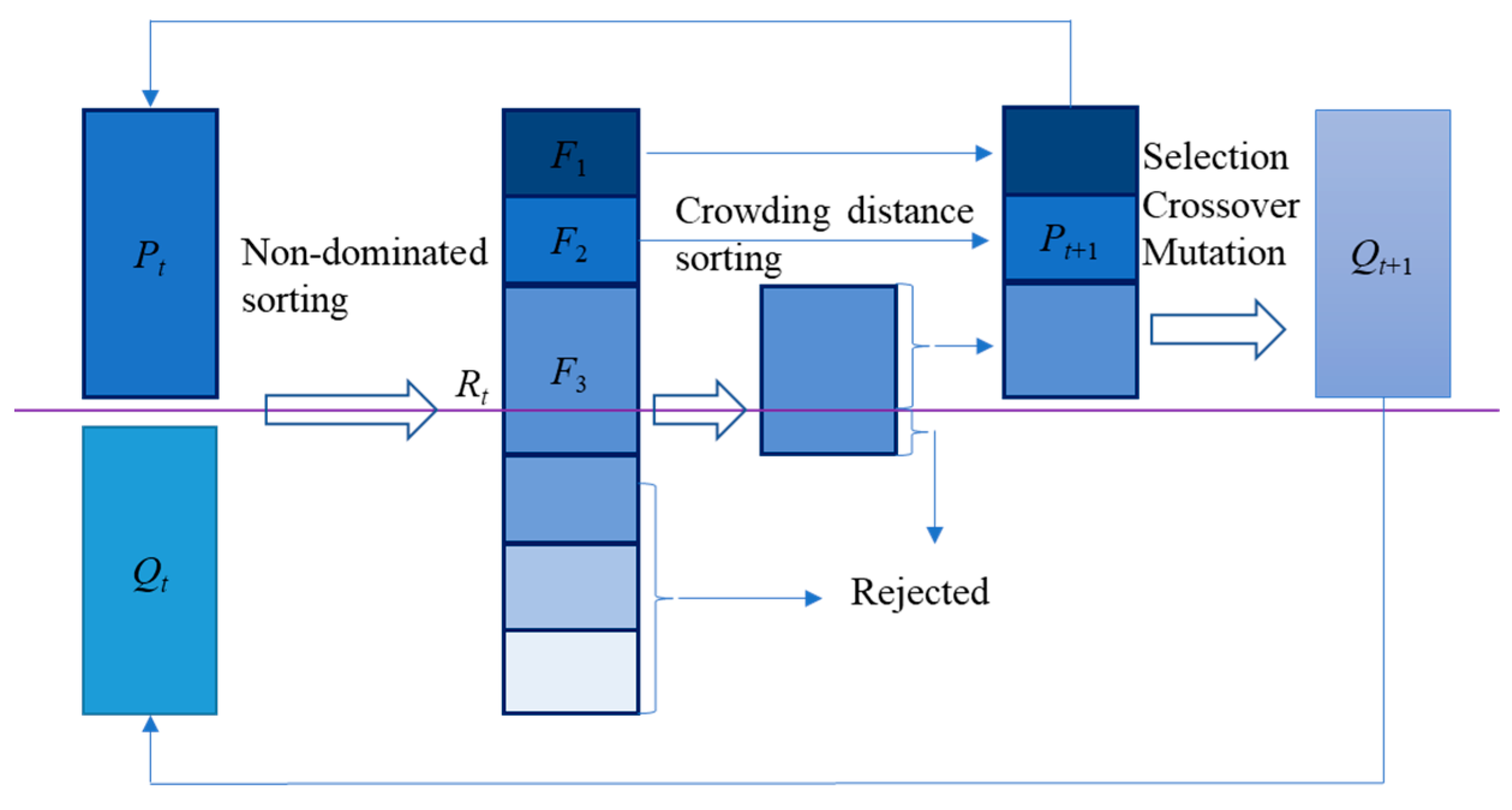
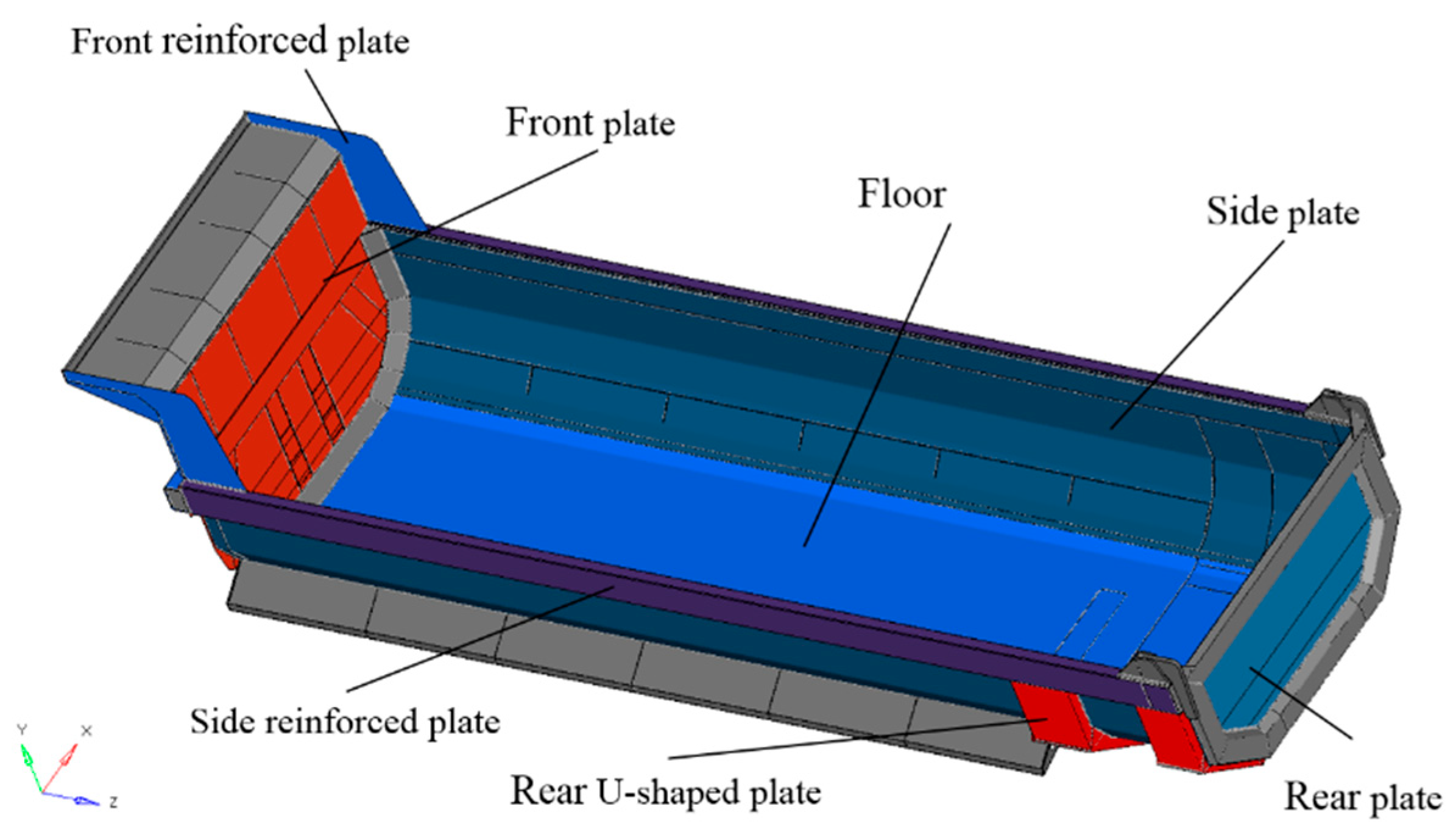
This paper proposes a multi-objective optimization method by integrating the Kriging surrogate model, NSGA-II algorithm and entropy weighted TOPSIS to optimize the dump truck carriage plate thickness, for realizing its lightweight design. Firstly, the finite element model of the U-carriage is developed to carry out its modal and strength analysis. The Kriging surrogate models for fitting the relationship of the design variables of plate thickness and the performance indexes of the U-carriage are constructed, with the samples generated by the optimal Latin Hypercube method. Then the multi-objective optimization of the U-carriage is modeled with the objective function of minimizing the weight and maximizing the first-order natural frequency, while considering the constraints of the maximum stress under the full load and lifting condition. The Pareto solutions are acquired by the NSGA-II algorithm. Finally, the optimal parameters of U-carriage are determined using entropy weighted TOPSIS method, so as to achieve weight reduction and performance improvement.

The rest of this paper is structured as follows. The next section explains some basic theories used for the proposed multi-objective optimization approach. In Section 3, the finite element model of the dump truck carriage is established to calculate its performance. In Section 4, the presented multi-objective optimization method is applied to perform the lightweight design of the carriage and the optimization results are discussed and analyzed. Finally, the main conclusions are outlined in Section 5.

2. Multi-Objective Optimization Procedure

2.1. Kriging Surrogate Model

Generally, there are a large number of iterations for solving engineering optimization problems, making the optimization time-consuming, especially when the problem is complex. Surrogate model-based optimization provides an alternative approach for improving optimization efficiency [25,26,27], in which the Kriging model is one of the most used surrogate models because of its high accuracy for predicting nonlinear response.

Kriging surrogate model includes two parts: polynomial function and random distribution. The approximate function expression of the Kriging surrogate model is:

$$\widehat{y}\left(x\right)=f^{\mathrm{T}}\left(x\right)\cdot \beta +z\left(x\right)$$

(1)

where β represents the regression coefficient vector. $f^{\mathrm{T}}\left(x\right)$ is the polynomial of design variable vector x for representing the global approximation model of design space.z(x) represents the random distribution, which can be expressed as a random process with mean of zero and standard deviation of σ.

Thus, the covariance matrix of random distribution z(x) can be expressed as:

$$Cov\left[z\left(x_i\right),z\left(x_j\right)\right]={\sigma }^{2}R$$

(2)

where R represents the correlation symmetric matrix with n × n order diagonal 1. $R(x_i，x_j)$ represents the spatial correlation equation of two random sample points $x_i$ and $x_j$ in n sample points, which plays an absolute key role in the simulation accuracy.

$R(x_i，x_j)$ can be expressed by Gaussian correlation equation, which, featuring good calculation effect, is widely used. It is formulated as:

$$R\left(x_i,x_j\right)=EXP\left(-{\displaystyle \sum _{k=1}^m{\lambda }_k{\left|x_{ik}-x_{jk}\right|}^2}\right)$$

(3)

where m represents the number of design variables. ${\lambda }_k$ represents the correlation coefficient of the fitting surrogate model. $x_{ik}$ and $x_{jk}$ represent the kth value of $x_i$ and $x_j$, respectively.

In order to ensure the unbiasedness of the simulation process, after determining the correlation function, the relational expression of the estimated value $\widehat{y}\left(x\right)$ of the approximate response, the regression coefficient matrix $\widehat{\beta }$ and the estimated value ${\widehat{\sigma }}^2$ of the variance can be obtained as follows:

$$\{\begin{array}{l}\widehat{y}\left(x\right)=f^{\mathrm{T}}\left(x\right)\widehat{\beta }+r^{\mathrm{T}}\left(X^{\ast }\right)R^{-1}\left(y-F\widehat{\beta }\right)\\ \widehat{\beta }={\left(F^{\mathrm{T}}{R}^{-1}F\right)}^{-1}{F}^T{R}^{-1}y\\ {\widehat{\sigma }}^2=\frac{{\left(y-F\widehat{\beta }\right)}^{\mathrm{T}}{R}^{-1}\left(y-F\widehat{\beta }\right)}{n}\end{array}$$

(4)

According to the above equations, the maximum natural estimation of parameter ${\lambda }_k$ can be obtained as follows:

$$\underset{{\lambda }_k>0}{\max \left({\lambda }_k\right)}=-\frac{\left[n\ln \left({\widehat{\sigma }}^2\right)+\ln \left|R\right|\right]}{2}$$

(5)

2.2. NSGA-II Algorithm

The elitist non-dominated sorting genetic algorithm (NSGA-II) is proposed by K. Deb [28], which improves the iterative convergence rate while ensures population diversity by employing the fast non-dominated sorting approach, elitist maintenance strategy and efficient crowding distance estimation method [29]. This makes it popular in solving complex optimization problems [30,31]. The principle of the NSGA-II algorithm is shown in Figure 1, and its basic steps are as follows:

Step 1: An initial population P_t of size N is randomly generated at generation t = 0, and it is used to generate offspring population Q_t.

Step 2: A new population R_t with a size of 2N is obtained by merging P_t and Q_t. Then it is classified into several fronts (F₁, F₂, F₃, ...) based on non-dominated sorting. Meanwhile, the crowding distance of population individuals is calculated for each front.

Step 3: Select N suitable individuals from R_t according to non-dominated sort and crowding distance to form a new parent population P_t+1. In this step, the individuals with lower non-dominated ranks are first selected, and then the individuals with larger crowding distances are chosen.

Step 4: A new offspring population Q_t+1 with a size of N is obtained from P_t+1 by performing GA operators of selection, crossover and mutation.

Step 5: The procedure from Step 2 is continued until the termination criterion is satisfied.

2.3. Entropy Weighted TOPSIS

The TOPSIS technique is a well-known multiple attribute decision-making method, used to rank the alternatives from the best to the worst, of which the best alternative should have the shortest distance to the positive ideal solution and the farthest distance to the negative ideal solution [32]. When it is used to choose the best compromise solution to the multi-objective optimization problem, the obtained Pareto set can be defined as the original decision-making matrix of the TOPSIS method, which is expressed as:

$$X=\left(\begin{array}{l}{x}_{11} x_{12} \dots x_{1n}\\ x_{21} x_{22} \dots x_{2n}\\ \dots \\ x_{m1} x_{m2} \dots x_{mn} \end{array}\right)$$

(6)

where $x_{ij},i=1,2,\cdots ,m; j=1,2,\cdots ,n$ represents the value of the jth evaluation index for the ith alternative; m and n are the number of alternatives and performance indexes, respectively.

To facilitate comparative analysis, the original data matrix needs to be regularized. The formula is:

$$r_{ij}=\frac{x_{ij}}{\sqrt{{\displaystyle \sum _{i=1}^m{x}_{ij}^2}}}$$

(7)

where $r_{ij}$ is the results after regularization of $x_{ij}$.

Information entropy can be used to describe the degree of disorder of the system. The smaller the information entropy of a certain index is, the greater the information content of the index is, and the higher the weight should be in the evaluation [33]. Thus, the entropy method is adopted to determine the weight coefficient of each evaluation index. The calculation formula of information entropy $e_j$ is:

$$e_j=-k{\displaystyle \sum _{i=1}^m{p}_{ij}\ln }{p}_{ij}$$

(8)

where k = 1/ln(m) is the adjustment coefficient; $p_{ij}=r_{ij}/{\displaystyle \sum _{i=1}^m{r}_{ij}}$ is the result of standardized processing of $r_{ij}$.

Using entropy weighted method to calculate the weight coefficient of each performance index, the formula is:

$$w_j=\frac{1-e_j}{{\displaystyle \sum _{j=1}^n(1-e_j)}}$$

(9)

Taking into account the weight coefficient of each performance index, the regularization results are weighted as follows:

$$v_{ij}=w_j{r}_{ij} {\displaystyle \sum _{j=1}^n{w}_j}=1$$

(10)

where $w_j$ is the weight factor for the jth index.

TOPSIS method ranks each alternative by calculating the distance between the ideal solution and the negative ideal solution. The ideal solution and negative ideal solution can be defined as:

$$\{\begin{array}{l}{A}^{+}=\left\{v_1^{+},v_2^{+},\cdots ,v_n^{+}\right\}\\ A^{-}=\left\{v_1^{-},v_2^{-},\cdots ,v_n^{-}\right\}\end{array}$$

(11)

where $A^{+}$ and $A^{-}$ denote the ideal solution set and the negative ideal solution set, respectively.

For the-smaller-the-better alternatives, such as the mass of the carriage, the stress of the full load case and the stress of the lifting load case, the ideal solution and negative ideal solution are calculated as follows:

$$\{\begin{array}{l}{v}_j^{+}={\min }_i\left\{v_{ij},j=1,2,\cdots ,n\right\}\\ v_j^{-}={\max }_i\left\{v_{ij},j=1,2,\cdots ,n\right\}\end{array}$$

(12)

where $v_j^{+}$ and $v_j^{-}$ represent the ideal solution and negative ideal solution for the jth index, respectively.

For the-larger-the-better alternatives, such as the first-order natural frequency, the calculation method of the ideal solution and negative ideal solution is:

$$\{\begin{array}{l}{v}_j^{+}={\max }_i\left\{v_{ij},j=1,2,\cdots ,n\right\}\\ v_j^{-}={\min }_i\left\{v_{ij},j=1,2,\cdots ,n\right\}\end{array}$$

(13)

The distance between each alternative and the ideal solution and negative ideal solution can be calculated by Euclidean distance, namely:

$$\{\begin{array}{l}{S}_i^{+}=\sqrt{{\displaystyle \sum _{j=1}^n{(v_{ij}-v_j^{+})}^2}}\\ S_i^{-}=\sqrt{{\displaystyle \sum _{j=1}^n{(v_{ij}-v_j^{-})}^2}}\end{array},$$

(14)

where $S_i^{+}$ and $S_i^{-}$ represent the distance between the alternative and the ideal solution and the negative ideal solution, respectively.

The relative closeness coefficient of each alternative can be defined as its relative proximity to the negative ideal solution, namely:

$$C_i=\frac{S_i^{-}}{S_i^{+}+S_i^{-}}$$

(15)

where C_i is the relative closeness coefficient of the ith alternative. The larger the value is the closer the alternative is to the optimal value.

2.4. Multi-Objective Optimization Procedure

In this paper, a multi-objective optimization procedure integrating the Kriging surrogate model, the NSGA-II algorithm and entropy-based TOPSIS is proposed to perform the lightweight design of the dump truck carriage. In this method, the optimal Latin Hypercube sampling method is firstly applied to generate the sample points of the design variables, and the corresponding responses are calculated by finite element simulations. Then, the Kriging surrogate model is adopted to present the numerical relationship between the design variables and the responses. On this basis, the NSGA-II algorithm is utilized to perform the multi-objective optimization based on the Kriging model, for searching the Pareto front. Finally, the optimal solution is determined from the Pareto set through the entropy-weighted TOPSIS method. The flowchart of the proposed multi-objective optimization procedure is presented in Figure 2.

3. Finite element Analysis of Dump Truck Carriage

3.1. Finite Element Modeling of Dump Truck U-Carriage

A dump truck is a special purpose vehicle, which has been widely used to transport sand, garbage, construction materials and so on, because of its capacity of self-uploading freight through hydraulic lifting devices. It is equipped with the carriage, which is an open box, for storing the freight. The mass reduction of the carriage is an effective way to cut transportation costs as well as to realize energy conservation and environmental protection.

Thus, a U-shaped dump truck carriage, as shown in Figure 3, is selected as the research object, for studying the lightweight design method of the commercial vehicle component. The U-carriage, with a dimension size of 7600 mm × 2300 mm × 1730 mm, is made of high-strength steel with a yield strength of 1200 MPa. The basic material properties are given in

Table 1. Material basic properties of high-strength steel used for carriage.

Material	σs/MPa	E/MPa	µ
High-strength steel	1200	2.10 × 105	0.28

.

The finite element model of the dump truck carriage was established by the finite element preprocessing software HyperMesh, and this model would be solved by OptiStruct. In the modeling process, the three-dimensional solid model of the U-carriage is first imported into the finite element software. After geometric cleaning, the plates of the carriage are meshed by shell elements with a size of 10 mm. The hinge support and lifting support are meshed using solid elements. The welded parts are simulated by the rigid elements, which can be used for connecting two nodes to model a rigid welded type connection. Through meshing, the U-carriage is divided into 790,503 elements and 896,499 nodes, and its finite element model is shown in Figure 4.

3.2. Definition of Boundary Conditions

The strength of the dump truck carriage is an important performance for guaranteeing it can store freight safely. In this paper, there are two load cases to carry out the static structural analysis of the U-carriage with the finite element method. One is the full load case, which is used to obtain the stress distribution of the U-carriage under full load working conditions. The other is the lifting load case, which is adopted to simulate the critical separation state between the carriage and frame when the dump truck uploads freight.

In the full load case, the translational freedom in the x, y and z directions and the rotational freedom around the y and z axes are constrained at the joints between the carriage hinge support and the frame, as well as the joints between the carriage lifting support and the hydraulic cylinder (denoted as 1, 2, 3, 5, 6). Meanwhile, the y-direction translational freedom for the nodes in the contact area of carriage and frame is constrained (denoted as 2).

In the lifting load case, the constraints are the same as the full load case, except that a displacement of 10 mm is applied to the carriage lifting support point, which is adopted to simulate the critical separation state between the carriage and frame. Moreover, the y-direction translational constraint for the nodes in the contact area of carriage and frame is canceled. The constraint condition of the U-carriage in the full load case and lifting load case are shown in Figure 5.

The dump truck carriage is usually for storing loose material. In this paper, the load of sandy loam soil applied on the plates of the carriage is calculated according to Rankine’s theory of active earth pressure [34]. The pressure of sandy loam soil exerted on the floor, front, rear and side plates are shown in Figure 6.

The pressure of sandy loam soil applied on floor can be calculated as:

$$q=H\gamma$$

(16)

where H is the height of loaded sandy loam soil and γ is its bulk density.

The bulk density γ of sandy loam soil can be formulated as:

$$\gamma =\rho g$$

(17)

where ρ is the density of sandy loam soil; g denotes the acceleration of gravity.

It is assumed that the upper surface of the sandy loam soil loaded in the carriage is horizontal, and the sandy loam soil is in the limit equilibrium state before sliding. According to Rankine’s theory of active earth pressure, at a depth h below the upper surface of the sandy loam soil, the horizontal pressure $q_2$ of the sandy loam soil acting on the front, rear and side plates of the carriage can be calculated as:

$$q_2=q_1{\tan }^2\left(45°-\varphi /2\right)$$

(18)

where $q_1$ is the vertical pressure at the depth of h, $q_1=h\gamma$; ϕ is the internal friction angle of sandy loam soil.

To simplify the calculation of loading of the dump truck carriage, the depth h is calculated by the vertical distance between the geometric center of each plate and the upper surface of the loaded soil. Accordingly, the applied pressure is divided into five equivalent loading areas, as shown in Figure 7. The pressure is obtained according to the full load condition, with consideration of a dynamic load coefficient of 1.5 caused by road roughness. Since the lift angle is very small at the beginning of unloading freight, it is assumed that the load condition for the lifting load case is the same as the applied load of the full load case.

3.3. Initial Performance Analysis of U-Carriage

The strength analyses of the finite element model of the U-carriage are solved by OptiStruct, under the full load condition and lifting load condition, and the stress distribution is obtained, as shown in Figure 8. The maximum stress is given in

Table 2. Initial performance analysis of carriage.

Performance		Initial Value
Mass m/kg		2193
Maximum stress/MPa	Full load σmz	316.32
	Lifting σjs	690.08
Natural frequency f/Hz	1st order	6.1
	2nd order	9.7
	3rd order	11.4
	4th order	12.7
	5th order	14.6
	6th order	20.9

. Moreover, the modal analysis of the U-carriage is conducted to calculate its natural frequencies in a free state. The first six order modes are obtained, as listed in Table 2.

4. Lightweight Design of Dump Truck Carriage

4.1. Construction of Kriging Surrogate Model

For saving the computation cost from lots of finite element simulations in multi-objective optimization, as an effective alternative, the Kriging surrogate model is widely used to establish the mathematical relationship between the design variables and the performance responses, with high fitting accuracy [35,36,37]. The lightweight design of dump truck carriage is a multi-objective optimization design problem. Its aim is to minimize the dump truck carriage mass while improving its performance by optimizing the geometrical parameters. Therefore, the thickness of key plates of the dump truck carriage is taken as the design variable, as shown in Figure 3. That is to say, the design variables consist of the floor thickness, the thickness of the front, rear and side plates, and the thickness of front and rear reinforced plates and the rear U-shaped plate. Their value range is given in

Table 3. Value range of design variables.

Variables	Description	Initial	Lower	Upper
x1/mm	Floor	6.0	4.0	8
x2/mm	Front plate	3.0	2.0	4
x3/mm	Rear plate	3.0	2.0	4
x4/mm	Side plate	3.0	2.0	4
x5/mm	Side reinforced plate	4.0	2.5	5.5
x6/mm	Front reinforced plate	6.0	4.0	8
x7/mm	Rear U-shaped plate	8.0	6.0	10

. The initial values of the design variables are defined based on the original model of the dump truck carriage. On this basis, their upper and lower limits are determined by giving deviations from the initial values.

Then, the optimal Latin hypercube approach is utilized to search the sample points, and 30 points are acquired as a result, which is randomly and uniformly distributed in the design space. The corresponding performance responses are obtained through finite element analysis of U-carriage. The Kriging surrogate model is built, and its accuracy can be verified by the determination coefficient R², which is formulated as:

$$R^2=\frac{{\displaystyle \sum _{i=1}^n{\left({\widehat{y}}_i-\overline{y}\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$

(19)

where n is the number of sample points used to verify the accuracy of the surrogate model; ${\widehat{y}}_i$ and $y_i$ are the predictive value and numerical simulation value, respectively; $\overline{y}$ is the mean value.

The range of R² is [0,1], and the closer the value is to 1, indicating that the accuracy of the surrogate model is higher [38]. There are 10 sample points randomly selected from the sample points for accuracy validation. The determination coefficients of the surrogate models for the mass, the first-order natural frequency, the maximum stress of the full load case and the lifting load case are obtained, as shown in

Table 4. Determination coefficients of surrogate models.

Surrogate Model	R²
Mass m	0.9611
First-order natural frequency f1	0.9031
Maximum stress of full load case σmz	0.9151
Maximum stress of lifting load case σjs	0.9163

. The validation results for the mass and first-order frequency are given in Figure 9. Obviously, the Kriging surrogate models of the U-carriage exhibit sufficient accuracy.

4.2. Multi-Objective Optimization for Lightweight Design of Carriage

The lightweight multi-objective optimization of the dump truck carriage is carried out for minimizing the mass while maximizing the first-order natural frequency. Meanwhile, the maximum stress of the full load case and the lifting load case are taken as constraints. Then, the multi-objective optimization of the U-carriage can be formulated as:

$$\{\begin{array}{l}\mathrm{find}x=（x_1，x_2，x_3，x_4，x_5，x_6，x_7）\\ \min \left\{m(x)\right\},max\left\{f_1(x)\right\}\\ \mathrm{s}.\mathrm{t}.{\sigma }_1(x)\le \left[{\sigma }_{\mathrm{mz}}\right]\\ {\sigma }_2(x)\le \left[{\sigma }_{\mathrm{js}}\right]\\ x\in (x_L,x_U)\end{array}$$

(20)

where m is the mass of the carriage; $f_1$ is the first-order natural frequency; ${\sigma }_1$ is the maximum stress of the carriage under the full load condition, $\left[{\sigma }_{\mathrm{mz}}\right]$ = 316.32 MPa; ${\sigma }_2$ is the maximum stress of the lifting condition, $\left[{\sigma }_{\mathrm{js}}\right]$ = 690.08 MPa; $x_L$ and $x_U$ are the lower and upper limits of the design variable, respectively.

The NSGA-II algorithm is adopted to solve the multi-objective optimization problem with the population size of 20, generation of 40 and crossover probability of 0.85. After optimization iteration, the Pareto front of multi-objective optimization of the dump truck carriage is obtained, as shown in Figure 10.

4.3. Results and Discussion

In order to find the optimal solution for lightweighting the dump truck U-carriage from the Pareto front, 64 Pareto solutions are defined as the decision matrix according to the TOPSIS approach. Meanwhile, the weight coefficients of mass, the first-order natural frequency, the maximum stress of the full load case and the lifting load case are calculated by the entropy weight method, and the calculation results are listed in

Table 5. Weight coefficient of performance index.

Performance	Entropy	Weight
Mass	0.99804	0.25232
First-order natural frequency	0.998125	0.241376
Maximum stress for full load case	0.998013	0.255759
Maximum stress for lifting load case	0.998053	0.250569

. Then, the ideal and negative ideal solutions are determined from the weighted and regularized decision matrix. Moreover, the Euclidean distance between each Pareto solution and the ideal solution, as well as the distance between each Pareto solution and negative ideal solution, are obtained for calculating the relative closeness coefficient. On this basis, the 64 Pareto solutions are sorted by the relative closeness coefficient in descending order. The top 15 of the 64 Pareto solutions are illustrated in

Table 6. Sorting results of Pareto solutions.

Sample	S+	S−	Ci	Order
26	0.002106	0.004779	0.694092	1
47	0.002102	0.004668	0.689477	2
52	0.002102	0.00456	0.684501	3
49	0.002097	0.004549	0.684437	4
10	0.002087	0.0045	0.6832	5
20	0.002074	0.004423	0.68077	6
6	0.002027	0.004107	0.669589	7
63	0.002134	0.004161	0.660943	8
53	0.002136	0.003813	0.640888	9
34	0.002096	0.003672	0.636575	10
39	0.002138	0.003718	0.634826	11
19	0.002138	0.003709	0.634336	12
31	0.002211	0.003332	0.601195	13
42	0.002237	0.003356	0.600075	14
40	0.002227	0.003299	0.59694	15

.

It can be seen from Table 6 that the 26th Pareto solution is ranked first in terms of the relative closeness coefficient. Thus, it is chosen as the optimal solution for the lightweight design of the dump truck carriage, which is marked as “Optimal” in Figure 10. Additionally, there are two Pareto solutions randomly selected to compare with the optimal solution, which are marked as “Point A” and “Point B” in Figure 10. The comparisons among the original model and optimized models of the dump truck carriage are given in

Table 7. Comparison among the original model and optimized models of the carriage.

Parameter	Original	Point A	Point B	Optimal	Modification
x1/mm	6.00	6.24	7.00	6.32	6.50
x2/mm	3.00	2.06	2.07	2.12	2.00
x3/mm	3.00	2.02	2.01	2.54	2.50
x4/mm	3.00	2.12	2.67	2.90	3.00
x5/mm	4.00	3.73	5.13	3.65	4.00
x6/mm	6.00	5.54	5.82	4.43	4.50
x7/mm	8.00	6.00	6.33	6.08	6.00
m/kg	2193.00	2034.90	2083.92	2063.70	2112.00
f1/Hz	6.10	5.93	6.22	6.11	6.16
σmz/MPa	316.32	299.25	289.42	288.45	272.49
σjs/MPa	690.08	692.69	699.33	689.21	688.17

.

Obviously, the mass of the dump truck carriage achieves a remarkable reduction after the multi-objective optimization. The mass and the first-order natural frequency of the optimal solution is between Point A and Point B, which can be easily observed from the Pareto front. The maximum stress of the full load case and the lifting load case in the optimal solution are less than those in Point A and Point B, because the strength of the dump truck carriage is also considered in determining the optimal solution by the entropy weighted TOPSIS approach.

The design variables of the optimal solution are corrected according to practical engineering, and are listed in Table 7. Then, the finite element model of the dump truck carriage is modified and used to calculate the performance index. The first mode and stress contours of the full load case and lifting load case are shown in Figure 11. It can be seen that the stress distribution is improved compared with that before optimization. The mass of the U-carriage is reduced by 81 kg with a mass reduction of 3.7%, while guaranteeing sufficient performance, which achieves a significant lightweight. It is also proved the effectiveness of the proposed method for multi-objective lightweight optimization.

5. Conclusions

This paper proposed a multi-objective optimization approach integrating the NSGA-II algorithm and entropy weighted TOPSIS and its effectiveness was proved by its application to the lightweight design of the dump truck carriage. Firstly, the finite element model of the U-carriage was built to perform the static strength analysis and the modal analysis. The thickness of key plates of the carriage was taken as the design variable, and the optimal Latin Hypercube sampling technique was adopted to choose the randomly and uniformly distributed sample points in the design space. Then, the Kriging model was utilized to construct the numerical relationships between the design variables and the performance index of the dump truck carriage. On this basis, the NSGA-II algorithm was employed to carry out the multi-objective optimization of the lightweight design of the U-carriage for minimizing the mass while maximizing the first-order natural frequency, and the Pareto front was obtained. Finally, the entropy weighted TOPSIS approach was used to determine the optimal solution for lightweighting the carriage from the Pareto solutions. The optimization results indicate that the mass of the optimized carriage was reduced by 81 kg compared with the original carriage, achieving a mass reduction of 3.7%, while guaranteeing the performance to meet the design requirement. This proves that the proposed multi-objective optimization procedure could improve the optimization efficiency, and it provides a feasible method for the lightweight design of dump trucks.

The contribution of this paper is mainly reflected as follows. First, the Kriging surrogate model, instead of the finite element model, was used to perform the optimization, which can save the computation cost and improve the optimization efficiency. Second, the TOPSIS method provided a novel way to find the optimal solution from many Pareto solutions. It can help researchers or engineers to determine the optimal design of the optimization problem.

However, the above research still has some limitations. In this paper, the effectiveness of the proposed method is only proved by comparing the optimal design with the initial design. Although this optimization procedure can provide a technical reference for the development and design of the dump truck carriage, the potential for optimization has yet to be tapped.

Thus, future research could conduct a comparison between the proposed method and other optimization methods to demonstrate its superiority over other methods. Meanwhile, different optimization algorithms will be adopted to seek the Pareto solutions, to achieve a better reduction in mass.