3.1. Datasets
The following datasets were used in this work for evaluation of the proposed method.
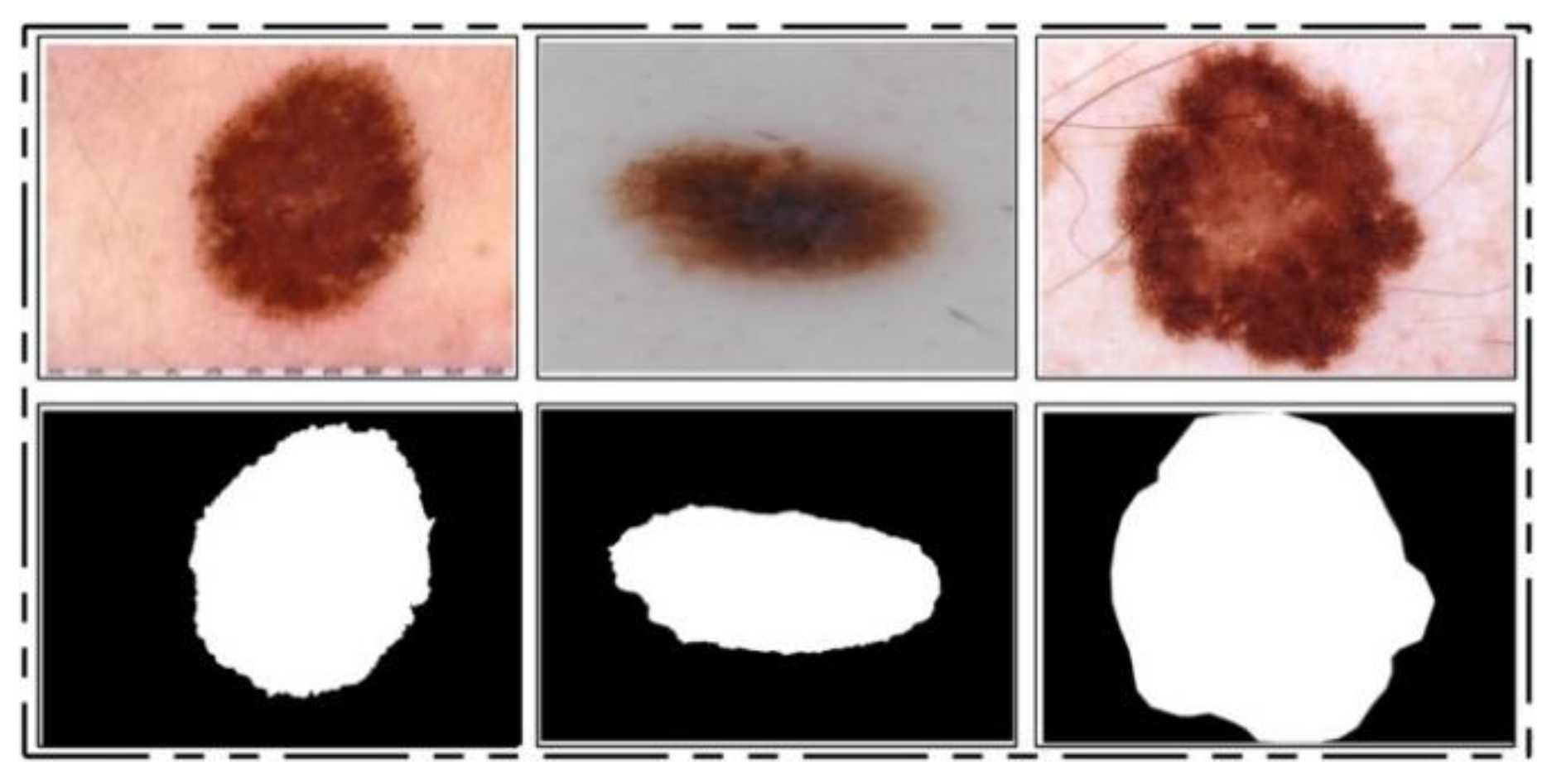
ISBI 2016 Dataset: This dataset [
24] entails a total of 900 training images and 379 testing images. The ground truth images are publicly available for validation of the segmentation task. The training images include melanoma and benign classes. These images were used for the training of a CNN model for the lesion segmentation task, while the rest of the testing images were utilized for testing the newly implemented CNN model for the segmentation task. Some sample images are reproduced in
Figure 1.
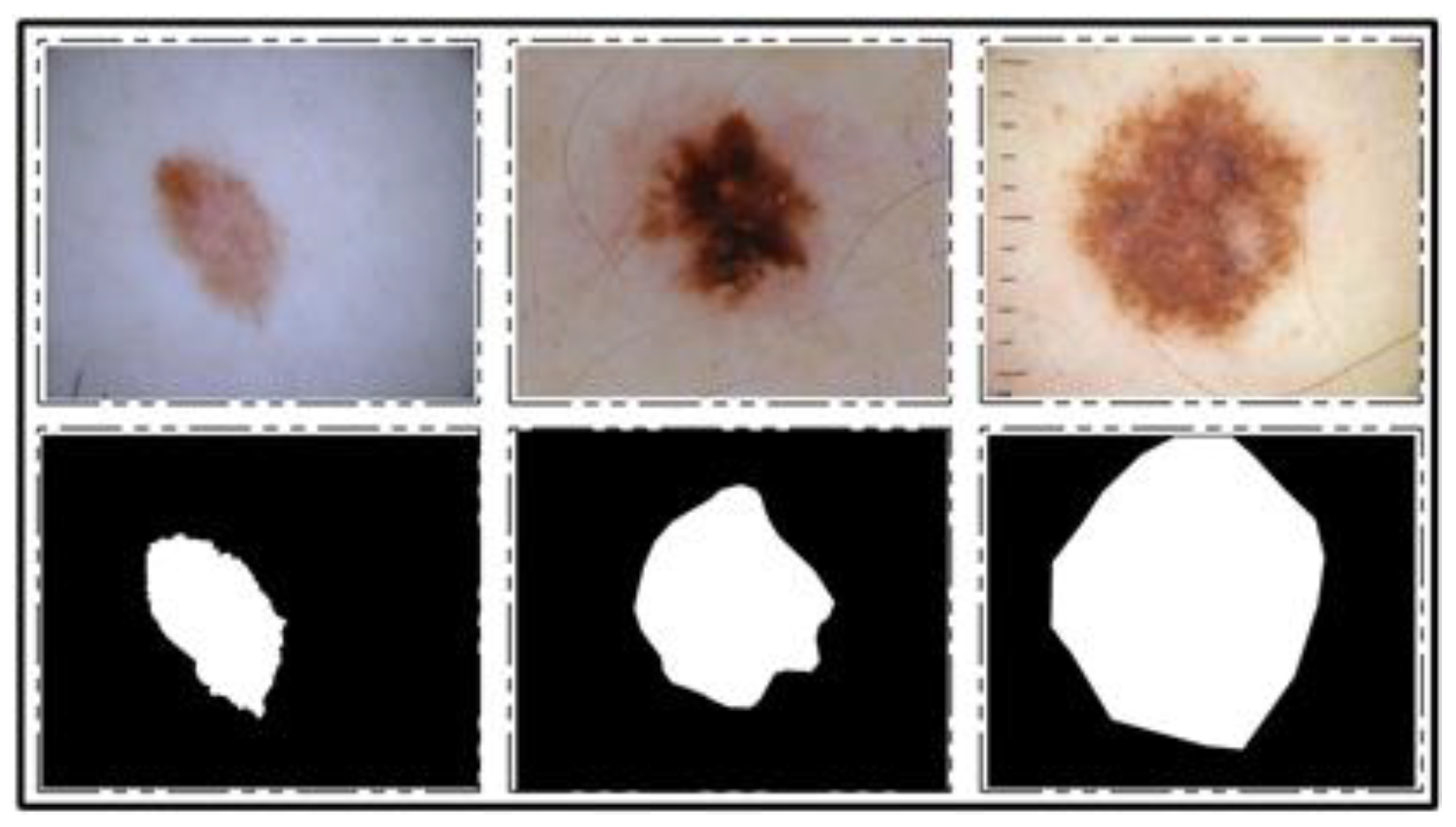
ISIC 2017 Dataset: This dataset [
25] consists of a total of 2750 dermoscopy images. From those, 2000 images are used for training, 150 for validation, and 600 for testing [
25]. The ground truth samples of this dataset are also publicly available, which were used for validation of the segmentation algorithm. A few sample images are shown in
Figure 2. For the classification task, images were classified into three categories, namely melanoma (374), seborrheic keratosis (254), and nevi (1372). As these classes are not balanced, we performed data augmentation.
ISBI 2018 Dataset: This dataset consists of three parts—lesion segmentation, attribute detection, and classification of the lesion into type [
26]. For segmentation, a total of 2594 training images are provided along with ground truth images, whereas 1000 and 100 images are given for testing and validation, respectively. A few sample images along with ground truth images are shown in
Figure 3.
HAM10000 Dataset: This dataset [
23] includes a total of 10,015 dermoscopy images. This dataset is known as one of the most complex imaging databases for multiclass skin lesion classification. Seven different types of skin lesions are included, namely AKIEC, BCC, BKL, DF, NV, MEL, and VASC. For each label, the number of images included is 327, 541, 1099, 155, 6705, 1113, and 142, respectively.
Figure 4 shows few sample images from this dataset.
3.3. Lesion Contrast Stretching
For image quality assessment, contrast enhancement is one of the imperative requirements. Image enhancement is the process of improving image quality by increasing the quality of a few features or decreasing haziness among distinct image pixels. The key objective of this step is to improve the image quality compared to the original image. Our main objective was to enhance the contrast of the lesion region to easily extract the region of interest (ROI). Many techniques are presented in the literature, and one of the most famous techniques is histogram equalization (HE) [
44]. In HE, all image pixels are increased, but lower and upper bounds are set to perform the enhancement only in the specific region of the lesion.
Motivated by HE, we implemented a hybrid contrast stretching technique named local color-controlled histogram intensity values (LCcHIV). In this approach, we initially create a histogram of the input image to find the lesion pixels and then improve the pixel range by multiplying variance values. The resultant variance value-based image is subjected to HE for further refinement. Later, the intensity values are increased and adjusted according to the lesion and background regions based on a fitness function. This process is described as follows.
Consider an input image
having dimensions
, where
and
, and
. Let
be the resultant contrast-enhanced image of the same dimensions as the input image
. First, the histogram of the image
is computed as follows:
where
is the histogram of an image
,
represents the frequency of occurrences,
represents the occurrence of gray levels, and
. Based on
, we find the range of infected pixels, represented by Equation (2).
where
represents the infected region patch and
represents the pixel values. The
is the entire infected region, and the range of the infected region is represented by
to
. Later, we compute the variance of the whole image
using Equation (3).
The output variance value is multiplied with Equation (2) as follows:
After that, we fuse
and
to obtain an infected patch. Furthermore, histogram equalization is applied on the infected patch and fused with the original image in Equation (6).
The process results are visually shown in
Figure 6b. In this figure, it is shown that the infection regions are highlighted more as compared to the original images. However, our interest is to separate the infection part from background based on contrast. Therefore, we define two fitness functions in sequential order and obtain more relevant information. Mathematically, the fitness functions are defined as follows:
These functions increase the range of pixel values by up to 5 times, each time in an increment of 1. After the images are passed through both fitness functions, the resultant images are more informative for correct lesion segmentation. The visual results of this step are shown in
Figure 6c,d. The final result shown in
Figure 6d is utilized in the next step for lesion segmentation.
3.4. Deep Saliency-Based Lesion Segmentation
Segmentation of skin lesions is a crucial step for the localization of infected regions. Many techniques are presented in the literature for lesion segmentation using saliency techniques and convolutional neural network-based techniques, to name a few [
40,
45,
46]. The saliency-based techniques are simple, but not more accurate as compared to CNN-based techniques. The techniques based on CNN [
47,
48] required a large number of ground truth images for training a model, which is further utilized for the detection process. However, in most medical applications, it is not possible to prepare the required number of ground truth images (e.g., for skin cancer, stomach infections, COVID-19, and lung cancer). Moreover, the existing techniques are also facing a few problems including low contrast of lesions, complex lesion boundaries, and irregularity in lesion shapes [
49]. We propose a new method named Deep Saliency Segmentation (DSS) for skin lesion detection in this work. The proposed method works as follows: (i) a simple CNN model is designed, which includes ten layers; (ii) features of the last convolutional layer are visualized and concatenated in one image; (iii) superpixels of the concatenated image are computed; (iv) a threshold is applied for the final segmentation; and (v) boundaries are drawn on segmented regions using an active contour approach for the localization of skin lesions.
Mathematically, this approach is formulated as follows: Given that
denotes output enhanced images with dimensions of
, we utilized these images to design a simple CNN model. The main use of this model is to learn and visualize the features of an image. Visually, the designed model is shown in
Figure 7. This model includes several layers, such as one input layer, three convolutional layers along with the ReLu layer, one max-pool layer, one fully connected layer (FC), one softmax layer, and, finally, an output layer. The size of the input layer was
; therefore, we resized all images to this size. In the first convolutional layer, the filter size was
, the number of channels was 3, the filter size was 64, and stride was
. After this layer, we obtained two feature matrices named the weight matrix and the bias matrix. The size of the weight matrix was
and the bias matrix was
.
The convolutional layer weight matrix and bias matrix are represented as follows:
where
denotes features of the first convolutional layer,
is an enhanced image,
is the weight matrix of the
layer, and
is the bias matrix of the
layer. After that, the ReLu activation layer was applied. In the second convolutional layer, the filter size was
, the number of channels was 64, the number of filters was 64, and stride was
. The weights and bias of this layer were updated as follows:
where
is the updated weight matrix,
is the updated bias matrix,
is the learning rate, and
is the momentum. The features of this layer were normalized using the ReLu activation function. Next, a max-pooling layer was applied of filter size
and stride of
. The main purpose of this layer was to obtain more active features and minimize the feature length. Mathematically, this layer is formulated as follows:
In the third convolutional layer, the filter size was , the number of channels was 64, the number of filters was 128, and the stride was . The weights and the bias matrix were updated using Equations (10) and (11). Later, the fully connected and softmax layers were added and training was performed.
After training, the features of the third convolutional layer were visualized, and in the output, 96 images were generated, as shown in
Figure 8. Then, all 96 output images were combined in one image to obtain a saliency map image. Visually, this resultant image is shown in
Figure 8. This figure shows that the output image is more informative, and the lesion is highlighted. By utilizing this saliency map image, superpixels were computed and the pixels were reconstructed. The main purpose of the superpixel technique is to group the important image pixels of a meaningful object. The second purpose of this approach is to remove image complexity. In this work, we used a simple linear iterative clustering approach [
50] for superpixel generation. This approach is shown in
Figure 9. This figure illustrates that initially, superpixels are generated, and then, they are combined based on color pixels.
After this technique, the constructed saliency map was clearer, which was further passed through a threshold function for final segmentation. Mathematically, the threshold function is defined as follows. Consider that
is a final saliency mapped image and
represents a threshold value; then, the threshold function is formulated as follows:
This threshold function converts images into binary format. Visually, the output is shown in
Figure 10 (binary image), which illustrates that the binary images include a few holes that need to be refined. Therefore, we applied a filling morphological operation. The final segmented images are shown in
Figure 10a. We drew boundaries based on the active contour approach (seen in
Figure 10b). This figure illustrates that the boundaries drawn on the original images are based on their segmented output. Hence, in the next step, deep learning features were extracted through these localized regions.
3.5. Multiclass Lesion Classification
Multiclass skin lesion classification is a new research area in which researchers are trying to improve the classification performance. Experiments have been performed on the ISBI 2018 and HAM10000 datasets. However, the images in these datasets are very similar to each other, and each dataset consists of seven classes, as mentioned in
Section 3.1. In the existing studies, the researchers faced high similarity, low contrast, and imbalanced data. In this work, for the multiclass classification, we initially balanced the data using a data augmentation step. For this purpose, we performed the following operations: right flip, left flip, and transposition of the original and both flipped images. After balancing the skin classes, we utilized two pre-trained deep learning models named ResNet101 and DenseNet201. We retrained both models by employing transfer learning for feature extraction. A detailed description is given below.
ResNet101 CNN Model: ResNet was proposed in 2015 [
28]; see
Figure 11A. In this model, a few connections are simply skipped, and the direct connections are made between the layers. In ResNet101, the “bottleneck” building blocks are used to reduce the parameters (see
Figure 11B). These blocks are formulated as follows:
where
represents an output vector,
is the residual mapping to be learned, and
is input localized lesion pixels. This equation is utilized for short connections, but the dimensions of input and output must be the same. However, if the input–output channels do not have the same dimension, then linear projection is performed. Mathematically, the linear projection is defined as follows:
where
represents a convolutional operation, which is utilized to adjust the input dimensions. Visually, the architecture of ResNet101 is shown in
Figure 12. The network incorporates five convolutional blocks: Conv1, represents the first convolutional layer; Conv2 includes three building blocks, and each block has three convolutional layers. The third convolutional layer includes four building blocks. In the fourth and fifth convolutional layers, there are 23 and 3 building blocks, respectively. Finally, the last layer is the FC layer used for classification.
DenseNet201: The main idea in ResNet101 was skipping the layers revised in the DenseNet architecture [
51]. In this architecture, all features are concatenated in sequential order. Mathematically, the concatenation process is defined as follows:
where
is a nonlinear transform defined as a composite function followed by a ReLu activation function. The convolution operation of
is
, which refers to the concatenated features for layer
. In this model, dense blocks are created for downsampling. These dense blocks are separated by the transition layer.
The architecture of DesnseNet201 is illustrated in
Figure 13. This figure describes that the first convolutional layer has a filter size of
and stride of
. After this layer, a max-pooling layer is added of a filter size of
. Afterward, a dense block is added and each dense block includes a convolutional layer of filter size
and
. The main purpose of adding this
convolutional layer is to reduce the feature map and decrease the computational cost. A total of four dense blocks have been added to this architecture, and for each dense block, convolutional bocks are added. The size of the convolutional blocks is 6, 12, 48, and 32, respectively. After each dense block, a transition layer has been added. After the fourth dense block, a global average pooling layer has been added of a filter size of
followed by an FC layer for final classification.
Transfer Learning-based model training: Transfer learning (TL) is a technique where an existing pre-trained model is reused for a new classification task [
52]. TL has been proven to achieve good performance on many image classification tasks [
53,
54,
55,
56]. Visually, this process is illustrated in
Figure 14, where the pre-trained models are trained on large datasets such as ResNet101 and DenseNet201 in this work. In TL, knowledge is transferred on a target model, and the target datasets used were ISBI 2017 and HAM10000. After reusing both models, two new models were obtained for the classification of multiclass skin lesions. In the TL phase, we selected 70% images for training the model and the remaining 30% were used for testing. The number of epochs was 20 and the learning rate was 0.0001. The mini-batch size was set as 64. Mathematically, we can define TL as follows.
Consider that
is a source domain and
is a source task; then, it can be defined as
. The target domain is denoted by
and the target source is denoted by
; then, it is represented as
. TL uses the knowledge of the source domain and transfer in the target domain based on the following objective function.
We selected a global average pool layer of both architectures and extract features. The feature matrix length of ResNet101 was and , denoted by and , respectively.
Feature Optimization: Feature selection is the removal of irrelevant, noisy, and redundant features from an original feature set. It improves machine learning algorithms’ performance in terms of faster training and ease of interpretation, cuts the complexity if the best features are selected, and reduces overfitting [
57].
In this work, we implemented an improved moth flame optimization (IMFO) to select the best features from high-dimensional data. MFO emulates the navigation mechanism of moths in nature [
58]. Initially, in this algorithm, a population is assigned, denoted by
and feasible solutions are assigned
with features dimension
. The search technique is defined as follows:
where
denotes an initial phase,
is an updated phase, and
is the stopping condition. In the initial phase, the population is randomly generated, where
. The fitness function is applied to evaluate the features by the following equation.
where
represents the fitness function. In the Cubic SVM, the selected kernel function is cubic, and the method is one vs. all;
is a random value between
used to balance the classifier accuracy,
denotes input features, and
denotes selected features in
iteration. After this operation, the moths are updated based on the flames, but first, we employ an activation function for first-stage feature selection. The activation function is defined as:
where
is a value obtained after the mean operation of each selected feature set
, and it is updated in each iteration. In our work, the value of is mostly 0.4 to 0.48. In this equation, 1 represents the feature that is selected for the next iteration and is considered in the updated phase, whereas 0 represents the feature that is discarded from the next iteration. Using this process, there is a chance that a few important features will be lost but there is also a high probability of good features being transferred for the next iteration. The features are updated through the following formulation.
where
,
, and
. Based on this expression, the new positions of moths are updated w.r.t flames. Here,
represents the new closest position to the flame and
represents the farthest position. Later, the updated flames are sorted in descending order, defined by
, and the entropy value
is computed. The activation function is updated for the final selection of features in the first iteration based on the entropy value.
The features passed in this function are again evaluated in the fitness function, and this process continues until the iterations are completed. In this work, the numbers of iterations was set to 100. This algorithm was applied on both deep feature vectors, and in the output, two optimized vectors were obtained. The length of the optimized feature vectors was and , denoted by and , respectively.
Later on, we fused both vectors and obtained a more informative feature matrix. The main purpose of feature fusion is to improve accuracy, but, on the other side, the computational time increases. For feature fusion, we first found the length of both vectors and then selected the feature vector of the maximum length. Based on the maximum length, we found the entropy of fewer length feature vectors and performed padding. After padding, we computed the correlation among pairs of features and selected only those features for the fused vector that have a maximum correlation. Mathematically, it was formulated as follows.
Given two optimal feature vectors
and
of dimension
and
, respectively, consider that we have a fused feature vector
of dimension
, where
represents the feature dimension of the fused vector. Initially, the maximum dimensional feature vector is found by employing the following equation:
This equation returns a maximum length feature vector of dimension
, where
; hence, it is required to equal the length of other feature vectors according to the length of the resultant vector. Mostly, zero padding is performed for an equal length of feature vectors, but we computed the entropy value of fewer feature vectors and performed padding. After this step, the maximal correlation coefficient was computed among pair features
as follows:
where
is the covariance among
and
,
is a supremum function [
59],
, and the interval is
, where
represents a strong negative correlation among features and
represents a strong positive correlation. Hence, we selected only those pair of features that have a maximum correlation (1 or near to 1). Selecting pairs of features through this process plays a key role in obtaining the optimal values. This process of selecting the features was continued until
was calculated for all feature pairs (1262 pairs). Finally, the resultant fused vector was obtained, and the dimension of
was
. This final vector was classified using the KELM [
60]. The classification results are shown in
Figure 15 as labeled images.