Artificial Intelligence-Driven Ensemble Model for Predicting Mortality Due to COVID-19 in East Africa
Abstract
:1. Introduction
“Artificial Intelligence could be the saviour of the COVID-19 pandemic in the coming year; we just need to prove it.”The Lancet Digital Health, 2021
2. Materials and Methods
2.1. Study Area
2.2. Data Source and Attribute Selection
2.3. Data Preprocessing and Analyses
2.4. Proposed Methods
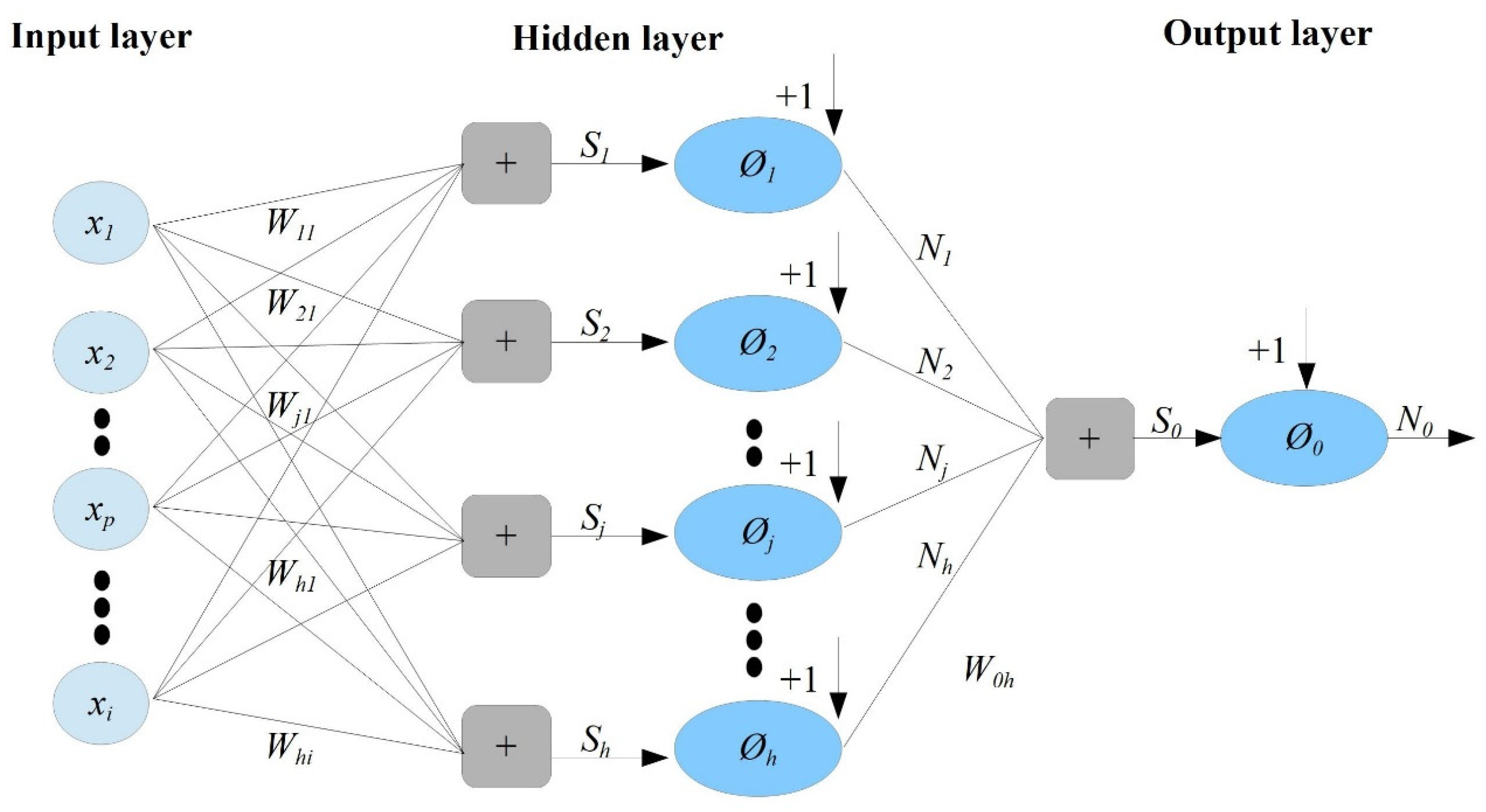
2.4.1. The Feedforward Neural Network (FFNN)
- compute , for i = 1…rk
- compute , for i = 1…rk
- Compute
- Compute , where the MLP uses the denotations below.
2.4.2. The Adaptive Neuro-Fuzzy Inference System (ANFIS)
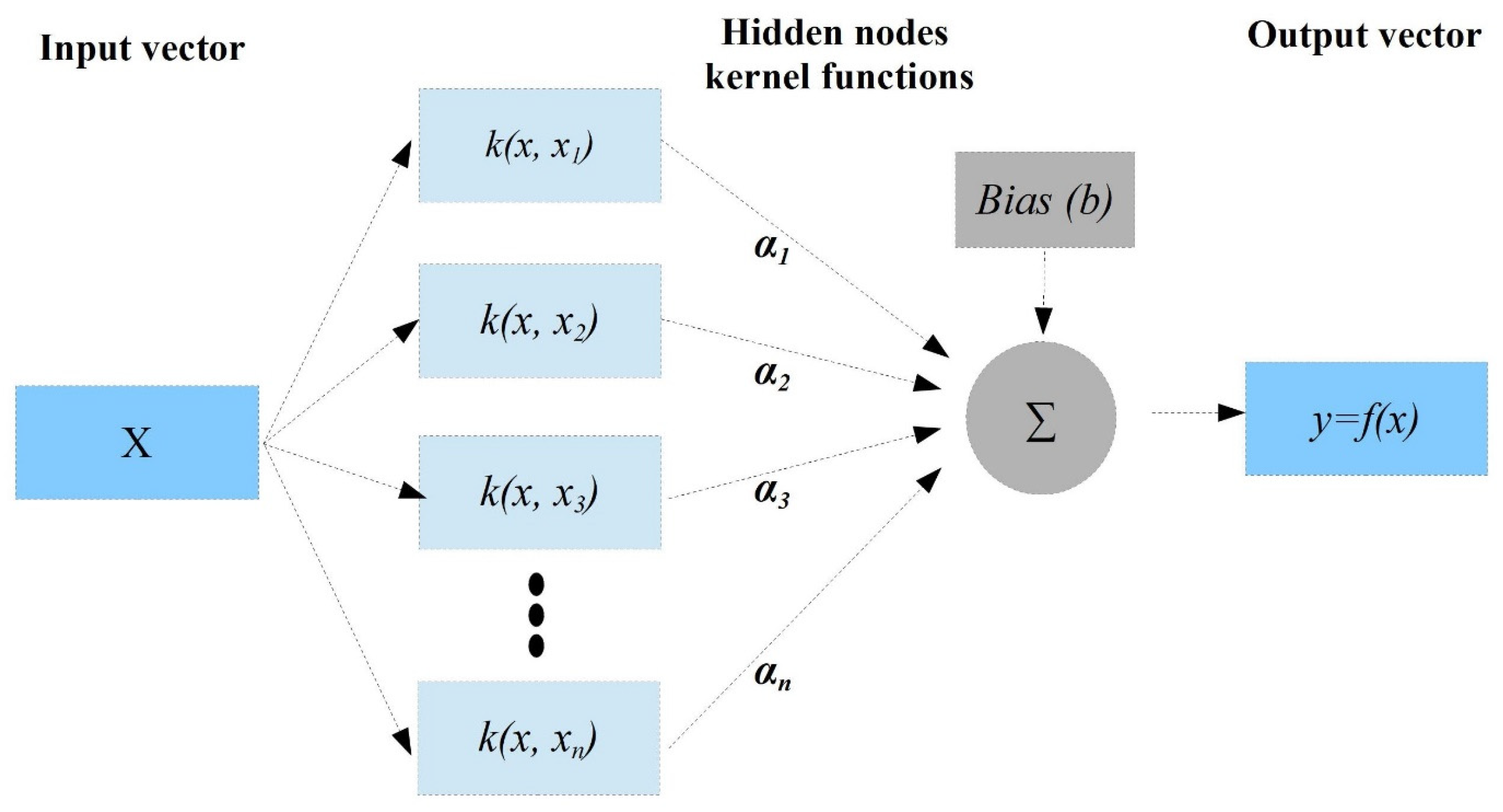
2.4.3. The Support Vector Machine (SVM)
2.4.4. The Multiple Linear Regression (MLR)
2.5. Ensemble Modelling
2.5.1. The Linear Ensemble Approaches
2.5.2. The Non-Linear Ensemble Approaches
2.5.3. Normalization and Evaluation of Models
3. Results and Discussions
3.1. Descriptive Statistics
3.2. Sensitivity Analysis
3.3. Single AI-Driven Black-Box Models
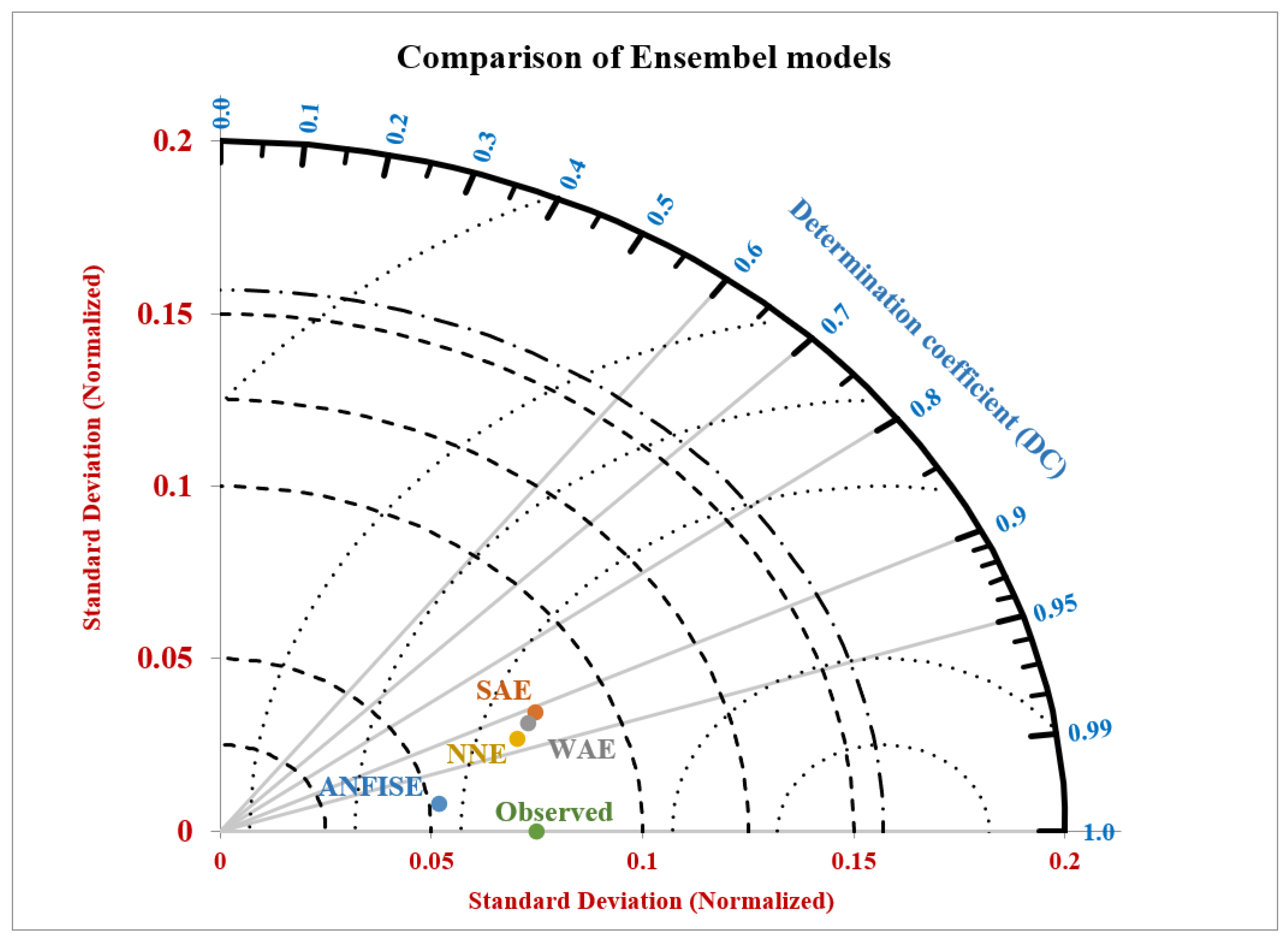
3.4. Ensemble Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, Y.; Chen, L.; Chi, J.; Zeng, S.; Feng, X.; Li, H.; Liu, D.; Feng, X.; Wang, S.; Wang, Y.; et al. Development and validation of an online model to predict critical COVID-19 with immune-inflammatory parameters. J. Intensive Care 2021, 9, 19. [Google Scholar] [CrossRef] [PubMed]
- Ko, H.; Chung, H.; Kang, W.S.; Park, C.; Kim, S.E.; Chung, C.R.; Ko, R.E.; Lee, H.; Seo, J.H.; Choi, T.Y.; et al. An artificial intelligence model to predict the mortality of COVID-19 patients at hospital admission time using routine blood samples: Development and validation of an ensemble model. J. Med. Internet Res. 2020, 22, e25442. [Google Scholar] [CrossRef] [PubMed]
- Arora, N.; Banerjee, A.K.; Narasu, M.L. The role of artificial intelligence in tackling COVID-19. Future Virol. 2020, 15, 717–724. [Google Scholar] [CrossRef]
- WHO. Coronavirus (COVID-19) Dashboard. Available online: https://covid19.who.int/ (accessed on 10 October 2021).
- Gavi, posted 1 June 2020. Available online: https://www.gavi.org/vaccineswork/how-does-COVID-19-compare-past-pandemic (accessed on 12 October 2021).
- Baik, S.M.; Lee, M.; Hong, K.S.; Park, D.J. Development of Machine-Learning Model to Predict COVID-19 Mortality: Application of Ensemble Model and Regarding Feature Impacts. Diagnostics 2022, 12, 1464. [Google Scholar] [CrossRef] [PubMed]
- Karaarslan, E.; Aydın, D. An artificial intelligence-based decision support and resource management system for COVID-19 pandemic. In Data Science for COVID-19; Academic Press: Cambridge, MA, USA, 2021; pp. 25–49. [Google Scholar]
- Vaishya, R.; Javaid, M.; Khan, I.H.; Haleem, A. Artificial Intelligence (AI) applications for COVID-19 pandemic. Diabetes Metab. Syndr. Clin. Res. Rev. 2020, 14, 337–339. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Ge, Q.; Jin, L.; Xiong, M. Artificial intelligence forecasting of COVID-19 in China. arXiv 2020, arXiv:2002.07112. [Google Scholar] [CrossRef]
- Chowdhury, D.; Banerjee, S.; Sannigrahi, M.; Chakraborty, A.; Das, A.; Dey, A.; Dwivedi, A.D. Federated learning-based Covid-19 detection. Expert Syst. 2022, e13173. [Google Scholar] [CrossRef]
- Schiaffino, S.; Codari, M.; Cozzi, A.; Albano, D.; Alì, M.; Arioli, R.; Avola, E.; Bnà, C.; Cariati, M.; Carriero, S.; et al. Machine learning to predict in-hospital mortality in covid-19 patients using computed tomography-derived pulmonary and vascular features. J. Pers. Med. 2021, 11, 501. [Google Scholar] [CrossRef]
- Relief Web. East & Horn of Africa COVID-19 Situation Report—#44, 10 March 2021 Update. 2021. Available online: https://reliefweb.int/report/ethiopia/east-horn-africa-COVID-19-situation-report-44-10-march-2021-update (accessed on 13 October 2021).
- UN.ECA. The Economic and Social Impacts of the COVID-19 Crisis on Eastern Africa: Strategies for Building-Back-Better. November 2020. Available online: https://www.uneca.org/ea-icsoe24 (accessed on 19 March 2021).
- Yaşar, Ş.; Çolak, C.; Yoloğlu, S. Artificial intelligence-based prediction of Covid-19 severity on the results of protein profiling. Comput. Methods Programs Biomed. 2021, 202, 105996. [Google Scholar] [CrossRef]
- Ullah, F.; Moon, J.; Naeem, H.; Jabbar, S. Explainable artificial intelligence approach in combating real-time surveillance of COVID-19 pandemic from CT scan and X-ray images using ensemble model. J. Supercomput. 2022, 78, 19246–19271. [Google Scholar] [CrossRef]
- Kolozsvári, L.R.; Bérczes, T.; Hajdu, A.; Gesztelyi, R.; Tiba, A.; Varga, I.; Ala’a, B.; Szőllősi, G.J.; Harsányi, S.; Garbóczy, S.; et al. Predicting the epidemic curve of the coronavirus (SARS-CoV-2) disease (COVID-19) using artificial intelligence: An application on the first and second waves. Inform. Med. Unlocked 2021, 25, 100691. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Wu, H.; Zhou, D.; Li, K.; Zhang, Y.; Ji, H.; Tong, Z.; Lou, S.; Liu, Z. Application of big data and artificial intelligence in COVID-19 prevention, diagnosis, treatment and management decisions in China. J. Med. Syst. 2021, 45, 84. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; He, Z. Prediction of the confirmed cases and deaths of global COVID-19 using artificial intelligence. Environ. Sci. Pollut. Res. 2021, 28, 11672–11682. [Google Scholar] [CrossRef]
- Gao, Y.; Cai, G.Y.; Fang, W.; Li, H.Y.; Wang, S.Y.; Chen, L.; Yu, Y.; Liu, D.; Xu, S.; Cui, P.F.; et al. Machine learning-based early warning system enables accurate mortality risk prediction for COVID-19. Nat. Commun. 2020, 11, 5033. [Google Scholar] [CrossRef]
- World Atlas. East African Countries. May 2021. Available online: https://www.worldatlas.com/geography/east-african-countries.html (accessed on 9 November 2021).
- USAID, East Africa Regional. Global Health. May 2021. Available online: https://www.usaid.gov/east-africa-regional/global-health (accessed on 9 November 2021).
- Mathieu, E.; Ritchie, H.; Ortiz-Ospina, E.; Roser, M.; Hasell, J.; Appel, C.; Giattino, C.; Rodés-Guirao, L. A global database of COVID-19 vaccinations. Nat. Hum. Behav. 2021, 5, 947–953. [Google Scholar] [CrossRef] [PubMed]
- Hasell, J.; Mathieu, E.; Beltekian, D.; Macdonald, B.; Giattino, C.; Ortiz-Ospina, E.; Roser, M.; Ritchie, H. A cross-country database of COVID-19 testing. Sci. Data 2020, 7, 345. [Google Scholar] [CrossRef] [PubMed]
- Tanty, R.; Desmukh, T.S. Application of artificial neural network in hydrology: A review. Int. J. Eng. Technol. Res. 2015, 4, 184–188. [Google Scholar]
- Nourani, V.; Gökçekuş, H.; Umar, I.K. Artificial intelligence-based ensemble model for prediction of vehicular traffic noise. Environ. Res. 2020, 180, 108852. [Google Scholar] [CrossRef]
- Brilliant.org Feedforward Neural Networks. Retrieved 17:22. Available online: https://brilliant.org/wiki/feedforward-neural-networks/ (accessed on 10 August 2022).
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing—A Computational Approach to Learning and Machine Intelligence; Prentice Hall: Trenton, NJ, USA, 1997. [Google Scholar]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Tsukamoto, Y. An approach to fuzzy reasoning method. Adv. Fuzzy Set Theory Appl. 1979, 137, 523–529. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modelling and control. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Kalteh, A.M. Monthly river flow forecasting using artificial neural network and support vector regression models coupled with wavelet transform. Comput. Geosci. 2013, 54, 1–8. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Behfar, N. Earthfill dam seepage analysis using ensemble artificial intelligence based modelling. J. Hydroinformatics 2018, 20, 1071–1084. [Google Scholar] [CrossRef]
- Wu, C.; Hwang, M.; Huang, T.H.; Chen, Y.M.; Chang, Y.J.; Ho, T.H.; Huang, J.; Hwang, K.S.; Ho, W.H. Application of artificial intelligence ensemble learning model in early prediction of atrial fibrillation. BMC Bioinform. 2021, 22, 93. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, C.; Yao, S.; Wang, L.; Zhao, Y.; Ren, J.; Li, Y. Estimating the COVID-19 prevalence and mortality using a novel data-driven hybrid model based on ensemble empirical mode decomposition. Sci. Rep. 2021, 11, 21413. [Google Scholar] [CrossRef]
- Edeh, M.O.; Dalal, S.; Dhaou, I.B.; Agubosim, C.C.; Umoke, C.C.; Richard-Nnabu, N.E.; Dahiya, N. Artificial Intelligence-Based Ensemble Learning Model for Prediction of Hepatitis C Disease. Front. Public Health 2022, 27, 847. [Google Scholar] [CrossRef]
- Kazienko, P.; Lughofer, E.; Trawinski, B. Hybrid and ensemble methods in machine learning J.UCS special issue. J. Univers. Comput. Sci. 2013, 19, 457–461. [Google Scholar]
- Ajami, N.K.; Duan, Q.; Gao, X.; Sorooshian, S. Multimodel combination techniques for analysis of hydrological simulations: Application to distributed model intercomparison project results. J. Hydrometeorol. 2006, 7, 755–768. [Google Scholar] [CrossRef]
- Abba, S.I.; Linh, N.T.T.; Abdullahi, J.; Ali, S.I.A.; Pham, Q.B.; Abdulkadir, R.A.; Costache, R.; Nam, V.T.; Anh, D.T. Hybrid machine learning ensemble techniques for modelling dissolved oxygen concentration. IEEE Access 2020, 8, 157218–157237. [Google Scholar] [CrossRef]
- Nourani, V.; Elkiran, G.; Abba, S.I. Wastewater treatment plant performance analysis using artificial intelligence—An ensemble approach. Water Sci. Technol. 2018, 78, 2064–2076. [Google Scholar] [CrossRef]
- Dawson, C.W.; Abrahart, R.J.; See, L.M. HydroTest: A web-based toolbox of evaluation metrics for the standardized assessment of hydrological forecasts. Environ. Model. Softw. 2007, 22, 1034–1052. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.-C.; Xu, D.-M.; Chau, K.-W.; Chen, S. Improved annual rainfall-runoff forecasting using PSO-SVM model based on EEMD. J. Hydroinformatics 2013, 15, 1377–1390. [Google Scholar] [CrossRef]
- Nourani, V.; Gokcekus, H.; Gelete, G. Estimation of suspended sediment load using artificial intelligence-based ensemble model. Complexity 2021, 2021, 6633760. [Google Scholar] [CrossRef]
- Sahoo, G.B.; Ray, C.; Wade, H.F. Pesticide prediction in groundwater in North Carolina domestic wells using artificial neural networks. Ecol. Model. 2005, 183, 29–46. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]




| Variables | The Description of Variables |
|---|---|
| New deaths | New deaths attributed to COVID-19 |
| New cases | New confirmed cases of COVID-19 |
| Positive rate | The share of COVID-19 tests that are positive |
| People vaccinated | Total number of people who received at least one vaccine dose |
| Stringency index | A composite metric based on 9 reaction indicators, such as school closures, workplace closures, and travel prohibitions, rescaled to a score between 0 and 100 (100 is the strict response) |
| GDP per capita/USD | Gross domestic product at purchasing power parity |
| Number of smokers | Share of male and female smokers |
| Prevalence of DM | Prevalence of people with diabetes aged 20 to 79 |
| Hospitals beds/1000 | Hospital beds per 1000 people |
| Population density | Number of people divided by land area, measured in square kilometers |
| Variables | Training Data (n = 584) | Verification Data (n = 146) | ||||
|---|---|---|---|---|---|---|
| Min | Mean ± SD | Max | Min | Mean + SD | Max | |
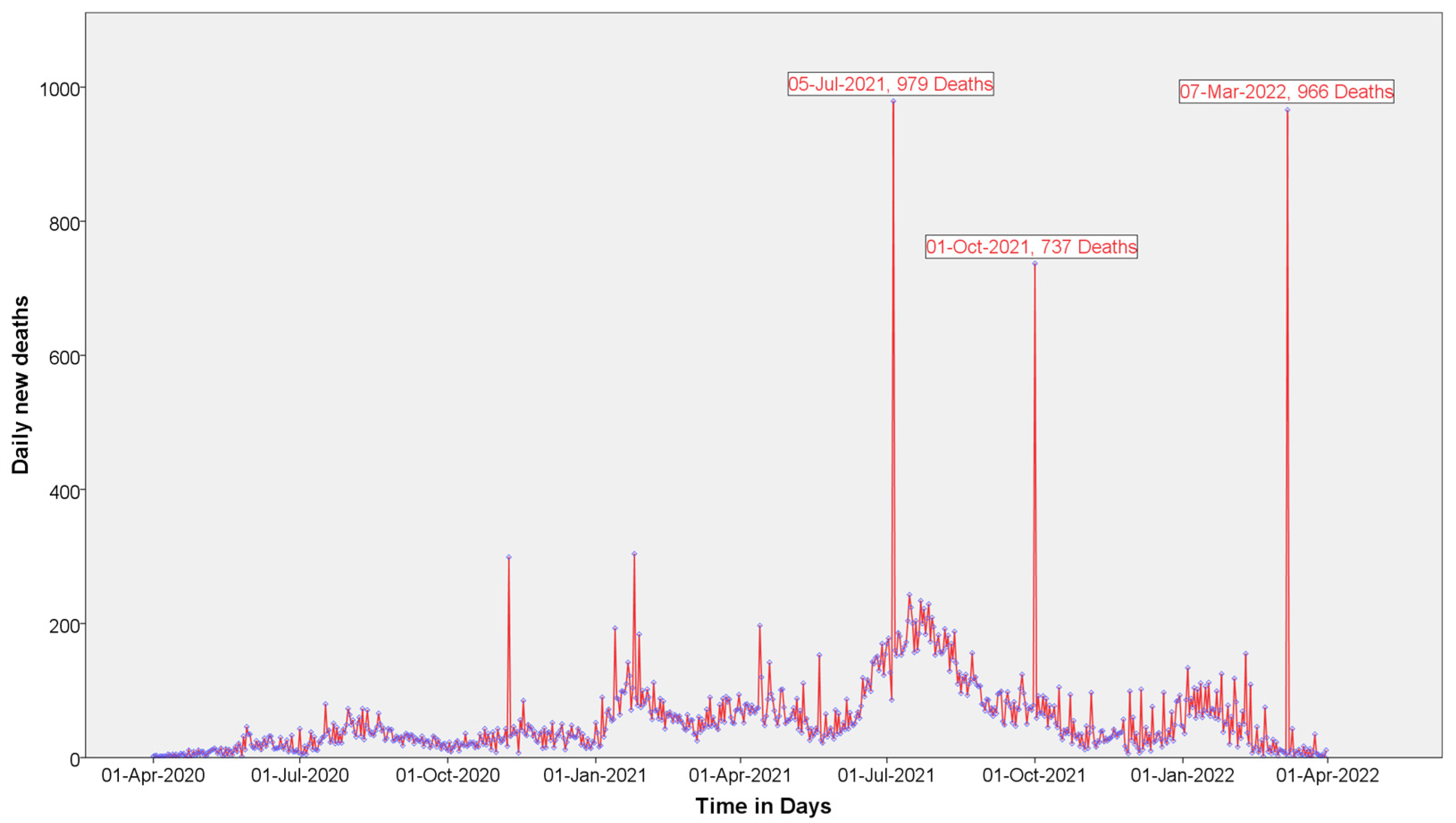
| New deaths | 0 | 61.03 ± 69.1 | 979 | 1 | 46.16 ± 83.59 | 966 |
| New cases | 11 | 2783.5 ± 2423 | 27,596 | 95 | 5724.66 ± 6522.3 | 34,125 |
| Rate of positive cases | 0.004 | 0.041 ± 0.022 | 0.102 | 0.0 | 0.05 ± 0.052 | 0.065 |
| Newly vaccinated | 0 | 26,234.2 ± 47,498.4 | 276,532 | 2915 | 220,514 ± 332,466 | 1,877,713 |
| Number of CVDs | 4655.45 | 4822.25 ± 17.263 | 5231.50 | 4252 | 4656 ± 0.5268 | 4986 |
| Stringency index | 40.14 | 51.71 ± 8.80 | 76.50 | 29 | 40.80 ± 2.192 | 44 |
| GDP per capita/USD | 76,254.42 | 76,321.52 ± 2.35 | 76,985.23 | 77,956 | 76,254 ± 2.589 | 78,962 |
| Number of smokers | 354.2 | 365.5 ± 56.32 | 420.5 | 332.1 | 354.2 ± 9.536 | 386.5 |
| Prevalence of DM | 6.61 | 6.71 ± 0.23 | 6.98 | 6.51 | 6.61 ± 0.2652 | 7.02 |
| Hospitals beds/1000 | 20.04 | 28.25 ± 3.50 | 35.23 | 18.1 | 20.4 ± 0.5623 | 22.6 |
| Population density | 2697.26 | 2725.25 ± 5.62 | 2756.85 | 2568.2 | 2697.25 ± 0.2562 | 2893.2 |
| Inputs | DC | Rank |
|---|---|---|
| Positive rate | 0.9178 | 1st |
| Hospital beds/1000 | 0.8962 | 2nd |
| New cases | 0.8617 | 3rd |
| People vaccinated | 0.8113 | 4th |
| Number of smokers | 0.2505 | 5th |
| GDP per capita/USD | 0.2220 | 6th |
| Number of CVDs | 0.2013 | 7th |
| Population density | 0.1902 | 8th |
| Prevalence of DM | 0.0663 | 9th |
| Stringency Index | 0.0524 | 10th |
| Model | Combination of Inputs | Selected Structure | Training | Verification | ||
|---|---|---|---|---|---|---|
| DC | RMSE | DC | RMSE | |||
| FFNN | Cases, Pos_rate, vaccine, Hosp_bed | Gaussian | 0.8792 | 0.001478 | 0.8586 | 0.001412 |
| ANFIS | Cases, Pos_rate, vaccine, Hosp_bed | 4-6-1 | 0.9146 | 0.000182 | 0.9273 | 0.000125 |
| SVM | Cases, Pos_rate, vaccine, Hosp_bed | RBF | 0.8650 | 0.000210 | 0.8490 | 0.000146 |
| MLR | Cases, Pos_rate, vaccine, Hosp_bed | 4-1 | 0.8021 | 0.000119 | 0.7956 | 0.000192 |
| Ensemble Method | Selected Structure | Calibration | Verification | ||
|---|---|---|---|---|---|
| DC | RMSE | DC | RMSE | ||
| SAE | 3-1 | 0.9446 | 0.000821 | 0.9073 | 0.000245 |
| WAE | 0.243, 0.269, 0.249, 0.22 | 0.9250 | 0.000123 | 0.9190 | 0.000156 |
| ANFIS_E | Gaussian 3 | 0.9292 | 0.001658 | 0.9886 | 0.000012 |
| NNE | 3-6-2 | 0.9286 | 0.000120 | 0.9356 | 0.000132 |
| Ensemble Models | Single Models | Ensemble vs. Single Models | The Difference in Percent (%) | |
|---|---|---|---|---|
| Verification | Training | |||
| NNE | FFNN | NNE vs. FFNN | 5.6% | 4.9% |
| ANFIS | NNE vs. ANFIS | 2.1% | 1.4% | |
| SVM | NNE vs. SVM | 7.1% | 6.4% | |
| MLR | NNE vs. MLR | 13.4% | 12.7% | |
| ANFIS_E | FFNN | ANFIS_E vs. FFNN | 13% | 5% |
| ANFIS | ANFIS_E vs. ANFIS | 6.1% | 1.4% | |
| SVM | ANFIS_E vs. SVM | 13.9% | 6.4% | |
| MLR | ANFIS_E vs. MLR | 19.3% | 12.7% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abegaz, K.H.; Etikan, İ. Artificial Intelligence-Driven Ensemble Model for Predicting Mortality Due to COVID-19 in East Africa. Diagnostics 2022, 12, 2861. https://doi.org/10.3390/diagnostics12112861
Abegaz KH, Etikan İ. Artificial Intelligence-Driven Ensemble Model for Predicting Mortality Due to COVID-19 in East Africa. Diagnostics. 2022; 12(11):2861. https://doi.org/10.3390/diagnostics12112861
Chicago/Turabian StyleAbegaz, Kedir Hussein, and İlker Etikan. 2022. "Artificial Intelligence-Driven Ensemble Model for Predicting Mortality Due to COVID-19 in East Africa" Diagnostics 12, no. 11: 2861. https://doi.org/10.3390/diagnostics12112861
APA StyleAbegaz, K. H., & Etikan, İ. (2022). Artificial Intelligence-Driven Ensemble Model for Predicting Mortality Due to COVID-19 in East Africa. Diagnostics, 12(11), 2861. https://doi.org/10.3390/diagnostics12112861







