Advancing Brain Metastases Detection in T1-Weighted Contrast-Enhanced 3D MRI Using Noisy Student-Based Training
Abstract
:1. Introduction
2. Materials and Methods
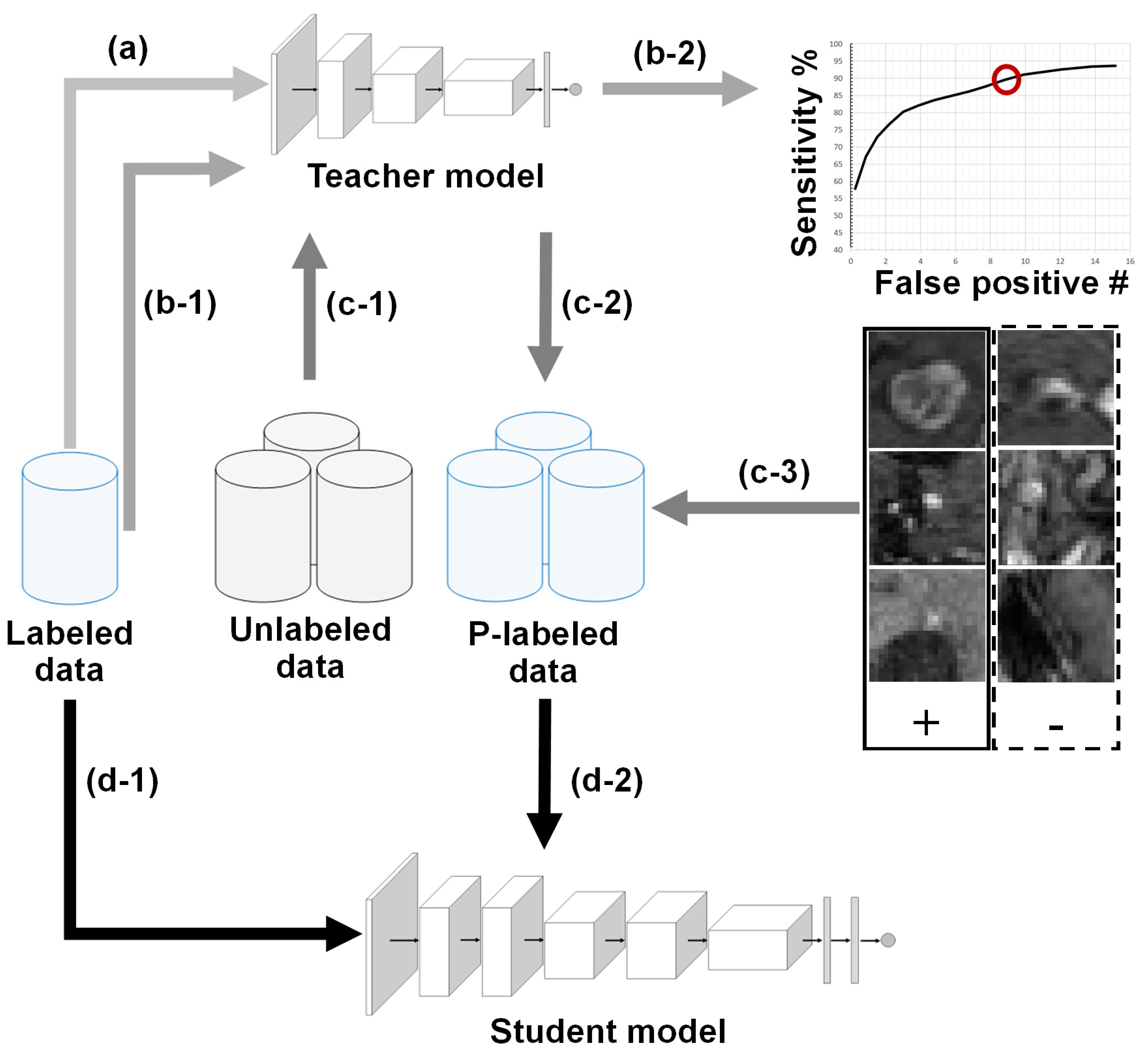
2.1. BM Detection Framework Overview
2.2. Teacher–Student Models and Noising Mechanisms
2.3. Technical Contribution: Sensitivity-Based NS Algorithm
2.4. Database
2.5. Validation Metric
3. Results
3.1. Validation Study
3.2. Experiments with System Parameters
3.2.1. Teacher Model Sensitivity
3.2.2. Unlabeled Data Weights (λ)
3.2.3. Student Model Iterations
3.2.4. Labeled-Data Utilization
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lester, S.C.; Taksler, G.B.; Kuremsky, J.G.; Lucas, J.T., Jr.; Ayala-Peacock, D.N.; Randolph, D.M.; Bourland, J.D.; Laxton, A.W.; Tatter, S.B.; Chan, M.D. Clinical and Economic Outcomes of Patients with Brain Metastases Based on Symptoms: An Argument for Routine Brain Screening of Those Treated with Upfront Radiosurgery. Cancer 2014, 120, 433–441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tong, E.; McCullagh, K.L.; Iv, M. Advanced Imaging of Brain Metastases: From Augmenting Visualization and Improving Diagnosis to Evaluating Treatment Response. Front. Neurol. 2020, 11, 270. [Google Scholar] [CrossRef] [PubMed]
- Charron, O.; Lallement, A.; Jarnet, D.; Noblet, V.; Clavier, J.-B.; Meyer, P. Automatic Detection and Segmentation of Brain Metastases on Multimodal MR Images with a Deep Convolutional Neural Network. Comput. Biol. Med. 2018, 95, 43–54. [Google Scholar] [CrossRef] [PubMed]
- Dikici, E.; Ryu, J.L.; Demirer, M.; Bigelow, M.; White, R.D.; Slone, W.; Erdal, B.S.; Prevedello, L.M. Automated Brain Metastases Detection Framework for T1-Weighted Contrast-Enhanced 3D MRI. IEEE J. Biomed. Health Inform. 2020, 24, 2883–2893. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Stojadinovic, S.; Hrycushko, B.; Wardak, Z.; Lau, S.; Lu, W.; Yan, Y.; Jiang, S.B.; Zhen, X.; Timmerman, R.; et al. A Deep Convolutional Neural Network-Based Automatic Delineation Strategy for Multiple Brain Metastases Stereotactic Radiosurgery. PLoS ONE 2017, 12, e0185844. [Google Scholar] [CrossRef] [Green Version]
- Grovik, E.; Yi, D.; Iv, M.; Tong, E.; Rubin, D.; Zaharchuk, G. Deep Learning Enables Automatic Detection and Segmentation of Brain Metastases on Multisequence MRI. J. Magn. Reson. Imaging 2019, 51, 175–182. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Vassantachart, A.; Jason, C.Y.; Yu, C.; Ruan, D.; Sheng, K.; Lao, Y.; Shen, Z.L.; Balik, S.; Bian, S.; et al. Automatic Detection and Segmentation of Multiple Brain Metastases on Magnetic Resonance Image Using Asymmetric UNet Architecture. Phys. Med. Biol. 2021, 66, 15003. [Google Scholar] [CrossRef]
- Bousabarah, K.; Ruge, M.; Brand, J.-S.; Hoevels, M.; Rueß, D.; Borggrefe, J.; Große Hokamp, N.; Visser-Vandewalle, V.; Maintz, D.; Treuer, H.; et al. Deep Convolutional Neural Networks for Automated Segmentation of Brain Metastases Trained on Clinical Data. Radiat. Oncol. 2020, 15, 1–9. [Google Scholar] [CrossRef]
- Cho, S.J.; Sunwoo, L.; Baik, S.H.; Bae, Y.J.; Choi, B.S.; Kim, J.H. Brain Metastasis Detection Using Machine Learning: A Systematic Review and Meta-Analysis. Neuro-Oncol. 2021, 23, 214–225. [Google Scholar] [CrossRef]
- Mongan, J.; Moy, L.; Kahn, C.E., Jr. Checklist for Artificial Intelligence in Medical Imaging (CLAIM): A Guide for Authors and Reviewers. Radiol. Artif. Intell. 2020, 2, e200029. [Google Scholar] [CrossRef] [Green Version]
- Whiting, P.F.; Rutjes, A.W.S.; Westwood, M.E.; Mallett, S.; Deeks, J.J.; Reitsma, J.B.; Leeflang, M.M.G.; Sterne, J.A.C.; Bossuyt, P.M.M. QUADAS-2: A Revised Tool for the Quality Assessment of Diagnostic Accuracy Studies. Ann. Intern. Med. 2011, 155, 529–536. [Google Scholar] [CrossRef] [PubMed]
- Xie, Q.; Luong, M.-T.; Hovy, E.; Le, Q. V Self-Training with Noisy Student Improves Imagenet Classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10687–10698. [Google Scholar]
- Ma, J.; Zhang, Y.; Gu, S.; Zhang, Y.; Zhu, C.; Wang, Q.; Liu, X.; An, X.; Ge, C.; Cao, S.; et al. AbdomenCT-1K: Is Abdominal Organ Segmentation a Solved Problem? arXiv 2020, arXiv:2010.14808. [Google Scholar] [CrossRef] [PubMed]
- Isensee, F.; Jäger, P.F.; Kohl, S.A.A.; Petersen, J.; Maier-Hein, K.H. Automated Design of Deep Learning Methods for Biomedical Image Segmentation. arXiv 2019, arXiv:1904.08128. [Google Scholar]
- Rajan, D.; Thiagarajan, J.J.; Karargyris, A.; Kashyap, S. Self-Training with Improved Regularization for Sample-Efficient Chest X-ray Classification. In Medical Imaging 2021: Computer-Aided Diagnosis, Proceedings of the SPIE Medical Imaging 2021, San Diego, CA, USA, 14–18 February 2021; SPIE: Cergy, France, 2021; Volume 11597, p. 115971S. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. Mixup: Beyond Empirical Risk Minimization. arXiv 2017, arXiv:1710.09412. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Shak, K.; Al-Shabi, M.; Liew, A.; Lan, B.L.; Chan, W.Y.; Ng, K.H.; Tan, M. A New Semi-Supervised Self-Training Method for Lung Cancer Prediction. arXiv 2020, arXiv:2012.09472. [Google Scholar]
- Li, Y.; Fan, Y. DeepSEED: 3D Squeeze-and-Excitation Encoder-Decoder Convolutional Neural Networks for Pulmonary Nodule Detection. In Proceedings of the 2020 IEEE 17th International Symposium on Biomedical Imaging (ISBI), Iowa City, IA, USA, 3–7 April 2020; pp. 1866–1869. [Google Scholar]
- Armato III, S.G.; McLennan, G.; Bidaut, L.; McNitt-Gray, M.F.; Meyer, C.R.; Reeves, A.P.; Zhao, B.; Aberle, D.R.; Henschke, C.I.; Hoffman, E.A.; et al. The Lung Image Database Consortium (LIDC) and Image Database Resource Initiative (IDRI): A Completed Reference Database of Lung Nodules on CT Scans. Med. Phys. 2011, 38, 915–931. [Google Scholar] [CrossRef] [PubMed]
- Team, N.L.S.T.R. The National Lung Screening Trial: Overview and Study Design. Radiology 2011, 258, 243–253. [Google Scholar]
- Lin, E.; Kuo, W.; Yuh, E. Noisy Student Learning for Cross-Institution Brain Hemorrhage Detection. arXiv 2021, arXiv:2105.00582. [Google Scholar]
- Kuo, W.; Häne, C.; Yuh, E.; Mukherjee, P.; Malik, J. PatchFCN for Intracranial Hemorrhage Detection. arXiv 2018, arXiv:1806.03265. [Google Scholar]
- Chilamkurthy, S.; Ghosh, R.; Tanamala, S.; Biviji, M.; Campeau, N.G.; Venugopal, V.K.; Mahajan, V.; Rao, P.; Warier, P. Development and Validation of Deep Learning Algorithms for Detection of Critical Findings in Head CT Scans. arXiv 2018, arXiv:1803.05854. [Google Scholar]
- Kim, G.; Park, S.; Oh, Y.; Seo, J.B.; Lee, S.M.; Kim, J.H.; Moon, S.; Lim, J.-K.; Ye, J.C. Severity Quantification and Lesion Localization of COVID-19 on CXR Using Vision Transformer. arXiv 2021, arXiv:2103.07062. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Irvin, J.; Rajpurkar, P.; Ko, M.; Yu, Y.; Ciurea-Ilcus, S.; Chute, C.; Marklund, H.; Haghgoo, B.; Ball, R.; Shpanskaya, K.; et al. Chexpert: A Large Chest Radiograph Dataset with Uncertainty Labels and Expert Comparison. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 590–597. [Google Scholar]
- Shiraishi, J.; Katsuragawa, S.; Ikezoe, J.; Matsumoto, T.; Kobayashi, T.; Komatsu, K.; Matsui, M.; Fujita, H.; Kodera, Y.; Doi, K. Development of a Digital Image Database for Chest Radiographs with and without a Lung Nodule: Receiver Operating Characteristic Analysis of Radiologists’ Detection of Pulmonary Nodules. Am. J. Roentgenol. 2000, 174, 71–74. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Xia, Q.; Hu, Z.; Yan, Z.; Li, Z.; Wu, Y.; Huang, N.; Gao, Y.; Metaxas, D.; Zhang, S. Few-Shot Learning by a Cascaded Framework with Shape-Constrained Pseudo Label Assessment for Whole Heart Segmentation. IEEE Trans. Med. Imaging 2021, 40, 2629–2641. [Google Scholar] [CrossRef]
- Milletari, F.; Navab, N.; Ahmadi, S.-A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Lindeberg, T. Scale Selection Properties of Generalized Scale-Space Interest Point Detectors. J. Math. Imaging Vis. 2013, 46, 177–210. [Google Scholar] [CrossRef] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland; pp. 234–241. [Google Scholar]
- Zhou, Z.; Sanders, J.W.; Johnson, J.M.; Gule-Monroe, M.K.; Chen, M.M.; Briere, T.M.; Wang, Y.; Son, J.B.; Pagel, M.D.; Li, J.; et al. Computer-Aided Detection of Brain Metastases in T1-Weighted MRI for Stereotactic Radiosurgery Using Deep Learning Single-Shot Detectors. Radiology 2020, 295, 407–415. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representation, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Louis, D.N.; Perry, A.; Reifenberger, G.; Von Deimling, A.; Figarella-Branger, D.; Cavenee, W.K.; Ohgaki, H.; Wiestler, O.D.; Kleihues, P.; Ellison, D.W. The 2016 World Health Organization Classification of Tumors of the Central Nervous System: A Summary. Acta Neuropathol. 2016, 131, 803–820. [Google Scholar] [CrossRef] [Green Version]
- Mutasa, S.; Sun, S.; Ha, R. Understanding Artificial Intelligence Based Radiology Studies: What Is Overfitting? Clin. Imaging 2020, 65, 96–99. [Google Scholar] [CrossRef]
- Huang, G.; Sun, Y.; Liu, Z.; Sedra, D.; Weinberger, K.Q. Deep Networks with Stochastic Depth. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 646–661. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 6105–6114. [Google Scholar]
- Dikici, E.; Bigelow, M.; White, R.D.; Erdal, B.S.; Prevedello, L.M. Constrained Generative Adversarial Network Ensembles for Sharable Synthetic Medical Images. J. Med. Imaging 2021, 8, 24004. [Google Scholar] [CrossRef]
- Park, S.; Kwak, N. Analysis on the Dropout Effect in Convolutional Neural Networks. In Proceedings of the Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; pp. 189–204. [Google Scholar]
- Cohen, R.Y.; Sodickson, A.D. An Orchestration Platform That Puts Radiologists in the Driver’s Seat of AI Innovation: A Methodological Approach. arXiv 2021, arXiv:2107.04409. [Google Scholar]
- Dikici, E.; Bigelow, M.; Prevedello, L.M.; White, R.D.; Erdal, B.S. Integrating AI into Radiology Workflow: Levels of Research, Production, and Feedback Maturity. J. Med. Imaging 2020, 7, 16502. [Google Scholar] [CrossRef] [PubMed] [Green Version]









| Labeled Data | Unlabeled Data | |
|---|---|---|
| Exam count | 217 | 1247 |
| Patient count | 158 | 867 |
| Acquisition date from | January 2015 | November 2016 |
| Acquisition date to | February 2016 | December 2019 |
| Mean patient age | 62 | 56 |
| Sex ratio | 0.89 | 1.09 |
| Detection Sensitivity | Teacher | Student ts = 90% | Student ts = 85% | Student ts = 80% |
|---|---|---|---|---|
| 80% | 2.94 | 2.91 | 3.18 | 3.82 |
| 85% | 5.74 | 4.82 | 5.41 | 6.37 |
| 90% | 9.23 | 8.44 | 9.97 | 10.84 |
| Detection Sensitivity | Teacher | Student λ = 1.0 | Student λ = 0.8 | Student λ = 0.6 |
|---|---|---|---|---|
| 80% | 2.94 | 2.91 | 3.19 | 2.97 |
| 85% | 5.74 | 4.82 | 5.36 | 5.55 |
| 90% | 9.23 | 8.44 | 8.71 | 9.12 |
| Detection Sensitivity | Teacher | Student Iter = 1 | Student Iter = 2 | Student Iter = 3 |
|---|---|---|---|---|
| 80% | 2.94 | 2.91 | 2.89 | 3.03 |
| 85% | 5.74 | 4.82 | 5.20 | 5.09 |
| 90% | 9.23 | 8.44 | 8.35 | 8.46 |
| Detection Sensitivity | Teacher LD:100% | Student LD:100% | Teacher LD:75% | Student LD:75% | Teacher LD:50% | Student LD:50% |
|---|---|---|---|---|---|---|
| 80% | 2.94 | 2.91 | 3.74 | 3.73 | 5.36 | 4.46 |
| 85% | 5.74 | 4.82 | 6.60 | 6.15 | 8.05 | 7.65 |
| 90% | 9.23 | 8.44 | 12.19 | 10.79 | 13.89 | 12.37 |
| Study | Patient # | Network | Acq. | BM Volume (mm3) | Validation Type | Sens % | AFP |
|---|---|---|---|---|---|---|---|
| Charron et al. [3] | 182-labeled | DeepMedic | Multi seq. a | Mean: 2400 Median: 500 | Fixed train/test | 93 | 7.8 |
| Liu et al. [5] | 490-labeled | En-DeepMedic | Multi seq. b | Mean: 672 | 5-fold CV | NA | NA |
| Bousabarah et al. [8] | 509-labeled | U-Net | Multi seq. c | Mean: 1920 Median: 470 | Fixed train/test | 77–82 | <1 |
| Grøvik et al. [6] | 156-labeled | GoogleNet | Multi seq. d | NA | Fixed train/test | 83 | 8.3 |
| Cao et al. [7] | 195-labeled | Asym-UNet | T1cMRI | NA g | Fixed train/test | 81–100 k | NA |
| Zhou et al. [33] | 266-labeled | Custom + SSD | T1c MRI e | NA h | Fixed train/test | 81 | 6 |
| Dikici et al. [4] | 158-labeled i | CropNet | T1c MRI | Mean: 160 Median: 50 | 5-fold CV | 90 | 9.12 |
| This study | 158-labeled 867-unlabeled | CropNet+NS | T1c MRI f | Mean: 160 j Median: 50 | 2-fold CV | 90 | 8.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dikici, E.; Nguyen, X.V.; Bigelow, M.; Ryu, J.L.; Prevedello, L.M. Advancing Brain Metastases Detection in T1-Weighted Contrast-Enhanced 3D MRI Using Noisy Student-Based Training. Diagnostics 2022, 12, 2023. https://doi.org/10.3390/diagnostics12082023
Dikici E, Nguyen XV, Bigelow M, Ryu JL, Prevedello LM. Advancing Brain Metastases Detection in T1-Weighted Contrast-Enhanced 3D MRI Using Noisy Student-Based Training. Diagnostics. 2022; 12(8):2023. https://doi.org/10.3390/diagnostics12082023
Chicago/Turabian StyleDikici, Engin, Xuan V. Nguyen, Matthew Bigelow, John L. Ryu, and Luciano M. Prevedello. 2022. "Advancing Brain Metastases Detection in T1-Weighted Contrast-Enhanced 3D MRI Using Noisy Student-Based Training" Diagnostics 12, no. 8: 2023. https://doi.org/10.3390/diagnostics12082023
APA StyleDikici, E., Nguyen, X. V., Bigelow, M., Ryu, J. L., & Prevedello, L. M. (2022). Advancing Brain Metastases Detection in T1-Weighted Contrast-Enhanced 3D MRI Using Noisy Student-Based Training. Diagnostics, 12(8), 2023. https://doi.org/10.3390/diagnostics12082023







