A Deep Learning Framework with Explainability for the Prediction of Lateral Locoregional Recurrences in Rectal Cancer Patients with Suspicious Lateral Lymph Nodes
Abstract
:1. Introduction
2. Materials and Methods
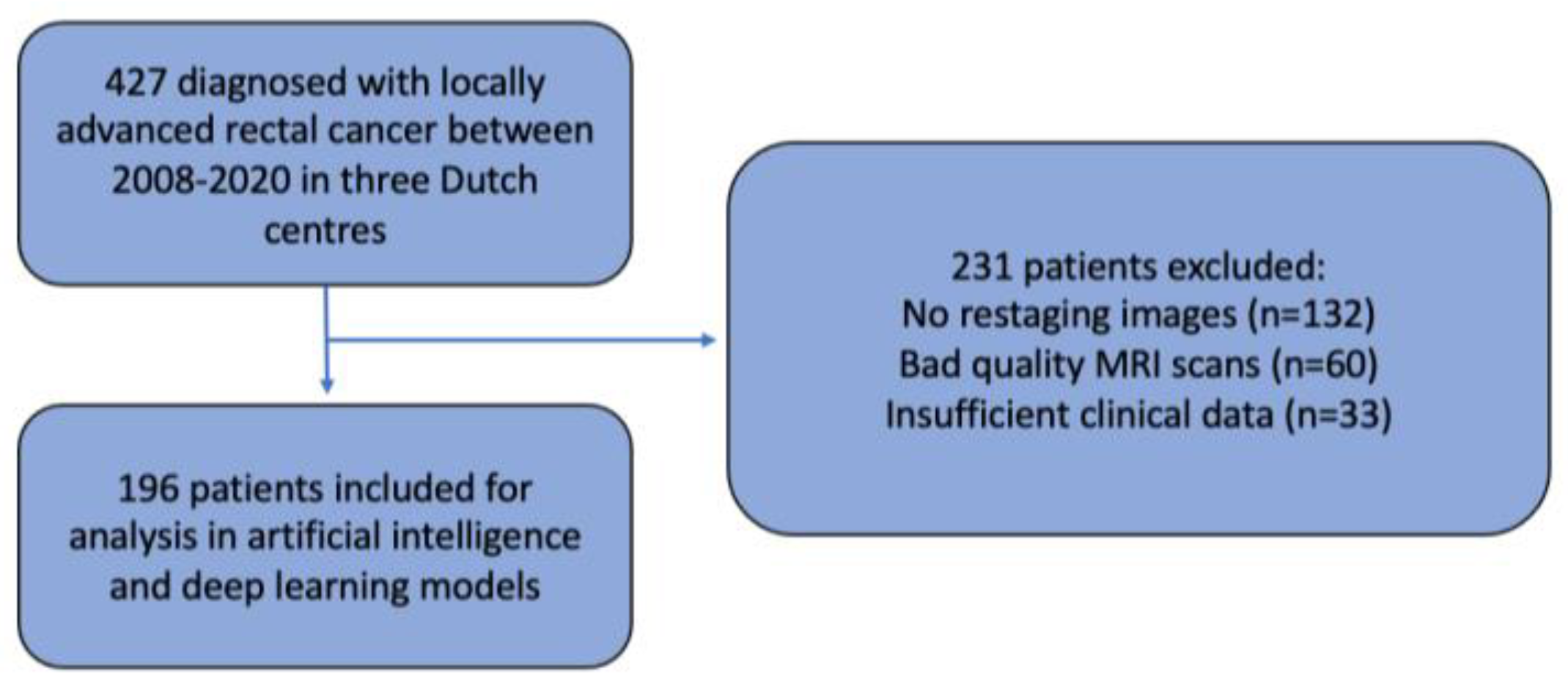
2.1. Study Population and Design
2.2. Initial MRI Re-Review
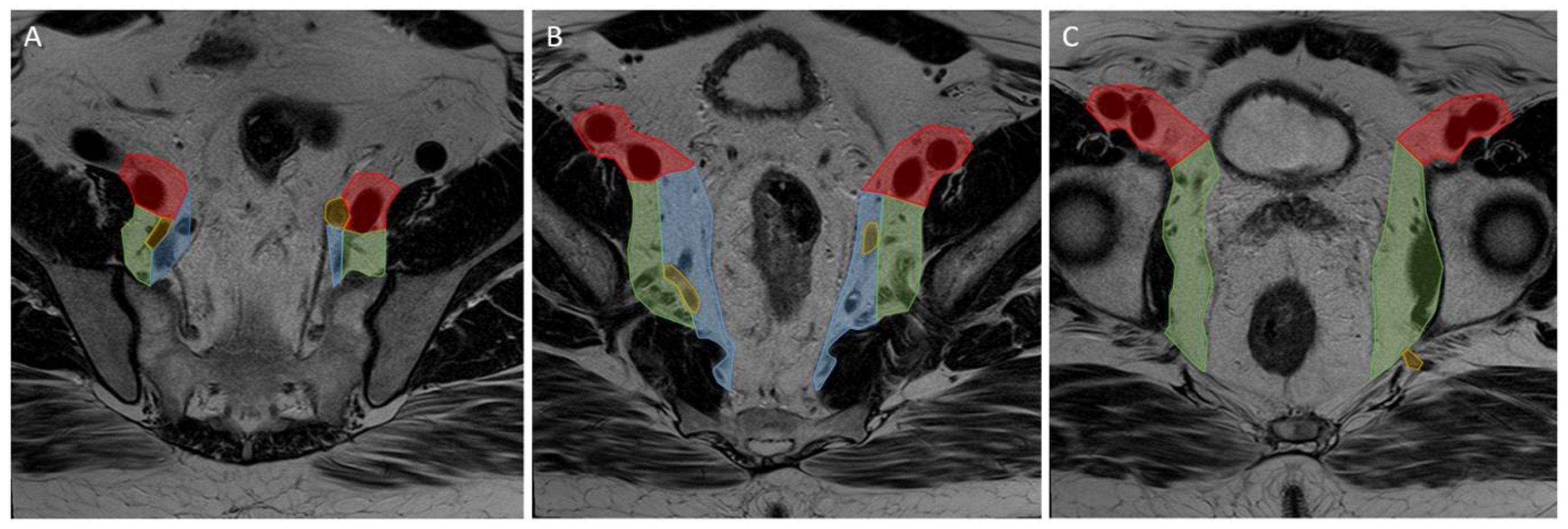
2.3. Image Segmentation
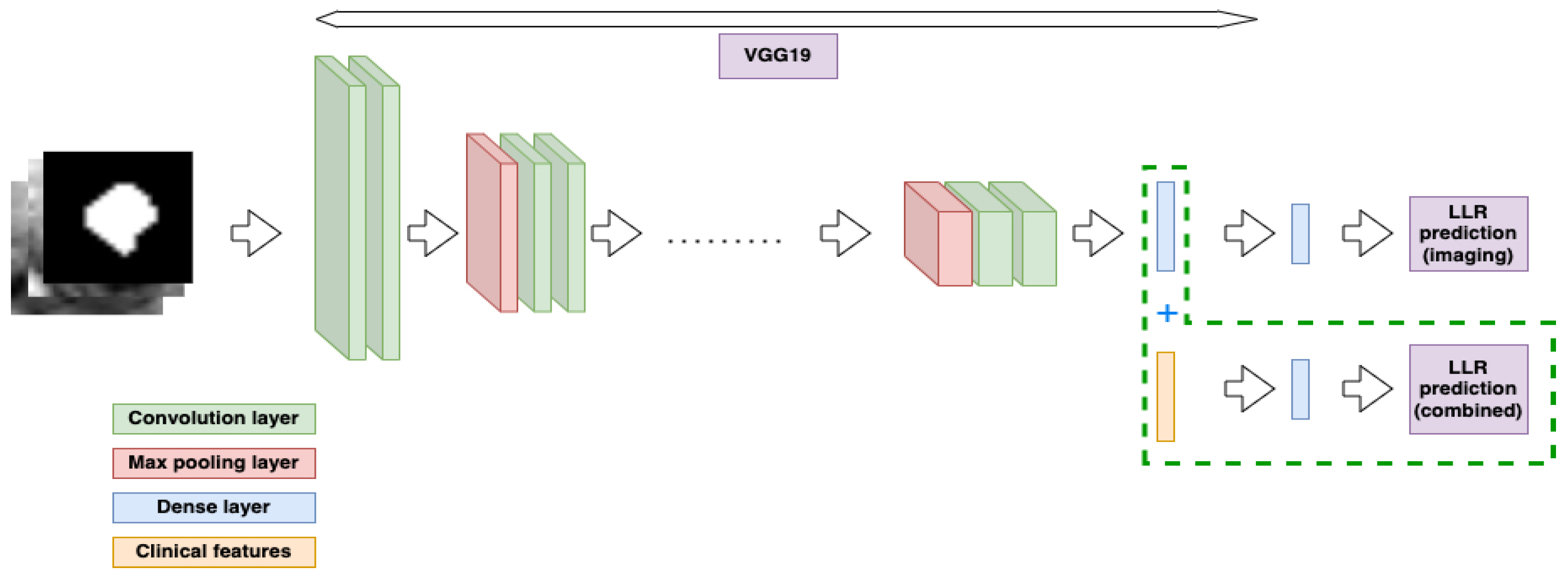
2.4. Feature Extraction and Classification
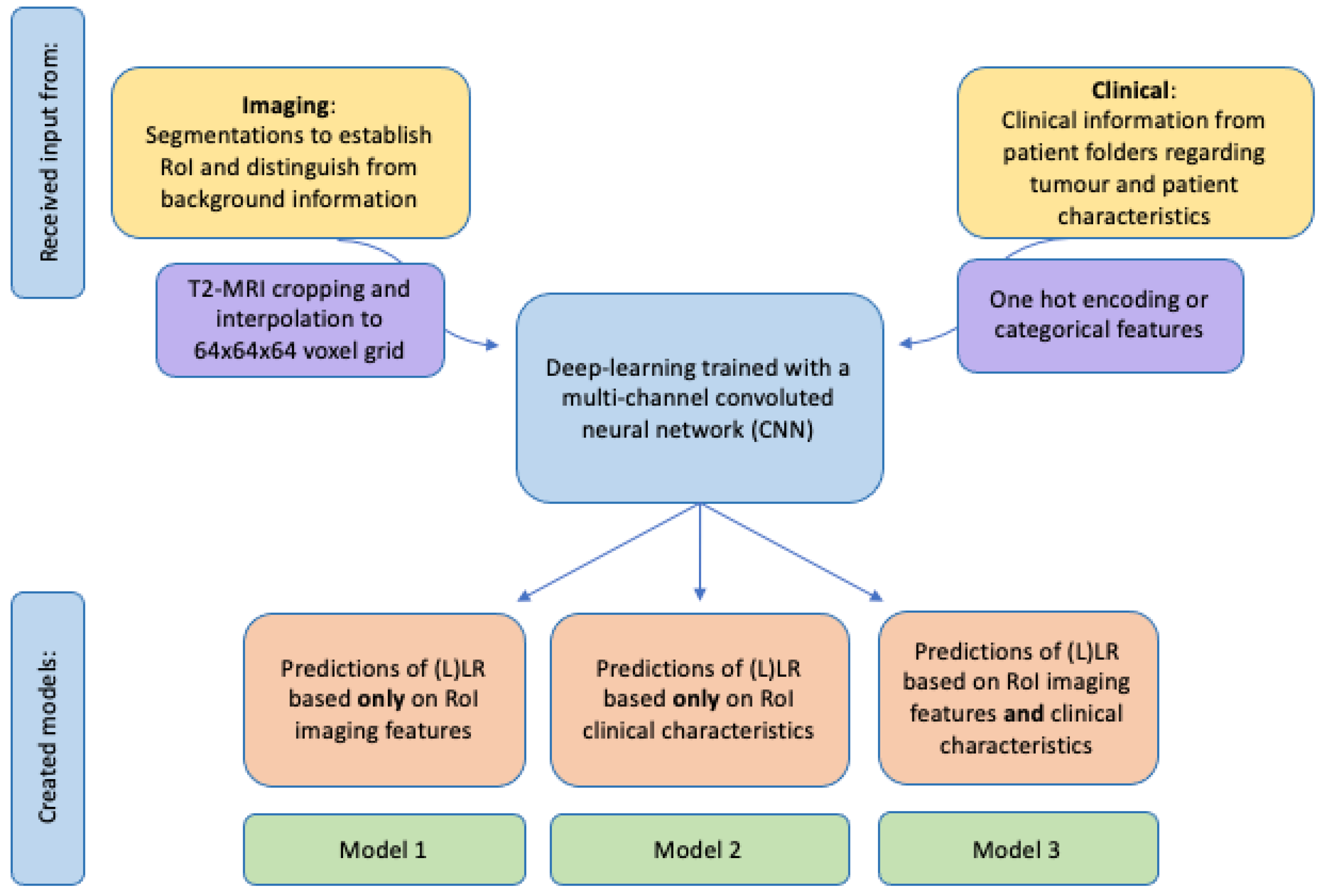
2.5. Models
2.6. Statistical Analyses
3. Results
3.1. Patient Characteristics
3.2. Deep Learning Model and Oncological Outcomes
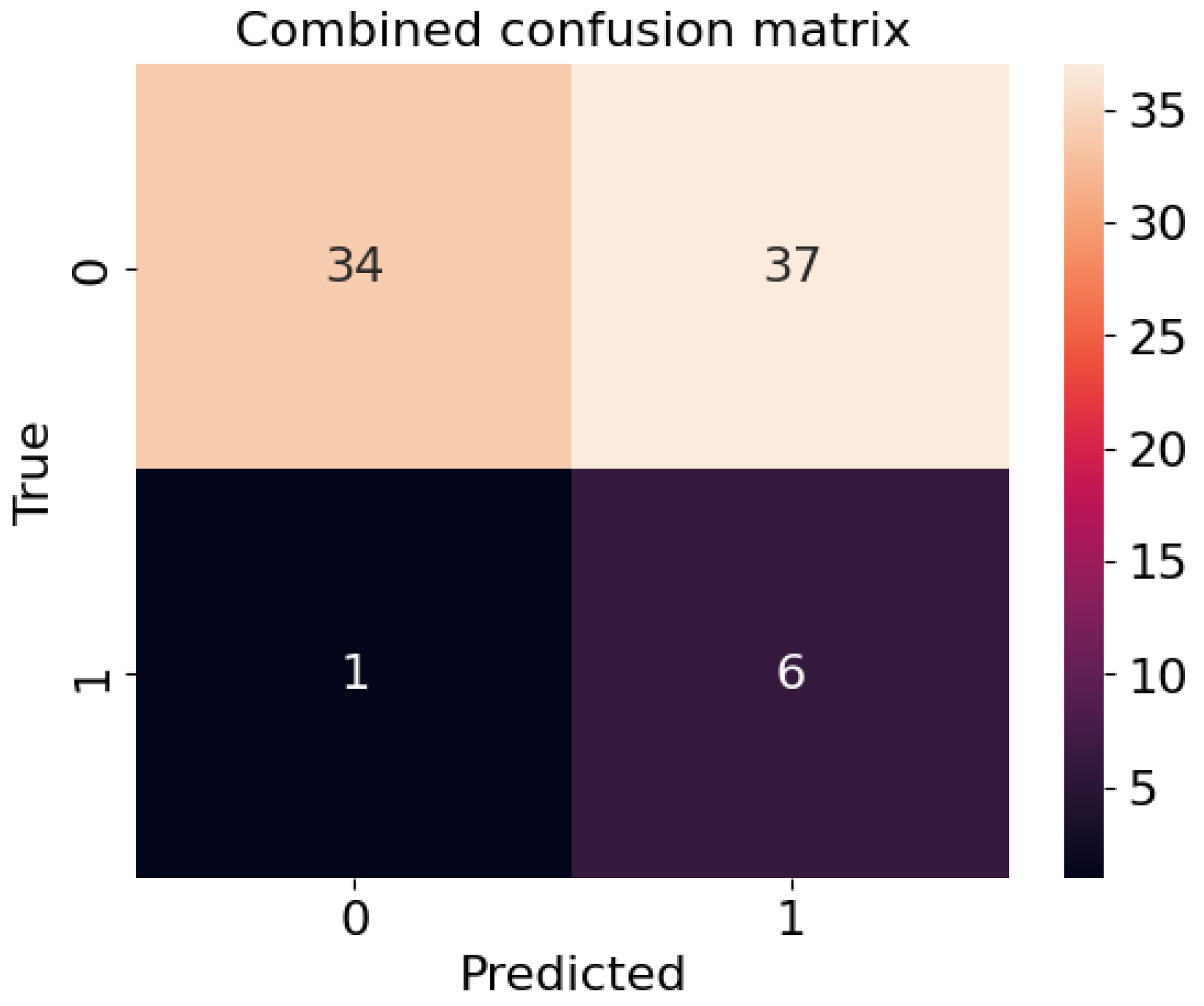
3.3. Sensitivity and Specificity
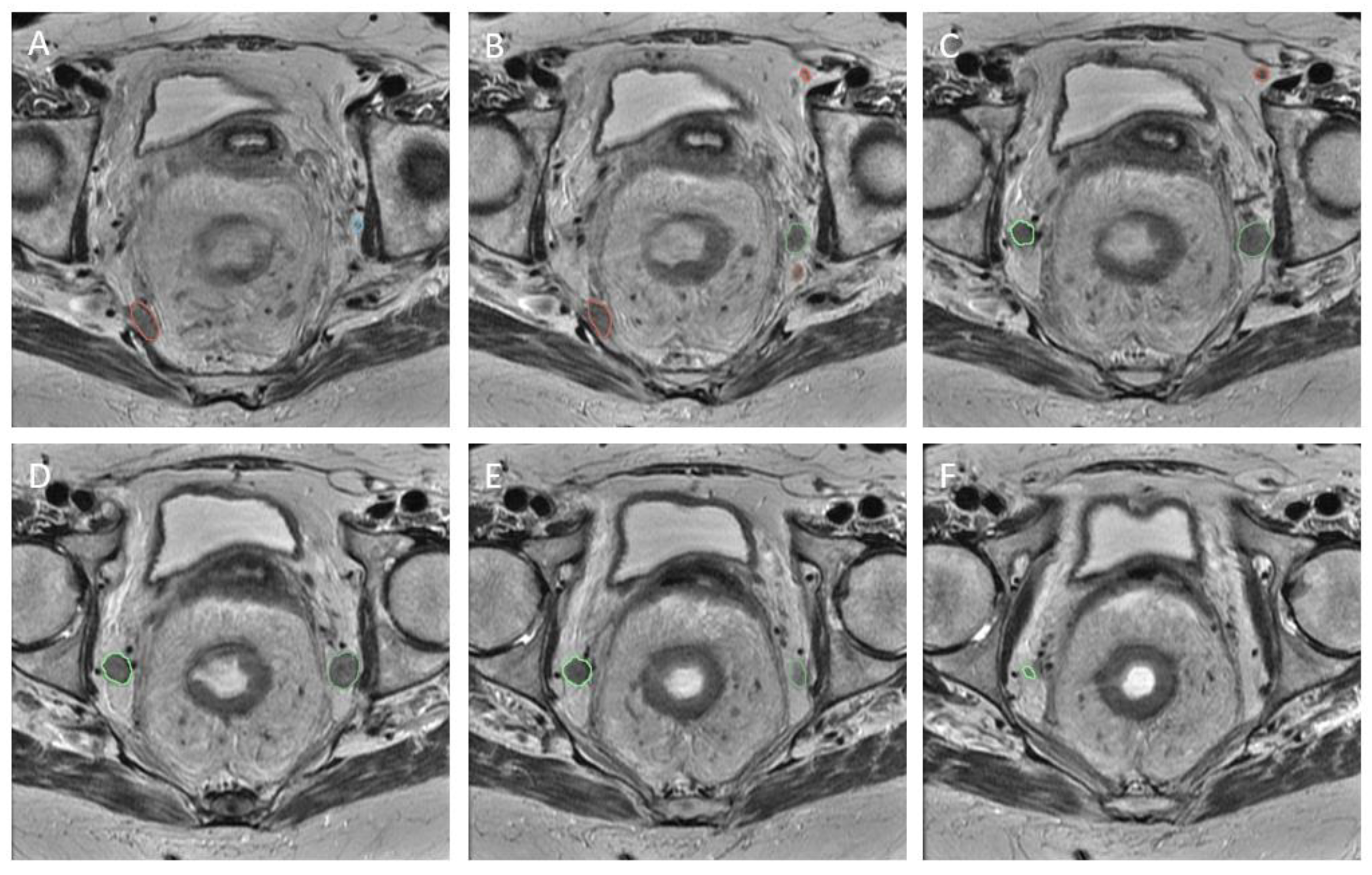
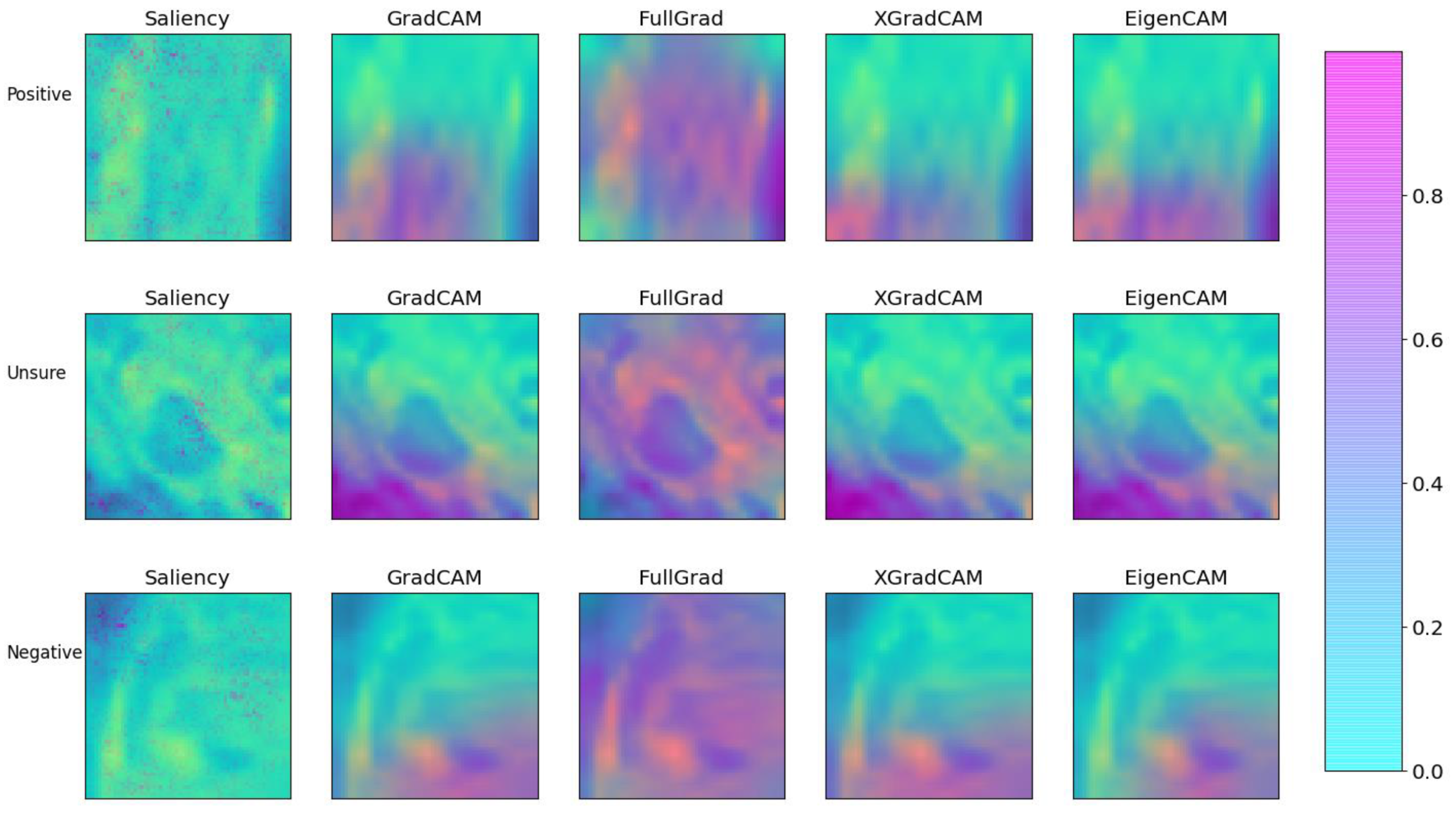
3.4. Explainability
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| MRI | SA Cut-Off Value | Sensitivity | Specificity | PPV | NPV |
|---|---|---|---|---|---|
| A: local recurrence | |||||
| Primary | 5 mm | 49.0% | 60.4% | 14.0% | 90.0% |
| Primary | 6 mm | 40.8% | 78.0% | 19.6% | 90.9% |
| Primary | 7 mm | 32.7% | 86.6% | 24.2% | 90.8% |
| Restaging | 4 mm | 55.6% | 63.7% | 18.3% | 90.7% |
| Restaging | 5 mm | 47.2% | 80.0% | 25.8% | 91.2% |
| Restaging | 6 mm | 36.1% | 90.2% | 35.1% | 90.6% |
| B: lateral local recurrence | |||||
| Primary | 5 mm | 60.9% | 60.5% | 8.1% | 96.4% |
| Primary | 6 mm | 56.5% | 77.7% | 12.7% | 96.9% |
| Primary | 7 mm | 43.5% | 86.0% | 15.2% | 96.4% |
| Restaging | 4 mm | 76.5% | 63.6% | 11.9% | 97.7% |
| Restaging | 5 mm | 64.7% | 79.2% | 16.7% | 97.2% |
| Restaging | 6 mm | 52.9% | 89.4% | 24.3% | 96.7% |
Appendix B
References
- Knol, J.; Keller, D.S. Total Mesorectal Excision Technique—Past, Present, and Future. In Clinics in Colon and Rectal Surgery; Georg Thieme Verlag KG: New York, NY, USA, 2020; Volume 33, pp. 134–143. [Google Scholar] [CrossRef]
- Haanappel, A.; Kroon, H.M.; Schaap, D.P.; Bedrikovetski, S.; Dudi-Venkata, N.N.; Lee, H.X.; Thomas, M.L.; Liu, J.; van der Valk, M.J.M.; Rutten, H.J.T.; et al. Lateral Lymph Node Metastases in Locally Advanced Low Rectal Cancers May Not Be Treated Effectively With Neoadjuvant (Chemo)Radiotherapy Only. Front. Oncol. 2019, 9, 1355. [Google Scholar] [CrossRef] [PubMed]
- Iversen, H.; Martling, A.; Johansson, H.; Nilsson, P.J.; Holm, T. Pelvic local recurrence from colorectal cancer: Surgical challenge with changing preconditions. Color. Dis. Off. J. Assoc. Coloproctology Great Br. Irel. 2018, 20, 399–406. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Shiomi, A. Lateral lymph node dissection in advanced low rectal cancer treatment. Int. J. Colorectal Dis. 2021, 36, 2361–2371. [Google Scholar] [CrossRef]
- Williamson, J.S.; Quyn, A.J.; Sagar, P.M. Rectal cancer lateral pelvic sidewall lymph nodes: A review of controversies and management. Br. J. Surg. 2020, 107, 1562–1569. [Google Scholar] [CrossRef] [PubMed]
- Sluckin, T.C.; Hazen, S.J.A.; Kusters, M. From “East vs West” towards international multidisciplinary collaboration: An appraisal of lateral lymph nodes in rectal cancer. Ann. Gastroenterol. Surg. 2021, 5, 731–737. [Google Scholar] [CrossRef] [PubMed]
- Ogura, A.; Konishi, T.; Cunningham, C.; Garcia-Aguilar, J.; Iversen, H.; Toda, S.; Lee, I.K.; Lee, H.X.; Uehara, K.; Lee, P.; et al. Neoadjuvant (Chemo)radiotherapy With Total Mesorectal Excision Only Is Not Sufficient to Prevent Lateral Local Recurrence in Enlarged Nodes: Results of the Multicenter Lateral Node Study of Patients With Low cT3/4 Rectal Cancer. J. Clin. Oncol. Off. J. Am. Soc. Clin. Oncol. 2019, 37, 33–43. [Google Scholar] [CrossRef]
- Ogura, A.; Konishi, T.; Beets, G.L.; Cunningham, C.; Garcia-Aguilar, J.; Iversen, H.; Toda, S.; Lee, I.K.; Lee, H.X.; Uehara, K.; et al. Lateral Nodal Features on Restaging Magnetic Resonance Imaging Associated With Lateral Local Recurrence in Low Rectal Cancer After Neoadjuvant Chemoradiotherapy or Radiotherapy. JAMA Surg. 2019, 154, e192172. [Google Scholar] [CrossRef]
- Akiyoshi, T.; Matsueda, K.; Hiratsuka, M.; Unno, T.; Nagata, J.; Nagasaki, T.; Konishi, T.; Fujimoto, Y.; Nagayama, S.; Fukunaga, Y.; et al. Indications for Lateral Pelvic Lymph Node Dissection Based on Magnetic Resonance Imaging Before and After Preoperative Chemoradiotherapy in Patients with Advanced Low-Rectal Cancer. Ann. Surg. Oncol. 2015, 22, S614–S620. [Google Scholar] [CrossRef]
- Malakorn, S.; Yang, Y.; Bednarski, B.K.; Kaur, H.; You, Y.N.; Holliday, E.B.; Dasari, A.; Skibber, J.M.; Rodriguez-Bigas, M.A.; Chang, G.J. Who Should Get Lateral Pelvic Lymph Node Dissection After Neoadjuvant Chemoradiation? Dis. Colon. Rectum. 2019, 62, 1158–1166. [Google Scholar] [CrossRef]
- Sluckin, T.C.; Hazen, S.J.A.; Horsthuis, K.; Lambregts, D.M.J.; Beets-Tan, R.G.H.; Tanis, P.J.; Kusters, M. Significant improvement after training in the assessment of lateral compartments and short-axis measurements of lateral lymph nodes in rectal cancer. Eur. Radiol. 2022, 33, 483–492. [Google Scholar] [CrossRef]
- Grimm, P.; Loft, M.K.; Dam, C.; Pedersen, M.R.V.; Timm, S.; Rafaelsen, S.R. Intra- and Interobserver Variability in Magnetic Resonance Imaging Measurements in Rectal Cancer Patients. Cancers 2021, 13, 5120. [Google Scholar] [CrossRef] [PubMed]
- Cattell, R.; Ying, J.; Lei, L.; Ding, J.; Chen, S.; Serrano Sosa, M.; Huang, C. Preoperative prediction of lymph node metastasis using deep learning-based features. Vis. Comput. Ind. Biomed. Art 2022, 5, 8. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Wang, S.; Zhang, S.; Wang, M.; Ding, Y.; Fang, J.; Wu, Q.; Qian, W.; Liu, Z.; Sun, K.; et al. Development of a Deep Learning Model to Identify Lymph Node Metastasis on Magnetic Resonance Imaging in Patients With Cervical Cancer. JAMA Netw. Open 2020, 3, e2011625. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Xie, P.; Wang, M.; Li, W.; Pickhardt, P.J.; Xia, W.; Xiong, F.; Zhang, R.; Xie, Y.; Jian, J.; et al. Deep learning-based fully automated detection and segmentation of lymph nodes on multiparametric-mri for rectal cancer: A multicentre study. EBioMedicine 2020, 56, 102780. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Yao, Z.; Huang, Y.; Yu, Y.; Wang, Y.; Liu, Y.; Mao, R.; Li, F.; Xiao, Y.; Wang, Y.; et al. Deep learning radiomics can predict axillary lymph node status in early-stage breast cancer. Nat. Commun. 2020, 11, 1236. [Google Scholar] [CrossRef]
- Sluckin, T.C.; Rooker, Y.F.L.; Kol, S.Q.; Hazen, S.J.A.; Tuynman, J.B.; Stoker, J.; Tanis, P.J.; Horsthuis, K.; Kusters, M. The awareness of radiologists for the presence of lateral lymph nodes in patients with locally advanced rectal cancer: A single-centre, retrospective cohort study. Eur. Radiol. 2022, 32, 6637–6645. [Google Scholar] [CrossRef]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef]
- Taghavi, M.; Benson, S. Tevien/dtor: DTOR beta 1. Zenodo 2021. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Foret, P.; Kleiner, A.; Mobahi, H.; Neyshabur, B. Sharpness-aware minimization for efficiently improving generalization. arXiv 2020, arXiv:2010.01412. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- IBM Corp. IBM SPSS Statistics for Windows; IBM Corp: Armonk, NY, USA, 2019. [Google Scholar]
- Hastie, T.; Rosset, S.; Zhu, J.; Zou, H. Multi-class AdaBoost. Stat. Interface 2010, 2, 349–360. [Google Scholar] [CrossRef]
- van Timmeren, J.E.; Cester, D.; Tanadini-Lang, S.; Alkadhi, H.; Baessler, B. Radiomics in medical imaging-“how-to” guide and critical reflection. Insights Imaging 2020, 11, 91. [Google Scholar] [CrossRef] [PubMed]
- Bedrikovetski, S.; Dudi-Venkata, N.N.; Maicas, G.; Kroon, H.M.; Seow, W.; Carneiro, G.; Moore, J.W.; Sammour, T. Artificial intelligence for the diagnosis of lymph node metastases in patients with abdominopelvic malignancy: A systematic review and meta-analysis. Artif. Intell. Med. 2021, 113, 102022. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, R.; Akiyoshi, T.; Toda, S.; Murakami, Y.; Taguchi, S.; Oba, K.; Hanaoka, Y.; Nagasaki, T.; Yamaguchi, T.; Konishi, T.; et al. Radiomics Approach Outperforms Diameter Criteria for Predicting Pathological Lateral Lymph Node Metastasis After Neoadjuvant (Chemo)Radiotherapy in Advanced Low Rectal Cancer. Ann. Surg. Oncol. 2020, 27, 4273–4283. [Google Scholar] [CrossRef] [PubMed]
- Kasai, S.; Shiomi, A.; Kagawa, H.; Hino, H.; Manabe, S.; Yamaoka, Y.; Chen, K.; Nanishi, K.; Kinugasa, Y. The Effectiveness of Machine Learning in Predicting Lateral Lymph Node Metastasis from Lower Rectal Cancer: A Single Center Development and Validation Study. Ann. Gastroenterol. Surg. 2022, 6, 92–100. [Google Scholar] [CrossRef]
- Benson, A.B.; Venook, A.P.; Al-Hawary, M.M.; Cederquist, L.; Chen, Y.J.; Ciombor, K.K.; Cohen, S.; Cooper, H.S.; Deming, D.; Engstrom, P.F.; et al. Rectal Cancer, Version 2.2018, NCCN Clinical Practice Guidelines in Oncology. J. Natl. Compr. Cancer Netw. 2018, 16, 874–901. [Google Scholar] [CrossRef]
- Cai, L.; Bodalal, Z.; Trebeschi, S.; Waktola, S.; Sluckin, T.C.; Kusters, M.; Maas, M.; Beets-Tan, R.; Benson, S. Imaging of colorectal nodal disease. In The lymphatic System in Colorectal Cacer; Academic Press: Cambridge, MA, USA, 2022; pp. 75–88. [Google Scholar]


| N = 196 | N (%) |
|---|---|
| Male | 127 (64.8) |
| Female | 69 (35.2) |
| Age in years, mean (SD) | 64.1 (10.8) |
| BMI, mean (SD) | 26.0 (4.9) |
| Centre | |
| Catharina Hospital (CH) | 116 (59.2) |
| Netherlands Cancer Institute (NKI) | 24 (12.2) |
| Amsterdam UMC (AUMC) | 56 (28.6) |
| ASA-score | |
| 1 | 27 (15.3) |
| 2 | 128 (72.7) |
| 3 | 20 (11.4) |
| 4 | 1 (0.6) |
| Distance tumour to anorectal junction in cm, mean (SD) | 3.0 (2.8) |
| Clinical T-stage | |
| cT2 | 5 (2.6) |
| cT3 | 113 (57.7) |
| cT4 | 78 (39.8) |
| Clinical N-stage | |
| cN0 | 48 (24.5) |
| cN1 | 77 (39.3) |
| cN2 | 71 (36.2) |
| Positive mesorectal fascia or T4 on primary MRI | 99 (50.5) |
| Anatomical location of largest lateral lymph node * | |
| Internal iliac | 19 (9.7) |
| External iliac | 18 (9.2) |
| Obturator | 159 (81.1) |
| Mean lateral lymph node size on primary MRI, mm (SD) * | 5.5 (2.7) |
| Mean number of lateral lymph nodes on primary MRI (SD) | 3.6 (2.1) |
| Neoadjuvant treatment * | |
| Short-course radiotherapy | 34 (17.3) |
| Chemoradiotherapy | 162 (82.7) |
| Operation | |
| No surgery/wait and see | 6 (3.1) |
| TEM/local excision | 1 (0.5) |
| TME/LAR | 108 (55.1) |
| APR | 79 (40.3) |
| Pelvic exenteration | 2 (1.0) |
| Lateral lymph node dissection (LLND) | |
| No | 186 (94.9) |
| LLND | 3 (1.5) |
| Node-picking | 7 (3.6) |
| Positive resection margins * | 15 (7.7) |
| Centre | AUC (Imaging) | AUC (Clinical) | AUC (Combined) |
|---|---|---|---|
| A: local recurrence | |||
| NKI | 0.67 (95% CI: 0.40–0.95) | 0.68 (95% CI: 0.47–0.89) | 0.79 (95% CI: 0.60–0.96) |
| AUMC | 0.85 (95% CI: 0.75–0.95) | 0.82 (95% CI: 0.70–0.93) | 0.68 (95% CI: 0.53–0.83) |
| CH | 0.60 (95% CI: 0.53–0.67) | 0.79 (95% CI: 0.73–0.84) | 0.50 (95% CI: 0.43–0.58) |
| B: lateral local recurrence | |||
| NKI | 0.57 (95% CI: 0.46–1.00) | 0.73 (95% CI: 0.46–1.00) | 0.80 (95% CI: 0.49–1.00) |
| AUMC | 0.82 (95% CI: 0.70–0.94) | 0.81 (95% CI: 0.70–0.93) | 0.61 (95% CI: 0.44–0.78) |
| CH | 0.64 (95% CI: 0.56–0.71) | 0.78 (95% CI: 0.71–0.84) | 0.53 (95% CI: 0.45–0.62) |
| Centre | F1 | Specificity | Sensitivity |
|---|---|---|---|
| A: local recurrence | |||
| NKI | 0.21/0.24/0.24 | 50.7%/67.6%/47.9% | 71.4%/57.1%/85.7% |
| AUMC | 0.20/0.25/0.16 | 51.7%/79.4%/44.4% | 91.7%/58.3%/83.3% |
| CH | 0.26/0.43/0.22 | 59.1%/71.0%/57.2% | 47.8%/71.6%/41.8% |
| B: lateral local recurrence | |||
| NKI | 0.11/0.17/0.13 | 45.6%/68.4%/52.6% | 66.7%/66.7%/66.7% |
| AUMC | 0.18/0.21/0.14 | 53.4%/77.9%/45.5% | 88.9%/55.6%/77.8% |
| CH | 0.28/0.42/0.24 | 58.6%/72.7%/58.6% | 53.7%/66.7%/44.4% |
| Case | Saliency | GradCAM | FullGRAD | XGradCAM | EigenCAM |
|---|---|---|---|---|---|
| SSIM | |||||
| Positive | 0.235 | 1.000 | 0.225 | 0.772 | 0.792 |
| Unsure | 0.220 | 1.000 | 0.233 | 0.839 | 0.912 |
| Negative | 0.271 | 1.000 | 0.266 | 0.930 | 0.916 |
| MSE | |||||
| Positive | 0.214 | 0.000 | 0.281 | 0.024 | 0.024 |
| Unsure | 0.245 | 0.000 | 0.347 | 0.014 | 0.003 |
| Negative | 0.212 | 0.000 | 0.346 | 0.010 | 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sluckin, T.C.; Hekhuis, M.; Kol, S.Q.; Nederend, J.; Horsthuis, K.; Beets-Tan, R.G.H.; Beets, G.L.; Burger, J.W.A.; Tuynman, J.B.; Rutten, H.J.T.; et al. A Deep Learning Framework with Explainability for the Prediction of Lateral Locoregional Recurrences in Rectal Cancer Patients with Suspicious Lateral Lymph Nodes. Diagnostics 2023, 13, 3099. https://doi.org/10.3390/diagnostics13193099
Sluckin TC, Hekhuis M, Kol SQ, Nederend J, Horsthuis K, Beets-Tan RGH, Beets GL, Burger JWA, Tuynman JB, Rutten HJT, et al. A Deep Learning Framework with Explainability for the Prediction of Lateral Locoregional Recurrences in Rectal Cancer Patients with Suspicious Lateral Lymph Nodes. Diagnostics. 2023; 13(19):3099. https://doi.org/10.3390/diagnostics13193099
Chicago/Turabian StyleSluckin, Tania C., Marije Hekhuis, Sabrine Q. Kol, Joost Nederend, Karin Horsthuis, Regina G. H. Beets-Tan, Geerard L. Beets, Jacobus W. A. Burger, Jurriaan B. Tuynman, Harm J. T. Rutten, and et al. 2023. "A Deep Learning Framework with Explainability for the Prediction of Lateral Locoregional Recurrences in Rectal Cancer Patients with Suspicious Lateral Lymph Nodes" Diagnostics 13, no. 19: 3099. https://doi.org/10.3390/diagnostics13193099
APA StyleSluckin, T. C., Hekhuis, M., Kol, S. Q., Nederend, J., Horsthuis, K., Beets-Tan, R. G. H., Beets, G. L., Burger, J. W. A., Tuynman, J. B., Rutten, H. J. T., Kusters, M., & Benson, S. (2023). A Deep Learning Framework with Explainability for the Prediction of Lateral Locoregional Recurrences in Rectal Cancer Patients with Suspicious Lateral Lymph Nodes. Diagnostics, 13(19), 3099. https://doi.org/10.3390/diagnostics13193099







