Impact of Misdiagnosis in Case-Control Studies of Myalgic Encephalomyelitis/Chronic Fatigue Syndrome
Abstract
:1. Introduction
2. Statistical Methodology
2.1. Formulation of the Problem
- I.
- ME/CFS-diagnosed cases are a mix of apparent and genuine patients of the disease;
- II.
- The causal factor is only associated with genuine ME/CFS patients;
- III.
- Apparent cases are similar to healthy controls as far as the association with the causal factor is concerned;
- VI.
- The chance of an ME/CFS misdiagnosis is only dependent on the true clinical status of the cases and not on the confounding factors;
- V.
- The true association is independent of disease duration and disease triggers, among other factors occurring during the disease course;
- VI.
- Healthy controls were not misdiagnosed as such;
- VII.
- The value of the candidate causal factor can be determined perfectly in each individual.
- VII.
- There are only two possible serological outcomes for each individual: seronegative or seropositive;
- VIII.
- The sensitivity and specificity of the serological classification are identical for all of the individuals.
2.2. Simulation Study
2.3. Application to Two ME/CFS Studies
3. Results
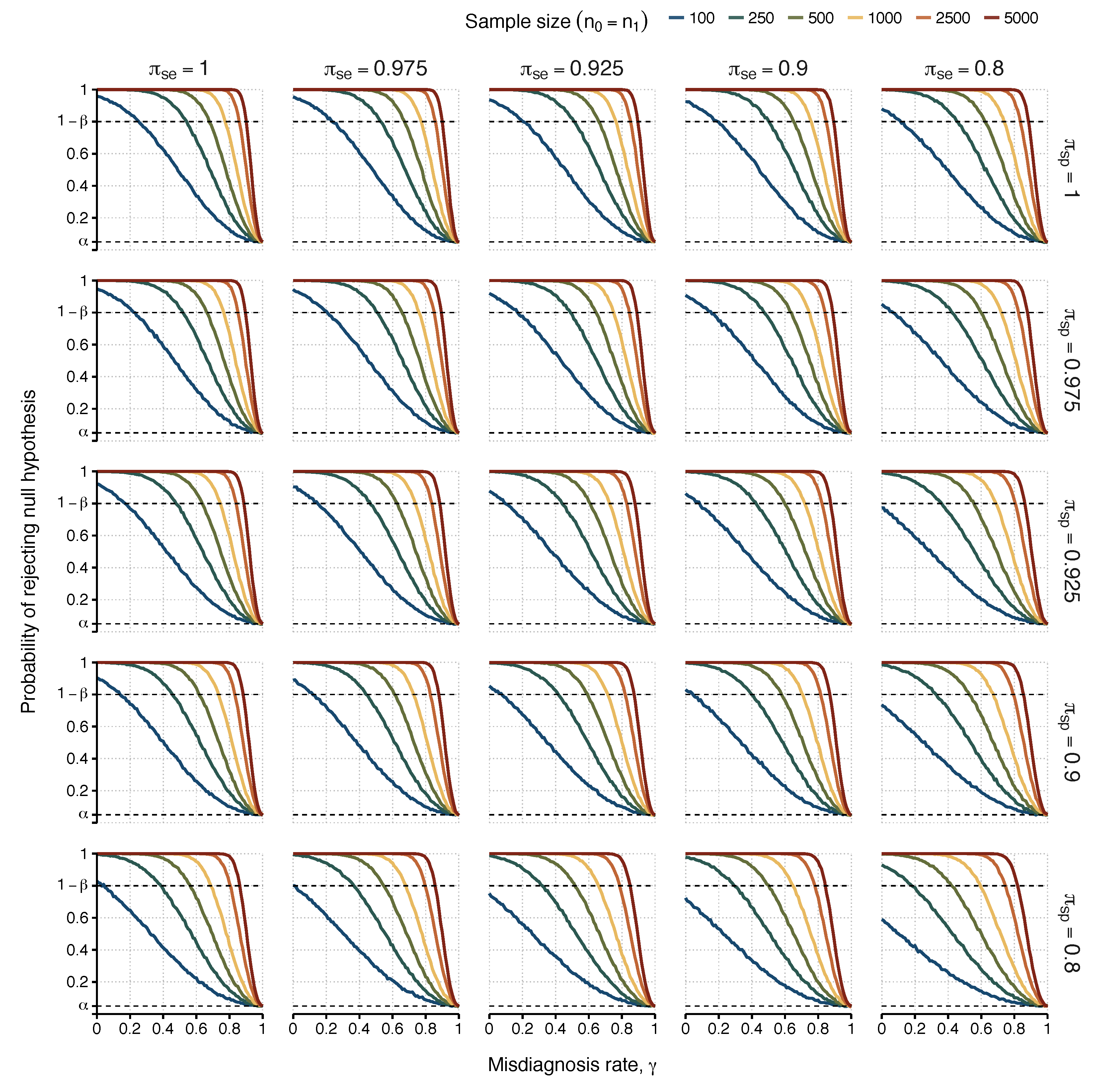
3.1. Simulation Study: Impact of ME/CFS Misdiagnosis
3.2. Simulation Study: Impact of ME/CFS Misdiagnosis and Misclassification on the Candidate Causal Factor
3.3. Application to Data from Two ME/CFS Studies
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ME/CFS | Myalgic Encephalomyelitis/Chronic Fatigue Syndrome |
| SNP | Single-nucleotide polymorphism |
| PTPN22 | Tyrosine phosphatase non-receptor type 22 |
| CTLA4 | Cytotoxic T-lymphocyte-associated protein 4 |
| TNF | Tumor necrosis factor |
| IRF5 | Interferon regulatory factor 5 |
| CMV | Human cytomegalovirus |
| EBV | Epstein–Barr virus |
| HSV1 | Herpes simplex virus 1 |
| HSV2 | Herpes simplex virus 2 |
| VZV | Varicella-zoster virus |
| HHV6 | Human herpesvirus |
| CI | Confidence interval |
Appendix A. Appendix Tables
| Causal Factor | Controls | ME/CFS-Diagnosed Cases | |
|---|---|---|---|
| (Apparent) | (True) | ||
| Present | |||
| Absent | |||
| Estimated Serological Status | True Serological Status | Controls | ME/CFS-Diagnosed Cases | |
|---|---|---|---|---|
| (Apparent) | (True) | |||
Appendix B. Mathematical Formulation
Appendix B.1. Sampling Distribution
Appendix B.2. Simulation Study Estimation of Parameter
References
- Fukuda, K.; Strausm, S.E.; Hickie, I.; Sharpe, M.C.; Dobbins, J.G.; Komaroff, A. The Chronic Fatigue Syndrome: A Comprehensive Approach to Its Definition and Study. Ann. Intern. Med. 1994, 121, 953. [Google Scholar] [CrossRef] [PubMed]
- Carruthers, B.M.; Jain, A.K.; De Meirleir, K.L.; Peterson, D.L.; Klimas, N.G.; Lerner, A.M.; Bested, A.C.; Flor-Henry, P.; Joshi, P.; Powles, A.C.P.; et al. Myalgic Encephalomyelitis/Chronic Fatigue Syndrome: Clinical Working Case Definition, Diagnostic and Treatment Protocols. J. Chronic Fatigue Syndr. 2003, 11, 7–115. [Google Scholar] [CrossRef]
- König, R.S.; Albrich, W.C.; Kahlert, C.R.; Bahr, L.S.; Löber, U.; Vernazza, P.; Scheibenbogen, C.; Forslund, S.K. The Gut Microbiome in Myalgic Encephalomyelitis (ME)/Chronic Fatigue Syndrome (CFS). Front. Immunol. 2022, 12, 628741. [Google Scholar] [CrossRef] [PubMed]
- Wirth, K.; Scheibenbogen, C. A Unifying Hypothesis of the Pathophysiology of Myalgic Encephalomyelitis/Chronic Fatigue Syndrome (ME/CFS): Recognitions from the finding of autoantibodies against ß2-adrenergic receptors. Autoimmun. Rev. 2020, 19, 102527. [Google Scholar] [CrossRef] [PubMed]
- Wood, E.; Hall, K.H.; Tate, W. Role of mitochondria, oxidative stress and the response to antioxidants in myalgic encephalomyelitis/chronic fatigue syndrome: A possible approach to SARS-CoV-2 ‘long-haulers’? Chronic Dis. Transl. Med. 2021, 7, 14–26. [Google Scholar] [CrossRef] [PubMed]
- Castro-Marrero, J.; Cordero, M.D.; Sáez-Francas, N.; Jimenez-Gutierrez, C.; Aguilar-Montilla, F.J.; Aliste, L.; Alegre-Martin, J. Could Mitochondrial Dysfunction Be a Differentiating Marker Between Chronic Fatigue Syndrome and Fibromyalgia? Antioxidants Redox Signal. 2013, 19, 1855–1860. [Google Scholar] [CrossRef]
- Rasa, S.; Nora-Krukle, Z.; Henning, N.; Eliassen, E.; Shikova, E.; Harrer, T.; Scheibenbogen, C.; Murovska, M.; Prusty, B.K. Chronic viral infections in myalgic encephalomyelitis/chronic fatigue syndrome (ME/CFS). J. Transl. Med. 2018, 16, 268. [Google Scholar] [CrossRef]
- Sepúlveda, N.; Carneiro, J.; Lacerda, E.; Nacul, L. Myalgic Encephalomyelitis/Chronic Fatigue Syndrome as a Hyper-Regulated Immune System Driven by an Interplay Between Regulatory T Cells and Chronic Human Herpesvirus Infections. Front. Immunol. 2019, 10, 2684. [Google Scholar] [CrossRef]
- Cortes Rivera, M.; Mastronardi, C.; Silva-Aldana, C.; Arcos-Burgos, M.; Lidbury, B. Myalgic Encephalomyelitis/Chronic Fatigue Syndrome: A Comprehensive Review. Diagnostics 2019, 9, 91. [Google Scholar] [CrossRef]
- Smith, M.E.B.; Nelson, H.D.; Haney, E.; Pappas, M.; Daeges, M.; Wasson, N.; McDonagh, M. Diagnosis and Treatment of Myalgic Encephalomyelitis/Chronic Fatigue Syndrome. Evid. Rep. Technol. Assess. 2014, 219, 1–433. [Google Scholar] [CrossRef]
- Malato, J.; Graça, L.; Nacul, L.; Lacerda, E.; Sepúlveda, N. Statistical challenges of investigating a disease with a complex diagnosis. In Estatística: Desafios Transversais às Ciências com Dados; Milheiro, P., Pacheco, A., de Sousa, B., Alves, I.F., Pereira, I., Polidoro, M.J., Ramos, S., Eds.; Sociedade Portuguesa de Estatística: Lisboa, Portugal, 2021; pp. 153–167. [Google Scholar]
- Jason, L.A.; Sunnquist, M.; Brown, A.; Evans, M.; Vernon, S.D.; Furst, J.D.; Simonis, V. Examining case definition criteria for chronic fatigue syndrome and myalgic encephalomyelitis. Fatigue Biomed. Health Behav. 2014, 2, 40–56. [Google Scholar] [CrossRef] [PubMed]
- Reeves, W.C.; Wagner, D.; Nisenbaum, R.; Jones, J.F.; Gurbaxani, B.; Solomon, L.; Papanicolaou, D.A.; Unger, E.R.; Vernon, S.D.; Heim, C. Chronic Fatigue Syndrome – A clinically empirical approach to its definition and study. BMC Med. 2005, 3, 19. [Google Scholar] [CrossRef] [PubMed]
- Jason, L.A.; Kot, B.; Sunnquist, M.; Brown, A.; Reed, J.; Furst, J.; Newton, J.L.; Strand, E.B.; Vernon, S.D. Comparing and contrasting consensus versus empirical domains. Fatigue Biomed. Health Behav. 2015, 3, 63–74. [Google Scholar] [CrossRef] [PubMed]
- Conroy, K.E.; Islam, M.F.; Jason, L.A. Evaluating case diagnostic criteria for myalgic encephalomyelitis/chronic fatigue syndrome (ME/CFS): Toward an empirical case definition. Disabil. Rehabil. 2022, 1–8. [Google Scholar] [CrossRef]
- Brown, D.; Birch, C.; Younger, J.; Worthey, E. ME/CFS: Whole genome sequencing uncovers a misclassified case of glycogen storage disease type 13 previously diagnosed as ME/CFS. Mol. Genet. Metab. 2021, 132, S194–S195. [Google Scholar] [CrossRef]
- Jason, L.A.; Ravichandran, S.; Katz, B.Z.; Natelson, B.H.; Bonilla, H.F. Establishing a consensus on ME/CFS exclusionary illnesses. Fatigue Biomed. Health Behav. 2023, 11, 1–13. [Google Scholar] [CrossRef]
- Nacul, L.; Lacerda, E.M.; Kingdon, C.C.; Curran, H.; Bowman, E.W. How have selection bias and disease misclassification undermined the validity of myalgic encephalomyelitis/chronic fatigue syndrome studies? J. Health Psychol. 2017, 24, 1765–1769. [Google Scholar] [CrossRef] [PubMed]
- Brurberg, K.G.; Fønhus, M.S.; Larun, L.; Flottorp, S.; Malterud, K. Case definitions for chronic fatigue syndrome/myalgic encephalomyelitis (CFS/ME): A systematic review. BMJ Open 2014, 4, e003973. [Google Scholar] [CrossRef] [PubMed]
- Lim, E.J.; Son, C.G. Review of case definitions for myalgic encephalomyelitis/chronic fatigue syndrome (ME/CFS). J. Transl. Med. 2020, 18, 289. [Google Scholar] [CrossRef]
- Steiner, S.; Becker, S.C.; Hartwig, J.; Sotzny, F.; Lorenz, S.; Bauer, S.; Löbel, M.; Stittrich, A.B.; Grabowski, P.; Scheibenbogen, C. Autoimmunity-Related Risk Variants in PTPN22 and CTLA4 Are Associated With ME/CFS With Infectious Onset. Front. Immunol. 2020, 11, 578. [Google Scholar] [CrossRef]
- Cliff, J.M.; King, E.C.; Lee, J.S.; Sepúlveda, N.; Wolf, A.S.; Kingdon, C.; Bowman, E.; Dockrell, H.M.; Nacul, L.; Lacerda, E.; et al. Cellular Immune Function in Myalgic Encephalomyelitis/Chronic Fatigue Syndrome (ME/CFS). Front. Immunol. 2019, 10, 796. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Pablos, M.; Paiva, B.; Montero-Mateo, R.; Garcia, N.; Zabaleta, A. Epstein-Barr Virus and the Origin of Myalgic Encephalomyelitis or Chronic Fatigue Syndrome. Front. Immunol. 2021, 12, 656797. [Google Scholar] [CrossRef] [PubMed]
- Sepúlveda, N.; Malato, J.T.; Sotzny, F.; Grabowska, A.D.; Fonseca, A.; Cordeiro, C.; Graça, L.; Biecek, P.; Behrends, U.; Mautner, J.; et al. Revisiting IgG antibody reactivity to Epstein-Barr virus in Myalgic Encephalomyelitis/Chronic Fatigue Syndrome and its potential application to disease diagnosis. Front. Med. 2022, 9, 921101. [Google Scholar] [CrossRef]
- Sepúlveda, N.; Stresman, G.; White, M.T.; Drakeley, C.J. Current Mathematical Models for Analyzing Anti-Malarial Antibody Data with an Eye to Malaria Elimination and Eradication. J. Immunol. Res. 2015, 2015, 1–21. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Malato, J.; Graça, L.; Sepúlveda, N. Impact of Misclassification and Imperfect Serological Tests in Association Analyses of ME/CFS Applied to COVID-19 Data. In Recent Developments in Statistics and Data Science; Bispo, R., Henriques-Rodrigues, L., Alpizar-Jara, R., de Carvalho, M., Eds.; Springer International Publishing: Cham, Switzderland, 2022; pp. 215–225. [Google Scholar]
- Domingues, T.D.; Mouriño, H.; Sepúlveda, N. Analysis of antibody data using Finite Mixture Models based on Scale Mixtures of Skew-Normal distributions. medRxiv 2021. medRxiv:2021.03.08.21252807. [Google Scholar] [CrossRef]
- Scheibenbogen, C.; Freitag, H.; Blanco, J.; Capelli, E.; Lacerda, E.; Authier, J.; Meeus, M.; Marrero, J.C.; Nora-Krukle, Z.; Oltra, E.; et al. The European ME/CFS Biomarker Landscape project: An initiative of the European network EUROMENE. J. Transl. Med. 2017, 15, 162. [Google Scholar] [CrossRef]
- Herrera, S.; de Vega, W.C.; Ashbrook, D.; Vernon, S.D.; McGowan, P.O. Genome-epigenome interactions associated with Myalgic Encephalomyelitis/Chronic Fatigue Syndrome. Epigenetics 2018, 13, 1174–1190. [Google Scholar] [CrossRef]
- Tanigawa, Y.; Li, J.; Justesen, J.M.; Horn, H.; Aguirre, M.; DeBoever, C.; Chang, C.; Narasimhan, B.; Lage, K.; Hastie, T.; et al. Components of genetic associations across 2,138 phenotypes in the UK Biobank highlight adipocyte biology. Nat. Commun. 2019, 10, 4064. [Google Scholar] [CrossRef]
- Dibble, J.J.; McGrath, S.J.; Ponting, C.P. Genetic risk factors of ME/CFS: A critical review. Hum. Mol. Genet. 2020, 29, R117–R124. [Google Scholar] [CrossRef]
- Hajdarevic, R.; Lande, A.; Mehlsen, J.; Rydland, A.; Sosa, D.D.; Strand, E.B.; Mella, O.; Pociot, F.; Fluge, Ø.; Lie, B.A.; et al. Genetic association study in myalgic encephalomyelitis/chronic fatigue syndrome (ME/CFS) identifies several potential risk loci. Brain, Behav. Immun. 2022, 102, 362–369. [Google Scholar] [CrossRef]
- Giri, A.; Hellwege, J.N.; Keaton, J.M.; Park, J.; Qiu, C.; Warren, H.R.; Torstenson, E.S.; Kovesdy, C.P.; Sun, Y.V.; Wilson, O.D.; et al. Trans-ethnic association study of blood pressure determinants in over 750,000 individuals. Nat. Genet. 2018, 51, 51–62. [Google Scholar] [CrossRef]
- International Multiple Sclerosis Genetics Consortium (IMSGC). Analysis of immune-related loci identifies 48 new susceptibility variants for multiple sclerosis. Nat. Genet. 2013, 45, 1353–1360. [Google Scholar] [CrossRef] [PubMed]
- Bjornevik, K.; Cortese, M.; Healy, B.C.; Kuhle, J.; Mina, M.J.; Leng, Y.; Elledge, S.J.; Niebuhr, D.W.; Scher, A.I.; Munger, K.L.; et al. Longitudinal analysis reveals high prevalence of Epstein-Barr virus associated with multiple sclerosis. Science 2022, 375, 296–301. [Google Scholar] [CrossRef] [PubMed]
- Pheby, D.F.H.; Araja, D.; Berkis, U.; Brenna, E.; Cullinan, J.; de Korwin, J.D.; Gitto, L.; Hughes, D.A.; Hunter, R.M.; Trepel, D.; et al. A Literature Review of GP Knowledge and Understanding of ME/CFS: A Report from the Socioeconomic Working Group of the European Network on ME/CFS (EUROMENE). Medicina 2020, 57, 7. [Google Scholar] [CrossRef]
- Lacerda, E.M.; Mudie, K.; Kingdon, C.C.; Butterworth, J.D.; O’Boyle, S.; Nacul, L. The UK ME/CFS Biobank: A Disease-Specific Biobank for Advancing Clinical Research Into Myalgic Encephalomyelitis/Chronic Fatigue Syndrome. Front. Neurol. 2018, 9, 1026. [Google Scholar] [CrossRef] [PubMed]
- Słomko, J.; Newton, J.L.; Kujawski, S.; Tafil-Klawe, M.; Klawe, J.; Staines, D.; Marshall-Gradisnik, S.; Zalewski, P. Prevalence and characteristics of chronic fatigue syndrome/myalgic encephalomyelitis (CFS/ME) in Poland: A cross-sectional study. BMJ Open 2019, 9, e023955. [Google Scholar] [CrossRef] [PubMed]
- Ariza, M.E. Commentary: Antibodies to Human Herpesviruses in Myalgic Encephalomyelitis/Chronic Fatigue Syndrome Patients. Front. Immunol. 2020, 11, 1400. [Google Scholar] [CrossRef]
- Grabowska, A.D.; Lacerda, E.M.; Nacul, L.; Sepúlveda, N. Review of the Quality Control Checks Performed by Current Genome-Wide and Targeted-Genome Association Studies on Myalgic Encephalomyelitis/Chronic Fatigue Syndrome. Front. Pediatr. 2020, 8, 293. [Google Scholar] [CrossRef]
- Hajdarevic, R.; Lande, A.; Rekeland, I.; Rydland, A.; Strand, E.B.; Sosa, D.D.; Creary, L.E.; Mella, O.; Egeland, T.; Saugstad, O.D.; et al. Fine mapping of the major histocompatibility complex (MHC) in myalgic encephalomyelitis/chronic fatigue syndrome (ME/CFS) suggests involvement of both HLA class I and class II loci. Brain, Behav. Immun. 2021, 98, 101–109. [Google Scholar] [CrossRef]
- Domingues, T.D.; Grabowska, A.D.; Lee, J.S.; Ameijeiras-Alonso, J.; Westermeier, F.; Scheibenbogen, C.; Cliff, J.M.; Nacul, L.; Lacerda, E.M.; Mouriño, H.; et al. Herpesviruses Serology Distinguishes Different Subgroups of Patients From the United Kingdom Myalgic Encephalomyelitis/Chronic Fatigue Syndrome Biobank. Front. Med. 2021, 8, 686736. [Google Scholar] [CrossRef]
- Szklarski, M.; Freitag, H.; Lorenz, S.; Becker, S.C.; Sotzny, F.; Bauer, S.; Hartwig, J.; Heidecke, H.; Wittke, K.; Kedor, C.; et al. Delineating the Association Between Soluble CD26 and Autoantibodies Against G-Protein Coupled Receptors, Immunological and Cardiovascular Parameters Identifies Distinct Patterns in Post-Infectious vs. Non-Infection-Triggered Myalgic Encephalomyelitis/Chronic Fatigue Syndrome. Front. Immunol. 2021, 12, 644548. [Google Scholar] [CrossRef] [PubMed]
- Cella, M.; Chalder, T. Measuring fatigue in clinical and community settings. J. Psychosom. Res. 2010, 69, 17–22. [Google Scholar] [CrossRef] [PubMed]
- Loebel, M.; Eckey, M.; Sotzny, F.; Hahn, E.; Bauer, S.; Grabowski, P.; Zerweck, J.; Holenya, P.; Hanitsch, L.G.; Wittke, K.; et al. Serological profiling of the EBV immune response in Chronic Fatigue Syndrome using a peptide microarray. PLoS ONE 2017, 12, e0179124. [Google Scholar] [CrossRef]
- Kaushik, N. Gene expression in peripheral blood mononuclear cells from patients with chronic fatigue syndrome. J. Clin. Pathol. 2005, 58, 826–832. [Google Scholar] [CrossRef] [PubMed]
- Johnston, S.; Staines, D.; Klein, A.; Marshall-Gradisnik, S. A targeted genome association study examining transient receptor potential ion channels, acetylcholine receptors, and adrenergic receptors in Chronic Fatigue Syndrome/Myalgic Encephalomyelitis. BMC Med Genet. 2016, 17, 79. [Google Scholar] [CrossRef] [PubMed]
- Lande, A.; Fluge, Ø.; Strand, E.B.; Flåm, S.T.; Sosa, D.D.; Mella, O.; Egeland, T.; Saugstad, O.D.; Lie, B.A.; Viken, M.K. Human Leukocyte Antigen alleles associated with Myalgic Encephalomyelitis/Chronic Fatigue Syndrome (ME/CFS). Sci. Rep. 2020, 10, 5267. [Google Scholar] [CrossRef]
- Kerr, J.R.; Petty, R.; Burke, B.; Gough, J.; Fear, D.; Sinclair, L.I.; Mattey, D.L.; Richards, S.C.M.; Montgomery, J.; Baldwin, D.A.; et al. Gene Expression Subtypes in Patients with Chronic Fatigue Syndrome/Myalgic Encephalomyelitis. J. Infect. Dis. 2008, 197, 1171–1184. [Google Scholar] [CrossRef]
- Zhang, L.; Gough, J.; Christmas, D.; Mattey, D.L.; Richards, S.C.M.; Main, J.; Enlander, D.; Honeybourne, D.; Ayres, J.G.; Nutt, D.J.; et al. Microbial infections in eight genomic subtypes of chronic fatigue syndrome/myalgic encephalomyelitis. J. Clin. Pathol. 2009, 63, 156–164. [Google Scholar] [CrossRef]
- Jason, L.A.; Unger, E.R.; Dimitrakoff, J.D.; Fagin, A.P.; Houghton, M.; Cook, D.B.; Marshall, G.D.; Klimas, N.; Snell, C. Minimum data elements for research reports on CFS. Brain Behav. Immun. 2012, 26, 401–406. [Google Scholar] [CrossRef]
- Nacul, L.; Authier, F.J.; Scheibenbogen, C.; Lorusso, L.; Helland, I.B.; Martin, J.A.; Sirbu, C.A.; Mengshoel, A.M.; Polo, O.; Behrends, U.; et al. European Network on Myalgic Encephalomyelitis/Chronic Fatigue Syndrome (EUROMENE): Expert Consensus on the Diagnosis, Service Provision, and Care of People with ME/CFS in Europe. Medicina 2021, 57, 510. [Google Scholar] [CrossRef]


| Causal Factor | Controls | ME/CFS-Diagnosed Cases |
|---|---|---|
| Present | ||
| Absent |
| 0.05 | 0.1 | 0.25 | 0.5 | n (per Group) | ||
|---|---|---|---|---|---|---|
| 10 | 0.59 | 0.65 | 0.64 | 0.53 | 100 | |
| 5 | 0.24 | 0.43 | 0.50 | 0.42 | ||
| 3 | − | 0.02 | 0.25 | 0.23 | ||
| 2 | − | − | − | − | ||
| 1.5 | − | − | − | − | ||
| 1.25 | − | − | − | − | ||
| 10 | 0.77 | 0.79 | 0.77 | 0.70 | 250 | |
| 5 | 0.56 | 0.66 | 0.69 | 0.63 | ||
| 3 | 0.20 | 0.41 | 0.53 | 0.50 | ||
| 2 | − | − | 0.23 | 0.26 | ||
| 1.5 | − | − | − | − | ||
| 1.25 | − | − | − | − | ||
| 10 | 0.84 | 0.86 | 0.84 | 0.78 | 500 | |
| 5 | 0.70 | 0.76 | 0.78 | 0.73 | ||
| 3 | 0.47 | 0.60 | 0.67 | 0.65 | ||
| 2 | − | 0.27 | 0.46 | 0.47 | ||
| 1.5 | − | − | 0.04 | 0.13 | ||
| 1.25 | − | − | − | − | ||
| 10 | 0.89 | 0.90 | 0.89 | 0.84 | 1000 | |
| 5 | 0.80 | 0.84 | 0.85 | 0.81 | ||
| 3 | 0.64 | 0.72 | 0.77 | 0.75 | ||
| 2 | 0.32 | 0.50 | 0.62 | 0.62 | ||
| 1.5 | − | 0.05 | 0.32 | 0.38 | ||
| 1.25 | − | − | − | − | ||
| 10 | 0.93 | 0.94 | 0.93 | 0.90 | 2500 | |
| 5 | 0.88 | 0.90 | 0.90 | 0.88 | ||
| 3 | 0.78 | 0.83 | 0.85 | 0.84 | ||
| 2 | 0.58 | 0.69 | 0.76 | 0.76 | ||
| 1.5 | 0.18 | 0.42 | 0.58 | 0.59 | ||
| 1.25 | − | − | 0.20 | 0.28 | ||
| 10 | 0.95 | 0.95 | 0.95 | 0.93 | 5000 | |
| 5 | 0.91 | 0.93 | 0.93 | 0.91 | ||
| 3 | 0.84 | 0.88 | 0.90 | 0.88 | ||
| 2 | 0.71 | 0.78 | 0.83 | 0.83 | ||
| 1.5 | 0.44 | 0.59 | 0.70 | 0.72 | ||
| 1.25 | − | 0.20 | 0.44 | 0.49 | ||
| 1 | 0.975 | 0.925 | 0.9 | 0.8 | n (per Group) | ||
|---|---|---|---|---|---|---|---|
| 1 | 0.25 | 0.23 | 0.20 | 0.19 | 0.11 | ||
| 0.975 | 0.22 | 0.20 | 0.17 | 0.15 | 0.06 | ||
| 0.925 | 0.17 | 0.14 | 0.09 | 0.08 | − | 100 | |
| 0.9 | 0.13 | 0.11 | 0.07 | 0.04 | − | ||
| 0.8 | 0.03 | − | − | − | − | ||
| 1 | 0.53 | 0.52 | 0.51 | 0.50 | 0.45 | ||
| 0.975 | 0.51 | 0.50 | 0.48 | 0.47 | 0.42 | ||
| 0.925 | 0.47 | 0.46 | 0.43 | 0.42 | 0.36 | 250 | |
| 0.9 | 0.45 | 0.43 | 0.41 | 0.39 | 0.32 | ||
| 0.8 | 0.38 | 0.36 | 0.31 | 0.29 | 0.18 | ||
| 1 | 0.67 | 0.67 | 0.66 | 0.65 | 0.62 | ||
| 0.975 | 0.66 | 0.65 | 0.64 | 0.63 | 0.59 | ||
| 0.925 | 0.63 | 0.62 | 0.60 | 0.59 | 0.55 | 500 | |
| 0.9 | 0.61 | 0.61 | 0.59 | 0.57 | 0.52 | ||
| 0.8 | 0.56 | 0.54 | 0.51 | 0.50 | 0.42 | ||
| 1 | 0.77 | 0.77 | 0.76 | 0.75 | 0.73 | ||
| 0.975 | 0.76 | 0.75 | 0.74 | 0.74 | 0.72 | ||
| 0.925 | 0.74 | 0.73 | 0.72 | 0.71 | 0.68 | 1000 | |
| 0.9 | 0.73 | 0.72 | 0.71 | 0.70 | 0.67 | ||
| 0.8 | 0.68 | 0.67 | 0.65 | 0.64 | 0.59 | ||
| 1 | 0.85 | 0.85 | 0.85 | 0.84 | 0.83 | ||
| 0.975 | 0.85 | 0.85 | 0.84 | 0.84 | 0.82 | ||
| 0.925 | 0.84 | 0.83 | 0.82 | 0.82 | 0.80 | 2500 | |
| 0.9 | 0.83 | 0.82 | 0.81 | 0.81 | 0.79 | ||
| 0.8 | 0.80 | 0.79 | 0.78 | 0.78 | 0.74 | ||
| 1 | 0.90 | 0.90 | 0.89 | 0.89 | 0.88 | ||
| 0.975 | 0.89 | 0.89 | 0.89 | 0.88 | 0.87 | ||
| 0.925 | 0.88 | 0.88 | 0.87 | 0.87 | 0.86 | 5000 | |
| 0.9 | 0.88 | 0.87 | 0.87 | 0.87 | 0.85 | ||
| 0.8 | 0.86 | 0.85 | 0.84 | 0.84 | 0.81 | ||
| SNP | Gene | 95% CI ( ) | p-Value | ||
|---|---|---|---|---|---|
| rs3087243 | CTLA4 | 0.56 | 1.54 | (1.17, 2.03) | 0.002 |
| rs2476601 | PTPN22 | 0.08 | 1.63 | (1.04, 2.55) | 0.033 |
| rs1799724 | TNF | 0.13 | 0.84 | (0.56, 1.27) | 0.409 |
| rs1800629 | TNF | 0.16 | 0.89 | (0.61, 1.30) | 0.551 |
| rs3807306 | IRF5 | 0.51 | 0.94 | (0.72, 1.22) | 0.637 |
| Herpes Virus | 95% CI () | p-Value | ||
|---|---|---|---|---|
| HSV1 | 0.42 | 1.60 | (0.83, 3.09) | 0.163 |
| HSV2 | 0.34 | 1.36 | (0.69, 2.66) | 0.377 |
| EBV | 0.93 | 0.65 | (0.21, 1.97) | 0.442 |
| CMV | 0.37 | 0.84 | (0.42, 1.67) | 0.613 |
| VZV | 0.97 | 0.75 | (0.12, 4.63) | 0.757 |
| HHV6 | 0.95 | 1.27 | (0.24, 6.79) | 0.776 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malato, J.; Graça, L.; Sepúlveda, N. Impact of Misdiagnosis in Case-Control Studies of Myalgic Encephalomyelitis/Chronic Fatigue Syndrome. Diagnostics 2023, 13, 531. https://doi.org/10.3390/diagnostics13030531
Malato J, Graça L, Sepúlveda N. Impact of Misdiagnosis in Case-Control Studies of Myalgic Encephalomyelitis/Chronic Fatigue Syndrome. Diagnostics. 2023; 13(3):531. https://doi.org/10.3390/diagnostics13030531
Chicago/Turabian StyleMalato, João, Luís Graça, and Nuno Sepúlveda. 2023. "Impact of Misdiagnosis in Case-Control Studies of Myalgic Encephalomyelitis/Chronic Fatigue Syndrome" Diagnostics 13, no. 3: 531. https://doi.org/10.3390/diagnostics13030531
APA StyleMalato, J., Graça, L., & Sepúlveda, N. (2023). Impact of Misdiagnosis in Case-Control Studies of Myalgic Encephalomyelitis/Chronic Fatigue Syndrome. Diagnostics, 13(3), 531. https://doi.org/10.3390/diagnostics13030531






