A Novel Framework of Manifold Learning Cascade-Clustering for the Informative Frame Selection
Abstract
:1. Introduction
1.1. Early Diagnosis and Narrow-Band Imaging
1.2. Informative Frame Selection for CADx
1.3. Organization
2. Related Work
2.1. Criterion-Based Feature Extraction
2.2. Learning-Based Feature Extraction
2.3. Contributions
- A new scheme couples the state-of-the-art dimensionality reduction techniques and clustering methods for solving the issue. The proposed scheme extracts feature faster than the baseline method [17] and require no effort on the labeling data. This ensures the reliability and effectiveness of the proposed scheme in a clinical setting datasets.
- For the frame reduction or video summarization, the future direction for unsupervised learning methods should involve cluster determination [28]. In this work, we introduce a metric under our scheme, the Calinski-Harabasz Index, to automatically determine cluster numbers.
- In this work, we propose an automatic cluster labeling algorithm using bijections mapping for evaluating the classification performance of unsupervised methods. We further propose a Bayesian optimization cost function algorithm to boost classification performance.
- To the best of the authors’ knowledge, none of the existing works in the literature on computer-aided diagnosis of laryngoscopy attempt to solve the problem using an unsupervised scheme based on the feature learning method. In addition, our methods achieved comparable performance to state-of-the-art supervised learning methods [17,38,39].
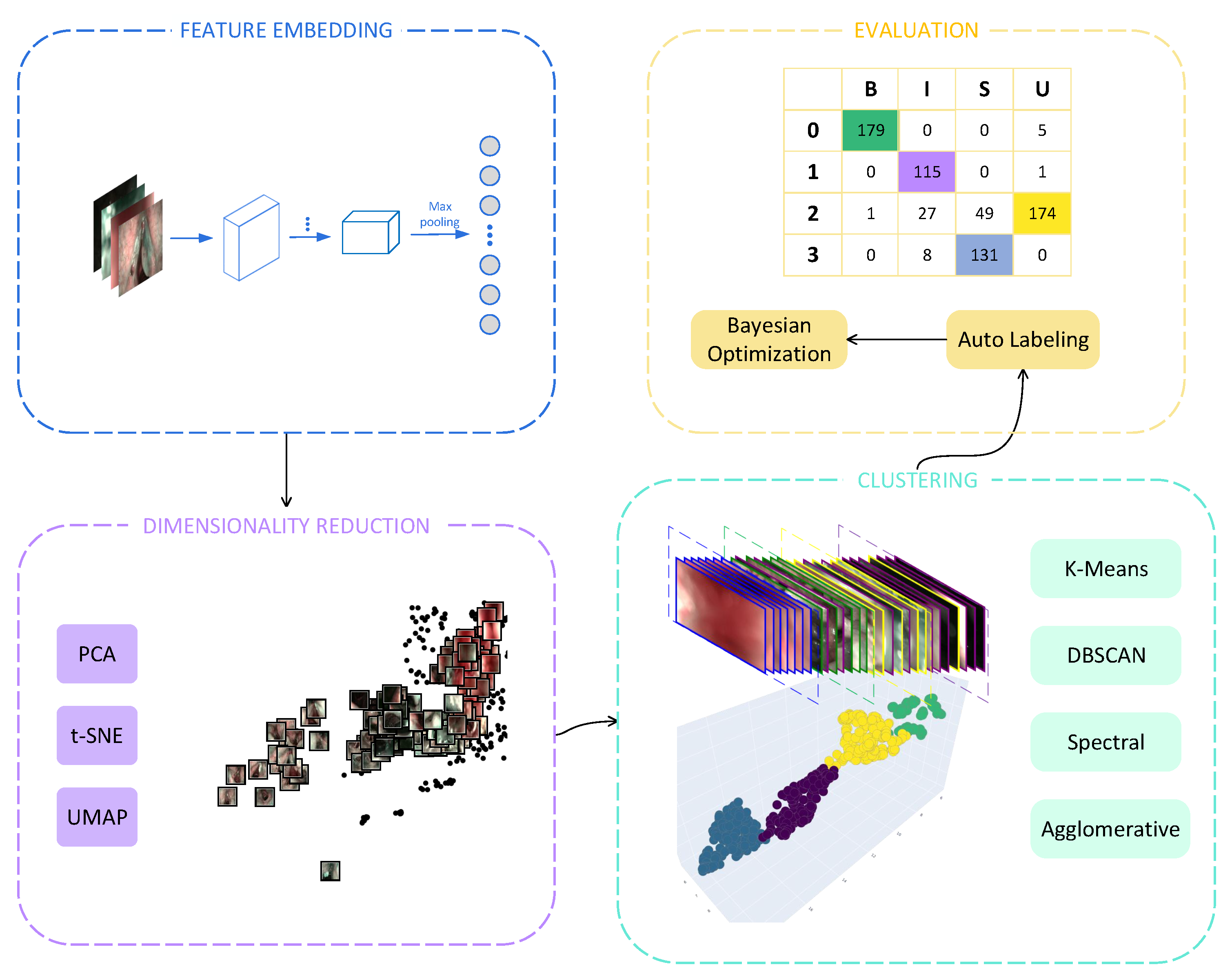
3. Methods
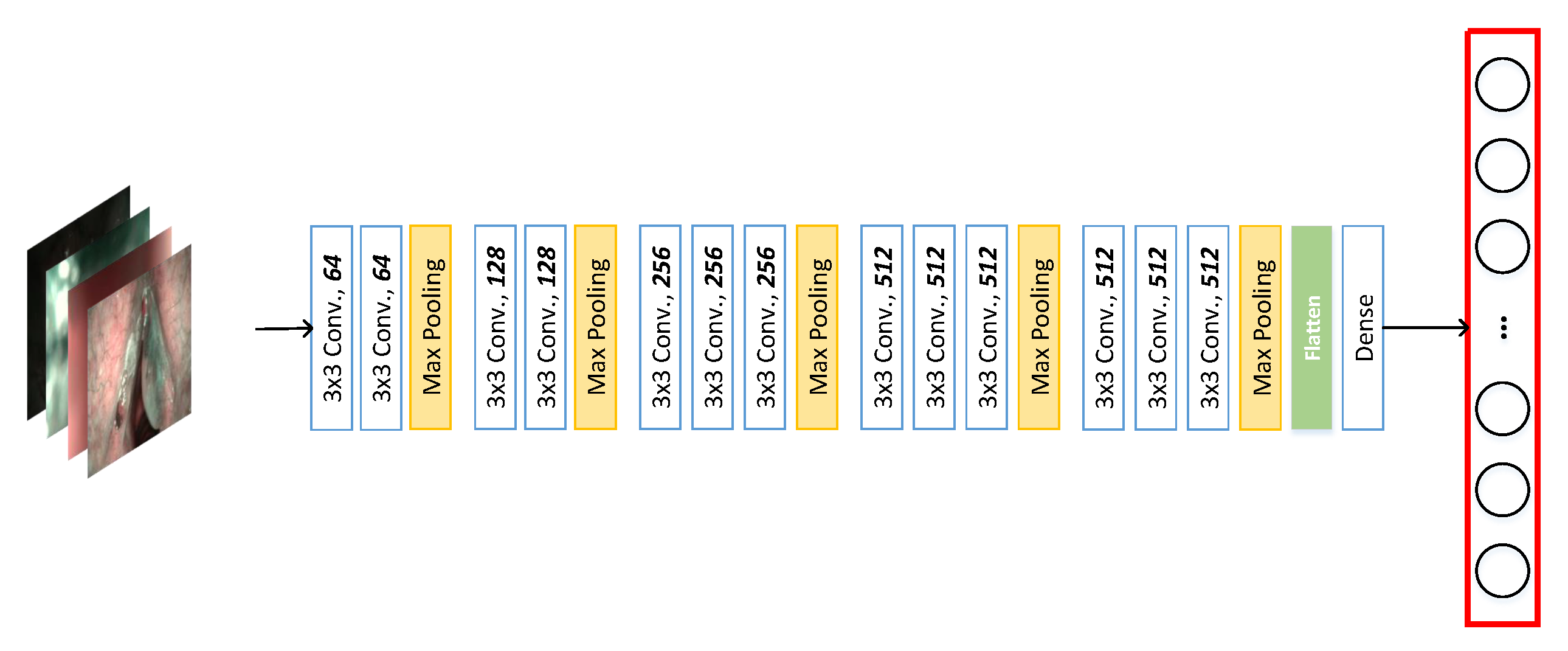
3.1. Feature Embedding
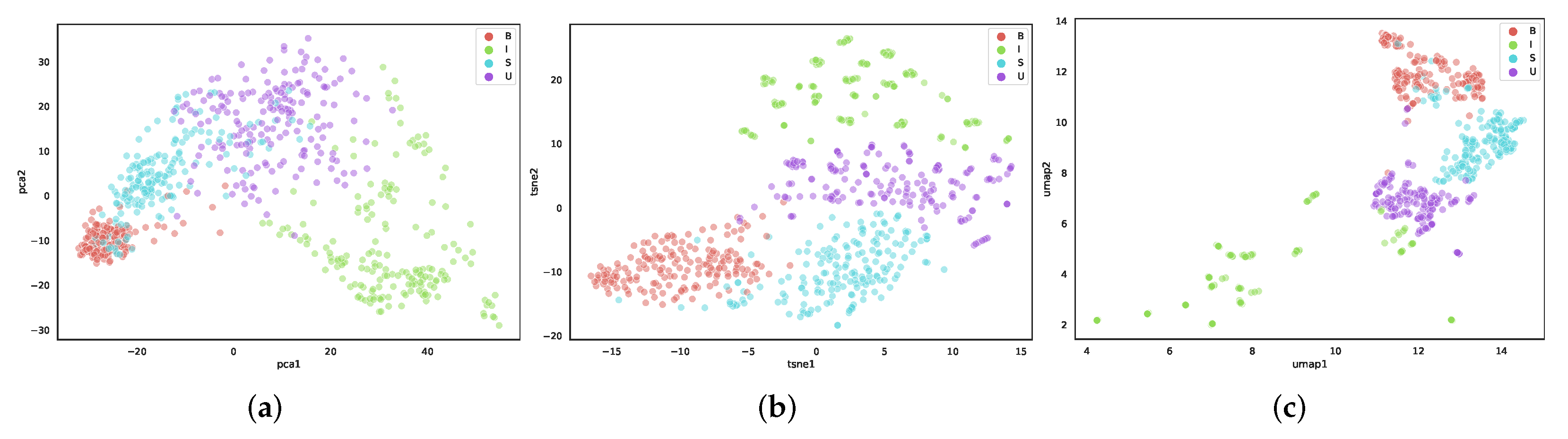
3.2. Dimensionality Reduction
3.2.1. PCA
3.2.2. t-SNE
3.2.3. UMAP
3.3. Clustering
3.3.1. Agglomerative
3.3.2. K-Means
3.3.3. Spectral Clustering
3.3.4. DBSCAN
| Algorithm 1 Cost function for the Bayesian optimization searching |
| Require: , recall of the method; , precision of the method; , parameter space |
| Ensure: number of clusters K = 4 |
| ▹ penalty the label counts deviation |
| ▹ weight for the impact of the variance |
| repeat |
| if method is MinibatchKMeans or Agglomerative or Spectral then |
| , s.t. |
| else if menthod is DBSCAN then |
| count the outlier labels, −1 in the cluster, |
| count the number of kinds of labels except for outliers in the cluster, |
| calculate the variance of the counts of each group deviate from 180, |
| , s.t. |
| end if |
| C. |
| until stop-iteration criteria satisfied |
| return best parameters in |
4. Evaluation
4.1. Dataset
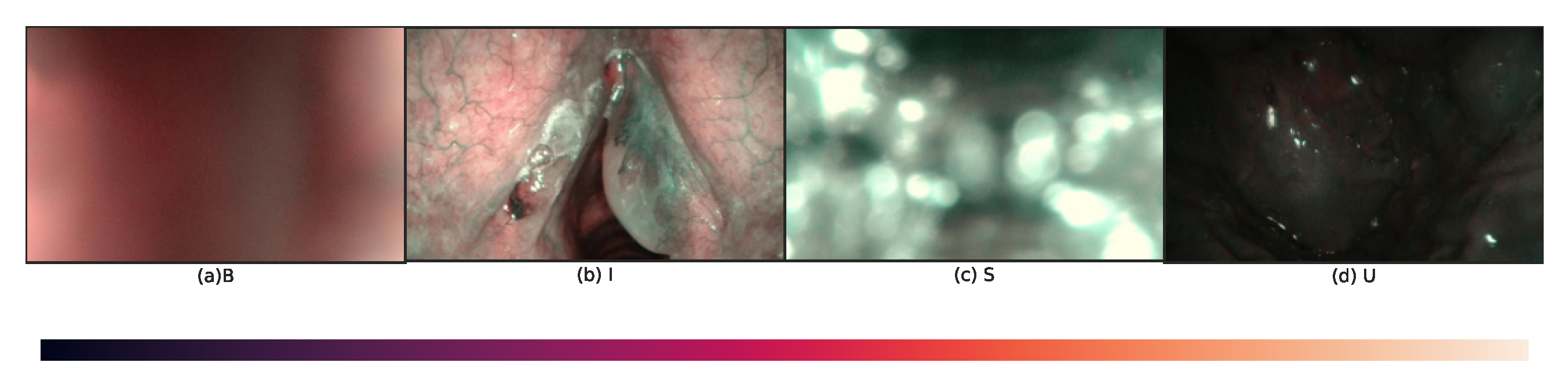
- B, frames should show a homogeneous and widespread blur.
- I, frames should have adequate exposure and visible blood vessels; they may also present micro-blur and small portions of specular reflections (up to 10 per cent of the image area).
- S, frames should present bright white/light-green bubbles or blobs, overlapping with at least half of the image area.
- U, frames should present a high percentage of dark pixels, even though small image portions (up to 10 per cent of the image area) with over or regular exposure are allowed.
4.2. Evaluation Metrics
4.3. Automatic Cluster Labeling
| Algorithm 2 Automatic cluster labeling |
| Require: , images grouped by cluster labels; , images with meaningful intent labels |
| Ensure: number of clusters is 4 |
| for each cluster in do |
| for each class in do |
| calculate intersection number of the and , |
| end for |
| find the max intersection number of in , max |
| update the mapping relationship, |
| end for |
| return f |
4.4. Cost Function in Hyperparameter Tuning
5. Experiments and Results
5.1. Comparison of Dimensionality Reduction Methods
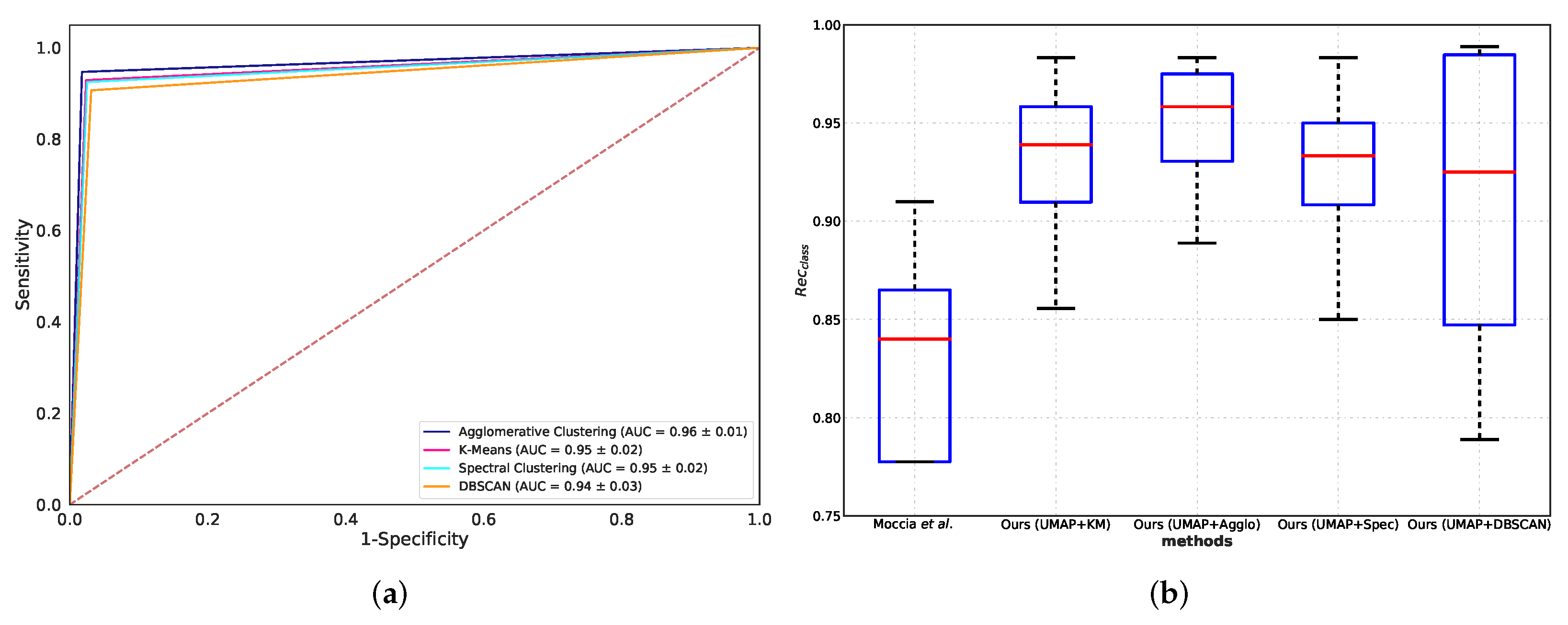
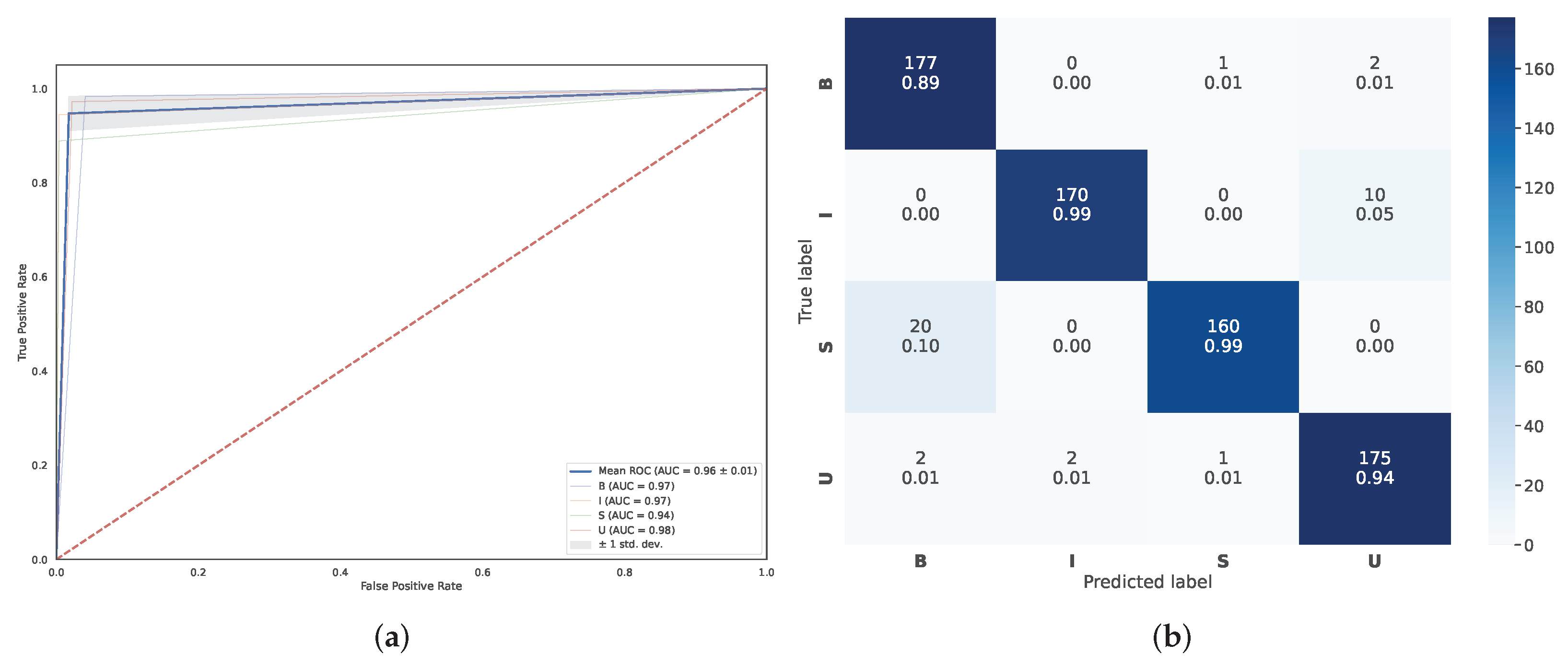
5.2. Classification Performance Comparison
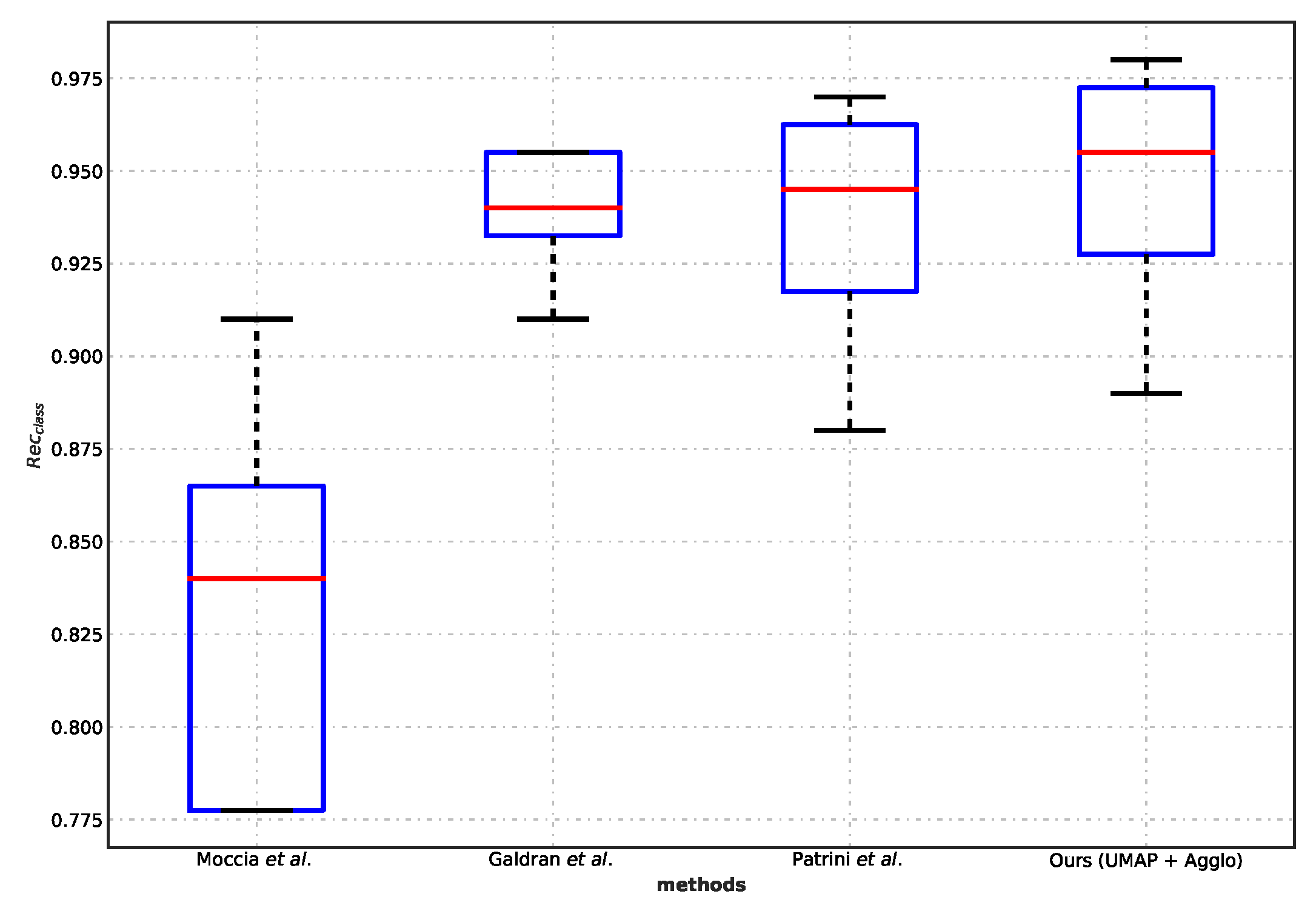
5.3. Comparison with Benchmarks
5.4. Cluster Number Determination
6. Discussion
- We extracted the features using a suitable scale convolutional neural network.
- We employed a persevering global-structure features method, which keeps a minimal number of features for the subsequent clustering.
- The agglomerative clustering maintained a bottom-up fashion dendrogram, which is efficient for the small dataset.
- The introduced metric for cluster number determination needs to be further demonstrated in the dataset close to the clinical setting.
- The proposed automatic cluster labeling algorithm is conditioned on the number of clusters, which should be identical to the defined number of the class.
- The cost function in Bayesian optimization aims to find the best average recall of all classes; thus, the time consumption of the searching algorithm is enormous (Appendix C).
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. NBI-InfFrmaes Dataset
| Video ID | I | B | S | U | |
|---|---|---|---|---|---|
| Fold 1 | 1 | 10 | 10 | 20 | 11 |
| 2 | 10 | 0 | 6 | 9 | |
| 3 | 10 | 0 | 0 | 2 | |
| 4 | 10 | 40 | 23 | 20 | |
| 5 | 10 | 10 | 11 | 3 | |
| 6 | 10 | 0 | 0 | 15 | |
| total | 60 | 60 | 60 | 60 | |
| Fold 2 | 7 | 10 | 28 | 19 | 0 |
| 8 | 10 | 8 | 21 | 5 | |
| 9 | 10 | 3 | 10 | 10 | |
| 10 | 10 | 21 | 10 | 16 | |
| 11 | 10 | 0 | 0 | 14 | |
| 12 | 10 | 0 | 0 | 15 | |
| total | 60 | 60 | 60 | 60 | |
| Fold 3 | 13 | 10 | 17 | 0 | 10 |
| 14 | 10 | 21 | 34 | 22 | |
| 15 | 10 | 0 | 11 | 10 | |
| 16 | 10 | 0 | 9 | 5 | |
| 17 | 10 | 12 | 0 | 2 | |
| 18 | 10 | 10 | 6 | 11 | |
| total | 60 | 60 | 60 | 60 |
Appendix B. Understanding UMAP from Cost Function
Appendix C. Time Consumption Analysis
Appendix C.1. Feature Extraction
Appendix C.2. Hyperparameter Tuning
| K-Means | Agglomerative | Spectral | DBSCAN | |
|---|---|---|---|---|
| Parameters (num) | 4320 | 35,840 | 26,880 | 54,000 |
| CPU time (sec) | 13,078 | 37,523 | 37,039 | 19,940 |
| BO search (step) | 1000 | 5000 | 3000 | 2000 |
| CPU time (sec)/per step | 13.08 | 7.50 | 12.35 | 9.97 |
References
- Bradley, P.J.; Piazza, C.; Paderno, A. A Roadmap of Six Different Pathways to Improve Survival in Laryngeal Cancer Patients. Curr. Opin. Otolaryngol. Head Neck Surg. 2021, 29, 65–78. [Google Scholar] [CrossRef] [PubMed]
- Lauwerends, L.J.; Galema, H.A.; Hardillo, J.A.U.; Sewnaik, A.; Monserez, D.; van Driel, P.B.A.A.; Verhoef, C.; Baatenburg de Jong, R.J.; Hilling, D.E.; Keereweer, S. Current Intraoperative Imaging Techniques to Improve Surgical Resection of Laryngeal Cancer: A Systematic Review. Cancers 2021, 13, 1895. [Google Scholar] [CrossRef]
- Sasco, A.; Secretan, M.; Straif, K. Tobacco Smoking and Cancer: A Brief Review of Recent Epidemiological Evidence. Lung Cancer 2004, 45, S3–S9. [Google Scholar] [CrossRef] [PubMed]
- Brawley, O.W. The Role of Government and Regulation in Cancer Prevention. Lancet Oncol. 2017, 18, e483–e493. [Google Scholar] [CrossRef] [PubMed]
- Zuo, J.J.; Tao, Z.Z.; Chen, C.; Hu, Z.W.; Xu, Y.X.; Zheng, A.Y.; Guo, Y. Characteristics of Cigarette Smoking without Alcohol Consumption and Laryngeal Cancer: Overall and Time-Risk Relation. A Meta-Analysis of Observational Studies. Eur. Arch. Oto-Rhino-Laryngol. 2017, 274, 1617–1631. [Google Scholar] [CrossRef]
- Zhou, X.; Tang, C.; Huang, P.; Mercaldo, F.; Santone, A.; Shao, Y. LPCANet: Classification of Laryngeal Cancer Histopathological Images Using a CNN with Position Attention and Channel Attention Mechanisms. Interdiscip. Sci. Comput. Life Sci. 2021, 13, 666–682. [Google Scholar] [CrossRef]
- Xiong, H.; Lin, P.; Yu, J.G.; Ye, J.; Xiao, L.; Tao, Y.; Jiang, Z.; Lin, W.; Liu, M.; Xu, J.; et al. Computer-Aided Diagnosis of Laryngeal Cancer via Deep Learning Based on Laryngoscopic Images. EBioMedicine 2019, 48, 92–99. [Google Scholar] [CrossRef] [Green Version]
- Cancer.Net. Laryngeal and Hypopharyngeal Cancer: Statistics. Available online: https://www.cancer.net/cancer-types/laryngeal-and-hypopharyngeal-cancer/statistics (accessed on 30 April 2022).
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer Statistics, 2020. CA Cancer J. Clin. 2020, 70, 7–30. [Google Scholar] [CrossRef]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer Statistics, 2016. CA Cancer J. Clin. 2016, 66, 7–30. [Google Scholar] [CrossRef] [Green Version]
- Steuer, C.E.; El-Deiry, M.; Parks, J.R.; Higgins, K.A.; Saba, N.F. An Update on Larynx Cancer. CA: Cancer J. Clin. 2017, 67, 31–50. [Google Scholar] [CrossRef] [Green Version]
- Marioni, G.; Marchese-Ragona, R.; Cartei, G.; Marchese, F.; Staffieri, A. Current Opinion in Diagnosis and Treatment of Laryngeal Carcinoma. Cancer Treat. Rev. 2006, 32, 504–515. [Google Scholar] [CrossRef]
- Paderno, A.; Holsinger, F.C.; Piazza, C. Videomics: Bringing Deep Learning to Diagnostic Endoscopy. Curr. Opin. Otolaryngol. Head Neck Surg. 2021, 29, 143–148. [Google Scholar] [CrossRef]
- Ni, X.G.; Zhang, Q.Q.; Wang, G.Q. Narrow Band Imaging versus Autofluorescence Imaging for Head and Neck Squamous Cell Carcinoma Detection: A Prospective Study. J. Laryngol. Otol. 2016, 130, 1001–1006. [Google Scholar] [CrossRef]
- Qureshi, W.A. Current and Future Applications of the Capsule Camera. Nat. Rev. Drug Discov. 2004, 3, 447–450. [Google Scholar] [CrossRef]
- Ali, H.; Sharif, M.; Yasmin, M.; Rehmani, M.H.; Riaz, F. A Survey of Feature Extraction and Fusion of Deep Learning for Detection of Abnormalities in Video Endoscopy of Gastrointestinal-Tract. Artif. Intell. Rev. 2020, 53, 2635–2707. [Google Scholar] [CrossRef]
- Moccia, S.; Vanone, G.O.; Momi, E.D.; Laborai, A.; Guastini, L.; Peretti, G.; Mattos, L.S. Learning-Based Classification of Informative Laryngoscopic Frames. Comput. Methods Programs Biomed. 2018, 158, 21–30. [Google Scholar] [CrossRef] [Green Version]
- Paolanti, M.; Frontoni, E. Multidisciplinary Pattern Recognition Applications: A Review. Comput. Sci. Rev. 2020, 37, 100276. [Google Scholar] [CrossRef]
- Maghsoudi, O.H.; Talebpour, A.; Soltanian-Zadeh, H.; Alizadeh, M.; Soleimani, H.A. Informative and Uninformative Regions Detection in WCE Frames. J. Adv. Comput. 2014, 3, 12–34. [Google Scholar] [CrossRef]
- Ren, J.; Jing, X.; Wang, J.; Ren, X.; Xu, Y.; Yang, Q.; Ma, L.; Sun, Y.; Xu, W.; Yang, N.; et al. Automatic Recognition of Laryngoscopic Images Using a Deep-Learning Technique. Laryngoscope 2020, 130, E686–E693. [Google Scholar] [CrossRef]
- Cho, W.K. Comparison of Convolutional Neural Network Models for Determination of Vocal Fold Normality in Laryngoscopic Images. J. Voice 2020, 36, 590–598. [Google Scholar] [CrossRef] [PubMed]
- Cho, W.K.; Lee, Y.J.; Joo, H.A.; Jeong, I.S.; Choi, Y.; Nam, S.Y.; Kim, S.Y.; Choi, S.H. Diagnostic Accuracies of Laryngeal Diseases Using a Convolutional Neural Network-Based Image Classification System. Laryngoscope 2021, 131, 2558–2566. [Google Scholar] [CrossRef] [PubMed]
- Yin, L.; Liuy, Y.; Pei, M.; Li, J.; Wu, M.; Jia, Y. Laryngoscope8: Laryngeal Image Dataset and Classification of Laryngeal Disease Based on Attention Mechanism. Pattern Recognit. Lett. 2021, 150, 207–213. [Google Scholar] [CrossRef]
- Yao, P.; Usman, M.; Chen, Y.H.; German, A.; Andreadis, K.; Mages, K.; Rameau, A. Applications of Artificial Intelligence to Office Laryngoscopy: A Scoping Review. Laryngoscope 2021, 132, 1993–2016. [Google Scholar] [CrossRef]
- Kuo, C.F.J.; Chu, Y.H.; Wang, P.C.; Lai, C.Y.; Chu, W.L.; Leu, Y.S.; Wang, H.W. Using Image Processing Technology and Mathematical Algorithm in the Automatic Selection of Vocal Cord Opening and Closing Images from the Larynx Endoscopy Video. Comput. Methods Programs Biomed. 2013, 112, 455–465. [Google Scholar] [CrossRef]
- Atasoy, S.; Mateus, D.; Meining, A.; Yang, G.Z.; Navab, N. Endoscopic Video Manifolds for Targeted Optical Biopsy. IEEE Trans. Med. Imaging 2012, 31, 637–653. [Google Scholar] [CrossRef] [Green Version]
- Bashar, M.K.; Mori, K.; Suenaga, Y.; Kitasaka, T.; Mekada, Y. Detecting Informative Frames from Wireless Capsule Endoscopic Video Using Color and Texture Features. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI, New York, NY, USA, 6–10 September 2008; Metaxas, D., Axel, L., Fichtinger, G., Székely, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 603–610. [Google Scholar] [CrossRef] [Green Version]
- Iakovidis, D.; Tsevas, S.; Polydorou, A. Reduction of Capsule Endoscopy Reading Times by Unsupervised Image Mining. Comput. Med. Imaging Graph. 2010, 34, 471–478. [Google Scholar] [CrossRef]
- Perperidis, A.; Akram, A.; Altmann, Y.; McCool, P.; Westerfeld, J.; Wilson, D.; Dhaliwal, K.; McLaughlin, S. Automated Detection of Uninformative Frames in Pulmonary Optical Endomicroscopy. IEEE Trans. Biomed. Eng. 2017, 64, 87–98. [Google Scholar] [CrossRef] [Green Version]
- Yao, H.; Zhang, X.; Zhou, X.; Liu, S. Parallel Structure Deep Neural Network Using CNN and RNN with an Attention Mechanism for Breast Cancer Histology Image Classification. Cancers 2019, 11, 1901. [Google Scholar] [CrossRef] [Green Version]
- Krotkov, E. Focusing. Int. J. Comput. Vis. 1988, 1, 223–237. [Google Scholar] [CrossRef]
- Bashar, M.; Kitasaka, T.; Suenaga, Y.; Mekada, Y.; Mori, K. Automatic Detection of Informative Frames from Wireless Capsule Endoscopy Images. Med. Image Anal. 2010, 14, 449–470. [Google Scholar] [CrossRef]
- Park, S.; Sargent, D.; Spofford, I.; Vosburgh, K.; A-Rahim, Y. A Colon Video Analysis Framework for Polyp Detection. IEEE Trans. Biomed. Eng. 2012, 59, 1408–1418. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.F.J.; Kao, C.H.; Dlamini, S.; Liu, S.C. Laryngopharyngeal Reflux Image Quantization and Analysis of Its Severity. Sci. Rep. 2020, 10, 10975. [Google Scholar] [CrossRef]
- Kuo, C.F.J.; Lai, W.S.; Barman, J.; Liu, S.C. Quantitative Laryngoscopy with Computer-Aided Diagnostic System for Laryngeal Lesions. Sci. Rep. 2021, 11, 10147. [Google Scholar] [CrossRef]
- Islam, A.B.M.R.; Alammari, A.; Oh, J.; Tavanapong, W.; Wong, J.; de Groen, P.C. Non-Informative Frame Classification in Colonoscopy Videos Using CNNs. In Proceedings of the 2018 3rd International Conference on Biomedical Imaging, Signal Processing. Association for Computing Machinery, Bari, Italy, 11–12 October 2018; pp. 53–60. [Google Scholar] [CrossRef]
- Yao, H.; Stidham, R.W.; Soroushmehr, R.; Gryak, J.; Najarian, K. Automated Detection of Non-Informative Frames for Colonoscopy through a Combination of Deep Learning and Feature Extraction. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 2402–2406. [Google Scholar] [CrossRef]
- Patrini, I.; Ruperti, M.; Moccia, S.; Mattos, L.S.; Frontoni, E.; De Momi, E. Transfer Learning for Informative-Frame Selection in Laryngoscopic Videos through Learned Features. Med. Biol. Eng. Comput. 2020, 58, 1225–1238. [Google Scholar] [CrossRef]
- Galdran, A.; Costa, P.; Campilho, A. Real-Time Informative Laryngoscopic Frame Classification with Pre-Trained Convolutional Neural Networks. In Proceedings of the IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 87–90. [Google Scholar] [CrossRef]
- Yao, P.; Witte, D.; Gimonet, H.; German, A.; Andreadis, K.; Cheng, M.; Sulica, L.; Elemento, O.; Barnes, J.; Rameau, A. Automatic Classification of Informative Laryngoscopic Images Using Deep Learning. Laryngoscope Investig. Otolaryngol. 2022, 7, 460–466. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.; van Ginneken, B.; Sánchez, C.I. A Survey on Deep Learning in Medical Image Analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [Green Version]
- Ravì, D.; Wong, C.; Deligianni, F.; Berthelot, M.; Andreu-Perez, J.; Lo, B.; Yang, G.Z. Deep Learning for Health Informatics. IEEE J. Biomed. Health Inform. 2017, 21, 4–21. [Google Scholar] [CrossRef] [Green Version]
- Van Der Maaten, L.; Postma, E.; Van den Herik, J. Dimensionality reduction: A comparative review. J. Mach. Learn. Res. 2009, 10, 13. [Google Scholar]
- Van Der Maaten, L.; Hinton, G. Visualizing Data Using T-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2020, arXiv:1802.03426. [Google Scholar]
- Conlen, M.; Hohman, F. The Beginner’s Guide to Dimensionality Reduction. In Proceedings of the Workshop on Visualization for AI Explainability (VISxAI) at IEEE VIS, Berlin, Germany, 21–26 October 2018. [Google Scholar]
- Coenen, A.; Pearce, A. Understanding UMAP. Available online: https://pair-code.github.io/understanding-umap/ (accessed on 29 March 2022).
- Kotsiantis, S.; Pintelas, P. Recent Advances in Clustering: A Brief Survey. WSEAS Trans. Inf. Sci. Appl. 2004, 1, 73–81. [Google Scholar]
- Ackermann, M.R.; Blömer, J.; Kuntze, D.; Sohler, C. Analysis of Agglomerative Clustering. Algorithmica 2014, 69, 184–215. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data Clustering: A Review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Von Luxburg, U. A Tutorial on Spectral Clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Caliński, T.; Harabasz, J. A Dendrite Method for Cluster Analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Turner, R.; Eriksson, D.; McCourt, M.; Kiili, J.; Laaksonen, E.; Xu, Z.; Guyon, I. Bayesian Optimization Is Superior to Random Search for Machine Learning Hyperparameter Tuning: Analysis of the Black-Box Optimization Challenge 2020. arXiv 2021, arXiv:2104.10201. [Google Scholar] [CrossRef]
- Tang, J.; Liu, J.; Zhang, M.; Mei, Q. Visualizing Large-scale and High-dimensional Data. In Proceedings of the 25th International Conference on World Wide Web, Montréal, Québec, QC, Canada, 11–15 April 2016; pp. 287–297. [Google Scholar] [CrossRef] [Green Version]
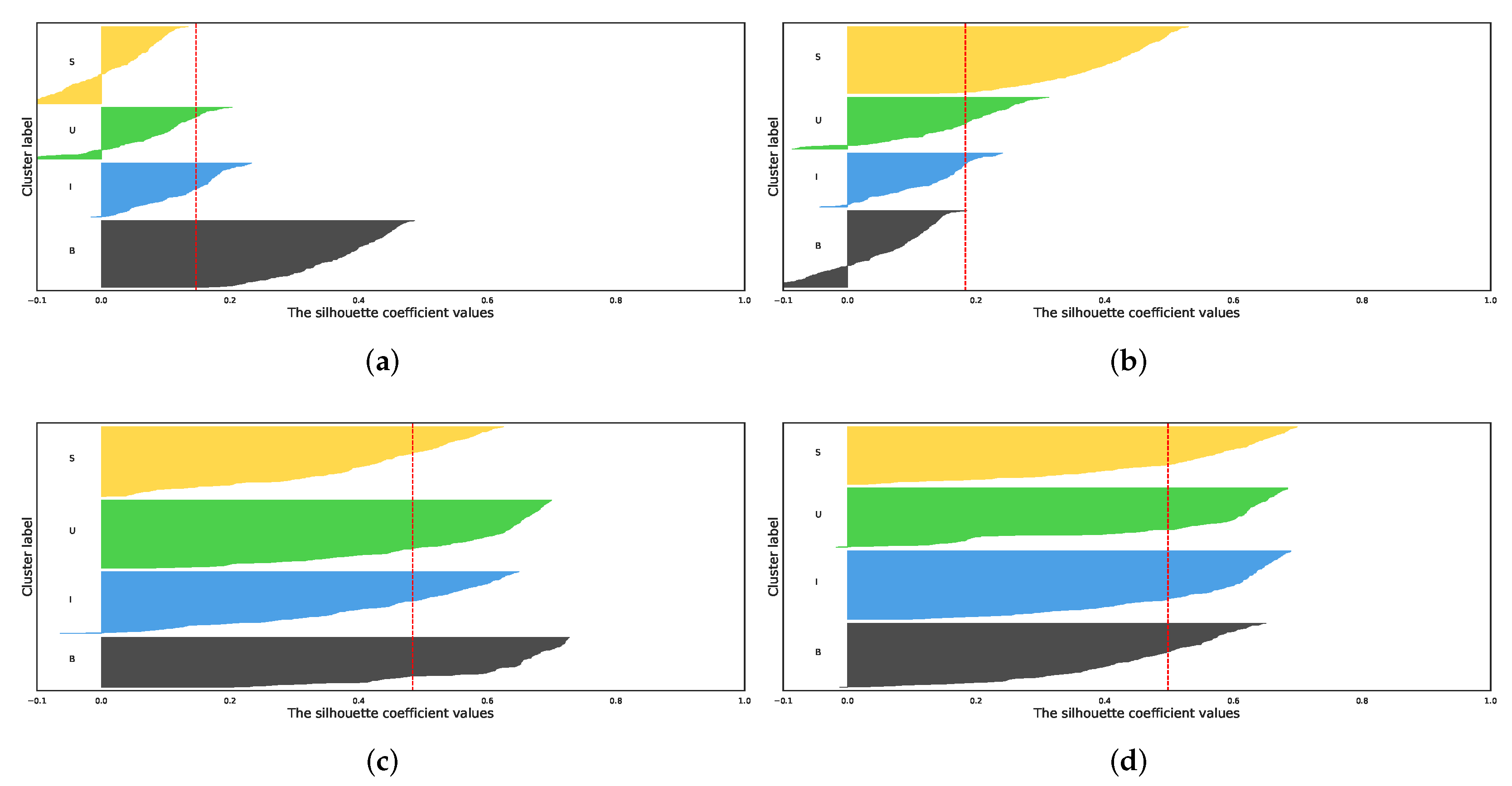
| Vanilla K-Means | PCA + K-Means | t-SNE + K-Means | UMAP + K-Means | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | 0.90 | 0.97 | 0.93 | 0.90 | 0.97 | 0.93 | 0.89 | 0.97 | 0.93 | 0.89 | 0.98 | 0.94 |
| I | 1.00 | 0.87 | 0.93 | 1.00 | 0.87 | 0.93 | 1.00 | 0.81 | 0.89 | 1.00 | 0.95 | 0.97 |
| S | 0.94 | 0.78 | 0.85 | 0.94 | 0.78 | 0.85 | 0.88 | 0.87 | 0.87 | 0.93 | 0.86 | 0.89 |
| U | 0.78 | 0.97 | 0.87 | 0.79 | 0.97 | 0.87 | 0.80 | 0.89 | 0.85 | 0.90 | 0.93 | 0.92 |
| Median | 0.92 | 0.92 | 0.90 | 0.92 | 0.92 | 0.90 | 0.89 | 0.88 | 0.88 | 0.92 | 0.94 | 0.93 |
| IQR | 0.13 | 0.15 | 0.07 | 0.13 | 0.15 | 0.07 | 0.11 | 0.09 | 0.05 | 0.07 | 0.07 | 0.05 |
| Spectral Clustering | PCA + Spectral Clustering | t-SNE + Spectral Clustering | UMAP + Spectral Clustering | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | 0.25 | 1.00 | 0.40 | 0.25 | 1.00 | 0.40 | 0.31 | 1.00 | 0.47 | 0.89 | 0.98 | 0.93 |
| I | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.74 | 0.85 | 0.99 | 0.94 | 0.97 |
| S | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.92 | 0.85 | 0.88 |
| U | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.91 | 0.93 | 0.92 |
| Median | - | - | - | - | - | - | - | - | - | 0.92 | 0.94 | 0.93 |
| IQR | - | - | - | - | - | - | - | - | - | 0.06 | 0.07 | 0.05 |
| Agglomerative Clustering | PCA + Agglomerative Clustering | t-SNE + Agglomerative Clustering | UMAP + Agglomerative Clustering | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | 0.89 | 0.98 | 0.93 | 0.91 | 0.94 | 0.93 | 0.89 | 0.99 | 0.93 | 0.89 | 0.98 | 0.93 |
| I | 1.00 | 0.83 | 0.91 | 1.00 | 0.83 | 0.91 | 0.95 | 0.92 | 0.93 | 0.99 | 0.94 | 0.97 |
| S | 0.99 | 0.88 | 0.93 | 0.90 | 0.91 | 0.91 | 0.99 | 0.60 | 0.75 | 0.99 | 0.89 | 0.94 |
| U | 0.84 | 0.99 | 0.91 | 0.84 | 0.95 | 0.89 | 0.71 | 0.93 | 0.81 | 0.94 | 0.97 | 0.95 |
| Median | 0.94 | 0.93 | 0.92 | 0.91 | 0.93 | 0.91 | 0.92 | 0.93 | 0.87 | 0.97 | 0.96 | 0.95 |
| IQR | 0.13 | 0.13 | 0.02 | 0.09 | 0.08 | 0.02 | 0.17 | 0.20 | 0.15 | 0.08 | 0.06 | 0.03 |
| SVM [17] | Fine-tuned SqueezeNet [39] | Fine-tuned VGG16 [38] | Ours (UMAP + Agglo) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | 0.76 | 0.83 | 0.79 | 0.94 | 0.94 | 0.94 | 0.92 | 0.96 | 0.94 | 0.89 | 0.98 | 0.93 |
| I | 0.91 | 0.91 | 0.91 | 0.97 | 1.00 | 0.98 | 0.97 | 0.97 | 0.97 | 0.99 | 0.94 | 0.97 |
| S | 0.78 | 0.62 | 0.69 | 0.93 | 0.91 | 0.91 | 0.93 | 0.88 | 0.91 | 0.99 | 0.89 | 0.94 |
| U | 0.76 | 0.85 | 0.80 | 0.97 | 0.94 | 0.95 | 0.92 | 0.93 | 0.93 | 0.94 | 0.97 | 0.95 |
| Median | 0.77 | 0.84 | 0.80 | 0.96 | 0.94 | 0.95 | 0.93 | 0.95 | 0.94 | 0.97 | 0.96 | 0.95 |
| IQR | 0.09 | 0.16 | 0.12 | 0.04 | 0.05 | 0.04 | 0.03 | 0.06 | 0.04 | 0.08 | 0.06 | 0.03 |
| n_cluster | Vanilla↑ | PCA ↑ | t-SNE ↑ | UMAP ↑ |
|---|---|---|---|---|
| 2 | 185.55 | 226.95 | 1445.76 | 1097.70 |
| 3 | 148.47 | 186.72 | 1470.55 | 1285.14 |
| 4 | 122.82 | 157.26 | 1696.34 | 1529.70 |
| 5 | 104.90 | 136.15 | 1564.44 | 1384.12 |
| 6 | 93.23 | 122.66 | 1500.42 | 1357.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wu, L.; Wei, L.; Wu, H.; Lin, Y. A Novel Framework of Manifold Learning Cascade-Clustering for the Informative Frame Selection. Diagnostics 2023, 13, 1151. https://doi.org/10.3390/diagnostics13061151
Zhang L, Wu L, Wei L, Wu H, Lin Y. A Novel Framework of Manifold Learning Cascade-Clustering for the Informative Frame Selection. Diagnostics. 2023; 13(6):1151. https://doi.org/10.3390/diagnostics13061151
Chicago/Turabian StyleZhang, Lei, Linjie Wu, Liangzhuang Wei, Haitao Wu, and Yandan Lin. 2023. "A Novel Framework of Manifold Learning Cascade-Clustering for the Informative Frame Selection" Diagnostics 13, no. 6: 1151. https://doi.org/10.3390/diagnostics13061151
APA StyleZhang, L., Wu, L., Wei, L., Wu, H., & Lin, Y. (2023). A Novel Framework of Manifold Learning Cascade-Clustering for the Informative Frame Selection. Diagnostics, 13(6), 1151. https://doi.org/10.3390/diagnostics13061151






