SAA-UNet: Spatial Attention and Attention Gate UNet for COVID-19 Pneumonia Segmentation from Computed Tomography
Abstract
:1. Introduction
- We propose the spatial attention and attention gate UNet model (SAA-UNet) based on attention UNet (Att-UNet) and spatial attention UNet (SA-UNet). We took the attention approach proposed by Ozan Oktay et al. [25] to focus on COVID-19 infection regions. The local features vector of infection improved the performance compared to gating established on a global feature vector. We took the spatial attention module (SAM) approach proposed by Changlu Guo et al. [26] to deal with features fed to the bridge of SAA-UNet from the encoder to the decoder. This makes it take essential features needed in spatial information and helps reduce the number of parameters.
- SAA-UNet proved to be effective in segmenting the infection areas in CT images of COVID-19 patients.
- SAA-UNet showed good generalization when applied to different datasets.
2. Related Work
3. Methodology
3.1. Pre-Processing of Images
3.2. Spatial Attention and Attention UNet Model
3.3. Spatial Attention Module
3.4. Attention Gating Module
| Algorithm 1: The pseudocode of the proposed SAA-UNet model |
|
3.5. Combination of Weighted Cross-Entropy Loss Function, Dice Loss, and Boundary Loss
3.6. Performance Metrics
4. Datasets
5. Data Analysis and Preprocessing
5.1. Preprocessing of MedSeg and Radiopaedia 9P Datasets
5.2. Preprocessing of Zenodo 20P Dataset
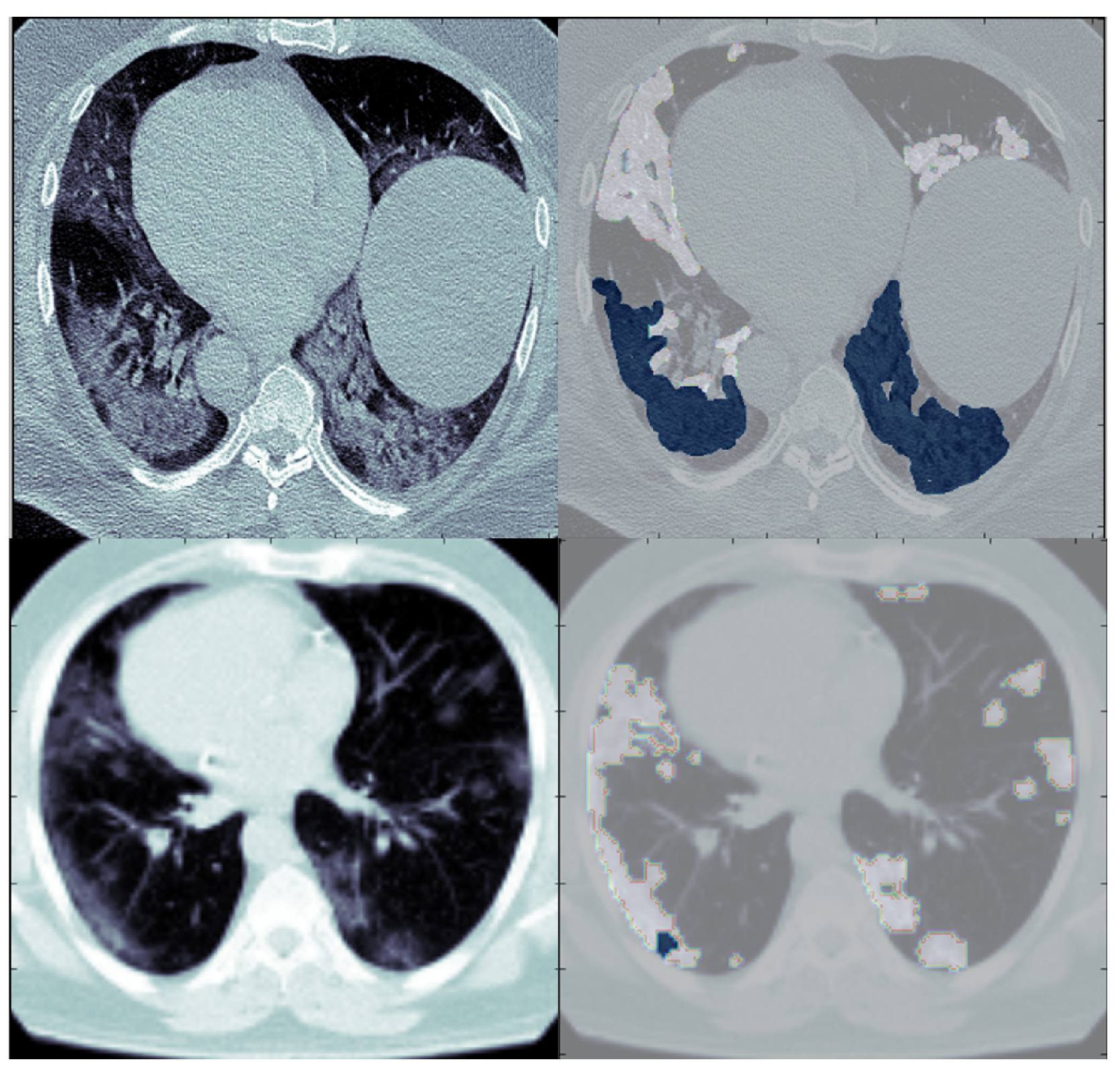
6. Experiments and Results
6.1. Implementation Details
6.2. Binary Class Classification
6.3. Multi-Class Classification
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, H.; Stratton, C.W.; Tang, Y.W. Outbreak of pneumonia of unknown etiology in Wuhan, China: The mystery and the miracle. J. Med. Virol. 2020, 92, 401–402. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Statement on the Second Meeting of the International Health Regulations (2005) Emergency Committee Regarding the Outbreak of Novel Coronavirus (2019-nCoV). Available online: https://www.who.int/news/item/30-01-2020-statement-on-the-second-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov) (accessed on 30 August 2021).
- Singhal, T. A review of coronavirus disease-2019 (COVID-19). Indian J. Pediatr. 2020, 87, 281–286. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. WHO Director-General’s Remarks at the Media Briefing on 2019-nCoV on 11 February 2020. 2020. Available online: https://www.who.int/director-general/speeches/detail/who-director-general-s-remarks-at-the-media-briefing-on-2019-ncov-on-11-february-2020 (accessed on 30 August 2021).
- Ahmed, S.F.; Quadeer, A.A.; McKay, M.R. Preliminary identification of potential vaccine targets for the COVID-19 coronavirus (SARS-CoV-2) based on SARS-CoV immunological studies. Viruses 2020, 12, 254. [Google Scholar] [CrossRef] [PubMed]
- Greenberg, S.B. Update on human rhinovirus and coronavirus infections. In Seminars in Respiratory and Critical Care Medicine; Thieme Medical Publishers: New York, NY, USA, 2016; Volume 37, pp. 555–571. [Google Scholar]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- Rothe, C.; Schunk, M.; Sothmann, P.; Bretzel, G.; Froeschl, G.; Wallrauch, C.; Zimmer, T.; Thiel, V.; Janke, C.; Guggemos, W.; et al. Transmission of 2019-nCoV infection from an asymptomatic contact in Germany. N. Engl. J. Med. 2020, 382, 970–971. [Google Scholar] [CrossRef]
- WHO Director-General’s Opening Remarks at the Media Briefing on COVID-19—11 March 2020. Available online: https://www.who.int/director-general/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-COVID-19—11-march-2020 (accessed on 30 August 2021).
- WHO Coronavirus (COVID-19) 2021. Available online: https://covid19.who.int/ (accessed on 2 September 2021).
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.; Lau, E.H.; Wong, J.Y.; et al. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef]
- Daamen, A.R.; Bachali, P.; Owen, K.A.; Kingsmore, K.M.; Hubbard, E.L.; Labonte, A.C.; Robl, R.; Shrotri, S.; Grammer, A.C.; Lipsky, P.E. Comprehensive transcriptomic analysis of COVID-19 blood, lung, and airway. Sci. Rep. 2021, 11, 7052. [Google Scholar] [CrossRef]
- Bai, H.X.; Hsieh, B.; Xiong, Z.; Halsey, K.; Choi, J.W.; Tran, T.M.L.; Pan, I.; Shi, L.B.; Wang, D.C.; Mei, J.; et al. Performance of radiologists in differentiating COVID-19 from non-COVID-19 viral pneumonia at chest CT. Radiology 2020, 296, E46–E54. [Google Scholar] [CrossRef]
- Dai, W.C.; Zhang, H.W.; Yu, J.; Xu, H.J.; Chen, H.; Luo, S.P.; Zhang, H.; Liang, L.H.; Wu, X.L.; Lei, Y.; et al. CT imaging and differential diagnosis of COVID-19. Can. Assoc. Radiol. J. 2020, 71, 195–200. [Google Scholar] [CrossRef]
- Jain, U. Effect of COVID-19 on the Organs. Cureus 2020, 12, e9540. [Google Scholar] [CrossRef]
- Li, B.; Shen, J.; Li, L.; Yu, C. Radiographic and clinical features of children with coronavirus disease (COVID-19) pneumonia. Indian Pediatr. 2020, 57, 423–426. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, P.; Vig, R.; Bhadoria, S.; Dethe, C. Role of segmentation in medical imaging: A comparative study. Int. J. Comput. Appl. 2011, 29, 54–61. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder–decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: 4th International Workshop, DLMIA 2018, and 8th International Workshop, ML-CDS 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 20 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–11. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Overview of Open Access COVID-19 Imaging Datasets for Teaching, Training and Research. Available online: https://www.eibir.org/covid-19-imaging-datasets/ (accessed on 22 August 2021).
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention u-net: Learning where to look for the pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Guo, C.; Szemenyei, M.; Yi, Y.; Wang, W.; Chen, B.; Fan, C. Sa-unet: Spatial attention u-net for retinal vessel segmentation. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 1236–1242. [Google Scholar]
- Voulodimos, A.; Protopapadakis, E.; Katsamenis, I.; Doulamis, A.; Doulamis, N. Deep learning models for COVID-19 infected area segmentation in CT images. In Proceedings of the 14th PErvasive Technologies Related to Assistive Environments Conference, Virtual, Greece, 29 June–2 July 2021; pp. 404–411. [Google Scholar]
- Walvekar, S.; Shinde, S. Efficient medical image segmentation of COVID-19 chest ct images based on deep learning techniques. In Proceedings of the 2021 International Conference on Emerging Smart Computing and Informatics (ESCI), Pune, India, 5–7 March 2021; pp. 203–206. [Google Scholar]
- Ahmed, I.; Chehri, A.; Jeon, G. A Sustainable Deep Learning-Based Framework for Automated Segmentation of COVID-19 Infected Regions: Using UNet with an Attention Mechanism and Boundary Loss Function. Electronics 2022, 11, 2296. [Google Scholar] [CrossRef]
- Zhou, T.; Canu, S.; Ruan, S. Automatic COVID-19 CT segmentation using UNet integrated spatial and channel attention mechanism. Int. J. Imaging Syst. Technol. 2021, 31, 16–27. [Google Scholar] [CrossRef]
- Saeedizadeh, N.; Minaee, S.; Kafieh, R.; Yazdani, S.; Sonka, M. COVID TV-Unet: Segmenting COVID-19 chest CT images using connectivity imposed Unet. Comput. Method. Programs Biomed. Update 2021, 1, 100007. [Google Scholar] [CrossRef]
- Ben-Haim, T.; Sofer, R.M.; Ben-Arie, G.; Shelef, I.; Raviv, T.R. A Deep Ensemble Learning Approach to Lung CT Segmentation for COVID-19 Severity Assessment. In Proceedings of the 2022 IEEE International Conference on Image Processing (ICIP), Bordeaux, France, 16–19 October 2022; pp. 151–155. [Google Scholar]
- Zhang, Z.; Xue, H.; Zhou, G. A plug-and-play attention module for CT-based COVID-19 segmentation. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 2078, p. 012041. [Google Scholar]
- Wang, Z.; Voiculescu, I. Quadruple augmented pyramid network for multi-class COVID-19 segmentation via CT. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Virtual, 1–5 November 2021; pp. 2956–2959. [Google Scholar]
- Yang, Q.; Li, Y.; Zhang, M.; Wang, T.; Yan, F.; Xie, C. Automatic segmentation of COVID-19 CT images using improved MultiResUNet. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 1614–1618. [Google Scholar]
- Ibtehaz, N.; Rahman, M.S. MultiResUNet: Rethinking the UNet architecture for multimodal biomedical image segmentation. Neural Netw. 2020, 121, 74–87. [Google Scholar] [CrossRef]
- Enshaei, N.; Afshar, P.; Heidarian, S.; Mohammadi, A.; Rafiee, M.J.; Oikonomou, A.; Fard, F.B.; Plataniotis, K.N.; Naderkhani, F. An ensemble learning framework for multi-class COVID-19 lesion segmentation from chest ct images. In Proceedings of the 2021 IEEE International Conference on Autonomous Systems (ICAS), Montreal, QC, Canada, 11–13 August 2021; pp. 1–6. [Google Scholar]
- Uçar, M. Automatic segmentation of COVID-19 from computed tomography images using modified UNet model-based majority voting approach. Neural Comput. Appl. 2022, 34, 21927–21938. [Google Scholar] [CrossRef]
- Pei, H.Y.; Yang, D.; Liu, G.R.; Lu, T. MPS-net: Multi-point supervised network for ct image segmentation of COVID-19. IEEE Access 2021, 9, 47144–47153. [Google Scholar] [CrossRef]
- Budak, Ü.; Çıbuk, M.; Cömert, Z.; Şengür, A. Efficient COVID-19 segmentation from CT slices exploiting semantic segmentation with integrated attention mechanism. J. Digit. Imaging 2021, 34, 263–272. [Google Scholar] [CrossRef]
- Raj, A.N.J.; Zhu, H.; Khan, A.; Zhuang, Z.; Yang, Z.; Mahesh, V.G.; Karthik, G. ADID-UNET—A segmentation model for COVID-19 infection from lung CT scans. PeerJ Comput. Sci. 2021, 7, e349. [Google Scholar]
- Chen, Y.; Zhou, T.; Chen, Y.; Feng, L.; Zheng, C.; Liu, L.; Hu, L.; Pan, B. HADCNet: Automatic segmentation of COVID-19 infection based on a hybrid attention dense connected network with dilated convolution. Comput. Biol. Med. 2022, 149, 105981. [Google Scholar] [CrossRef] [PubMed]
- Khalifa, N.E.M.; Manogaran, G.; Taha, M.H.N.; Loey, M. A deep learning semantic segmentation architecture for COVID-19 lesions discovery in limited chest CT datasets. Expert Syst. 2022, 39, e12742. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Liu, Y.; Li, S.; Xu, J. MiniSeg: An Extremely Minimum Network for Efficient COVID-19 Segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Wu, X.; Zhang, Z.; Guo, L.; Chen, H.; Luo, Q.; Jin, B.; Gu, W.; Lu, F.; Chen, J. FAM: Focal attention module for lesion segmentation of COVID-19 CT images. J. Real-Time Image Process. 2022, 19, 1091–1104. [Google Scholar] [CrossRef] [PubMed]
- DUDA-Net: A double U-shaped dilated attention network for automatic infection area segmentation in COVID-19 lung CT images. Int. J. Comput. Assist. Radiol. Surg. 2021, 16, 1425–1434. [CrossRef] [PubMed]
- Singh, V.K.; Abdel-Nasser, M.; Pandey, N.; Puig, D. Lunginfseg: Segmenting COVID-19 infected regions in lung ct images based on a receptive-field-aware deep learning framework. Diagnostics 2021, 11, 158. [Google Scholar] [CrossRef]
- Karthik, R.; Menaka, R.; M, H.; Won, D. Contour-enhanced attention CNN for CT-based COVID-19 segmentation. Pattern Recognit. 2022, 125, 108538. [Google Scholar] [CrossRef]
- Rajamani, K.T.; Siebert, H.; Heinrich, M.P. Dynamic deformable attention network (DDANet) for COVID-19 lesions semantic segmentation. J. Biomed. Inform. 2021, 119, 103816. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, X.; Huang, L.; Huang, C.; Wei, Y.; Liu, W. Ccnet: Criss-cross attention for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 603–612. [Google Scholar]
- Bressem, K.K.; Niehues, S.M.; Hamm, B.; Makowski, M.R.; Vahldiek, J.L.; Adams, L.C. 3D UNet for segmentation of COVID-19 associated pulmonary infiltrates using transfer learning: State-of-the-art results on affordable hardware. arXiv 2021, arXiv:2101.09976. [Google Scholar]
- Aswathy, A.L.; Chandra, S.S.V. Cascaded 3D UNet architecture for segmenting the COVID-19 infection from lung CT volume. Sci. Rep. 2022, 12, 3090. [Google Scholar] [CrossRef]
- Modeling Data with NumPy Image Volumes. Available online: https://oak-tree.tech/blog/numpy-image-volumes (accessed on 20 October 2022).
- Bradski, G. The openCV library. Dr. Dobb’s J. Softw. Tools Prof. Program. 2000, 25, 120–123. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Topsøe, F. Bounds for entropy and divergence for distributions over a two-element set. J. Ineq. Pure Appl. Math 2001, 2, 300. [Google Scholar]
- Kervadec, H.; Bouchtiba, J.; Desrosiers, C.; Granger, E.; Dolz, J.; Ayed, I.B. Boundary loss for highly unbalanced segmentation. In Proceedings of the International Conference on Medical Imaging with Deep Learning, London, UK, 8–10 July 2019; pp. 285–296. [Google Scholar]
- Boykov, Y.; Kolmogorov, V.; Cremers, D.; Delong, A. An integral solution to surface evolution PDEs via geo-cuts. In Proceedings of the Computer Vision—ECCV 2006: 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 409–422. [Google Scholar]
- COVID-19 CT Segmentation Dataset 2020. Available online: http://medicalsegmentation.com/covid19/ (accessed on 22 August 2021).
- Italian Society of Medical and Interventional. Available online: https://sirm.org/# (accessed on 15 September 2021).
- COVID-19 CT Images Segmentation. Available online: https://www.kaggle.com/c/covid-segmentation (accessed on 22 August 2021).
- Jun, M.; Cheng, G.; Yixin, W.; Xingle, A.; Jiantao, G.; Ziqi, Y.; Minqing, Z.; Xin, L.; Xueyuan, D.; Shucheng, C.; et al. COVID-19 CT Lung and Infection Segmentation Dataset. 2020. Available online: https://zenodo.org/record/3757476#.ZFhtJs5BxPY (accessed on 24 April 2023).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Müller, D.; Soto-Rey, I.; Kramer, F. Robust chest CT image segmentation of COVID-19 lung infection based on limited data. Inform. Med. Unlocked 2021, 25, 100681. [Google Scholar] [CrossRef]
- Shiri, I.; Arabi, H.; Salimi, Y.; Sanaat, A.; Akhavanallaf, A.; Hajianfar, G.; Askari, D.; Moradi, S.; Mansouri, Z.; Pakbin, M.; et al. COLI-Net: Deep learning-assisted fully automated COVID-19 lung and infection pneumonia lesion detection and segmentation from chest computed tomography images. Int. J. Imaging Syst. Technol. 2022, 32, 12–25. [Google Scholar] [CrossRef]














| Dataset | Patients CT Cases | # of Slices | COVID-19 Infection | Non- COVID-19 | Annotation | Training Slices in Each Fold | Validation Slices in Each Fold | Testing |
|---|---|---|---|---|---|---|---|---|
| MedSeg | >40 | 100 | 96 | 4 | GGO, Consolidation, Lungs, Background | 81 | 9 | 10 |
| Radiopaedia 9P | 9 | 829 | 373 | 456 | GGO, Consolidation, Lungs, Background | 671 | 75 | 83 |
| MedSeg+Radiopaedia9P | >49 | 929 | 469 | 460 | GGO, Consolidation, Lungs, Background | 752 | 84 | 93 |
| Zenodo 20P | 20 | 3520 | 1793 | 1727 | Infection, Left Lung, Right Lung, Background | 2851 | 317 | 352 |
| Parameter Name | Parameter Value |
|---|---|
| Number of parameters | 18,713,274 |
| Optimizer | Adam |
| Learning rate | 10−4 |
| Batch size | 2 |
| Epoch | 150 |
| Image size | 512 × 512, 128 × 128 |
| Data augmentation method | Without |
| Dataset | Mean Dice | Dice Inf | Dice Back | Mean IOU | Accuracy | Specificity | Sensitivity | Precision | F1-Score |
|---|---|---|---|---|---|---|---|---|---|
| MedSeg | 0.854 ± 0.13 | 0.725 ± 0.04 | 0.983 ± 0.003 | 0.803 ± 0.4 | 0.970 ± 0.005 | 0.968 ± 0.005 | 0.872 ± 0.03 | 0.892 ± 0.03 | 0.880 ± 0.03 |
| Radiopaedia 9P | 0.945 ± 0.05 | 0.892 ± 0.01 | 0.999 ± 0.0002 | 0.891 ± 0.01 | 0.997 ± 0.0006 | 0.997 ± 0.0004 | 0.934 ± 0.01 | 0.943 ± 0.007 | 0.938 ± 0.008 |
| MedSeg + Radiopaedia 9P | 0.917 ± 0.08 | 0.837 ± 0.03 | 0.997 ± 0.0009 | 0.849 ± 0.03 | 0.994 ± 0.001 | 0.994 ± 0.002 | 0.904 ± 0.03 | 0.92 ± 0.02 | 0.911 ± 0.02 |
| Zenodo 20P | 0.951 ± 0.05 | 0.902 ± 0.05 | 0.999 ± 0.0004 | 0.894 ± 0.05 | 0.998 ± 0.0008 | 0.998 ± 0.0008 | 0.935 ± 0.03 | 0.944 ± 0.03 | 0.939 ± 0.03 |
| Dataset | Mean Dice | Dice Inf | Dice Back | Mean IOU | Accuracy | Specificity | Sensitivity | Precision | F1-Score |
|---|---|---|---|---|---|---|---|---|---|
| MedSeg | 0.848 ± 0.14 | 0.708 ± 0.01 | 0.988 ± 0.0004 | 0.783 ± 0.005 | 0.978 ± 0.0008 | 0.976 ± 0.0009 | 0.858 ± 0.01 | 0.872 ± 0.01 | 0.865 ± 0.004 |
| Radiopaedia 9P | 0.936 ± 0.06 | 0.875 ± 0.009 | 0.998 ± 5.5 × 10−5 | 0.899 ± 0.003 | 0.997 ± 0.0001 | 0.996 ± 9.38 × 10−5 | 0.940 ± 0.005 | 0.948 ± 0.003 | 0.943 ± 0.002 |
| MedSeg + Radiopaedia 9P | 0.914 ± 0.08 | 0.831 ± 0.03 | 0.997 ± 6.1 × 10−5 | 0.857 ± 0.003 | 0.995 ± 0.0001 | 0.995 ± 0.0002 | 0.911 ± 0.005 | 0.924 ± 0.005 | 0.917 ± 0.002 |
| Zenodo 20P | 0.93 ± 0.07 | 0.861 ± 0.007 | 0.999 ± 1.6 × 10 | 0.87 ± 0.002 | 0.998 ± 3.3 × 10 | 0.998 ± 4.1 × 10 | 0.921 ± 0.005 | 0.930 ± 0.005 | 0.926 ± 0.001 |
| Contrast Enhancement | Mean Dice | Dice Inf | Dice Back | Mean IOU | Accuracy | Specificity | Sensitivity | Precision | F1-Score |
|---|---|---|---|---|---|---|---|---|---|
| MedSeg (without) | 0.824 ± 0.16 | 0.66± 0.07 | 0.987 ± 0.001 | 0.761 ± 0.04 | 0.976 ± 0.003 | 0.974 ± 0.006 | 0.839 ± 0.03 | 0.865 ± 0.06 | 0.846 ± 0.03 |
| MedSeg (with) | 0.848 ± 0.14 | 0.708 ± 0.01 | 0.988 ± 0.0004 | 0.783 ± 0.005 | 0.978 ± 0.0008 | 0.976 ± 0.0009 | 0.858 ± 0.01 | 0.872 ± 0.01 | 0.865 ± 0.004 |
| Radiopaedia 9P (without) | 0.923 ± 0.1 | 0.847 ± 0.04 | 0.998 ± 0.0003 | 0.899 ± 0.01 | 0.997 ± 0.0004 | 0.996 ± 0.0008 | 0.939 ± 0.01 | 0.948 ± 0.005 | 0.943 ± 0.007 |
| Radiopaedia 9P (with) | 0.936 ± 0.06 | 0.875 ± 0.009 | 0.998 ± 5.5 × 10 | 0.899 ± 0.003 | 0.997 ± 0.0001 | 0.996 ± 9.38 × 10 | 0.940 ± 0.005 | 0.948 ± 0.003 | 0.943 ± 0.002 |
| Trained Dataset | Tested Dataset | Mean Dice | Dice Inf | Dice Back | Mean IOU | Accuracy | Specificity | Sensitivity | Precision | F1-Score |
|---|---|---|---|---|---|---|---|---|---|---|
| Radiopaedia 9P | MedSeg | 0.71 ± 0.2 | 0.462 ± 0.02 | 0.957 ± 0.009 | 0.645 ± 0.02 | 0.920 ± 0.0003 | 0.922 ± 0.02 | 0.773 ± 0.03 | 0.731 ± 0.007 | 0.744 ± 0.02 |
| Radiopaedia 9P | Zenodo 20P | 0.579 ± 0.4 | 0.172 ± 0.04 | 0.977 ± 0.007 | 0.522 ± 0.01 | 0.957 ± 0.01 | 0.956 ± 0.01 | 0.78 ± 0.03 | 0.545 ± 0.002 | 0.567 ± 0.01 |
| Zenodo 20P | MedSeg | 0.770 ± 0.2 | 0.566 ± 0.03 | 0.973 ± 0.002 | 0.686 ± 0.02 | 0.957 ± 0.002 | 0.952 ± 0.003 | 0.724 ± 0.02 | 0.908 ± 0.003 | 0.783 ± 0.02 |
| Zenodo 20P | Radiopaedia 9P | 0.802 ± 0.2 | 0.609 ± 0.03 | 0.996 ± 0.0002 | 0.607 ± 0.01 | 0.992 ± 0.0004 | 0.991 ± 0.0004 | 0.782 ± 0.01 | 0.730 ± 0.01 | 0.657 ± 0.02 |
| Zenodo 20P | MedSeg + Radiopaedia 9P | 0.809 ± 0.2 | 0.624 ± 0.02 | 0.994 ± 0.0003 | 0.619 ± 0.01 | 0.988 ± 0.0006 | 0.988 ± 0.0006 | 0.80 ± 0.02 | 0.735 ± 0.008 | 0.673 ± 0.01 |
| MedSeg | Radiopaedia 9P | 0.71 ± 0.3 | 0.424 ± 0.06 | 0.996 ± 0.0002 | 0.649 ± 0.01 | 0.993 ± 0.0003 | 0.993 ± 0.0003 | 0.859 ± 0.02 | 0.719 ± 0.007 | 0.701 ± 0.01 |
| MedSeg | Zenodo 20P | 0.441 ± 0.4 | 0.04 ± 0.002 | 0.839 ± 0.02 | 0.371 ± 0.02 | 0.724 ± 0.03 | 0.721 ± 0.03 | 0.646 ± 0.02 | 0.505 ± 0.001 | 0.436 ± 0.01 |
| MedSeg + Radiopaedia 9P | Zenodo 20P | 0.57 ± 0.4 | 0.169 ± 0.04 | 0.971 ± 0.008 | 0.507 ± 0.014 | 0.945 ± 0.014 | 0.943 ± 0.012 | 0.785 ± 0.02 | 0.535 ± 0.008 | 0.549 ± 0.02 |
| Dataset | Mean Dice | Dice GGO | Dice Con | Dice Inf | Dice Back | Dice Lung | Mean IOU | Accuracy | Specificity | Sensitivity | Precision | F1-Score |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MedSeg | 0.685 ± 0.25 | 0.530 ± 0.07 | 0.367 ± 0.07 | - | 0.992 ± 0.003 | 0.85 ± 0.04 | 0.659 ± 0.03 | 0.952 ± 0.009 | 0.984 ± 0.003 | 0.759 ± 0.05 | 0.785 ± 0.03 | 0.762 ± 0.03 |
| Radiopaedia 9P | 0.897 ± 0.07 | 0.794 ± 0.04 | 0.871 ± 0.04 | - | 0.998 ± 0.0001 | 0.926 ± 0.02 | 0.839 ± 0.02 | 0.994 ± 0.0007 | 0.998 ± 0.0001 | 0.894 ± 0.02 | 0.917 ± 0.02 | 0.904 ± 0.01 |
| MedSeg + Radiopaedia 9P | 0.873 ± 0.1 | 0.751 ± 0.04 | 0.81 ± 0.03 | - | 0.997 ± 0.0004 | 0.933 ± 0.01 | 0.775 ± 0.03 | 0.989 ± 0.002 | 0.996 ± 0.0006 | 0.846 ± 0.02 | 0.875 ± 0.02 | 0.855 ± 0.02 |
| Zenodo 20P | 0.940 ± 0.04 | - | - | 0.880 ± 0.05 | 0.999 ± 0.0005 | L = 0.952 ± 0.02 R = 0.931 ± 0.03 | 0.909 ± 0.04 | 0.995 ± 0.002 | 0.998 ± 0.0007 | 0.946 ± 0.02 | 0.953 ± 0.02 | 0.949 ± 0.02 |
| Dataset | Mean Dice | Dice GGO | Dice Con | Dice Inf | Dice Back | Dice Lung | Mean IOU | Accuracy | Specificity | Sensitivity | Precision | F1-Score |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MedSeg | 0.693 ± 0.27 | 0.557 ± 0.05 | 0.311 ± 0.03 | - | 0.993 ± 0.001 | 0.909 ± 0.08 | 0.679 ± 0.02 | 0.964 ± 0.002 | 0.988 ± 0.0008 | 0.775 ± 0.03 | 0.795 ± 0.02 | 0.78 ± 0.02 |
| Radiopaedia 9P | 0.891 ± 0.09 | 0.768 ± 0.03 | 0.859 ± 0.02 | - | 0.997 ± 0.0001 | 0.941 ± 0.01 | 0.865 ± 0.007 | 0.993 ± 0.0003 | 0.998 ± 8.95 × 10 | 0.917 ± 0.01 | 0.931 ± 0.01 | 0.923 ± 0.005 |
| MedSeg + Radiopaedia 9P | 0.870 ± 0.10 | 0.752 ± 0.02 | 0.794 ± 0.02 | - | 0.997 ± 6.5 × 10 | 0.937 ± 0.008 | 0.783 ± 0.003 | 0.99 ± 0.0001 | 0.997 ± 4.5 × 10 | 0.854 ± 0.004 | 0.88 ± 0.005 | 0.864 ± 0.002 |
| Zenodo 20P | 0.926 ± 0.06 | - | - | 0.84 ± 0.01 | 0.998 ± 0.0001 | L = 0.945 ± 0.004 R = 0.919 ± 0.004 | 0.894 ± 0.005 | 0.994 ± 0.0003 | 0.998 ± 9.3 × 10 | 0.937 ± 0.005 | 0.945 ± 0.002 | 0.941 ± 0.003 |
| Dataset | Class Classification | Model | Mean Dice | Mean IOU | Accuracy | Specificity | Sensitivity | Precision | F1-Score |
|---|---|---|---|---|---|---|---|---|---|
| MedSeg | Binary | Plug-and-play Attention UNet [33] | 0.84 | 0.74 | - | - | - | - | - |
| Binary | HADCNet [42] | 0.792 | - | 0.970 | 0.985 | 0.871 | - | - | |
| Binary | MiniSeg [44] | 0.759 | 0.822 | - | 0.977 | 0.8495 | - | - | |
| Binary | SAA-UNet1 | 0.854 | 0.803 | 0.970 | 0.968 | 0.872 | 0.892 | 0.88 | |
| Binary | SAA-UNet2 | 0.85 | 0.78 | 0.978 | 0.976 | 0.858 | 0.872 | 0.865 | |
| Multi-class | SAA-UNet1 | 0.685 | 0.659 | 0.952 | 0.984 | 0.759 | 0.785 | 0.762 | |
| Multi-class | SAA-UNet2 | 0.693 | 0.679 | 0.964 | 0.988 | 0.775 | 0.795 | 0.78 | |
| Radiopaedia 9P | Binary | MPS-Net [39] | 0.83 | 0.74 | - | 0.9988 | 0.8406 | - | - |
| Binary | DUDA-Net [46] | 0.87 | 0.771 | 0.991 | 0.996 | 0.909 | - | - | |
| Binary | HADCNet [42] | 0.796 | - | 0.991 | 0.994 | 0.912 | - | - | |
| Binary | MiniSeg [44] | 0.80 | 0.853 | - | 0.992 | 0.906 | - | - | |
| Binary | SAA-UNet1 | 0.945 | 0.891 | 0.997 | 0.997 | 0.934 | 0.943 | 0.938 | |
| Binary | SAA-UNet2 | 0.94 | 0.90 | 0.997 | 0.996 | 0.940 | 0.948 | 0.943 | |
| Multi-class | SAA-UNet1 | 0.897 | 0.839 | 0.994 | 0.998 | 0.894 | 0.917 | 0.904 | |
| Multi-class | SAA-UNet2 | 0.89 | 0.87 | 0.993 | 0.998 | 0.917 | 0.931 | 0.923 | |
| MedSeg+ Radiopaedia 9P | Binary | TV UNet [31] | 0.864 | 0.995 | - | - | 0.85 | 0.87 | - |
| Binary | Channel-attention UNet [30] | 0.83 | - | - | - | - | - | - | |
| Binary | Ensemble UNet & majority voting [38] | 0.85 | - | - | 0.994 | 0.891 | - | - | |
| Binary | ADID-UNet [41] | 0.803 | - | 0.97 | 0.9966 | 0.797 | 0.848 | 0.82 | |
| Binary | A-SegNet [40] | 0.896 | - | - | 0.995 | 0.927 | - | - | |
| Binary | SAA-UNet1 | 0.917 | 0.849 | 0.994 | 0.994 | 0.904 | 0.92 | 0.911 | |
| Binary | SAA-UNet2 | 0.90 | 0.84 | 0.993 | 0.998 | 0.917 | 0.931 | 0.923 | |
| Multi-class | DDANet [49] | 0.78 | - | - | 0.992 | 0.884 | - | - | |
| Multi-class | SAA-UNet1 | 0.873 | 0.775 | 0.989 | 0.996 | 0.846 | 0.875 | 0.855 | |
| Multi-class | SAA-UNet2 | 0.87 | 0.78 | 0.99 | 0.997 | 0.854 | 0.88 | 0.864 | |
| Zenodo 20P | Binary | FCN-8s Light-UNet [27] | - | - | (1) 0.98 (2) 0.98 | - | (1) 0.50 (2) 0.57 | (1) 0.85 (2) 0.96 | (1) 0.57 (2) 0.64 |
| Binary | 3-Encoder, 3Decoder [43] | - | 0.799 | 0.972 | 0.9499 | 0.9499 | 0.993 | - | |
| Binary | LungINFseg [47] | 0.803 | 0.688 | 0.989 | 0.995 | 0.831 | - | - | |
| Binary | contour-enhanced attention decoder CNN [48] | 0.88 | 0.75 | - | 0.998 | 0.90 | 0.856 | - | |
| Binary | Focal attention module with DeepLabV3+ [45] | 0.885 | - | - | - | - | - | - | |
| Binary | HADCNet [42] | 0.723 | - | 0.987 | 0.997 | 0.694 | - | - | |
| Binary | MiniSeg [44] | 0.763 | 0.845 | - | 0.991 | 0.851 | - | - | |
| Binary | SAA-UNet1 | 0.951 | 0.894 | 0.998 | 0.998 | 0.935 | 0.944 | 0.939 | |
| Binary | SAA-UNet2 | 0.93 | 0.88 | 0.998 | 0.998 | 0.921 | 0.93 | 0.926 | |
| Multi-class | QAP-Net [34] | - | 0.816 | 0.9976 | 0.998 | 0.958 | 0.846 | - | |
| Multi-class | MultiResUNet [35] | 0.88 | - | - | - | - | - | - | |
| Multi-class | SAA-UNet1 | 0.940 | 0.909 | 0.995 | 0.998 | 0.946 | 0.953 | 0.949 | |
| Multi-class | SAA-UNet2 | 0.931 | 0.899 | 0.994 | 0.998 | 0.937 | 0.945 | 0.941 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshomrani, S.; Arif, M.; Al Ghamdi, M.A. SAA-UNet: Spatial Attention and Attention Gate UNet for COVID-19 Pneumonia Segmentation from Computed Tomography. Diagnostics 2023, 13, 1658. https://doi.org/10.3390/diagnostics13091658
Alshomrani S, Arif M, Al Ghamdi MA. SAA-UNet: Spatial Attention and Attention Gate UNet for COVID-19 Pneumonia Segmentation from Computed Tomography. Diagnostics. 2023; 13(9):1658. https://doi.org/10.3390/diagnostics13091658
Chicago/Turabian StyleAlshomrani, Shroog, Muhammad Arif, and Mohammed A. Al Ghamdi. 2023. "SAA-UNet: Spatial Attention and Attention Gate UNet for COVID-19 Pneumonia Segmentation from Computed Tomography" Diagnostics 13, no. 9: 1658. https://doi.org/10.3390/diagnostics13091658
APA StyleAlshomrani, S., Arif, M., & Al Ghamdi, M. A. (2023). SAA-UNet: Spatial Attention and Attention Gate UNet for COVID-19 Pneumonia Segmentation from Computed Tomography. Diagnostics, 13(9), 1658. https://doi.org/10.3390/diagnostics13091658






