Osteoporosis Assessment Using Bone Density Measurement in Hounsfield Units in the Femoral Native CT Cross-Section: A Comparison with Computed Tomography X-Ray Absorptiometry of the Hip
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Design and Ethical Approval
2.2. Study Population
2.3. Diagnostic Procedures
2.4. Statistical Analysis
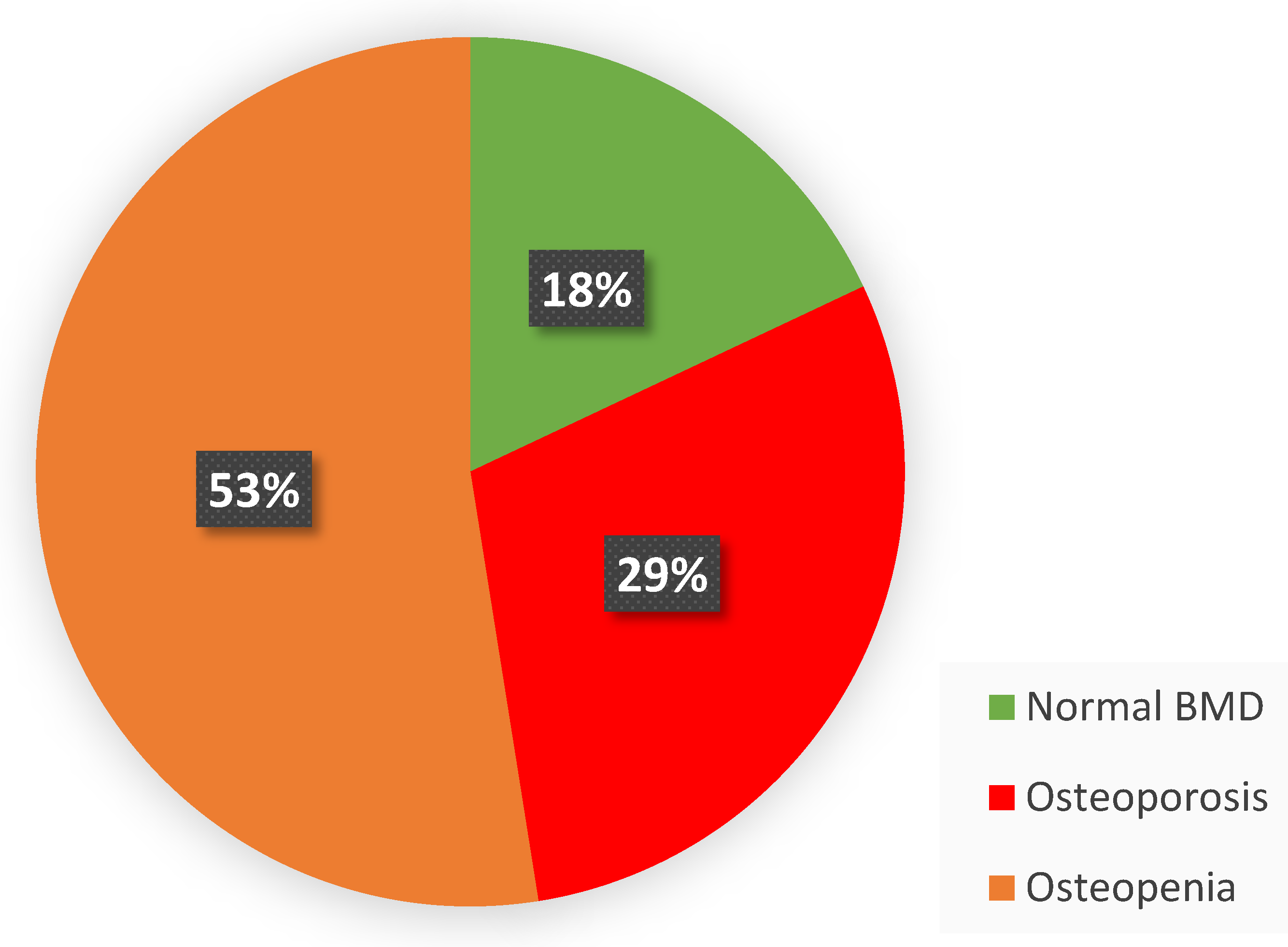
3. Results
4. Discussion
5. Limitations and Strengths
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUC | Area under the curve |
| BMD | Bone mineral density |
| BMI | Body mass index |
| CTXA | Computed tomography X-ray absorptiometry |
| DEXA | Dual-energy X-ray absorptiometry |
| Fig. | Figure |
| GE | General Electric |
| HU | Hounsfield unit |
| MA | Mean age |
| n | Number |
| OVF | Osteoporotic vertebral fracture |
| Q1-Q3 | First to third quartiles |
| ROC | Receiver operating characteristic |
| ROI | Region of interest |
| SD | Standard deviation |
| Tab. | Table |
References
- Andresen, R.; Radmer, S.; Banzer, D. Bone Mineral Density and Spongiosa Architecture in Correlation to Vertebral Body Insufficiency Fractures. Acta Radiol. 1998, 39, 538–542. [Google Scholar] [CrossRef]
- Schröder, G.; Andresen, J.R.; Hiepe, L.; Schulze, M.; Kullen, C.M.; Kopetsch, C.; Burmeister, J.; Schober, H.-C.; Andresen, R. Interobserver Variability in the Determination of Bone Mineral Density in Hounsfield Units from Differently Configured Fields of Measurement in the Cancellous Bone of Vertebral Bodies from Elderly Body Donors. J. Orthop. 2024, 49, 48–55. [Google Scholar] [CrossRef]
- Andresen, J.R.; Schröder, G.; Haider, T.; Kopetsch, C.; Kullen, C.M.; Schober, H.C.; Andresen, R. Vergleichende Bewertung der spongiösen Knochendichte in Hounsfield-Einheiten im lumbalen nativen CT-Schnittbild zur Osteoporosediagnostik und Frakturrisikobestimmung durch verschiedene Untersucher. Orthopädie 2025, 54, 48–60. [Google Scholar] [CrossRef]
- Johnell, O.; Kanis, J. Epidemiology of Osteoporotic Fractures. Osteoporos. Int. 2005, 16, S3–S7. [Google Scholar] [CrossRef]
- Kelly, M.A.; McCabe, E.; Bergin, D.; Kearns, S.R.; McCabe, J.P.; Armstrong, C.; Heaney, F.; Carey, J.J. Osteoporotic Vertebral Fractures Are Common in Hip Fracture Patients and Are Under-Recognized. J. Clin. Densitom. 2021, 24, 183–189. [Google Scholar] [CrossRef]
- Cooper, C.; Campion, G.; Melton, L.J. Hip Fractures in the Elderly: A World-Wide Projection. Osteoporos. Int. 1992, 2, 285–289. [Google Scholar] [CrossRef]
- Icks, A.; Haastert, B.; Wildner, M.; Becker, C.; Meyer, G. Trend of Hip Fracture Incidence in Germany 1995–2004: A Population-Based Study. Osteoporos. Int. 2008, 19, 1139–1145. [Google Scholar] [CrossRef]
- Rupp, M.; Walter, N.; Pfeifer, C.; Lang, S.; Kerschbaum, M.; Krutsch, W.; Baumann, F.; Alt, V. The Incidence of Fractures among the Adult Population of Germany. Dtsch. Ärzteblatt. Int. 2021, 118, 665–669. [Google Scholar] [CrossRef]
- Johansson, H.; Siggeirsdóttir, K.; Harvey, N.C.; Odén, A.; Gudnason, V.; McCloskey, E.; Sigurdsson, G.; Kanis, J.A. Imminent Risk of Fracture after Fracture. Osteoporos. Int. 2017, 28, 775–780. [Google Scholar] [CrossRef]
- Chau, P.H.; Wong, M.; Lee, A.; Ling, M.; Woo, J. Trends in Hip Fracture Incidence and Mortality in Chinese Population from Hong Kong 2001-09. Age Ageing 2013, 42, 229–233. [Google Scholar] [CrossRef]
- Karampampa, K.; Ahlbom, A.; Michaëlsson, K.; Andersson, T.; Drefahl, S.; Modig, K. Declining Incidence Trends for Hip Fractures Have Not Been Accompanied by Improvements in Lifetime Risk or Post-Fracture Survival—A Nationwide Study of the Swedish Population 60 years and Older. Bone 2015, 78, 55–61. [Google Scholar] [CrossRef]
- Guzon-Illescas, O.; Perez Fernandez, E.; Crespí Villarias, N.; Quirós Donate, F.J.; Peña, M.; Alonso-Blas, C.; García-Vadillo, A.; Mazzucchelli, R. Mortality after Osteoporotic Hip Fracture: Incidence, Trends, and Associated Factors. J. Orthop. Surg. Res. 2019, 14, 203. [Google Scholar] [CrossRef]
- Cree, M.; Soskolne, C.L.; Belseck, E.; Hornig, J.; McElhaney, J.E.; Brant, R.; Suarez-Almazor, M. Mortality and Institutionalization Following Hip Fracture. J. Am. Geriatr. Soc. 2000, 48, 283–288. [Google Scholar] [CrossRef]
- Gosch, M.; Hoffmann-Weltin, Y.; Roth, T.; Blauth, M.; Nicholas, J.A.; Kammerlander, C. Orthogeriatric Co-Management Improves the Outcome of Long-Term Care Residents with Fragility Fractures. Arch. Orthop. Trauma Surg. 2016, 136, 1403–1409. [Google Scholar] [CrossRef]
- Hayward-Livingston, A.; Ozdag, Y.; Kolessar, D.; Weinberg, J.; Pamul, A.; Koury, K.; Balsamo, A. A 10-Year Experience of an Integrated Geriatric Hip Fracture Treatment Protocol: Outcomes at a Minimum 2-Year Follow-Up. Geriatr. Orthop. Surg. Rehabil. 2024, 15, 21514593241273155. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, Y.; Lin, W.; Lee, D.H.; Yang, F.; Fan, Y. Quantitative Computed Tomography Analysis of Proximal Femur Bone Mineral Density and Its Relation to Hip Fracture Risk. Quant. Imaging Med. Surg. 2024, 14, 9385–9393. [Google Scholar] [CrossRef]
- Kanis, J.A.; Oden, A.; Johnell, O.; Johansson, H.; De Laet, C.; Brown, J.; Burckhardt, P.; Cooper, C.; Christiansen, C.; Cummings, S.; et al. The Use of Clinical Risk Factors Enhances the Performance of BMD in the Prediction of Hip and Osteoporotic Fractures in Men and Women. Osteoporos. Int. 2007, 18, 1033–1046. [Google Scholar] [CrossRef]
- Baum, E.; Rintelen, B.; Siggelkow, H.; Engelke, K.; Glüer, C.-C.; Thomasius, F. Osteoporose-Risikofaktoren. Osteologie 2023, 32, 92–96. [Google Scholar] [CrossRef]
- Damilakis, J.; Maris, T.G.; Karantanas, A.H. An Update on the Assessment of Osteoporosis Using Radiologic Techniques. Eur. Radiol. 2007, 17, 1591–1602. [Google Scholar] [CrossRef]
- Dachverband Osteologie e.V. S3-Leitlinie Prophylaxe, Diagnostik und Therapie der Osteoporose bei Postmenopausalen Frauen und bei Männern ab dem 50. Lebensjahr. Available online: https://register.awmf.org/de/leitlinien/detail/183-001 (accessed on 4 February 2025).
- Khoo, B.C.C.; Brown, K.; Cann, C.; Zhu, K.; Henzell, S.; Low, V.; Gustafsson, S.; Price, R.I.; Prince, R.L. Comparison of QCT-Derived and DXA-Derived Areal Bone Mineral Density and T Scores. Osteoporos. Int. 2009, 20, 1539–1545. [Google Scholar] [CrossRef]
- Cann, C.E.; Adams, J.E.; Brown, J.K.; Brett, A.D. CTXA Hip—An Extension of Classical DXA Measurements Using Quantitative CT. PLoS ONE 2014, 9, e91904. [Google Scholar] [CrossRef]
- American College of Radiology. ACR-SPR SSR Practice Parameter for the Performance of Musculoskeletal Quantitative Computed Tomography (QCT). Am. Coll. Radiol. Rest. 2018, 1076, 6. [Google Scholar]
- Andresen, J.R.; Schröder, G.; Haider, T.; Kullen, C.M.; Kopetsch, C.; Schober, H.-C.; Andesen, R. Comparative Assessment of Cancellous Bone Density in Hounsfield Units in the Lumbar Native CT Cross-Sectional Image for Osteoporosis Diagnosis and Fracture Risk Determination by Different Examiners—A Comparison with QCT and CTXA. J. Bone Miner. Res. 2024, 39, 146–147. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Z.; Ren, Q.; Nie, G.; Zhao, D. Measurement of Hounsfield Units on Proximal Femur Computed Tomography for Predicting Regional Osteoporosis. Radiologie 2023, 63, 90–97. [Google Scholar] [CrossRef]
- Lee, S.Y.; Kwon, S.-S.; Kim, H.S.; Yoo, J.H.; Kim, J.; Kim, J.Y.; Min, B.C.; Moon, S.J.; Sung, K.H. Reliability and Validity of Lower Extremity Computed Tomography as a Screening Tool for Osteoporosis. Osteoporos. Int. 2015, 26, 1387–1394. [Google Scholar] [CrossRef]
- Kılınc, R.M.; Açan, A.E.; Türk, G.; Kılınç, C.Y.; Yeniçeri, İ.Ö. Evaluation of Femoral Head Bone Quality by Hounsfield Units: A Comparison with Dual-Energy X-Ray Absorptiometry. Acta Radiol. 2022, 63, 933–941. [Google Scholar] [CrossRef]
- Fan, J.; Lv, Y.; Xu, X.; Zhou, F.; Zhang, Z.; Tian, Y.; Ji, H.; Guo, Y.; Yang, Z.; Hou, G. Evaluation of Femoral Head Bone Quality by Hounsfield Units: A Predictor of Implant Failure for Intertrochanteric Fractures after Intramedullary Nail Fixation. Front. Surg. 2023, 9, 816742. [Google Scholar] [CrossRef]
- Uemura, K.; Takao, M.; Otake, Y.; Iwasa, M.; Hamada, H.; Ando, W.; Sato, Y.; Sugano, N. The Effect of Region of Interest on Measurement of Bone Mineral Density of the Proximal Femur: Simulation Analysis Using CT Images. Calcif. Tissue Int. 2022, 111, 475–484. [Google Scholar] [CrossRef]
- Christensen, D.L.; Nappo, K.E.; Wolfe, J.A.; Tropf, J.G.; Berge, M.J.; Wheatley, B.M.; Saxena, S.; Yow, B.G.; Tintle, S.M. Ten-Year Fracture Risk Predicted by Proximal Femur Hounsfield Units. Osteoporos. Int. 2020, 31, 2123–2130. [Google Scholar] [CrossRef]
- Imren, Y.; Karslioglu, B.; Semih Dedeoğlu, S.; Keskin, A.; Firat Berkay, A.; Cagri Tekin, A. Feasibility of Diagnosing Osteoporosis Using Routine Computed Tomography Scans for Hip Fractures: Correlation with Histopathological Diagnosis of Head and Neck Regions. Acta Orthop. Traumatol. Turc. 2024, 57, 384–388. [Google Scholar] [CrossRef]
- Lim, H.K.; Ha, H.I.; Park, S.-Y.; Lee, K. Comparison of the Diagnostic Performance of CT Hounsfield Unit Histogram Analysis and Dual-Energy X-Ray Absorptiometry in Predicting Osteoporosis of the Femur. Eur. Radiol. 2019, 29, 1831–1840. [Google Scholar] [CrossRef]
- Ye, K.; Xing, Y.; Zou, D.; Zhou, F.; Zhang, Z.; Du, G.; Tian, Y. Positive Correlation between the Proximal Femur Hounsfield Units from Routine CT and DXA Results. J. Orthop. Res. 2023, 41, 2648–2656. [Google Scholar] [CrossRef]
- Xu, C.; Li, H.; Zhang, C.; Ge, F.; He, Q.; Chen, H.; Zhang, L.; Bai, X. Quantitative Analysis of Primary Compressive Trabeculae Distribution in the Proximal Femur of the Elderly. Orthop. Surg. 2024, 16, 2030–2039. [Google Scholar] [CrossRef]
- Buenger, F.; Eckardt, N.; Sakr, Y.; Senft, C.; Schwarz, F. Correlation of Bone Density Values of Quantitative Computed Tomography and Hounsfield Units Measured in Native Computed Tomography in 902 Vertebral Bodies. World Neurosurg. 2021, 151, e599–e606. [Google Scholar] [CrossRef]
- Simion, G.; Eckardt, N.; Ullrich, B.W.; Senft, C.; Schwarz, F. Bone Density of the Cervical, Thoracic and Lumbar Spine Measured Using Hounsfield Units of Computed Tomography—Results of 4350 Vertebras. BMC Musculoskelet. Disord. 2024, 25, 200. [Google Scholar] [CrossRef]
- Feng, N.; Zhou, S.; Yu, X.; Guan, J.; Li, W.; Yang, K.; Yue, X.; Qiu, Z.; Jiang, G. Feasibility Study in Quantitative Identification of Fresh and Old Osteoporotic Vertebral Compression Fracture by Vertebral CT Value and CT Value Difference. BMC Musculoskelet. Disord. 2024, 25, 821. [Google Scholar] [CrossRef]
- Andresen, J.R.; Schröder, G.; Haider, T.; Andresen, R. Opportunistic Osteoporosis Assessment and Fracture Risk Determination Using Cancellous Density Measurement in Hounsfield Units of Native Lumbar Computed Tomography Images—A Comparative Study with Conventional Bone Density Evaluation. J. Clin. Med. 2025, 14, 1226. [Google Scholar] [CrossRef]
- Simion, G.; Eckardt, N.; Senft, C.; Schwarz, F. Bone Density of the Axis (C2) Measured Using Hounsfield Units of Computed Tomography. J. Orthop. Surg. Res. 2023, 18, 93. [Google Scholar] [CrossRef]
- Liu, G.; Li, L.; Yang, C.; Wei, L.; Li, T.; Zhu, L.; Hu, J. Hounsfield Units Predicts the Occurrence but Not the Patterns of Proximal Humerus Fracture in the Elderly Patients. BMC Musculoskelet. Disord. 2023, 24, 342. [Google Scholar] [CrossRef]
- Uemura, K.; Otake, Y.; Takashima, K.; Hamada, H.; Imagama, T.; Takao, M.; Sakai, T.; Sato, Y.; Okada, S.; Sugano, N. Development and Validation of an Open-Source Tool for Opportunistic Screening of Osteoporosis from Hip CT Images: A Multicentre Study of 978 Hips. Bone Jt. Res. 2023, 12, 590–597. [Google Scholar] [CrossRef]
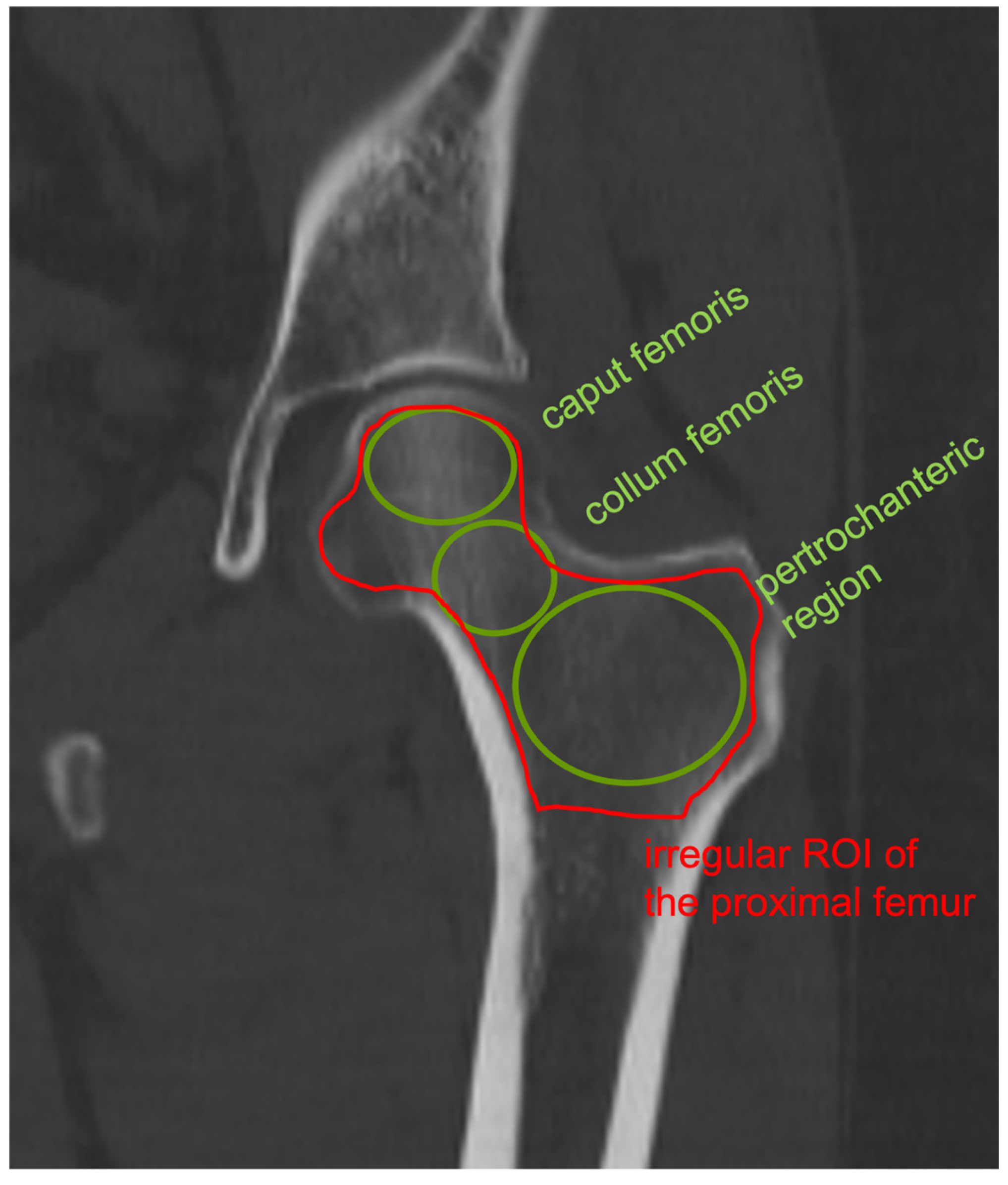
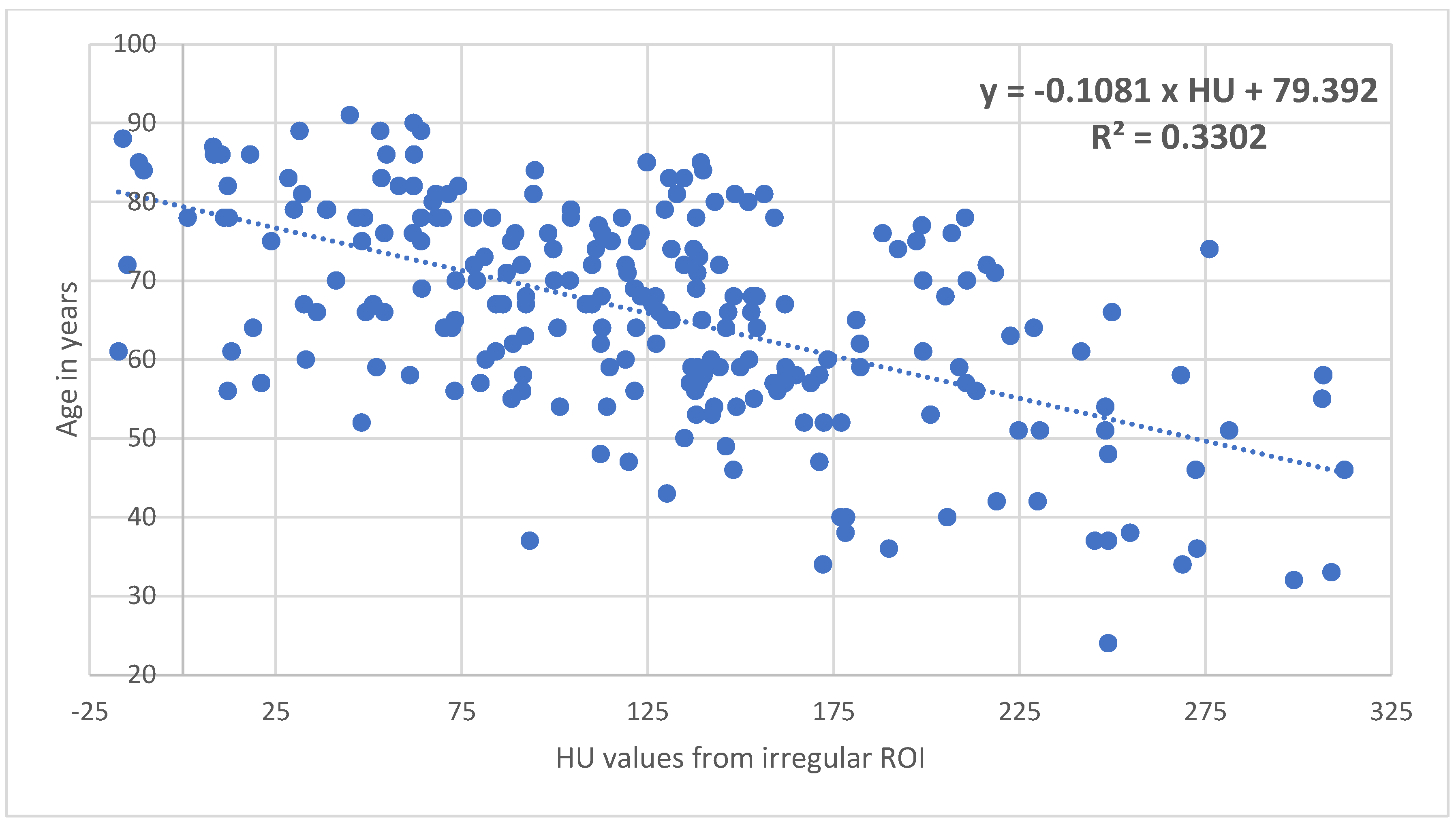
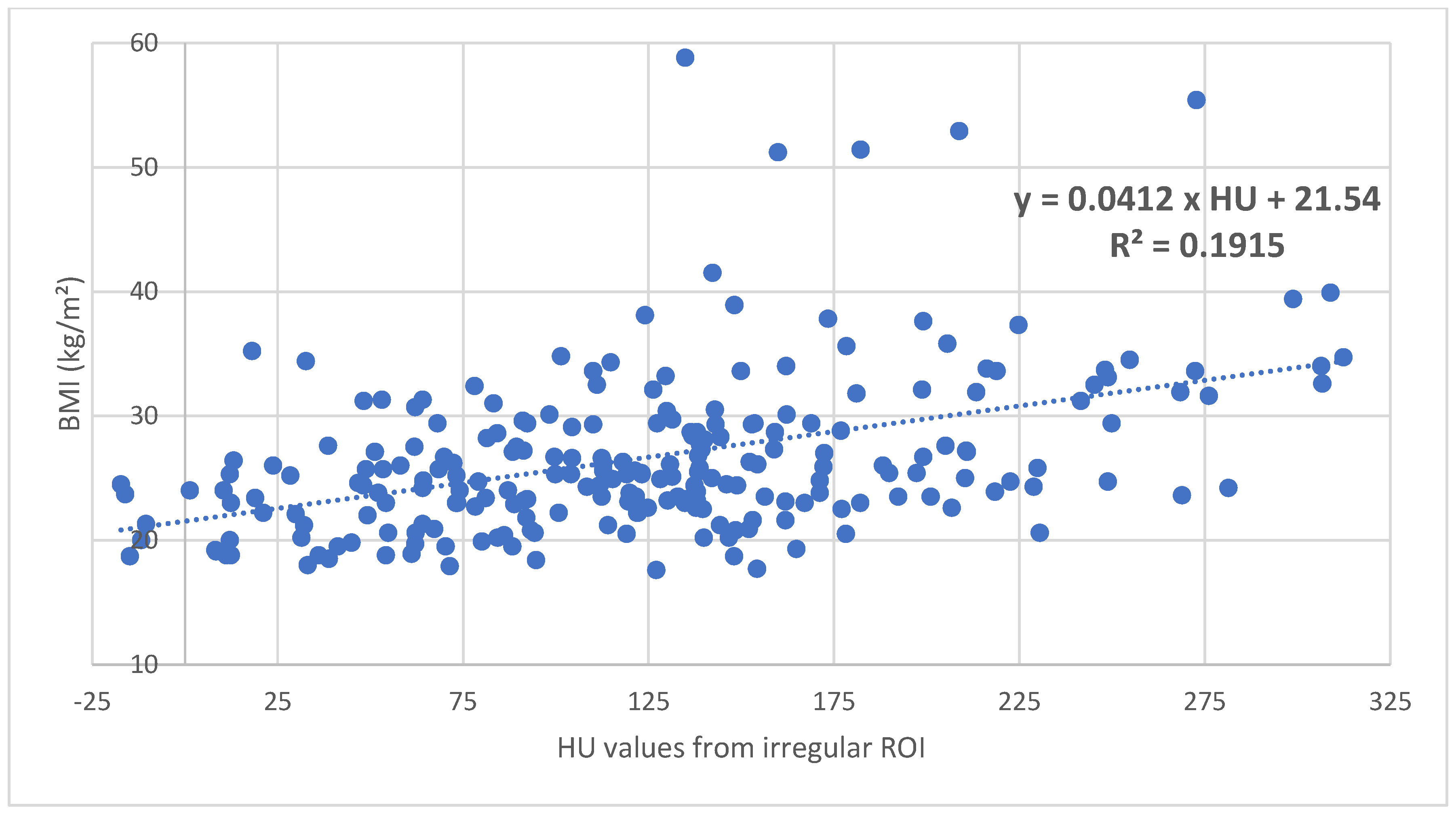
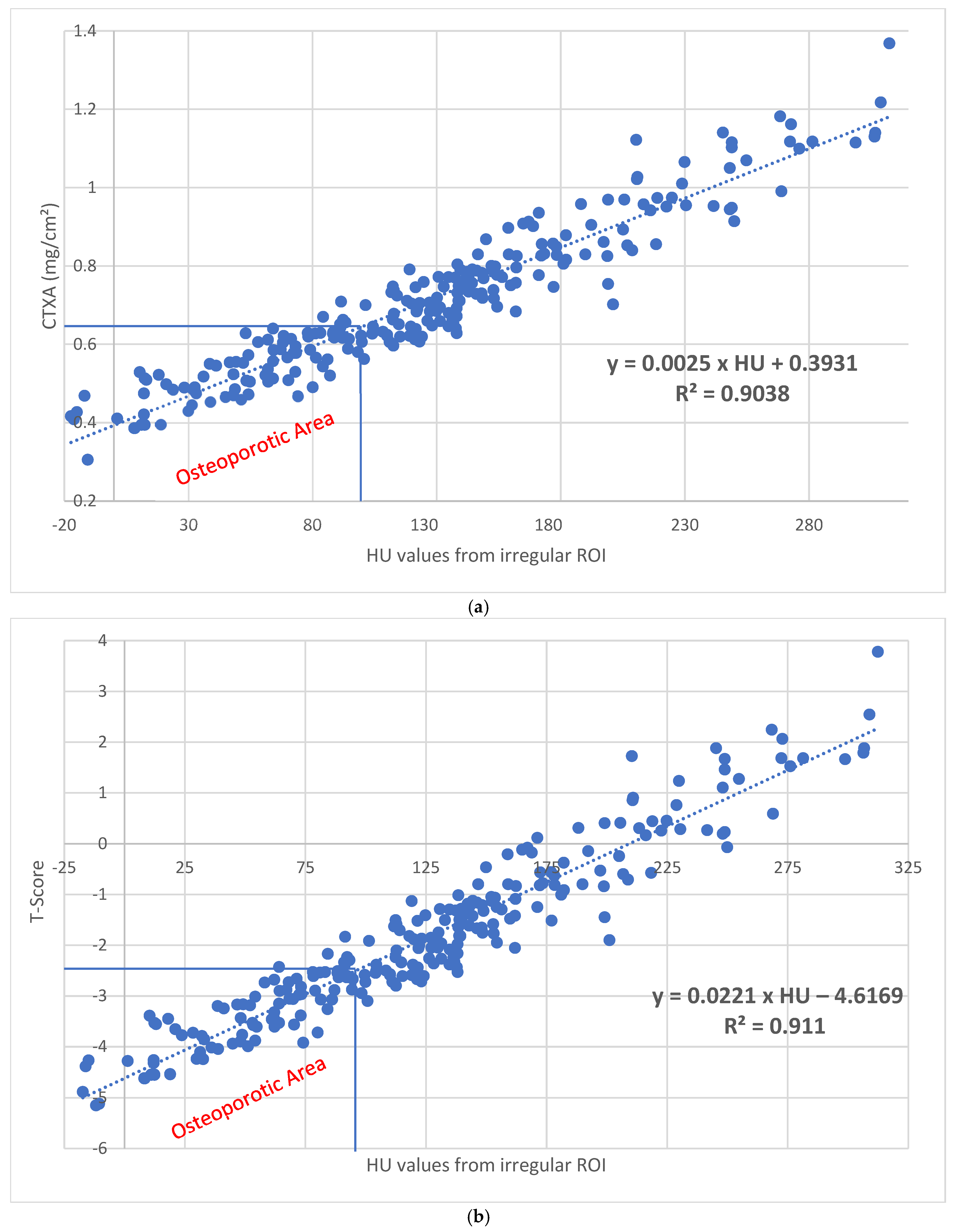

| Characterization of the Total Sample | |||
|---|---|---|---|
| Patients (n = 240) | Men (n = 40) | Women (n = 200) | |
| Age | ⌀ 65.9 | ⌀ 68.5 | ⌀ 65.3 |
| (in years) | (min.: 24; max.: 91) | (min.: 42; max.: 84) | (min.: 24; max.: 91) |
| BMI | ⌀ 26.7 | ⌀ 24.9 | ⌀ 27.1 |
| (kg/m2) | (min.: 17.6; max.: 60.6) | (min.: 17.6; max.: 33.8) | (min.: 17.7; max.: 60.6) |
| CTXA and T Values of the Hip | ||||
|---|---|---|---|---|
| n | Min | Max | Median | |
| CTXA (mg/cm2) | 240 | 0.3055 | 1.368 | 0.684 |
| T-value | 240 | −5.15 | 3.78 | −2.06 |
| HU Values of the Different ROIs | ||||
|---|---|---|---|---|
| ROI | n | Min | Max | Median |
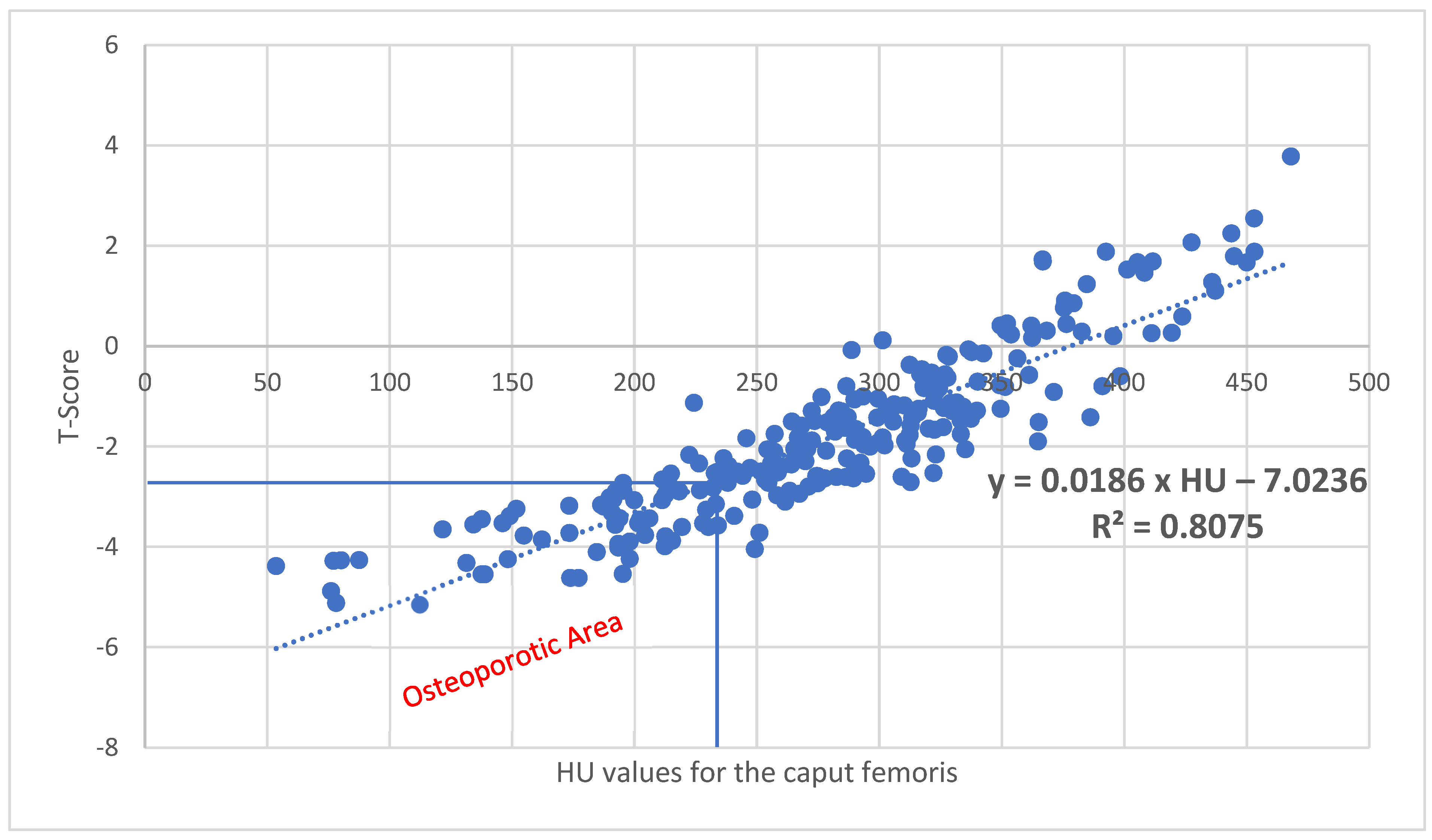
| Caput femoris | 240 | 53.6 | 468.1 | 281.65 |
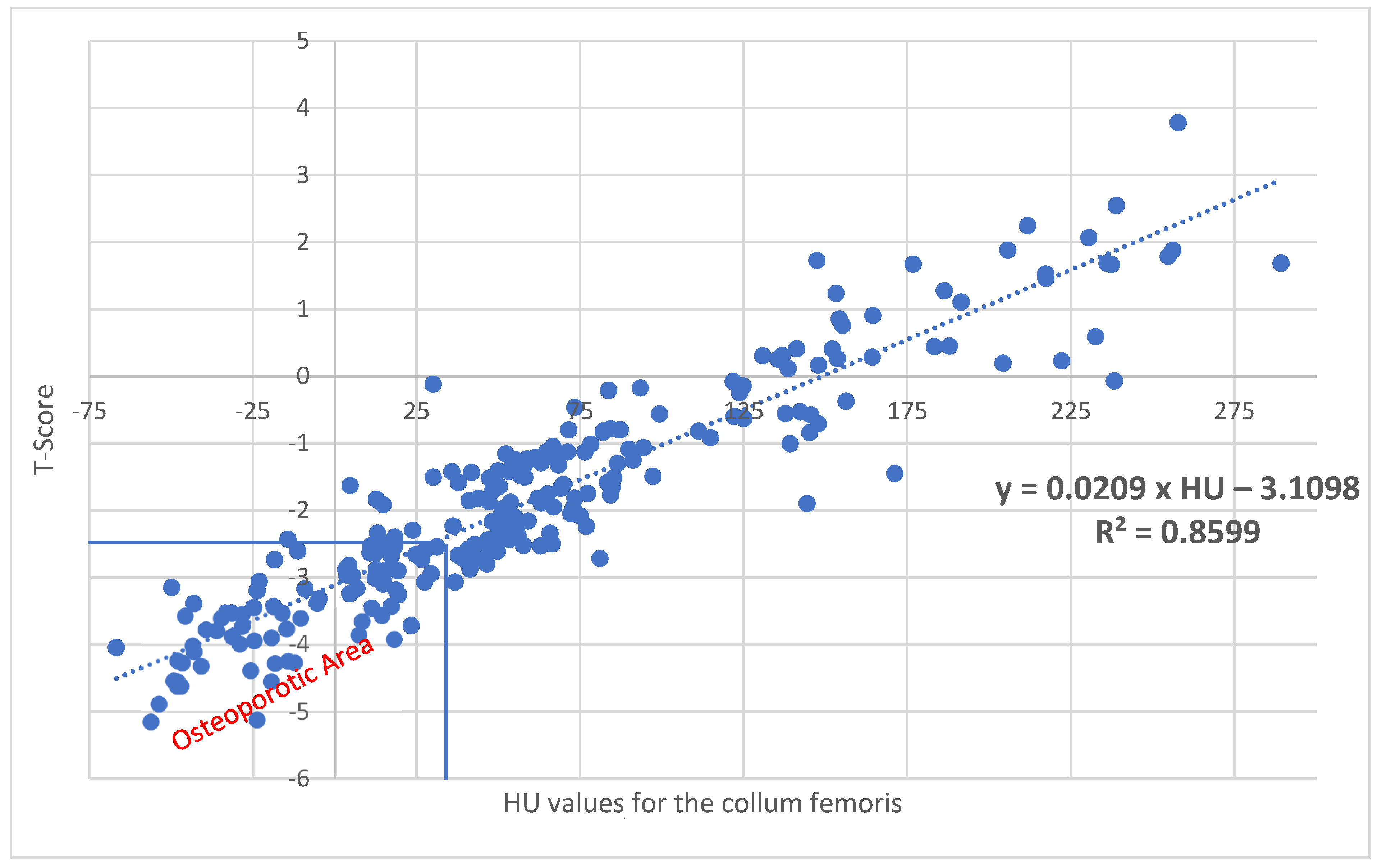
| Collum femoris | 240 | −66.8 | 289.3 | 51.75 |
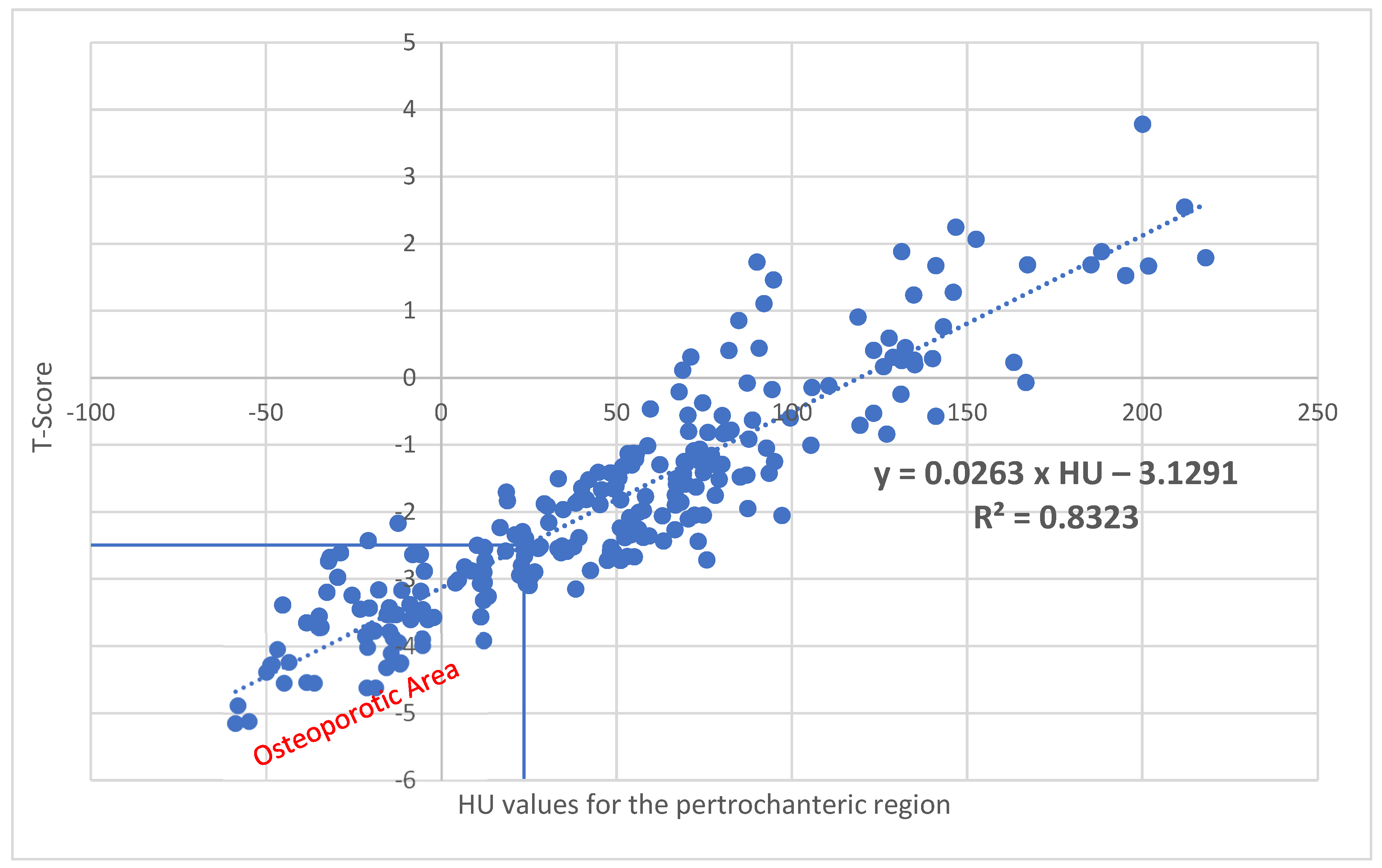
| Pertrochanteric region | 240 | −58.8 | 218.1 | 50.9 |
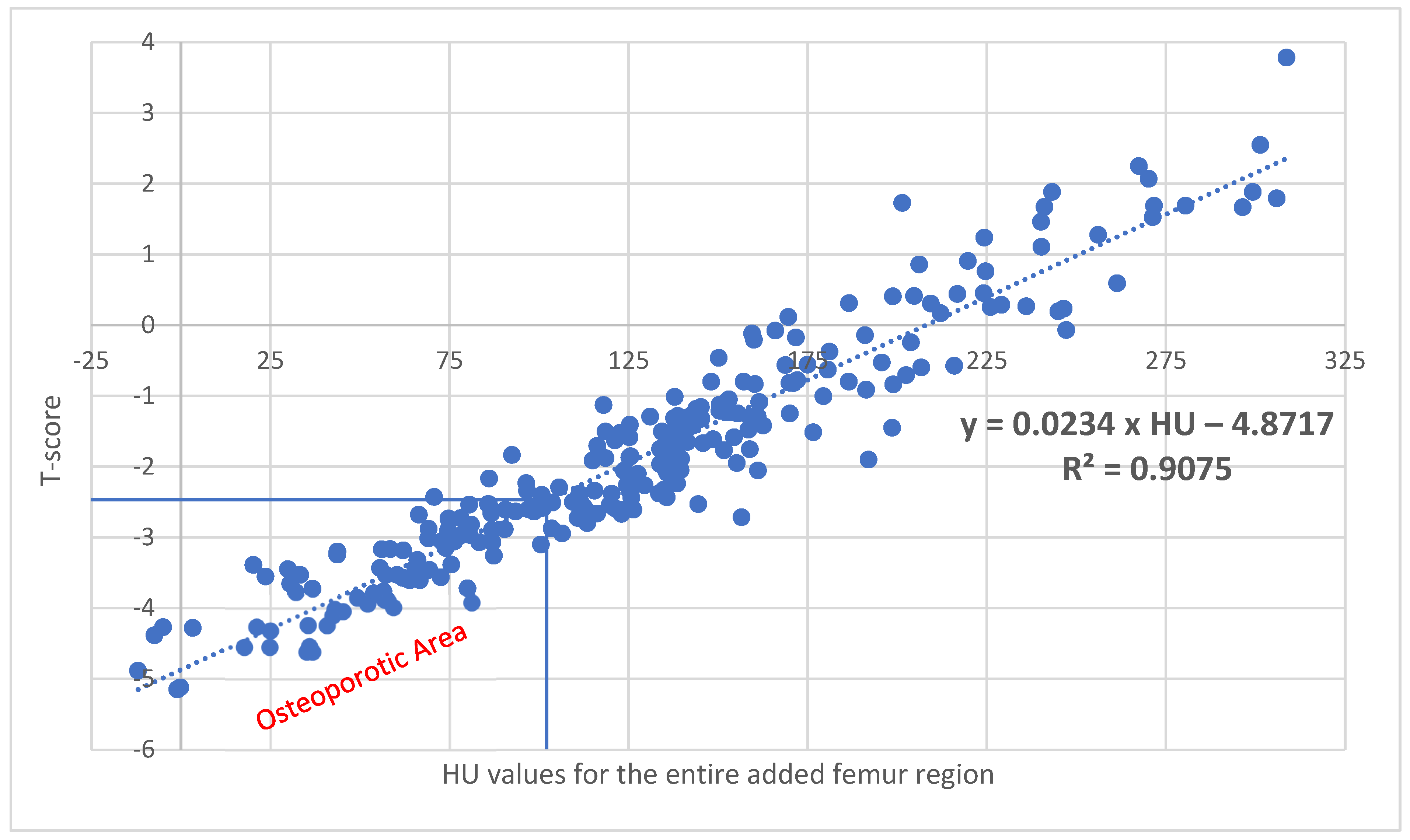
| Average values from the upper three ROIs | 240 | −24 | 325.17 | 128.1 |
| Irregular-surface ROI of the prox. femur | 240 | −17.3 | 312.4 | 123.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andresen, J.R.; Schröder, G.; Haider, T.; Schober, H.-C.; Andresen, R. Osteoporosis Assessment Using Bone Density Measurement in Hounsfield Units in the Femoral Native CT Cross-Section: A Comparison with Computed Tomography X-Ray Absorptiometry of the Hip. Diagnostics 2025, 15, 1014. https://doi.org/10.3390/diagnostics15081014
Andresen JR, Schröder G, Haider T, Schober H-C, Andresen R. Osteoporosis Assessment Using Bone Density Measurement in Hounsfield Units in the Femoral Native CT Cross-Section: A Comparison with Computed Tomography X-Ray Absorptiometry of the Hip. Diagnostics. 2025; 15(8):1014. https://doi.org/10.3390/diagnostics15081014
Chicago/Turabian StyleAndresen, Julian Ramin, Guido Schröder, Thomas Haider, Hans-Christof Schober, and Reimer Andresen. 2025. "Osteoporosis Assessment Using Bone Density Measurement in Hounsfield Units in the Femoral Native CT Cross-Section: A Comparison with Computed Tomography X-Ray Absorptiometry of the Hip" Diagnostics 15, no. 8: 1014. https://doi.org/10.3390/diagnostics15081014
APA StyleAndresen, J. R., Schröder, G., Haider, T., Schober, H.-C., & Andresen, R. (2025). Osteoporosis Assessment Using Bone Density Measurement in Hounsfield Units in the Femoral Native CT Cross-Section: A Comparison with Computed Tomography X-Ray Absorptiometry of the Hip. Diagnostics, 15(8), 1014. https://doi.org/10.3390/diagnostics15081014







