Effect of Surface Texture on the Sliding Pair Lubrication Efficiency
Abstract
1. Introduction
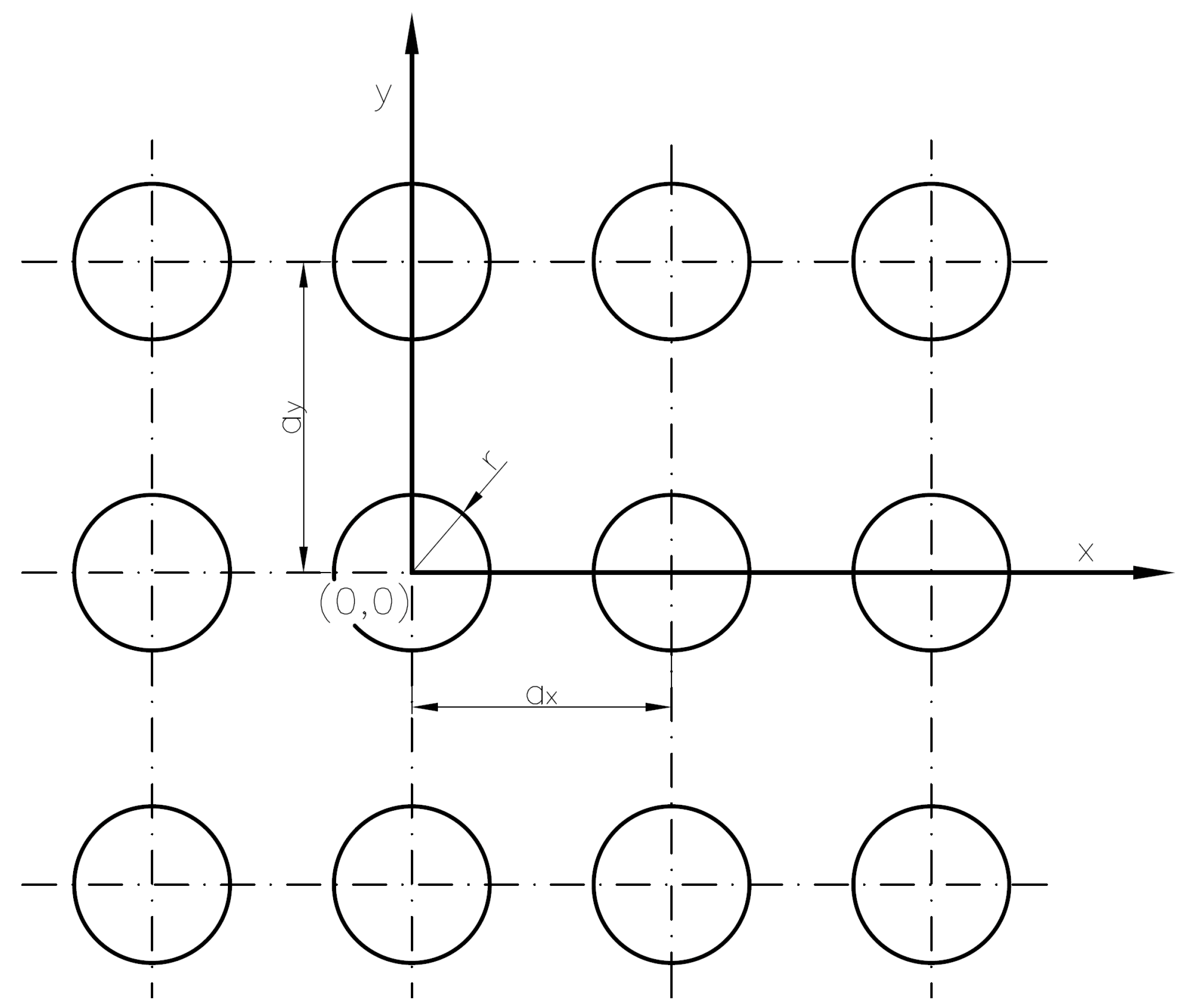
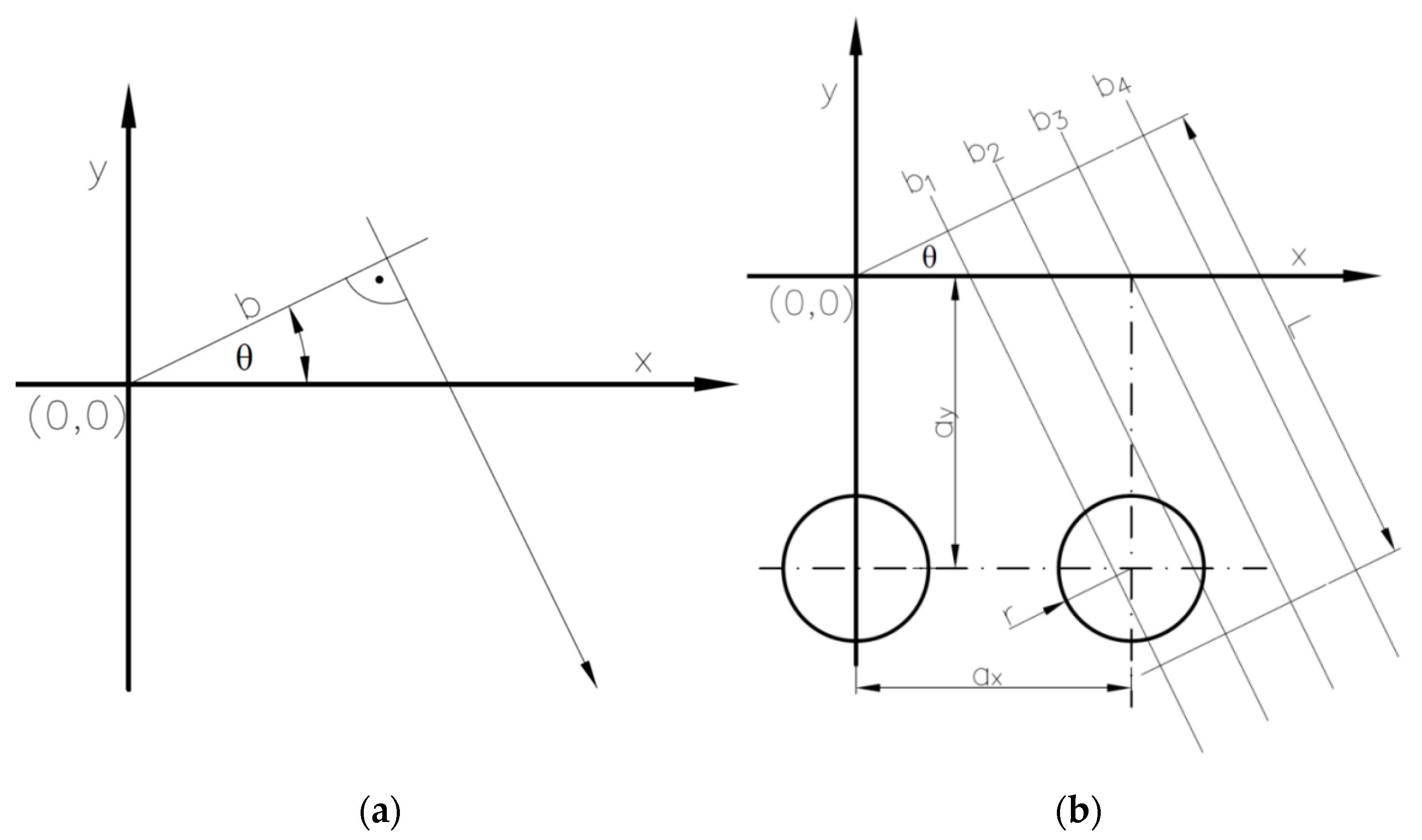
2. Textured Surface Lubrication—Theoretical Analysis
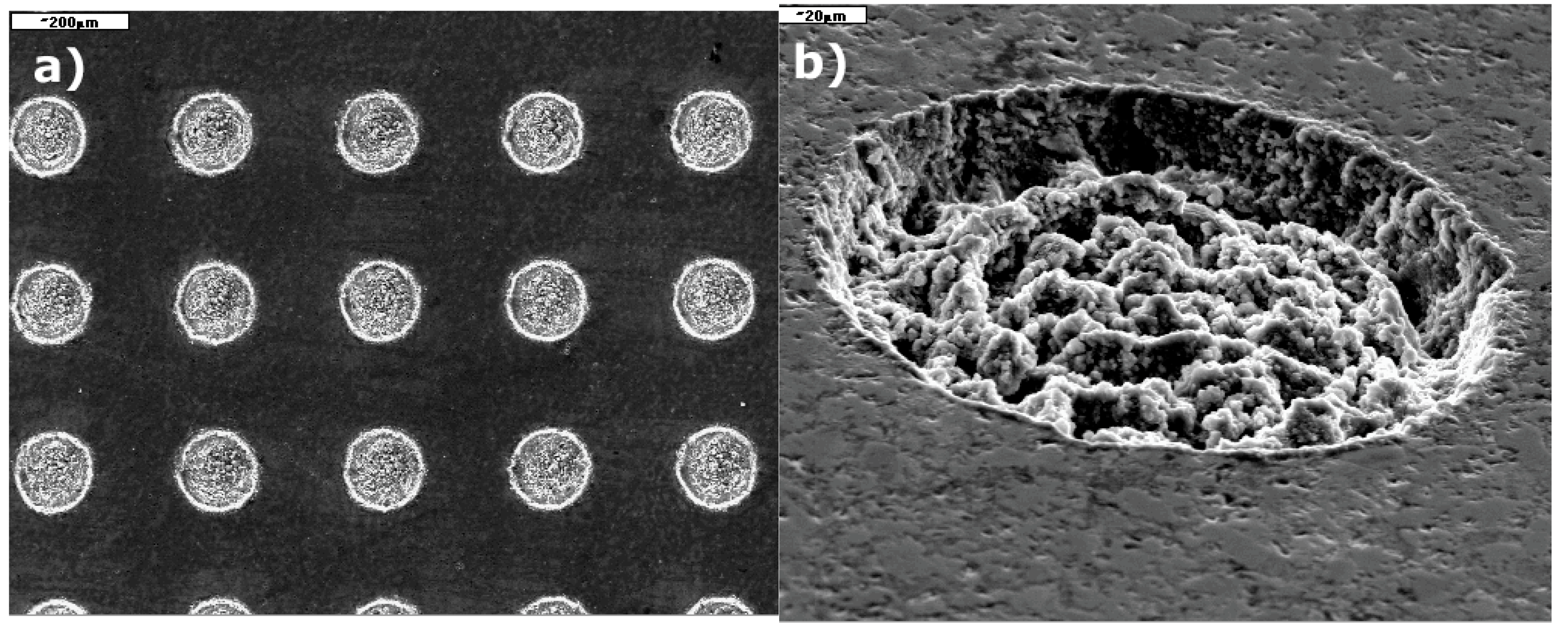
3. Laser Production of Textured Surface
4. Tribological Testing
- Anton Paar TRB3 Tribometer with reciprocating motion;
- Modified T-01M Ball-on-Ring Tester.
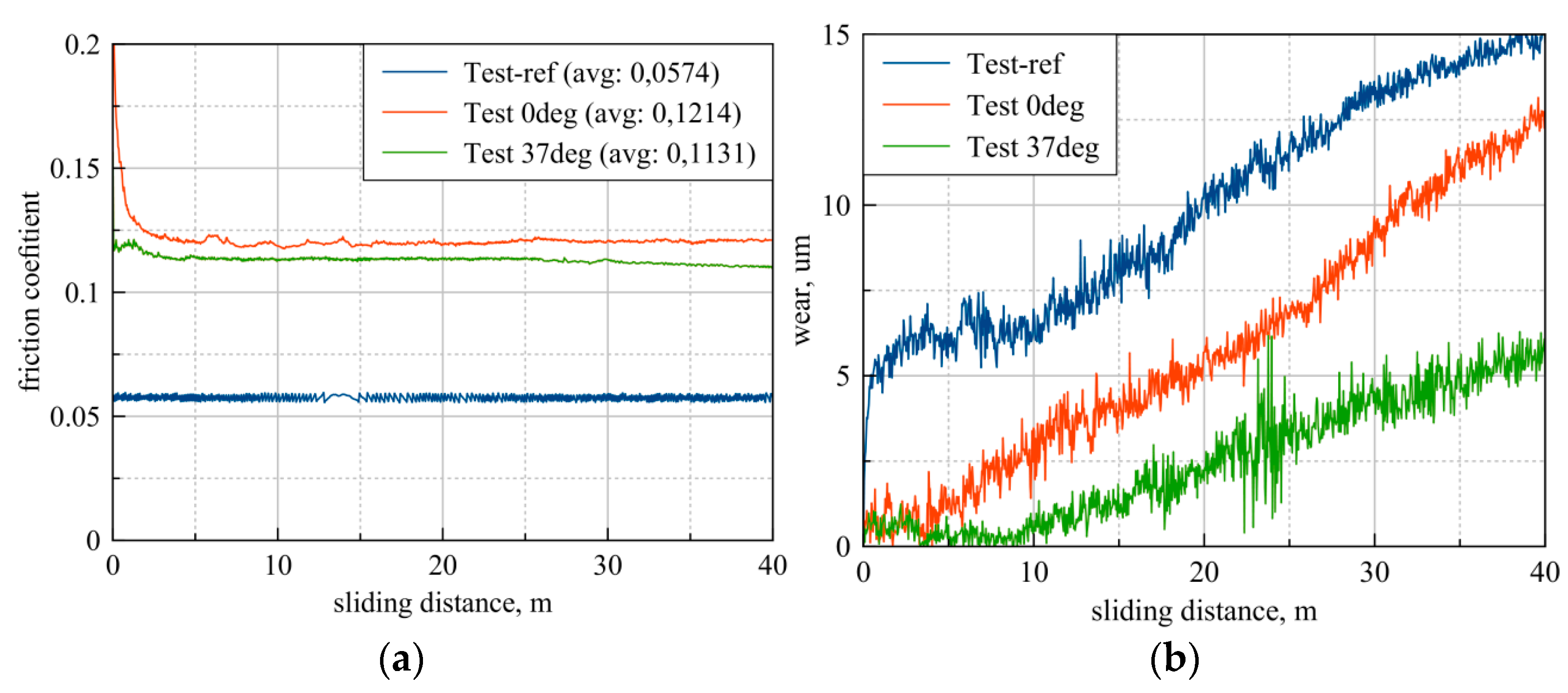
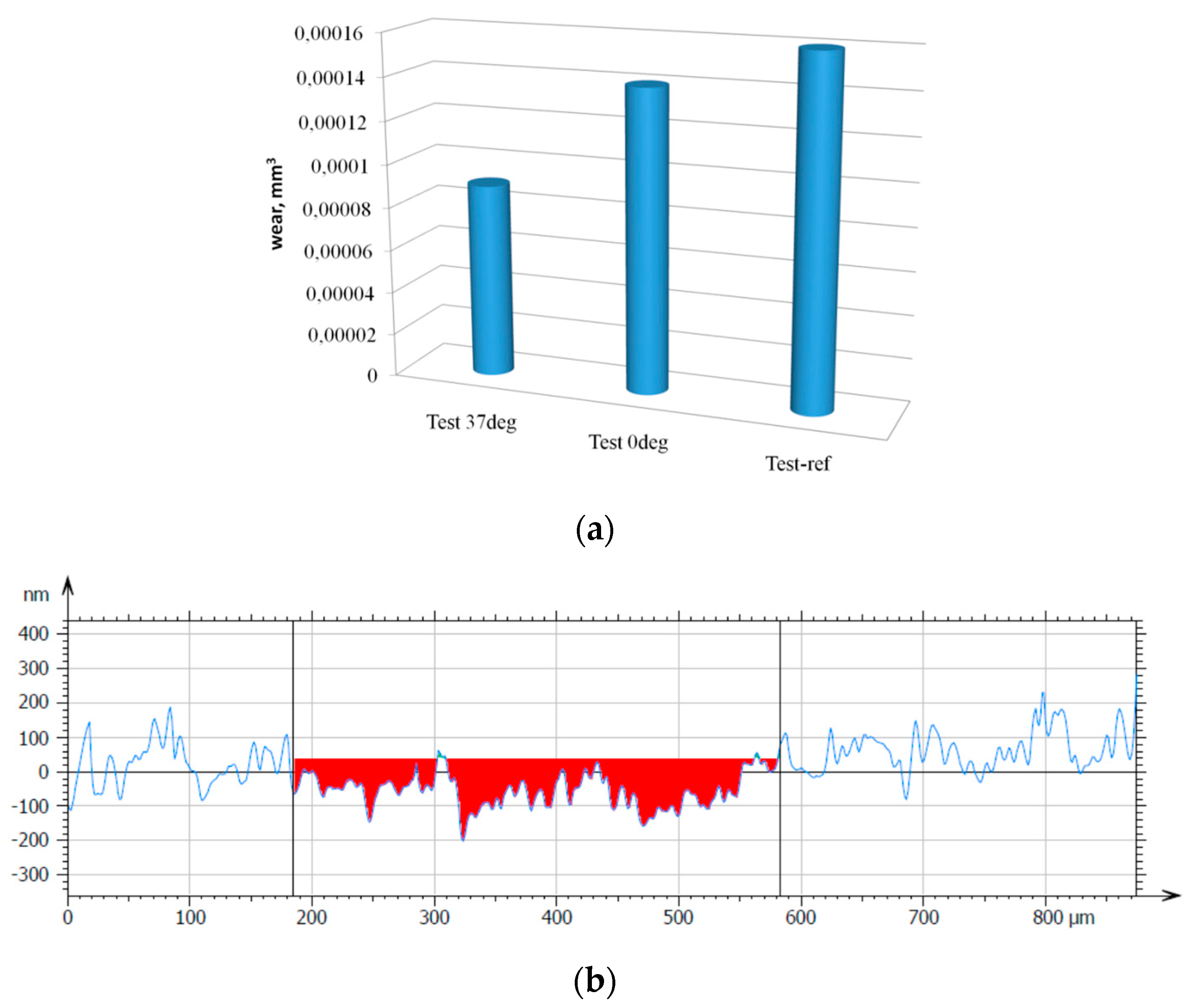
4.1. Anton Paar TRB3 Tribometer Tests
- Load—30 N;
- Sliding distance—40 m;
- Number of cycles—4000;
- Sliding frequency—1 Hz.
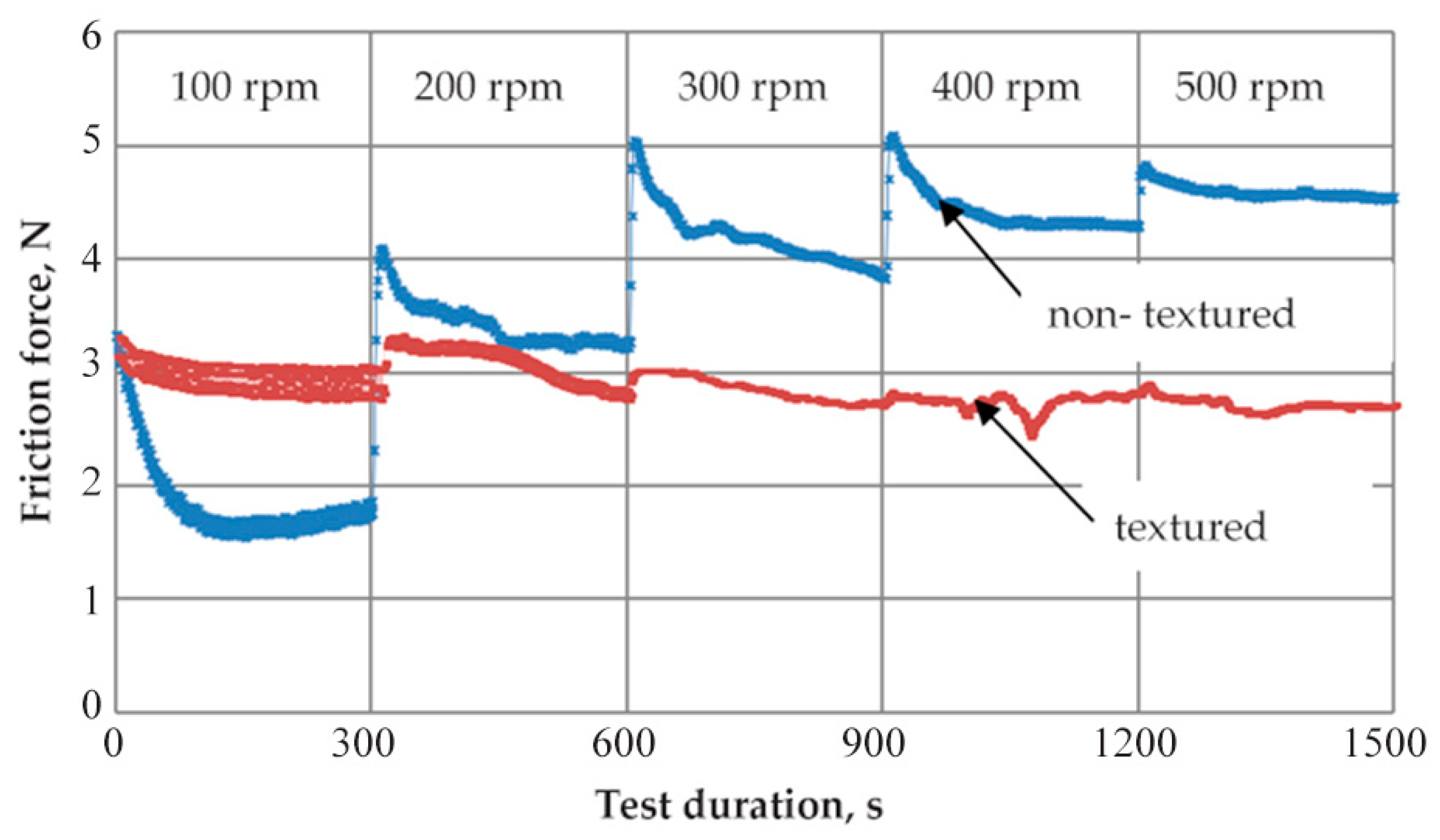
4.2. T-01M Ball-on-Ring (Modified) Tests
- Rotation speed changed gradually from 100 to 500 rpm;
- Friction pair load with normal force from 4.9 to 39.2 N.
5. Conclusions
- The presented findings, both theoretical and experimental, proved that the motion trajectory analysis during friction depending on texture distribution of elements has a significant impact on exploitation parameters, such as the friction coefficient and wear;
- The experimental results concerning relationship influence between the motion trajectory and texture mesh confirmed theoretical analyzes and proved that there is a clear dependence between studied parameters. If “dry” trajectories occur during friction, the value of the friction coefficient and the intensity of wear increase;
- Presented analyzes and tests herein have proved that the surface texture improves lubrication efficiency, especially at higher loads and higher sliding speeds. The final effect depends on the type, size and mutual arrangement of the individual texture elements and the sliding pair load parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, C.; Bai, S.; Peng, X.; Meng, Y. Improving hydrophobicity of laser textured SiC surface with micro-square convexes. Appl. Surf. Sci. 2013, 266, 51–56. [Google Scholar] [CrossRef]
- Erdemir, A. Review of engineered tribological interfaces for improved boundary lubrication. Tribol. Int. 2005, 38, 249–256. [Google Scholar] [CrossRef]
- Kovaci, H.; Secer, Y. Improved tribological performance of AISI 316L stainless steel by a combined surface treatment: Surface texturing by selective laser melting and plasma nitriding. Surf. Coat. Technol. 2020, 400, 126178. [Google Scholar] [CrossRef]
- McGeough, J.A.; Rasmussen, H. A theoretical model of electrodischarge texturing. J. Mater. Processing Technol. 1997, 68, 172–178. [Google Scholar] [CrossRef]
- Tarelnyk, V.; Konoplianchenko, I.; Martsynkovskyy, V.; Zhukov, A.; Kurp, P. Comparative tribological tests for face impulse seals sliding surfaces formed by various methods. In Advances in Design, Simulation and Manufacturing; DSMIE 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–10. [Google Scholar]
- Kovalchenko, A.; Ajayi, A.; Erdemir, A.; Fenske, G.; Etison, I. The effect of laser surface texturing on transitions in lubrication regimes during unidirectional sliding contact. Tribol. Int. 2005, 38, 219–225. [Google Scholar] [CrossRef]
- Antoszewski, B.; Sęk, P. Influence of laser beam intensity on geometry parameters of a single surface texture element. Arch. Metall. Mater. 2015, 60, 2215–2219. [Google Scholar] [CrossRef][Green Version]
- Sęk, P. The use of statistical functions for the selection of laser texturing parameters. Open Eng. 2020, 10, 454–461. [Google Scholar] [CrossRef]
- Powell, P.M. Laser-Based Micromachining Gets Practical. In Photonics Spectra; Photonics Media: Pittsfield, MA, USA, 2003; p. 70. [Google Scholar]
- Steen, W.M.; Mazumder, J. Laser Material Processing; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Xue, X.; Li, Y.; Guan, Y. Improving tribological behavior of laser textured Ti-20Zr-10Nb-4Ta alloy with dimple surface. Mater. Lett. 2021, 305, 130876. [Google Scholar] [CrossRef]
- Lu, Y.; Deng, J.; Wang, R.; Wu, J.; Meng, Y. Tribological performance of micro textured surface machined by Nd:YAG laser with different incident angle. Opt. Laser Technol. 2022, 148, 107768. [Google Scholar] [CrossRef]
- Wang, X.; Kato, K.; Adachi, K.; Aizawa, K. The effect of laser texturing of SiC surface on the critical load for transition of water lubrication mode from hydrodynamic to mixed. Tribol. Int. 2001, 34, 703–711. [Google Scholar] [CrossRef]
- Sani, E. Tailoring optical properties of surfaces in wide spectral ranges by multi-scale femtosecond-laser texturing: A case-study for TaB2 ceramics. Opt. Mater. 2020, 109, 110347. [Google Scholar] [CrossRef]
- Xing, Y.; Deng, J.; Feng, X.; Yu, S. Effect of laser surface texturing on Si3N4/TiC ceramic sliding against steel under dry friction. Mater. Des. 2013, 52, 234–245. [Google Scholar] [CrossRef]
- Hsu, S.; Jing, Y.; Zhao, F. Self-adaptive surface texture design for friction reduction across the lubrication regimes. Surf. Topogr. Metrol. Prop. 2015, 4, 014004. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Q.; Zhang, Z.; Fu, Y.; Xu, J. Surface micro-texture on sapphire fabricated by laser ablation trajectory regulation. Chin. J. Aeronaut. 2022, 35, 525–536. [Google Scholar] [CrossRef]
- Volchok, A.; Halperin, G.; Etsion, I. The effect of surface regular microtopography on fretting fatigue life. Wear 2002, 235, 509–515. [Google Scholar] [CrossRef]
- Pakuła, D.; Staszuk, M.; Dziekońska, M.; Kožmín, P.; Čermák, A. Laser micro-texturing of sintered tool materials surface. Materials 2019, 12, 3152. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Yi, S.; Ge, X.; Chen, X.; Luo, J. Enhancement of friction performance of fluorinated graphene and molybdenum disulfide coating by microdimple arrays. Carbon 2020, 167, 122–131. [Google Scholar] [CrossRef]
- Yan, H.; Chen, Z.; Zhao, J.; Zhang, P.; Yu, Z.; Lu, Q. Enhancing tribological properties of WS2/NbC/Co-based self-lubricating coating via laser texturing and laser cladding two-step process. J. Mater. Res. Technol. 2020, 9, 9907–9919. [Google Scholar] [CrossRef]
- Murzin, S.P.; Balyakin, V.B. Microstructuring the surface of silicon carbide ceramic by laser action for reducing friction losses in rolling bearings. Opt. Laser Technol. 2017, 88, 96–98. [Google Scholar] [CrossRef]
- Schille, J. High-rate laser surface texturing for advanced tribological functionalit. Lubricants 2020, 8, 33. [Google Scholar] [CrossRef]
- Wang, H.; Sun, A.; Qi, X.; Fan, Y.D.B. Wear properties of textured lubricant films filled with graphite and polytetrafluoroethylene (PTFE) via laser surface texturing (LST). Tribol. Int. 2022, 167, 107414. [Google Scholar] [CrossRef]
- Ryk, G.; Klingerman, Y.; Etison, I. Experimental investigation of laser surface texturing for reciprocating automotive components. Tribol. Trans. 2002, 45, 444–449. [Google Scholar] [CrossRef]
- Behera, R.; Das, A.; Hasan, A.; Pamu, D.; Pandey, L.; Sankar, M. Deposition of biphasic calcium phosphate film on laser surface textured Ti-6Al-4V and its effect on different biological properties for orthopedic applications. J. Alloys Compd. 2020, 842, 155683. [Google Scholar] [CrossRef]
- Yu, X.Q.; He, S.; Cai, R.L. Frictional characteristics of mechanical seals with a laser textured seal face. J. Mater. Processing Technol. 2002, 129, 463–466. [Google Scholar] [CrossRef]
- Wang, X.; Adachi, K.; Otsuka, K.; Kato, K. Optimization of the surface texture for silicon carbide sliding in water. Appl. Surf. Sci. 2006, 253, 1282–1286. [Google Scholar] [CrossRef]
- Maldonado-Cortés, D.; Peña-Parás, L.; Rodríguez, N.; Marcelo, M.; Leal, O.; Iván, D.; Correa, Q. Tribological characterization of different geometries generated with laser surface texturing for tooling applications. Wear 2021, 477, 203856. [Google Scholar] [CrossRef]
- Sharma, S.C.; Tomar, A.K. Study on MR fluid hybrid hole-entry spherical journal bearing with micro-grooves. Int. J. Mech. Sci. 2021, 202–203, 106504. [Google Scholar] [CrossRef]
- Tomar, A.K.; Sharma, S.C. An investigation into surface texture effect on hole-entry hybrid spherical journal bearing performance. Tribol. Int. 2020, 151, 106417. [Google Scholar] [CrossRef]
- Antoszewski, B.; Tarelnyk, V. Laser texturing of sliding surfaces of bearings and pump seals. Appl. Mech. Mater. 2014, 630, 301–307. [Google Scholar] [CrossRef]
- Kumar, V.; Sharma, S.C. Influence of dimple geometry and micro-roughness orientation on performance of textured hybrid thrust pad bearing. Meccanica 2018, 53, 3579–3606. [Google Scholar] [CrossRef]
- Mishra, S.; Choudhury, A.; Sahu, S. CFD investigation of influences of reverse textures on bearing surface of a journal bearing. J. Appl. Fluid Mech. 2014, 7, 395–399. [Google Scholar]
- Khatri, C.B.; Sharma, S.C. Influence of textured surface on the performance of non-recessed hybrid journal bearing operating with non-Newtonian lubricant. Tribol. Int. 2016, 95, 221–235. [Google Scholar] [CrossRef]
- Antoszewski, B. Mechanical seals with sliding surface texture—model fluid flow and some aspects of the laser forming of the texture. Procedia Eng. 2012, 39, 51–62. [Google Scholar] [CrossRef]
- Etison, I. State of the art in laser surface texturing. J. Tribol. 2005, 127, 248–253. [Google Scholar] [CrossRef]
- Etison, I. A laser surface textured hydrostatic mechanical seal. Tribol. Trans. 2002, 45, 430–434. [Google Scholar] [CrossRef]
- Bronsztejn, I.N.; Muhlig, H.; Musiol, G.; Siemiendiajew, K.A. Nowoczesne Kompendium Matematyki; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2022. (In Polish) [Google Scholar]
- da Silva, W.M.; Suarez, M.P.; Machado, A.R.; Costa, H.L. Effect of laser surface modification on the micro-abrasive wear resistance of coated cemented carbide tools. Wear 2013, 302, 1230–1240. [Google Scholar] [CrossRef]
- Antoszewski, B. Properties of Laser and Plasma Modified Sliding Nodes of Friction on the Example of Face Seals; Kielce University of Technology: Kielce, Poland, 1999. (In Polish) [Google Scholar]
- Eberhart, J.G.; Horner, S. Bond-energy and surface-energy calculations in metals. J. Chem. Educ. 2010, 87, 608–612. [Google Scholar] [CrossRef]





| θ | +0° | +1° | +2° | +3° | +4° | +5° | +6° | +7° | +8° | +9° |
|---|---|---|---|---|---|---|---|---|---|---|
| 0° | 18.2 | 0.13 | 0.28 | 0.14 | 0.10 | 0.40 | 0.51 | 0.06 | 0.06 | 0.21 |
| 10° | 0.11 | 0.47 | 0.14 | 1.10 | 4.55 | 0.09 | 0.15 | 0.61 | 0.40 | 0.27 |
| 20° | 1.22 | 0.37 | 0.10 | 0.10 | 0.13 | 0.29 | 0.26 | 0.77 | 0.42 | 0.11 |
| 30° | 0.05 | 2.44 | 1.70 | 0.21 | 0.13 | 2.60 | 0.17 | 0.08 | 0.13 | 0.12 |
| 40° | 0.20 | 0.12 | 2.43 | 0.07 | 0.18 | 9.29 | 0.17 | 0.60 | 0.32 | 0.12 |
| 50° | 0.04 | 0.21 | 0.23 | 0.11 | 2.59 | 0.13 | 0.36 | 0.28 | 0.78 | 0.80 |
| 60° | 0.24 | 0.25 | 0.95 | 0.09 | 0.08 | 0.53 | 0.07 | 0.13 | 0.09 | 1.22 |
| 70° | 1.18 | 0.23 | 0.11 | 0.46 | 1.31 | 0.06 | 4.23 | 0.21 | 0.13 | 0.40 |
| 80° | 0.07 | 0.11 | 0.13 | 0.21 | 0.36 | 0.07 | 0.18 | 0.11 | 0.14 | 0.30 |
| 90° | 18.75 | - | - | - | - | - | - | - | - | - |
| Recess Diameter d [μm] | Distance between the Recess Symmetry Axles’ Centers Ca [μm] | Degree of Blackening Sp [%] | Mutual Distance between the Recess’ Edges Ca—d [μm] | Total Surface Energy Ep [mJ/m2] |
|---|---|---|---|---|
| 78 | 162 | 18.2 | 84 | 60.6 |
| 134 | 279 | 17.9 | 145 | 63.4 |
| 78 | 106 | 42.5 | 28 | 56.2 |
| 134 | 183 | 41.8 | 49 | 55.9 |
| 150 | 256 | 27.4 | 106 | 56.7 |
| 70 | 119 | 27.1 | 49 | 55.9 |
| 102 | 128 | 49.9 | 26 | 58.8 |
| 102 | 233 | 15.1 | 131 | 60.9 |
| 102 | 174 | 26.9 | 72 | 56.5 |
| Load [N] | Sliding Velocity [rpm] | Friction Type | AverageFriction Coefficient f | c0 | c1 (d) | c2 (γ) | c3 (Ca-d) | c4 (Sp) | Correlation Coefficient Cc |
|---|---|---|---|---|---|---|---|---|---|
| 24.5 | (200) | fluid | 0.12 | 0.4439 | −0.0017 | −0.0072 | +0.0013 | +0.0039 | 0.5795 |
| 29.4 | (200) | fluid | 0.10 | 0.8588 | −0.0031 | −0.0171 | +0.034 | +0.0093 | 0.8544 |
| 24.5 | (600) | mixed | 0.14 | −0.543 | +0.0001 | +0.0157 | −0.0018 | −0.0053 | 0.8572 |
| 29.4 | (600) | mixed | 0.12 | −0.448 | −0.0010 | +0.0118 | −0.0003 | −0.0002 | 0.9062 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antoszewski, B.; Kurp, P. Effect of Surface Texture on the Sliding Pair Lubrication Efficiency. Lubricants 2022, 10, 80. https://doi.org/10.3390/lubricants10050080
Antoszewski B, Kurp P. Effect of Surface Texture on the Sliding Pair Lubrication Efficiency. Lubricants. 2022; 10(5):80. https://doi.org/10.3390/lubricants10050080
Chicago/Turabian StyleAntoszewski, Bogdan, and Piotr Kurp. 2022. "Effect of Surface Texture on the Sliding Pair Lubrication Efficiency" Lubricants 10, no. 5: 80. https://doi.org/10.3390/lubricants10050080
APA StyleAntoszewski, B., & Kurp, P. (2022). Effect of Surface Texture on the Sliding Pair Lubrication Efficiency. Lubricants, 10(5), 80. https://doi.org/10.3390/lubricants10050080






