Numerical Optimization Analysis of Floating Ring Seal Performance Based on Surface Texture
Abstract
:1. Introduction
2. Theory Model
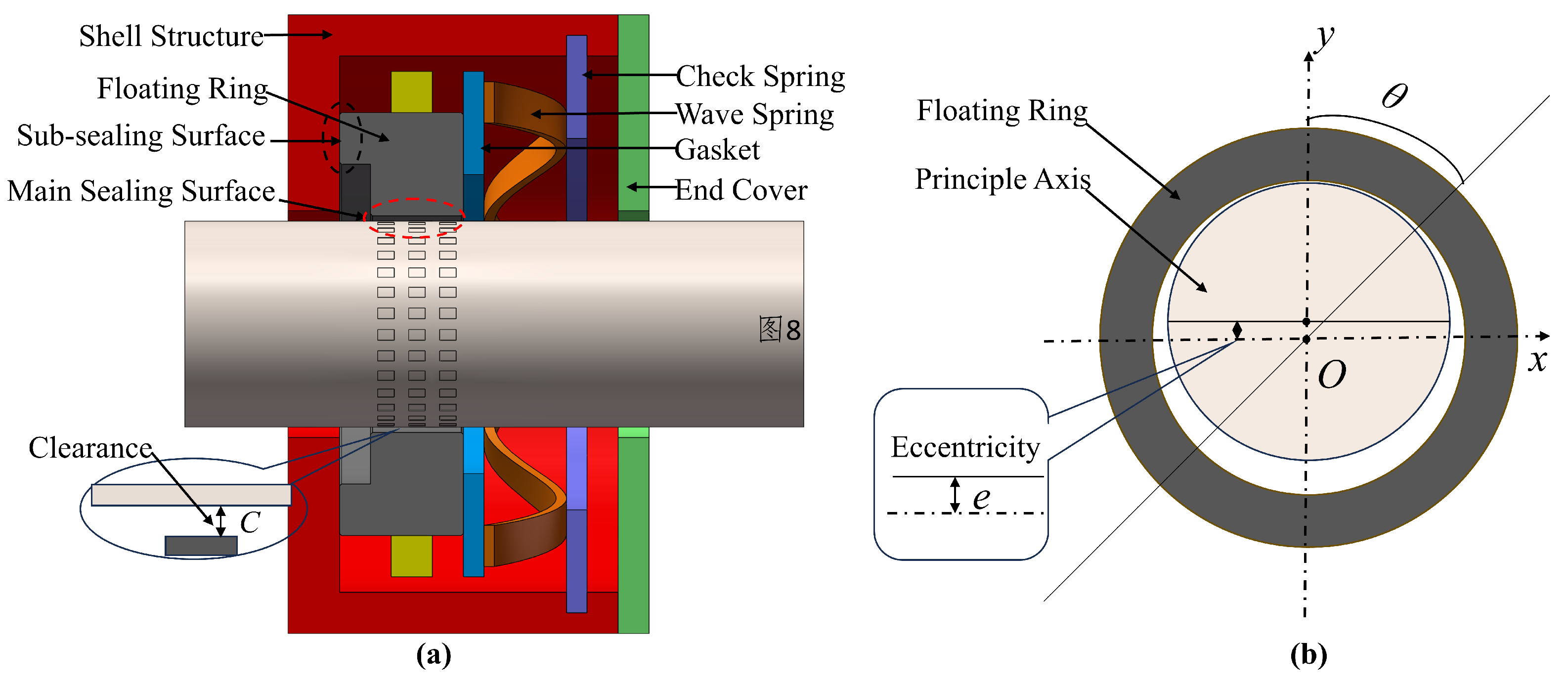
2.1. Working Principle
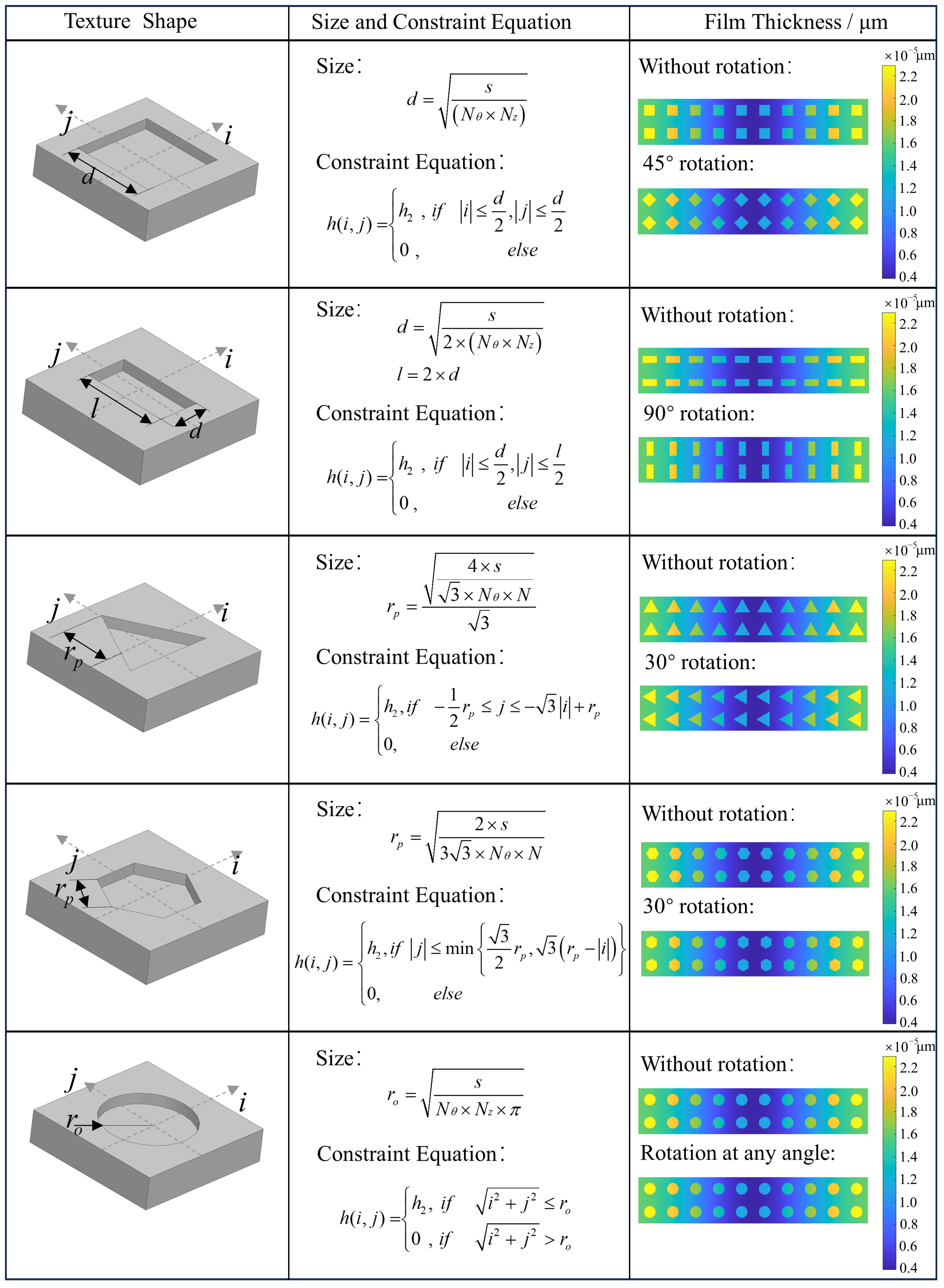
2.2. Surface Texture Model
2.3. Surface Roughness Model
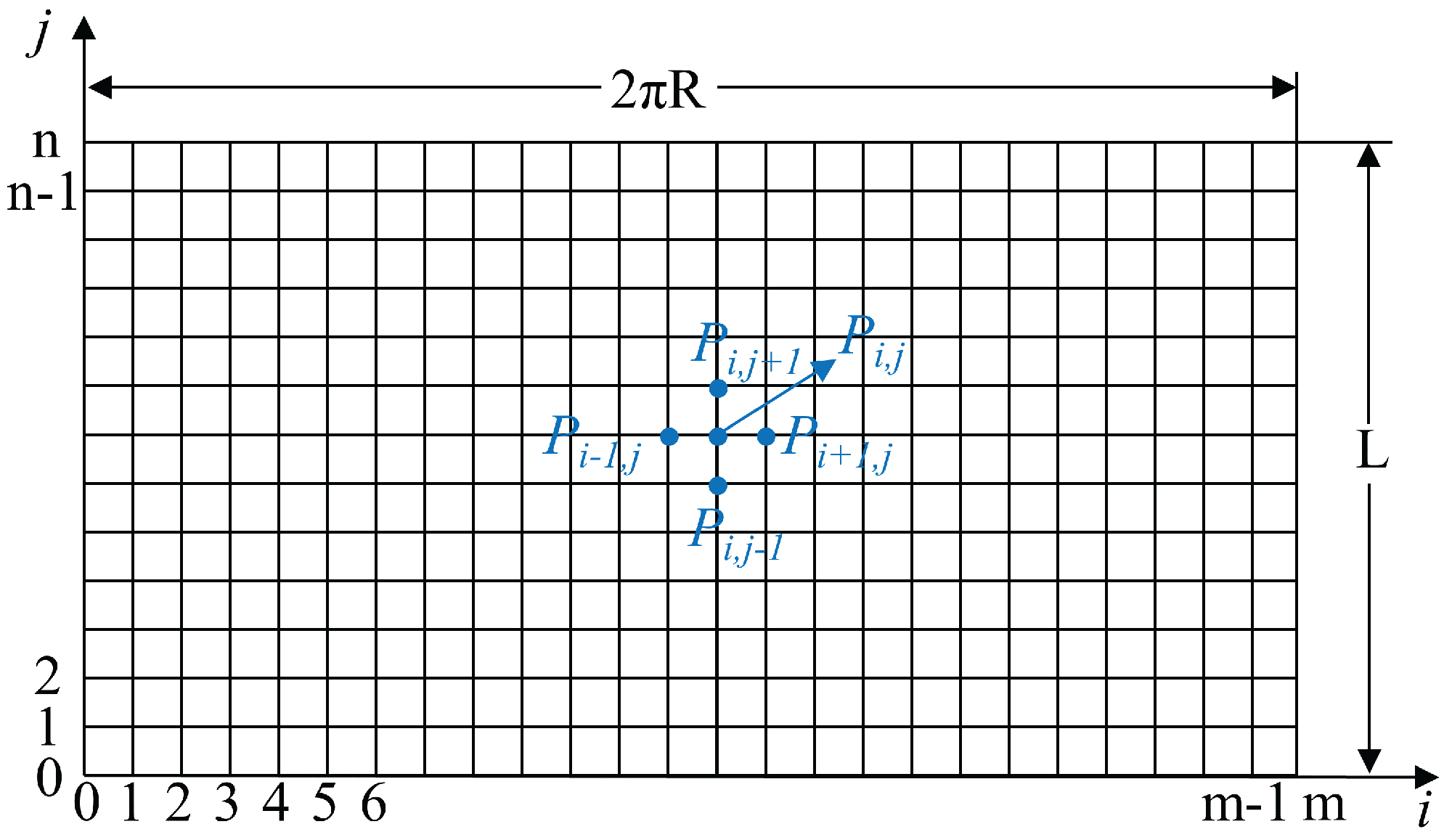
2.4. Differential Grids and Iteration
2.5. Performance Evaluation
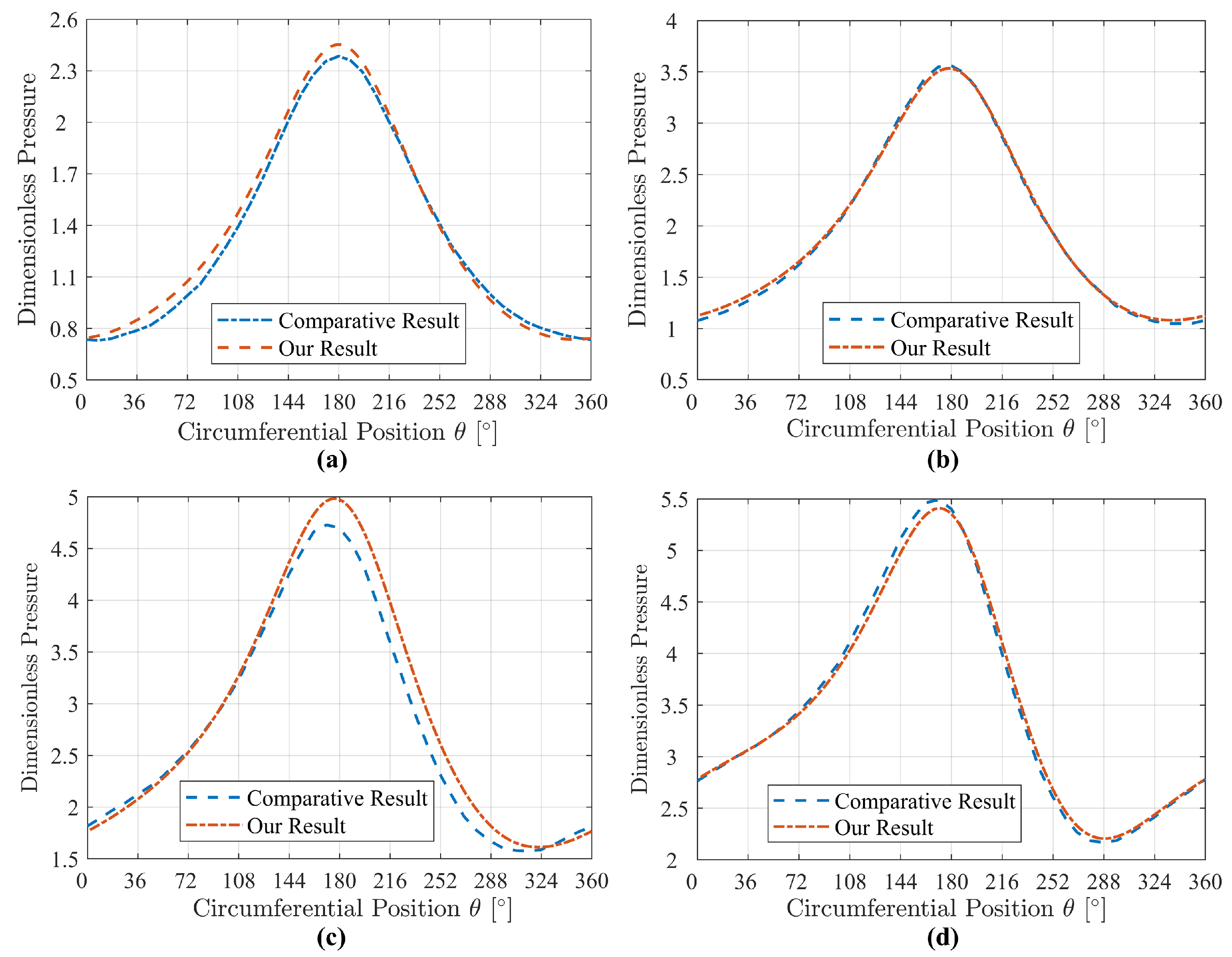
3. Validation
4. Result and Discussion
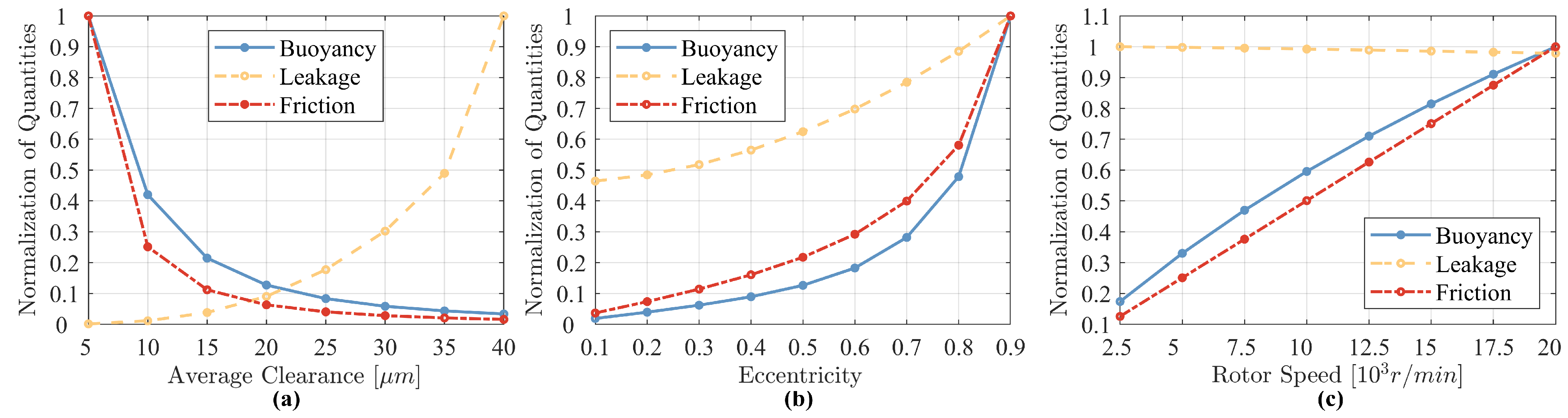
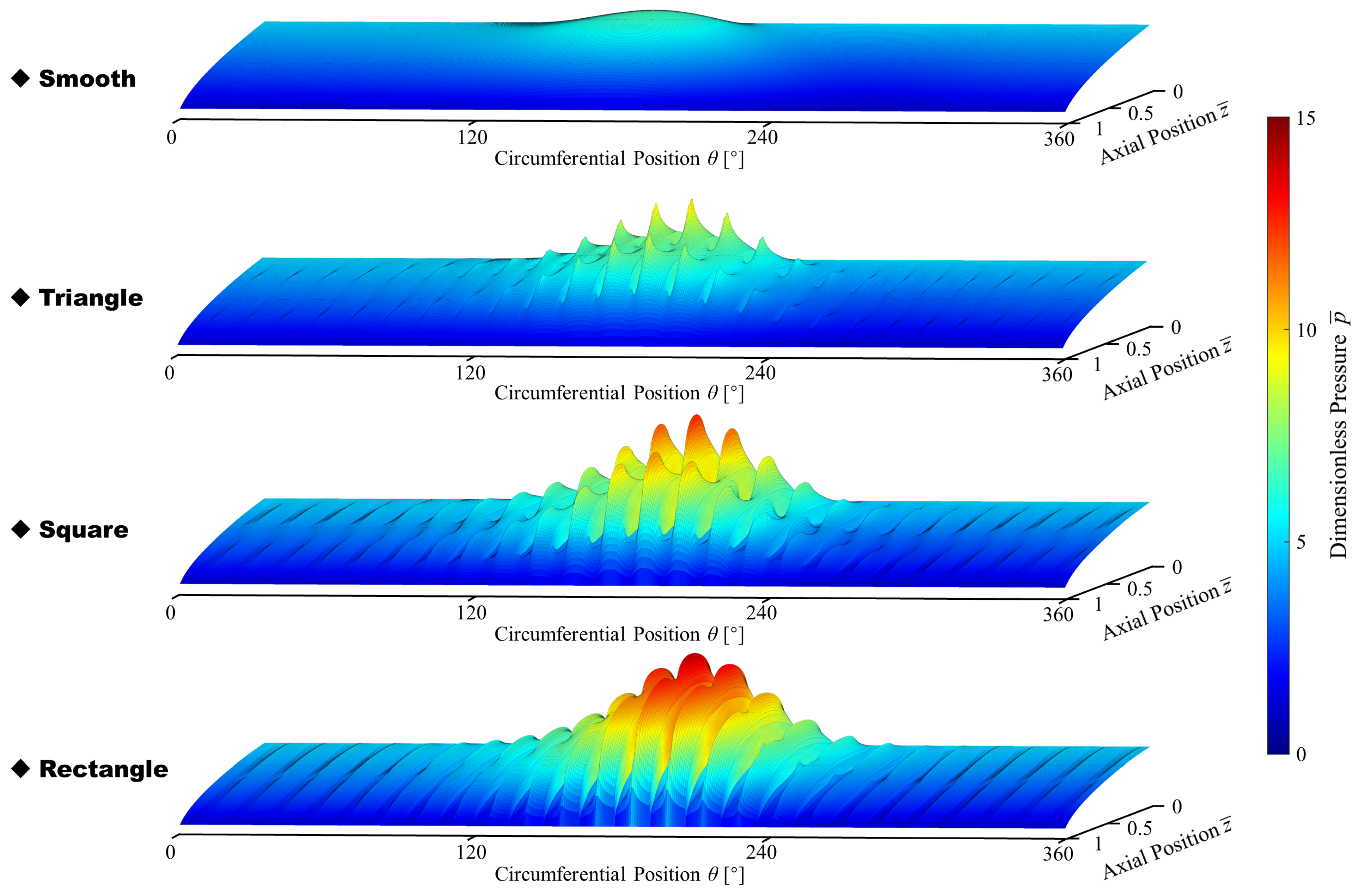
4.1. Seal Mechanism
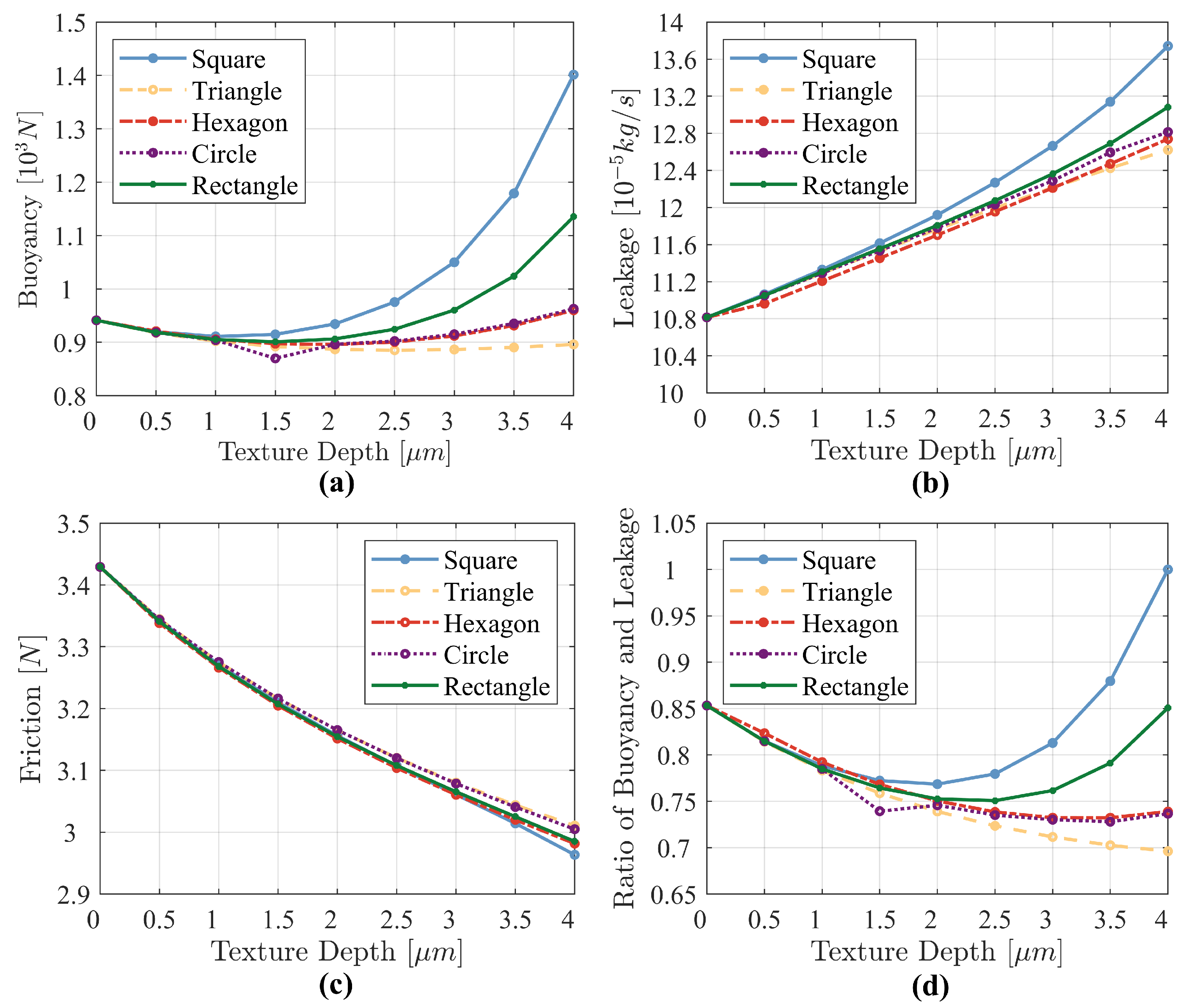
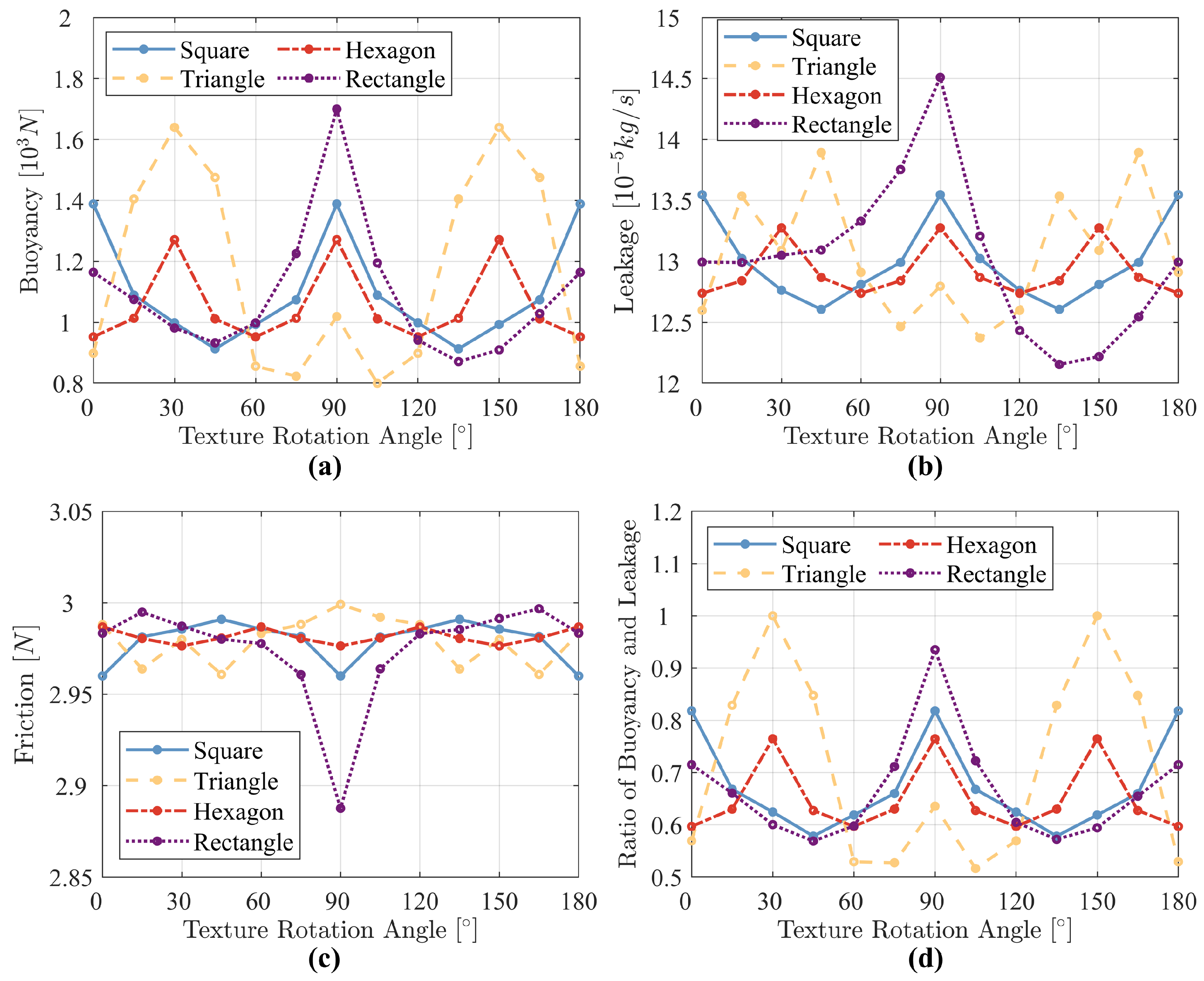
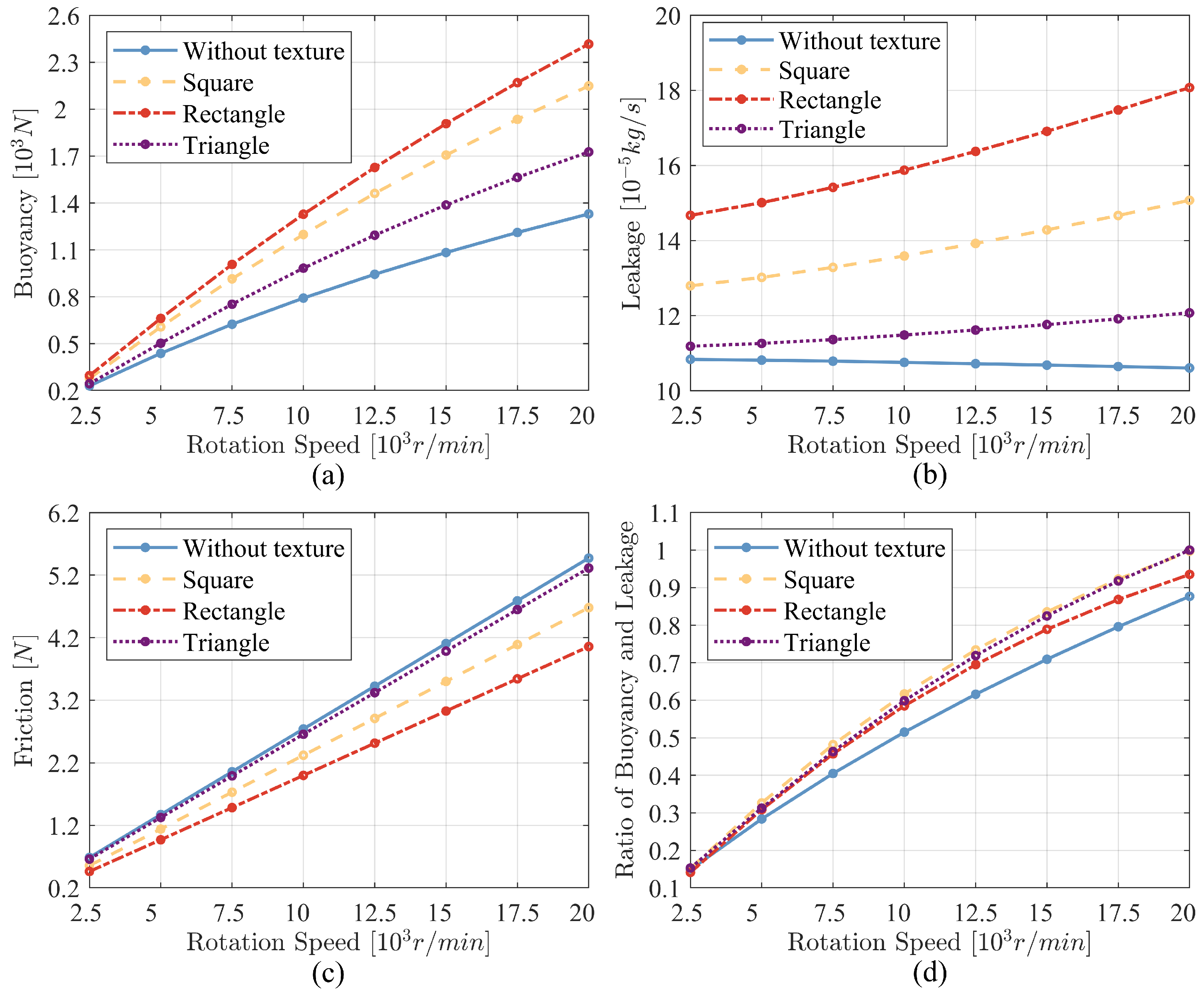
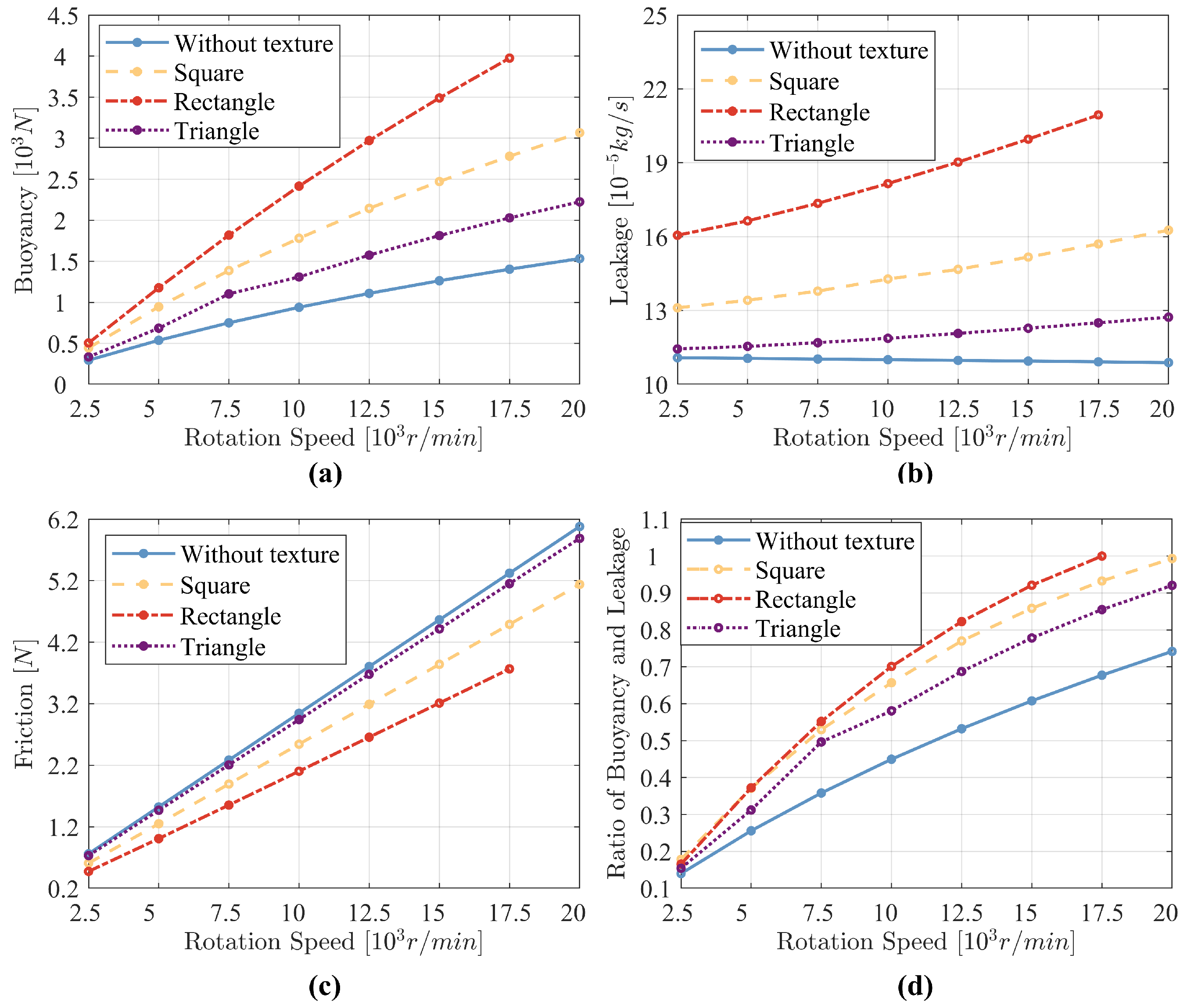
4.2. Effect of Texture
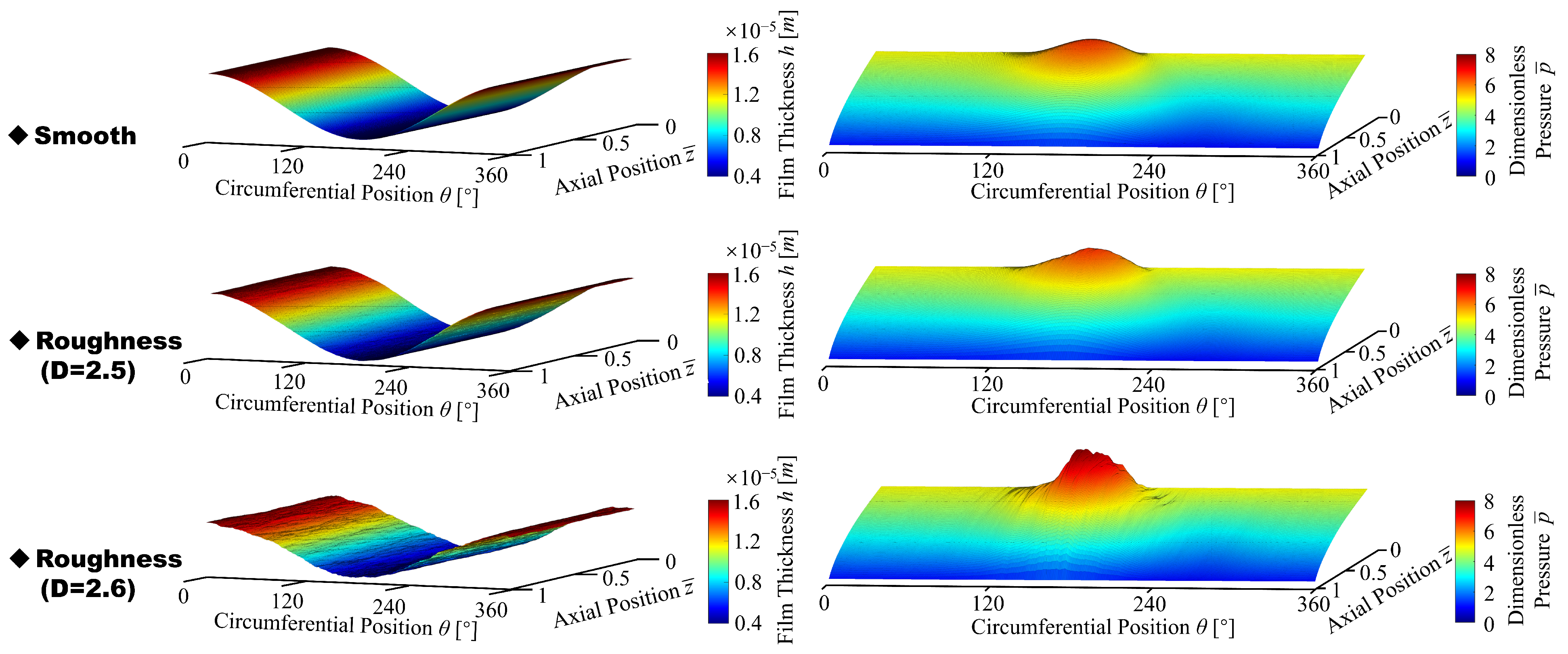
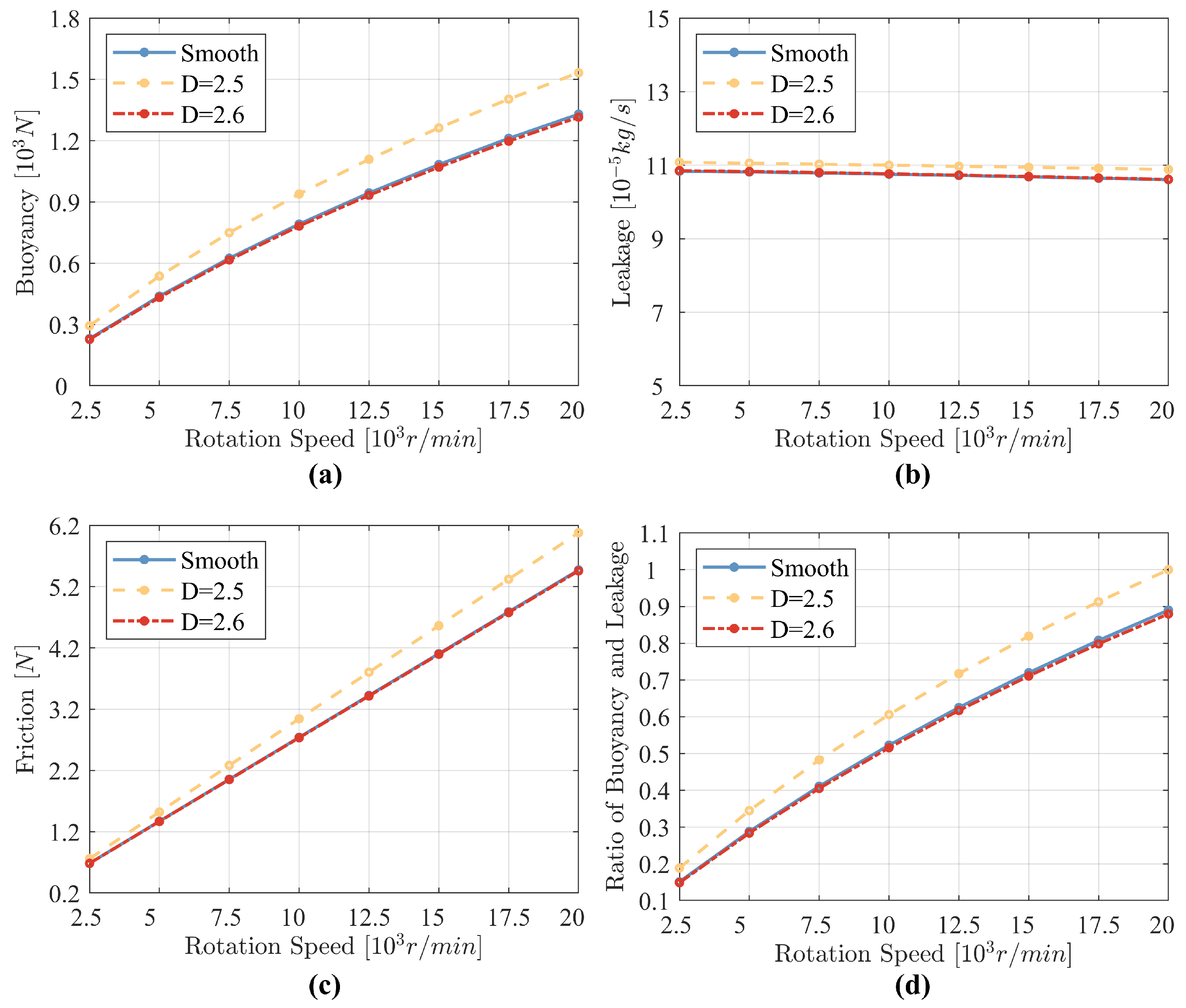
4.3. Effect of Texture with Roughness
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | textured area |
| random numbers in the interval [0, ] | |
| b | position of the shaft surface |
| random numbers in the interval [0, ] | |
| c | radial clearance, m |
| C | height coefficient of the surface |
| a normally distributed random variable with a mean of 0 and variance of 1 | |
| d | lengths of square textures; the width of the rectangular texture, m |
| D | fractal dimension |
| theoretical fractal dimension | |
| e | eccentricity, m |
| G | feature scale parameter |
| h | gas film thickness, m |
| distribution of depth of texture | |
| distribution of depth of surface roughness | |
| depth of texture, m | |
| H | dimensionless film thickness |
| k | ratio of buoyancy and leakage, N· kg/s |
| l | length of the rectangular texture, m |
| L | size of the simulated image, m |
| sampling length, m | |
| a number which is determined by the instrument resolution | |
| m | frequency coefficient |
| M | number of spatial undulations |
| n | frequency coefficient |
| maximum frequency coefficient | |
| p | gas film pressure, Pa |
| dimensionless film pressure | |
| air pressure, Pa | |
| pressure in the low-pressure side, Pa | |
| pressure in the high-pressure side, Pa | |
| Q | leakage, kg/s |
| R | radius of the rotating shaft, m |
| radius of the outer circle of a triangular or hexagonal texture, m | |
| radius of the outer circle of a triangular or hexagonal texture, m | |
| dimensionless friction component in the x-direction | |
| dimensionless friction component in the y-direction | |
| U | linear velocity of rotating shaft, m/s |
| w | buoyancy of gas film, N |
| dimensionless buoyancy of gas film, N | |
| dimensionless buoyancy component in the x-direction | |
| dimensionless buoyancy component in the y-direction | |
| characteristic parameter | |
| seal coefficient | |
| aerodynamic viscosity, Pa · m | |
| a series of random phases between 0 and | |
| gas density, kg/m3 |
References
- Xia, P.; Chen, H.; Liu, Z.; Ma, W.; Yang, B. Analysis of whirling motion for the dynamic system of floating ring seal and rotor. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 1221–1235. [Google Scholar] [CrossRef]
- Duan, W.; Chu, F.; Kim, C.H.; Lee, Y.B. A bulk-flow analysis of static and dynamic characteristics of floating ring seals. Tribol. Int. 2007, 40, 470–478. [Google Scholar] [CrossRef]
- Lee, Y.B.; Kim, C.H.; Duan, W.; Chu, F. Analysis of Leakage Flow and Dynamic Characteristics in Floating Ring Seals for High Pressure Turbopump. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; Volume 42401, pp. 1341–1349. [Google Scholar]
- Bae, J.H.; Kwak, H.D.; Heo, S.J.; Choi, C.H.; Choi, J.S. Numerical and experimental study of nose for Lox floating ring seal in turbopump. Aerospace 2022, 9, 667. [Google Scholar] [CrossRef]
- Shi, R.J.; Li, S.X.; Zhen, R.; Ma, L.j.; Zhang, J.B. Design method and research of high temperature gas floating ring seal with slightly variable gap. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1081, 012005. [Google Scholar] [CrossRef]
- Anbarsooz, M.; Amiri, M.; Erfanian, A.; Benini, E. Effects of the ring clearance on the aerodynamic performance of a CO2 centrifugal compressors annular seal: A numerical study. Tribol. Int. 2022, 170, 107501. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Q.; Huang, E.; Lei, Z.; Wu, H.; Xu, G. Leakage performance of floating ring seal in cold/hot state for aero-engine. Chin. J. Aeronaut. 2019, 32, 2085–2094. [Google Scholar] [CrossRef]
- Nagai, K.; Kaneko, S.; Taura, H.; Watanabe, Y. Numerical and experimental analyses of dynamic characteristics for liquid annular seals with helical grooves in seal stator. J. Tribol. 2018, 140, 052201. [Google Scholar] [CrossRef]
- Lu, X.; Andrés, L.S. Leakage and Rotordynamic Force Coefficients of a Three-Wave (Air in Oil) Wet Annular Seal: Measurements and Predictions. J. Eng. Gas Turbines Power 2019, 141, 032503. [Google Scholar] [CrossRef]
- Zhang, G.H.; Wang, G.L.; Liu, Z.S.; Ma, R.X. Stability Characteristics of Steam Turbine Rotor Seal System with Analytical Floating Ring Seal Force Model. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air. American Society of Mechanical Engineers, San Antonio, TX, USA, 3–7 June 2013; Volume 55270, p. V07BT30A004. [Google Scholar]
- Kirk, R.; Miller, W. The influence of high pressure oil seals on turbo-rotor stability. ASLE Trans. 1979, 22, 14–24. [Google Scholar] [CrossRef]
- Adjemout, M.; Brunetiere, N.; Bouyer, J. Numerical analysis of the texture effect on the hydrodynamic performance of a mechanical seal. Surf. Topogr. Metrol. Prop. 2015, 4, 014002. [Google Scholar] [CrossRef]
- Pei, S.; Xu, H.; Yun, M.; Shi, F.; Hong, J. Effects of surface texture on the lubrication performance of the floating ring bearing. Tribol. Int. 2016, 102, 143–153. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, Y.; Chen, S.; Zhu, W. Comparative research on gas seal performance textured with microgrooves and microdimples. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 280. [Google Scholar] [CrossRef]
- Wang, S.; Ding, X.; Li, N.; Ding, J.; Zhang, L. Orientation effect on sealing characteristics of rectangular micro-textured floating ring gas film seal. J. Beijing Univ. Aeronaut. Astronaut. 2023, 1–18. Available online: https://kns.cnki.net/kcms2/detail/11.2625.V.20230710.1709.004.html (accessed on 30 June 2024).
- He, Z.; Song, Q.; Liu, Q.; Xin, J.; Yang, C.; Liu, M.; Li, B.; Yan, F. Analysis of the effect of texturing parameters on the static characteristics of radial rigid bore aerodynamic journal bearings. Surf. Topogr. Metrol. Prop. 2022, 10, 035025. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, X.; Xu, J.; Jiang, H.; Li, N.; Si, J. A study on building and testing fractal model for predicting end face wear of Aeroengine’s floating ring seal. Wear 2023, 532, 205079. [Google Scholar] [CrossRef]
- Pattnayak, M.R.; Ganai, P.; Pandey, R.; Dutt, J.; Fillon, M. An overview and assessment on aerodynamic journal bearings with important findings and scope for explorations. Tribol. Int. 2022, 174, 107778. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, K.; Han, J.; Huang, Y.; Gong, W.; Guo, Y.; Huang, Z.; Luo, X.; Liang, B. Performance of textured foil journal bearing considering the influence of relative texture depth. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 2105–2117. [Google Scholar] [CrossRef]
- Tewelde, F.B.; Allen, Q.; Zhou, T. Multiscale Texture Features to Enhance Lubricant Film Thickness for Prosthetic Hip Implant Bearing Surfaces. Lubricants 2024, 12, 187. [Google Scholar] [CrossRef]
- Yan, W.; Komvopoulos, K. Contact analysis of elastic-plastic fractal surfaces. J. Appl. Phys. 1998, 84, 3617–3624. [Google Scholar] [CrossRef]
- Ausloos, M.; Berman, D. A multivariate Weierstrass–Mandelbrot function. Proc. R. Soc. London. A Math. Phys. Sci. 1985, 400, 331–350. [Google Scholar]
- Zhang, X.; Xu, Y.; Jackson, R.L. An analysis of generated fractal and measured rough surfaces in regards to their multi-scale structure and fractal dimension. Tribol. Int. 2017, 105, 94–101. [Google Scholar] [CrossRef]
- Xiao, H.; Sun, Y.; Chen, Z. Fractal modeling of normal contact stiffness for rough surface contact considering the elastic–plastic deformation. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 11. [Google Scholar] [CrossRef]
- Flores Alarcón, J.L.; Figueroa, C.G.; Jacobo, V.H.; Velázquez Villegas, F.; Schouwenaars, R. Statistical Study of the Bias and Precision for Six Estimation Methods for the Fractal Dimension of Randomly Rough Surfaces. Fractal Fract. 2024, 8, 152. [Google Scholar] [CrossRef]
- Liu, Y. Digital Modeling for Functional Surface Structure Based on Fractal Representation. Master’s Thesis, South China University of Technology, Guangdong, China, 2011. [Google Scholar]
- Jiang, S.; Zheng, Y. An analytical model of thermal contact resistance based on the Weierstrass—Mandelbrot fractal function. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 959–967. [Google Scholar] [CrossRef]
- Xu, J. Analysis and Experimental Research on Dynamic Pressure Lubrication Characteristics of Compliant Foil Gas Film Seal. Ph.D. Thesis, Lanzhou University of Technology, Lanzhou, China, 2022. [Google Scholar]
- Youssef, I.K.; Taha, A. On the modified successive overrelaxation method. Appl. Math. Comput. 2013, 219, 4601–4613. [Google Scholar] [CrossRef]
- Ma, G.; Ping, X.; Shen, X.; Hu, G. Analysis of quasi-dynamic characteristics of compliant floating ring gas cylinder seal. J. Aerosp. Power 2010, 25, 1190–1196. [Google Scholar]
- Chen, T. The Groove Parameters Optimization and Numerical Simulation on Cylindrical Gas Seal. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2015. [Google Scholar]
- Shipeng, W.; Xuexing, D.; Junhua, D.; Jingmo, W. Numerical Analysis on Improving the Rectangular Texture Floating Ring Gas-film Seal Characteristics with Different Bottom Shapes. J. Appl. Fluid Mech. 2023, 16, 1371–1385. [Google Scholar]
- Ye, S.; Tang, H.; Ren, Y.; Xiang, J. Study on the load-carrying capacity of surface textured slipper bearing of axial piston pump. Appl. Math. Model. 2020, 77, 554–584. [Google Scholar] [CrossRef]
- Ding, X.; Wu, J.; Wang, Y.; Cui, B.; An, S.; Su, B.; Wang, Y. Influence of surface texture on sealing performance of PTFE materials. Macromol 2022, 2, 225–235. [Google Scholar] [CrossRef]
- Luz, F.K.C.; Profito, F.J.; dos Santos, M.B.; Silva, S.A.; Costa, H.L. Deterministic Simulation of Surface Textures for the Piston Ring/Cylinder Liner System in a Free Piston Linear Engine. Lubricants 2024, 12, 12. [Google Scholar] [CrossRef]
- Yuan, Z.; Chen, J. Influences of Floating-ring Seal Parameters on Clearance Leakage. IOP Conf. Ser. Mater. Sci. Eng. 2020, 790, 012077. [Google Scholar] [CrossRef]
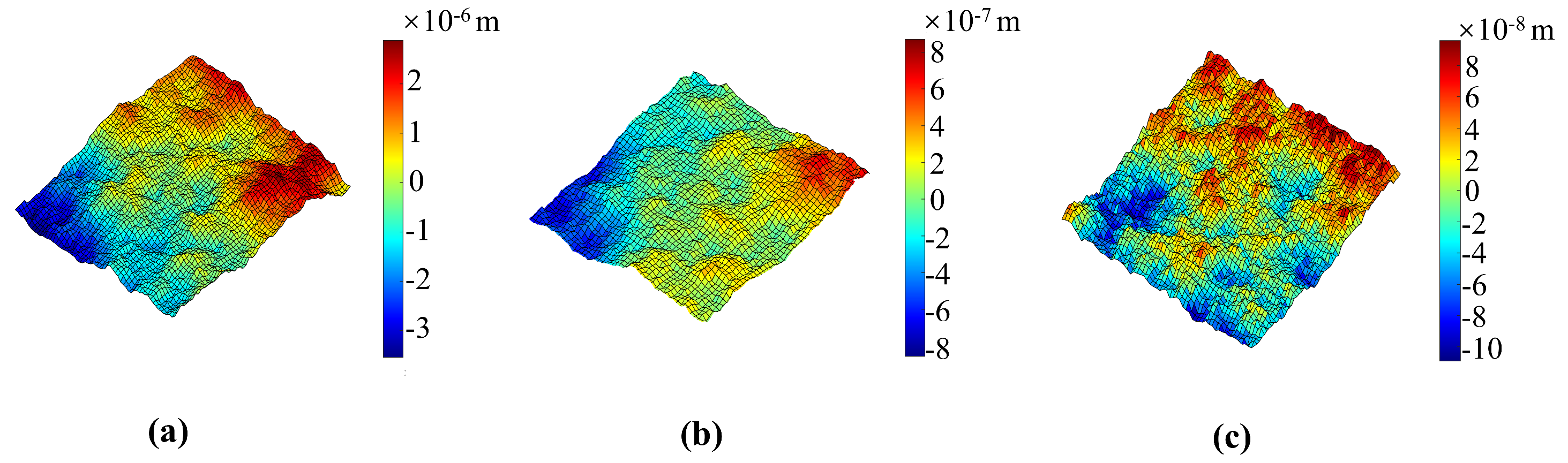


| Fractal Dimension | |||
|---|---|---|---|
| Arithmetic Mean Deviation/m | |||
| Maximum Height of Profile/m |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Eccentricity | 0.5 | Viscosity [ Pa· s] | 1.932 |
| Clearance [ m] | 10 | Density [kg/m3] | 1.1614 |
| Width of seal [ m] | 40 | Pressure of low side [MPa] | 0.11 |
| Diameter of rotor [ m] | 160 | Pressure of high side [MPa] | {0.11 0.20 |
| Speed of rotor [r/min] | 25,000 | 0.32 0.45} |
| Parameters of Seal | Value | Parameters of Textures | Value |
|---|---|---|---|
| Eccentricity | 0.5 | Texture depth [ m] | 4 |
| Clearance [ m] | 10 | Texture area ratio | 0.2 |
| Width of seal [ m] | 40 | Texture distribution | 25 × 2 |
| Diameter of rotor [ m] | 160 | Texture angle | 0 |
| Speed of rotor [r/min] | 12,500 | ||
| Pressure of low side [MPa] | 0.101325 | ||
| Pressure of high side [MPa] | 0.5 | ||
| Viscosity [ Pa· s] | 1.932 | ||
| Density [kg/m3] | 1.1614 |
| Texture Shape | Texture Depth | Rotation Angle | Area Ratio |
|---|---|---|---|
| Square | 4 m | 0° | 25% |
| Rectangle | 4 m | 90° | 40% |
| Triangle | 4 m | 30° | 5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Guo, Y.; Si, J.; Li, N.; Jia, L.; Zou, Y.; Wang, H. Numerical Optimization Analysis of Floating Ring Seal Performance Based on Surface Texture. Lubricants 2024, 12, 241. https://doi.org/10.3390/lubricants12070241
He Z, Guo Y, Si J, Li N, Jia L, Zou Y, Wang H. Numerical Optimization Analysis of Floating Ring Seal Performance Based on Surface Texture. Lubricants. 2024; 12(7):241. https://doi.org/10.3390/lubricants12070241
Chicago/Turabian StyleHe, Zhenpeng, Yuhang Guo, Jiaxin Si, Ning Li, Lanhao Jia, Yuchen Zou, and Hongyu Wang. 2024. "Numerical Optimization Analysis of Floating Ring Seal Performance Based on Surface Texture" Lubricants 12, no. 7: 241. https://doi.org/10.3390/lubricants12070241
APA StyleHe, Z., Guo, Y., Si, J., Li, N., Jia, L., Zou, Y., & Wang, H. (2024). Numerical Optimization Analysis of Floating Ring Seal Performance Based on Surface Texture. Lubricants, 12(7), 241. https://doi.org/10.3390/lubricants12070241






