Sprint and Jump Mechanical Profiles in Academy Rugby League Players: Positional Differences and the Associations between Profiles and Sprint Performance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Design
2.2. Participants
2.3. Procedures
2.3.1. Squat Jump Testing Procedures
2.3.2. Sprint Testing Procedures
2.3.3. Anthropometric, Position and Environmental Measures for Mechanical Profile Calculations
2.4. Data Analysis
2.4.1. Mechanical Profile Computation
Squat Jump Mechanical Variables
Sprint Mechanical Variables
2.4.2. Sprint Performance Data
2.5. Statistical Analysis
3. Results
3.1. Descriptive Statistics
3.2. Positional Differences
3.3. Associations between Jump and Sprint Mechanical Variables
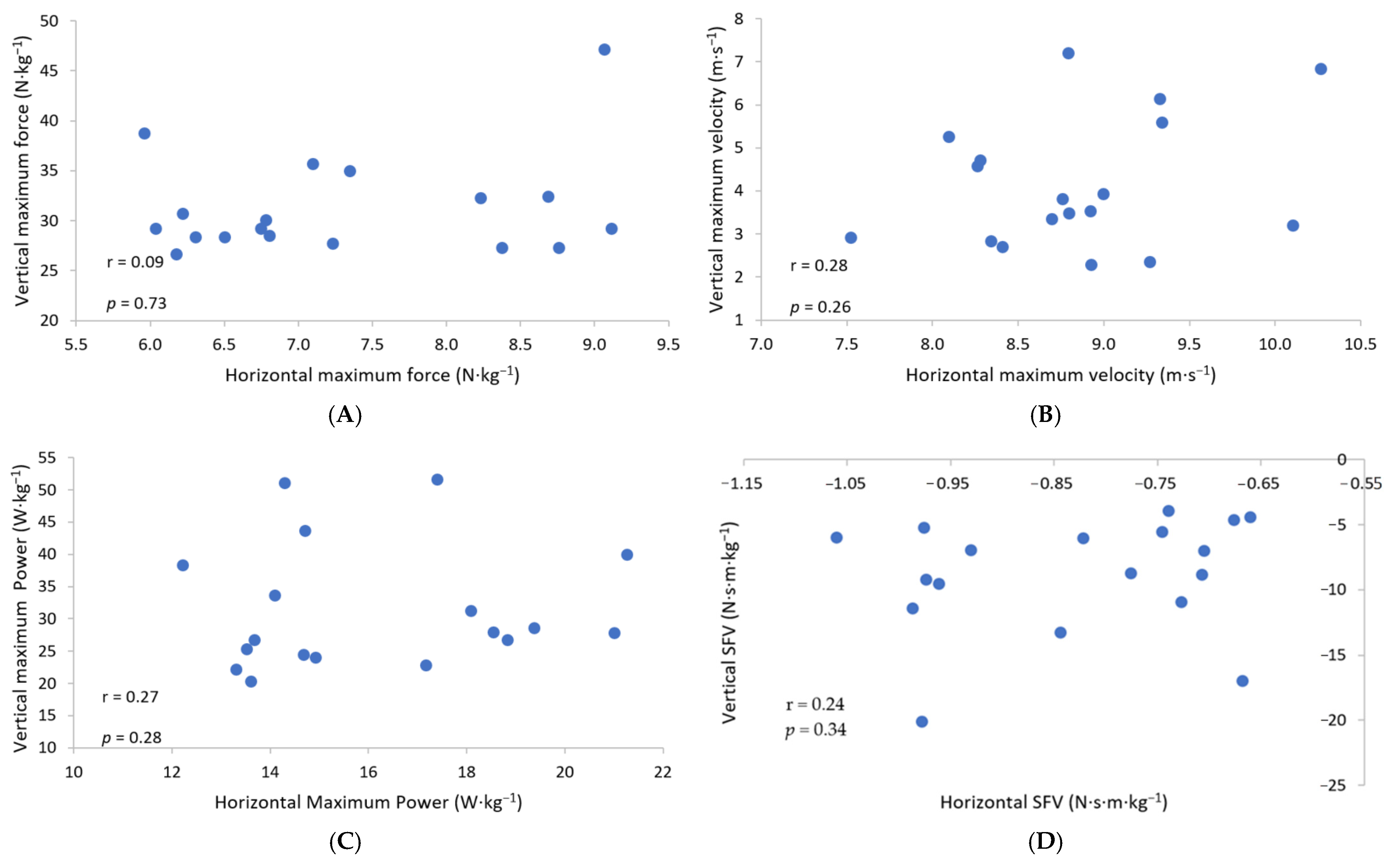
3.3.1. The Association between Relative Theoretical Maximal Force Variables
3.3.2. The Association between Velocity Variables
3.3.3. The Association between Relative Theoretical Maximal Power Variables
3.3.4. The Association between the Slope of the Linear F-v Relationships
3.4. Associations between Jump and Sprint Mechanical Profiles and Sprint Performance Outcomes
3.4.1. Theoretical Maximal Horizontal Force (FH0)
3.4.2. Relative Theoretical Maximal Horizontal Force (FH0rel)
3.4.3. Theoretical Maximal Horizontal Velocity (vH0)
3.4.4. Theoretical Maximal Horizontal Power (PHmax)
3.4.5. Relative Theoretical Maximal Horizontal Power (PHmaxrel)
3.4.6. Slope of Horizontal Force-Velocity Relationship (SHFv)
3.4.7. Rate of Decrease in Ratio of Force with Increasing Velocity during Sprint Acceleration (DRF)
3.4.8. Maximum Ratio of Step-Averaged Horizontal Ground Reaction Force to the Corresponding Resultant Force (RFmax)
3.4.9. Maximum Sprinting Velocity (vmax)
3.4.10. Maximum Sprinting Acceleration (amax)
3.4.11. Acceleration Relative to a Time Constant (τ)
4. Discussion
4.1. Mechanical Variables in Academy Rugby League Players
4.1.1. Jump Profiles
4.1.2. Sprint Profiles
4.2. Positional Comparisons
4.3. F-v Imbalances in Profiles
4.4. Associations between Jump Mechanical and Sprint Variables
4.5. Associations between Sprint Mechanical Variables and Sprint Performance
4.6. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiménez-Reyes, P.; Samozino, P.; Brughelli, M.; Morin, J.-B. Effectiveness of an Individualized Training Based on Force-Velocity Profiling during Jumping. Front. Physiol. 2017, 7, 677. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morin, J.-B.; Samozino, P. Interpreting Power-Force-Velocity Profiles for Individualized and Specific Training. Int. J. Sports Physiol. Perform. 2016, 11, 267–272. [Google Scholar] [CrossRef]
- Samozino, P.; Edouard, P.; Sangnier, S.; Brughelli, M.; Gimenez, P.; Morin, J.-B. Force-Velocity Profile: Imbalance Determination and Effect on Lower Limb Ballistic Performance. Int. J. Sports Med. 2014, 35, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Morin, J.-B.; Edouard, P.; Samozino, P. Technical Ability of Force Application as a Determinant Factor of Sprint Performance. Med. Sci. Sports Exerc. 2011, 43, 1680–1688. [Google Scholar] [CrossRef] [PubMed]
- Baker, D.; Nance, S. The Relation Between Running Speed and Measures of Strength and Power in Professional Rugby League Players. J. Strength Cond. 1999, 13, 230–235. [Google Scholar]
- Gabbett, T.J.; Jenkins, D.G.; Abernethy, B. Relationships between physiological, anthropometric, and skill qualities and playing performance in professional rugby league players. J. Sports Sci. 2011, 29, 1655–1664. [Google Scholar] [CrossRef] [PubMed]
- Zabaloy, S.; Carlos-Vivas, J.; Freitas, T.T.; Pareja-Blanco, F.; Pereira, L.; LoTurco, I.; Comyns, T.; Gálvez-González, J.; Alcaraz, P.E. Relationships between Resisted Sprint Performance and Different Strength and Power Measures in Rugby Players. Sports 2020, 8, 34. [Google Scholar] [CrossRef] [Green Version]
- LoTurco, I.; Pereira, L.; Moraes, J.E.; Kitamura, K.; Abad, C.C.C.; Kobal, R.; Nakamura, F.Y. Jump-Squat and Half-Squat Exercises: Selective Influences on Speed-Power Performance of Elite Rugby Sevens Players. PLoS ONE 2017, 12, e0170627. [Google Scholar] [CrossRef] [Green Version]
- Simperingham, K.D.; Cronin, J.B.; Ross, A.A. Advances in Sprint Acceleration Profiling for Field-Based Team-Sport Athletes: Utility, Reliability, Validity and Limitations. Sports Med. 2016, 46, 1619–1645. [Google Scholar] [CrossRef]
- Cross, M.R.; Brughelli, M.; Samozino, P.; Morin, J.-B. Methods of Power-Force-Velocity Profiling during Sprint Running: A Narrative Review. Sports Med. 2016, 47, 1255–1269. [Google Scholar] [CrossRef]
- Contreras-Diaz, G.; Jerez-Mayorga, D.; Delgado-Floody, P.; Arias-Poblete, L. Methods of evaluating the force-velocity profile through the vertical jump in athletes: A systematic review. Arch. Med. Deporte 2018, 35, 333–339. [Google Scholar]
- Till, K.; Scantlebury, S.; Jones, B. Anthropometric and Physical Qualities of Elite Male Youth Rugby League Players. Sports Med. 2017, 47, 2171–2186. [Google Scholar] [CrossRef] [Green Version]
- Johnston, R.D.; Gabbett, T.J.; Jenkins, D.G. Applied Sport Science of Rugby League. Sports Med. 2014, 44, 1087–1100. [Google Scholar] [CrossRef]
- de Lacey, J.; Brughelli, M.; McGuigan, M.; Hansen, K.; Samozino, P.; Morin, J.-B. The Effects of Tapering on Power-Force-Velocity Profiling and Jump Performance in Professional Rugby League Players. J. Strength Cond. Res. 2014, 28, 3567–3570. [Google Scholar] [CrossRef] [PubMed]
- Cross, M.R.; Brughelli, M.; Brown, S.; Samozino, P.; Gill, N.D.; Cronin, J.B.; Morin, J.-B. Mechanical Properties of Sprinting in Elite Rugby Union and Rugby League. Int. J. Sports Physiol. Perform. 2015, 10, 695–702. [Google Scholar] [CrossRef] [PubMed]
- Dobbin, N.; Clarke, J.; Cushman, S. The effects of an 8-week off-season period on the mechanical properties of sprinting in professional rugby league players: Implications for training recommendations. J. Trainology 2020, 9, 15–19. [Google Scholar] [CrossRef]
- Till, K.; Cobley, S.; O’Hara, J.; Brightmore, A.; Cooke, C.; Chapman, C. Using anthropometric and performance characteristics to predict selection in junior UK Rugby League players. J. Sci. Med. Sport 2011, 14, 264–269. [Google Scholar] [CrossRef] [PubMed]
- Till, K.; Jones, B.; Darrall-Jones, J.; Emmonds, S.; Cooke, C. Longitudinal Development of Anthropometric and Physical Characteristics Within Academy Rugby League Players. J. Strength Cond. Res. 2015, 29, 1713–1722. [Google Scholar] [CrossRef]
- Gabbett, T.; Kelly, J.; Ralph, S.; Driscoll, D. Physiological and anthropometric characteristics of junior elite and sub-elite rugby league players, with special reference to starters and non-starters. J. Sci. Med. Sport 2009, 12, 215–222. [Google Scholar] [CrossRef] [PubMed]
- Haugen, T.A.; Breitschädel, F.; Seiler, S. Sprint mechanical properties in soccer players according to playing standard, position, age and sex. J. Sports Sci. 2020, 38, 1–7. [Google Scholar] [CrossRef]
- Weaving, D.; Sawczuk, T.; Williams, S.; Scott, T.; Till, K.; Beggs, C.; Johnston, R.D.; Jones, B. The peak duration-specific locomotor demands and concurrent collision frequencies of European Super League rugby. J. Sports Sci. 2018, 37, 322–330. [Google Scholar] [CrossRef] [Green Version]
- Marcote-Pequeño, R.; García-Ramos, A.; Cuadrado-Peñafiel, V.; González-Hernández, J.M.; Gómez, M.Á.; Jiménez-Reyes, P. Association Between the Force–Velocity Profile and Performance Variables Obtained in Jumping and Sprinting in Elite Female Soccer Players. Int. J. Sports Physiol. Perform. 2019, 14, 209–215. [Google Scholar] [CrossRef]
- Jiménez-Reyes, P.; Samozino, P.; García-Ramos, A.; Cuadrado-Peñafiel, V.; Brughelli, M.; Morin, J.-B. Relationship between vertical and horizontal force-velocity-power profiles in various sports and levels of practice. PeerJ 2018, 6, e5937. [Google Scholar] [CrossRef]
- Stavridis, I.; Tsopanidou, A.; Tsolakis, C.; Zacharogiannis, E.; Koulouvaris, P.; Paradisis, G. Force-Velocity Relationship Between Sprinting and Jumping Testing Procedures. ISBS Proc. Arch. 2020, 38, 12. [Google Scholar]
- Samozino, P.; Rejc, E.; di Prampero, P.E.; Belli, A.; Morin, J.-B. Optimal Force–Velocity Profile in Ballistic Movements—Altius. Med. Sci. Sports Exerc. 2012, 44, 313–322. [Google Scholar] [CrossRef] [PubMed]
- Buchheit, M.; Samozino, P.; Glynn, J.A.; Michael, B.S.; Al Haddad, H.; Mendez-Villanueva, A.; Morin, J.B. Mechanical determinants of acceleration and maximal sprinting speed in highly trained young soccer players. J. Sports Sci. 2014, 32, 1906–1913. [Google Scholar] [CrossRef] [PubMed]
- Samozino, P.; Morin, J.-B.; Hintzy, F.; Belli, A. A simple method for measuring force, velocity and power output during squat jump. J. Biomech. 2008, 41, 2940–2945. [Google Scholar] [CrossRef] [PubMed]
- Samozino, P.; Rabita, G.; Dorel, S.; Slawinski, J.; Peyrot, N.; de Villarreal, E.S.; Morin, J.-B. A simple method for measuring power, force, velocity properties, and mechanical effectiveness in sprint running. Scand. J. Med. Sci. Sports 2016, 26, 648–658. [Google Scholar] [CrossRef]
- Morin, J.-B.; Samozino, P.; Murata, M.; Cross, M.R.; Nagahara, R. A simple method for computing sprint acceleration kinetics from running velocity data: Replication study with improved design. J. Biomech. 2019, 94, 82–87. [Google Scholar] [CrossRef] [Green Version]
- Janicijevic, D.; Knezevic, O.M.; Mirkov, D.M.; Pérez-Castilla, A.; Petrovic, M.; Samozino, P.; Garcia-Ramos, A. Assessment of the force-velocity relationship during vertical jumps: Influence of the starting position, analysis procedures and number of loads. Eur. J. Sport Sci. 2020, 20, 614–623. [Google Scholar] [CrossRef]
- Perez, J.; Guilhem, G.; Brocherie, F. Reliability of the force-velocity-power variables during ice hockey sprint acceleration. Sports Biomech. 2019, 1–15. [Google Scholar] [CrossRef]
- Hopkins, W.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive Statistics for Studies in Sports Medicine and Exercise Science. Med. Sci. Sports Exerc. 2009, 41, 3–12. [Google Scholar] [CrossRef] [Green Version]
- Matheson, G.J. We need to talk about reliability: Making better use of test-retest studies for study design and interpretation. PeerJ 2019, 7, e6918. [Google Scholar] [CrossRef] [Green Version]
- Barr, M.J.; Sheppard, J.M.; Gabbett, T.J.; Newton, R.U. Long-Term Training-Induced Changes in Sprinting Speed and Sprint Momentum in Elite Rugby Union Players. J. Strength Cond. Res. 2014, 28, 2724–2731. [Google Scholar] [CrossRef] [PubMed]
- Simperingham, K.D.; Cronin, J.B.; Pearson, S.N.; Ross, A. Reliability of horizontal force–velocity–power profiling during short sprint-running accelerations using radar technology. Sports Biomech. 2017, 18, 88–99. [Google Scholar] [CrossRef] [PubMed]
- Morin, J.-B.; Samozino, P. Spreadsheet for Sprint Acceleration Force-Velocity-Power Profiling. Available online: https://www.researchgate.net/publication/321767606_Spreadsheet_for_Sprint_acceleration_force-velocity-power_profiling (accessed on 18 June 2021).
- Morin, J.-B.; Samozino, P. Jump FVP Profile Spreadsheet. Available online: https://www.researchgate.net/publication/320146284_JUMP_FVP_profile_spreadsheet (accessed on 18 June 2021).
- Baker, D. Differences in strength and power among junior-high, senior-high, college-aged, and elite professional rugby league players. J. Strength Cond. Res. 2002, 16, 581–585. [Google Scholar]
- Till, K.; Jones, B.; Geeson-Brown, T. Do physical qualities influence the attainment of professional status within elite 16–19 year old rugby league players? J. Sci. Med. Sport 2016, 19, 585–589. [Google Scholar] [CrossRef]
- Wadhi, T.; Rauch, J.T.; Tamulevicius, N.; Andersen, J.C.; de Souza, E.O. Validity and Reliability of the GymAware Linear Position Transducer for Squat Jump and Counter-Movement Jump Height. Sports 2018, 6, 177. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giroux, C.; Rabita, G.; Chollet, D.; Guilhem, G. What is the Best Method for Assessing Lower Limb Force-Velocity Relationship? Int. J. Sports Med. 2015, 36, 143–149. [Google Scholar] [CrossRef]
- Till, K.; Tester, E.; Jones, B.; Emmonds, S.; Fahey, J.; Cooke, C. Anthropometric and Physical Characteristics of English Academy Rugby League Players. J. Strength Cond. Res. 2014, 28, 319–327. [Google Scholar] [CrossRef]
- Kirkpatrick, J.; Comfort, P. Strength, Power, and Speed Qualities in English Junior Elite Rugby League Players. J. Strength Cond. Res. 2013, 27, 2414–2419. [Google Scholar] [CrossRef]
- Geeson-Brown, T.; Jones, B.; Till, K.; Chantler, S.; Deighton, K. Body composition differences by age and playing standard in male rugby union and rugby league: A systematic review and meta-analysis. J. Sports Sci. 2020, 38, 2161–2176. [Google Scholar] [CrossRef]
- Haugen, T.A.; Breitschädel, F.; Seiler, S. Sprint mechanical variables in elite athletes: Are force-velocity profiles sport specific or individual? PLoS ONE 2019, 14, e0215551. [Google Scholar] [CrossRef]
- Giroux, C.; Rabita, G.; Chollet, D.; Guilhem, G. Optimal Balance between Force and Velocity Differs Among World-Class Athletes. J. Appl. Biomech. 2016, 32, 59–68. [Google Scholar] [CrossRef]
- Ross, A.; Gill, N.; Cronin, J.; Cross, M. The effects of Two Power Training Programmes on the Sprint Speed, Mechanical Sprint Characteristics, and Lower Body Power of Rugby Sevens Players. Ph.D. Thesis, Auckland University of Technology, Auckland, New Zealand, 2015. [Google Scholar]
- Hicks, D.S.; Schuster, J.G.; Samozino, P.; Morin, J.-B. Improving Mechanical Effectiveness during Sprint Acceleration: Practical Recommendations and Guidelines. Strength Cond. J. 2020, 42, 45–62. [Google Scholar] [CrossRef]
- Seitz, L.B.; Reyes, A.; Tran, T.T.; de Villarreal, E.S.; Haff, G.G. Increases in Lower-Body Strength Transfer Positively to Sprint Performance: A Systematic Review with Meta-Analysis. Sports Med. 2014, 44, 1693–1702. [Google Scholar] [CrossRef]
- Tillin, N.A.; Pain, M.T.; Folland, J.P. Identification of contraction onset during explosive contractions. Response to Thompson et al. Consistency of rapid muscle force characteristics: Influence of muscle contraction onset detection methodology J. Electromyogr. Kinesiol. 2012, 22, 893–900. J. Electromyogr. Kinesiol. 2013, 23, 991–994. [Google Scholar] [CrossRef]
- Jiménez-Reyes, P.; Samozino, P.; Cuadrado-Peñafiel, V.; Conceição, F.; González-Badillo, J.J.; Morin, J.-B. Effect of countermovement on power–force–velocity profile. Graefe’s Arch. Clin. Exp. Ophthalmol. 2014, 114, 2281–2288. [Google Scholar] [CrossRef] [PubMed]
- Wild, J.J.; Bezodis, I.N.; North, J.S.; Bezodis, N.E. Differences in step characteristics and linear kinematics between rugby players and sprinters during initial sprint acceleration. Eur. J. Sport Sci. 2018, 18, 1–11. [Google Scholar] [CrossRef] [PubMed]
- McGuigan, M.R.; Doyle, T.L.; Newton, M.; Edwards, D.J.; Nimphius, S.; Newton, R.U. Eccentric Utilization Ratio: Effect of Sport and Phase of Training. J. Strength Cond. Res. 2006, 20, 992–995. [Google Scholar] [CrossRef] [PubMed]
- Till, K.; Jones, B.; O’Hara, J.; Barlow, M.; Brightmore, A.; Lees, M.; Hind, K. Three-Compartment Body Composition in Academy and Senior Rugby League Players. Int. J. Sports Physiol. Perform. 2016, 11, 191–196. [Google Scholar] [CrossRef] [PubMed]
- Gabbett, T.J. Physiological characteristics of junior and senior rugby league players. Br. J. Sports Med. 2002, 36, 334–339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dobbin, N.; Highton, J.; Moss, S.L.; Twist, C. Factors Affecting the Anthropometric and Physical Characteristics of Elite Academy Rugby League Players: A Multiclub Study. Int. J. Sports Physiol. Perform. 2019, 14, 958–965. [Google Scholar] [CrossRef] [PubMed]
- Morris, C.G.; Weber, J.A.; Netto, K.J. Relationship Between Mechanical Effectiveness in Sprint Running and Force-Velocity Characteristics of a Countermovement Jump in Australian Rules Football Athletes. J. Strength Cond. Res. 2020, 1. [Google Scholar] [CrossRef] [PubMed]
- Cross, M.; Brown, S.; Brughelli, M.; Samozino, P.; Morin, J.-B.; Dé, R. Mechanical determinants of sprinting acceleration in rugby athletes. In Proceedings of the 23rd annual Congress of the European College of Sports Science, Dublin, Ireland, 4–7 July 2018. [Google Scholar]
- Moir, G.; Brimmer, S.M.; Snyder, B.W.; Connaboy, C.; Lamont, H.S. Mechanical Limitations to Sprinting and Biomechanical Solutions: A Constraints-Led Framework for the Incorporation of Resistance Training to Develop Sprinting Speed. Strength Cond. J. 2018, 40, 47–67. [Google Scholar] [CrossRef]
- Haugen, T.; McGhie, D.; Ettema, G. Sprint running: From fundamental mechanics to practice—A review. Graefe’s Arch. Clin. Exp. Ophthalmol. 2019, 119, 1273–1287. [Google Scholar] [CrossRef] [PubMed]
- Waldron, M.; Worsfold, P.R.; Twist, C.; Lamb, K.L. The relationship between physical abilities, ball-carrying and tackling among elite youth rugby league players. J. Sports Sci. 2013, 32, 542–549. [Google Scholar] [CrossRef]
- Clark, K.P.; Rieger, R.H.; Bruno, R.F.; Stearne, D.J. The National Football League Combine 40-yd Dash: How Important is Maximum Velocity? J. Strength Cond. Res. 2019, 33, 1542–1550. [Google Scholar] [CrossRef]
- Haugen, T.; Tønnessen, E.; Seiler, S. 9.58 and 10.49: Nearing the Citius End for 100 m? Int. J. Sports Physiol. Perform. 2015, 10, 269–272. [Google Scholar] [CrossRef]
- Gabbett, T.J. Sprinting Patterns of National Rugby League Competition. J. Strength Cond. Res. 2012, 26, 121–130. [Google Scholar] [CrossRef]
| Variables | All (n = 20) | Playing Position | Between Position Comparison | ||
|---|---|---|---|---|---|
| Backs (n = 7) | Forwards (n = 13) | ES 90% CI | p-Value | ||
| Unloaded jump height (cm) | 34.8 ± 3.4 | 36.6 ± 3.8 | 33.7 ± 2.6 | 0.96 (0.05 to 1.77) | 0.04 |
| Jump Vertical Mechanical Variables | |||||
| FV0 (N) | 2869 ± 579 | 2426 ±218 | 3091 ± 580 | −1.34 (−2.17 to −0.38) | 0.01 |
| FV0rel (N·kg−1) | 31.3 ± 5.2 | 31 ± 2.4 | 31.5 ± 6.2 | −0.11 (−0.93 to 0.72) | 0.43 |
| vV0 (m·s−1) | 4.16 ± 1.51 | 4.69 ± 1.71 | 3.89 ± 1.41 | 0.53 (−0.33 to 1.34) | 0.35 |
| PVmax (W) | 2874 ± 889 | 2812 ± 981 | 2904 ± 884 | −0.10 (−0.92 to 0.73) | 0.64 |
| PVmaxrel (W·kg−1) | 31.5 ± 9.6 | 35.5 ± 11.3 | 29.5 ± 8.4 | 0.63 (−0.24 to 1.44) | 0.24 |
| SVFv (N·s·m·kg−1) | −8.80 ± 4.42 | −7.56 ± 3.22 | −9.42 ± 4.92 | 0.42 (−0.43 to 1.23) | 0.45 |
| Jump F-v Imbalances | |||||
| Jump Fvimb (%) | 58.4 ± 29.6 | 50.3 ± 25.1 | 62.4 ± 31.9 | −0.40 (−1.21 to 0.44) | 0.40 |
| High force deficit | n = 10 | n = 3 | n = 7 | ||
| Low force deficit | n = 5 | n = 3 | n = 2 | ||
| Well balanced | n = 1 | n = 0 | n = 1 | ||
| Low velocity deficit | n = 2 | n = 0 | n = 2 | ||
| High velocity deficit | n = 0 | n = 0 | n = 0 | ||
| Sprint Horizontal Mechanical Variables | |||||
| FH0 (N) | 672.3 ± 121.2 | 596.4 ± 113.2 | 713.1 ± 108 | −1.06 (−1.83 to −0.20) | 0.045 |
| FH0rel (N·kg−1) | 7.39 ± 1.08 | 7.42 ± 1.07 | 7.37 ± 1.13 | 0.05 (−0.72 to 0.82) | 0.92 |
| vH0 (m·s−1) | 8.80 ± 0.65 | 9.23 ± 0.76 | 8.57 ± 0.46 | 1.16 (0.28 to 1.93) | 0.06 |
| PHmax (W) | 1471 ± 245 | 1370 ± 238 | 1526 ± 241 | −0.65 (−1.41 to 0.17) | 0.18 |
| PHmaxrel (W·kg−1) | 16.3 ± 2.7 | 17.1 ± 2.5 | 15.8 ± 2.8 | 0.48 (−0.47 to 1.39) | 0.31 |
| SHFv (N·s·m·kg−1) | −0.84 ± 0.13 | −0.81 ± 0.15 | −0.86 ± 0.13 | 0.37 (−0.32 to 1.24) | 0.49 |
| Mechanical efficiency | |||||
| RFmax (%) | 0.50 ± 0.04 | 0.51 ± 0.04 | 0.50 ± 0.04 | 0.21 (−0.58 to 0.97) | 0.43 |
| DRF (%) | −0.08 ± 0.01 | −0.07 ± 0.01 | −0.08 ± 0.01 | 0.46 (−0.34 to 1.22) | 0.48 |
| Velocity trace characteristics | |||||
| vmax (m·s−1) | 8.51 ± 0.58 | 8.88 ± 0.67 | 8.31 ± 0.43 | 1.11 (0.25 to 1.88) | 0.07 |
| amax (m·s−2) | 7.46 ± 0.99 | 7.78 ± 1.26 | 7.28 ± 0.82 | 0.51 (−0.30 to 1.27) | 0.38 |
| τ (s) | 1.17 ± 0.18 | 1.22 ± 0.20 | 1.15 ± 0.17 | 0.37 (−0.42 to 1.14) | 0.45 |
| Split Times | |||||
| 0–2 m time (s) | 0.82 ± 0.06 | 0.80 ± 0.05 | 0.82 ± 0.06 | −0.33 (−1.09 to 0.46) | 0.52 |
| 0–5 m time (s) | 1.41 ± 0.08 | 1.38 ± 0.08 | 1.41 ± 0.09 | −0.35 (−1.11 to 0.44) | 0.50 |
| 0–10 m time (s) | 2.15 ± 0.12 | 2.12 ± 0.11 | 2.17 ± 0.13 | −0.40(−1.16 to 0.39) | 0.40 |
| 0–20 m time (s) | 3.46 ± 0.18 | 3.38 ± 0.16 | 3.50 ± 0.19 | −0.66 (−1.43 to 0.15) | 0.18 |
| 0–30 m time (s) | 4.68 ± 0.24 | 4.57 ± 0.21 | 4.73 ± 0.24 | −0.69 (−1.46 to 0.13) | 0.14 |
| 0–40 m time (s) | 5.87 ± 0.30 | 5.71 ± 0.27 | 5.96 ± 0.29 | −0.88 (−1.65 to −0.04) | 0.09 |
| Between split times | |||||
| ∆10–20 m time (s) | 1.31 ± 0.07 | 1.26 ± 0.06 | 1.33 ± 0.07 | −1.05 (−1.82 to −0.19) | 0.04 |
| ∆20–30 m time (s) | 1.22 ± 0.07 | 1.18 ± 0.07 | 1.24 ± 0.06 | −0.94 (−1.71 to −0.10) | 0.10 |
| ∆30–40 m time (s) | 1.20 ± 0.08 | 1.15 ± 0.08 | 1.22 ± 0.07 | −0.95 (−1.72 to −0.11) | 0.03 |
| Momentum | |||||
| 0–10 m Momentum (kg·s−1) | 424 ± 52 | 379 ± 40 | 448 ± 40 | −1.73 (−2.53 to −0.77) | 0.001 |
| 30–40 m Momentum (kg·s−1) | 761 ± 275 | 699 ± 61 | 794 ± 61 | −1.56 (−2.35 to −0.63) | 0.004 |
| Performance Outcomes | FV0 (N) | FV0rel (N·kg−1) | vV0 (m·s−1) | PVmax (W) | PVmaxrel (W·kg−1) | SVFv (N·s·m·kg−1) |
|---|---|---|---|---|---|---|
| Split Times | ||||||
| 0–2 m (s) | −0.10 | −0.18 | 0.15 | −0.01 | −0.07 | 0.17 |
| 0–5 m (s) | −0.07 | −0.17 | 0.11 | −0.04 | −0.10 | 0.14 |
| 0–10 m (s) | 0.02 | −0.18 | 0.07 | −0.08 | −0.20 | 0.07 |
| 0–20 m (s) | 0.17 | −0.26 | −0.01 | −0.10 | −0.32 | 0.01 |
| 0–30 m (s) | 0.14 | −0.30 | −0.05 | −0.12 | −0.32 | 0.01 |
| 0–40 m (s) | 0.20 | −0.30 | −0.10 | −0.15 | −0.38 | −0.05 |
| Between split time | ||||||
| ∆10–20 m (s) | 0.27 | −0.29 | −0.13 | −0.14 | −0.41 | −0.07 |
| ∆20–30 m (s) | 0.24 | −0.34 | −0.17 | −0.10 | −0.34 | −0.02 |
| ∆30–40 m (s) | 0.39 | −0.35 | −0.24 | −0.06 | −0.36 | −0.07 |
| Momentum | ||||||
| Mom@ 0–10m (kg·s−1) | 0.71 ** | −0.16 | −0.25 | 0.18 | −0.27 | −0.19 |
| Mom@ 30–40m (kg·s−1) | 0.75 ** | 0.06 | −0.11 | 0.17 | −0.28 | −0.25 |
| Velocity trace characteristics | ||||||
| vmax (m·s−1) | −0.18 | 0.31 | 0.26 | 0.11 | 0.40 | 0.10 |
| amax (m·s−2) | −0.31 | −0.01 | 0..29 | 0.12 | 0.36 | 0.23 |
| τ (s) | −0.29 | 0.03 | 0.30 | 0.00 | 0.13 | 0.20 |
| Performance Outcome Variables | FH0 (N) | FH0rel (N·kg−1) | vH0 (m·s−1) | PHmax (W) | PHmaxrel (W·kg−1) | SHFv (N·s·m·kg−1) | DRF (%) | RFmax (%) | vmax (m·s−1) | amax (m·s−2) | τ (s) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Split Times | |||||||||||
| 0–2 m (s) | −0.63 ** | −0.98 *** | −0.18 | −0.78 *** | −0.94 *** | 0.77 *** | 0.78 *** | −0.98 *** | −0.23 | −0.02 | 0.81 ** |
| 0–5 m (s) | −0.60 ** | −0.96 *** | −0.28 | −0.78 *** | −0.98 *** | 0.74 *** | 0.72 *** | −0.97 *** | −0.34 | 0.06 | 0.77 ** |
| 0–10 m (s) | −0.53 * | −0.94 *** | −0.38 | −0.74 *** | −0.99 *** | 0.65 ** | 0.62 ** | −0.94 *** | −0.43 | −0.01 | 0.70 ** |
| 0–20 m (s) | −0.36 | −0.83 *** | −0.58 ** | −0.66 ** | −0.99 *** | 0.43 | 0.40 | −0.84 *** | −0.63 ** | −0.07 | 0.48 * |
| 0–30 m (s) | −0.22 | −0.71 ** | −0.72 ** | −0.57 ** | −0.94 *** | 0.34 | 0.31 | −0.72 *** | −0.76 *** | −0.11 | 0.39 |
| 0–40 m (s) | −0.10 | −0.60 ** | −0.81 *** | −0.47 * | −0.88 *** | 0.24 | 0.19 | −0.61 ** | −0.85 *** | −0.13 | 0.28 |
| Between split time | |||||||||||
| ∆10–20 m (s) | −0.02 | −0.52 * | −0.86 *** | −0.41 | −0.84 *** | 0.14 | 0.11 | −0.53 * | −0.89 *** | −0.17 | 0.19 |
| ∆20–30 m (s) | 0.20 | −0.25 | −0.96 *** | −0.21 | −0.63 ** | −0.24 | −0.27 | −0.26 | −0.97 *** | −0.19 | −0.20 |
| ∆30–40 m (s) | 0.30 | −0.19 | −0.97 *** | −0.11 | −0.60 ** | −0.35 | −0.37 | −0.21 | −0.98 *** | −0.17 | −0.30 |
| Momentum | |||||||||||
| Mom 0–10m (kg·s−1) | 0.88 *** | 0.33 | −0.47 * | 0.75 *** | 0.09 | −0.49 * | −0.51 * | 0.32 | −0.43 | −0.34 | −0.51 * |
| Mom@ 30–40m (kg·s−1) | 0.60 ** | 0.00 | −0.15 | 0.57 ** | −0.06 | 0.07 | 0.03 | 0.00 | −0.14 | −0.32 | −0.04 |
| Velocity trace characteristics | |||||||||||
| vmax (m·s–1) | −0.35 | 0.09 | 1.00 *** | 0.06 | 0.51 * | 0.36 | 0.37 | 0.11 | |||
| amax (m·s–2) | −0.24 | −0.9 | 0.18 | −0.22 | 0.05 | 0.14 | 0.08 | −0.04 | |||
| τ (s) | −0.86 *** | −0.87 *** | 0.36 | −0.79 *** | −0.60 ** | 1.00 *** | 0.97 *** | −0.80 *** | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicholson, B.; Dinsdale, A.; Jones, B.; Till, K. Sprint and Jump Mechanical Profiles in Academy Rugby League Players: Positional Differences and the Associations between Profiles and Sprint Performance. Sports 2021, 9, 93. https://doi.org/10.3390/sports9070093
Nicholson B, Dinsdale A, Jones B, Till K. Sprint and Jump Mechanical Profiles in Academy Rugby League Players: Positional Differences and the Associations between Profiles and Sprint Performance. Sports. 2021; 9(7):93. https://doi.org/10.3390/sports9070093
Chicago/Turabian StyleNicholson, Ben, Alex Dinsdale, Ben Jones, and Kevin Till. 2021. "Sprint and Jump Mechanical Profiles in Academy Rugby League Players: Positional Differences and the Associations between Profiles and Sprint Performance" Sports 9, no. 7: 93. https://doi.org/10.3390/sports9070093
APA StyleNicholson, B., Dinsdale, A., Jones, B., & Till, K. (2021). Sprint and Jump Mechanical Profiles in Academy Rugby League Players: Positional Differences and the Associations between Profiles and Sprint Performance. Sports, 9(7), 93. https://doi.org/10.3390/sports9070093






