Development of a Nakazima Test Suitable for Determining the Formability of Ultra-Thin Copper Sheets
Abstract
1. Introduction
2. Experimental Procedure
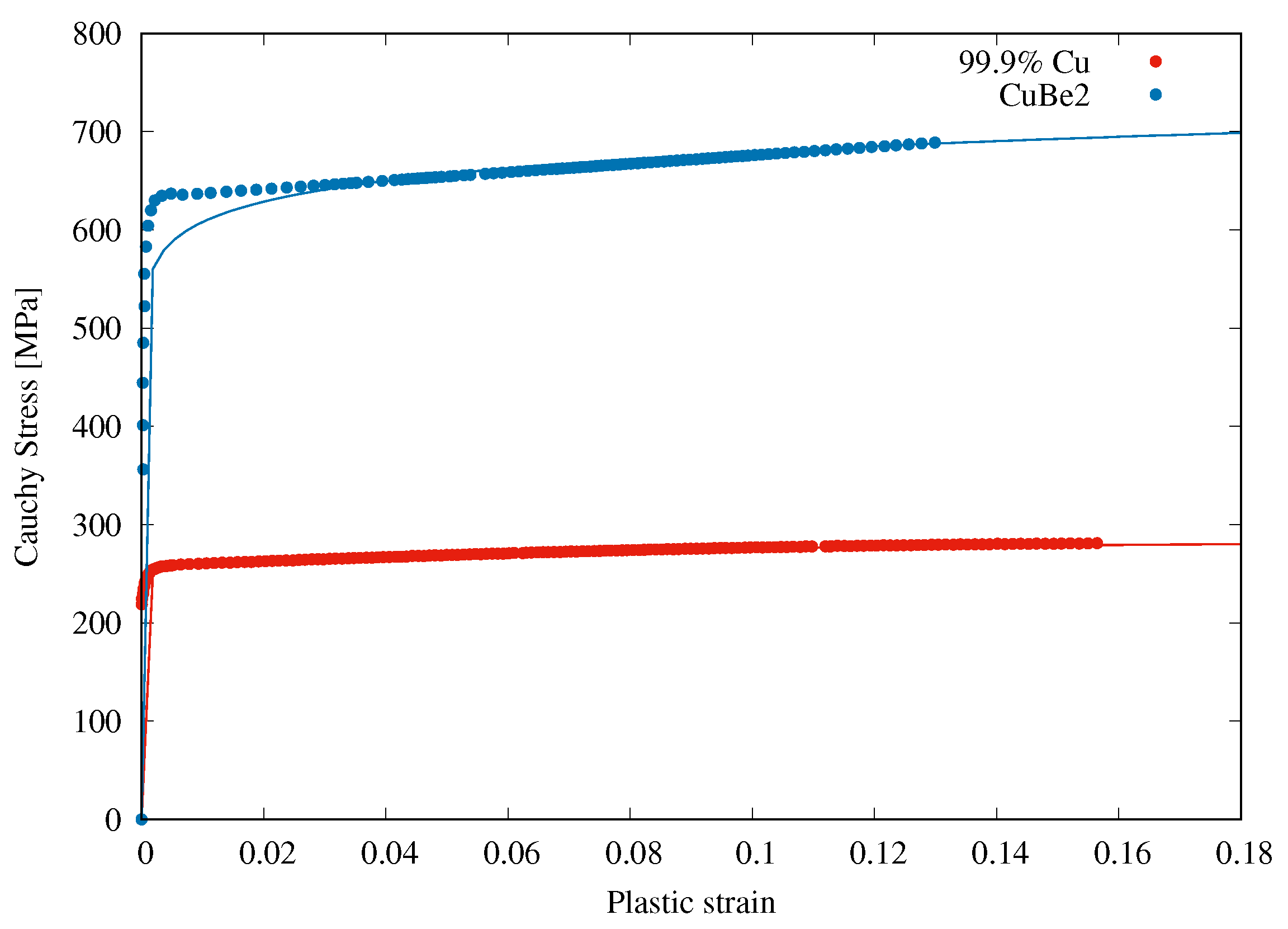
2.1. Materials
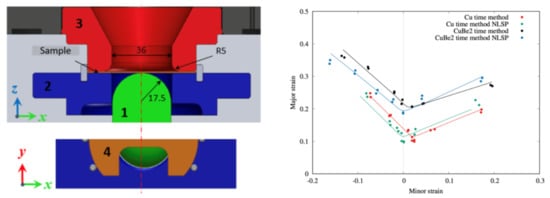
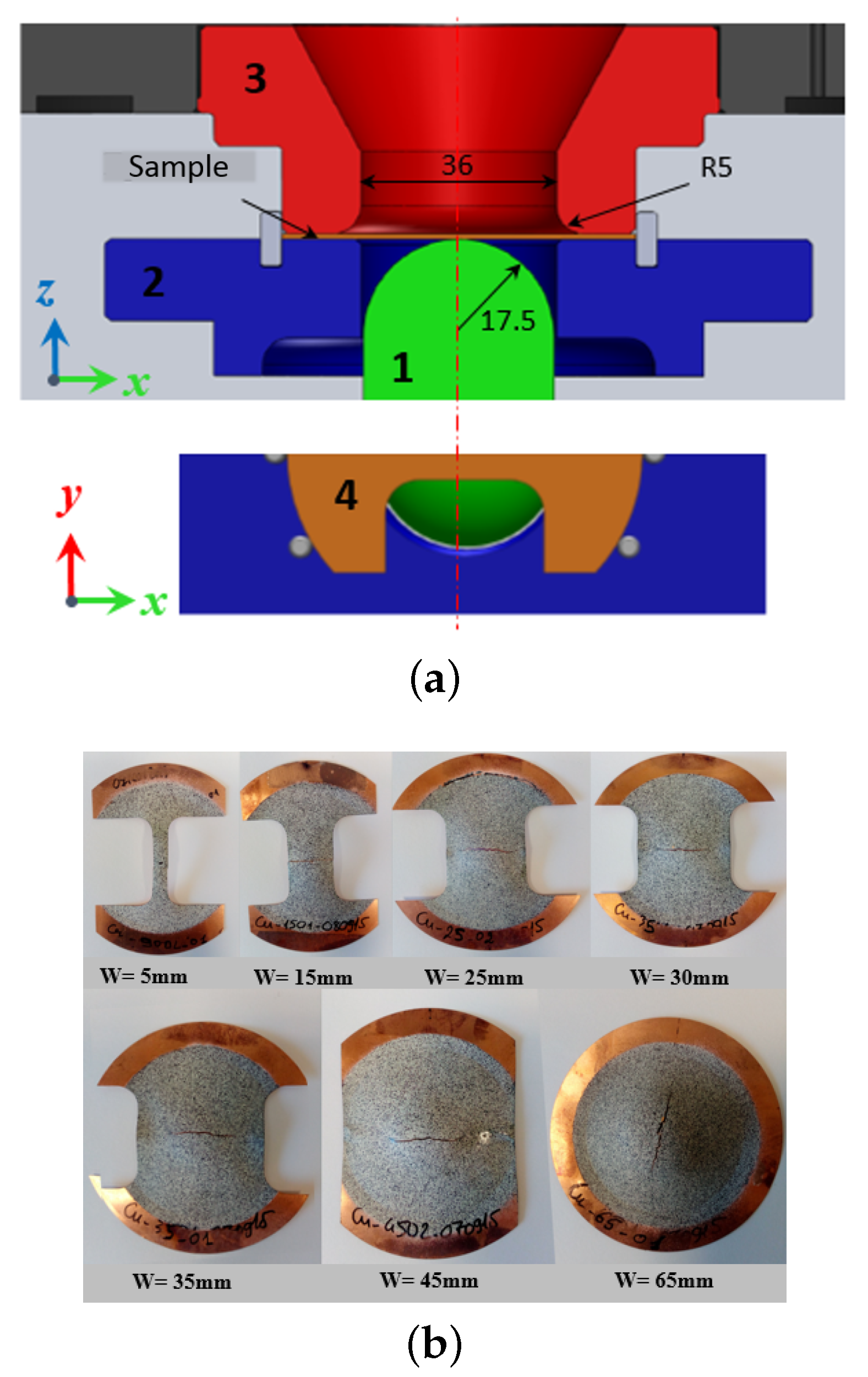
2.2. Nakazima Tests
2.3. Experimental Determination of Forming Limit Curves
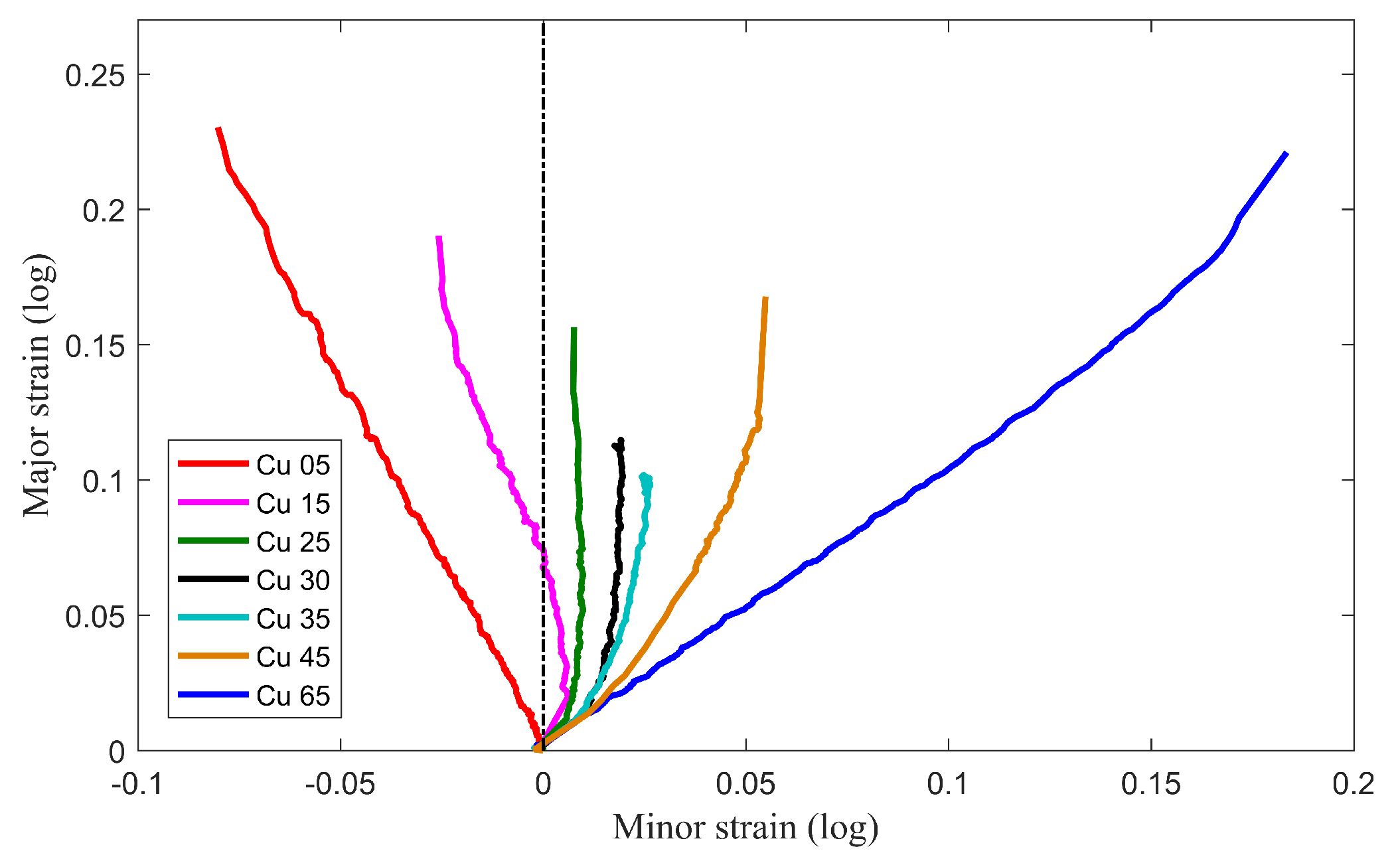
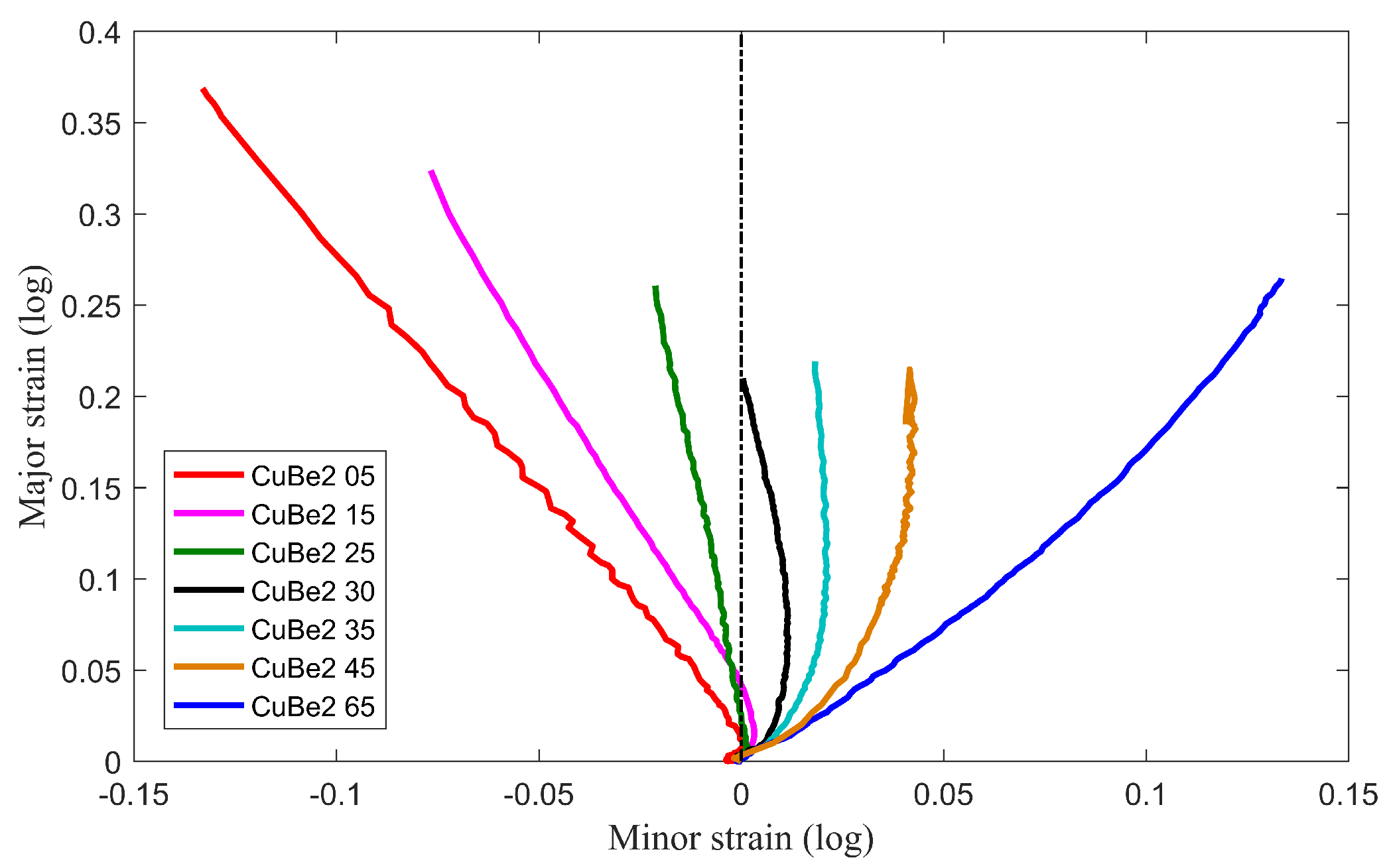
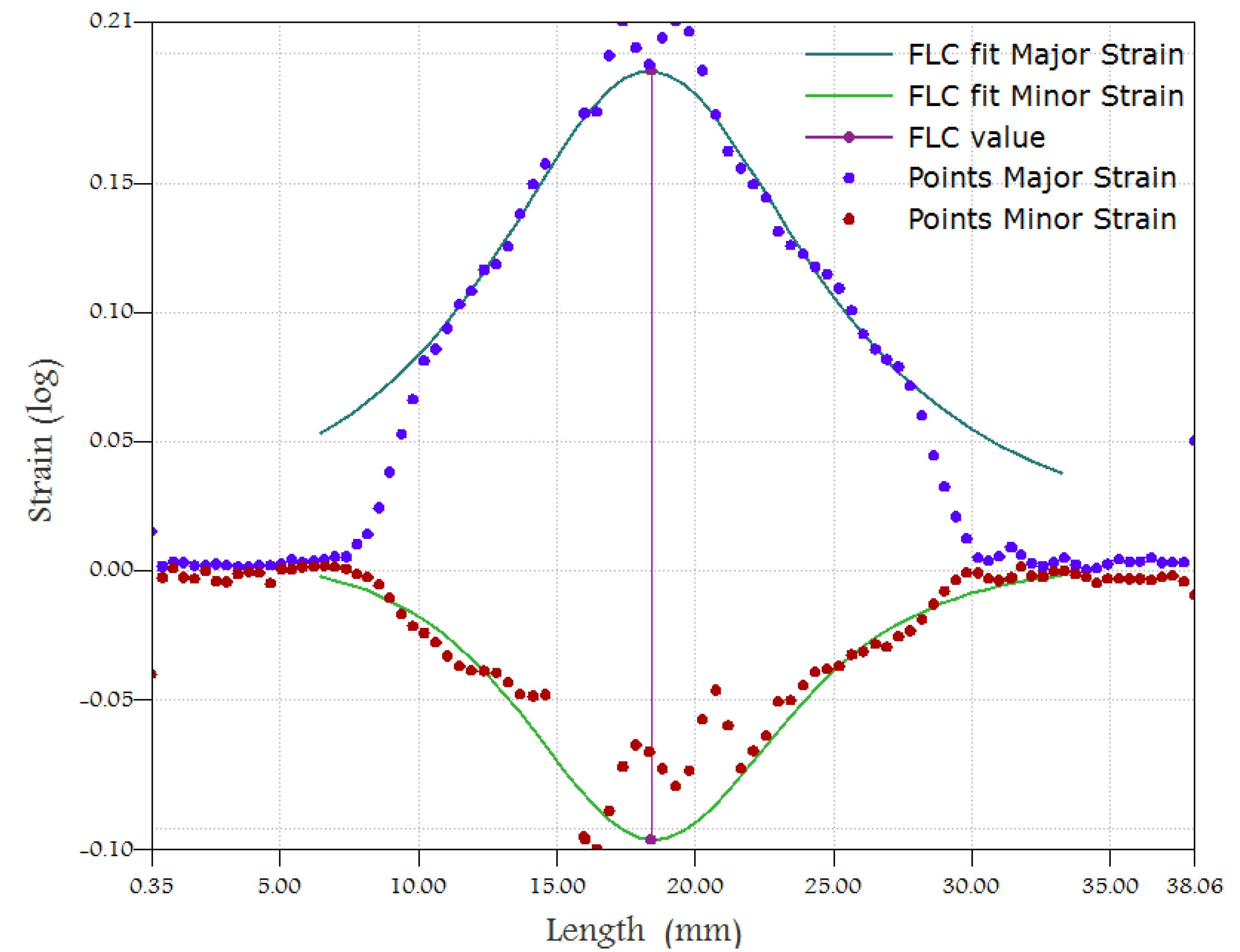
2.3.1. ISO 12004-2 Method
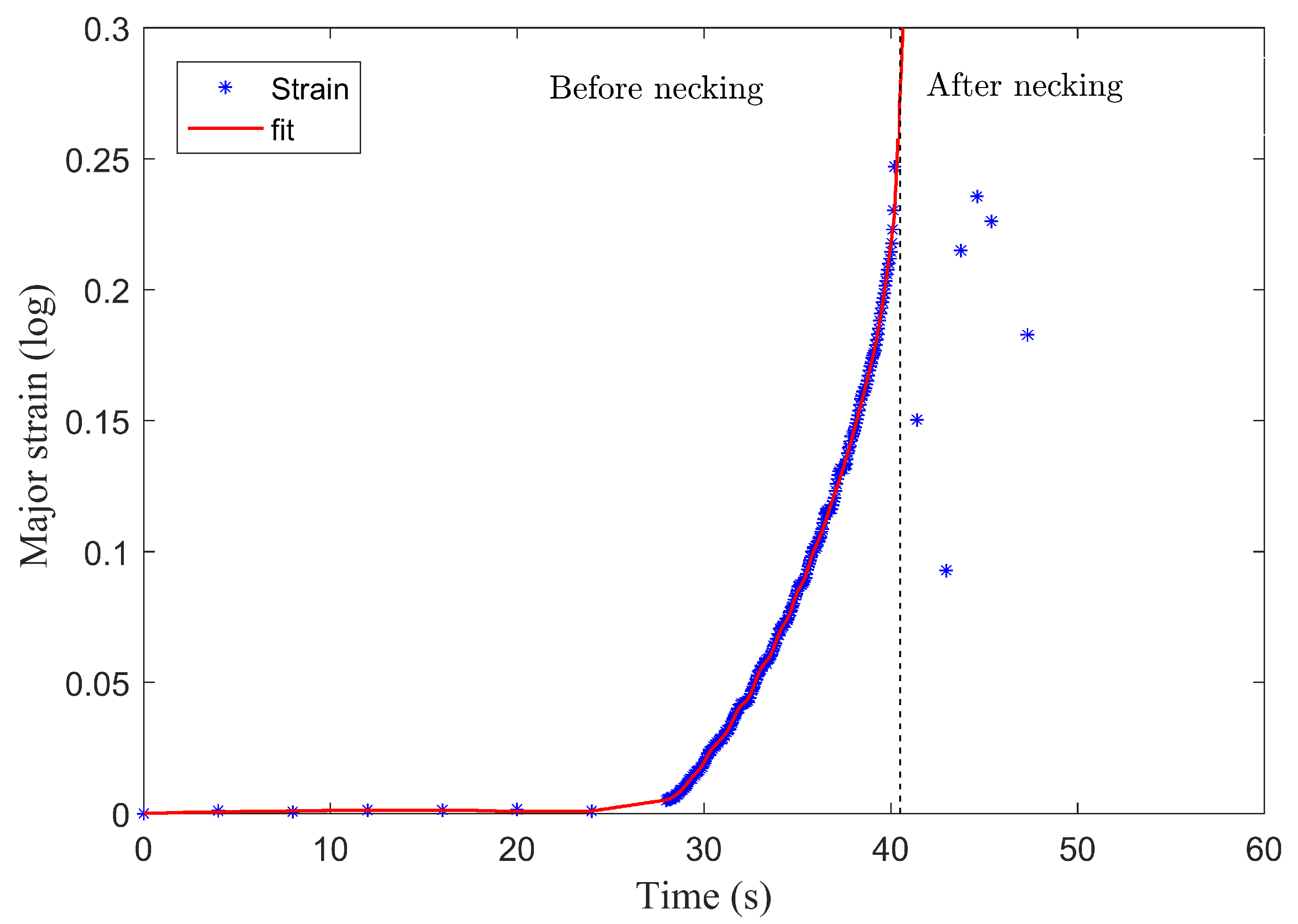
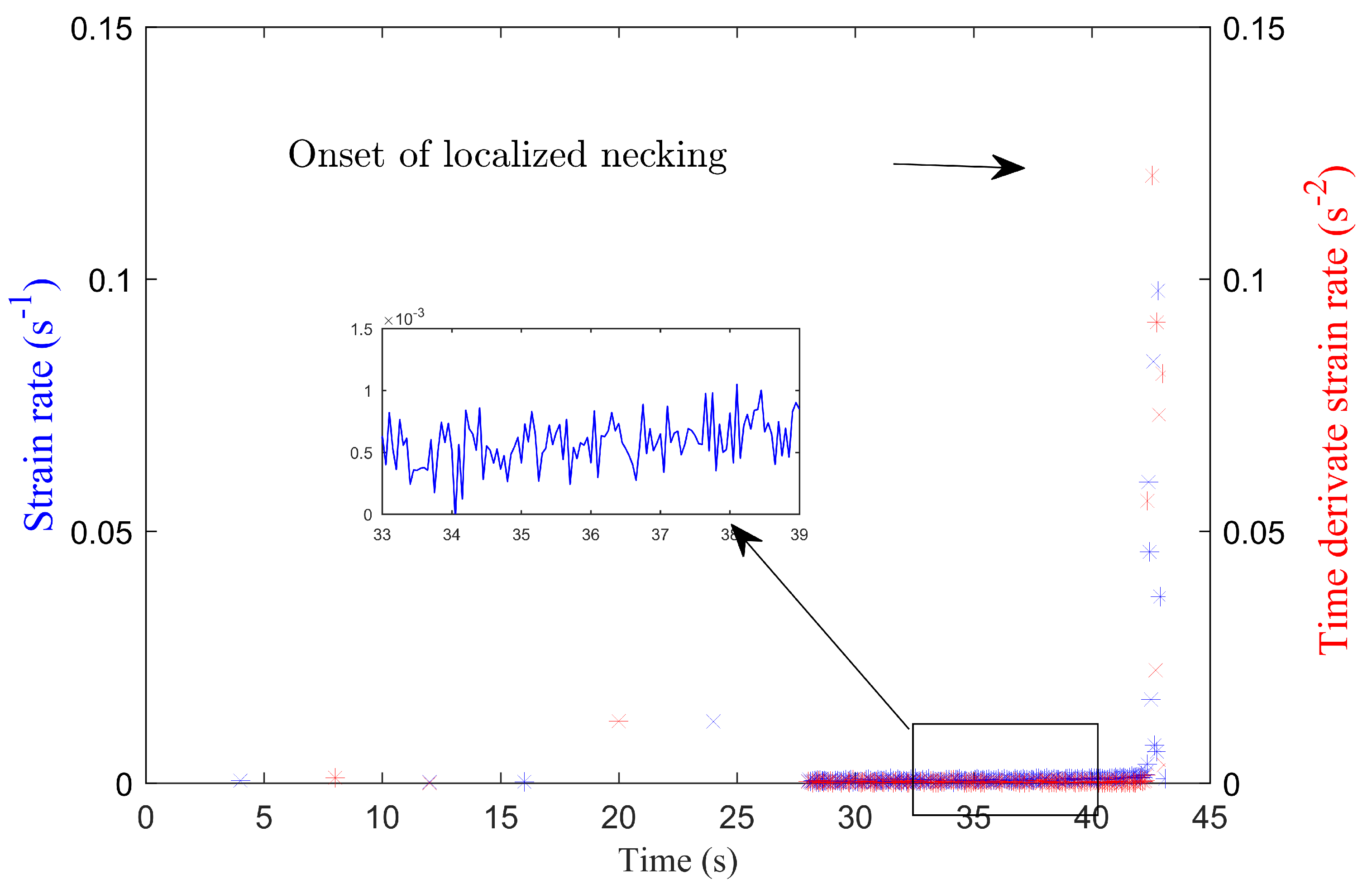
2.3.2. Time Dependent Method
3. Compensation of the FLC for Process-Dependent Effects
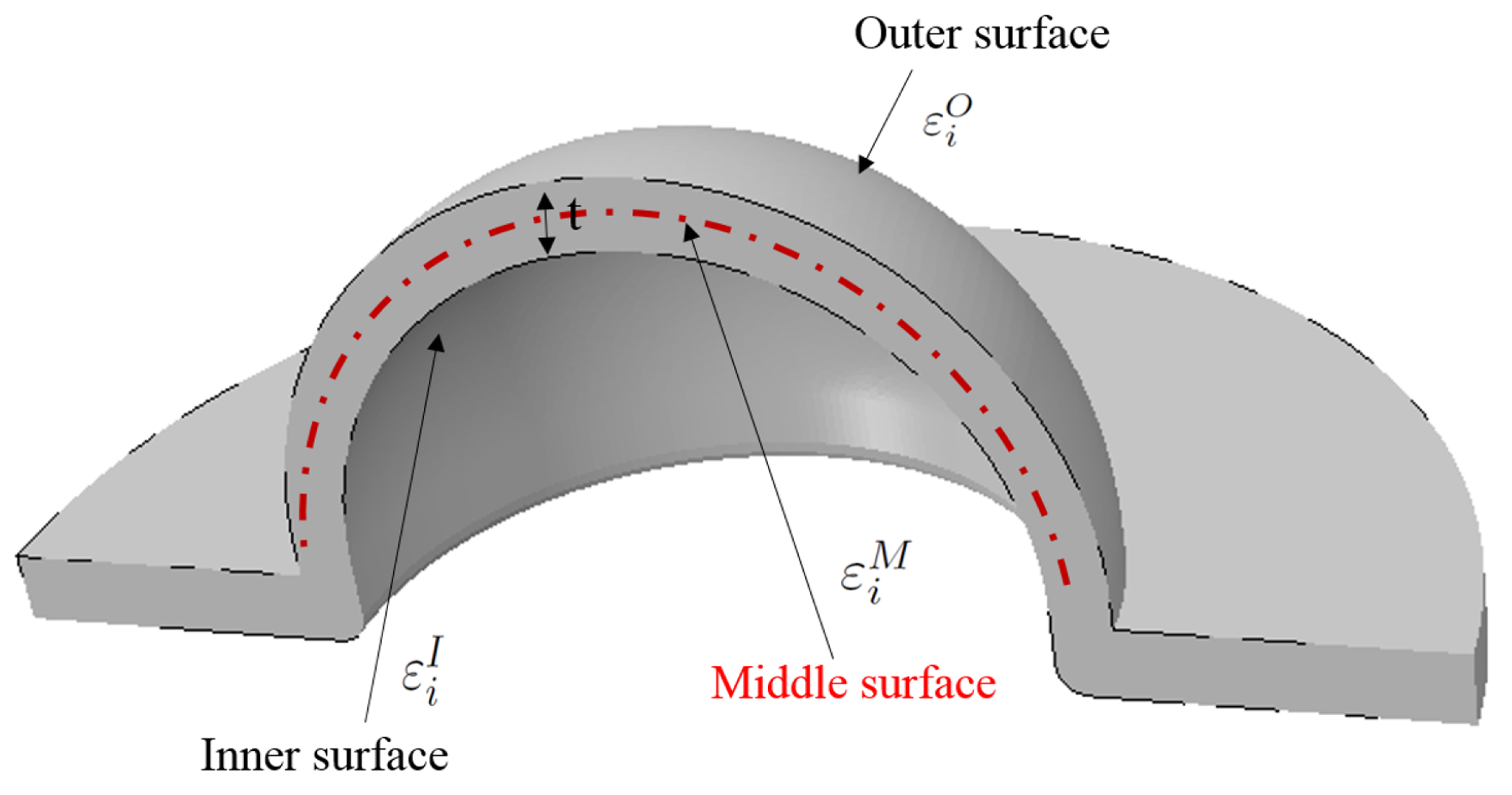
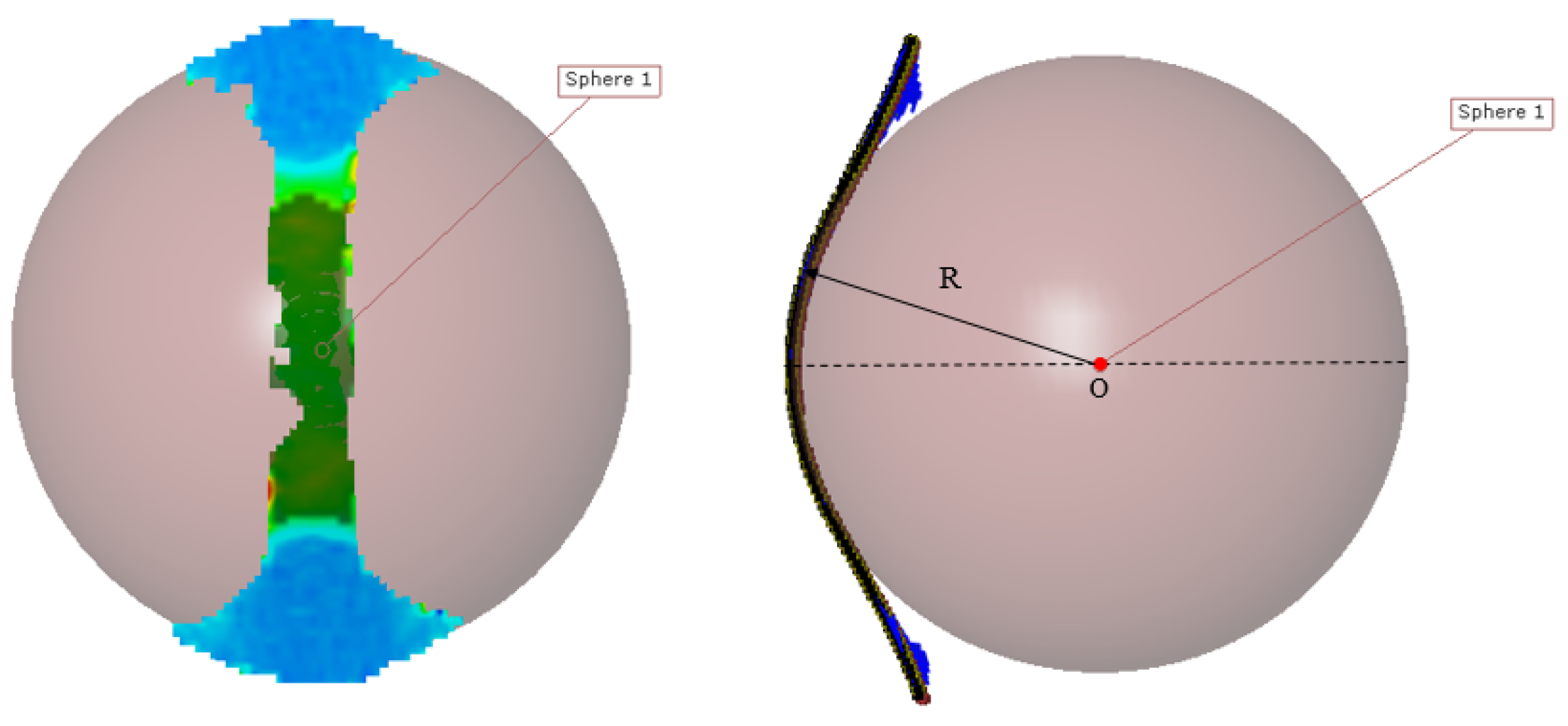
3.1. Determination of the Strain Path in the Thickness of the Sheet
3.2. Effects of Non-Linearity of the Strain Paths
3.3. Pressure Effects
4. Conclusions
- Our Nakazima test device is relevant for the study of the formability of ultra-thin sheets. Compared to other Nakazima or Marciniak devices that have been developed specifically for ultra-thin sheets, it remains macroscopic, avoiding any local or scale effects that can arise with very small tools.
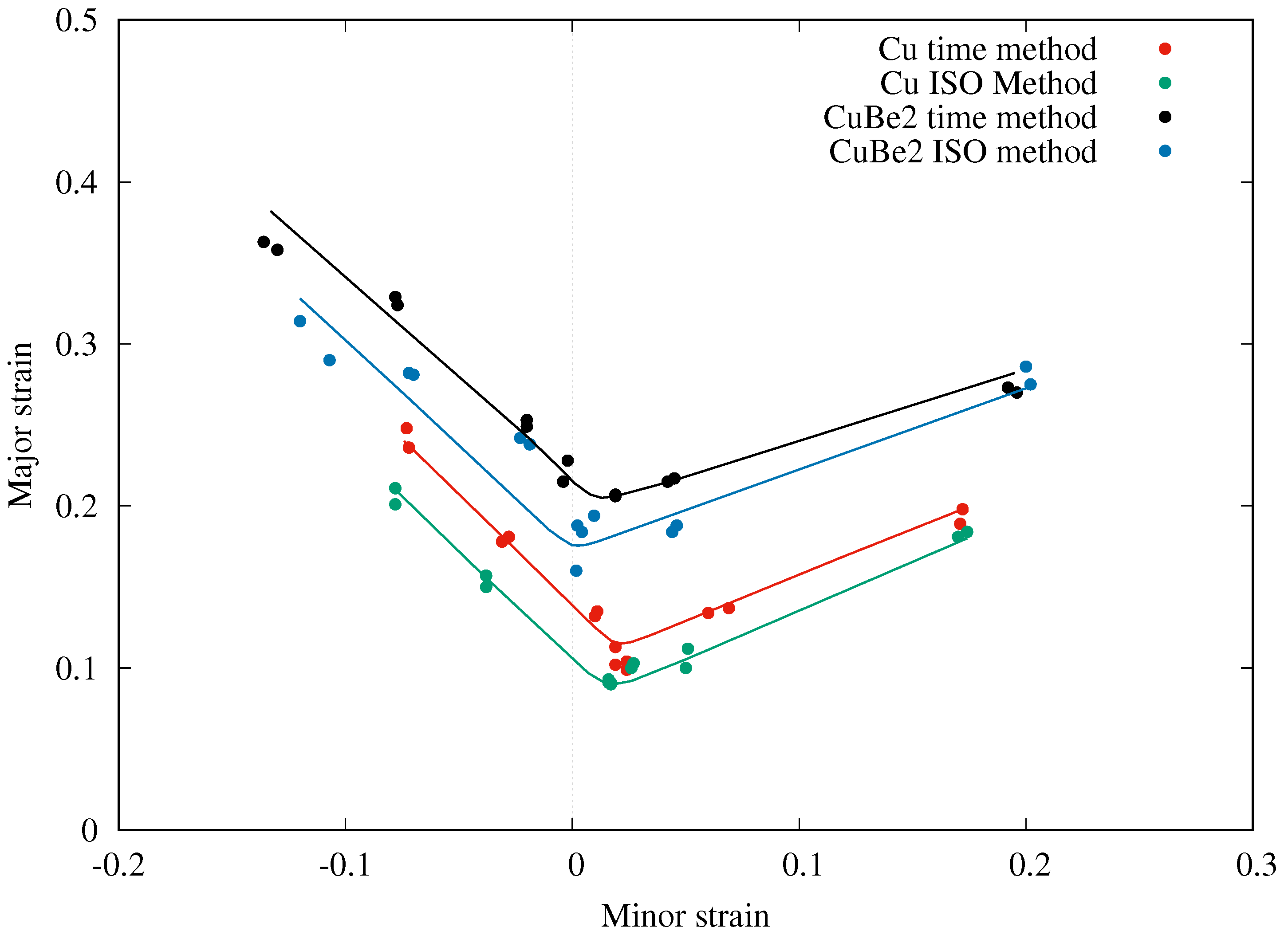
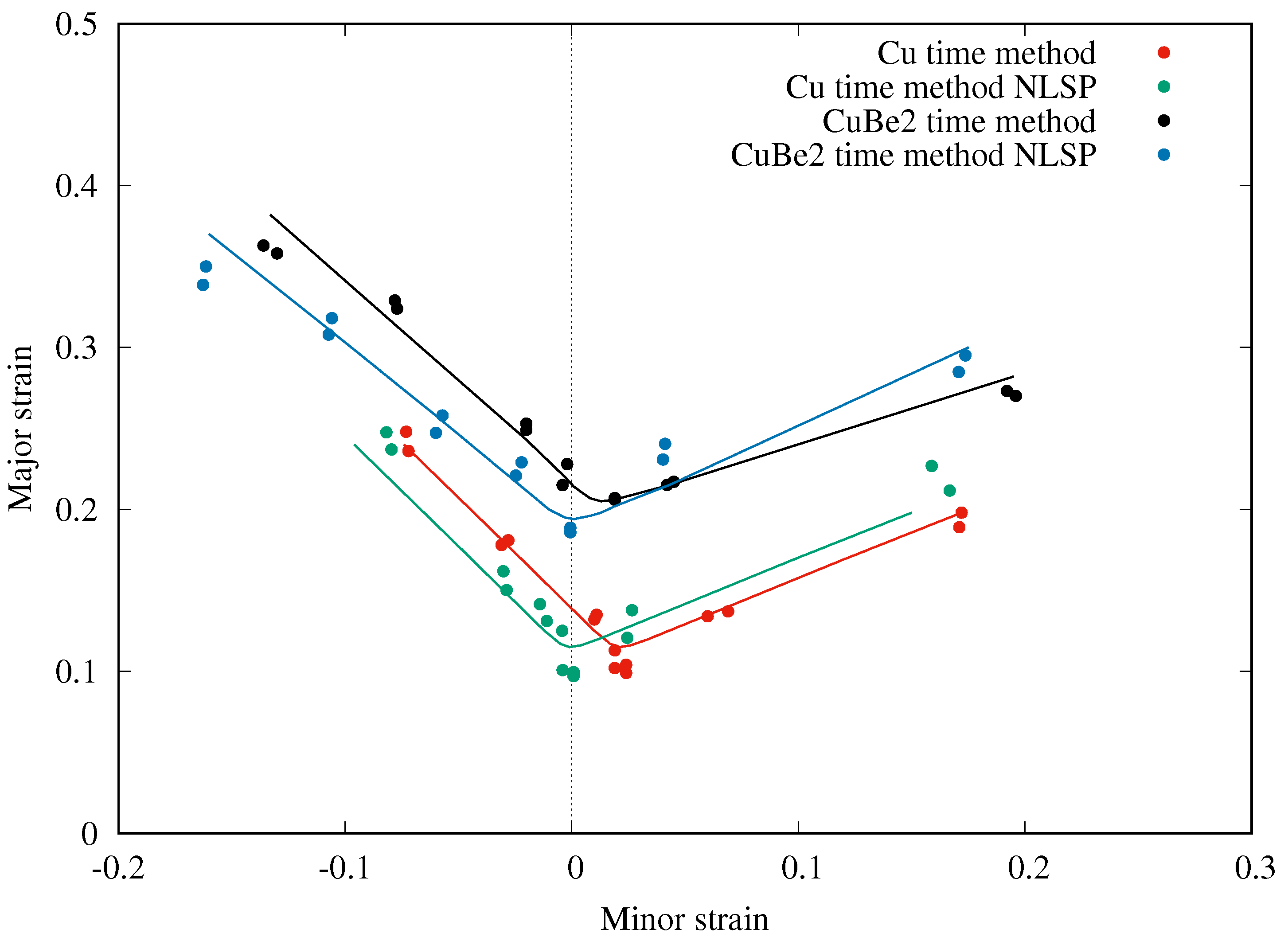
- The ISO 12004-2 method underestimates the FLCs for both materials. The time-dependent method, with its numerical based determination of the onset of necking, offers the possibility of generating objective and reproducible FLCs without any influence of the user. This method is more stable and enhance the measurement of the formability.
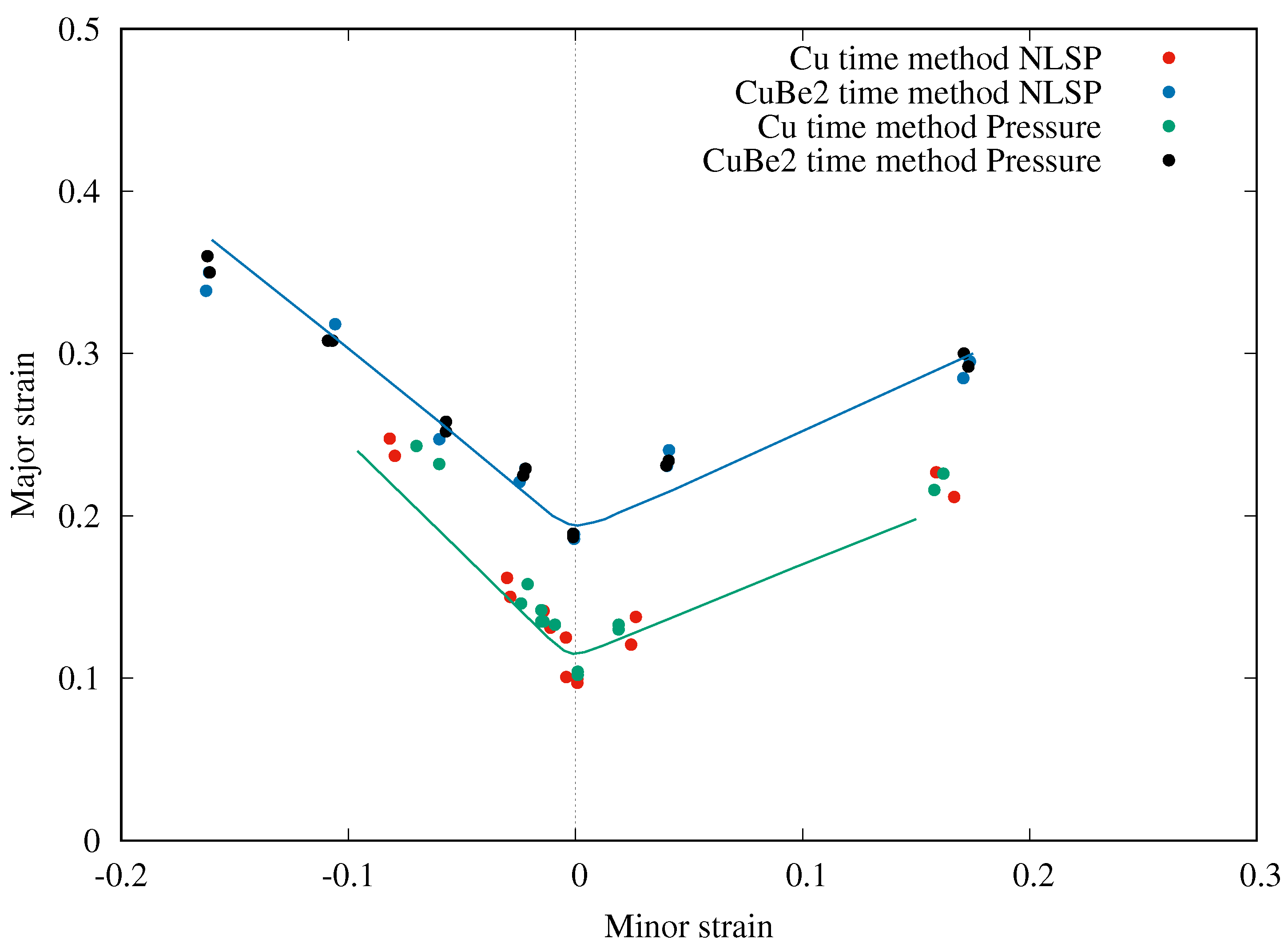
- Concerning the compensation method, the difference between the strains of the different layers is weak and the effect of curvature can be neglected for such thickness and punch diameter. Consequently, no influence was observed on the FLCs due to curvature effects.
- The correction process leads to a reduction of the necking strain in the major strain direction for both materials, but an increase in the expansion necking strain. The instantaneous strain path at the limit strain converges to the plane strain and the non-linear strain path correction significantly reduced the minor strain.
Author Contributions
Funding
Conflicts of Interest
Data Availability
References
- Adzima, F.; Balan, T.; Manach, P.Y. Springback prediction for a mechanical micro connector using CPFEM based numerical simulations. Int. J. Mater. Form. 2020, 13, 649–659. [Google Scholar] [CrossRef]
- Sène, N.A.; Balland, P.; Arrieux, R.; Sangharé, M. Numerical determination of micro-forming limit diagrams: Introduction of the effect of grain size heterogeneity. Modell. Simul. Mater. Sci. Eng. 2012, 20, 045020. [Google Scholar] [CrossRef]
- Pham, C.H.; Thuillier, S.; Manach, P.Y. Experimental and numerical investigation of the formability of an ultra-thin copper sheet. J. Phys. Conf. Ser. 2017, 896, 012109. [Google Scholar] [CrossRef]
- Xu, Z.; Peng, L.; Yi, P.; Lai, X. An investigation on the formability of sheet in the micro/meso scale hydroforming process. Int. J. Mech. Sci. 2019, 150, 265–276. [Google Scholar] [CrossRef]
- Erfanian, M.; Hashemi, R. A comparative study of the extended forming limit diagrams considering strain path, through-thickness normal and shear stress. Int. J. Mech. Sci. 2016, 148, 316–326. [Google Scholar] [CrossRef]
- Cao, J.; Li, F.; Ma, X.; Sun, Z. A modified elliptical fracture criterion to predict fracture forming limit diagrams for sheet metals. J. Mater. Process. Technol. 2018, 252, 116–127. [Google Scholar] [CrossRef]
- Leotoing, L.; Guines, D. Investigations of the effect of strain path changes on forming limit curves using an in-plane biaxial tensile test. Int. J. Mech. Sci. 2015, 99, 21–28. [Google Scholar] [CrossRef]
- Shinge, V.R.; Dabade, U.A. Experimental Investigation on Forming Limit Diagram of Mild Carbon Steel sheet. Int. J. Mech. Sci. 2018, 20, 141–146. [Google Scholar] [CrossRef]
- Xavier, M.D.; Plaut, R.L.; Schön, C.G. Uniaxial Near Plane Strain Tensile Tests Applied to the Determination of the FLC0 Formabillity Parameter. Mater. Res. 2014, 17, 982–986. [Google Scholar] [CrossRef]
- Rong, H.; Hu, P.; Ying, L.; Hou, W.; Zhang, J. Thermal forming limit diagram (TFLD) of AA7075 aluminum alloy based on a modified continuum damage model: Experimental and theoretical investigations. Int. J. Mech. Sci. 2019, 156, 59–73. [Google Scholar] [CrossRef]
- Schlosser, F.; Signorelli, J.; Leonard, M.; Roatta, A.; Milesi, M.; Bozzolo, N. Influence of the strain path changes on the formability of a zinc sheet. J. Mater. Process. Technol. 2019, 271, 101–110. [Google Scholar] [CrossRef]
- Toshniwal, K.; Pareddy, S.; Kotkunde, N.; Gupta, A.K. Numerical Investigation on Stress based Forming Limit Diagram for Ti-6Al-4V Alloy. Mater. Today Proc. 2017, 4, 8096–8103. [Google Scholar] [CrossRef]
- Park, N.; Huh, H.; Yoon, J.W. Anisotropic fracture forming limit diagram considering non-directionality of the equi-biaxial fracture strain. Int. J. Solids Struct. 2018, 151, 181–194. [Google Scholar] [CrossRef]
- Cheong, D.W.K. On the Influence of the Through-Thickness Strain Gradients for Characterization of Formability and Fracture of Sheet Metal Alloys. Master’s Thesis, University Of Waterloo, Waterloo, ON, Canada, 2019. [Google Scholar]
- Almeida, L.; Schöna, C.G. Evaluation of the formability of 90/10 brass produced by different casting processes and investigation of the effect of Forming Limit Diagram determination procedure. J. Mater. Res. Technol. 2019, 8, 4163–4172. [Google Scholar] [CrossRef]
- Bouktir, Y.; Chalal, H.; Haddad, M.; Abed-Meraim, F. Investigation of ductility limits based on bifurcation theory coupled with continuum damage mechanics. Mater. Design 2016, 90, 969–978. [Google Scholar] [CrossRef]
- Ben Hmida, R.; Thibaud, S.; Richard, F.; Hapsari, G.; Malécot, P. Numerical prediction of the forming limit diagrams of thin sheet metal using SPIF tests. Procedia Eng. 2017, 183, 113–118. [Google Scholar]
- Pham, Q.T.; Lee, B.H.; Park, K.C.; Kim, Y.S. Influence of the post-necking prediction of hardening law on the theoretical forming limit curve of aluminium sheets. Int. J. Mech. Sci. 2018, 140, 521–536. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczynski, K. Limit strains in the processes of stretch-forming sheet metal. Int. J. Mech. Sci. 1967, 9, 609–620. [Google Scholar] [CrossRef]
- Habibi, M.; Hashemi, R.; Fallah Tafti, M.; Assempour, A. Experimental investigation of mechanical properties, formability and forming limit diagrams for tailor-welded blanks produced by friction stir welding. J. Manuf. Process. 2018, 31, 310–323. [Google Scholar] [CrossRef]
- Nakazima, K.; Kikuma, T.; Hasuka, K. Study on the formability of steel sheets. Yawata Technol. Rep. 1968, 264, 8517–8530. [Google Scholar]
- Volk, W.; Groche, P.; Brosius, A.; Ghiotti, A.; Kinsey, B.L.; Liewald, M.; Madej, L.; Min, J.; Yanagimoto, J. Models and modelling for process limits in metal forming. CIRP Ann. Manuf. Technol. 2019, 68, 775–798. [Google Scholar] [CrossRef]
- Grolleau, V.; Roth, C.; Lafilé, V.; Galpin, B.; Mohr, D. Loading of mini-Nakazima specimens with a dihedral punch: Determining the strain to fracture for plane strain tension through stretch-bending. Int. J. Mech. Sci. 2019, 152, 329–345. [Google Scholar] [CrossRef]
- Min, J.; Stoughton, T.B.; Carsley, J.E.; Lin, J. Compensation for process-dependent effects in the determination of localized necking limits. Int. J. Mech. Sci. 2016, 117, 115–134. [Google Scholar] [CrossRef]
- Butuc, M.C.; Barlat, F.; Gracio, J.J. Study on plastic flow localization prediction using a physically-based hardening model. Comput. Mater. Sci. 2011, 50, 2688–2697. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, L.; Ouyang, Q.; Li, X.; Zhu, X.; Chen, J. Prediction of forming limits for anisotropic materials with non-linear strain paths by an instability approach. Int. J. Plast. 2018, 103, 143–167. [Google Scholar] [CrossRef]
- Abspoel, M.; Atzema, E.H.; Droog, J.M.M.; Khandeparkar, T.; Scholting, M.E.; Schouten, F.J.; Vegter, H. Inherent influence of strain path in Nakazima FLC testing. In Proceedings of the 8th IDDRG Conference, Mumbai, India, 5–8 June 2011; pp. 1–9. [Google Scholar]
- Zhao, L.R.; Sowerby, R.; Sklad, M.P. A theoretical and experimental investigation of limit strains in sheet metal forming. Int. J. Plast. 1996, 38, 1307–1317. [Google Scholar] [CrossRef]
- Stoughton, T.B. A general forming limit criterion for sheet metal forming. Int. J. Plast. 2000, 42, 1–27. [Google Scholar] [CrossRef]
- Stoughton, T.B. Stress-based forming limits in sheet metal forming. J. Eng. Mater. Technol. 2001, 123, 417–422. [Google Scholar] [CrossRef]
- Yoshida, K.; Kuwabara, T.; Kuroda, M. Path-dependence of the forming limit stresses in a sheet metal. Int. J. Plast. 2007, 23, 361–384. [Google Scholar] [CrossRef]
- ISO 12004-2 Metallic Materials-Sheet and Strip-Determination of Forming Limit Curves-Part 2; ISO: Geneva, Switzerland, 2008.
- Noder, J.; Butcher, C. A Comparative Investigation into the Influence of the Constitutive Model on the Prediction of In-Plane Formability for Nakazima and Marciniak Tests. Int. J. Mech. Sci. 2019, 163, 105–138. [Google Scholar] [CrossRef]
- Pham, C.H.; Thuillier, S.; Manach, P.Y. Mechanical properties involved in the micro-forming of ultra-thin stainless steel sheets. Metall. Mater. Trans. A 2015, 46, 3502–3515. [Google Scholar] [CrossRef]
- Sène, N.A.; Balland, P.; Arrieux, R.; Bouabdallah, K. An experimental study of the microformability of very thin materials. Exp. Mech. 2013, 53, 155–162. [Google Scholar] [CrossRef]
- Pham, C.H.; Thuillier, S.; Manach, P.Y. Prediction of flow stress and surface roughness of stainless steel sheets considering an inhomogeneous microstructure. Mater. Sci. Eng. A 2016, 678, 377–388. [Google Scholar] [CrossRef]
- Merklein, M.; Kuppert, A.; Geiger, M. Time dependent determination of forming limit diagrams. CIRP Ann. 2010, 59, 295–298. [Google Scholar] [CrossRef]
- Volk, W.; Gaber, C. Investigation and Compensation of Biaxial Pre-strain During the Standard Nakajima and Marciniak test Using Generalized Forming Limit Concept. Procedia Eng. 2017, 207, 568–573. [Google Scholar] [CrossRef]
- Martinez-Donaire, A.J.; Garcia-Lomas, F.J.; Vallellano, C. New approaches to detect the onset of localised necking in sheets under through-thickness strain gradients. Mater. Design 2014, 57, 135–145. [Google Scholar] [CrossRef]
- Magrinho, J.P.; Silva, M.B.; Genteno, G.; Moedas, F.; Vallellano, C.; Martins, P.A.F. On the determination of forming limits in thin-walled tubes. Int. J. Mech. Sci. 2019, 155, 381–391. [Google Scholar] [CrossRef]
- Min, J.; Stoughton, T.B.; Carsley, J.E.; Lin, J. An improved curvature method of detecting the onset of localized necking in Marciniak tests and its extension to Nakazima tests. Int. J. Mech. Sci. 2017, 123, 238–252. [Google Scholar] [CrossRef]
- Stoughton, T.B.; Zhu, X. Review of theoretical models of the strain-based FLD and their relevance to the stress-based FLD. Int. J. Plast. 2004, 20, 1463–1486. [Google Scholar] [CrossRef]


| Cu | Be | Co | Ni | Fe |
|---|---|---|---|---|
| 97 | 1.8–2 | 0.3 | 0.15 | 0.15 |
| Material | YS (MPa) | UTS (MPa) | K (MPa) | n | ||
|---|---|---|---|---|---|---|
| Cu 99.9% | 247 | 285 | 340 | |||
| CuBe2 | 430 | 590 | 787 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayachi, N.; Guermazi, N.; Pham, C.H.; Manach, P.-Y. Development of a Nakazima Test Suitable for Determining the Formability of Ultra-Thin Copper Sheets. Metals 2020, 10, 1163. https://doi.org/10.3390/met10091163
Ayachi N, Guermazi N, Pham CH, Manach P-Y. Development of a Nakazima Test Suitable for Determining the Formability of Ultra-Thin Copper Sheets. Metals. 2020; 10(9):1163. https://doi.org/10.3390/met10091163
Chicago/Turabian StyleAyachi, Nejia, Noamen Guermazi, Cong Hanh Pham, and Pierre-Yves Manach. 2020. "Development of a Nakazima Test Suitable for Determining the Formability of Ultra-Thin Copper Sheets" Metals 10, no. 9: 1163. https://doi.org/10.3390/met10091163
APA StyleAyachi, N., Guermazi, N., Pham, C. H., & Manach, P.-Y. (2020). Development of a Nakazima Test Suitable for Determining the Formability of Ultra-Thin Copper Sheets. Metals, 10(9), 1163. https://doi.org/10.3390/met10091163