Explanatory Machine Learning Accelerates the Design of Graphene-Reinforced Aluminium Matrix Composites with Superior Performance
Abstract
:1. Introduction
2. Methods
2.1. Establishment and Pre-Processing of Datasets
2.2. Machine Learning Methods
3. Results and Discussion
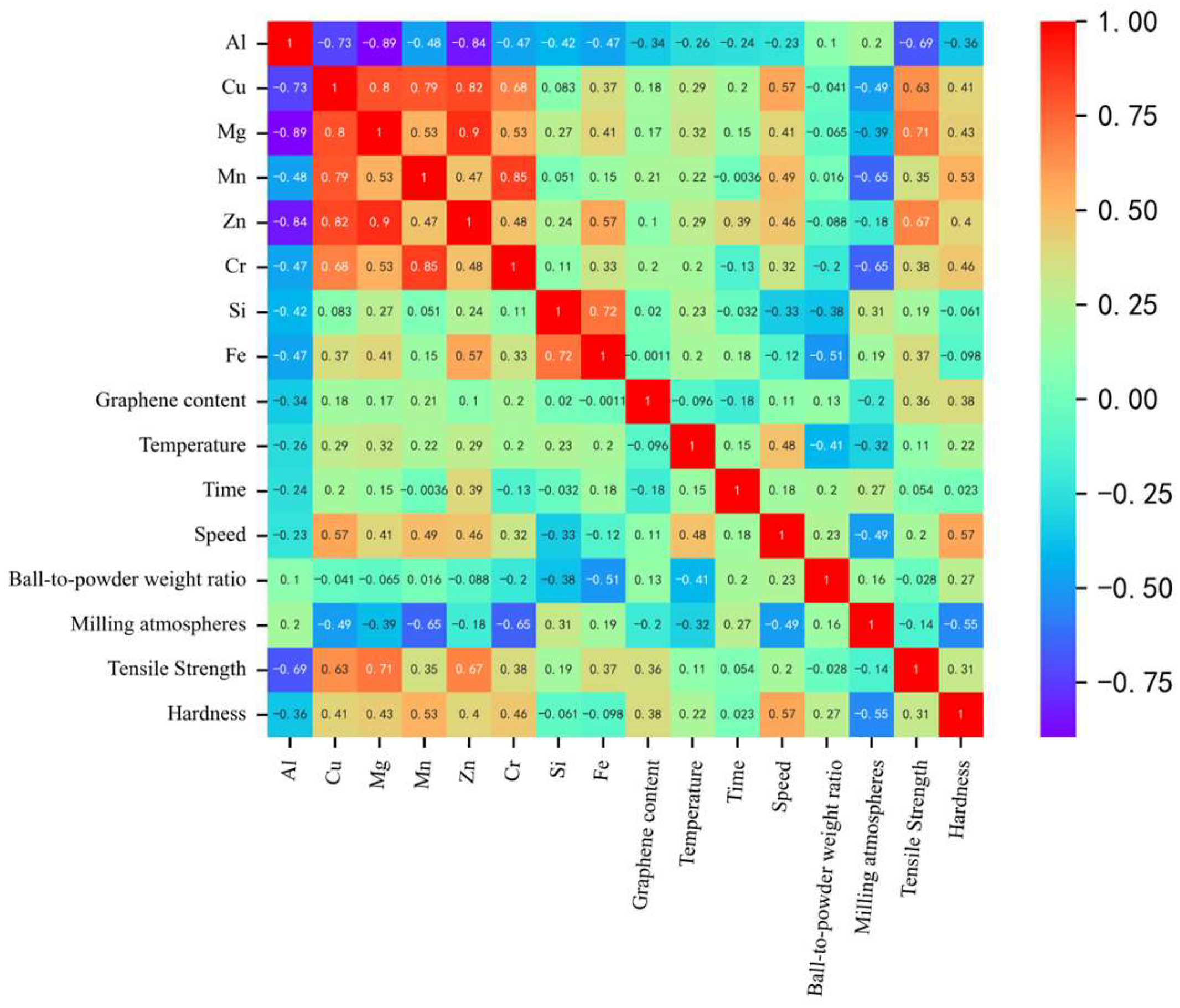
3.1. Dataset and Feature Engineering
3.2. Machine Learning Model Building and Optimisation
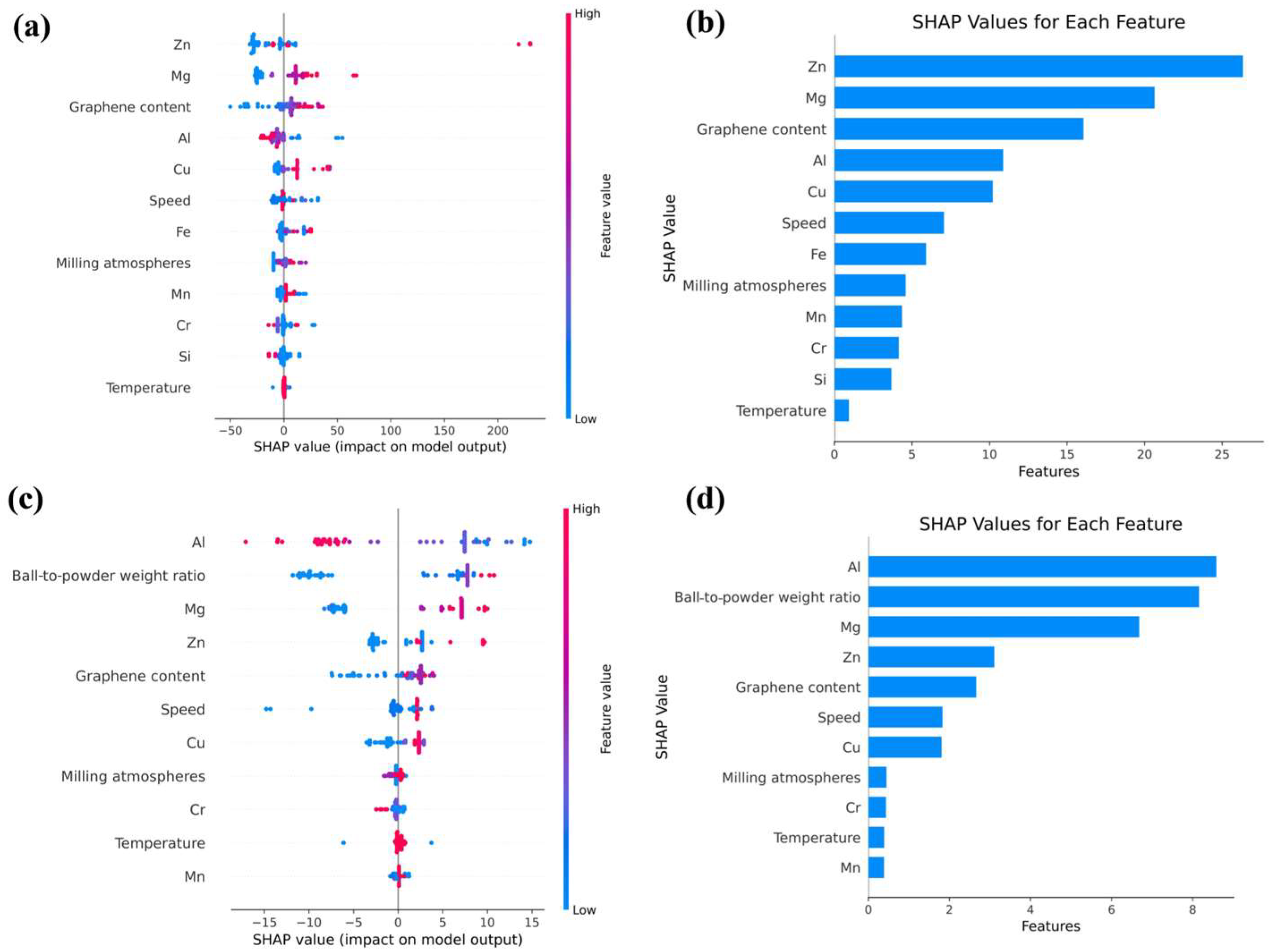
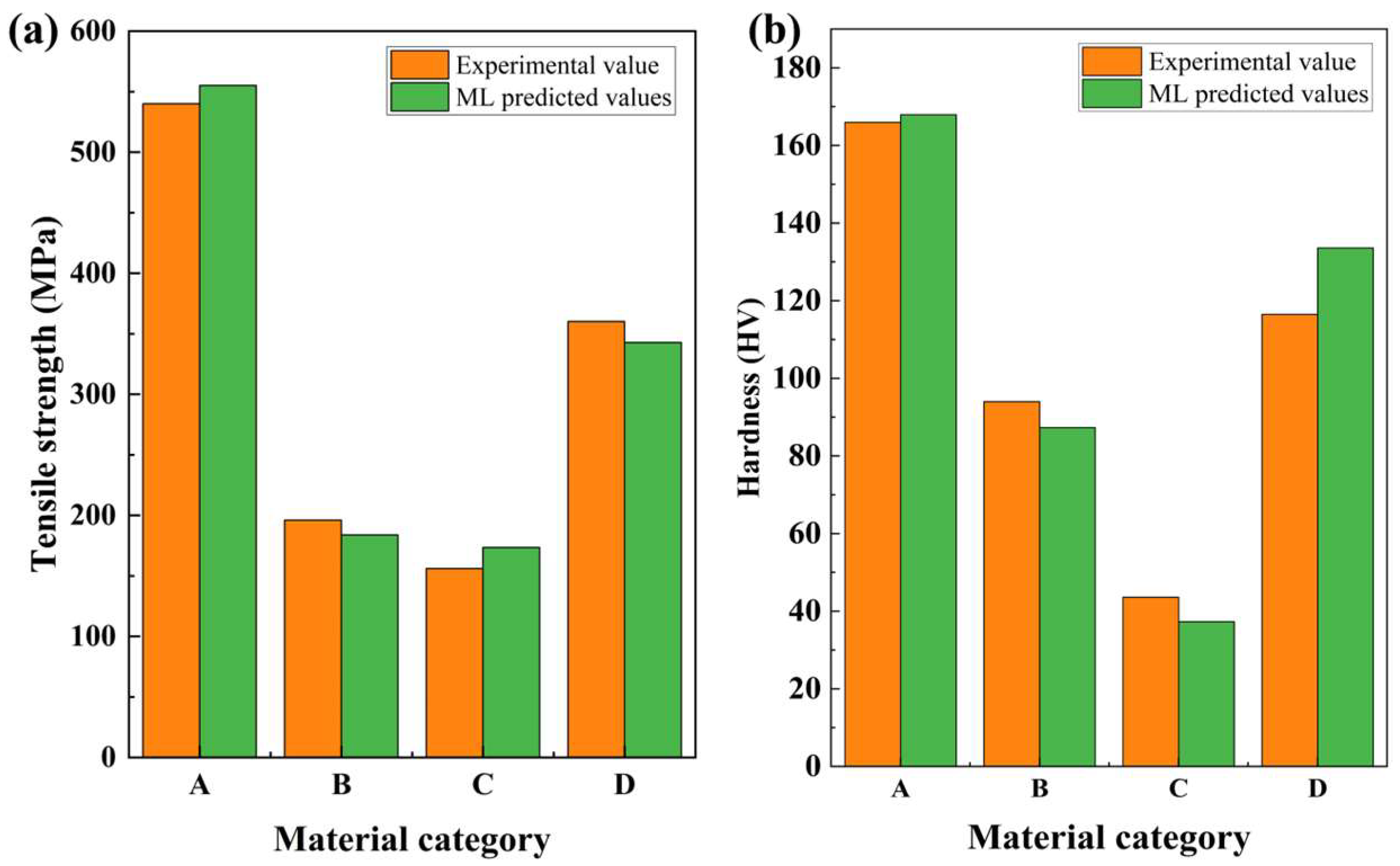
3.3. Interpretable Machine Learning and Validation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef]
- Soldano, C.; Mahmood, A.; Dujardin, E. Production, properties and potential of graphene. Carbon 2010, 48, 2127–2150. [Google Scholar] [CrossRef]
- Santos, M.C.; Machado, A.R.; Sales, W.F.; Barrozo, M.A.; Ezugwu, E.O. Machining of aluminum alloys: A review. Int. J. Adv. Manuf. Technol. 2016, 86, 3067–3080. [Google Scholar] [CrossRef]
- Starke, E.A., Jr.; Staley, J.T. Application of modern aluminum alloys to aircraft. Prog. Aerosp. Sci. 1996, 32, 131–172. [Google Scholar] [CrossRef]
- Miracle, D.B. Metal matrix composites–from science to technological significance. Compos. Sci. Technol. 2005, 65, 2526–2540. [Google Scholar] [CrossRef]
- Koria, C.S.; Kumar, R.; Chauhan, P.S. Reinforcement of micro and nano material with aluminum alloy (Al7075) metal matrix composite: A review. J. Phys. Conf. Ser. 2023, 2484, 012023. [Google Scholar] [CrossRef]
- Dixit, S.; Mahata, A.; Mahapatra, D.R.; Kailas, S.V.; Chattopadhyay, K. Multi-layer graphene reinforced aluminum–manufacturing of high strength composite by friction stir alloying. Compos. Part B Eng. 2018, 136, 63–71. [Google Scholar] [CrossRef]
- Palei, B.B.; Dash, T.; Biswal, S.K. Preparation of graphene reinforced aluminium composites: Investigation of microstructural, electrical conductivity and microhardness behaviour. Int. J. Mater. Prod. Technol. 2021, 62, 49–64. [Google Scholar] [CrossRef]
- Ju, J.M.; Wang, G.; Sim, K.H. Facile synthesis of graphene reinforced Al matrix composites with improved dispersion of graphene and enhanced mechanical properties. J. Alloy. Compd. 2017, 704, 585–592. [Google Scholar] [CrossRef]
- Rhee, H.; Whittington, W.R.; Oppedal, A.L.; Sherif, A.R.; King, R.L.; Kim, H.-J.; Lee, C. Mechanical properties of novel aluminum metal matrix metallic composites: Application to overhead conductors. Mater. Des. 2015, 88, 16–21. [Google Scholar] [CrossRef]
- Chen, F.; Gupta, N.; Behera, R.K.; Rohatgi, P.K. Graphene-reinforced aluminum matrix composites: A review of synthesis methods and properties. Jom 2018, 70, 837–845. [Google Scholar] [CrossRef]
- Mishra, T.K.; Kumar, P.; Jain, P. Effects of graphene content on the wear properties of aluminum matrix composites prepared by powder metallurgy route. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Lazarova, R.; Mourdjeva, Y.; Nihtianova, D.; Stefanov, G.; Petkov, V. Fabrication and Characterization of Aluminum-Graphene Nano-Platelets—Nano-Sized Al4C3 Composite. Metals 2022, 12, 2057. [Google Scholar] [CrossRef]
- Isametova, M.E.; Nussipali, R.; Martyushev, N.V.; Martyushev, N.V.; Malozyomov, B.V.; Efremenkov, E.A. Mathematical Modeling of the Reliability of Polymer Composite Materials. Mathematics 2022, 10, 3978. [Google Scholar] [CrossRef]
- Suzdaltsev, A.; Rakhmanova, O. Special Issue on Metal-Based Composite Materials: Preparation, Structure, Properties and Applications. Appl. Sci. 2023, 13, 4799. [Google Scholar] [CrossRef]
- Zhao, Z.; Chang, S.; Wang, J.; Bai, P.; Du, W.; Zhao, W. First-Principles Study on Graphene/Mg2Si Interface of Selective Laser Melting Graphene/Aluminum Matrix Composites. Metals 2021, 11, 941. [Google Scholar] [CrossRef]
- Kordijazi, A.; Zhao, T.; Zhang, J.; Rohatgi, P. A review of application of machine learning in design, synthesis, and characterization of metal matrix composites: Current status and emerging applications. Jom 2021, 73, 2060–2074. [Google Scholar] [CrossRef]
- Hasan, M.S.; Wong, T.; Rohatgi, P.K.; Nosonovsky, M. Analysis of the friction and wear of graphene reinforced aluminum metal matrix composites using machine learning models. Tribol. Int. 2022, 170, 107527. [Google Scholar] [CrossRef]
- Juan, Y.; Dai, Y.; Yang, Y.; Zhang, J. Accelerating materials discovery using machine learning. J. Mater. Sci. Technol. 2021, 79, 178–190. [Google Scholar] [CrossRef]
- Chen, C.; Zuo, Y.; Ye, W.; Li, X.; Deng, Z.; Ong, S.P. A critical review of machine learning of energy materials. Adv. Energy Mater. 2020, 10, 1903242. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, X.; Li, J.; Xiao, L.; Gao, H.; Zhao, F.; Ma, H. Progress on the application of graphene-based composites toward energetic materials: A review. Def. Technol. 2023, in press. [Google Scholar] [CrossRef]
- Chen, D.; Li, J.; Sun, K.; Fan, J. Graphene-reinforced metal matrix composites: Fabrication, properties, and challenges. Int. J. Adv. Manuf. Technol. 2023, 125, 2925–2965. [Google Scholar] [CrossRef]
- Ayub, S.; Guan, B.H.; Ahmad, F.; Javed, M.F.; Mosavi, A.; Felde, I. Preparation methods for graphene metal and polymer based composites for emi shielding materials: State of the art review of the conventional and machine learning methods. Metals 2021, 11, 1164. [Google Scholar] [CrossRef]
- Chaudry, U.M.; Hamad, K.; Abuhmed, T. Machine learning-aided design of aluminum alloys with high performance. Mater. Today Commun. 2021, 26, 101897. [Google Scholar] [CrossRef]
- Chan, C.H.; Sun, M.; Huang, B. Application of machine learning for advanced material prediction and design. EcoMat 2022, 4, e12194. [Google Scholar] [CrossRef]
- Cai, J.; Chu, X.; Xu, K.; Li, H.; Wei, J. Machine learning-driven new material discovery. Nanoscale Adv. 2020, 2, 3115–3130. [Google Scholar] [CrossRef]
- Morgan, D.; Jacobs, R. Opportunities and challenges for machine learning in materials science. Annu. Rev. Mater. Res. 2020, 50, 71–103. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Lundberg, S.M.; Nair, B.; Vavilala, M.S.; Horibe, M.; Eisses, M.J.; Adams, T.; Liston, D.E.; Low, D.K.-W.; Newman, S.-F.; Kim, J.; et al. Explainable machine-learning predictions for the prevention of hypoxaemia during surgery. Nat. Biomed. Eng. 2018, 2, 749–760. [Google Scholar] [CrossRef]
- Tang, M.; Zhang, D.; Wang, D.; Deng, J.; Kong, D.; Zhang, H. Performance prediction of 2D vertically stacked MoS2-WS2 heterostructures base on first-principles theory and Pearson correlation coefficient. Appl. Surf. Sci. 2022, 596, 153498. [Google Scholar] [CrossRef]
- Chen, W.C.; Schmidt, J.N.; Yan, D.; Vohra, Y.K.; Chen, C.-C. Machine learning and evolutionary prediction of superhard BCN compounds. npj Comput. Mater. 2021, 7, 114. [Google Scholar] [CrossRef]
- Kwon, H.; Mondal, J.; AlOgab, K.A.; Sammelselg, V.; Takamichi, M.; Kawaski, A.; Leparoux, M. Graphene oxide-reinforced aluminum alloy matrix composite materials fabricated by powder metallurgy. J. Alloy. Compd. 2017, 698, 807–813. [Google Scholar] [CrossRef]
- Gamil, M.; Ahmed, M.M.Z. Investigating the thermo-mechanical properties of aluminum/graphene nano-platelets composites developed by friction stir processing. Int. J. Precis. Eng. Manuf. 2020, 21, 1539–1546. [Google Scholar] [CrossRef]
- Li, M.; Gao, H.; Liang, J.; Gu, S.; You, W.; Shu, D.; Wang, J.; Sun, B. Microstructure evolution and properties of graphene nanoplatelets reinforced aluminum matrix composites. Mater. Charact. 2018, 140, 172–178. [Google Scholar] [CrossRef]
- Han, T.; Li, J.; Zhao, N.; He, C. Microstructure and properties of copper coated graphene nanoplates reinforced Al matrix composites developed by low temperature ball milling. Carbon 2020, 159, 311–323. [Google Scholar] [CrossRef]



| Code | Model | MAE/MPa | RMSE/MPa | R2 | MAPE/% |
|---|---|---|---|---|---|
| catboost | CatBoost Regressor | 23.6252 | 31.3978 | 0.8992 | 0.1099 |
| gbr | Gradient Boosting Regressor | 25.5935 | 32.3295 | 0.8889 | 0.1187 |
| et | Extra Trees Regressor | 25.7041 | 35.5107 | 0.8806 | 0.1170 |
| rf | Random Forest Regressor | 31.5405 | 41.6775 | 0.8348 | 0.1427 |
| ada | AdaBoost Regressor | 32.3919 | 39.1305 | 0.8328 | 0.1585 |
| dt | Decision Tree Regressor | 30.0533 | 37.294 | 0.8165 | 0.1337 |
| xgboost | Extreme Gradient Boosting | 29.2894 | 38.0660 | 0.8044 | 0.1343 |
| knn | K Neighbors Regressor | 62.6692 | 95.1768 | 0.4134 | 0.2825 |
| ridge | Ridge Regression | 60.9330 | 81.5503 | 0.1304 | 0.2720 |
| Code | Model | MAE/HV | RMSE/HV | R2 | MAPE/% |
|---|---|---|---|---|---|
| catboost | CatBoost Regressor | 7.7288 | 10.1066 | 0.8599 | 0.1173 |
| et | Extra Trees Regressor | 7.5516 | 10.2430 | 0.8332 | 0.1156 |
| rf | Random Forest Regressor | 9.4189 | 11.6678 | 0.8174 | 0.1489 |
| gbr | Gradient Boosting Regressor | 9.1669 | 11.3083 | 0.8160 | 0.1384 |
| xgboost | Extreme Gradient Boosting | 9.0745 | 11.5224 | 0.8107 | 0.1324 |
| ada | AdaBoost Regressor | 10.1792 | 12.7747 | 0.7797 | 0.1570 |
| knn | K Neighbors Regressor | 12.5199 | 15.6432 | 0.6636 | 0.1882 |
| dt | Decision Tree Regressor | 12.2699 | 16.044 | 0.6290 | 0.1868 |
| ridge | Ridge Regression | 13.3502 | 16.5541 | 0.6139 | 0.1980 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, J.; Huang, J.; Li, M.; Chen, J.; Wei, Z.; Cheng, Y.; Lai, Z.; Qu, N.; Liu, Y.; Zhu, J. Explanatory Machine Learning Accelerates the Design of Graphene-Reinforced Aluminium Matrix Composites with Superior Performance. Metals 2023, 13, 1690. https://doi.org/10.3390/met13101690
Xue J, Huang J, Li M, Chen J, Wei Z, Cheng Y, Lai Z, Qu N, Liu Y, Zhu J. Explanatory Machine Learning Accelerates the Design of Graphene-Reinforced Aluminium Matrix Composites with Superior Performance. Metals. 2023; 13(10):1690. https://doi.org/10.3390/met13101690
Chicago/Turabian StyleXue, Jingteng, Jingtao Huang, Mingwei Li, Jiaying Chen, Zongfan Wei, Yuan Cheng, Zhonghong Lai, Nan Qu, Yong Liu, and Jingchuan Zhu. 2023. "Explanatory Machine Learning Accelerates the Design of Graphene-Reinforced Aluminium Matrix Composites with Superior Performance" Metals 13, no. 10: 1690. https://doi.org/10.3390/met13101690
APA StyleXue, J., Huang, J., Li, M., Chen, J., Wei, Z., Cheng, Y., Lai, Z., Qu, N., Liu, Y., & Zhu, J. (2023). Explanatory Machine Learning Accelerates the Design of Graphene-Reinforced Aluminium Matrix Composites with Superior Performance. Metals, 13(10), 1690. https://doi.org/10.3390/met13101690







