The Parameter Identification of Physical-Based Constitutive Model by Inverse Analysis Method for Application in Near-Net Shape Forging of Aluminum Wheels
Abstract
:1. Introduction
2. Hot Compression Tests
2.1. Experimental Material and Procedures of Hot Compression Tests
2.2. Flow Stress–Strain Curves and Their Corrections
3. Identification of Modified Zerilli–Armstrong (M-ZA) Model Parameters by Inverse Analysis Method
3.1. Identification of M-ZA Model Parameters by Linear Fitting Method
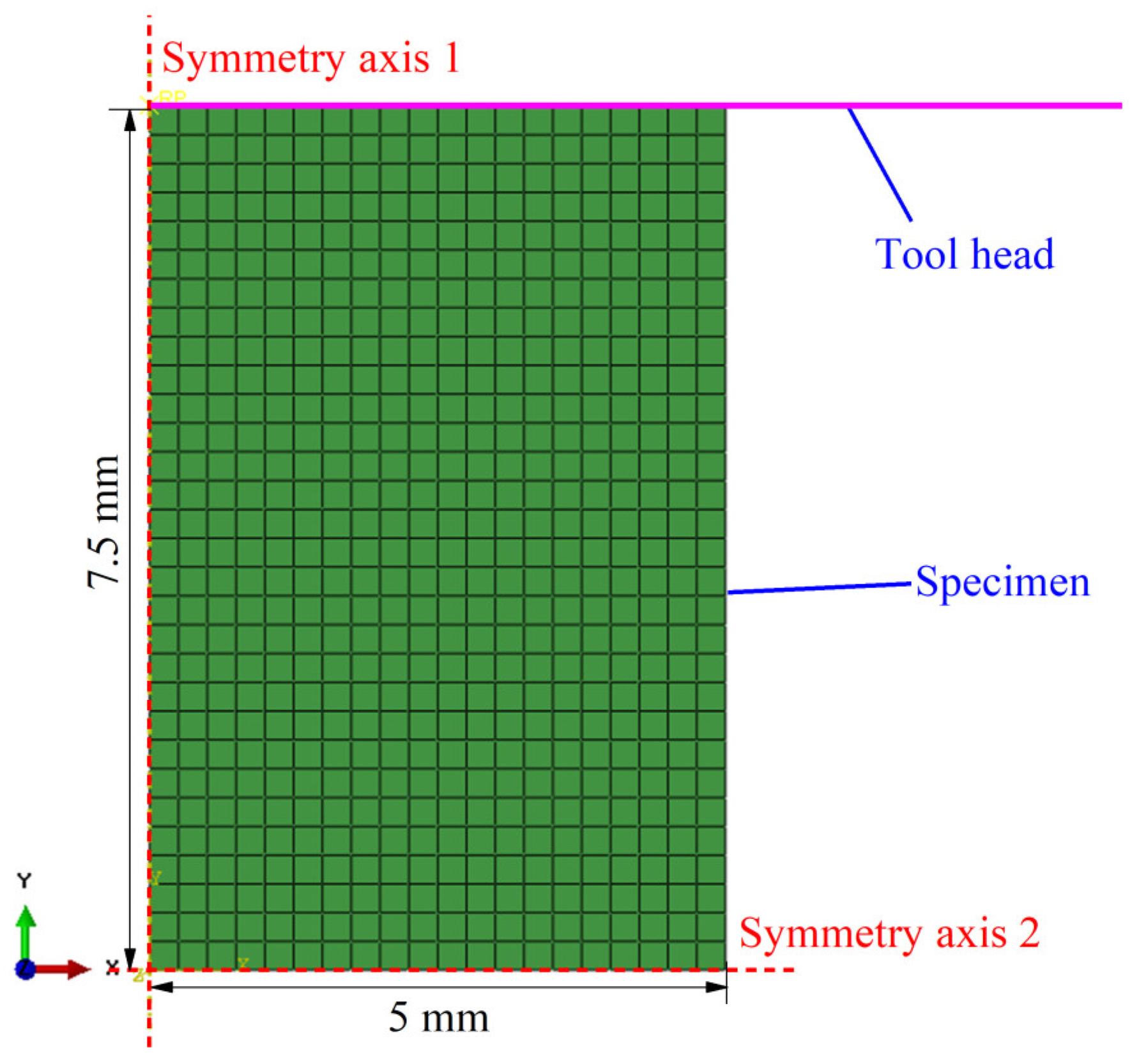
3.2. The Establishment of FEM Embedding M-ZA Model Based on Abaqus–Uhard Subroutine
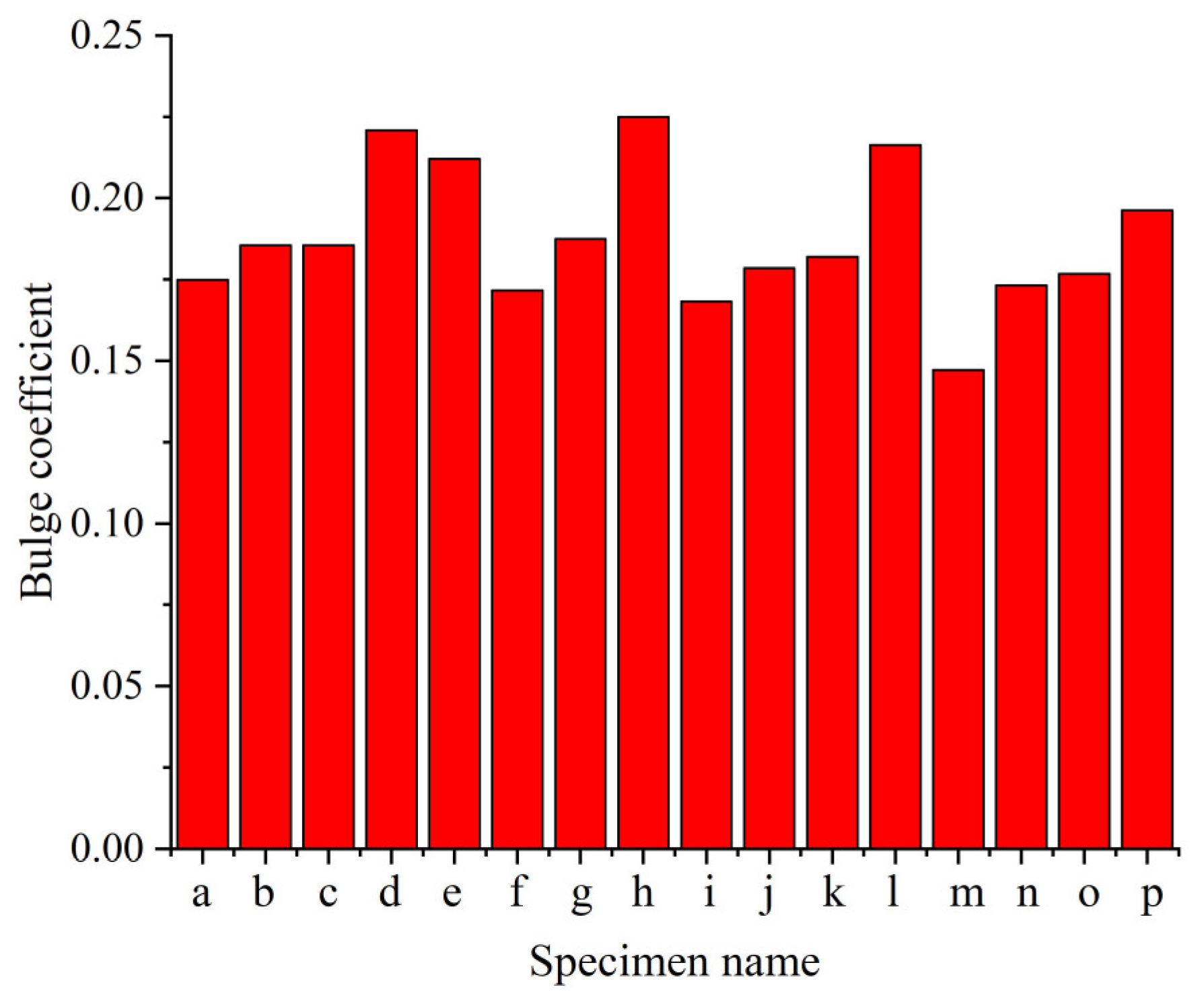
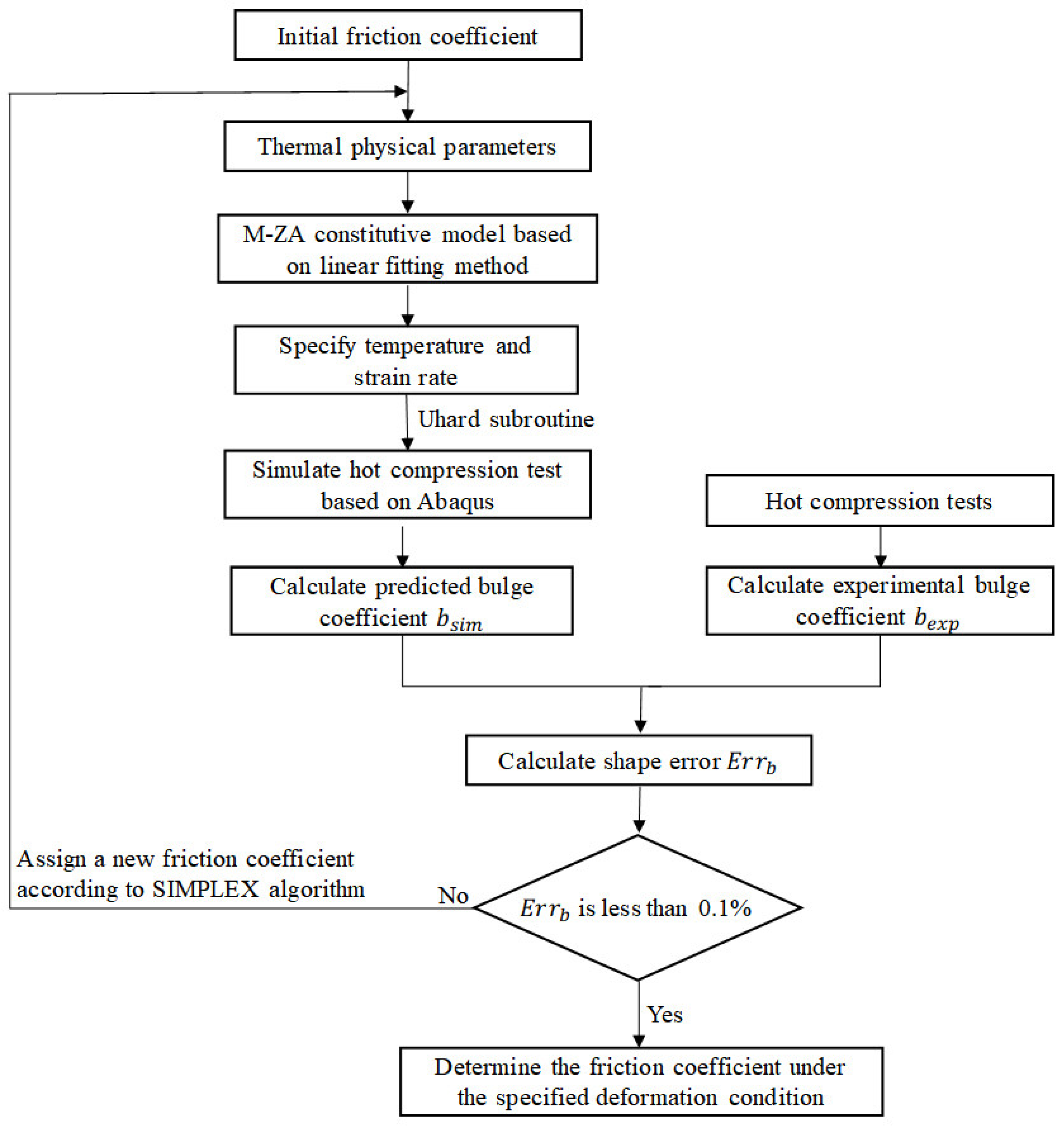
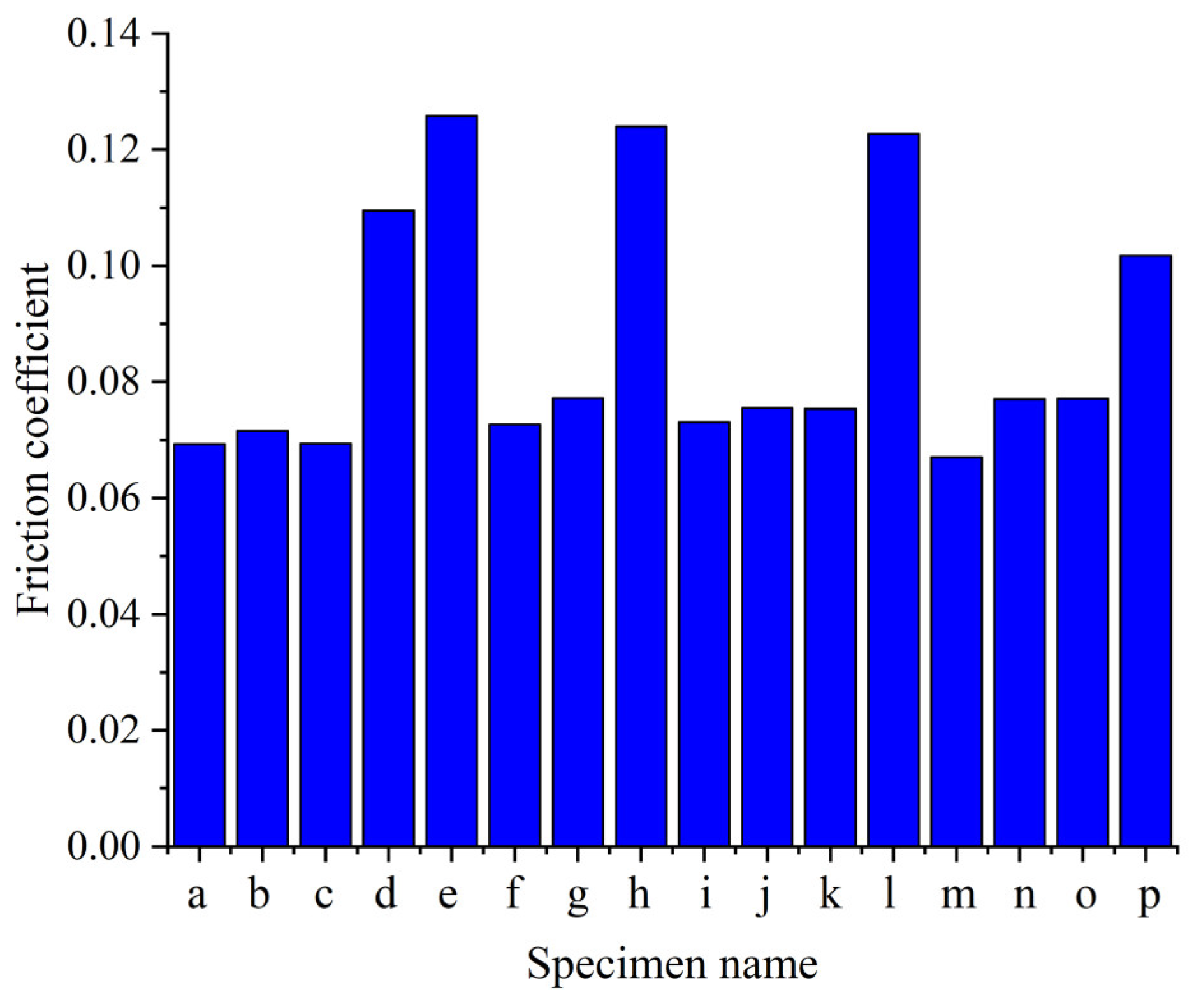
3.3. Determination of the Friction Coefficient under Each Deformation Condition
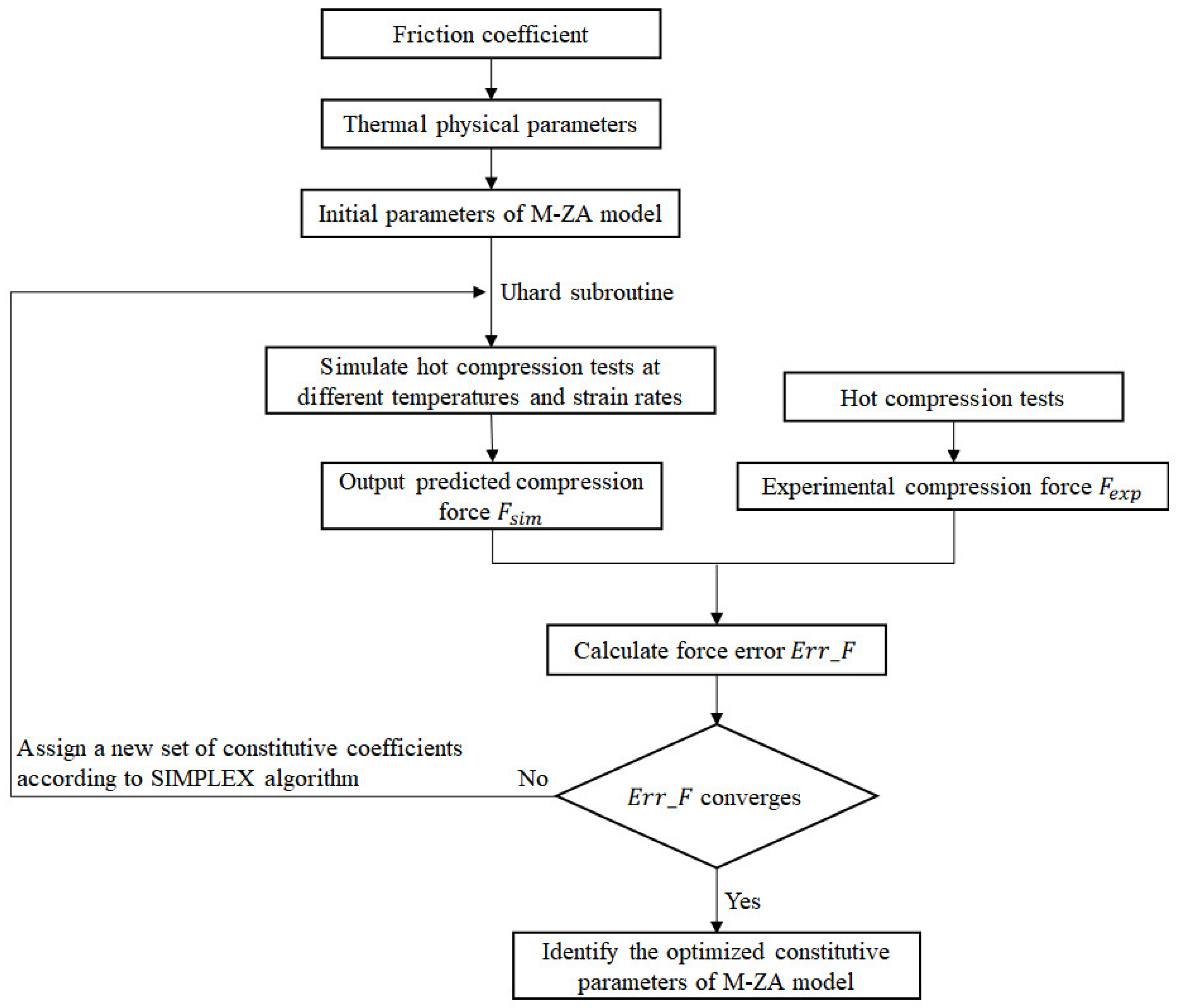
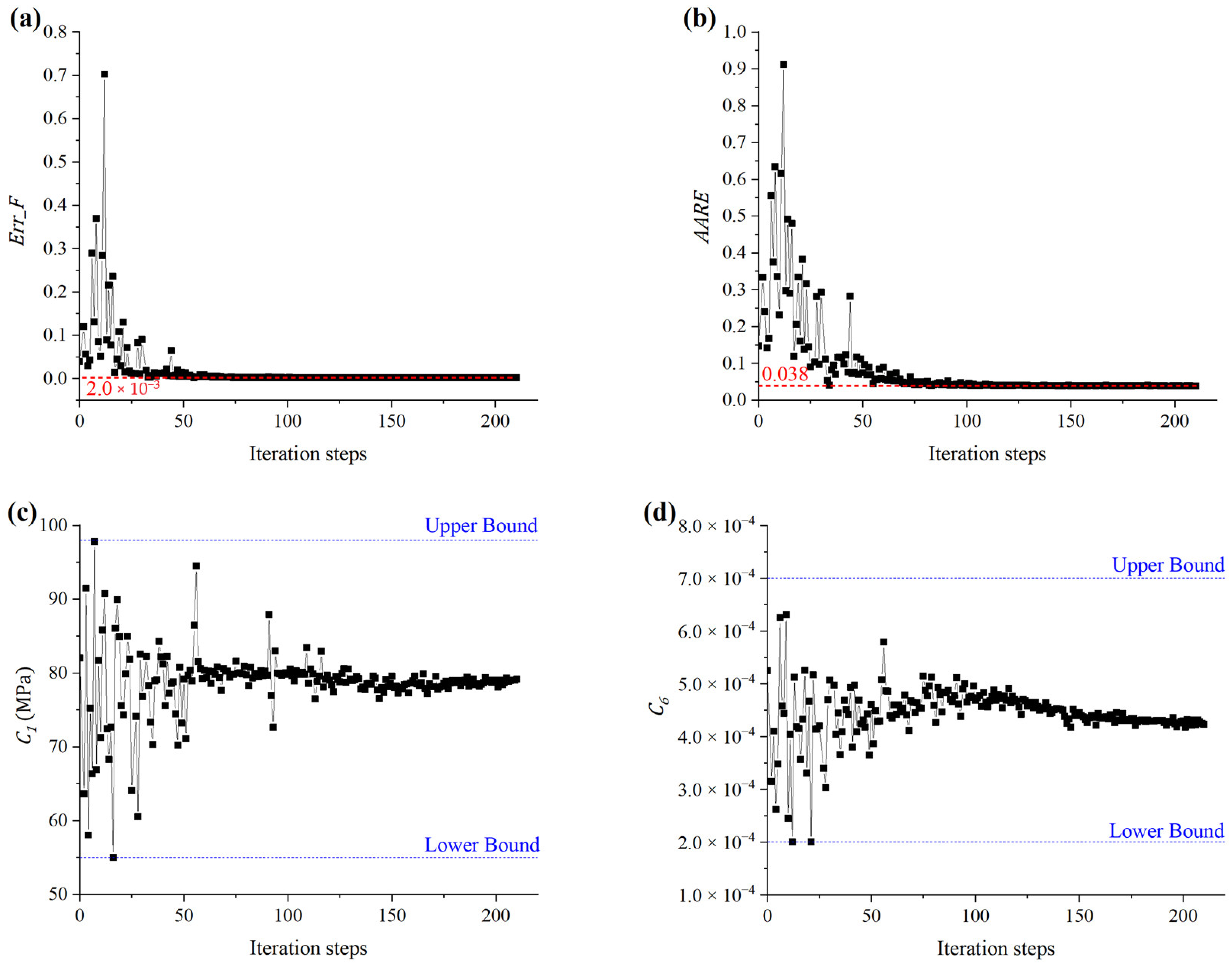
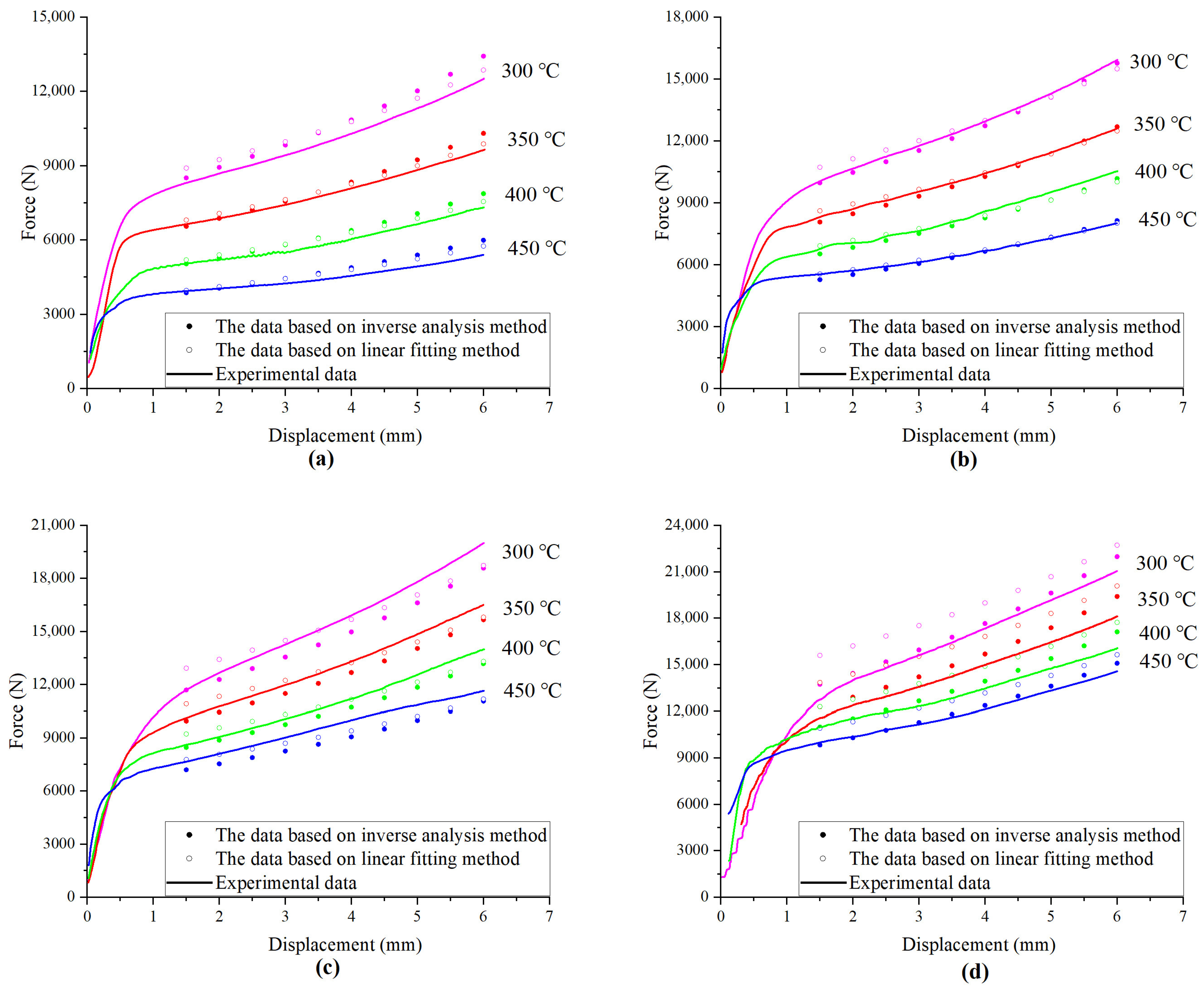
3.4. Identification of M-ZA Model Parameters by Inverse Analysis Method
4. Application of the M-ZA Model Determined by Inverse Analysis Method in the Near-Net Forging of Aluminum Alloy Wheels
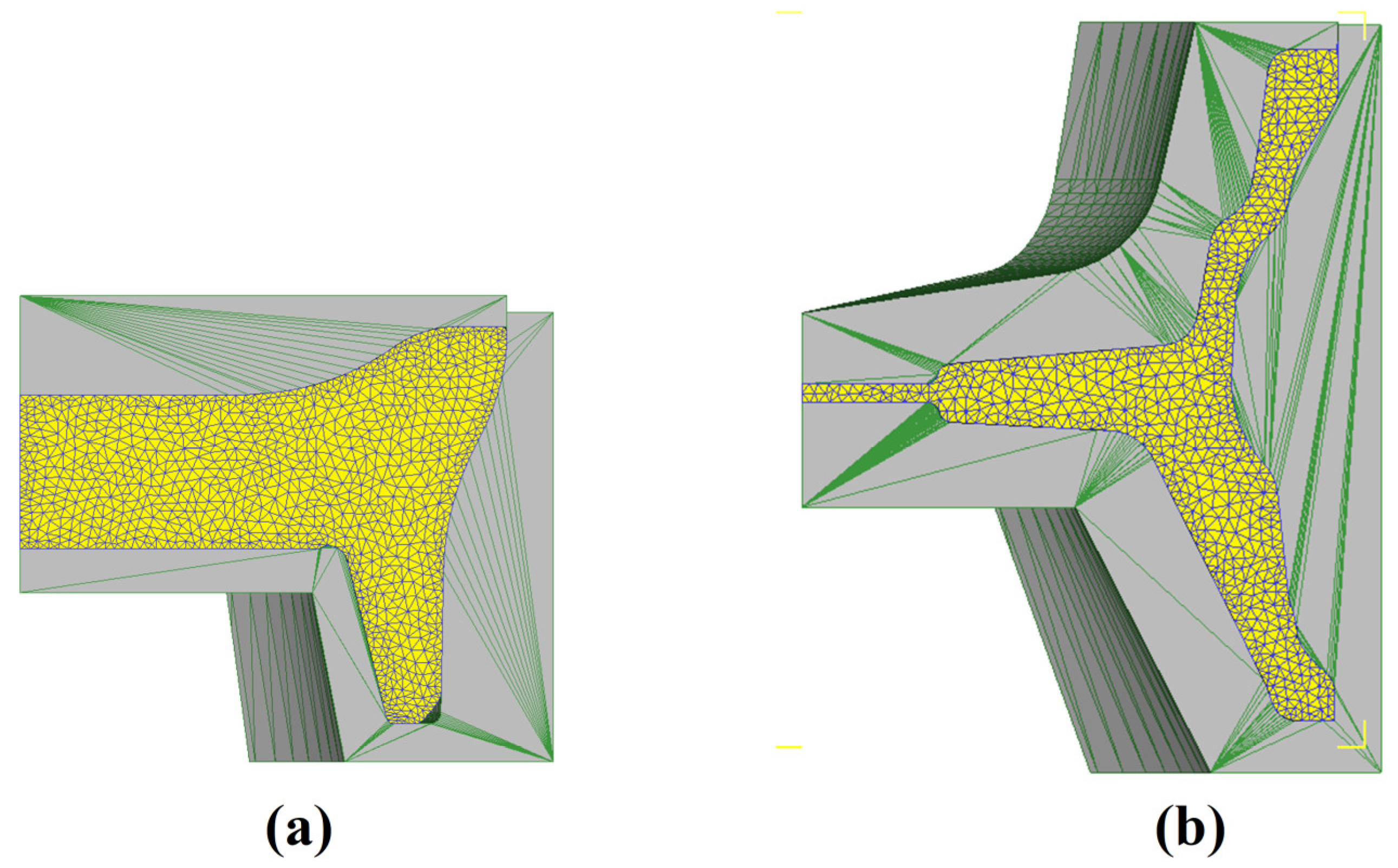
4.1. Finite Element Simulation of Near-Net Forging of Wheels
4.2. Experiments on Near-Net Shape Forging of Wheels
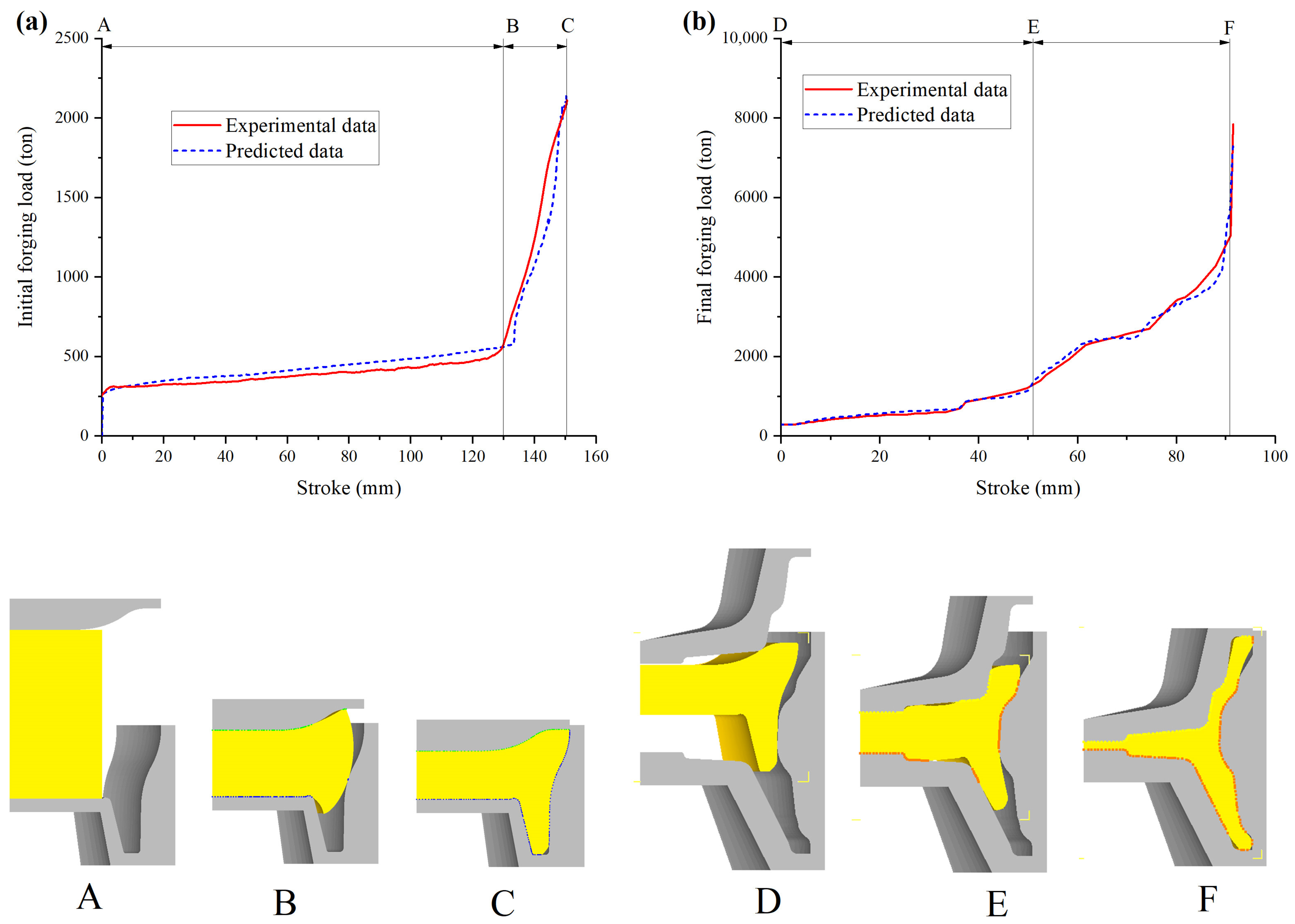
4.3. Comparisons of Experimental and Predicted Forging Load–Stroke Curves
5. Conclusions
- Based on the bulge coefficients of the compressed specimens, 16 friction coefficients between the compressed specimens and tool head at different temperatures and strain rates were determined by the inverse analysis method, where the maximal friction coefficient was 0.1258 and the minimum friction coefficient was 0.06706, and they differed by 46.69%.
- Based on the force–displacement data of the compressed specimens and the above 16 determined friction coefficients, nine material parameters of the M-ZA model were identified by the second inverse analysis technique, and the global average error between the experimental and predicted force–displacement curves was 3.8%. Moreover, the prediction accuracy of the compression force of the M-ZA model based on the inverse analysis method was higher apparently than that of the M-ZA model based on the traditional linear fitting method when the strain rate was 10 s−1, and the average prediction errors were 3.3% and 11.0%, respectively.
- The forging FE models of 7075 aluminum alloy wheels were built based on the Deform-3D platform, and the near-net shape forging processes of the wheels were simulated. The near-net shape forging experiments of aluminum alloy wheels were carried out. The experimental forgings were filled well and the flashes were thin. The predicted forging load–stroke curves were in good agreement with the experimental data in all stages of the initial and final forging processes, and the load average error in each stage during the final forging process was less than 10%. This not only verifies the reliability of the M-ZA model obtained by using the two-times inverse analysis method, but also provides theoretical guidance for the formulation and optimization of the near-net-shape forging process parameters of aluminum alloy wheels.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, Y.H.; Ryou, T.K.; Choi, H.J.; Hwang, B.B. An Analysis of the Forging Processes for 6061 Aluminum-Alloy Wheels. J. Mater. Process. Technol. 2002, 123, 270–276. [Google Scholar] [CrossRef]
- Li, L.; Wang, F. Simulation Study on Influence of Forming Process Parameters on Backward Extrusion Height of 6061 Aluminum-Alloy Wheel. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Zurich, Switzerland, 2012; pp. 363–366. [Google Scholar]
- Yang, T.S.; Luo, K.C. Friction Factor of 6061 Aluminum Alloy and Application to The Finite Element Analysis of Wheel Forging. Key Eng. Mater. 2017, 739, 231–234. [Google Scholar] [CrossRef]
- Ma, Z. Study on Closed-Die Forging Technology of Forging Aluminum Alloy Wheel. Forg. Stamp. Technol. 2015, 40, 1–4. [Google Scholar]
- Zhang, L.P.; Qi, B.N.; Zhao, D.J. One-Piece Forged Aluminum Alloy Wheel Process Steps Analysis and Dies Design. In Proceedings of the International Conference on Mechanical Engineering and Mechanics, Wuxi, China, 5–7 November 2007; Volume 1–2, pp. 1641–1646. [Google Scholar]
- Chen, S.Y.; Shu, X.D.; Lu, Y.J. Effect of 6061 Aluminum Alloy Wheel Forging and Spinning Process Parameters on Forming Quality. Metalurgija 2022, 61, 317–320. [Google Scholar]
- Lu, Y.J.; Shu, X.D. Effect of Aluminum Alloy Wheel Forging and Spinning Process Parameters on Forming Force. Metalurgija 2021, 60, 227–229. [Google Scholar]
- Samantaray, D.; Mandal, S.; Borah, U.; Bhaduri, A.K.; Sivaprasad, P.V. A Thermo-Viscoplastic Constitutive Model to Predict Elevated-Temperature Flow Behaviour in A Titanium-Modified Austenitic Stainless Steel. Mater. Sci. Eng. A 2009, 526, 1–6. [Google Scholar] [CrossRef]
- Yu, R.; Wang, P.; Li, G.; Fang, M.; Xu, G.; Zhang, M. Correction and Modeling of Flow Stress During Hot Deformation of 7055 Aluminum Alloy. J. Mater. Eng. Perform. 2022, 31, 6870–6879. [Google Scholar] [CrossRef]
- Rudra, A.; Ashiq, M.; Das, S.; Dasgupta, R. Constitutive Modeling for Predicting High-Temperature Flow Behavior in Aluminum 5083+10wtpct Sicp Composite. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2019, 50, 1060–1076. [Google Scholar] [CrossRef]
- Wang, G.; Ma, G.; Wu, J. Research on Constitutive Model of 2099-T83 Aluminum-Lithium Alloy. J. Plast. Eng. 2019, 26, 174–181. [Google Scholar]
- Paturi, U.M.R.; Narala, S.K.R.; Pundir, R.S. Constitutive Flow Stress Formulation, Model Validation and Fe Cutting Simulation for Aa7075-T6 Aluminum Alloy. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2014, 605, 176–185. [Google Scholar] [CrossRef]
- Ashtiani, H.R.R.; Shayanpoor, A.A. Prediction of The Hot Flow Behavior of Aa1070 Aluminum Using the Phenomenological and Physically-Based Models. Phys. Met. Met. 2021, 122, 1436–1445. [Google Scholar] [CrossRef]
- Venugopal, S.; Srinivasan, G.; Venkadesan, S.; Seetharaman, V. A Note on The Determination of the Friction Factor by Means of the Reduction-Capacity Test. J. Mech. Work. Technol. 1989, 19, 261–266. [Google Scholar] [CrossRef]
- Shen, G.; Vedhanayagam, A.; Kropp, E.; Altan, T. A Method for Evaluating Friction Using A Backward Extrusion-Type Forging. J. Mater. Process. Technol. 1992, 33, 109–123. [Google Scholar] [CrossRef]
- Dadras, P. A Semi-Empirical Solution to Upset Forging. J. Eng. Ind. Trans. Asme 1981, 103, 478–483. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Najafizadeh, A. A New Method for Evaluation of Friction in Bulk Metal Forming. J. Mater. Process. Technol. 2004, 152, 136–143. [Google Scholar] [CrossRef]
- Goetz, R.L.; Semiatin, S.L. The Adiabatic Correction Factor for Deformation Heating During the Uniaxial Compression Test. J. Mater. Eng. Perform. 2001, 10, 710–717. [Google Scholar] [CrossRef]
- Mostafaei, M.A.; Kazeminezhad, M. Hot Deformation Behavior of Hot Extruded Al–6mg Alloy. Mater. Sci. Eng. A 2012, 535, 216–221. [Google Scholar] [CrossRef]
- Peng, N.; Tang, G.; Liu, Z. Correcting Method of Flow Stress Curve for Hot Compression. Hot Work. Technol. 2012, 41, 12–15. [Google Scholar]
- Slooff, F.A.; Zhou, J.; Duszczyk, J.; Katgerman, L. Constitutive Analysis of Wrought Magnesium Alloy Mg–Al4–Zn1. Scr. Mater. 2007, 57, 759–762. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, J.; Dong, Y.; Zhao, G.; Gao, A.; Wang, L. Identification of Friction Coefficients and Strain-Compensated Arrhenius-Type Constitutive Model by A Two-Stage Inverse Analysis Technique. Int. J. Mech. Sci. 2015, 98, 195–204. [Google Scholar] [CrossRef]
- Plumeri, J.E.; Madej, Ł.; Misiolek, W.Z. Constitutive Modeling and Inverse Analysis of the Flow Stress Evolution During High Temperature Compression of a New Ze20 Magnesium Alloy for Extrusion Applications. Mater. Sci. Eng. A 2019, 740–741, 174–181. [Google Scholar] [CrossRef]
- Gawad, J.; Kuziak, R.; Madej, L.; Szeliga, D.; Pietrzyk, M. Identification of Rheological Parameters on The Basis of Various Types of Compression and Tension Tests. Steel Res. Int. 2005, 76, 131–137. [Google Scholar] [CrossRef]
- Yanagida, A.; Liu, J.; Yanagimoto, J. Flow Curve Determination for Metal Under Dynamic Recrystallization Using Inverse Analysis. Mater. Trans. 2003, 44, 2303–2310. [Google Scholar] [CrossRef] [Green Version]
- Ding, S.; Khan, S.A.; Yanagimoto, J. Flow Behavior and Dynamic Recrystallization Mechanism of A5083 Aluminum Alloys with Different Initial Microstructures During Hot Compression. Mater. Sci. Eng. A 2020, 787, 139522. [Google Scholar] [CrossRef]
- Xu, L.; Yao, Z.; Liu, J.; Xue, Z.; Xu, C.; He, H.; Li, L. Constitutive Model Parameter Identification for 6063 Aluminum Alloy Using Inverse Analysis Method for Extrusion Applications. J. Mater. Eng. Perform. 2021, 30, 7449–7460. [Google Scholar] [CrossRef]
- Mulyadi, M.; Rist, M.A.; Edwards, L.; Brooks, J.W. Parameter Optimisation in Constitutive Equations for Hot Forging. J. Mater. Process. Technol. 2006, 177, 311–314. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, J.H.; Zhao, H.W. Microstructure Evolution and Mechanical Responses of Al-Zn-Mg-Cu Alloys During Hot Deformation Process. J. Mater. Sci. 2021, 56, 13429–13478. [Google Scholar] [CrossRef]
- Salvado, F.C.; Teixeira-Dias, F.; Walley, S.M.; Lea, L.J.; Cardoso, J.B. A Review on The Strain Rate Dependency of the Dynamic Viscoplastic Response of Fcc Metals. Prog. Mater. Sci. 2017, 88, 186–231. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Ji, H.C.; Pei, W.C.; Wang, S.F.; Li, Y.G. Constitutive Relationship of 7075 Aluminum Alloy Based on Modified Zerilli-Armstrong (M-ZA) Model. Metalurgija 2021, 60, 269–272. [Google Scholar]
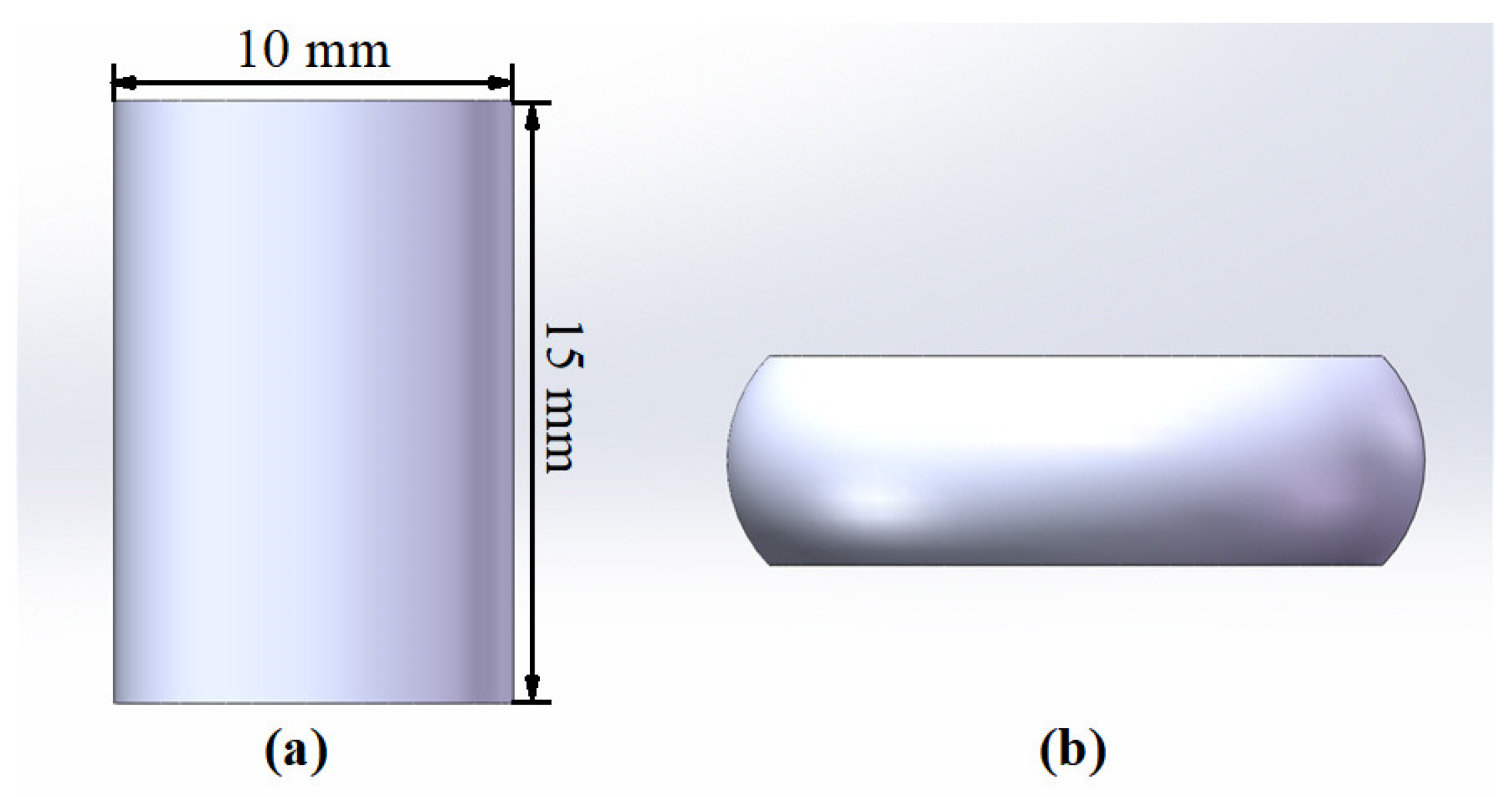
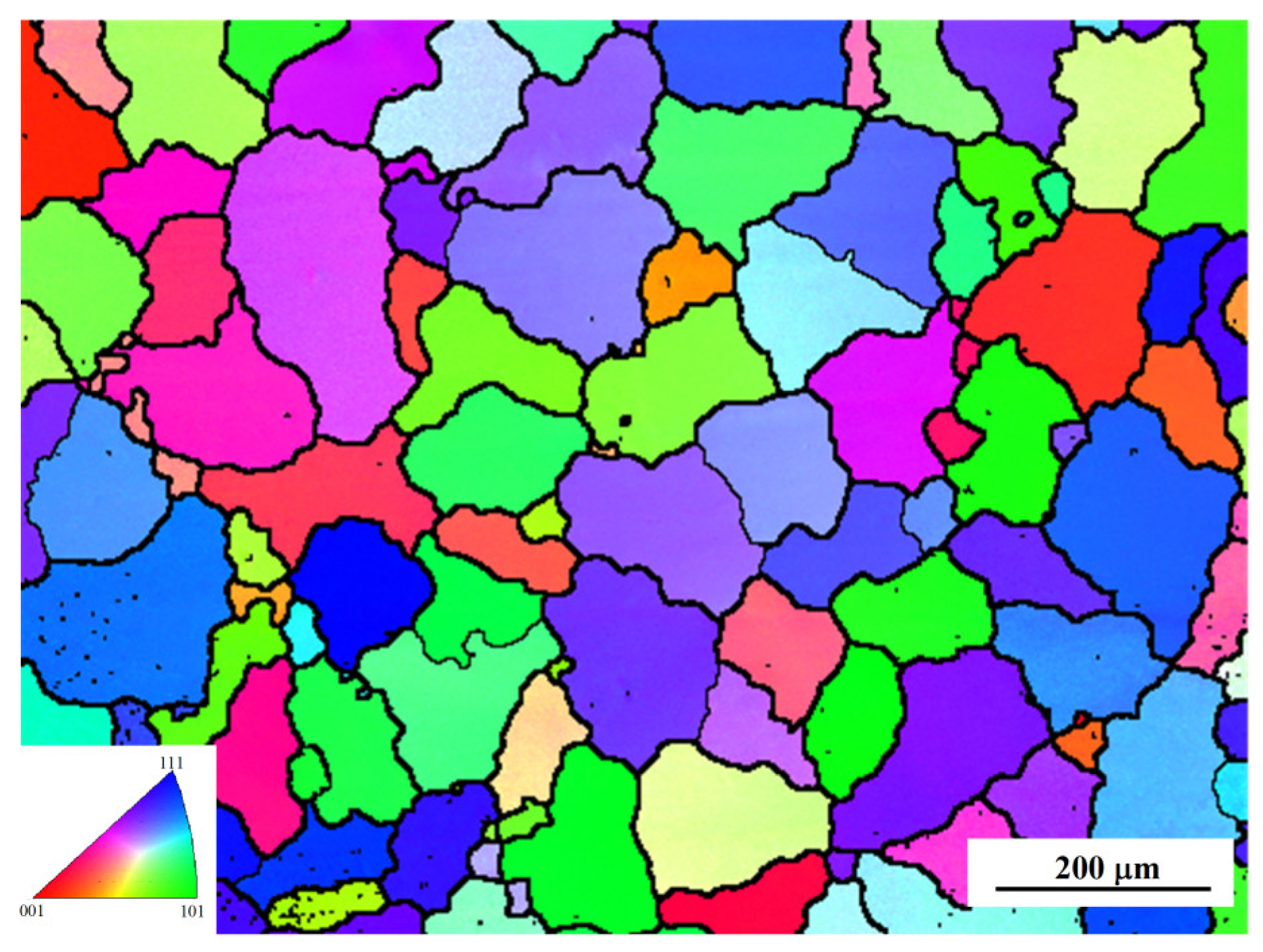

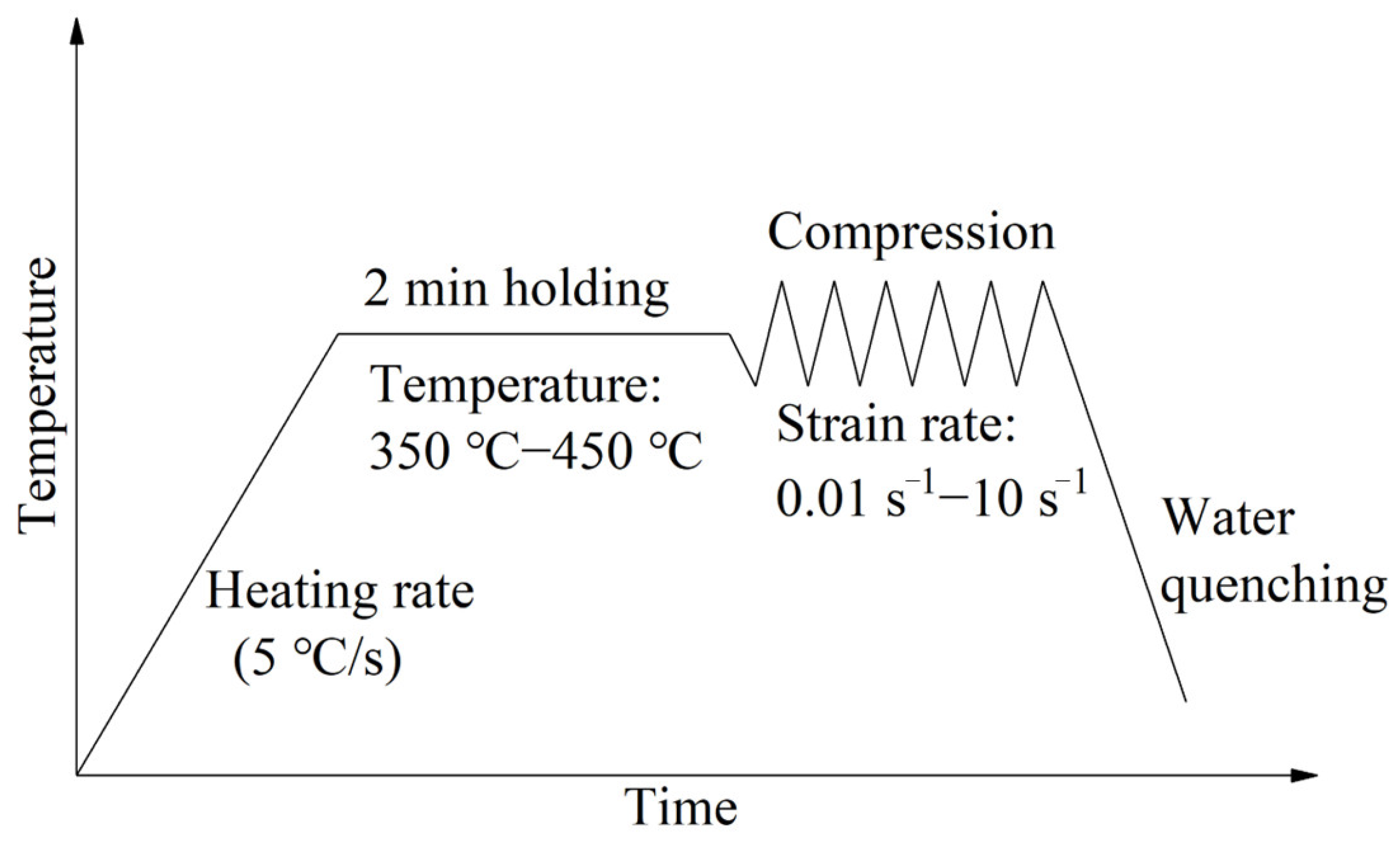

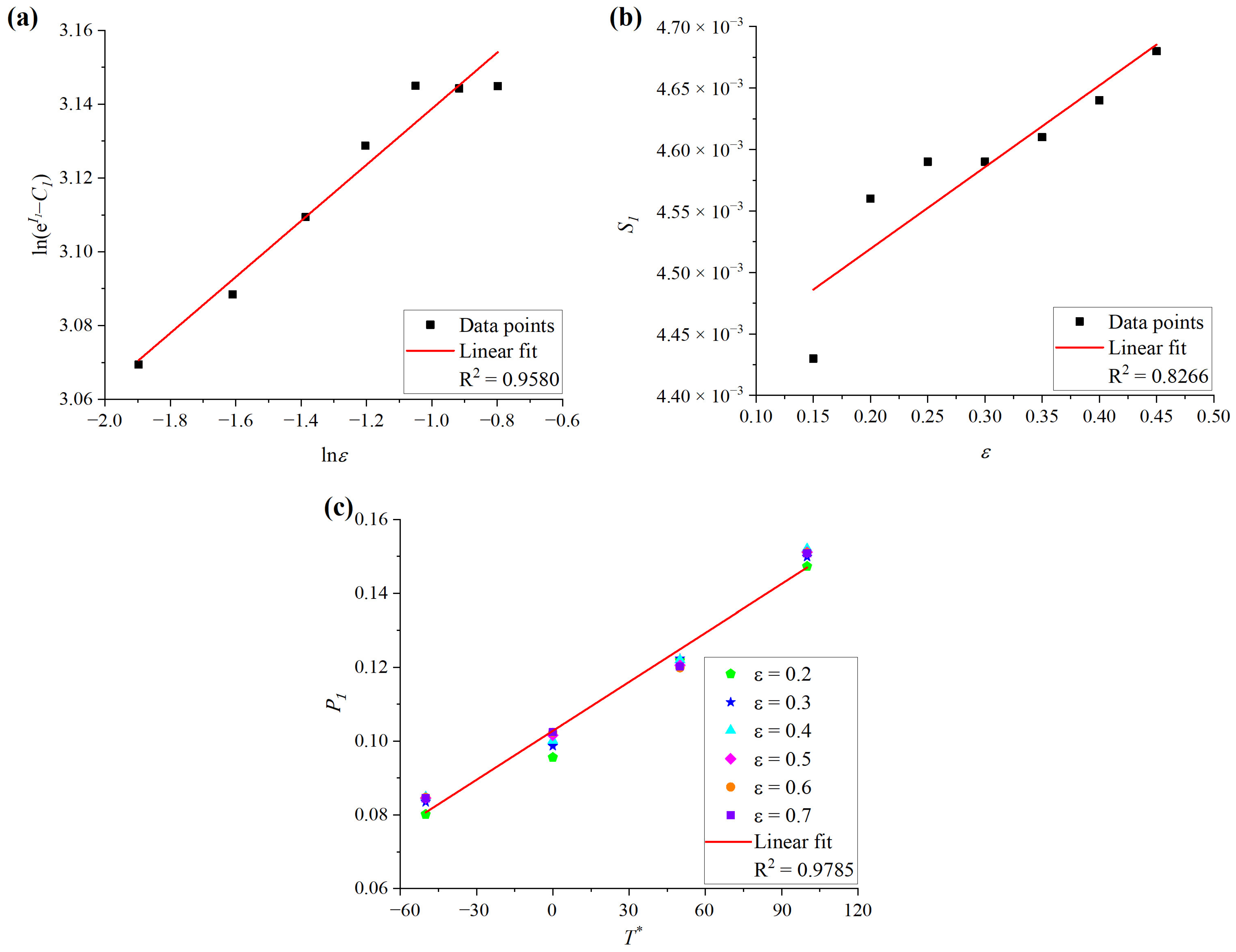


| Composition | Zn | Mg | Cu | Si | Ti | Cr | Mn | Fe | Al |
|---|---|---|---|---|---|---|---|---|---|
| Wt./% | 5.88 | 2.66 | 1.67 | 0.26 | 0.18 | 0.24 | 0.15 | 0.14 | Bal. |
| (MPa) | (MPa) | |||||
|---|---|---|---|---|---|---|
| 77.30 | 24.90 | 4.386 × 10−3 | 6.643 × 10−4 | 0.1028 | 4.420 × 10−4 | 7.605 × 10−2 |
| Thermal Conductivity (W/(m·K)) | Specific Heat (J/(kg·K)) | Density (kg/m3) | Inelastic Heat Fraction |
|---|---|---|---|
| 130 | 960 | 2800 | 0.9 |
| Boundaries | (MPa) | (MPa) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Upper boundary | 55 | 15 | 0 | 0 | 0.05 | 0.0002 | 0 | 300 | −2 |
| Lower boundary | 98 | 45 | 0.006 | 0.002 | 0.14 | 0.0007 | 3 | 450 | 1 |
| (MPa) | (MPa) | |||||||
|---|---|---|---|---|---|---|---|---|
| 79.18 | 24.04 | 4.993 × 10−3 | 1.084 × 10−3 | 7.899 × 10−2 | 4.229 ×10−4 | 0.5460 | 325.72 | 1.167 × 10−2 |
| Billet Diameter | Billet Height | Billet Temperature | Die Temperature | Forging Speed | Transfer Time |
|---|---|---|---|---|---|
| 250 mm | 229 mm | 430 °C | 400 °C | 16 mm/s | 10 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Yuan, C.; Wu, R.; Jiao, W.; Jiang, H.; Zhou, X. The Parameter Identification of Physical-Based Constitutive Model by Inverse Analysis Method for Application in Near-Net Shape Forging of Aluminum Wheels. Metals 2023, 13, 700. https://doi.org/10.3390/met13040700
Chen L, Yuan C, Wu R, Jiao W, Jiang H, Zhou X. The Parameter Identification of Physical-Based Constitutive Model by Inverse Analysis Method for Application in Near-Net Shape Forging of Aluminum Wheels. Metals. 2023; 13(4):700. https://doi.org/10.3390/met13040700
Chicago/Turabian StyleChen, Lingling, Chaolong Yuan, Rendong Wu, Wei Jiao, Haishun Jiang, and Xingyou Zhou. 2023. "The Parameter Identification of Physical-Based Constitutive Model by Inverse Analysis Method for Application in Near-Net Shape Forging of Aluminum Wheels" Metals 13, no. 4: 700. https://doi.org/10.3390/met13040700
APA StyleChen, L., Yuan, C., Wu, R., Jiao, W., Jiang, H., & Zhou, X. (2023). The Parameter Identification of Physical-Based Constitutive Model by Inverse Analysis Method for Application in Near-Net Shape Forging of Aluminum Wheels. Metals, 13(4), 700. https://doi.org/10.3390/met13040700





