Analysis of a New Process for Forming Two Flanges Simultaneously in a Hollow Part by Extrusion with Two Moving Dies
Abstract
:1. Introduction
2. Materials and Methods
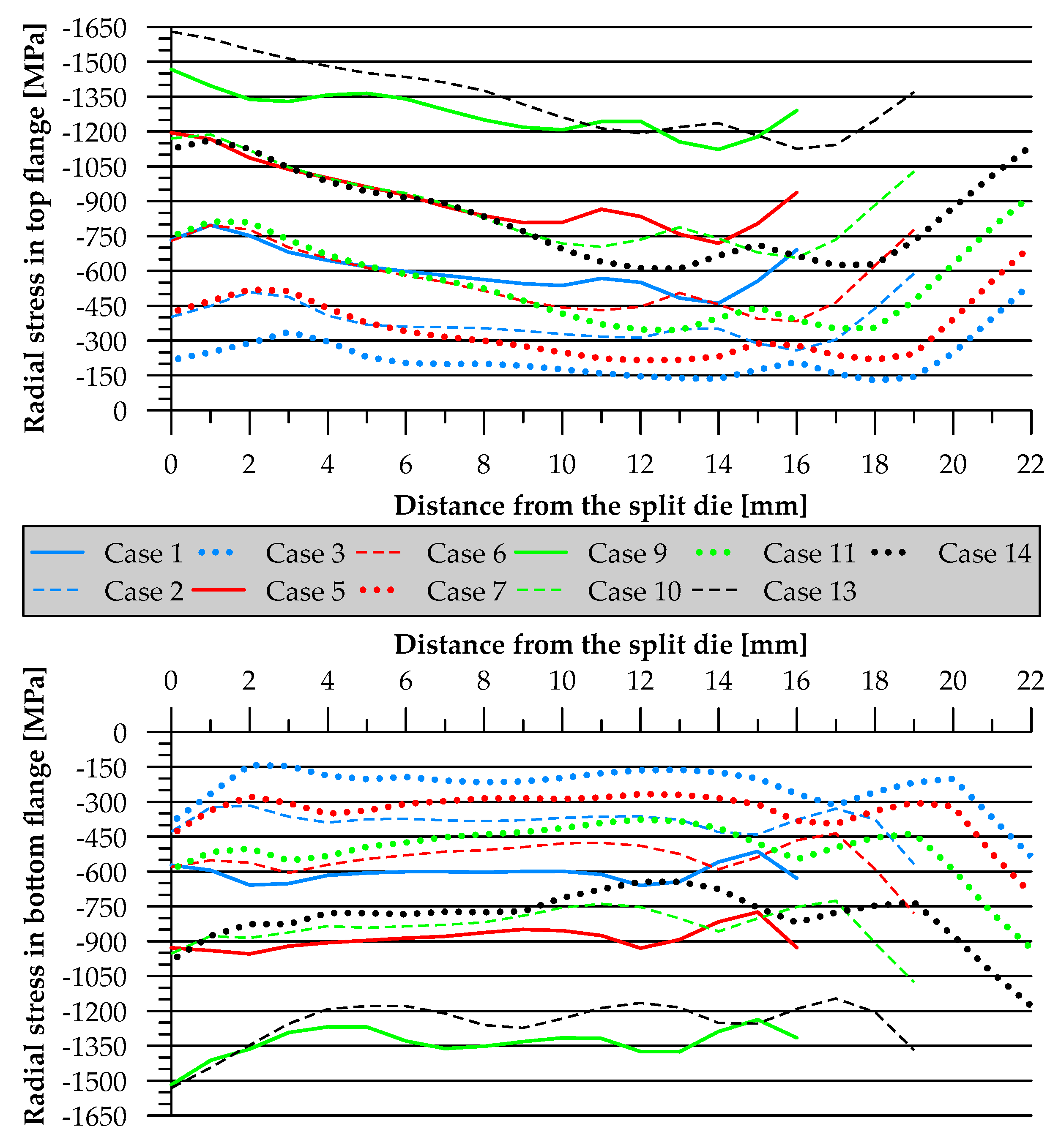
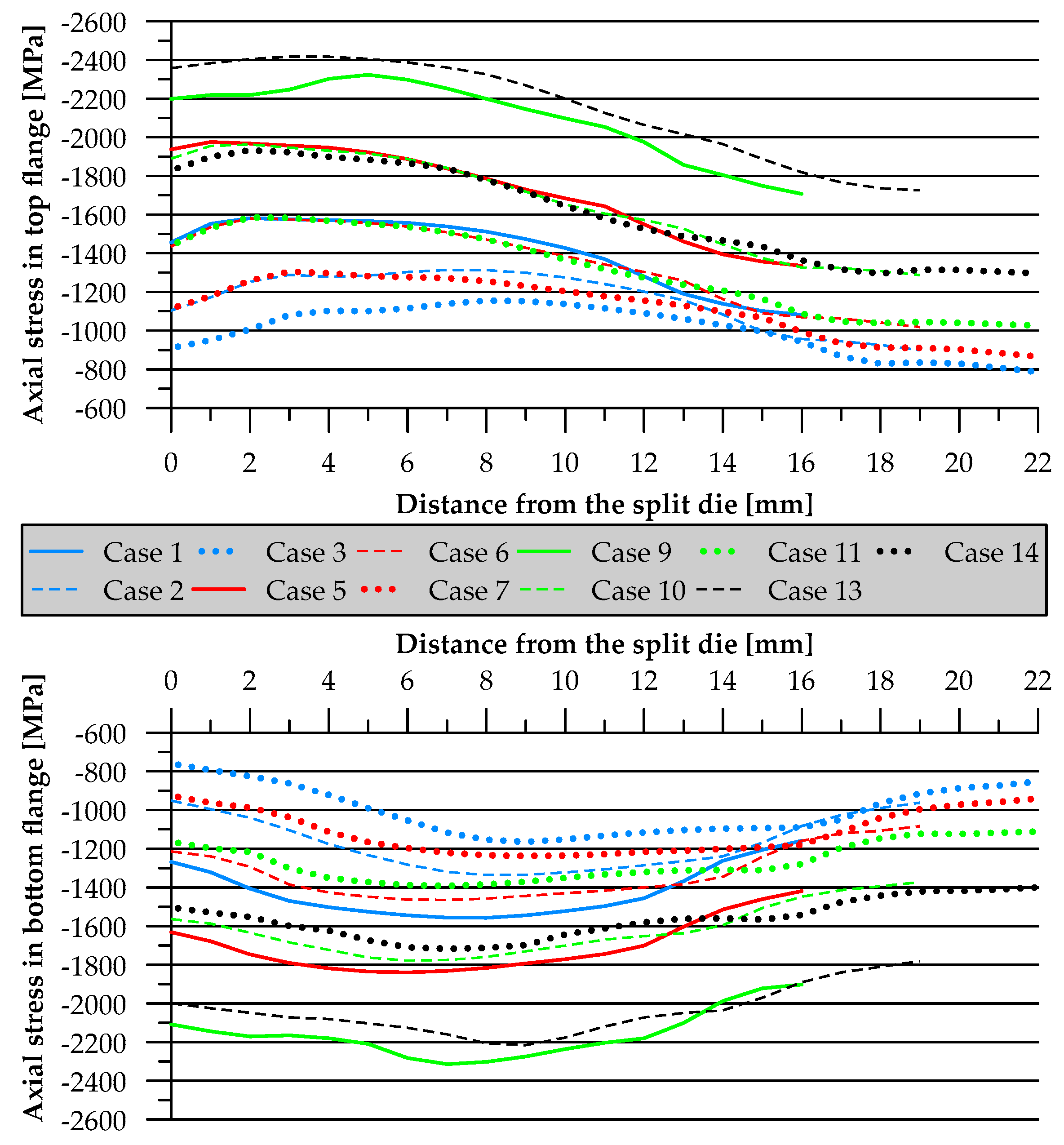
3. Results and Discussion
4. Conclusions
- The extrusion process conducted with two moving dies makes it possible to form two flanges simultaneously in one tool pass.
- The maximum achievable flange height is constrained by the possibility of contact loss between the workpiece and the mandrel; this can occur at the beginning of extrusion when only the punches are moving or when the dies are moving and flange height is increased.
- An analysis of the state of stresses at the beginning of the extrusion process, i.e., before the dies began to move, showed that the smaller the die impression height was, the lower the risk of workpiece/mandrel contact loss became.
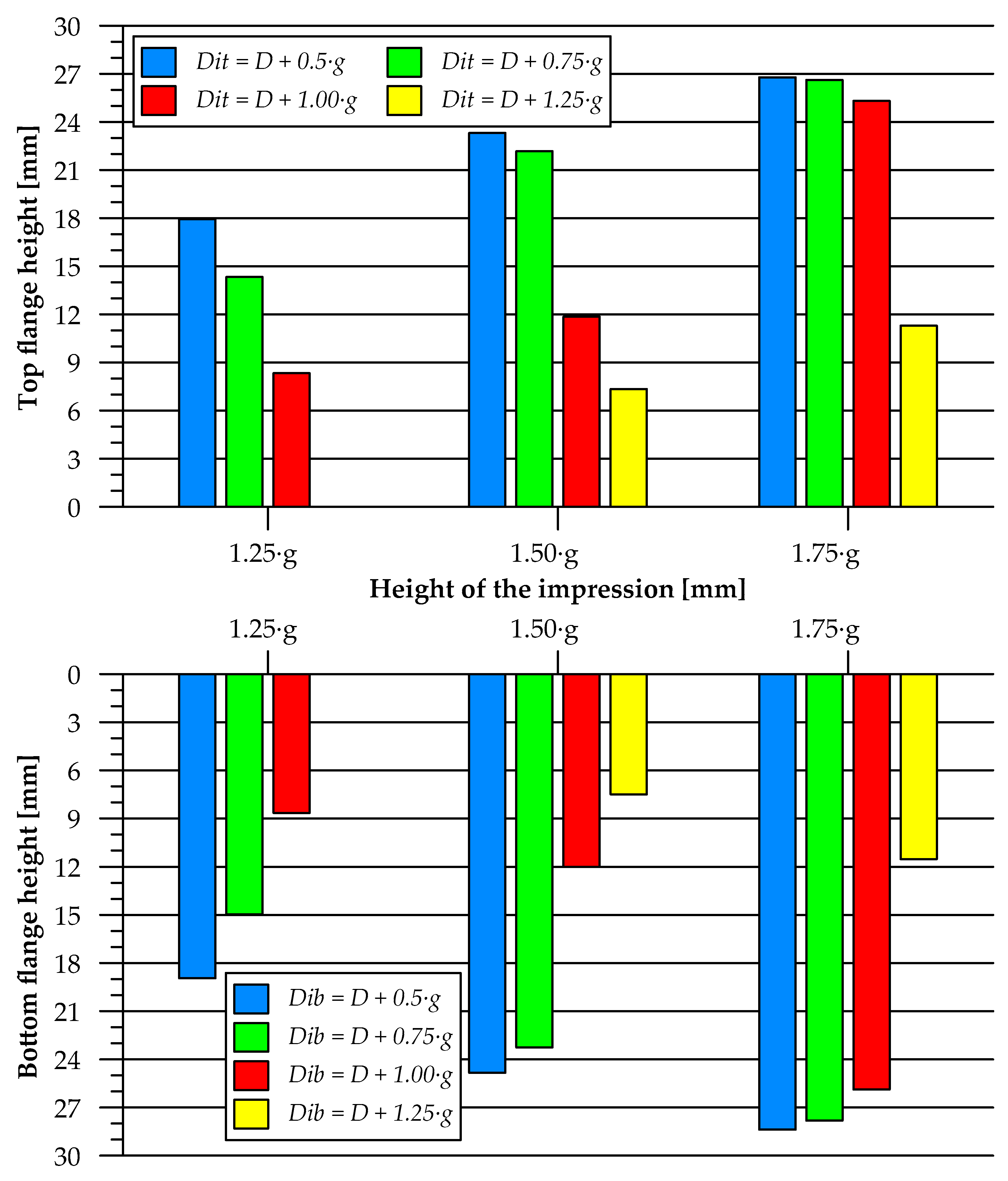
- The highest flanges were obtained for the cases of the extrusion process where the die impression diameter was greater than the outside diameter of the billet by 0.5 and 0.75 of its wall thickness and the impression height was 1.75 times the billet wall thickness.
- An increase in the die impression height led to an increase in the maximum flange height, while an increase in the die impression diameter caused a decrease in the maximum achievable flange height.
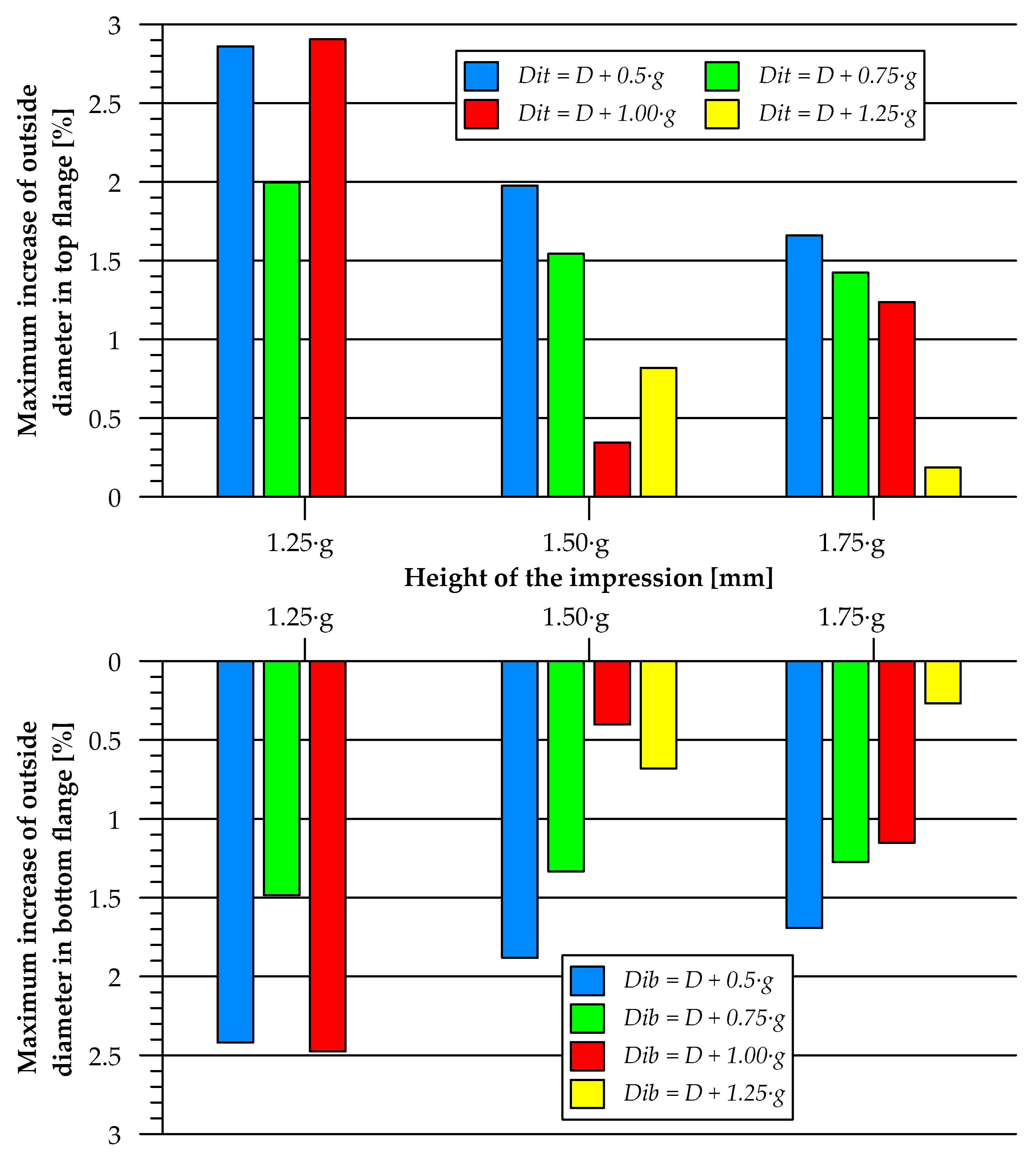
- An increase in the flange height caused a slight (below 3%) increase in the outside diameter of the flange; for higher die impression diameters, the maximum flange diameter increase was smaller, while an increase in the die impression height resulted in a smaller increase in the outside diameter of the flange.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ku, T.W.; Kang, B.S. Tool design for inner race cold forging with skew-type cross ball grooves. J. Mater. Process. Technol. 2014, 214, 1482–1502. [Google Scholar] [CrossRef]
- Ku, T.W.; Kang, B.S. Hardness-controlled tool fabrication and application to cold forging of inner race with skewed ball grooves. Int. J. Adv. Manuf. Technol. 2014, 74, 1337–1354. [Google Scholar] [CrossRef]
- Ku, T.W.; Kim, L.H.; Kang, B.S. Multi-stage cold forging and experimental investigation for the outer race of constant velocity joints. Mater. Design 2013, 49, 368–385. [Google Scholar] [CrossRef]
- Ku, T.W.; Kang, B.S. Tool design and experimental verification for multi-stage cold forging process of the outer race. Int. J. Precis. Eng. Man. 2014, 15, 1995–2004. [Google Scholar] [CrossRef]
- Chen, S.; Qin, Y.; Chen, J.G.; Choy, C.M. A forging method for reducing process steps in the forming of automotive fasteners. Int. J. Mech. Sci. 2018, 137, 1–14. [Google Scholar] [CrossRef]
- Ku, T.W. A study on two-stage cold forging for a drive shaft with internal spline and spur gear geometries. Metals 2018, 8, 953. [Google Scholar] [CrossRef]
- Ku, T.W. A combined cold extrusion for a drive shaft: A parametric study on tool geometry. Materials 2020, 13, 2244. [Google Scholar] [CrossRef]
- Schiemann, T.; Liewald, M.; Beiermeister, C.; Till, M. Influence of process chain on fold formation during flange upsetting of tubular cold forged parts. Procedia Eng. 2014, 81, 352–357. [Google Scholar] [CrossRef]
- Pang, H.; Lowrie, J.; Ngaile, G. Development of a non-isothermal forging process for hollow axle shafts. Procedia Engineer. 2017, 207, 454–459. [Google Scholar] [CrossRef]
- Pang, H.; Ngaile, G. Development of a non-isothermal forging process for hollow power transmission shafts. Procedia Manuf. 2018, 26, 1509–1516. [Google Scholar] [CrossRef]
- Pang, H.; Ngaile, G. Development of a non-isothermal forging process for hollow power transmission shafts. J. Manuf. Process. 2019, 47, 22–31. [Google Scholar] [CrossRef]
- Alves, L.M.; Afonso, R.M.; Silva, C.M.A.; Martins, P.A.F. Boss forming of annular flanges in thin-walled tubes. J. Mater. Process. Technol. 2017, 250, 182–189. [Google Scholar] [CrossRef]
- Malhotra, R.; Xue, L.; Belytschko, T.; Cao, J. Mechanics of fracture in single point incremental forming. J. Mater. Process. Technol. 2012, 212, 1573–1590. [Google Scholar] [CrossRef]
- Yang, C.; Wen, T.; Liu, L.T.; Zhang, S.; Wang, H. Dieless incremental hole-flanging of thin-walled tube for producing branched tubing. J. Mater. Process. Technol. 2014, 214, 2461–2467. [Google Scholar] [CrossRef]
- Hou, X.; Li, Y.; Xiao, X.; Qiu, X.; Yang, M.; Gao, X. Modeling and analysis of multi-pass progressive flanging force of copper tube end. Int. J. Adv. Manuf. Technol. 2022, 121, 4703–4712. [Google Scholar] [CrossRef]
- Cao, T.; Lu, B.; Ou, H.; Long, H.; Chen, J. Investigation on a new hole-flanging approach by incremental sheet forming through a featured tool. Int. J. Mach. Tool. Manu. 2016, 110, 1–17. [Google Scholar] [CrossRef]
- Alves, L.M.; Gameiro, J.; Silva, C.M.A.; Martins, P.A.F. Sheet-bulk forming of tubes for joining applications. J. Mater. Process. Technol. 2017, 240, 154–161. [Google Scholar] [CrossRef]
- Alves, L.M.; Afonso, R.M.; Silva, C.M.A.; Martins, P.A.F. Joining tubes to sheets by boss forming and upsetting. J. Mater. Process. Technol. 2018, 252, 773–781. [Google Scholar] [CrossRef]
- Zhu, S.; Zhuang, X.; Xu, D.; Zhu, Y.; Zhao, Z. Flange forming at an arbitrary tube location through upsetting with a controllable deformation zone. J. Mater. Process. Technol. 2019, 273, 116230. [Google Scholar] [CrossRef]
- Zhu, S.; Zhuang, X.; Yang, Y.; Zhu, Y.; Zhao, Z. Investigation of a tailored blank for the elimination of forging laps during cup sidewall upsetting. Int. J. Adv. Manuf. Technol. 2020, 109, 2311–2324. [Google Scholar] [CrossRef]
- Zhuang, X.; Liang, M.; Zhu, S.; Zhu, Y.; Zhao, Z. Sheet bulk forming of thin-walled components with external gearing through upsetting using controllable deformation zone method. Chin. J. Mech. Eng. 2021, 34, 138. [Google Scholar] [CrossRef]
- Zhu, S.; Zhuang, X.; Zhu, Y.; Zhao, Z. Thickening of cup sidewall through sheet-bulk forming with controllable deformation zone. J. Mater. Process. Technol. 2018, 262, 597–604. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, S.; Zhuang, X.; Zhao, Z. Die structure optimization for eliminating premature folding of sidewall upsetting with a controllable deformation zone. Int. J. Adv. Manuf. Technol. 2019, 105, 1411–1424. [Google Scholar] [CrossRef]
- Winiarski, G.; Gontarz, A. Numerical and experimental study of producing two-step flanges by extrusion with a movable sleeve. Arch. Metall. Mater. 2017, 62, 495–499. [Google Scholar] [CrossRef]
- Winiarski, G.; Bulzak, T.A.; Wójcik, Ł.; Szala, M. Effect of tool kinematics on tube flanging by extrusion with a moving sleeve. Adv. Sci. Technol. Res. J. 2019, 13, 210–216. [Google Scholar] [CrossRef] [PubMed]
- Winiarski, G.; Bulzak, T.A.; Wójcik, Ł.; Szala, M. A new method of flanges extrusion in hollow products—Analysis of the limiting phenomena. Adv. Sci. Technol. Res. J. 2020, 14, 78–85. [Google Scholar] [CrossRef]
- Winiarski, G. Theoretical and experimental study on the effect of selected parameters in a new method of extrusion with a movable sleeve. Materials 2022, 15, 4585. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.C.; Liu, C.H. The study of multi-stage cold forming process for the manufacture of relief valve regulating nuts. Appl. Sci. 2023, 13, 6299. [Google Scholar] [CrossRef]
- Wan, N.; He, Q.; Jing, X.; Jiang, Y.; Zhou, H. Numerical and experimental investigation of the effect of cold extrusion process on residual stress and fatigue life of internal thread of high-strength steel. Int. J. Adv. Manuf. Technol. 2023, 127, 4713–4726. [Google Scholar] [CrossRef]

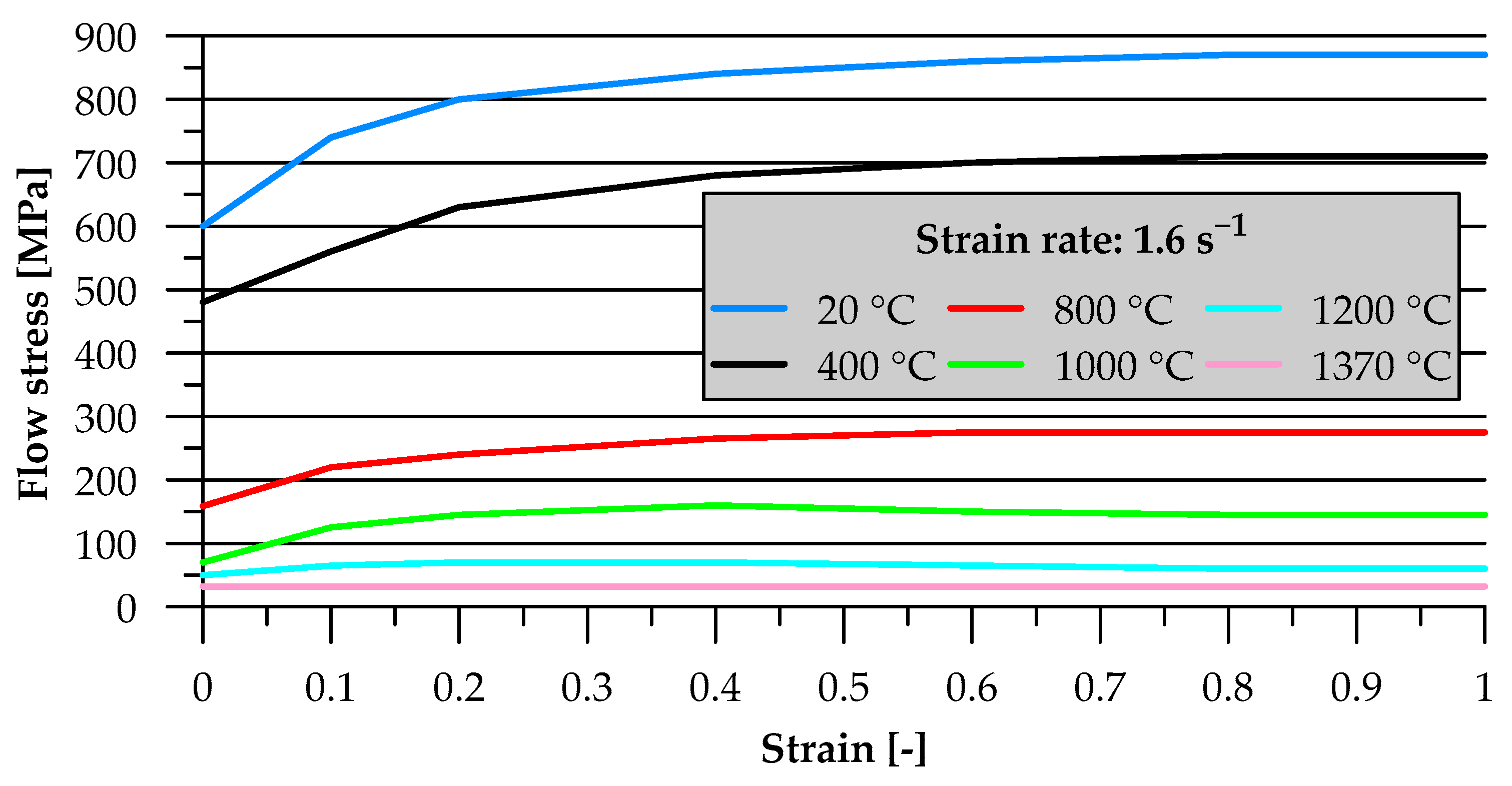
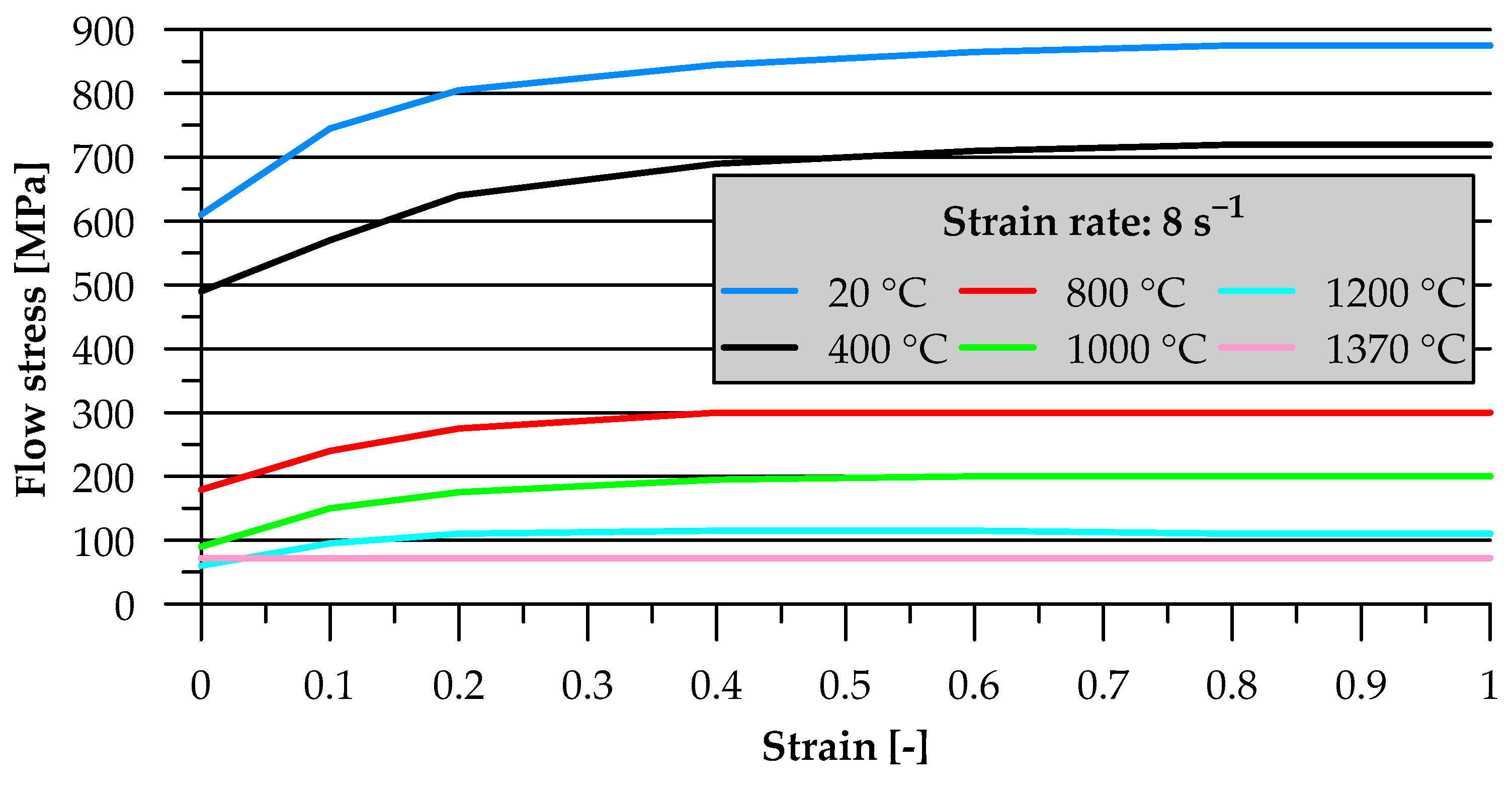
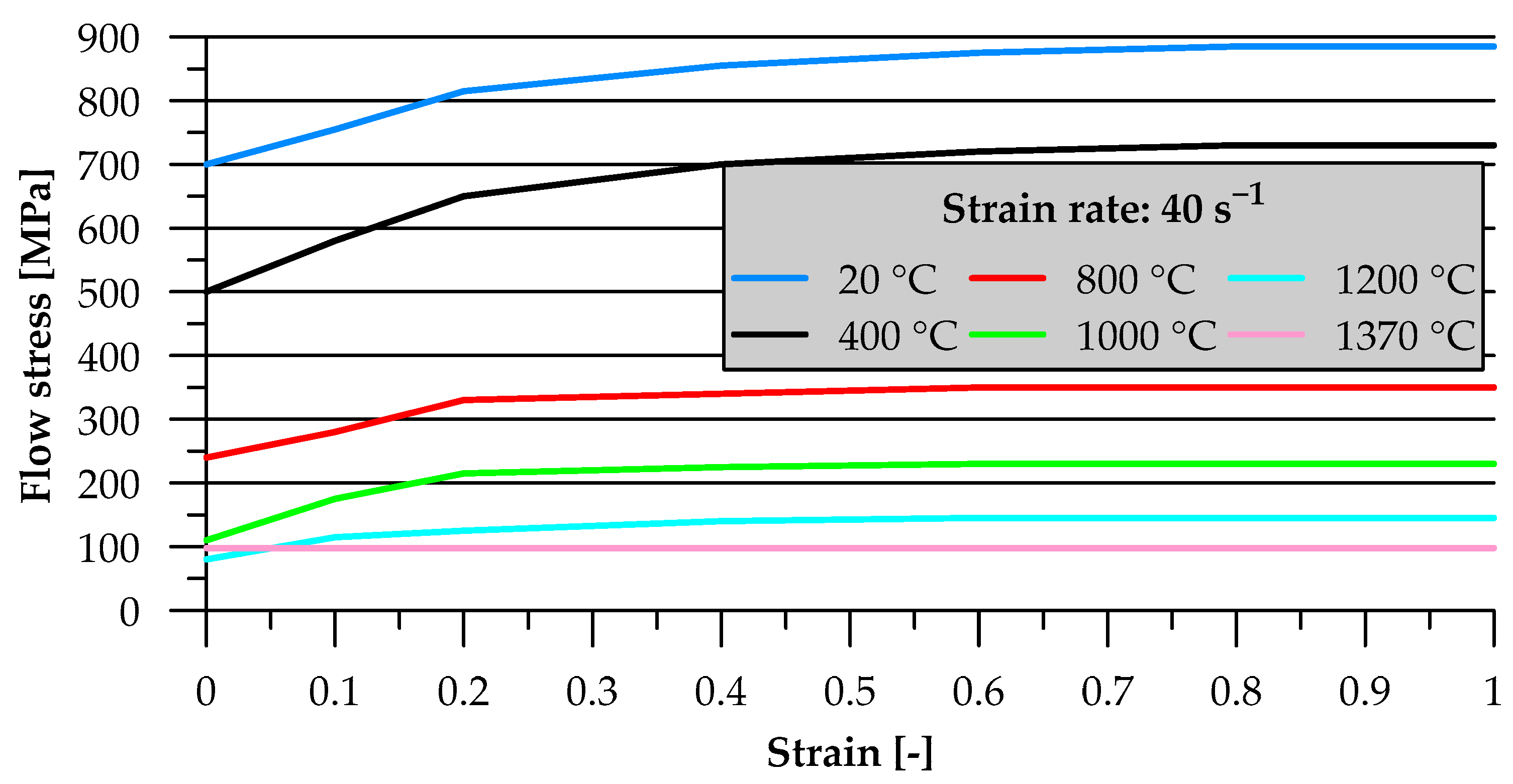
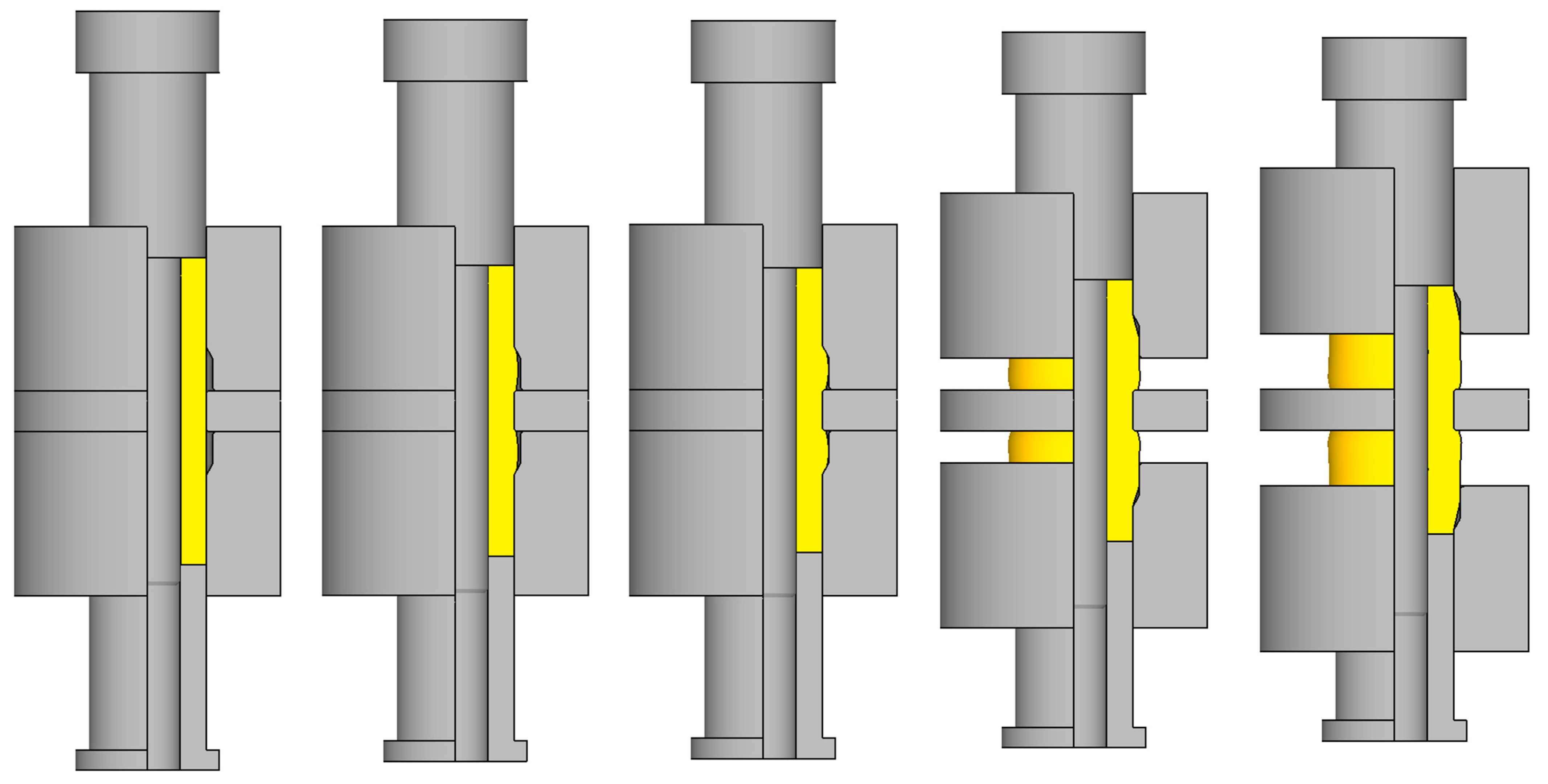
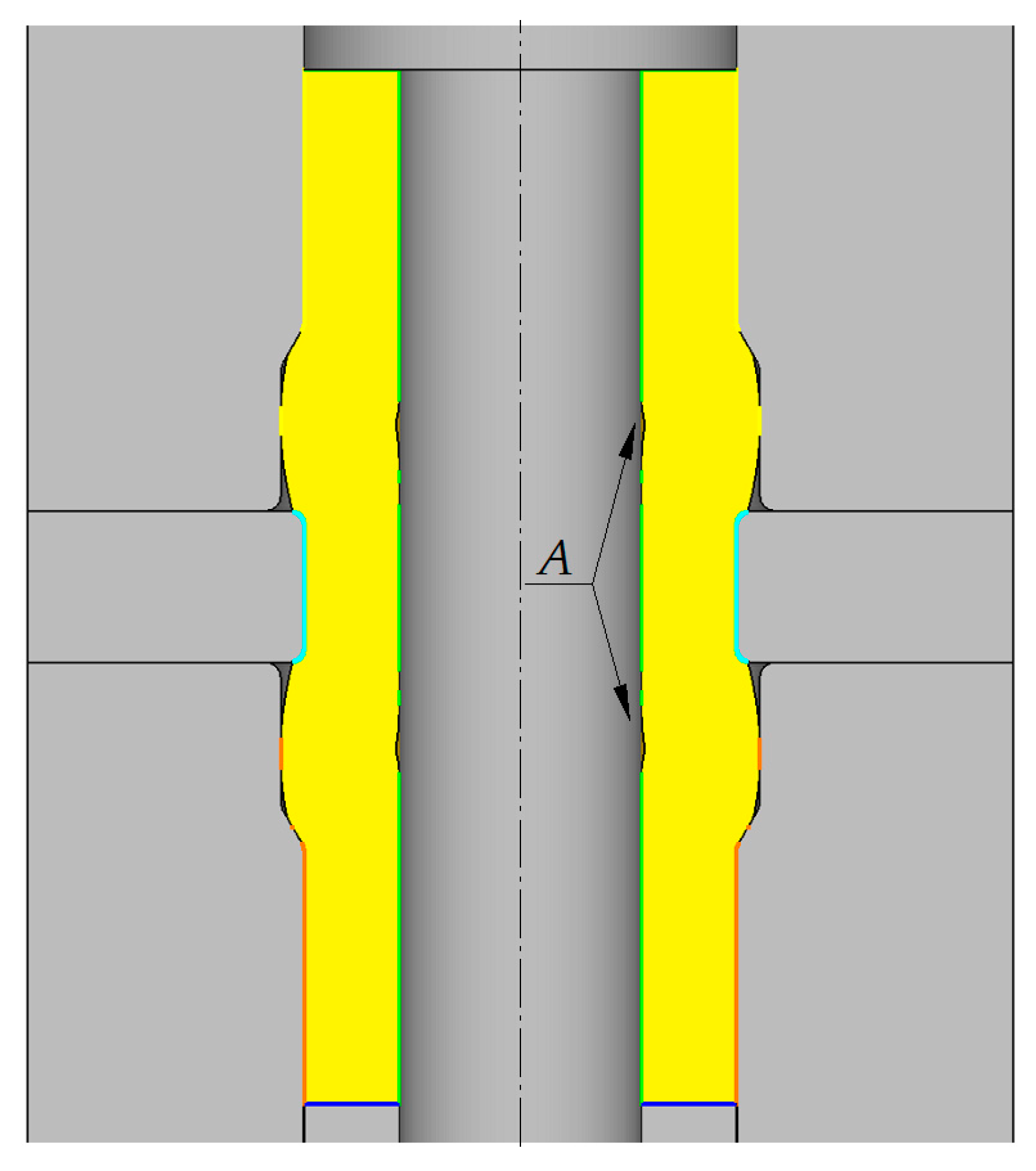
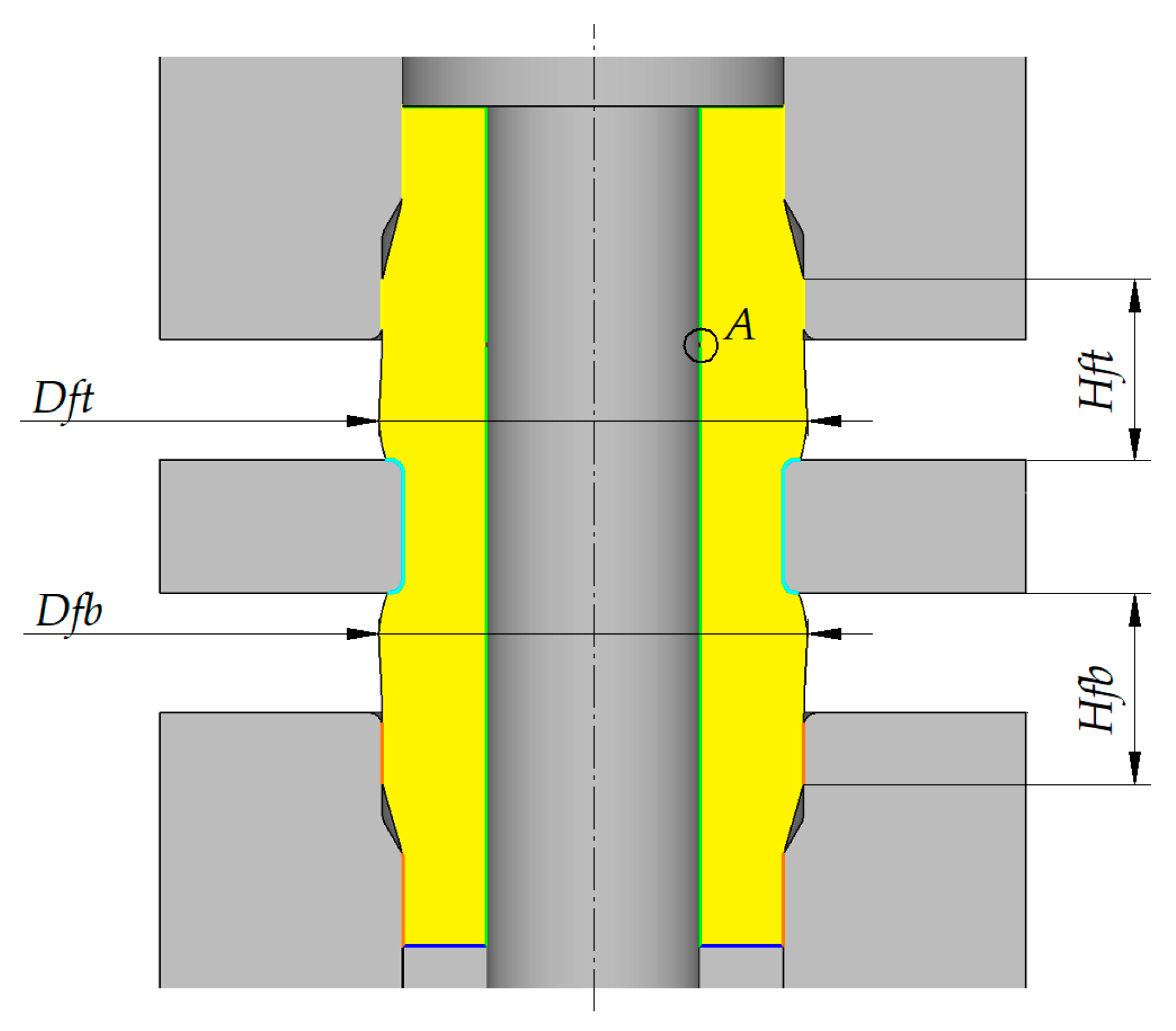



| Dimension | Unit | Value |
|---|---|---|
| L | mm | 150 |
| Lt | mm | 65 |
| Lb | mm | 65 |
| g | mm | 12.5 |
| D | mm | 57 |
| Rt | mm | 2 |
| Rb | mm | 2 |
| αt | degree | 30 |
| αb | degree | 30 |
| υpt | mm/s | 10 |
| υpb | mm/s | 10 |
| υct | mm/s | according to Equation (1) |
| υcb | mm/s | according to Equation (2) |
| Case Number | Dit = Dib Equation | Ht = Hb Equation | Dit = Dib Value [mm] | Ht = Hb Value [mm] |
|---|---|---|---|---|
| Case 1 | D + 0.50∙g | 1.25∙g | 63.25 | 15.63 |
| Case 2 | D + 0.50∙g | 1.50∙g | 63.25 | 18.75 |
| Case 3 | D + 0.50∙g | 1.75∙g | 63.25 | 21.88 |
| Case 4 | D + 0.50∙g | 2.00∙g | 63.25 | 25.00 |
| Case 5 | D + 0.75∙g | 1.25∙g | 66.38 | 15.63 |
| Case 6 | D + 0.75∙g | 1.50∙g | 66.38 | 18.75 |
| Case 7 | D + 0.75∙g | 1.75∙g | 66.38 | 21.88 |
| Case 8 | D + 0.75∙g | 2.00∙g | 66.38 | 25.00 |
| Case 9 | D + 1.00∙g | 1.25∙g | 69.50 | 15.63 |
| Case 10 | D + 1.00∙g | 1.50∙g | 69.50 | 18.75 |
| Case 11 | D + 1.00∙g | 1.75∙g | 69.50 | 21.88 |
| Case 12 | D + 1.00∙g | 2.00∙g | 69.50 | 25.00 |
| Case 13 | D + 1.25∙g | 1.50∙g | 72.63 | 18.75 |
| Case 14 | D + 1.25∙g | 1.75∙g | 72.63 | 21.88 |
| Case 15 | D + 1.25∙g | 2.00∙g | 72.63 | 25.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winiarski, G.; Gontarz, A.; Skrzat, A.; Wójcik, M.; Wencel, S. Analysis of a New Process for Forming Two Flanges Simultaneously in a Hollow Part by Extrusion with Two Moving Dies. Metals 2024, 14, 612. https://doi.org/10.3390/met14060612
Winiarski G, Gontarz A, Skrzat A, Wójcik M, Wencel S. Analysis of a New Process for Forming Two Flanges Simultaneously in a Hollow Part by Extrusion with Two Moving Dies. Metals. 2024; 14(6):612. https://doi.org/10.3390/met14060612
Chicago/Turabian StyleWiniarski, Grzegorz, Andrzej Gontarz, Andrzej Skrzat, Marta Wójcik, and Sylwia Wencel. 2024. "Analysis of a New Process for Forming Two Flanges Simultaneously in a Hollow Part by Extrusion with Two Moving Dies" Metals 14, no. 6: 612. https://doi.org/10.3390/met14060612
APA StyleWiniarski, G., Gontarz, A., Skrzat, A., Wójcik, M., & Wencel, S. (2024). Analysis of a New Process for Forming Two Flanges Simultaneously in a Hollow Part by Extrusion with Two Moving Dies. Metals, 14(6), 612. https://doi.org/10.3390/met14060612








