Crystal Plasticity Modeling of Dislocation Density Evolution in Cellular Dislocation Structures
Abstract
:1. Introduction
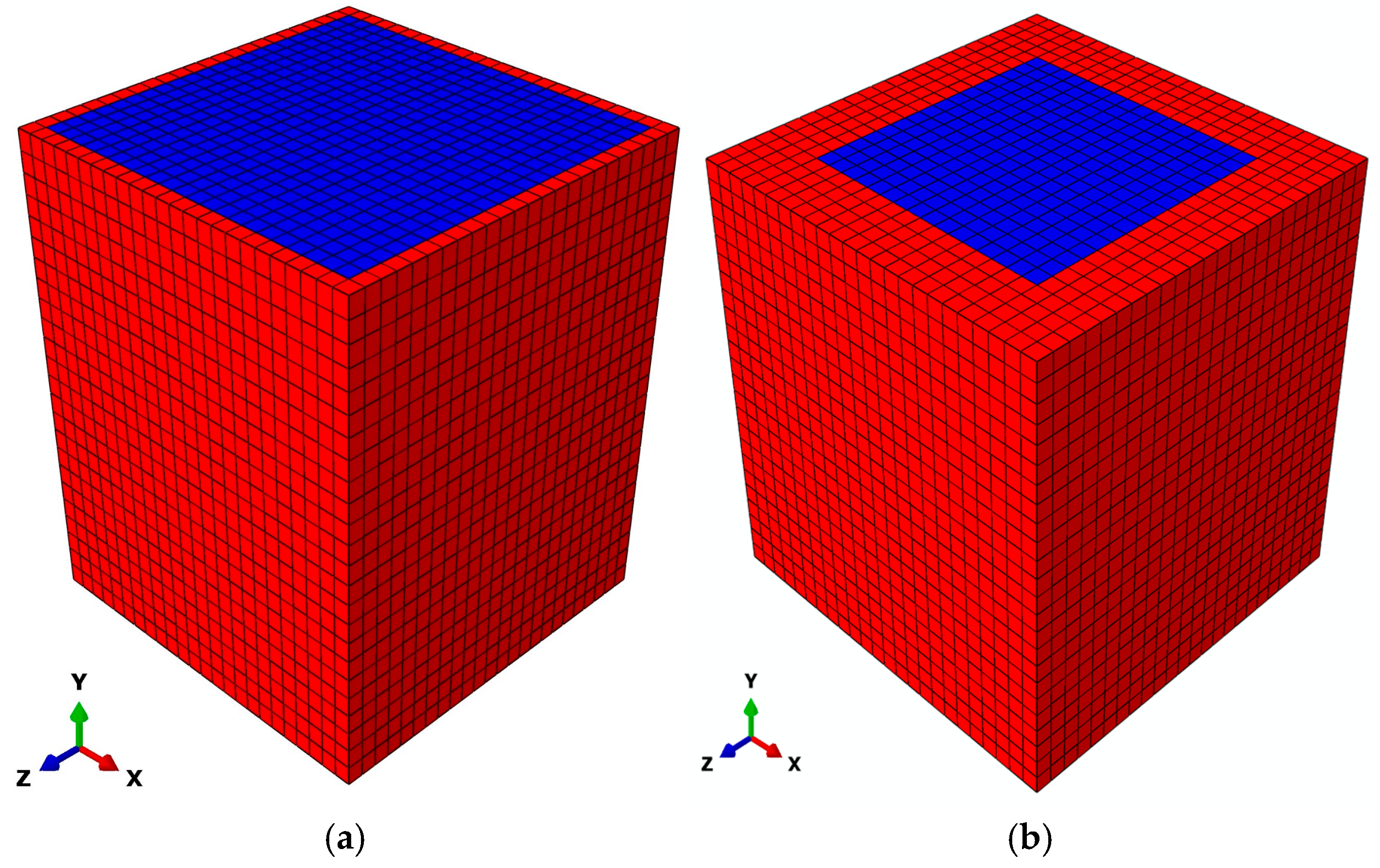
2. Methods
3. Results and Discussion
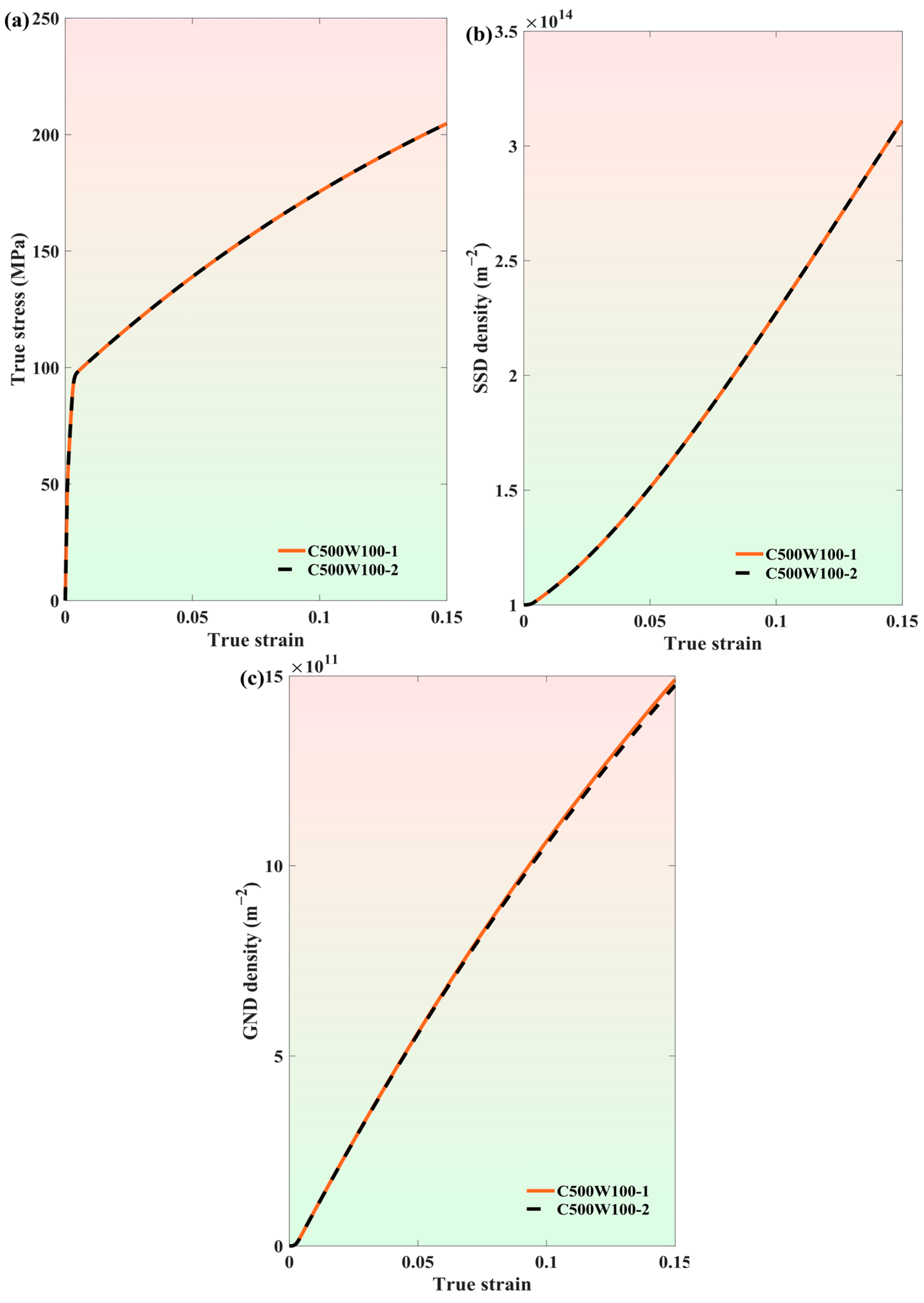
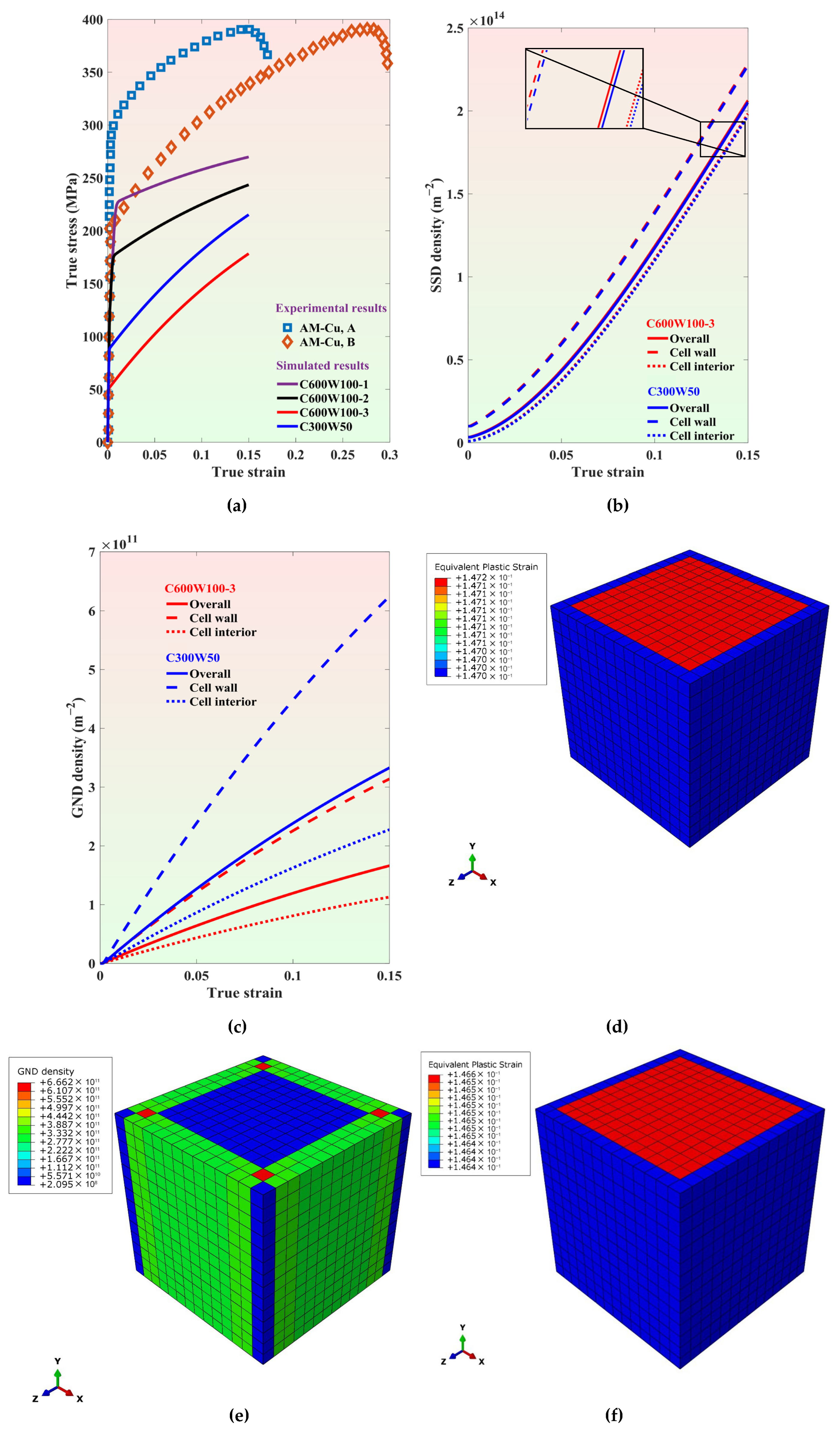
3.1. Mesh Sensitivity
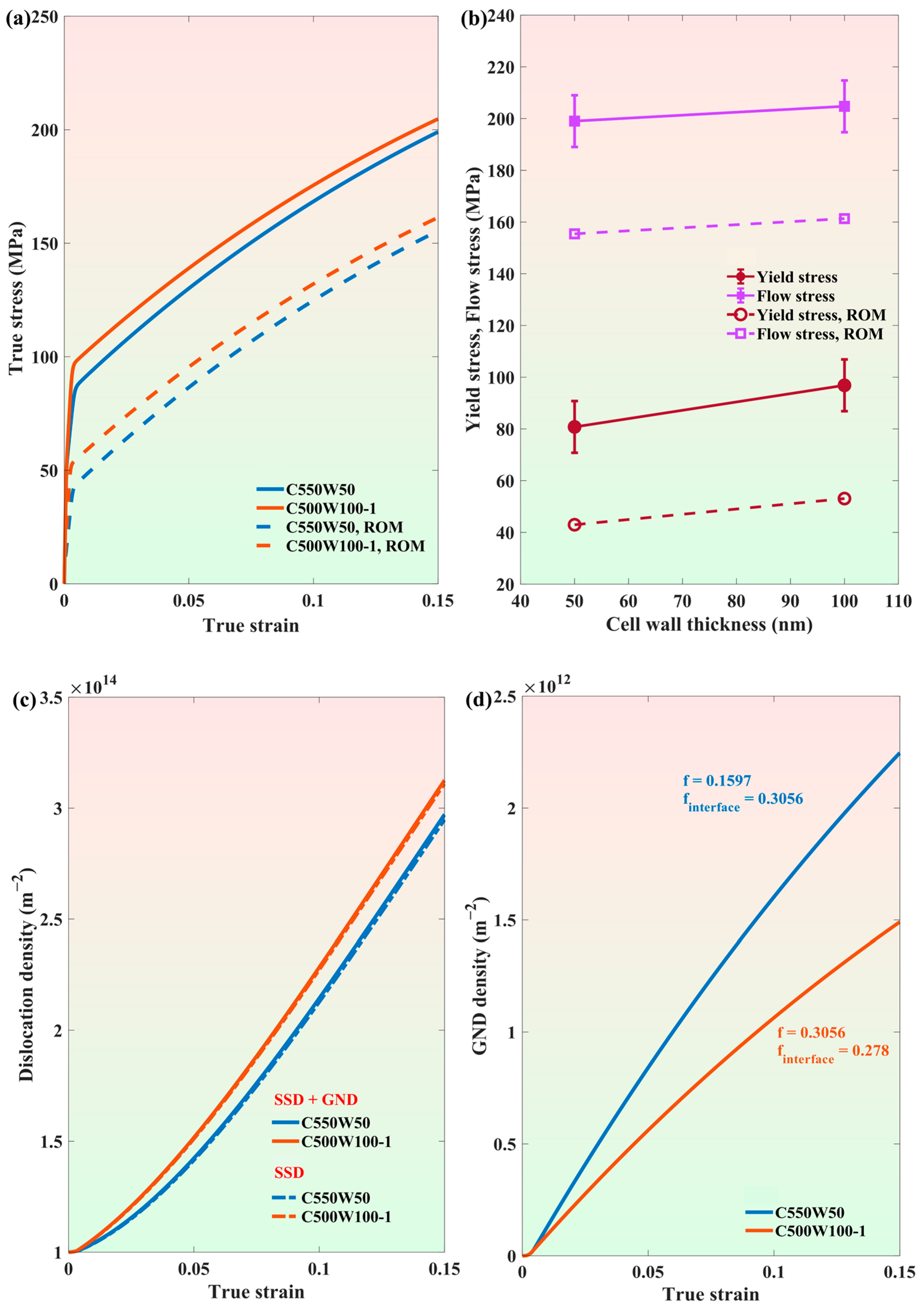
3.2. Effect of Cell Structure on Mechanical Response
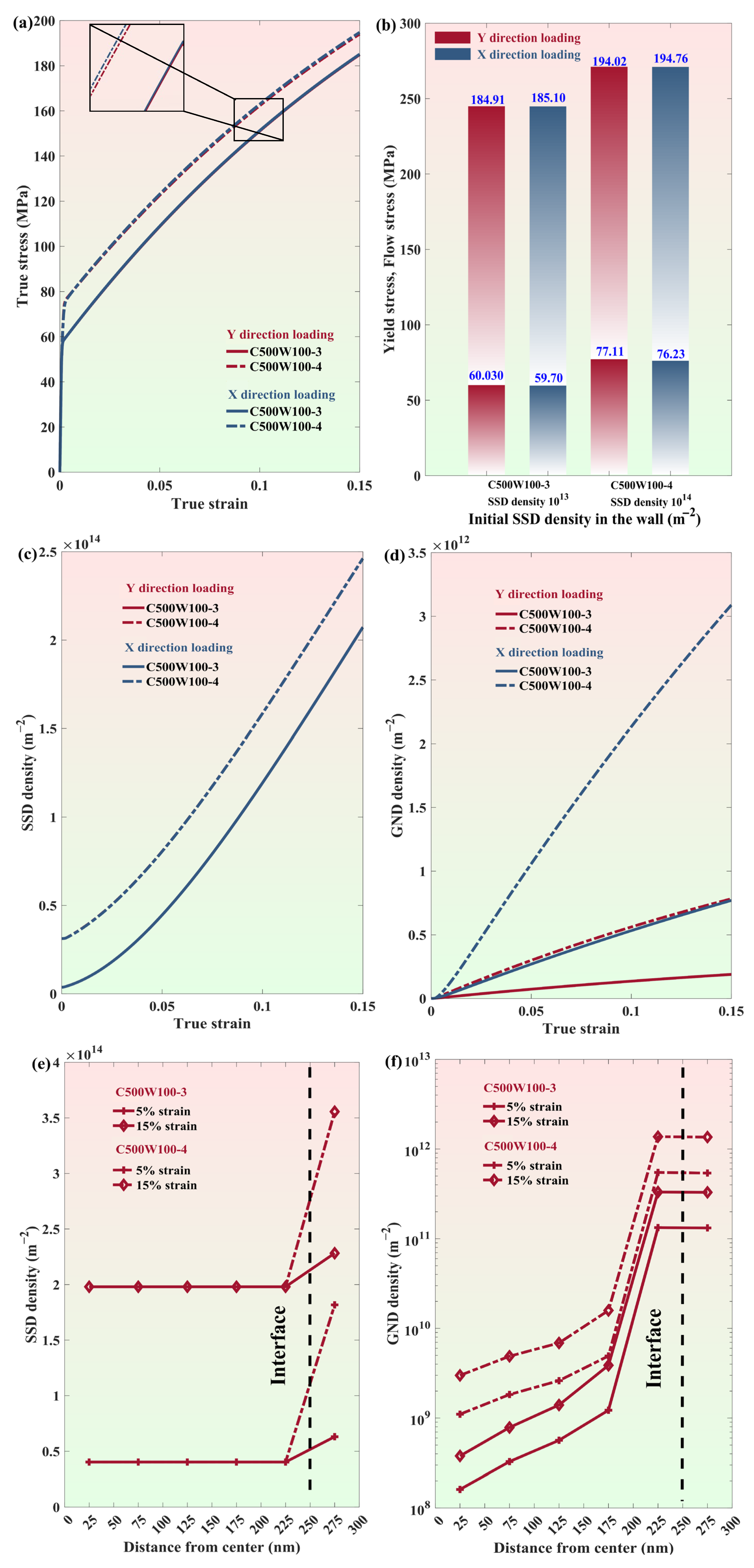
3.3. Impact of Initial Dislocation Density on Yield and Flow Stress
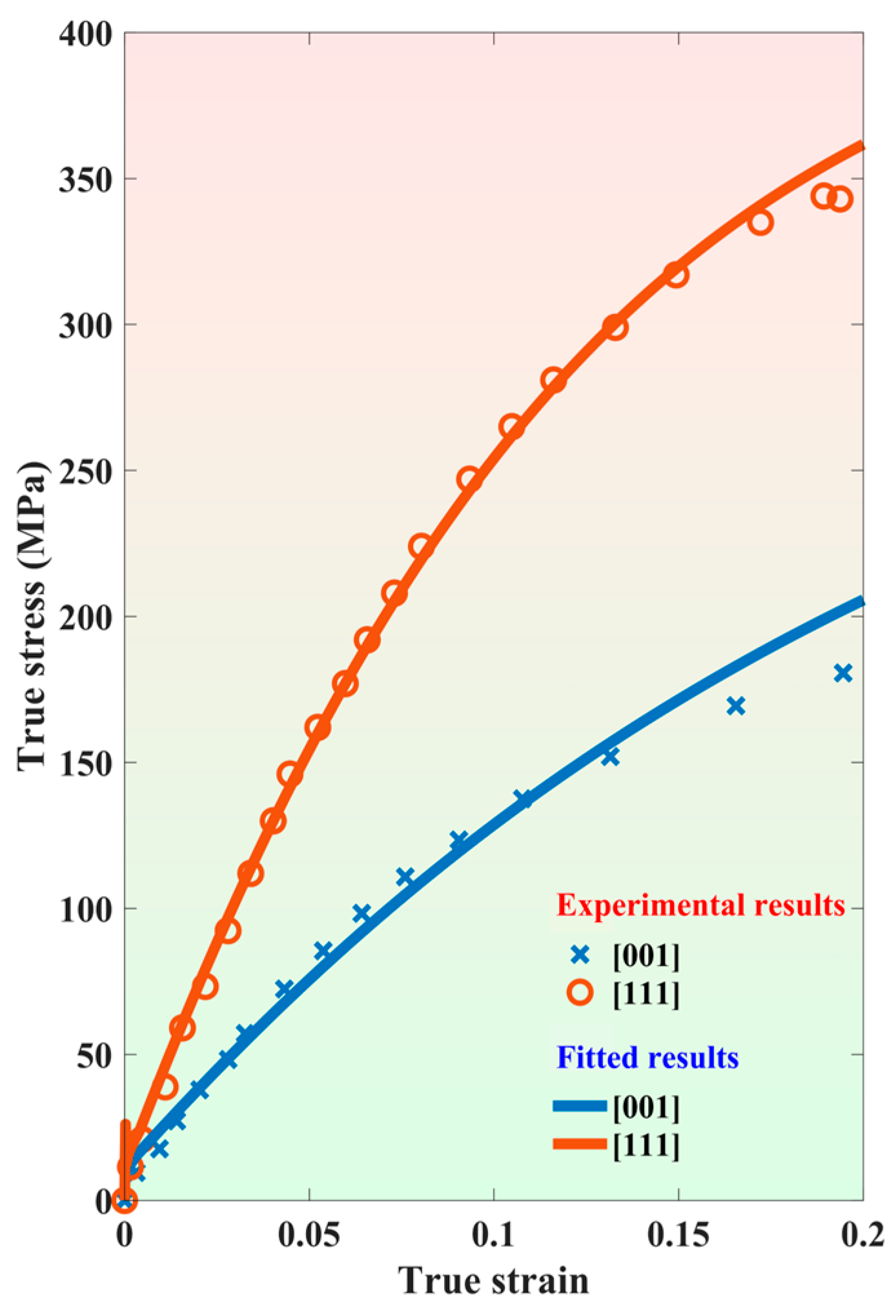
3.4. Anisotropy
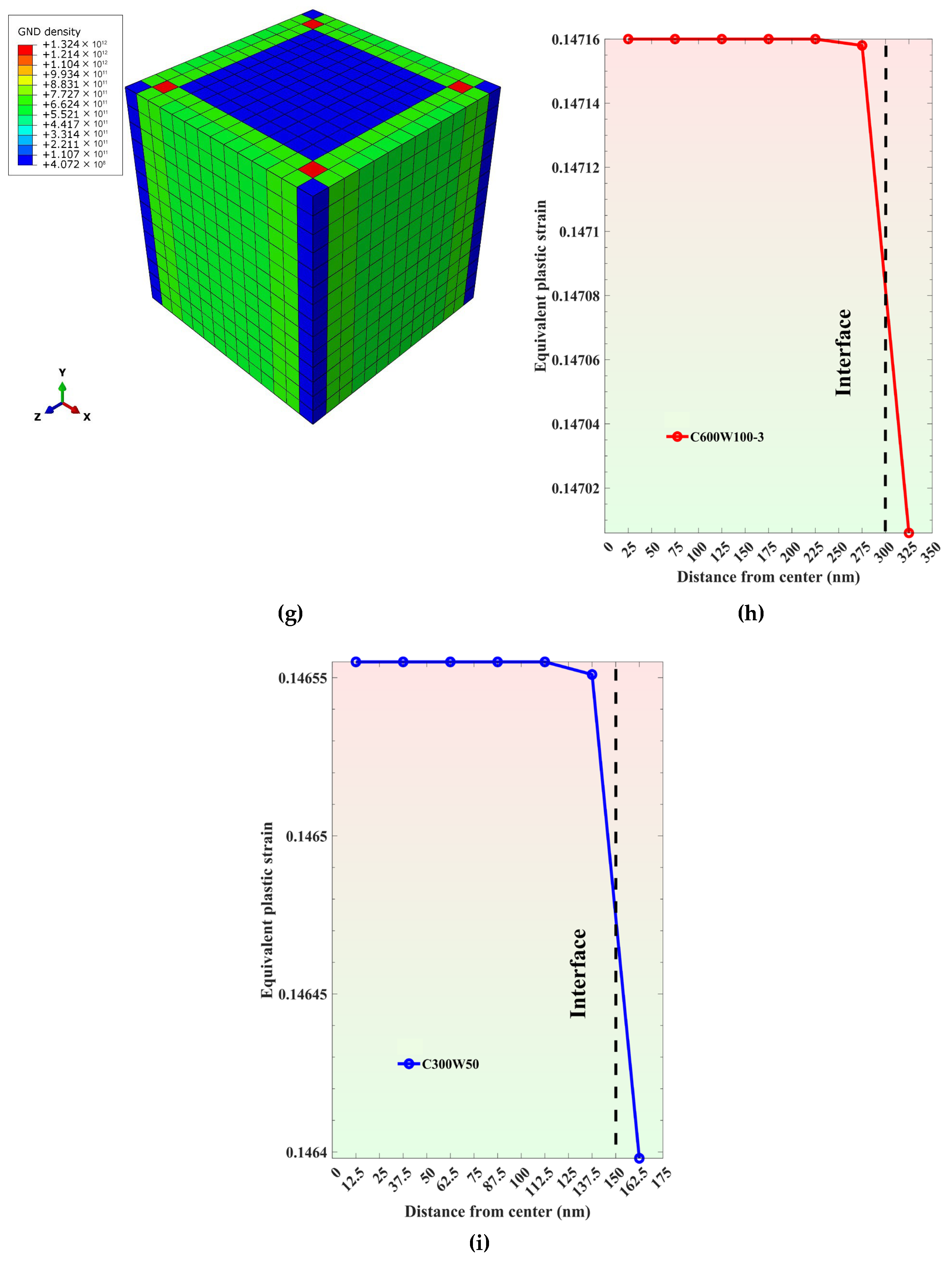
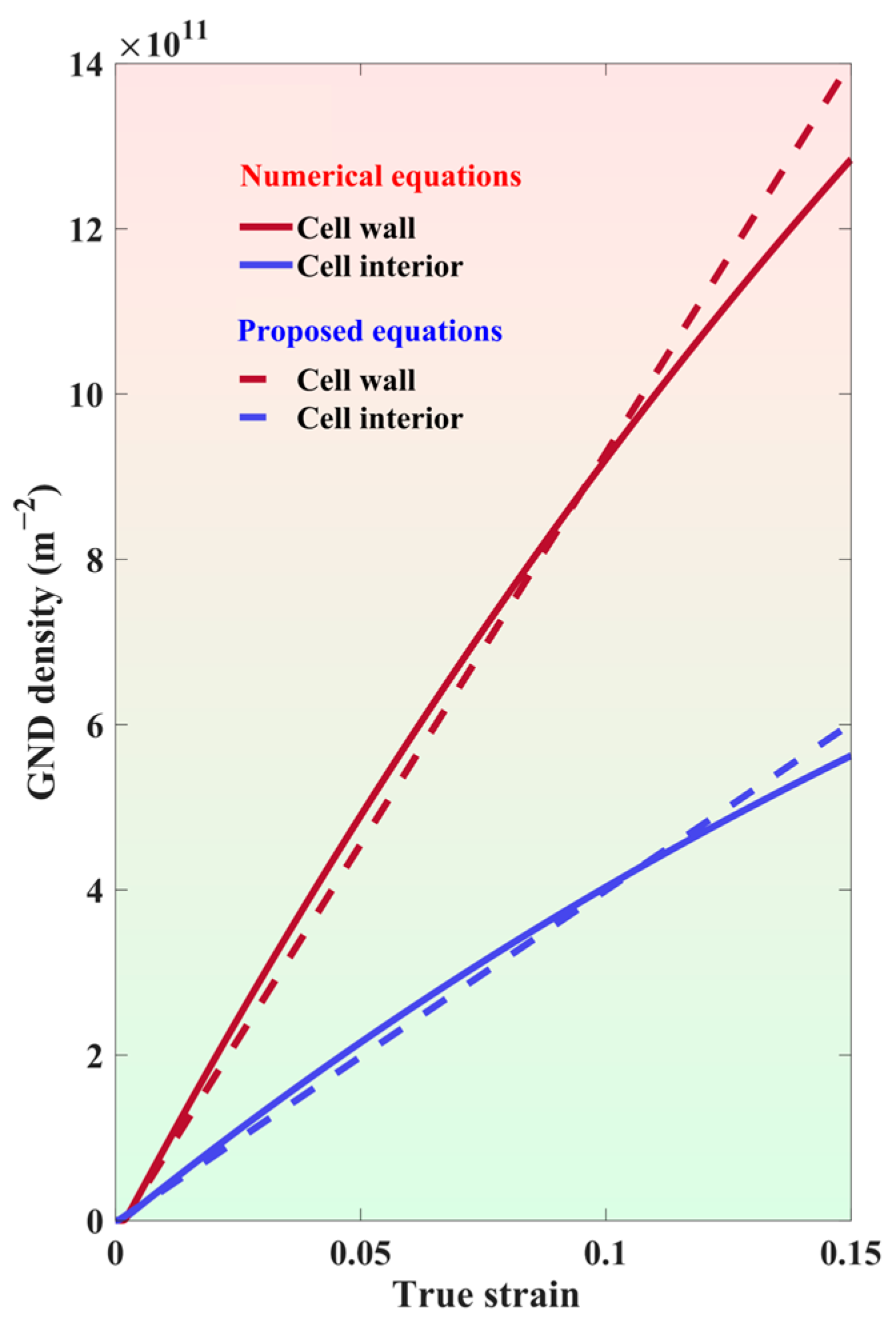
3.5. Quantifying GND
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lewandowski, J.J.; Seifi, M. Metal Additive Manufacturing: A Review of Mechanical Properties. Annu. Rev. Mater. Res. 2016, 46, 151–186. [Google Scholar] [CrossRef]
- Frazier, W.E. Metal additive manufacturing: A review. J. Mater. Eng. Perform. 2014, 23, 1917–1928. [Google Scholar] [CrossRef]
- Niendorf, T.; Leuders, S.; Riemer, A.; Richard, H.A.; Tröster, T.; Schwarze, D. Highly anisotropic steel processed by selective laser melting. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2013, 44, 794–796. [Google Scholar] [CrossRef]
- Kwon, J.; Karthik, G.M.; Estrin, Y.; Kim, H.S. Constitutive modeling of cellular-structured metals produced by additive manufacturing. Acta Mater. 2022, 241, 118421. [Google Scholar] [CrossRef]
- Prashanth, K.G.; Eckert, J. Formation of metastable cellular microstructures in selective laser melted alloys. J. Alloys Compd. 2017, 707, 27–34. [Google Scholar] [CrossRef]
- Bajaj, P.; Hariharan, A.; Kini, A.; Kürnsteiner, P.; Raabe, D.; Jägle, E.A. Steels in additive manufacturing: A review of their microstructure and properties. Mater. Sci. Eng. A 2020, 772, 138633. [Google Scholar] [CrossRef]
- Liu, L.; Ding, Q.; Zhong, Y.; Zou, J.; Wu, J.; Chiu, Y.L.; Li, J.; Zhang, Z.; Yu, Q.; Shen, Z. Dislocation network in additive manufactured steel breaks strength–ductility trade-off. Mater. Today 2018, 21, 354–361. [Google Scholar] [CrossRef]
- Shamsujjoha, M.; Agnew, S.R.; Fitz-Gerald, J.M.; Moore, W.R.; Newman, T.A. High Strength and Ductility of Additively Manufactured 316L Stainless Steel Explained. Metall. Mater. Trans. A 2018, 49, 3011–3027. [Google Scholar] [CrossRef]
- Sun, Z.; Tan, X.; Tor, S.B.; Chua, C.K. Simultaneously enhanced strength and ductility for 3D-printed stainless steel 316L by selective laser melting. NPG Asia Mater. 2018, 10, 127–136. [Google Scholar] [CrossRef]
- Nes, E. Modelling of work hardening and stress saturation in FCC metals. Prog. Mater. Sci. 1997, 41, 129–193. [Google Scholar] [CrossRef]
- Nes, E.; Marthinsen, K. Modeling the evolution in microstructure and properties during plastic deformation of f.c.c.-metals and alloys—An approach towards a unified model. Mater. Sci. Eng. A 2002, 322, 176–193. [Google Scholar] [CrossRef]
- Pinomaa, T.; Lindroos, M.; Walbrühl, M.; Provatas, N.; Laukkanen, A. The significance of spatial length scales and solute segregation in strengthening rapid solidification microstructures of 316L stainless steel. Acta Mater. 2020, 184, 1–16. [Google Scholar] [CrossRef]
- Bronkhorst, C.A.; Mayeur, J.R.; Livescu, V.; Pokharel, R.; Brown, D.W.; Gray, G.T. Structural representation of additively manufactured 316L austenitic stainless steel. Int. J. Plast. 2019, 118, 70–86. [Google Scholar] [CrossRef]
- Shimanek, J.D.; Liu, Z.K.; Beese, A.M. Effects of misorientation on single crystal plasticity by finite element methods. Comput. Mater. Sci. 2024, 237, 112879. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Thamburaja, P.; Anand, L. Polycrystalline shape-memory materials: Effect of crystallographic texture. J. Mech. Phys. Solids 2001, 49, 709–737. [Google Scholar] [CrossRef]
- Salem, A.A.; Kalidindi, S.R.; Semiatin, S.L. Strain hardening due to deformation twinning in α-titanium: Constitutive relations and crystal-plasticity modeling. Acta Mater. 2005, 53, 3495–3502. [Google Scholar] [CrossRef]
- Sedighiani, K.; Traka, K.; Roters, F.; Raabe, D.; Sietsma, J.; Diehl, M. Determination and analysis of the constitutive parameters of temperature-dependent dislocation-density-based crystal plasticity models. Mech. Mater. 2022, 164, 104117. [Google Scholar] [CrossRef]
- Kergaßner, A.; Mergheim, J.; Steinmann, P. Modeling of additively manufactured materials using gradient-enhanced crystal plasticity. Comput. Math. Appl. 2019, 78, 2338–2350. [Google Scholar] [CrossRef]
- Galera-Rueda, C.; Nieto-Valeiras, E.; Gardon, M.; Pérez-Prado, M.T.; LLorca, J. Effect of ZrH2 particles on the microstructure and mechanical properties of IN718 manufactured by selective laser melting. Mater. Sci. Eng. A 2021, 813, 141123. [Google Scholar] [CrossRef]
- Zhang, X.X.; Knoop, D.; Andrä, H.; Harjo, S.; Kawasaki, T.; Lutz, A.; Lahres, M. Multiscale constitutive modeling of additively manufactured Al–Si–Mg alloys based on measured phase stresses and dislocation density. Int. J. Plast. 2021, 140, 102972. [Google Scholar] [CrossRef]
- Li, Z.; Li, Z.; Tan, Z.; Xiong, D.-B.; Guo, Q. Stress relaxation and the cellular structure-dependence of plastic deformation in additively manufactured AlSi10Mg alloys. Int. J. Plast. 2020, 127, 102640. [Google Scholar] [CrossRef]
- Estrin, Y.; Mecking, H. A unified phenomenological description of work hardening and creep based on one-parameter models. Acta Metall. 1984, 32, 57–70. [Google Scholar] [CrossRef]
- Ghorbanpour, S.; Alam, M.E.; Ferreri, N.C.; Kumar, A.; McWilliams, B.A.; Vogel, S.C.; Bicknell, J.; Beyerlein, I.J.; Knezevic, M. Experimental characterization and crystal plasticity modeling of anisotropy, tension-compression asymmetry, and texture evolution of additively manufactured Inconel 718 at room and elevated temperatures. Int. J. Plast. 2020, 125, 63–79. [Google Scholar] [CrossRef]
- Biswas, A.; Prasad, M.R.G.; Vajragupta, N.; ul Hassan, H.; Brenne, F.; Niendorf, T.; Hartmaier, A. Influence of Microstructural Features on the Strain Hardening Behavior of Additively Manufactured Metallic Components. Adv. Eng. Mater. 2019, 21, 1900275. [Google Scholar] [CrossRef]
- Pokharel, R.; Patra, A.; Brown, D.W.; Clausen, B.; Vogel, S.C.; Gray, G.T. An analysis of phase stresses in additively manufactured 304L stainless steel using neutron diffraction measurements and crystal plasticity finite element simulations. Int. J. Plast. 2019, 121, 201–217. [Google Scholar] [CrossRef]
- Lindroos, M.; Pinomaa, T.; Ammar, K.; Laukkanen, A.; Provatas, N.; Forest, S. Dislocation density in cellular rapid solidification using phase field modeling and crystal plasticity. Int. J. Plast. 2022, 148, 103139. [Google Scholar] [CrossRef]
- Marin, E.B.; Dawson, P.R. On modelling the elasto-viscoplastic response of metals using polycrystal plasticity. Comput. Methods Appl. Mech. Eng. 1998, 165, 1–21. [Google Scholar] [CrossRef]
- Anand, L. Constitutive Equations for the Rate-Dependent Deformation of Metals at Elevated Temperatures. J. Eng. Mater. Technol. 1982, 104, 12–17. [Google Scholar] [CrossRef]
- Asaro, R.J.; Needleman, A. Overview no. 42 Texture development and strain hardening in rate dependent polycrystals. Acta Metall. 1985, 33, 923–953. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C.N. A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: Application to zirconium alloys. Acta Metall. Mater. 1993, 41, 2611–2624. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Obata, M. Rate-dependent, finite elasto-plastic deformation of polycrystals. Proc. R. Soc. Lond. A Math. Phys. Sci. 1986, 407, 343–375. [Google Scholar] [CrossRef]
- Kocks, U.F.; Argon, A.S.; Ashby, M.F. Thermodynamics and kinetics of slip. Prog. Mater. Sci. 1975, 19, 1–281. [Google Scholar]
- Houtte, P.V. Simulation of the rolling and shear texture of brass by the Taylor theory adapted for mechanical twinning. Acta Metall. 1978, 26, 591–604. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. An analysis of nonuniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic strain in metals. J. Inst. Met. 1938, 62, 307–324. [Google Scholar]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Ma, A.; Roters, F.; Raabe, D. A dislocation density based constitutive model for crystal plasticity FEM including geometrically necessary dislocations. Acta Mater. 2006, 54, 2169–2179. [Google Scholar] [CrossRef]
- Takeuchi, T. Work Hardening of Copper Single Crystals with Multiple Glide Orientations. Trans. Jpn. Inst. Met. 1975, 16, 629–640. [Google Scholar] [CrossRef]
- Wang, Y.M.; Voisin, T.; McKeown, J.T.; Ye, J.; Calta, N.P.; Li, Z.; Zeng, Z.; Zhang, Y.; Chen, W.; Roehling, T.T.; et al. Additively manufactured hierarchical stainless steels with high strength and ductility. Nat. Mater. 2018, 17, 63–71. [Google Scholar] [CrossRef]
- Wang, G.; Ouyang, H.; Fan, C.; Guo, Q.; Li, Z.; Yan, W.; Li, Z. The origin of high-density dislocations in additively manufactured metals. Mater. Res. Lett. 2020, 8, 283–290. [Google Scholar] [CrossRef]
- Zhu, Z.G.; Nguyen, Q.B.; Ng, F.L.; An, X.H.; Liao, X.Z.; Liaw, P.K.; Nai, S.M.L.; Wei, J. Hierarchical microstructure and strengthening mechanisms of a CoCrFeNiMn high entropy alloy additively manufactured by selective laser melting. Scr. Mater. 2018, 154, 20–24. [Google Scholar] [CrossRef]
- Gallmeyer, T.G.; Moorthy, S.; Kappes, B.B.; Mills, M.J.; Amin-Ahmadi, B.; Stebner, A.P. Knowledge of process-structure-property relationships to engineer better heat treatments for laser powder bed fusion additive manufactured Inconel 718. Addit. Manuf. 2020, 31, 100977. [Google Scholar] [CrossRef]
- Li, Z.; Cui, Y.; Yan, W.; Zhang, D.; Fang, Y.; Chen, Y.; Yu, Q.; Wang, G.; Ouyang, H.; Fan, C.; et al. Enhanced strengthening and hardening via self-stabilized dislocation network in additively manufactured metals. Mater. Today 2021, 50, 79–88. [Google Scholar] [CrossRef]
- Freeman, F.S.H.B.; Sharp, J.; Xi, J.; Todd, I. Influence of solidification cell structure on the martensitic transformation in additively manufactured steels. Addit. Manuf. 2019, 30, 100917. [Google Scholar] [CrossRef]
- Boussinot, G.; Apel, M.; Zielinski, J.; Hecht, U.; Schleifenbaum, J.H. Strongly Out-of-Equilibrium Columnar Solidification during Laser Powder-Bed Fusion in Additive Manufacturing. Phys. Rev. Appl. 2019, 11, 014025. [Google Scholar] [CrossRef]
- Kadkhodapour, J.; Butz, A.; Ziaei-Rad, S.; Schmauder, S. A micro mechanical study on failure initiation of dual phase steels under tension using single crystal plasticity model. Int. J. Plast. 2011, 27, 1103–1125. [Google Scholar] [CrossRef]
- Choi, K.S.; Liu, W.N.; Sun, X.; Khaleel, M.A. Influence of Martensite Mechanical Properties on Failure Mode and Ductility of Dual-Phase Steels. Metall. Mater. Trans. A 2009, 40, 796–809. [Google Scholar] [CrossRef]
- Rao, S.I.; Dimiduk, D.M.; Tang, M.; Parthasarathy, T.A.; Uchic, M.D.; Woodward, C. Estimating the strength of single-ended dislocation sources in micron-sized single crystals. Philos. Mag. 2007, 87, 4777–4794. [Google Scholar] [CrossRef]
- Li, J.; Yi, M.; Wu, H.; Fang, Q.; Liu, Y.; Liu, B.; Zhou, K.; Liaw, P.K. Fine-grain-embedded dislocation-cell structures for high strength and ductility in additively manufactured steels. Mater. Sci. Eng. A 2020, 790, 139736. [Google Scholar] [CrossRef]
- Bertsch, K.M.; Meric de Bellefon, G.; Kuehl, B.; Thoma, D.J. Origin of dislocation structures in an additively manufactured austenitic stainless steel 316L. Acta Mater. 2020, 199, 19–33. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chawla, K.K. Mechanical Behavior of Materials; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Kong, D.; Dong, C.; Wei, S.; Ni, X.; Zhang, L.; Li, R.; Wang, L.; Man, C.; Li, X. About metastable cellular structure in additively manufactured austenitic stainless steels. Addit. Manuf. 2021, 38, 101804. [Google Scholar] [CrossRef]
- Qu, S.; Ding, J.; Fu, J.; Fu, M.; Song, X. Anisotropic material properties of pure copper with fine-grained microstructure fabricated by laser powder bed fusion process. Addit. Manuf. 2022, 59, 103082. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. J. Theor. Exp. Appl. Phys. 1970, 21, 399–424. [Google Scholar] [CrossRef]

| (m−1) | (s−1) | m | |
|---|---|---|---|
| 109 (fitted) | 28 (fitted) | 0.003 (fitted) | 0.1 (fitted) |
| (m−2) | (m−2) | b (nm) | G (GPa) |
| 1012 (fitted) | 0 | 0.256 | 42 |
| C11 (GPa) | C12 (GPa) | C44 (GPa) | |
| 168.15 | 125.60 | 78.80 | 0.35 (fitted) |
| Process Parameters | [7] | [43] | [44] | [53] | [54] |
|---|---|---|---|---|---|
| Laser power (W) | 200 | 150–350 | 230 | 225 | 275 |
| Scanning speed (mm/s) | 850 | 700–1700 | 500 | 1000 | 8.5 |
| Hatch spacing (µm) | 100 | 75–105 | 60 | 90 | 350 |
| Rotated scanning direction (degree) | 67 | 0 | 67 | 67 | 90 |
| Laser spot size (µm) | 70 | 54 | 60 | 80 | 80 |
| Layer thickness (µm) | 20 | 30 | 20 | 30 | 254 |
| Average cell diameter (nm) | 500 | 580,930 | 200–500 | 500 | 470 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rohoman, M.M.; Zhou, C. Crystal Plasticity Modeling of Dislocation Density Evolution in Cellular Dislocation Structures. Metals 2025, 15, 419. https://doi.org/10.3390/met15040419
Rohoman MM, Zhou C. Crystal Plasticity Modeling of Dislocation Density Evolution in Cellular Dislocation Structures. Metals. 2025; 15(4):419. https://doi.org/10.3390/met15040419
Chicago/Turabian StyleRohoman, Md Mahabubur, and Caizhi Zhou. 2025. "Crystal Plasticity Modeling of Dislocation Density Evolution in Cellular Dislocation Structures" Metals 15, no. 4: 419. https://doi.org/10.3390/met15040419
APA StyleRohoman, M. M., & Zhou, C. (2025). Crystal Plasticity Modeling of Dislocation Density Evolution in Cellular Dislocation Structures. Metals, 15(4), 419. https://doi.org/10.3390/met15040419





