Stress Determination by IHD in Additively Manufactured Austenitic Steel Samples: A Validation Study
Abstract
1. Introduction
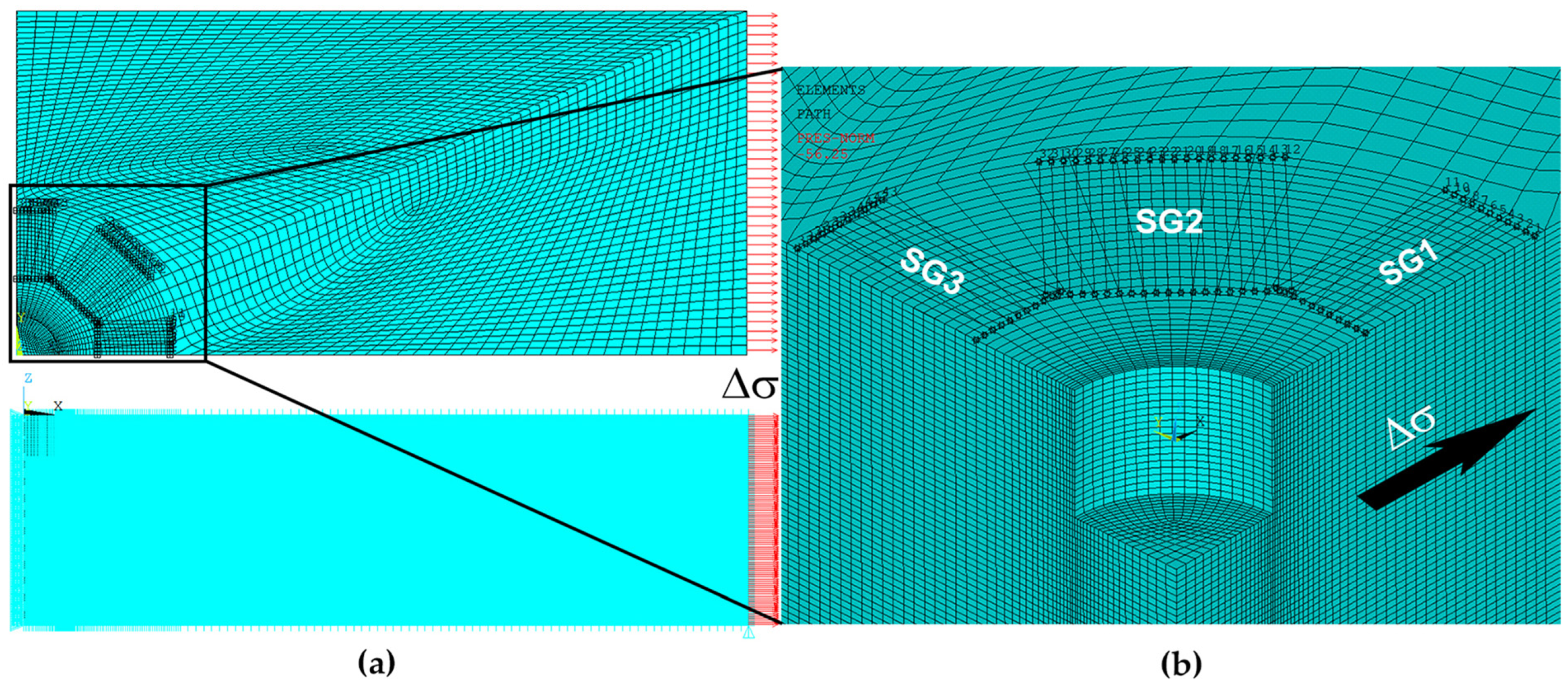
2. The Hybrid Experimental-Numerical Method (HENM)
3. The Integral Method for IHD Stress Calculation
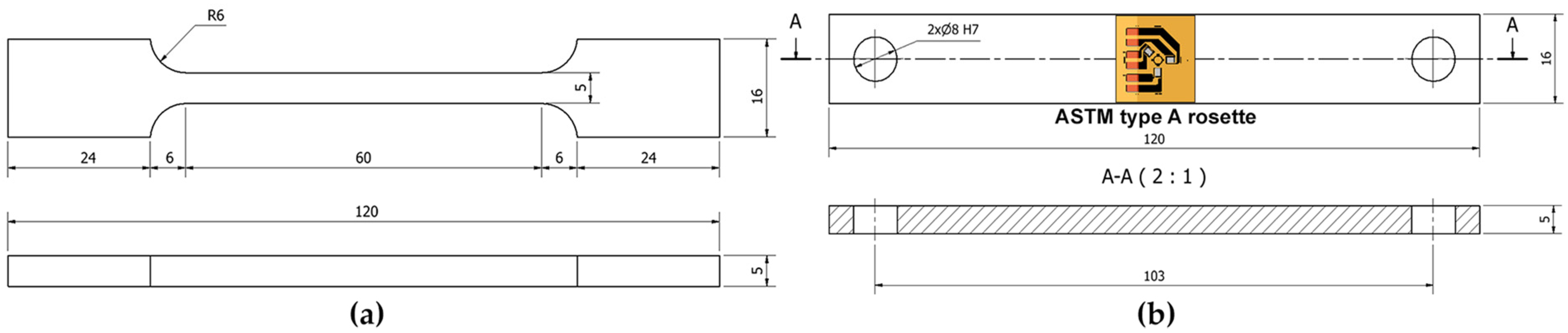
4. Material and Procedures
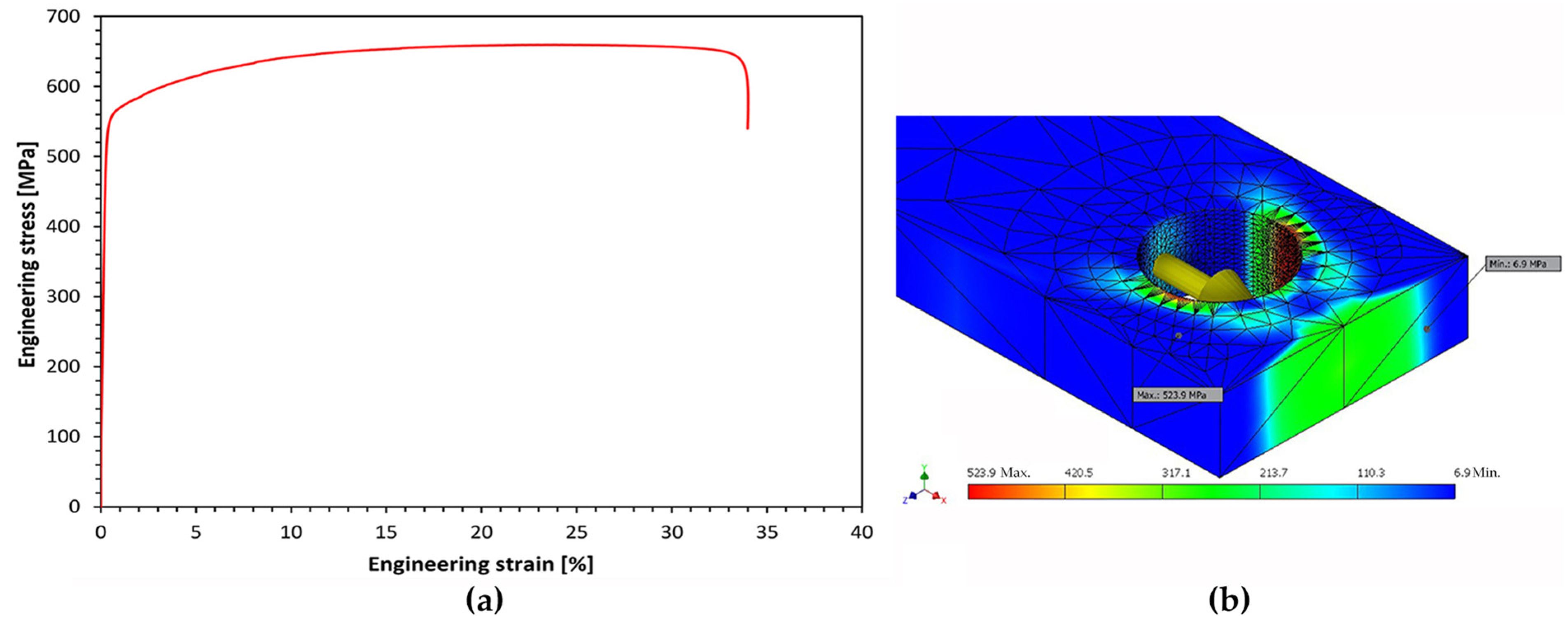
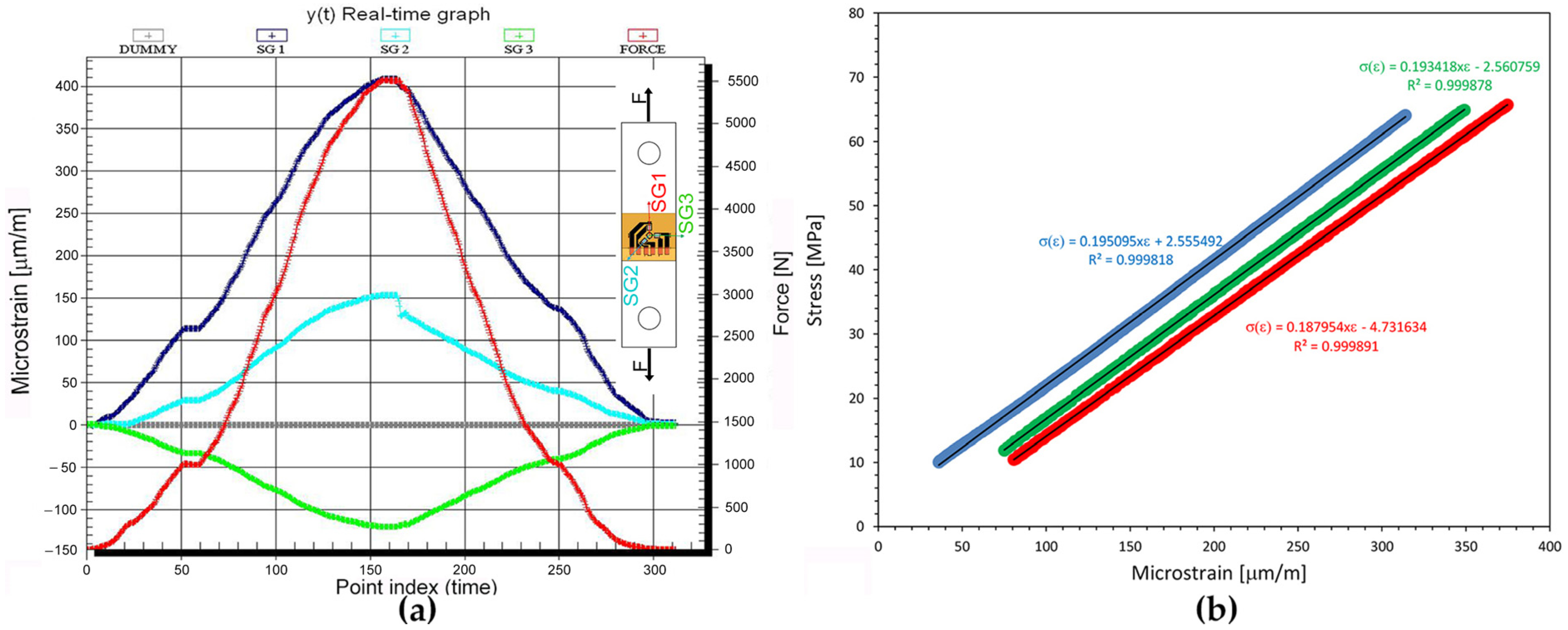
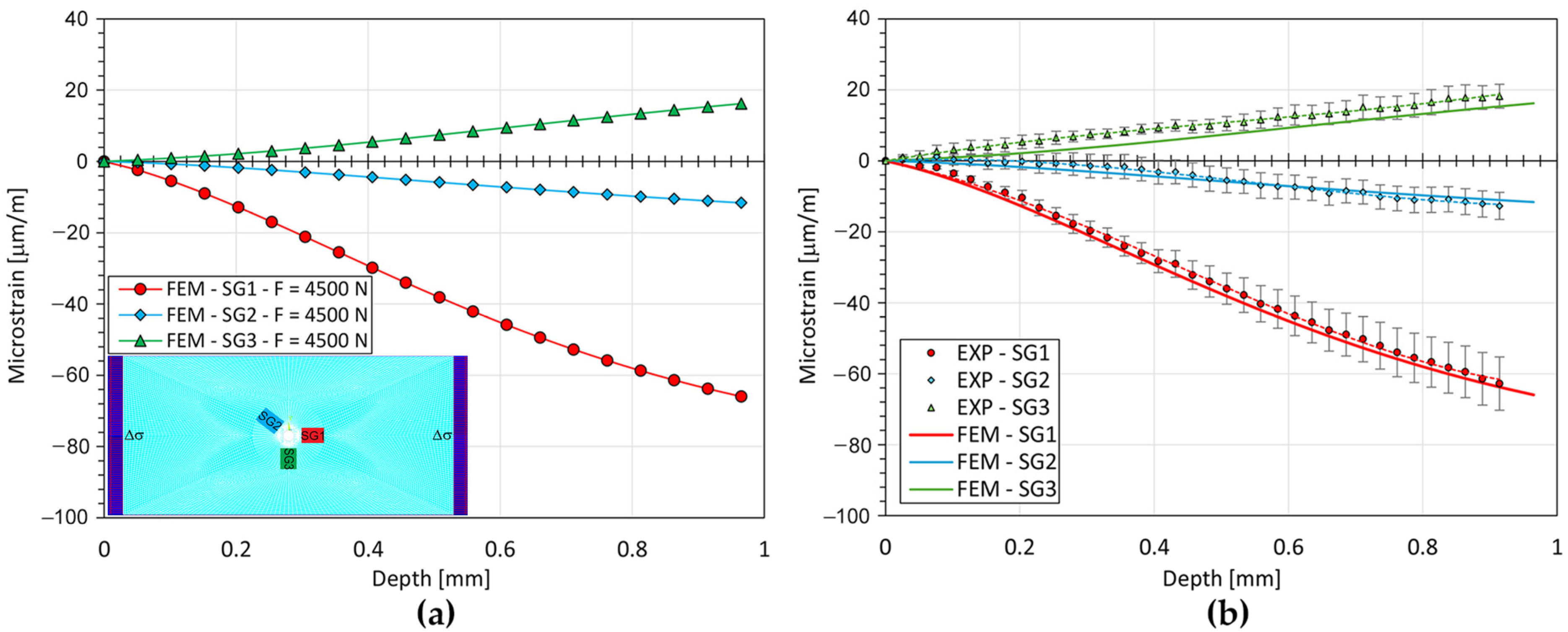
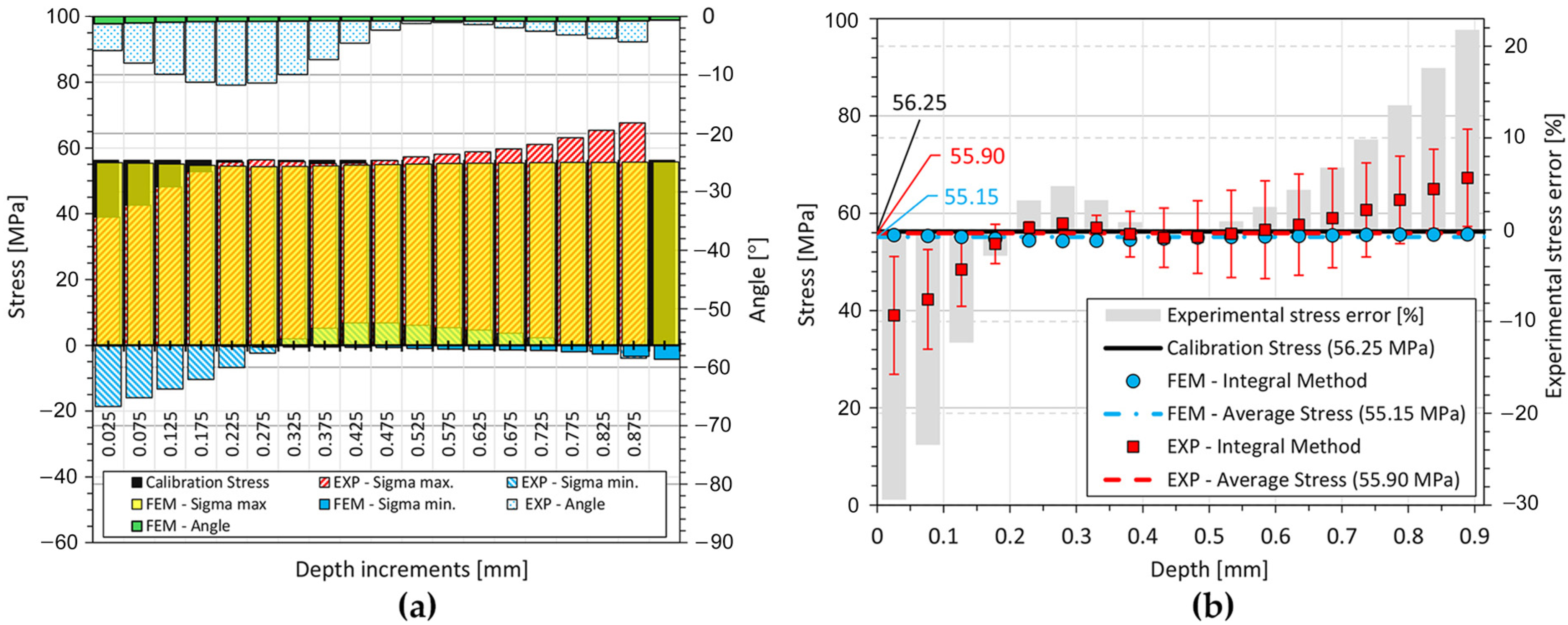
5. Experimental Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sefene, E.M. State-of-the-art of selective laser melting process: A comprehensive review. J. Manuf. Syst. 2022, 63, 250–274. [Google Scholar] [CrossRef]
- Mansoura, A.; Omidi, N.; Barka, N.; Karganroudi, S.S.; Dehghan, S. Selective Laser Melting of Stainless Steels: A review of Process, Microstructure and Properties. Met. Mat. Int. 2024, 30, 2343–2371. [Google Scholar] [CrossRef]
- Salmi, A.; Atzeni, E.; Iuliano, L.; Galati, M. Experimental Analysis of Residual Stresses on AlSi10Mg Parts Produced by Means of Selective Laser Melting (SLM). Procedia CIRP 2017, 62, 458–463. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Wang, D. A study on the residual stress during selective laser melting (SLM) of metallic powder. Int. J. Adv. Manuf. Technol. 2016, 87, 647–656. [Google Scholar] [CrossRef]
- ASTM-E837-20; Standard Test Method for Determining Residual Stresses by the Hole-Drilling Strain-Gage Method. ASTM International: West Conshohocken, PA, USA, 2020.
- Schajer, G.S.; Whitehead, P.S. Hole-Drilling Method for Measuring Residual Stresses; Springer: Cham, Switzerland, 2018; pp. 1–172. [Google Scholar] [CrossRef]
- Barsanti, M.; Beghini, M.; Santus, C.; Benincasa, A.; Bertelli, L. Integral method coefficients for the ring-core technique to evaluate non-uniform residual stresses. J. Strain Anal. Eng. Des. 2018, 53, 210–224. [Google Scholar] [CrossRef]
- Leggatt, R.H.; Smith, D.J.; Smith, S.D.; Faure, F. Development and experimental validation of the deep hole method for residual stress measurement. J. Strain Anal. Eng. Des. 1996, 31, 177–186. [Google Scholar] [CrossRef]
- Hill, M.R. The Slitting Method. In Practical Residual Stress Measurement Methods; Schajer, G.S., Ed.; Wiley: Hoboken, NJ, USA, 2013; pp. 89–108. [Google Scholar] [CrossRef]
- Prime, M.B.; DeWald, A.T. The Contour Method. In Practical Residual Stress Measurement Methods; Schajer, G.S., Ed.; Wiley: Hoboken, NJ, USA, 2013; pp. 109–138. [Google Scholar] [CrossRef]
- Hauk, V. Structural and Residual Stress Analysis by Nondestructive Methods; Elsevier Science B.V.: Amsterdam, The Netherlands, 1997. [Google Scholar] [CrossRef]
- Santa-aho, S.; Kiviluoma, M.; Jokiaho, T.; Gundgire, T.; Honkanen, M.; Lindgren, M.; Vippola, M. Additive Manufactured 316L Stainless-Steel Samples: Microstructure, Residual Stress and Corrosion Characteristics after Post-Processing. Metals 2021, 11, 182. [Google Scholar] [CrossRef]
- Geľatko, M.; Hatala, M.; Botko, F.; Vandžura, R. Residual Stress Evaluation in L-PBF-Produced SS 316L Specimens. Materials 2024, 17, 2270. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Yadroitsava, I. Evaluation of residual stress in stainless steel 316L and Ti6Al4V samples produced by selective laser melting. Virtual Phys. Prototyp. 2015, 10, 67–76. [Google Scholar] [CrossRef]
- Cheng, M.; Zou, X.; Chang, T.; Cao, Q.; Ju, H.; Luo, G.; Zou, Z.; Wu, Z. Residual Stresses of 316L Stainless Steel Laser Direct Metal During Pulsed-Wave and Continuous-Wave Laser Additive Manufacturing: A Comparative Study. Coatings 2024, 14, 1598. [Google Scholar] [CrossRef]
- Chen, W.; Voisin, T.; Zhang, Y.; Forien, J.-B.; Spadaccini, C.M.; McDowell, D.L.; Zhu, T.; Wang, Y.M. Microscale residual stresses in additively manufactured stainless steel. Nat. Commun. 2019, 10, 4338. [Google Scholar] [CrossRef] [PubMed]
- Simson, T.; Emmel, A.; Dwars, A.; Böhm, J. Residual stress measurements on AISI 316L samples manufactured by selective laser melting. Addit. Manuf. 2017, 17, 183–189. [Google Scholar] [CrossRef]
- Beltrami, M.; Pelegatti, M.; Magnan, M.; Lanzutti, A.; Avdeev, M.; Luzin, V.; Leoni, M.; De Bona, F.; Salvati, E. Microstructure and residual stress evolution during cyclic elastoplastic deformation of AISI316L fabricated via laser powder bed fusion. Mater. Sci. Eng. A 2024, 898, 146416. [Google Scholar] [CrossRef]
- Piscopo, G.; Salmi, A.; Atzeni, E. Influence of High-Productivity Process Parameters on the Surface Quality and Residual Stress State of AISI 316L Components Produced by Directed Energy Deposition. J. Mater. Eng. Perform. 2021, 30, 6691–6702. [Google Scholar] [CrossRef]
- Gu, J.; Li, R.; Qiu, Y.; Yue, H.; Liu, B.; Gu, H. Microstructure, Mechanical Properties, and Residual Stress Distribution of AISI 316L Stainless Steel Part Fabricated by Laser Metal Deposition. Scanning 2020, 4831798. [Google Scholar] [CrossRef]
- D’Andrea, D. Additive Manufacturing of AISI 316L Stainless Steel: A Review. Metals 2023, 13, 1370. [Google Scholar] [CrossRef]
- Schajer, G.S. Measurement of Non-Uniform Residual Stress Using the Hole-Drilling Method. Part II-Practical Application of The Integral Method. J. Eng. Mater. Technol. 1988, 110, 344–349. [Google Scholar] [CrossRef]
- Schajer, G.S. Hole-Drilling Residual Stress Profiling with Automated Smoothing. J. Eng. Mater. Technol. 2007, 129, 440–445. [Google Scholar] [CrossRef]
- Nobre, J.P.; Kornmeier, M.; Scholtes, B. Plasticity Effects in the Hole-Drilling Residual Stress Measurement in Peened Surfaces. Exp. Mech. 2018, 58, 369–380. [Google Scholar] [CrossRef]
- Shokrani, A.; Dhokia, V.; Newman, S.T. Environmentally conscious machining of difficult-to-machine materials with regard to cutting fluids. Int. J. Mach. Tools Manuf. 2012, 57, 83–101. [Google Scholar] [CrossRef]
- Flaman, M.T. Brief investigation of induced drilling stresses in the center-hole method of residual-stress measurement. Exp. Mech. 1982, 22, 26–30. [Google Scholar] [CrossRef]
- Flaman, M.T.; Herring, J.A. Comparison of Four Hole-Producing Techniques for the Center-Hole Residual-Stress Measurement Method. Exp. Tech. 1985, 9, 30–32. [Google Scholar] [CrossRef]
- Schajer, G.S.; Altus, E. Stress Calculation Error Analysis for Incremental Hole-Drilling Residual Stress Measurements. J. Eng. Mater. Technol. 1996, 118, 120–126. [Google Scholar] [CrossRef]
- Weng, C.C.; Lin, Y.C.; Chou, C.P. A new approach for determining the induced drilling stresses in the hole-drilling method of residual-stress measurement. Exp. Tech. 1992, 16, 33–35. [Google Scholar] [CrossRef]
- Lee, H.T.; Liu, C.; Hsu, F.C.; Hsu, J.M. An Enhanced Calibration Scheme for the EDM Hole-Drilling Strain Gage Method for the Measurement of Residual Stress in Ferrous Materials. Mater. Trans. 2008, 49, 1905–1910. [Google Scholar] [CrossRef]
- Simmons, J.C.; Chen, X.; Azizi, A.; Daeumer, M.A.; Zavalij, P.Y.; Zhou, G.; Schiffres, S.N. Influence of processing and microstructure on the local and bulk thermal conductivity of selective laser melted 316L stainless steel. Addit. Manuf. 2020, 32, 100996. [Google Scholar] [CrossRef]
- Nobre, J.P.; Stiffel, J.H.; Paepegem, W.V.; Nau, A.; Batista, A.C.; Marques, M.J.; Scholtes, B. Quantifying the Drilling Effect during the Application of Incremental Hole-Drilling Technique in Laminate Composites. Mater. Sci. Forum. 2011, 681, 510–515. [Google Scholar] [CrossRef]
- Nobre, J.P.; Smit, T.C.; Reid, R.; Qhola, Q.; Wu, T.; Niendorf, T. Stress Evaluation Through the Layers of a Fibre-Metal Hybrid Composite by IHD: An Experimental Study. Exp. Mech. 2024, 64, 487–500. [Google Scholar] [CrossRef]
- Schajer, G.S. Measurement of Non-Uniform Residual Stress Using the Hole-Drilling Method. Part I—Stress Calculation Procedures. J. Eng. Mater. Technol. 1988, 110, 338–343. [Google Scholar] [CrossRef]
- Schajer, G.; Prime, M. Use of Inverse Solutions for Residual Stress Measurement. J. Eng. Mater. Technol. 2006, 128, 375–382. [Google Scholar] [CrossRef]
- Schajer, G.S. Application of Finite Element Calculations to Residual Stress Measurements. J. Eng. Mater. Technol. 1981, 103, 157–163. [Google Scholar] [CrossRef]
- Zuccarello, B. Optimal calculation steps for the evaluation of residual stress by the incremental hole-drilling method. Exp. Mech. 1999, 39, 117–124. [Google Scholar] [CrossRef]
- Valentini, E.; Bertelli, L.; Benincasa, A.; Gulisano, S. Recent Advancements in the Hole-Drilling Strain-Gage Method for Determining Residual Stresses. In New Challenges in Residual Stress Measurements and Evaluation; Casavola, C., Barile, C., Moramarco, V., Pappalettera, G., Eds.; IntechOpen: Rijeka, Croatia, 2019; Chapter 4. [Google Scholar] [CrossRef]
- Simon, N.; Gibmeier, J. Consideration of Tool Chamfer for Realistic Application of the Incremental Hole-Drilling Method. Mater. Res. Proc. 2017, 2, 473–478. [Google Scholar] [CrossRef]
- Blödorn, R.; Bonomo, L.A.; Viotti, M.R.; Schroeter, R.B.; Albertazzi, A. Calibration Coefficients Determination Through Fem Simulations for the Hole-Drilling Method Considering the Real Hole Geometry. Exp. Tech. 2017, 41, 37–44. [Google Scholar] [CrossRef]



| Element | C | Cr | N | Mn | Mo | Ni | P | S | Si | O | Fe |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Weight (%) | <0.03 | 16–18 | <0.10 | <2 | 2–3 | 10–14 | <0.045 | <0.03 | <1 | <0.1 | bal |
| Laser Power | Layer Thickness | Scan Speed | Particle ∅ | Distance Between Paths |
|---|---|---|---|---|
| 300 W | 50 μm | 1 ms−1 | 15–45 μm | 110 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nobre, J.P.; Marques, M.J.; Batista, A.C. Stress Determination by IHD in Additively Manufactured Austenitic Steel Samples: A Validation Study. Metals 2025, 15, 485. https://doi.org/10.3390/met15050485
Nobre JP, Marques MJ, Batista AC. Stress Determination by IHD in Additively Manufactured Austenitic Steel Samples: A Validation Study. Metals. 2025; 15(5):485. https://doi.org/10.3390/met15050485
Chicago/Turabian StyleNobre, João Paulo, Maria José Marques, and António Castanhola Batista. 2025. "Stress Determination by IHD in Additively Manufactured Austenitic Steel Samples: A Validation Study" Metals 15, no. 5: 485. https://doi.org/10.3390/met15050485
APA StyleNobre, J. P., Marques, M. J., & Batista, A. C. (2025). Stress Determination by IHD in Additively Manufactured Austenitic Steel Samples: A Validation Study. Metals, 15(5), 485. https://doi.org/10.3390/met15050485









