Solidification Window in Al-Based Casting Alloys
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
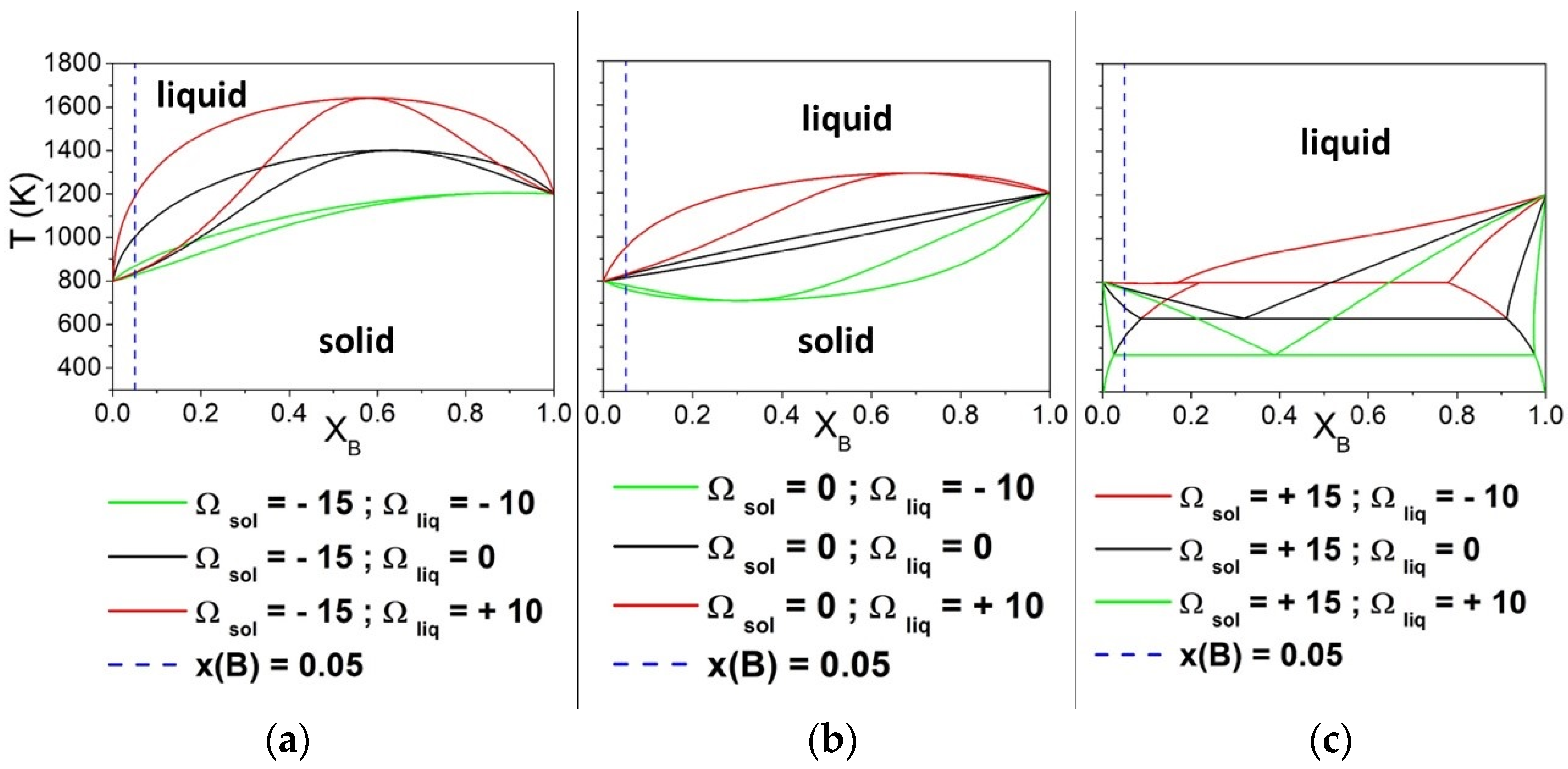
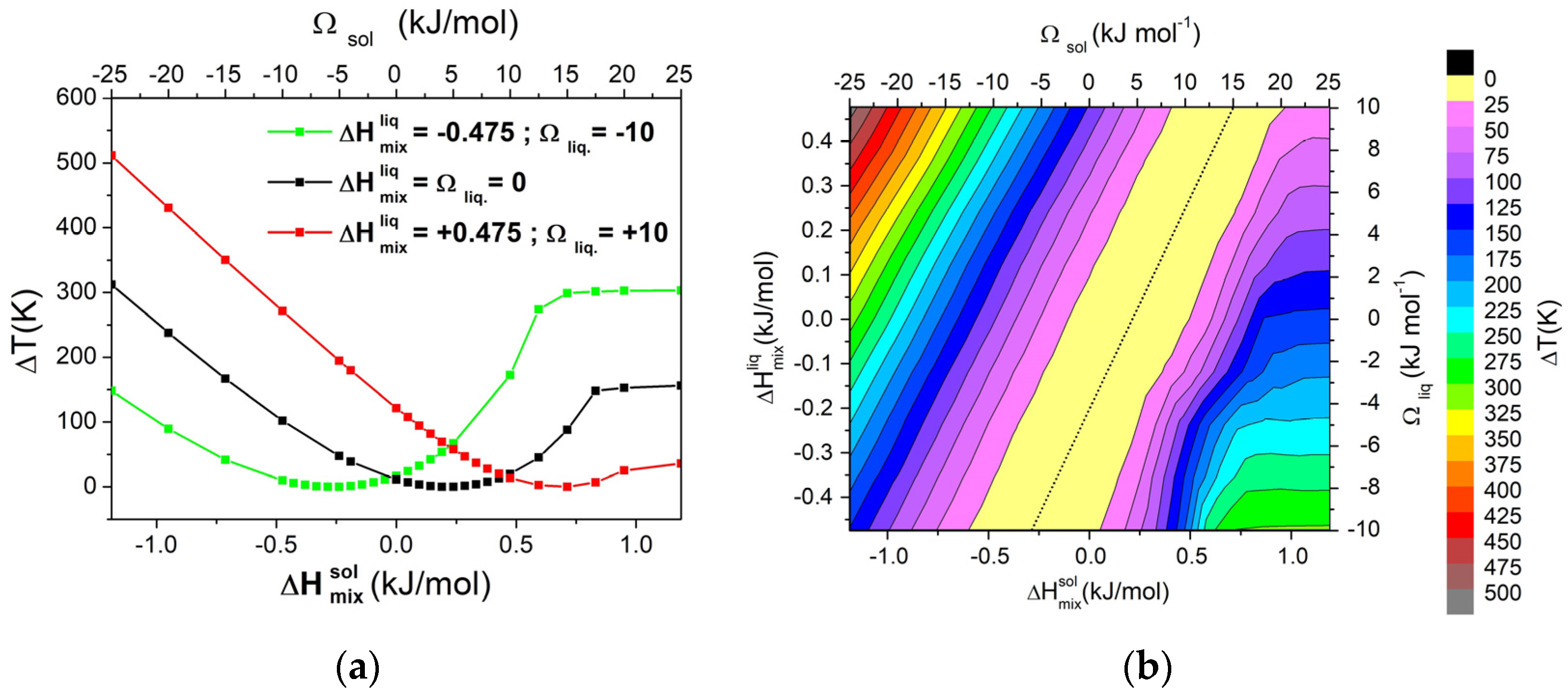
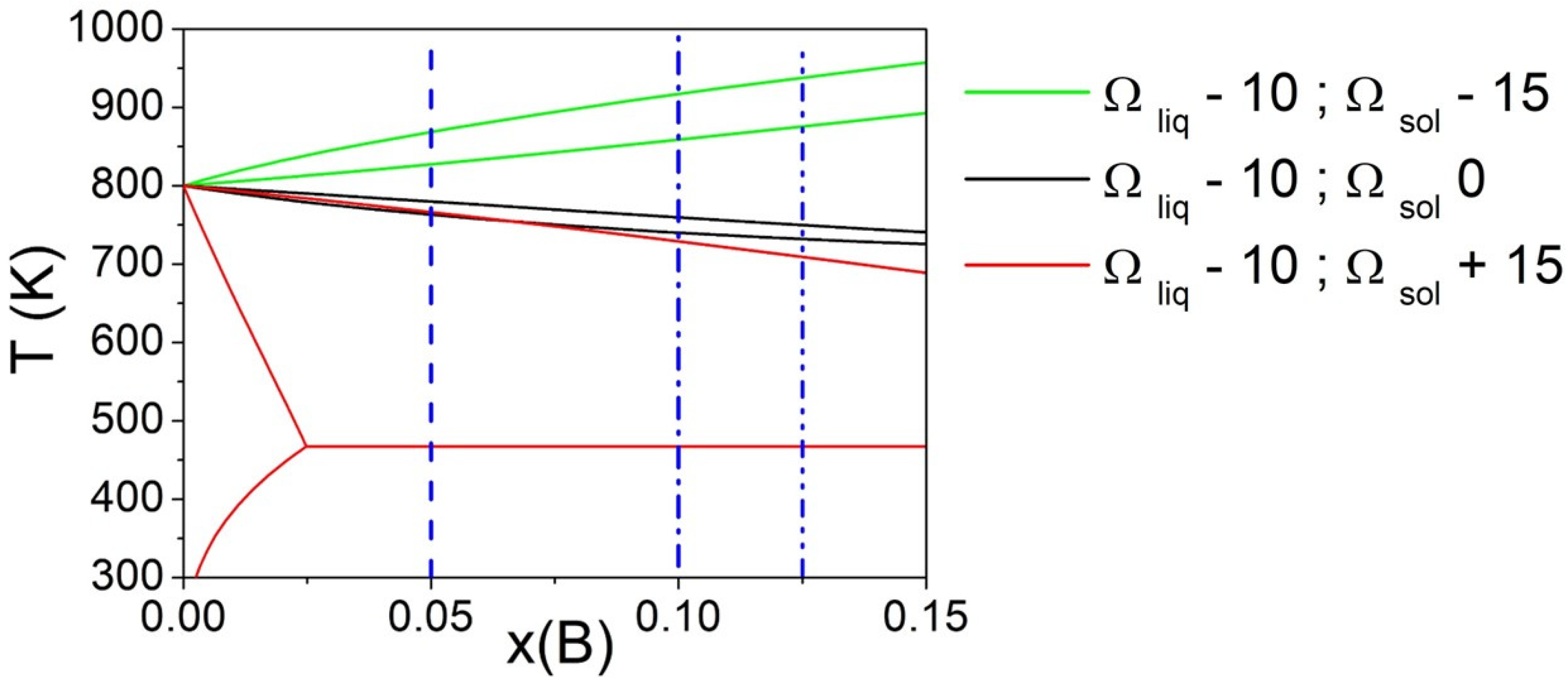
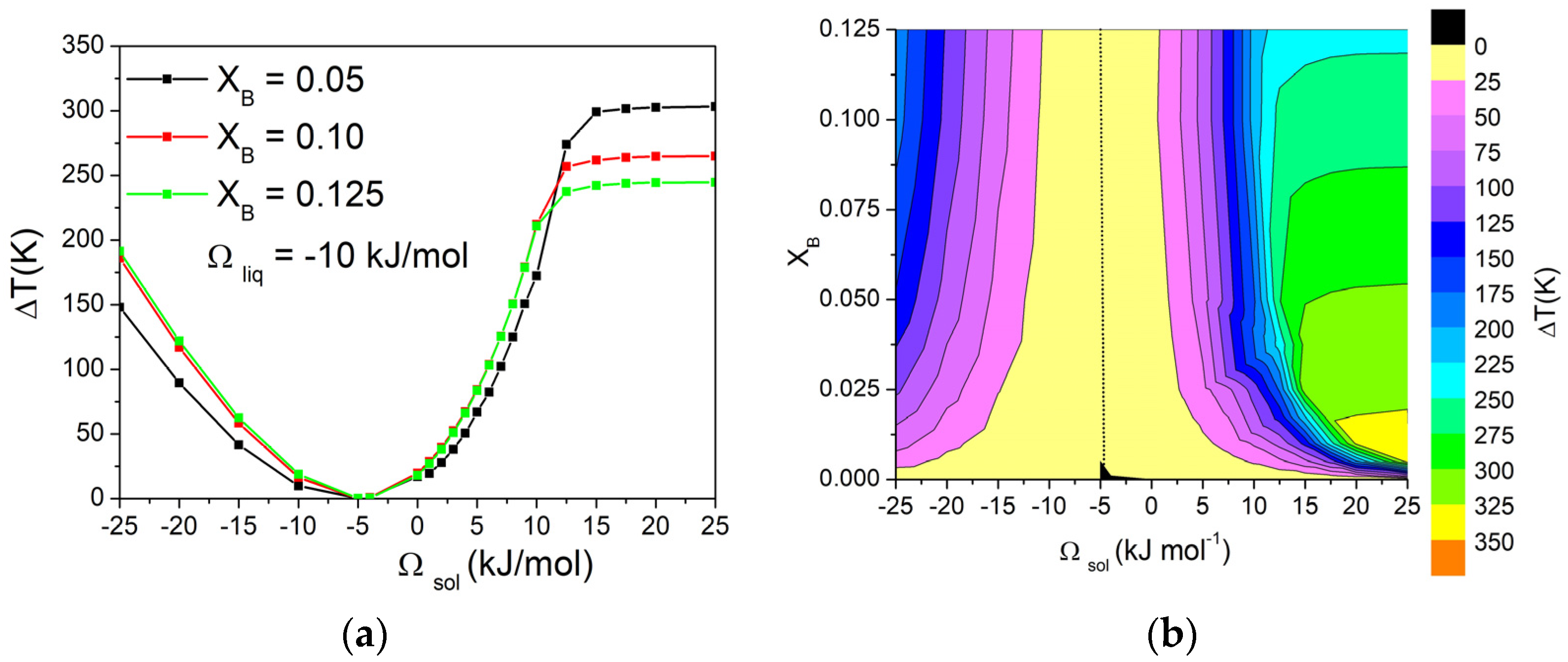
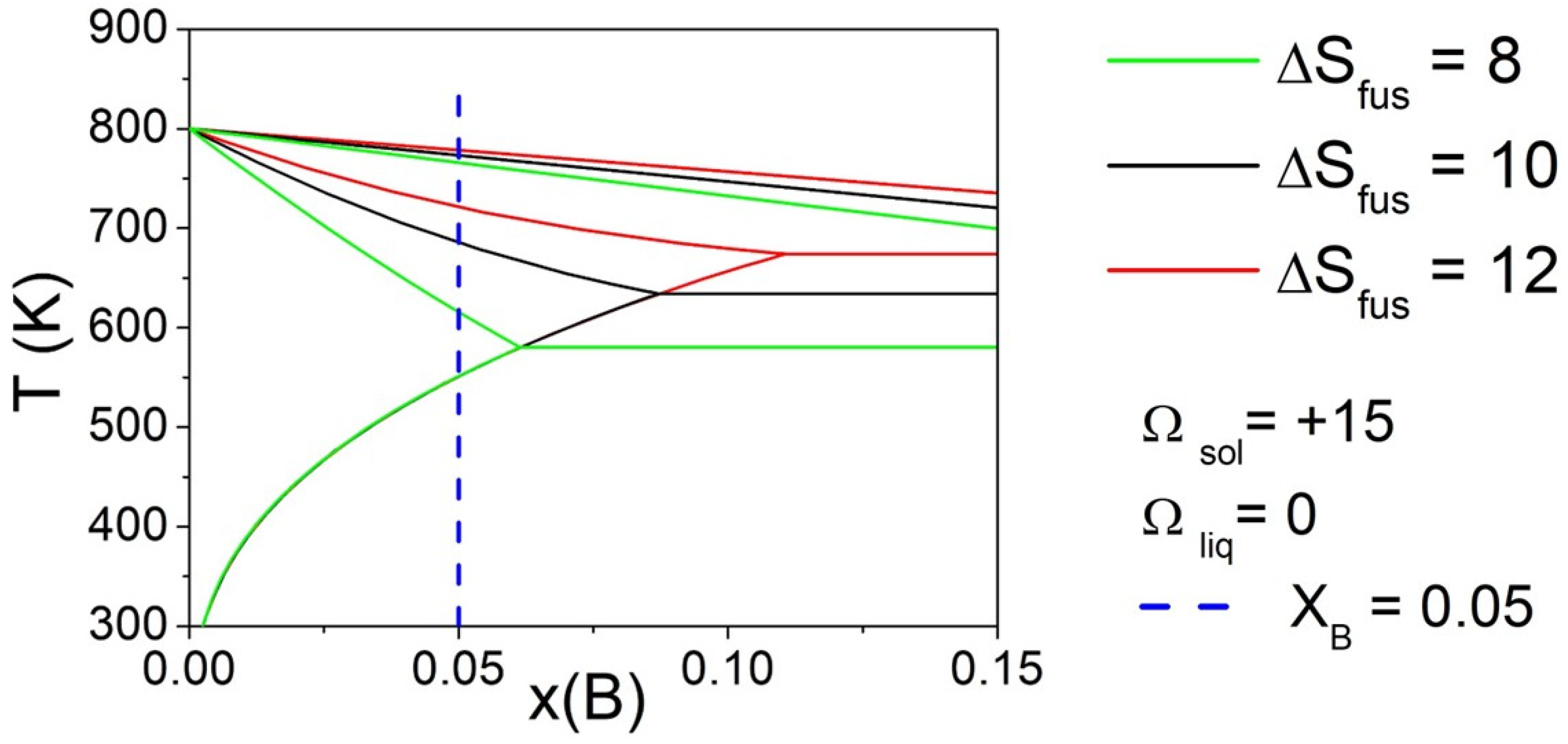
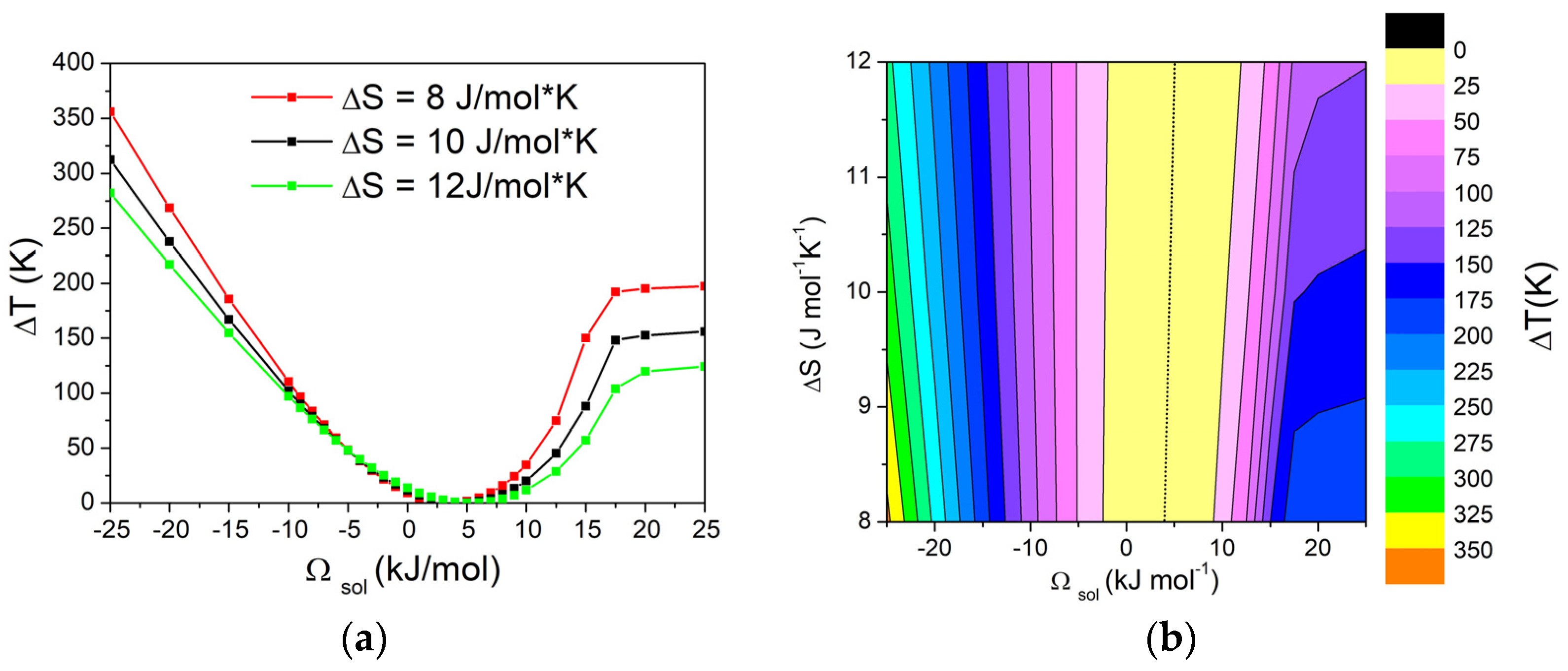
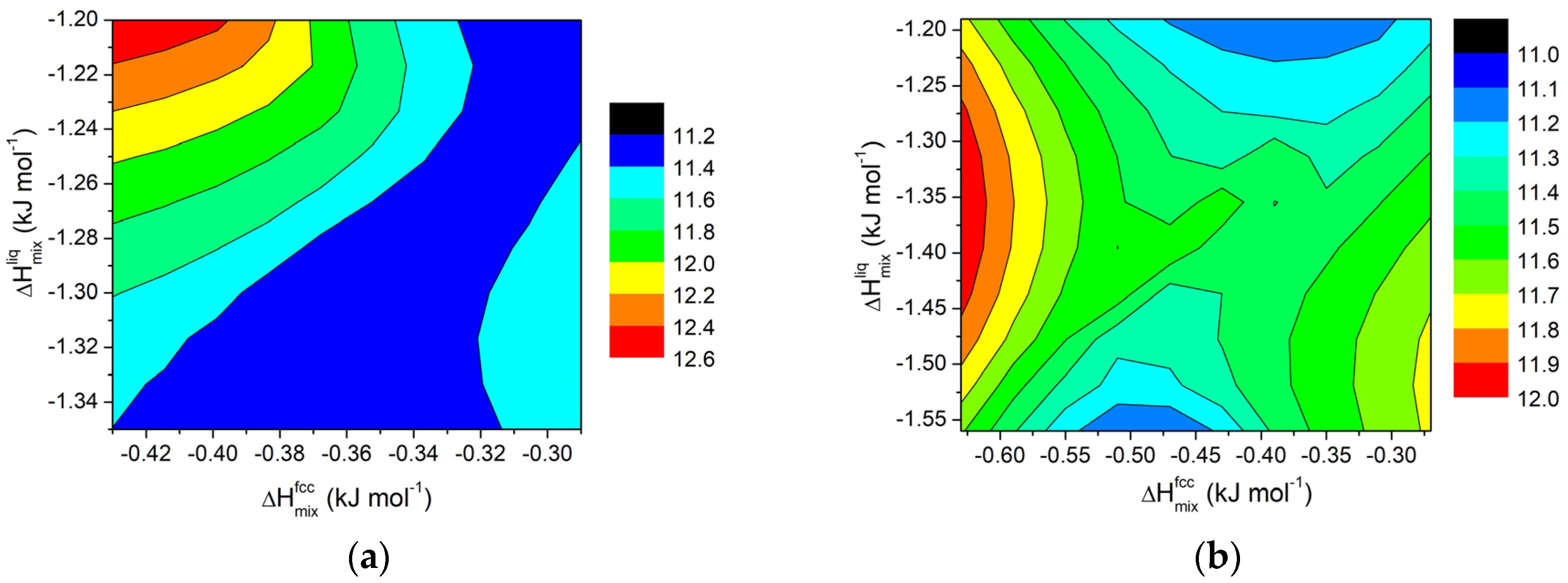
3.1. Regular Solutions
3.2. Al Binary Systems
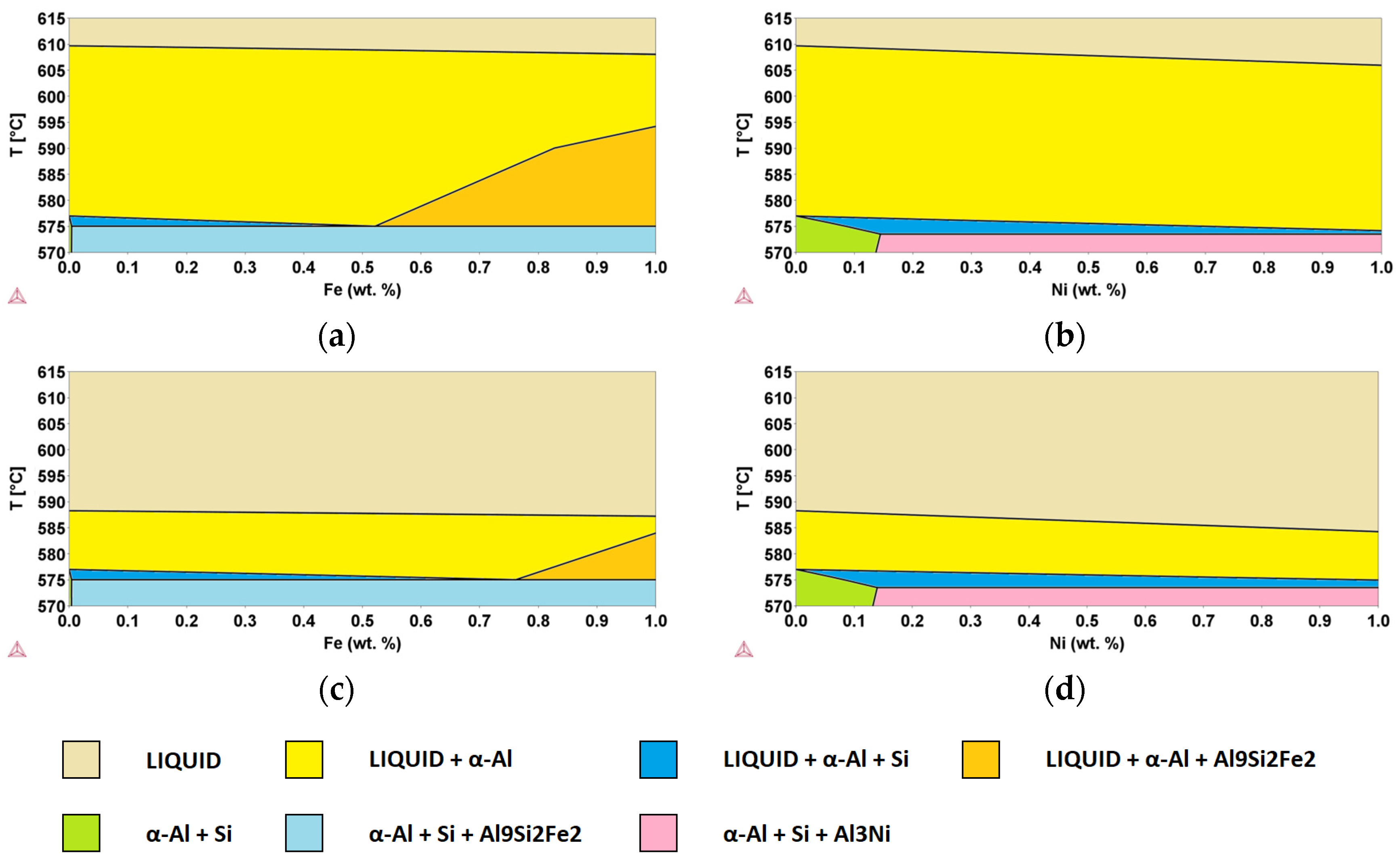
3.3. Al-Si8 and Al-Si11 Ternary Systems
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CALPHAD | Computer Coupling of Phase Diagrams and Thermochemistry |
| CEF | Compound Energy Formalism |
| fcc | Face-centred cubic |
| HPDC | High-pressure die casting |
| INSTM | Consorzio Interuniversitario Nazionale per la Scienza e Tecnologia dei Materiali |
| SSM | Semi-solid metallurgy |
References
- Modigell, M.; Pola, A.; Tocci, M. Rheological characterization of semi-solid metals: A review. Metals 2018, 8, 245. [Google Scholar] [CrossRef]
- Kirkwood, D.; Kapranos, P.; Suéry, M.; Atkinson, H.V.; Young, K.P. Semi-Solid Processing of Alloys, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Atkinson, H.V. Alloys for semi-solid processing. Solid State Phenom. 2013, 192–193, 16–27. [Google Scholar] [CrossRef]
- Jarfors, A.E.W. A comparison between semisolid casting methods for aluminium alloys. Metals 2020, 10, 1368. [Google Scholar] [CrossRef]
- Barbé, J.C.; Perez, M.; Papoular, M. Microstructure and viscosity of semi-solid mixtures. J. Phys. Condens. Matter. 2000, 12, 2567–2577. [Google Scholar] [CrossRef]
- Solomon, A.D.; Wilson, D.G.; Alexiades, V. A mushy zone model with an exact solution. Lett. Heat Mass Transf. 1982, 9, 319–324. [Google Scholar] [CrossRef]
- Guggenheim, E.A. The statistical mechanics of regular solutions. Proc. R. Soc. London. Ser. A—Math. Phys. Sci. 1935, 148, 304–312. [Google Scholar] [CrossRef]
- Oates, W.A.; Flanagan, T.B. Thermodynamic properties of regular interstitial solutions. J. Mater. Sci. 1981, 16, 3235–3243. [Google Scholar] [CrossRef]
- Sundman, B.; Dupin, N.; Sluiter, M.H.F.; Fries, S.G.; Guéneau, C.; Hallstedt, B.; Kattner, U.R.; Selleby, M. The Legacy of “The Regular Solution Model for Stoichiometric Phases and Ionic Melts”. J. Phase Equilibria Diffus. 2024, 45, 934–964. [Google Scholar] [CrossRef]
- Jung, J.G.; Cho, Y.H.; Lee, J.M.; Kim, H.W.; Euh, K. Designing the composition and processing route of aluminum alloys using CALPHAD: Case studies. Calphad 2019, 64, 236–247. [Google Scholar] [CrossRef]
- Ferraro, S.; Bongiovanni, A.; Lopez, I.S.; Palumbo, M.; Baricco, M.; Castellero, A. CALPHAD Optimization of the Composition of EN AC-46000 Secondary Alloys for Semi-Solid Casting Processes. Solid State Phenom. 2023, 347, 171–176. [Google Scholar] [CrossRef]
- Porter, D.A.; Easterling, K.E.; Sherif, M.Y. Phase Transformations in Metals and Alloys, third ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- David, R.L. CRC Handbook of Chemistry and Physics for the 21st Century; CRC Press: Boca Raton, FL, USA, 1989. [Google Scholar]
- Dinsdale, A.T. SGTE data for pure elements. Calphad 1991, 15, 317–425. [Google Scholar] [CrossRef]
- Tiwari, G.P. Modification of richard’s rule and correlation between entropy of fusion and allotropic behaviour. Met. Sci. 1978, 12, 317–320. [Google Scholar] [CrossRef]
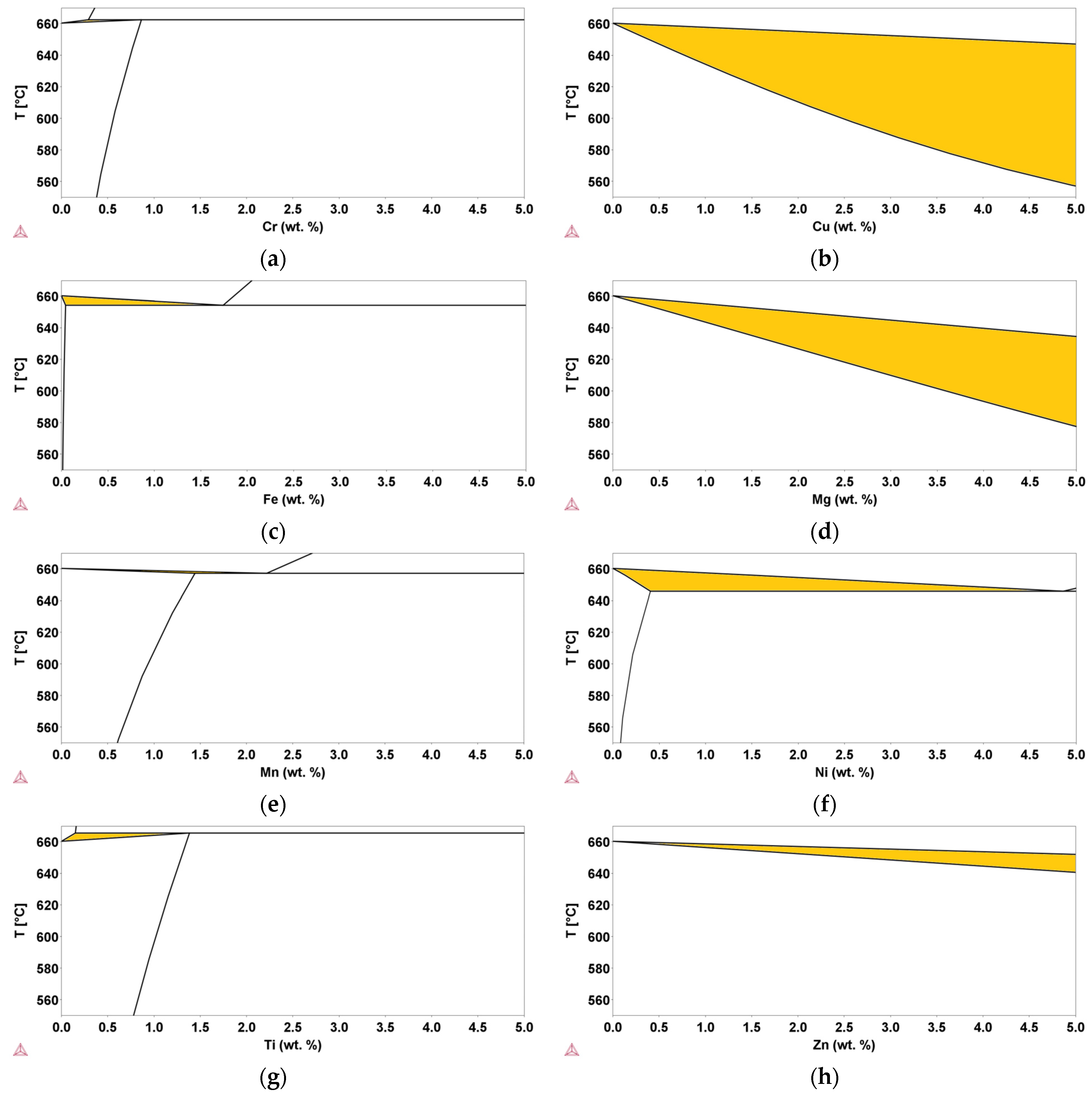
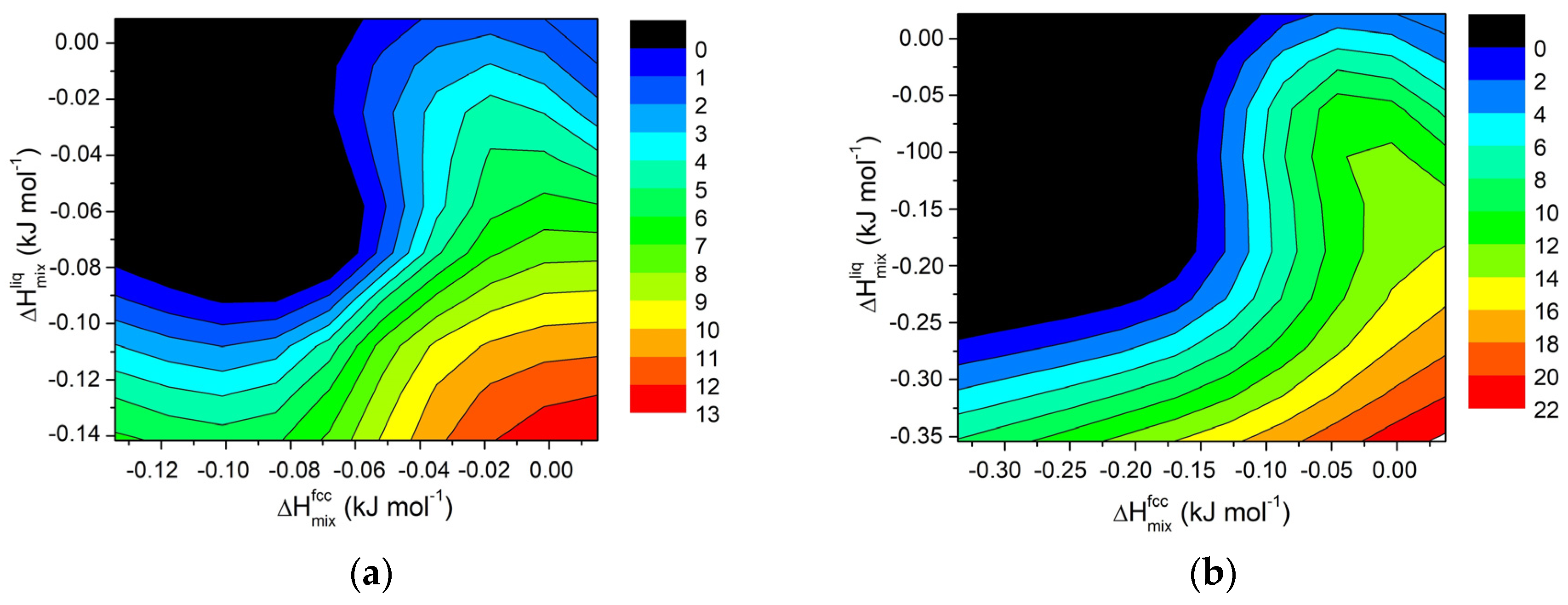

| Si (wt.%) | Cr (wt.%) | Cu (wt.%) | Fe (wt.%) | Mg (wt.%) | Mn (wt.%) | Ni (wt.%) | Ti (wt.%) | Zn (wt.%) |
|---|---|---|---|---|---|---|---|---|
| 8.0–11.0 | <0.15 | 2.00–4.00 | 0.60–1.10 | 0.15–0.55 | <0.55 | <0.55 | <0.20 | <1.20 |
| wt.% | Cr | Cu | Fe | Mg | Mn | Ni | Ti | Zn |
|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.99 | 4.76 | 5.35 | 1.70 | 0.19 | 6.13 | 4.47 | 0.46 |
| 0.5 | 0.90 | 12.17 | 4.31 | 5.79 | 0.45 | 13.05 | 3.34 | 1.15 |
| 1.0 | - | 23.93 | 2.57 | 12.45 | 0.83 | 11.61 | 1.45 | 2.30 |
| 5.0 | - | 91.07 | - | 58.27 | - | - | - | 11.39 |
| 0.2 wt.% | 0.5 wt.% | |||
|---|---|---|---|---|
| fcc | Liquid | fcc | Liquid | |
| Al-Mn | −0.06 | −0.08 | −0.15 | −0.21 |
| Al-Zn | 0.01 | 0.01 | 0.02 | 0.02 |
| Al-Cr | −0.06 | −0.03 | −0.14 | −0.08 |
| Al-Mg | 0.01 | −0.02 | 0.04 | −0.05 |
| Al-Ti | −0.13 | −0.12 | −0.34 | −0.30 |
| Al-Cu | −0.01 | −0.03 | −0.03 | −0.07 |
| Al-Fe | −0.05 | −0.09 | −0.13 | −0.24 |
| Al-Ni | −0.08 | −0.14 | −0.20 | −0.35 |
| x wt.% | Cr | Cu | Fe | Mg | Mn | Ni | Ti | Zn |
|---|---|---|---|---|---|---|---|---|
| 0.2 | 33.8 | 32.7 | 33.1 | 33.1 | 33.0 | 32.5 | 33.6 | 32.5 |
| 0.5 | 34.4 | 32.7 | 33.8 | 33.7 | 33.2 | 32.2 | 34.1 | 32.3 |
| 1.0 | 35.4 | 32.6 | 33.1 | 34.7 | 33.1 | 31.8 | 34.9 | 31.8 |
| x wt.% | Cr | Cu | Fe | Mg | Mn | Ni | Ti | Zn |
|---|---|---|---|---|---|---|---|---|
| 0.2 | 11.7 | 11.1 | 11.6 | 11.4 | 11.5 | 10.9 | 12.8 | 11.1 |
| 0.5 | 12.2 | 10.8 | 12.1 | 11.6 | 11.9 | 10.3 | 15.0 | 10.7 |
| 1.0 | 12.9 | 10.2 | 12.2 | 11.9 | 9.3 | 9.3 | 18.0 | 10.2 |
| 0.2 wt.% | 0.5 wt.% | 1.0 wt.% | ||||
|---|---|---|---|---|---|---|
| fcc | Liquid | fcc | Liquid | fcc | Liquid | |
| Al-Si8-Cr | −0.27 | −0.95 | −0.34 | −0.91 | −0.45 | −1.11 |
| Al-Si8-Fe | −0.28 | −1.01 | −0.37 | −1.17 | −0.52 | −1.44 |
| Al-Si8-Mg | −0.21 | −0.91 | −0.19 | −0.92 | −0.16 | −0.94 |
| Al-Si8-Mn | −0.29 | −0.99 | −0.40 | −1.12 | −0.57 | −1.34 |
| Al-Si8-Ti | −0.36 | −1.04 | −0.55 | −1.23 | −0.88 | −1.56 |
| Al-Si8-Cu | −0.24 | −0.93 | −0.26 | −0.96 | −0.29 | −1.02 |
| Al-Si8-Ni | −0.31 | −1.05 | −0.45 | −1.26 | −0.68 | −1.62 |
| Al-Si8-Zn | −0.22 | −0.90 | −0.20 | −0.88 | −0.18 | −0.86 |
| 0.2 wt.% | 0.5 wt.% | 1.0 wt.% | ||||
|---|---|---|---|---|---|---|
| fcc | Liquid | fcc | Liquid | fcc | Liquid | |
| Al-Si11-Cr | −0.34 | −1.25 | −0.40 | −1.32 | −0.51 | −1.43 |
| Al-Si11-Fe | −0.36 | −1.32 | −0.45 | −1.48 | −0.60 | −1.76 |
| Al-Si11-Mg | −0.29 | −1.21 | −0.27 | −1.22 | −0.24 | −1.23 |
| Al-Si11-Mn | −0.37 | −1.29 | −0.48 | −1.43 | −0.67 | −1.65 |
| Al-Si11-Ti | −0.43 | −1.34 | −0.63 | −1.55 | −0.95 | −1.89 |
| Al-Si11-Cu | −0.31 | −1.23 | −0.34 | −1.26 | −0.37 | −1.31 |
| Al-Si11-Ni | −0.39 | −1.35 | −0.54 | −1.56 | −0.78 | −1.92 |
| Al-Si11-Zn | −0.29 | −1.20 | −0.28 | −1.19 | −0.26 | −1.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferraro, S.; Palumbo, M.; Baricco, M.; Castellero, A. Solidification Window in Al-Based Casting Alloys. Metals 2025, 15, 489. https://doi.org/10.3390/met15050489
Ferraro S, Palumbo M, Baricco M, Castellero A. Solidification Window in Al-Based Casting Alloys. Metals. 2025; 15(5):489. https://doi.org/10.3390/met15050489
Chicago/Turabian StyleFerraro, Simone, Mauro Palumbo, Marcello Baricco, and Alberto Castellero. 2025. "Solidification Window in Al-Based Casting Alloys" Metals 15, no. 5: 489. https://doi.org/10.3390/met15050489
APA StyleFerraro, S., Palumbo, M., Baricco, M., & Castellero, A. (2025). Solidification Window in Al-Based Casting Alloys. Metals, 15(5), 489. https://doi.org/10.3390/met15050489







