Unveiling High-Pressure Behavior of Sc3AlC MAX Phase: A Comprehensive Theoretical Study on Structural, Mechanical, Dislocation, and Electronic Properties
Abstract
1. Introduction
2. Methodology
3. Results and Discussions
3.1. Structure Properties and Stability
3.2. Mechanical Properties
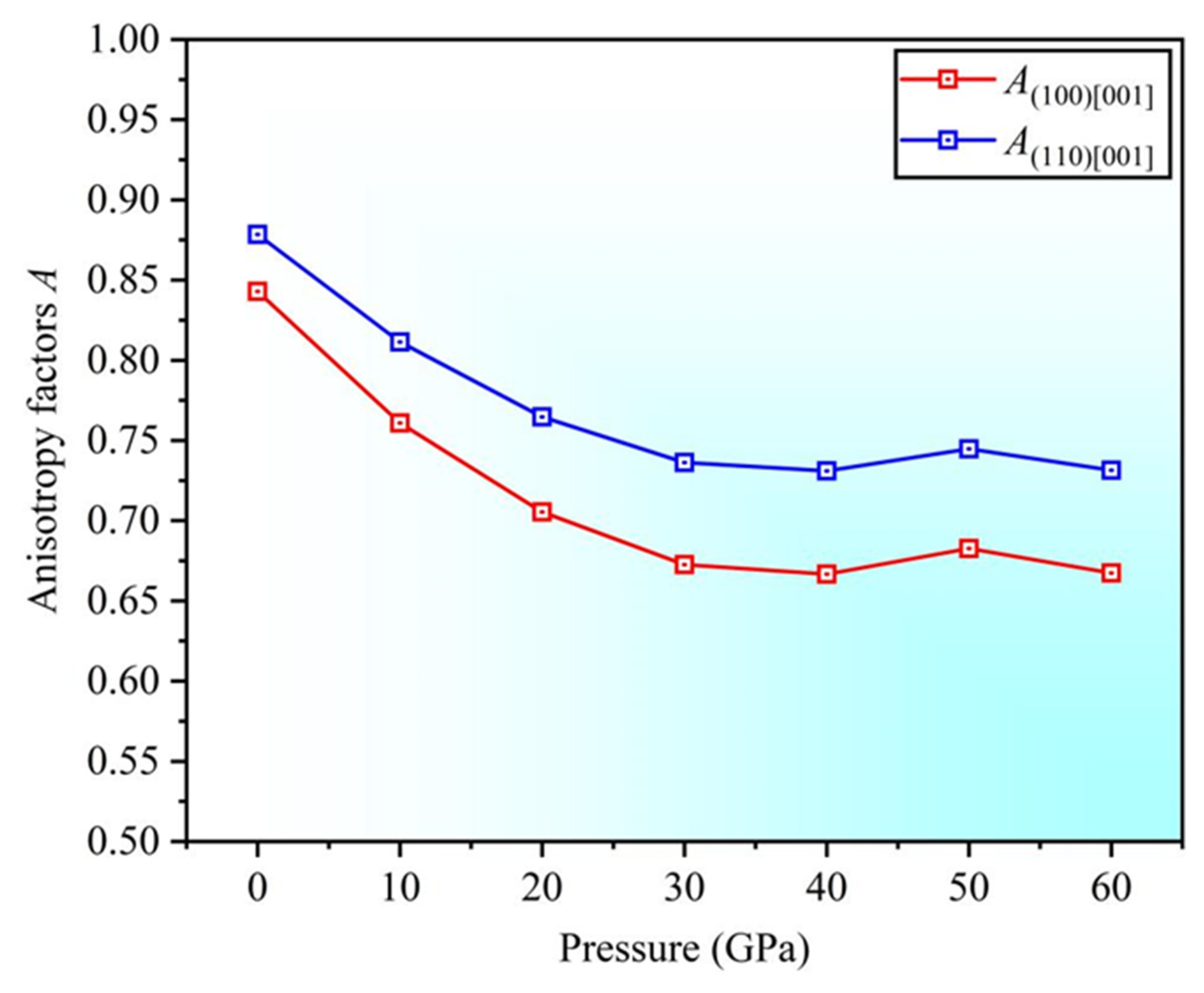
3.3. Anisotropy
3.4. Hardness and Yield Strength
3.5. Energy Factor K
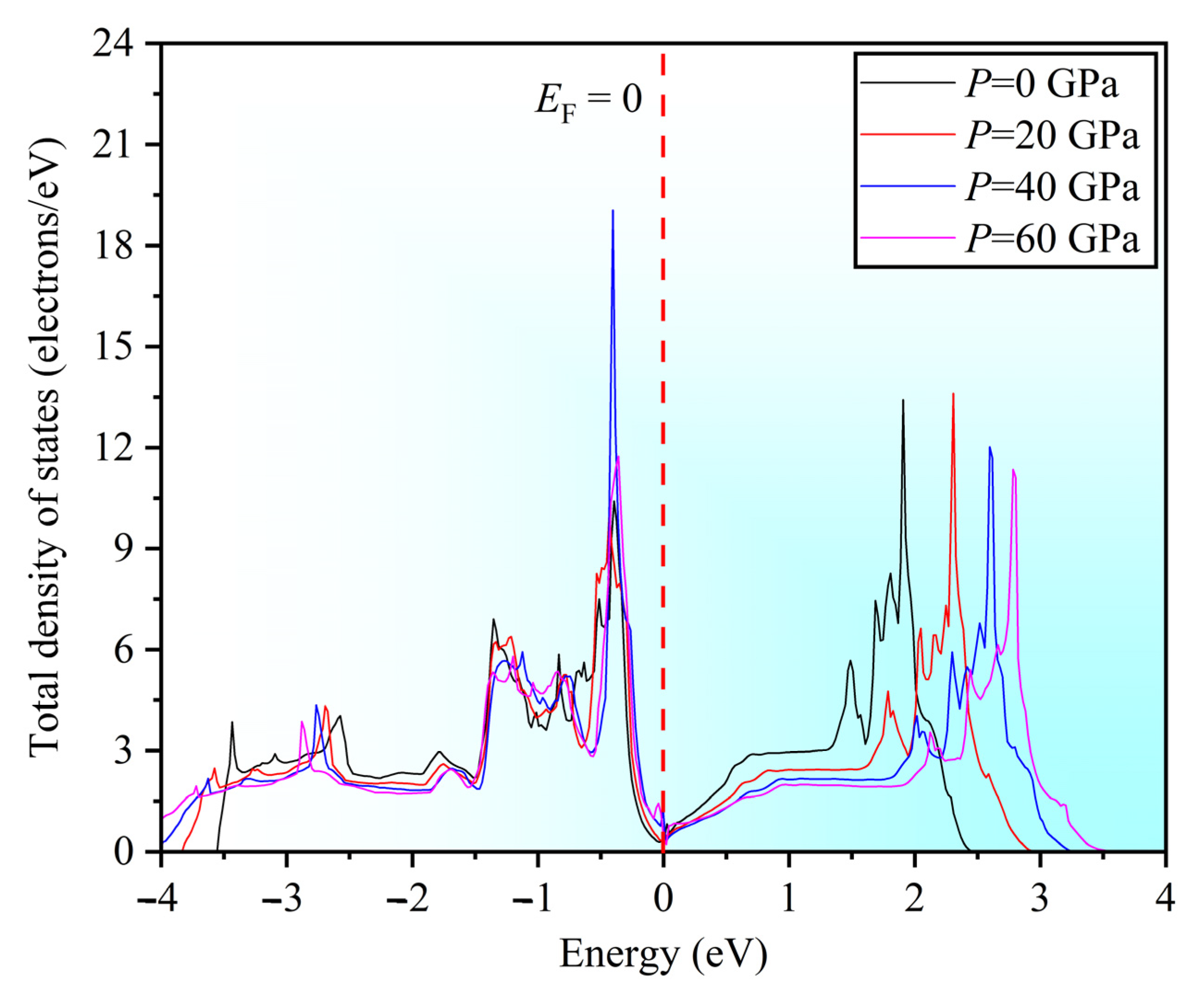
3.6. Electronic Properties
4. Conclusions
- (1)
- Under pressures ranging from 0 to 60 GPa, the lattice constant ratio and volume ratio decrease. The elastic constants satisfy stability criteria, indicating that the structure remains stable under high pressure.
- (2)
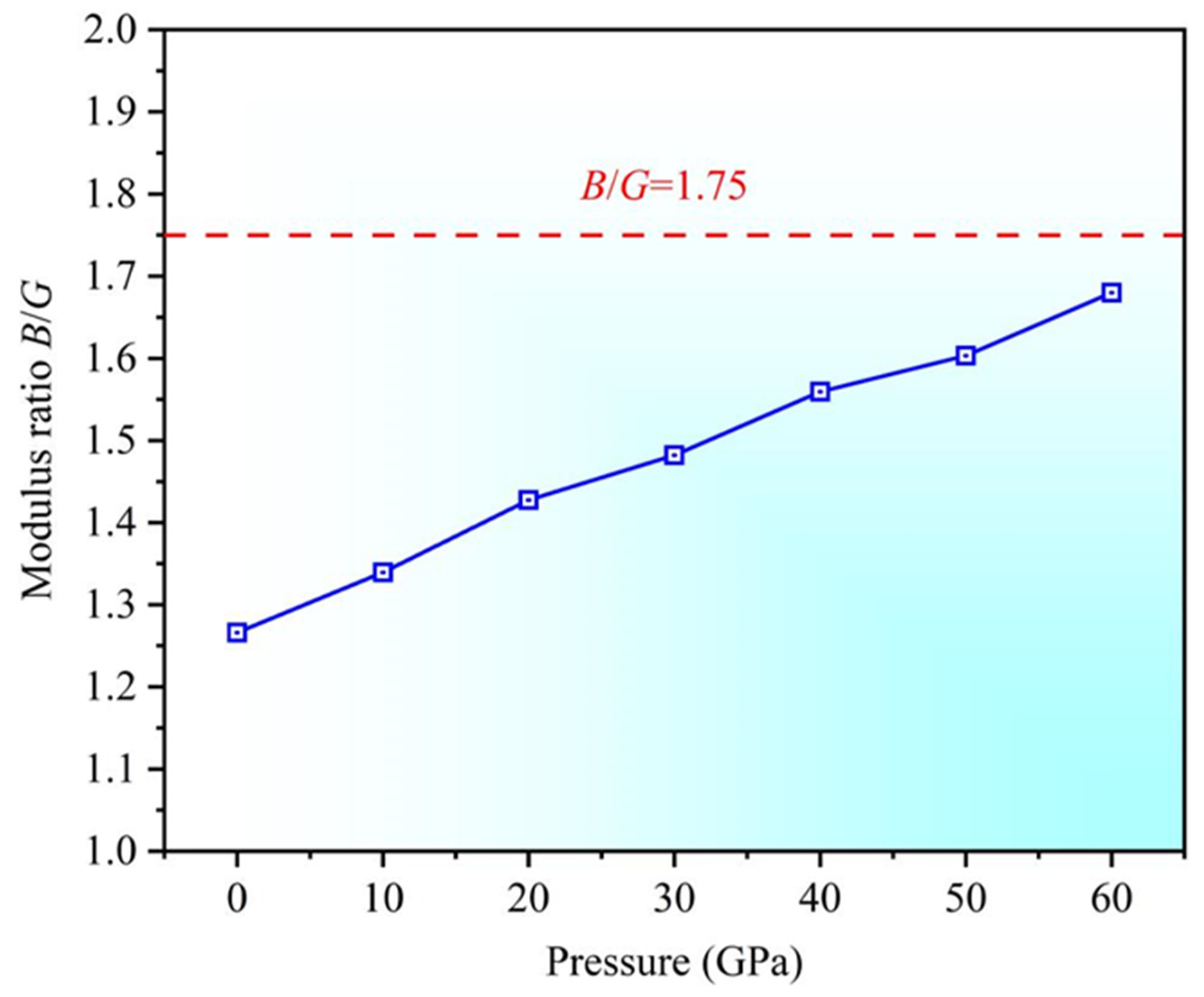
- As the pressure increases, the bulk modulus, Young’s modulus, and shear modulus increase, enhancing resistance to material deformation. The B/G ratio rises, approaching 1.75, suggesting a tendency toward ductile behavior, but the material still maintains its brittle characteristics.
- (3)
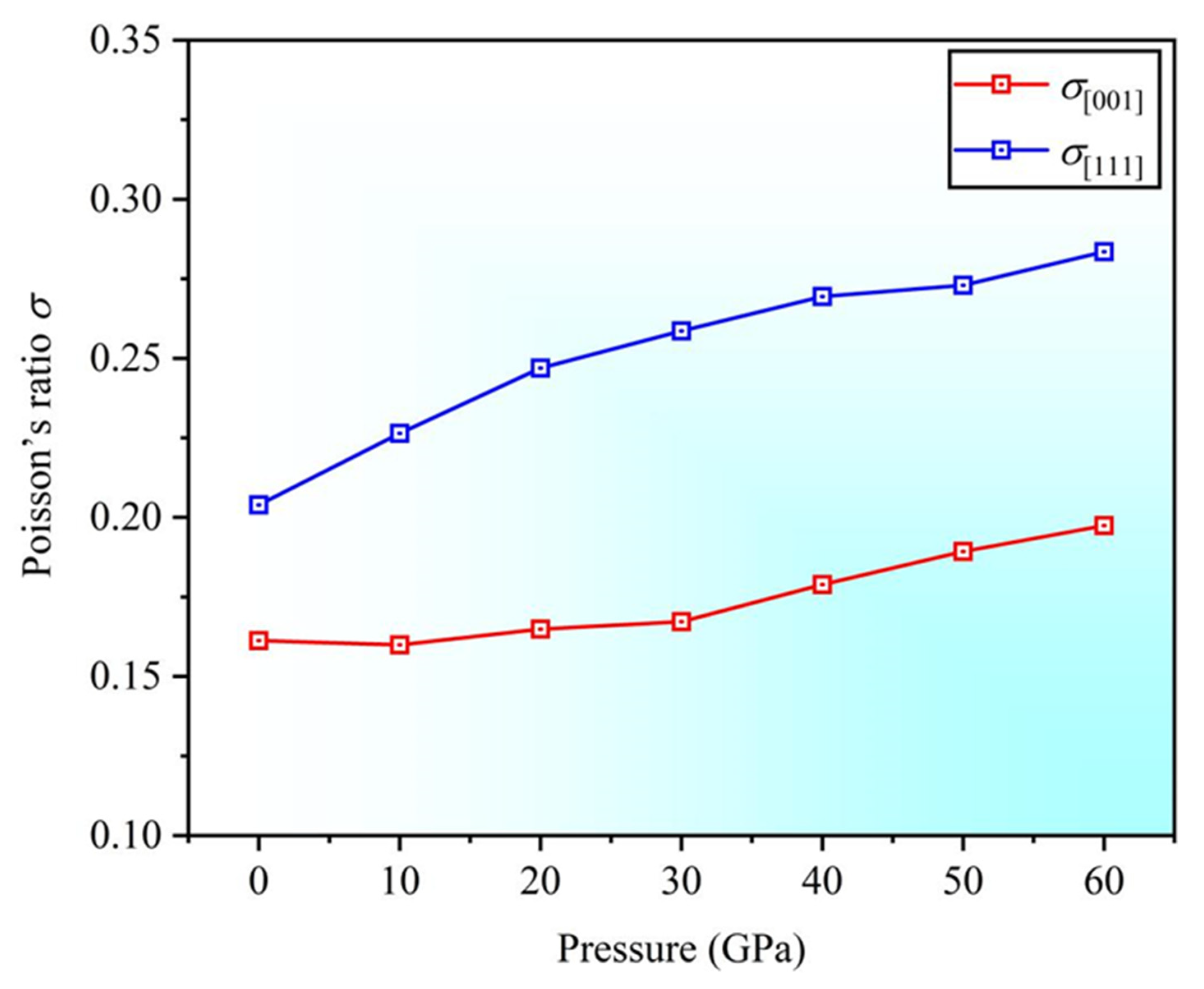
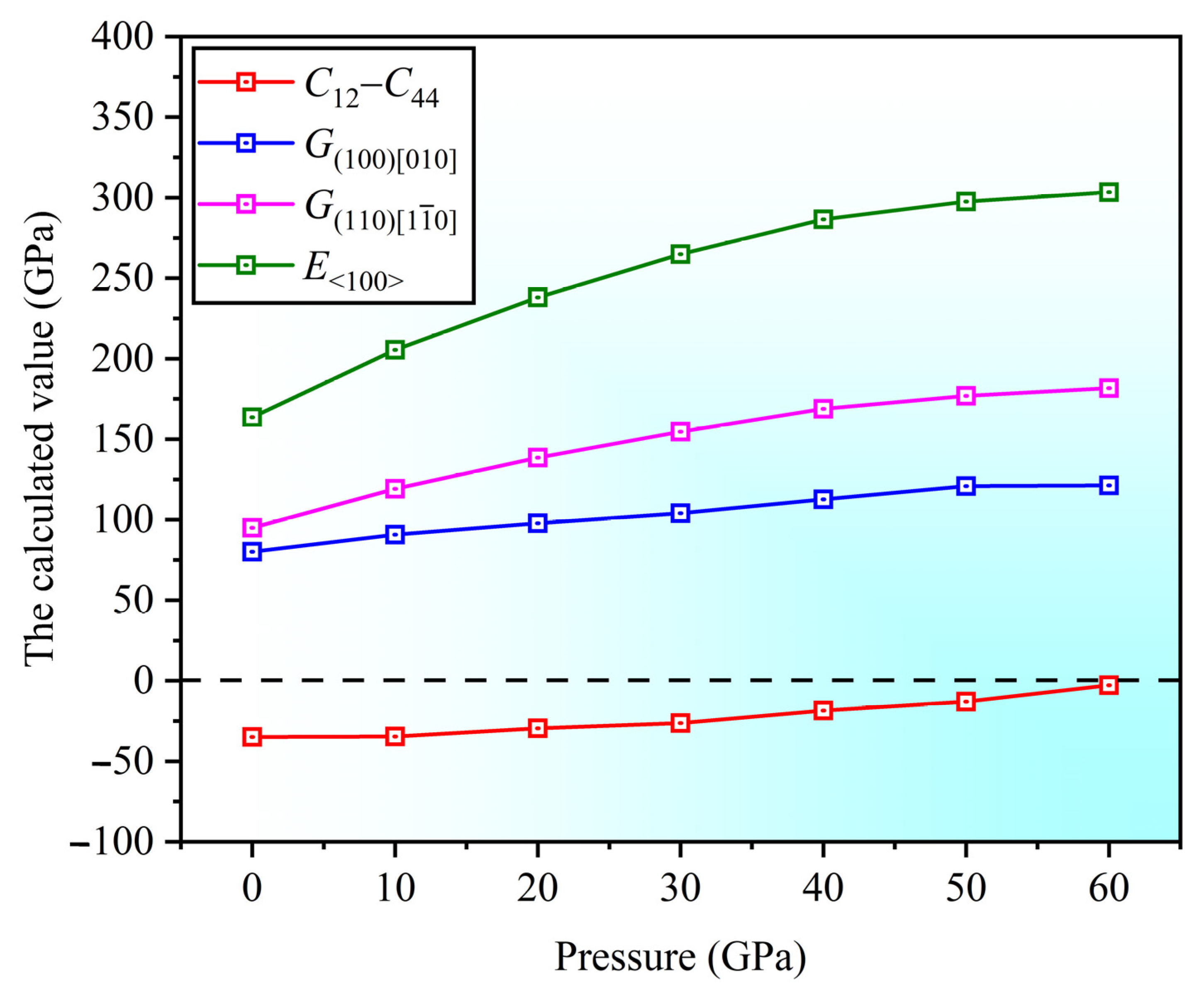
- As the pressure increases, the anisotropy in the and directions also increases. The Poisson’s ratio in the [001] and [111] directions increases, resulting in the enhanced plasticity, with better plasticity along the [111] direction. The negative Cauchy pressure indicates the directional characteristics of interatomic bonding.
- (4)
- Vickers hardness and yield strength increase under pressures of 0 to 10 GPa and remain relatively stable between 10 and 50 GPa, and then decrease sharply above 50 GPa.
- (5)
- High pressure increases the energy factors of edge and screw dislocations, suppressing dislocation nucleation. The mixed dislocation factor increases with increasing pressure, and the dislocation core width reduces, which may inhibit twinning deformation.
- (6)
- High pressure enhances the interatomic bonding in the Sc3AlC MAX phase, while the enhancement effect is not substantial.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, H.; Yu, Y.; Jin, X.; Tian, X.; He, W.; Ma, W. Microstructure and mechanical properties of SiC-SiC joints joined by spark plasma sintering. Ceram. Int. 2016, 42, 14463–14468. [Google Scholar] [CrossRef]
- Shrivastava, V. Microwave processed SrBi2Nb2O9 ferroelectric ceramics with controlled dielectric relaxation and metallic conduction. Ceram. Int. 2016, 42, 10122–10126. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, A.; Duan, Y.; Peng, M. Structural stability, electronic and optical properties of MAX-phase ternary nitrides β-TM4AlN3 (TM = V, Nb, and Ta) using the first-principles explorations. Vacuum 2021, 193, 110529. [Google Scholar] [CrossRef]
- Zhang, Z.; Duan, X.; Jia, D.; Zhou, Y.; Zwaag, S.V.D. On the formation mechanisms and properties of MAX phases: A review. J. Eur. Ceram. Soc. 2021, 41, 3851–3878. [Google Scholar] [CrossRef]
- Ching, W.Y.; Mo, Y.; Aryal, S.; Rulis, P. Intrinsic mechanical properties of 20 MAX-phase compounds. J. Am. Ceram. Soc. 2013, 96, 2292–2297. [Google Scholar] [CrossRef]
- Sokol, M.; Natu, V.; Kota, S.; Barsoum, M.W. On the chemical diversity of the MAX phases. Trends Chem. 2019, 1, 210–223. [Google Scholar] [CrossRef]
- Sauceda, D.; Singh, P.; Falkowski, A.; Chen, Y.; Doung, T.; Vazquez, G.; Radovic, M.; Arroyave, R. High-throughput reaction engineering to assess the oxidation stability of MAX phases. NPJ Comput. Mater. 2021, 7, 6. [Google Scholar] [CrossRef]
- Badie, S.; Sebold, D.; Vaßen, R.; Guillon, O.; Gonzalez-Julian, J. Mechanism for breakaway oxidation of the Ti2AlC MAX phase. Acta Mater. 2021, 215, 117025. [Google Scholar] [CrossRef]
- Bao, W.; Wang, X.G.; Ding, H.; Lu, P.; Zhu, C.; Zhang, G.J.; Xu, F. High-entropy M2AlC-MC (M = Ti, Zr, Hf, Nb, Ta) composite: Synthesis and microstructures. Scripta Mater. 2020, 183, 33–38. [Google Scholar] [CrossRef]
- Nowotny, H.; Boller, H.; Beckmann, O. Alloy phases crystallizing with structures which occur with nonmetallic compounds. J. Solid State Chem. 1970, 2, 462–471. [Google Scholar] [CrossRef]
- Nowotny, V.H. Strukturchemie einiger verbindungen der übergangsmetalle mit den elementen C, Si, Ge, Sn. Prog. Solid State Chem. 1971, 5, 27–70. [Google Scholar] [CrossRef]
- Ghule, A.; Ghule, S.; Garde, C.; Pandey, B.; Ramakrishnan, S. Ab initio study of Sc3MO (M = Al, Ga, In, Tl) and systematics in Sc3MZ (Z = B, C, N, O). Comput. Condens. Matter 2020, 25, e00509. [Google Scholar] [CrossRef]
- Chern, M.Y.; Vennos, D.; DiSalvo, F. Synthesis, structure, and properties of anti-perovskite nitrides Ca3MN, M = P, As, Sb, Bi, Ge, Sn, and Pb. J. Solid State Chem. 1992, 96, 415–425. [Google Scholar] [CrossRef]
- Deng, Z.; Ni, D.; Chen, D.; Bian, Y.; Li, S.; Wang, Z.; Zhao, Y. Anti-perovskite materials for energy storage batteries. InfoMat 2022, 4, e12252. [Google Scholar] [CrossRef]
- Lenggenhager, P.M.; Liu, X.; Neupert, T.; Bzdušek, T. Universal higher-order bulk-boundary correspondence of triple nodal points. Phys. Rev. B 2022, 106, 085129. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projected augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533. [Google Scholar] [CrossRef]
- Pack, J.D.; Monkhorst, H.J. Special Points for Brillonin-Zone Integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
- Gesing, T.M.; Wachtmann, K.H.; Jeitschko, W. The Perovskite Carbides A3MC (A = Sc, Y, La-Nd, Sm, Gd-Lu; M = AI, Ga, In, Tl, Sn, Pb). Z. Naturforsch. B 1997, 52, 176–182. [Google Scholar] [CrossRef]
- Haddadi, K.; Bouhemadou, A.; Zerarga, F.; Bin-Omran, S. First-principles investigation of the ternary scandium based inverse-perovskite carbides Sc3AC (A = Al, Ga, In and Tl). Solid State Sci. 2012, 14, 1175–1185. [Google Scholar] [CrossRef]
- Kanchana, V.; Ram, S. Electronic structure and mechanical properties of Sc3AC (A = Al, Ga, In, Tl) and Sc3BN (B = Al, In): Ab-initio study. Intermetallics 2012, 23, 39–48. [Google Scholar] [CrossRef]
- Medkour, Y.; Roumili, A.; Maouche, D.; Saoudi, A. A first-principles study on the structural, elastic and electronic properties of AlCSc3 and AlNSc3. Solid State Commun. 2009, 149, 1840–1842. [Google Scholar] [CrossRef]
- Rayhan, M.; Ali, M.; Jahan, N.; Hossain, M.; Uddin, M.; Islam, A.; Naqib, S. Insights into the unrevealed physical properties of Sc2Al2C3 compared with other Sc-Al-C systems via ab-initio investigation. Phys. Open 2024, 19, 100217. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, X.; Wang, F. Exploring the electronic, mechanical, anisotropic and optical properties of the Sc-Al-C MAX phases from a first principles calculations. Chem. Phys. Lett. 2024, 836, 141024. [Google Scholar] [CrossRef]
- Patil, S.K.R.; Khare, S.V.; Tuttle, B.R.; Bording, J.K.; Kodambaka, S. Mechanical stability of possible structures of PtN investigated using first-principles calculations. Phys. Rev. B 2006, 73, 104118. [Google Scholar] [CrossRef]
- Wang, J.; Yip, S.; Phillpot, S.R.; Wolf, D. Crystal instabilities at finite strain. Phys. Rev. Lett. 1993, 71, 4182. [Google Scholar] [CrossRef]
- Wallace, D.C.; Callen, H. Thermodynamics of Crystals. Am. J. Phys. 1972, 40, 1718–1719. [Google Scholar] [CrossRef]
- Yang, X.W.; Zhu, J.C.; Lai, Z.H.; Liu, Y.; He, D.; Nong, Z.S. Finite element analysis of quenching temperature field, residual stress and distortion in A357 aluminum alloy large complicated thin-wall workpieces. T. Nonferr. Metal. Soc. 2013, 23, 1751–1760. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, Y.; Zheng, F.; Wang, B.T.; Zhang, P. Electronic, mechanical, and thermodynamic properties of americium dioxide. J. Nucl. Mater. 2013, 441, 411–420. [Google Scholar] [CrossRef]
- Hill, R. The elastic behavior of crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Iotova, D.; Kioussis, N.; Lim, S.P. Electronic structure and elastic properties of the Ni3X (X = Mn, Al, Ga, Si, Ge) intermetallics. Phys. Rev. B 1996, 54, 14413–14422. [Google Scholar] [CrossRef] [PubMed]
- Cottrel, A.H. Advanced Structural Materials. In Proceedings of the 2nd European Conference on Advanced Materials and Processes, Cambridge, UK, 22–24 July 1991. [Google Scholar]
- Fu, H.; Li, D.; Peng, F.; Gao, T.; Cheng, X. Structural and elastic properties of γTiAl under high pressure from electronic structure calculations. J. Alloys Comp. 2009, 473, 255–261. [Google Scholar] [CrossRef]
- Mattesini, M.; Ahuja, R.; Johansson, B. Cubic Hf3N4 and Zr3N4: A class of hard materials. Phys. Rev. B 2003, 68, 184108. [Google Scholar] [CrossRef]
- Yoo, M.H. On the theory of anomalous yield behavior of Ni3Al—Effect of elastic anisotropy. Scripta Metall. 1986, 20, 915–920. [Google Scholar] [CrossRef]
- Fu, H.; Li, X.F.; Liu, W.F.; Ma, Y.; Tao, G.; Hong, X. Electronic and dynamical properties of NiAl studied from first principles. Intermetallics 2011, 19, 1959–1967. [Google Scholar] [CrossRef]
- Lau, K.; McCurdy, A.K. Elastic anisotropy factors for orthorhombic, tetragonal, and hexagonal crystals. Phys. Rev. B 1998, 58, 8980–8984. [Google Scholar] [CrossRef]
- Friák, M.; Šob, M.; Vitek, V. Ab initio calculation of tensile strength in iron. Philos. Mag. 2003, 83, 3529–3537. [Google Scholar] [CrossRef]
- Zhu, Y.M.; Weyland, M.; Morton, A.J.; Oh-ishi, K.; Hono, K.; Nie, J.F. The building block of long-period structures in Mg-RE-Zn alloys. Scripta Mater. 2009, 60, 980–983. [Google Scholar] [CrossRef]
- Fu, H.; Li, D.; Peng, F.; Gao, T.; Cheng, X. Ab initio calculations of elastic constants and thermodynamic properties of NiAl under high pressures. Comp. Mater. Sci. 2008, 44, 774–778. [Google Scholar] [CrossRef]
- Johnson, R.A. Analytic nearest-neighbor model for fcc metals. Phys. Rev. B 1988, 37, 3924–3931. [Google Scholar] [CrossRef]
- Pettifor, D. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Tse, J.S. Intrinsic hardness of crystalline solids. J. Superhard Mater. 2010, 32, 177–191. [Google Scholar] [CrossRef]
- Smedskjaer, M.M.; Mauro, J.C.; Yue, Y. Prediction of glass hardness using temperature-dependent constraint theory. Phys. Rev. Lett. 2010, 105, 115503. [Google Scholar] [CrossRef]
- Li, K.; Wang, X.; Zhang, F.; Xue, D. Electronegativity identification of novel superhard materials. Phys. Rev. Lett. 2008, 100, 235504. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; He, J.; Wu, E.; Liu, S.; Yu, D.; Li, D.; Zhang, S.; Tian, Y. Hardness of covalent crystals. Phys. Rev. Lett. 2003, 91, 015502. [Google Scholar] [CrossRef]
- Šimůnek, A.; Vackář, J. Hardness of covalent and ionic crystals: First-principle calculations. Phys. Rev. Lett. 2006, 96, 085501. [Google Scholar] [CrossRef]
- Chen, X.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Savin, M.M.; Chernov, V.M.; Strokova, A.M. Energy factor of dislocations in hexagonal crystals. Phys. Status Solidi A 1976, 35, 747–754. [Google Scholar] [CrossRef]
- Foreman, A.J.E. Dislocation energies in anisotropic crystals. Acta Metall. 1955, 3, 322–330. [Google Scholar] [CrossRef]
- Reid, C.N. Dislocation widths in anisotropic B.C.C. crystals. Acta Metall. 1966, 14, 13–16. [Google Scholar] [CrossRef]
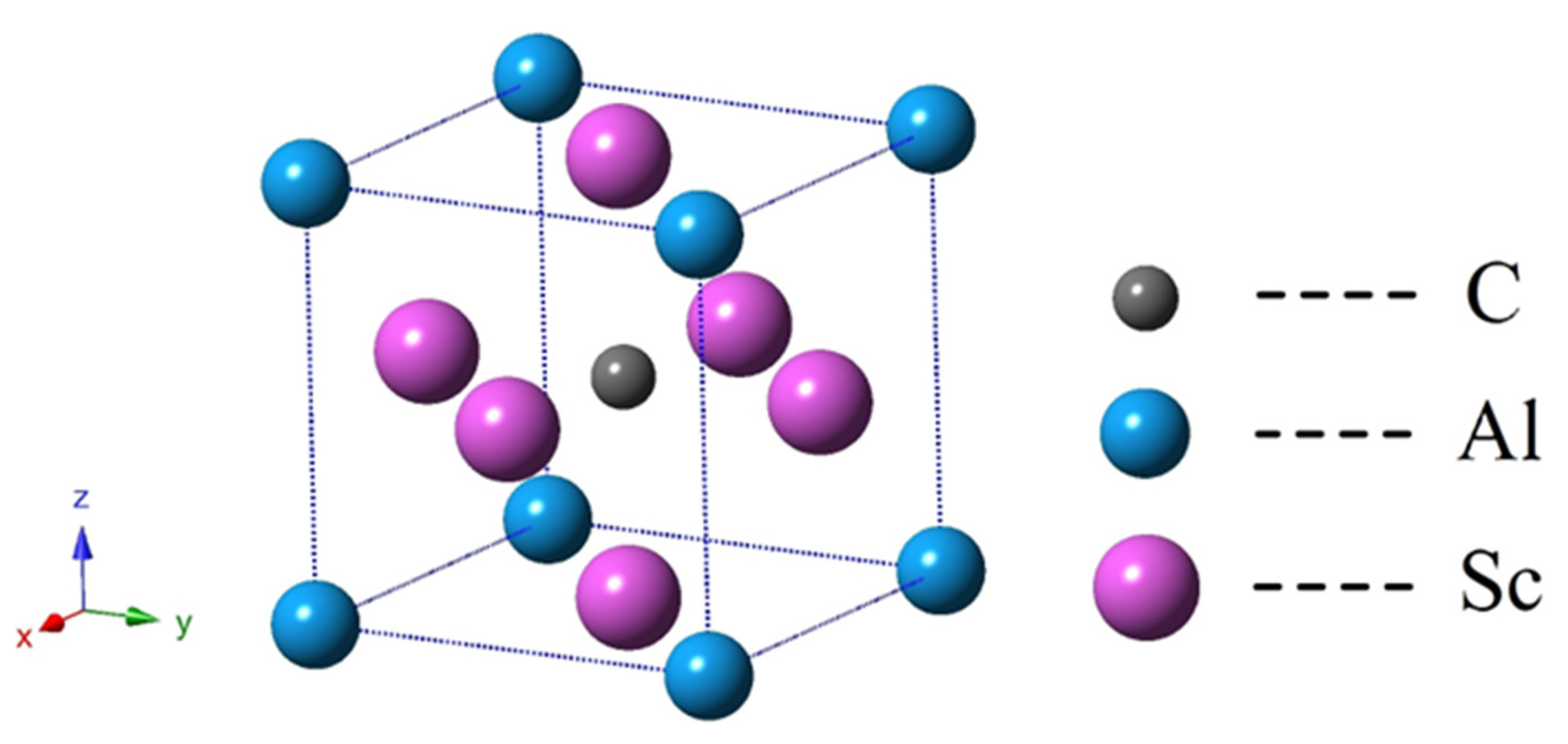
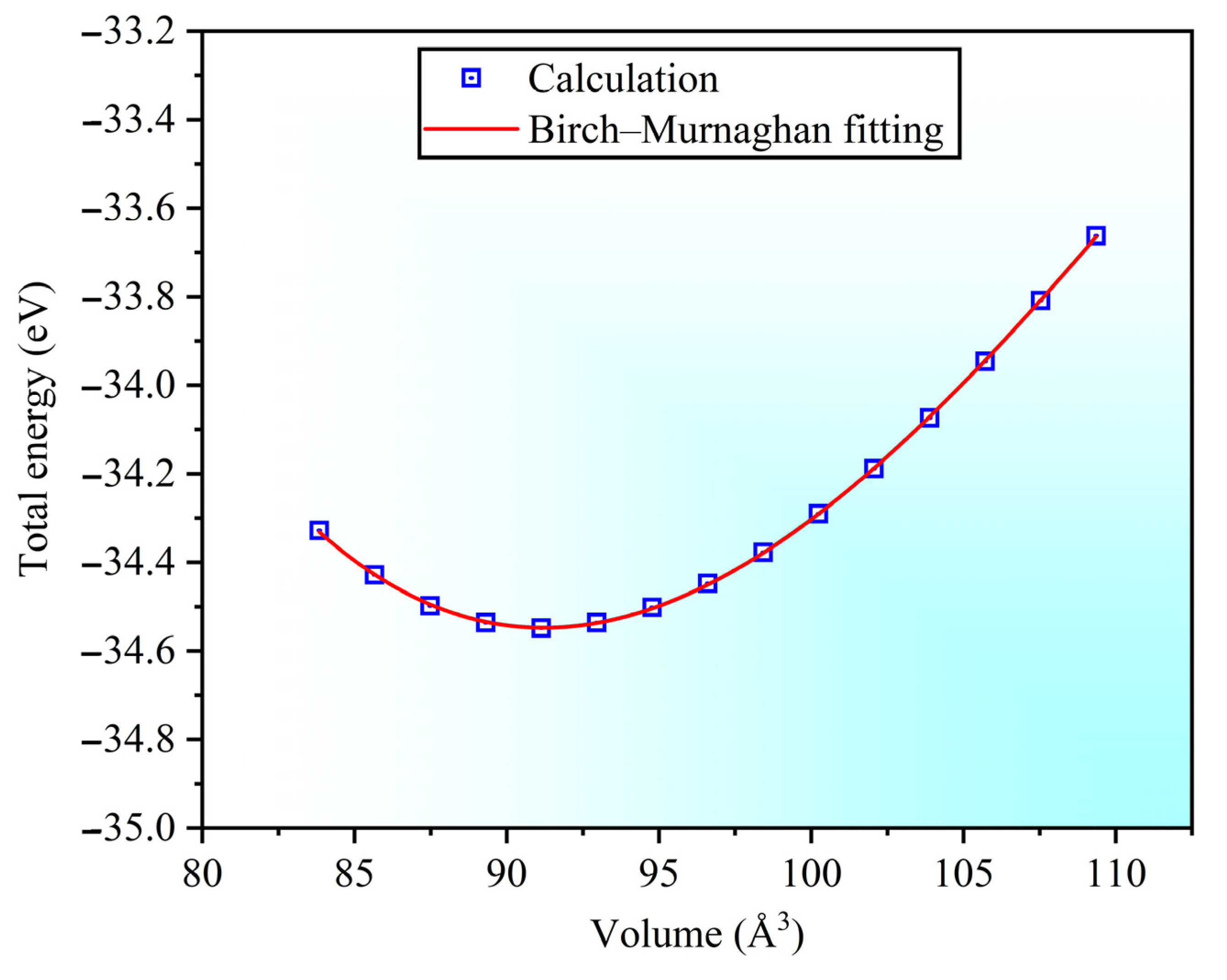
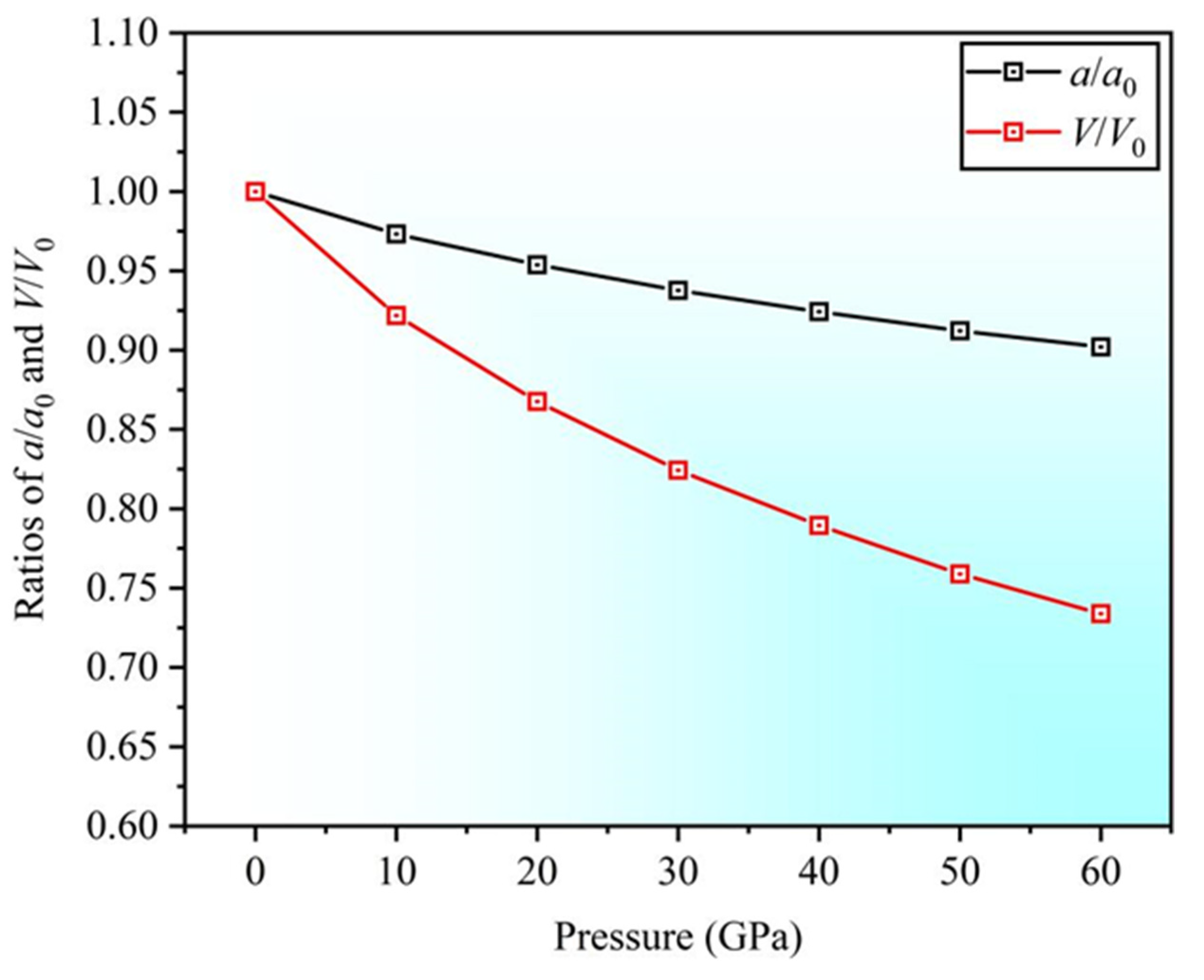
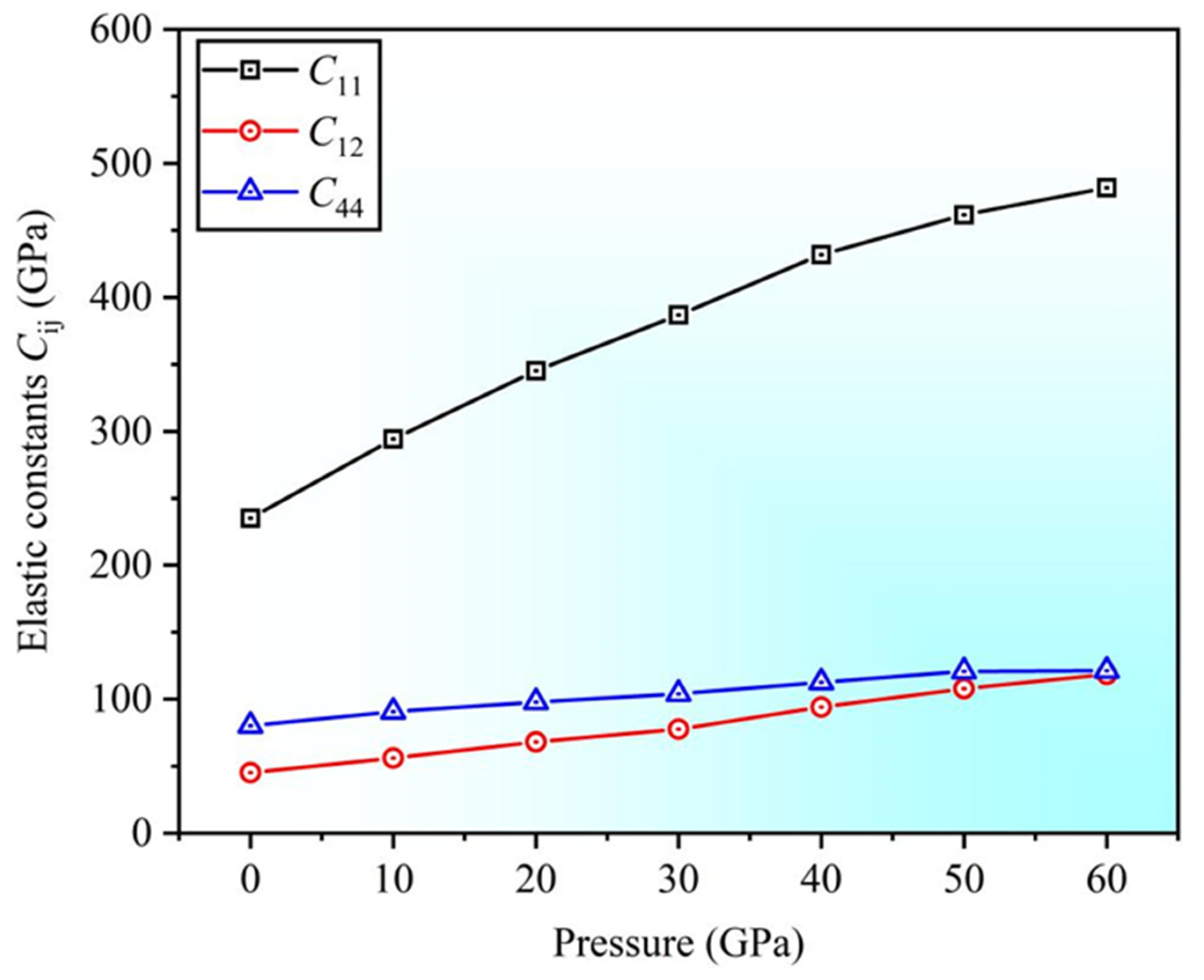




| Sc3AlC | Present | Experimental Values | Theoretical Values |
|---|---|---|---|
| Lattice parameter | 4.500 | 4.498 [22], 4.48 [10], | 4.508 [26], 4.480 [25], 4.508 [23], |
| 4.5004 [12] | 4.51 [27], 4.51 [24], 4.5119 [12] |
| Sc3AlC | Present | Theoretical Data |
|---|---|---|
| C11 | 235.2 | 220.85 [26], 224.90 [25], 219.20 [23], 220 [24], 225 [27], 220 [22] |
| C12 | 45.21 | 42.15 [26], 40.50 [25], 40.35 [23], 40 [24], 41.5 [27], 43 [22] |
| C44 | 80.08 | 80.12 [26], 80.80 [25], 80.19 [23], 79 [24], 80.3 [27], 79 [22] |
| B | 108.54 | 101.72 [26], 101.60 [25], 99.98 [23], 99.91 [24], 102.70 [27], 102 [22] |
| E | 203.62 | 197.03 [26], 199.70 [25], 196.40 [23], 195 [24], 199.27 [27] |
| G | 85.74 | 83.69 [26], 85.10 [25], 83.80 [23], 83.26 [24], 84.68 [27], 83 [22] |
| σ | 0.16 | 0.18 [26], 0.17 [25], 0.17 [23], 0.17 [24], 0.18 [27], 0.18 [22] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, J.; Wang, Z.; Zhang, L.; Ma, L.; Tang, P. Unveiling High-Pressure Behavior of Sc3AlC MAX Phase: A Comprehensive Theoretical Study on Structural, Mechanical, Dislocation, and Electronic Properties. Metals 2025, 15, 492. https://doi.org/10.3390/met15050492
Xi J, Wang Z, Zhang L, Ma L, Tang P. Unveiling High-Pressure Behavior of Sc3AlC MAX Phase: A Comprehensive Theoretical Study on Structural, Mechanical, Dislocation, and Electronic Properties. Metals. 2025; 15(5):492. https://doi.org/10.3390/met15050492
Chicago/Turabian StyleXi, Junping, Zhipeng Wang, Linkun Zhang, Li Ma, and Pingying Tang. 2025. "Unveiling High-Pressure Behavior of Sc3AlC MAX Phase: A Comprehensive Theoretical Study on Structural, Mechanical, Dislocation, and Electronic Properties" Metals 15, no. 5: 492. https://doi.org/10.3390/met15050492
APA StyleXi, J., Wang, Z., Zhang, L., Ma, L., & Tang, P. (2025). Unveiling High-Pressure Behavior of Sc3AlC MAX Phase: A Comprehensive Theoretical Study on Structural, Mechanical, Dislocation, and Electronic Properties. Metals, 15(5), 492. https://doi.org/10.3390/met15050492






