Mechanical Property Model of Q620 High-Strength Steel with Corrosion Effects
Abstract
1. Introduction
2. Materials and Methods
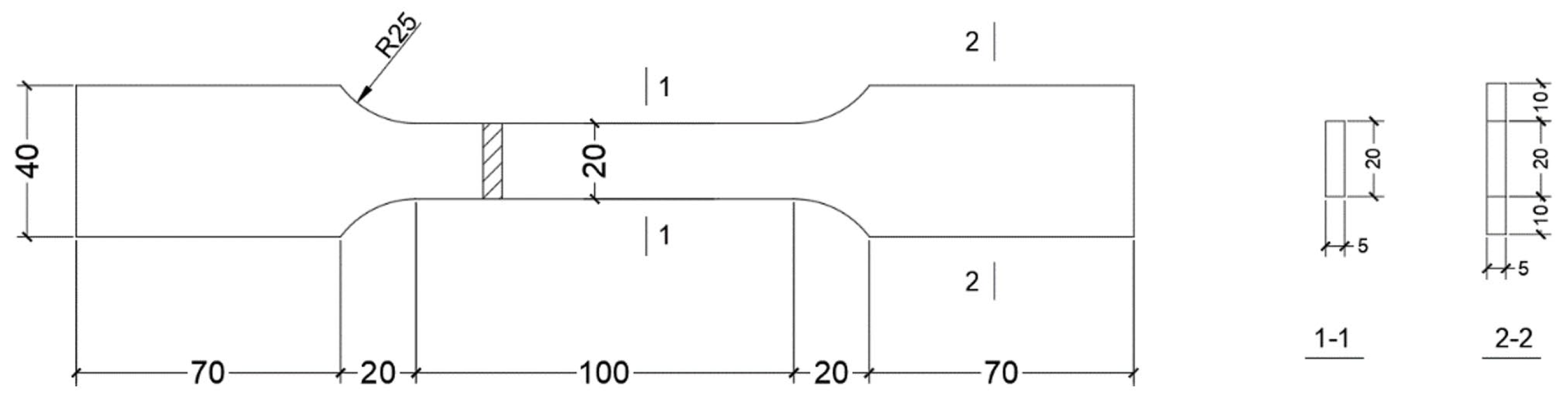
2.1. Test Specimen
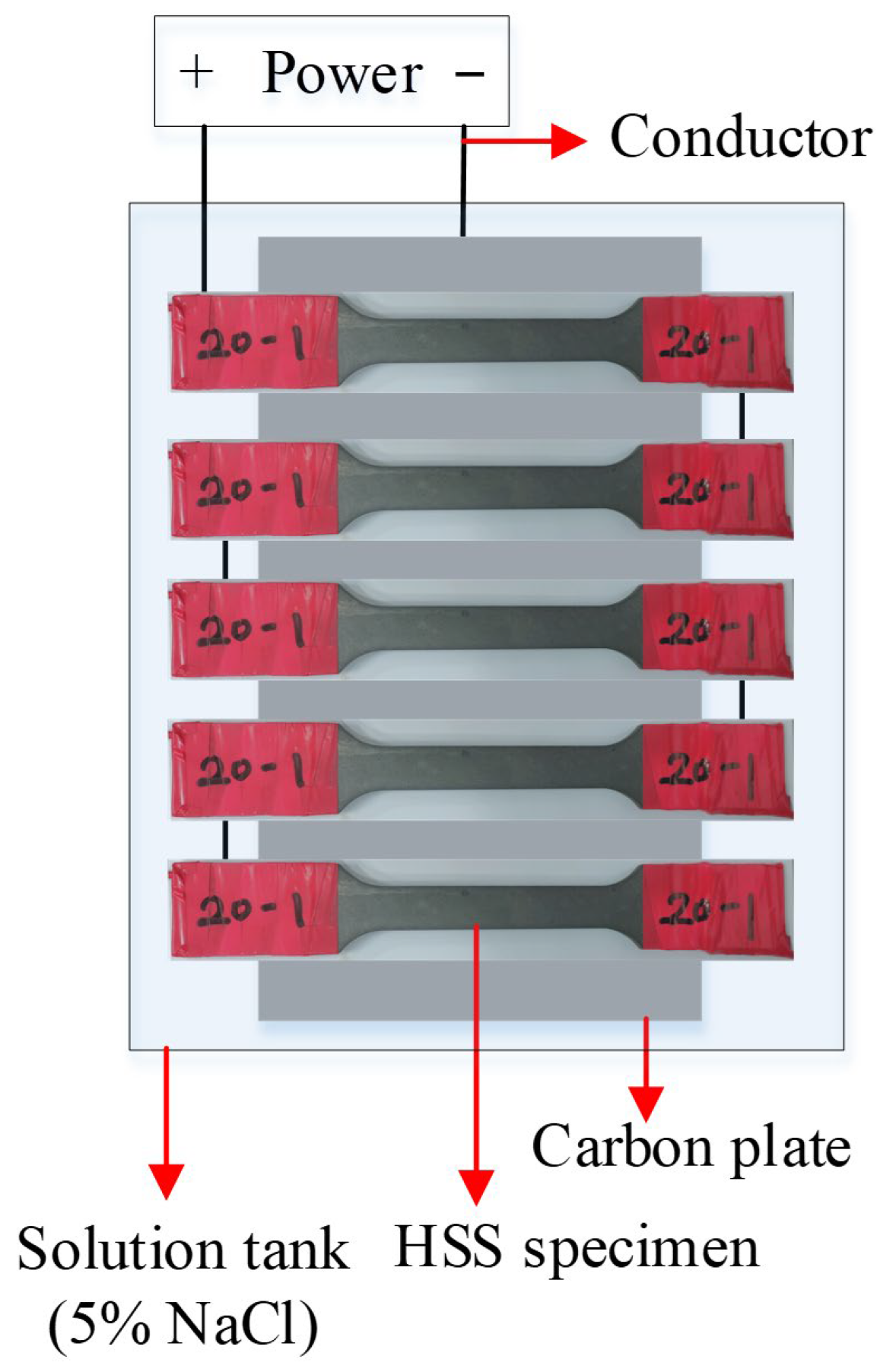
2.2. Electrochemical Accelerated Corrosion Test Procedure
2.3. Tensile Coupon Test Procedure
3. Results
3.1. Corrosion Test Result
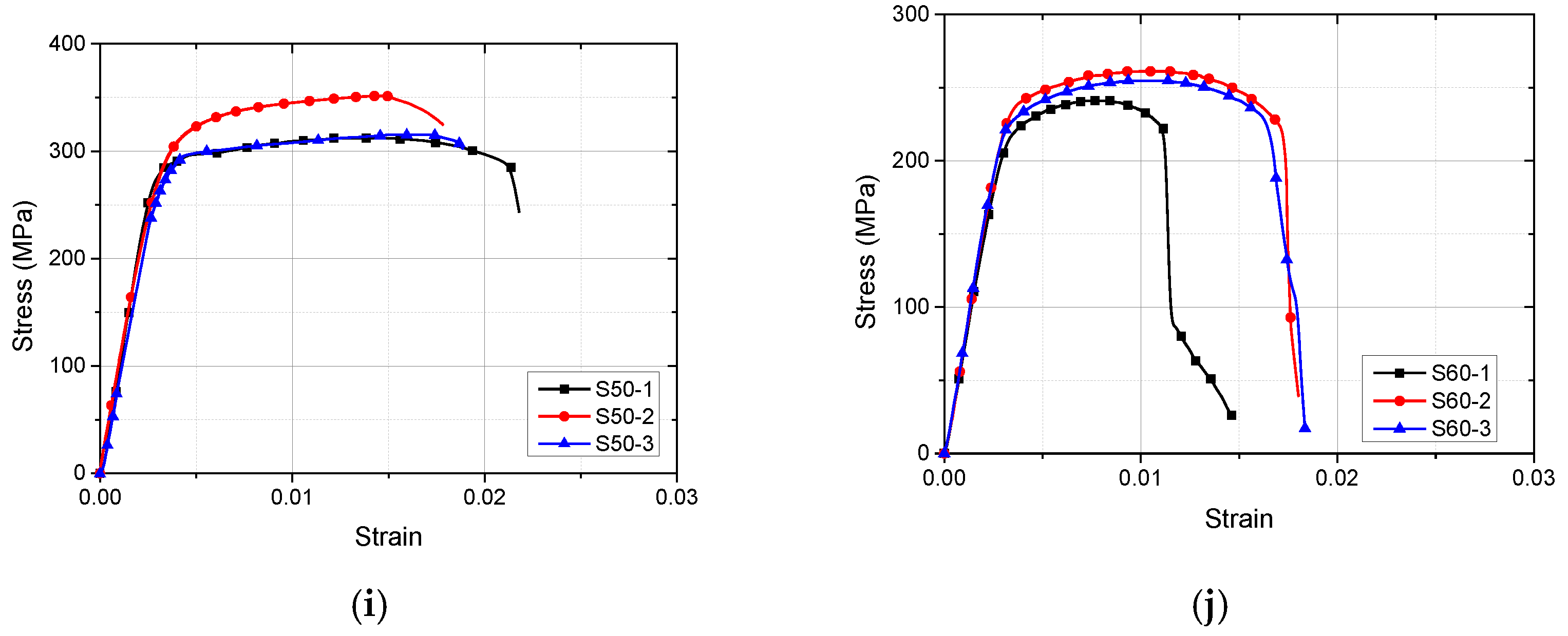
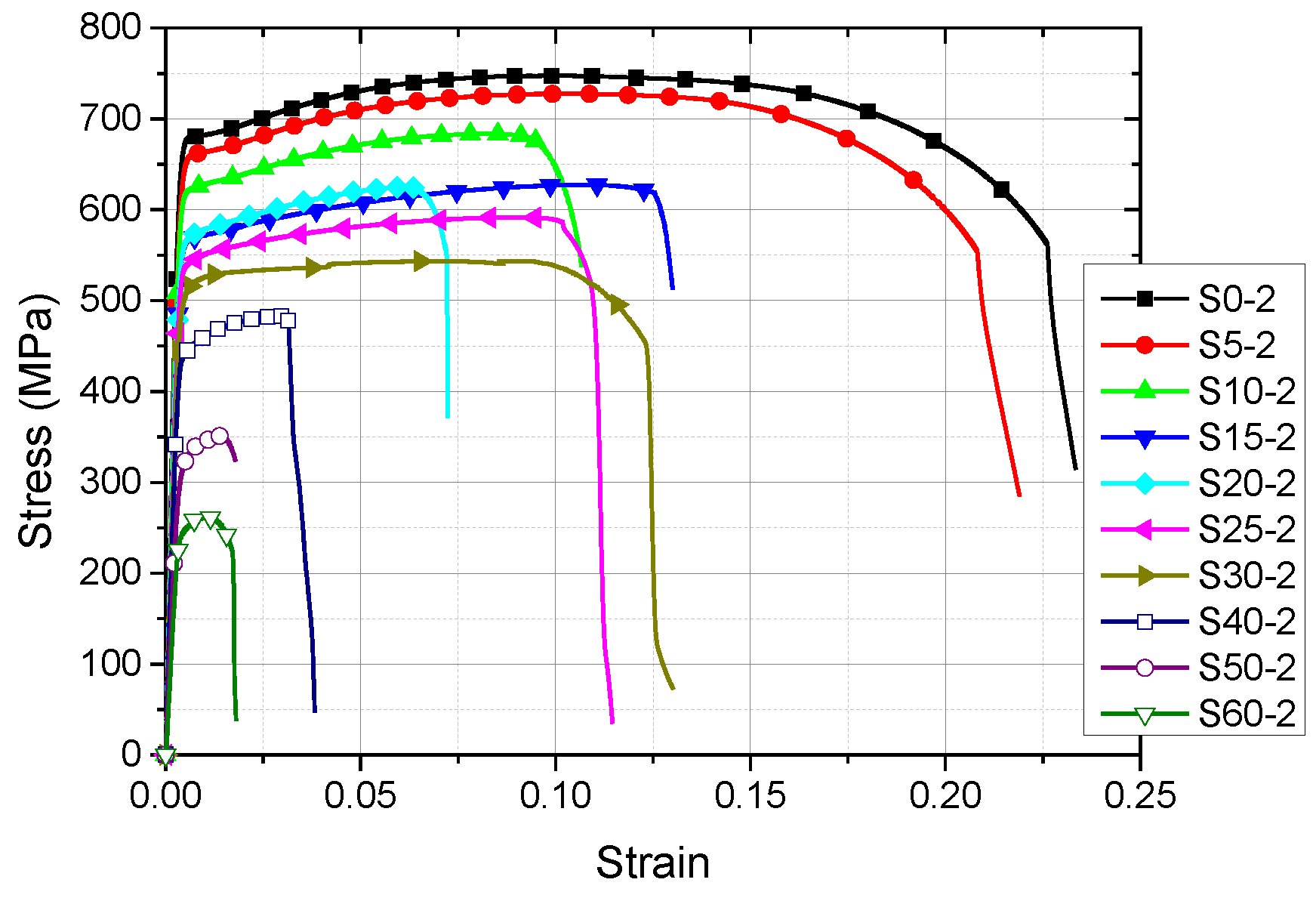
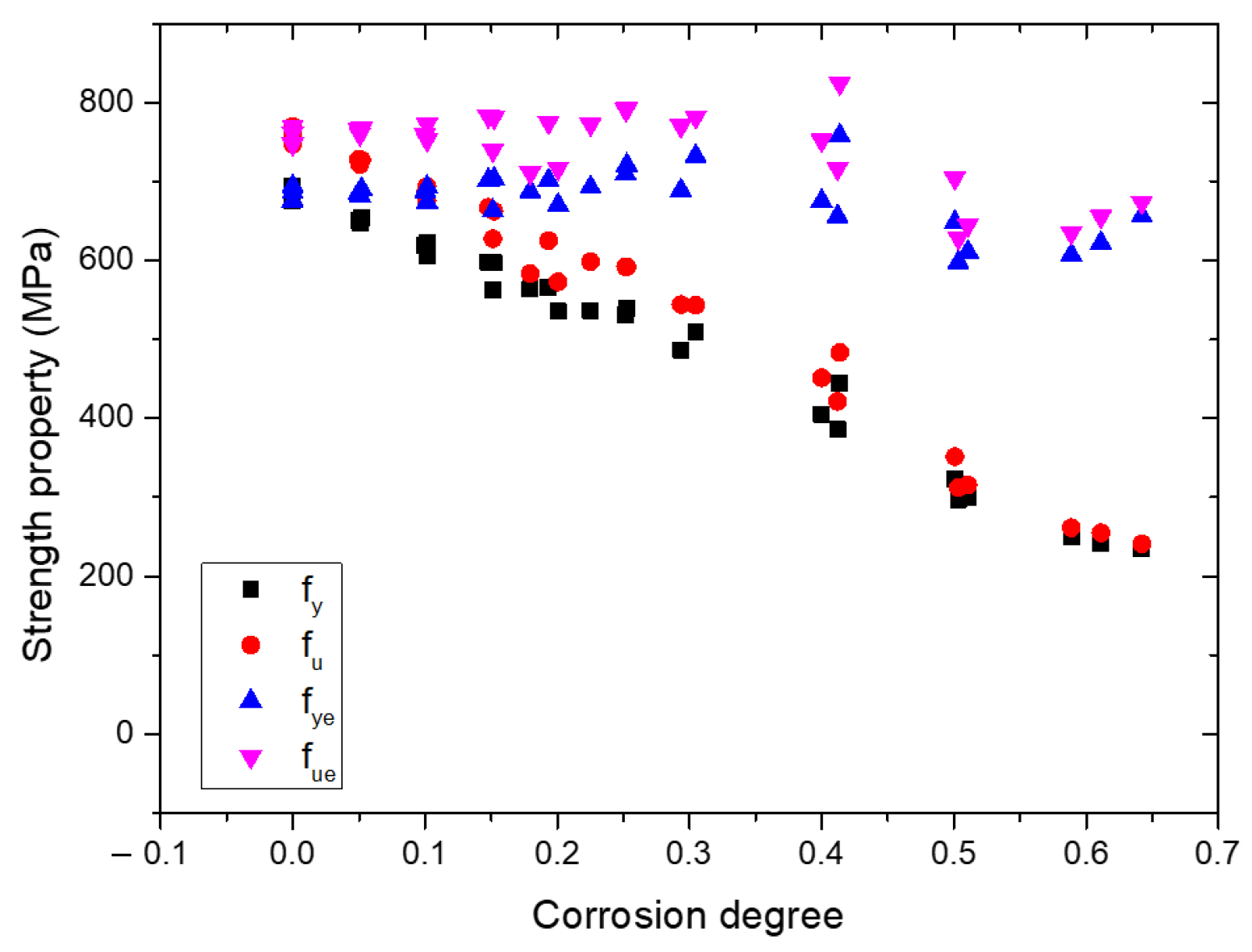
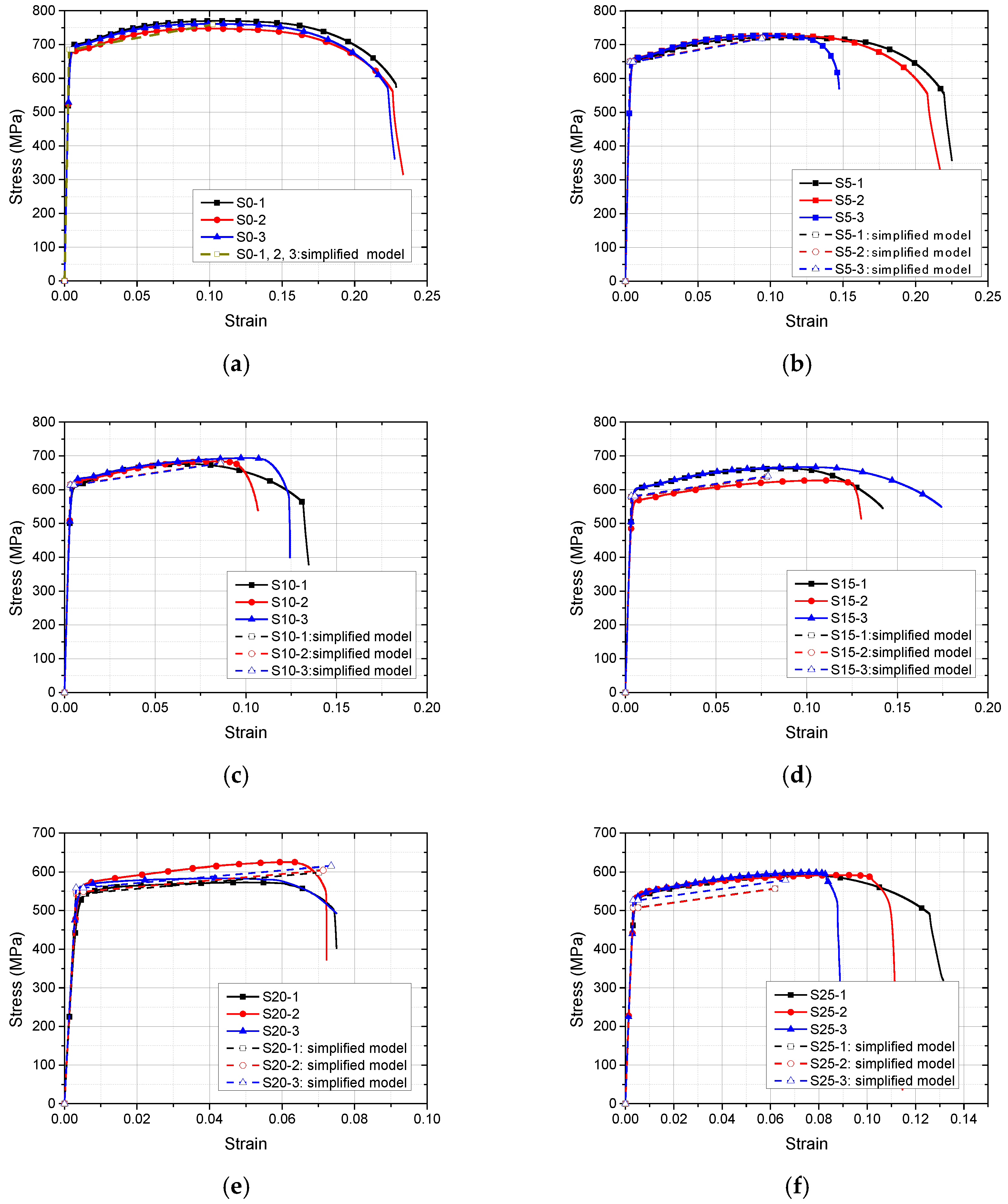
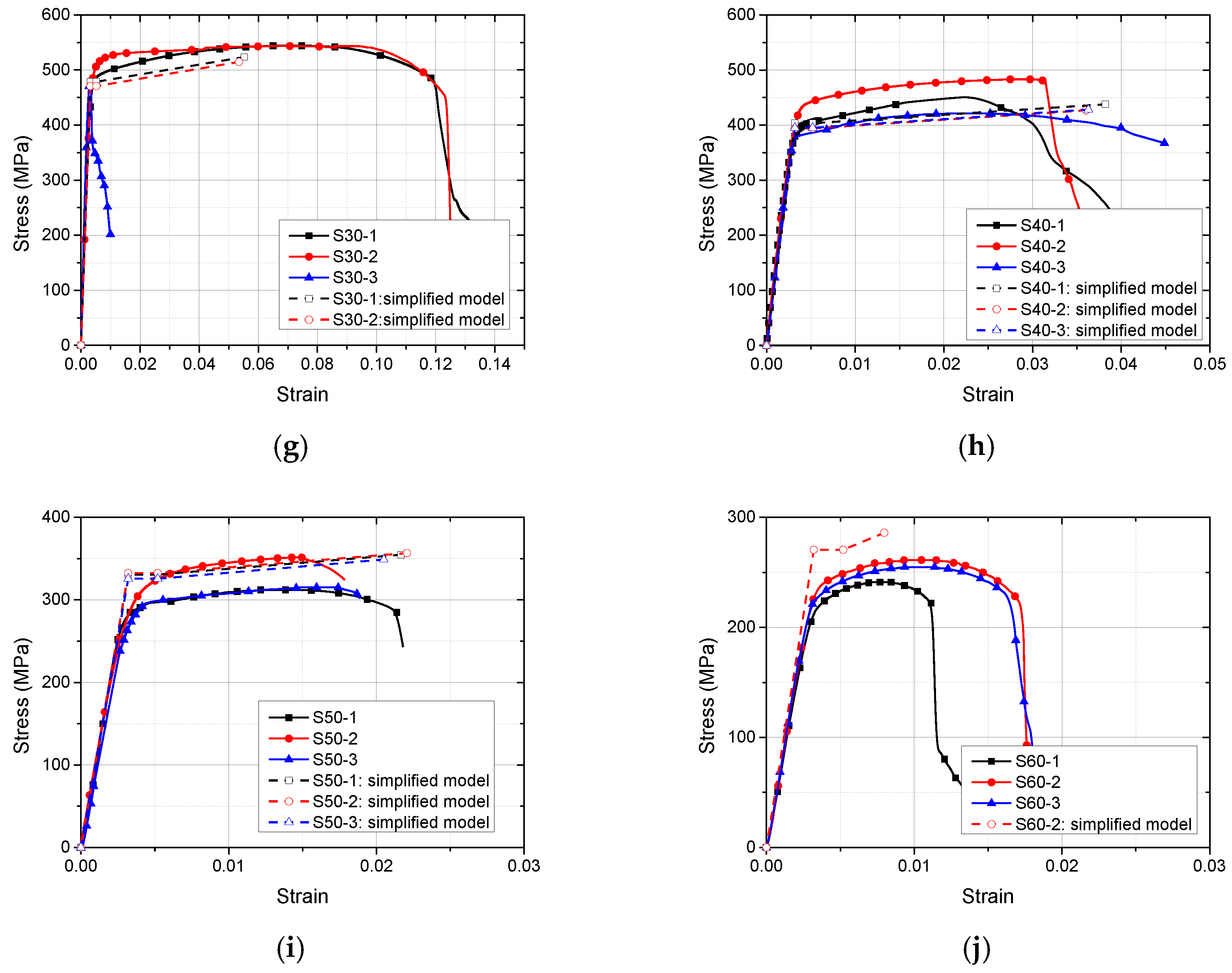
3.2. Stress–Strain Property
3.3. Failure Performance
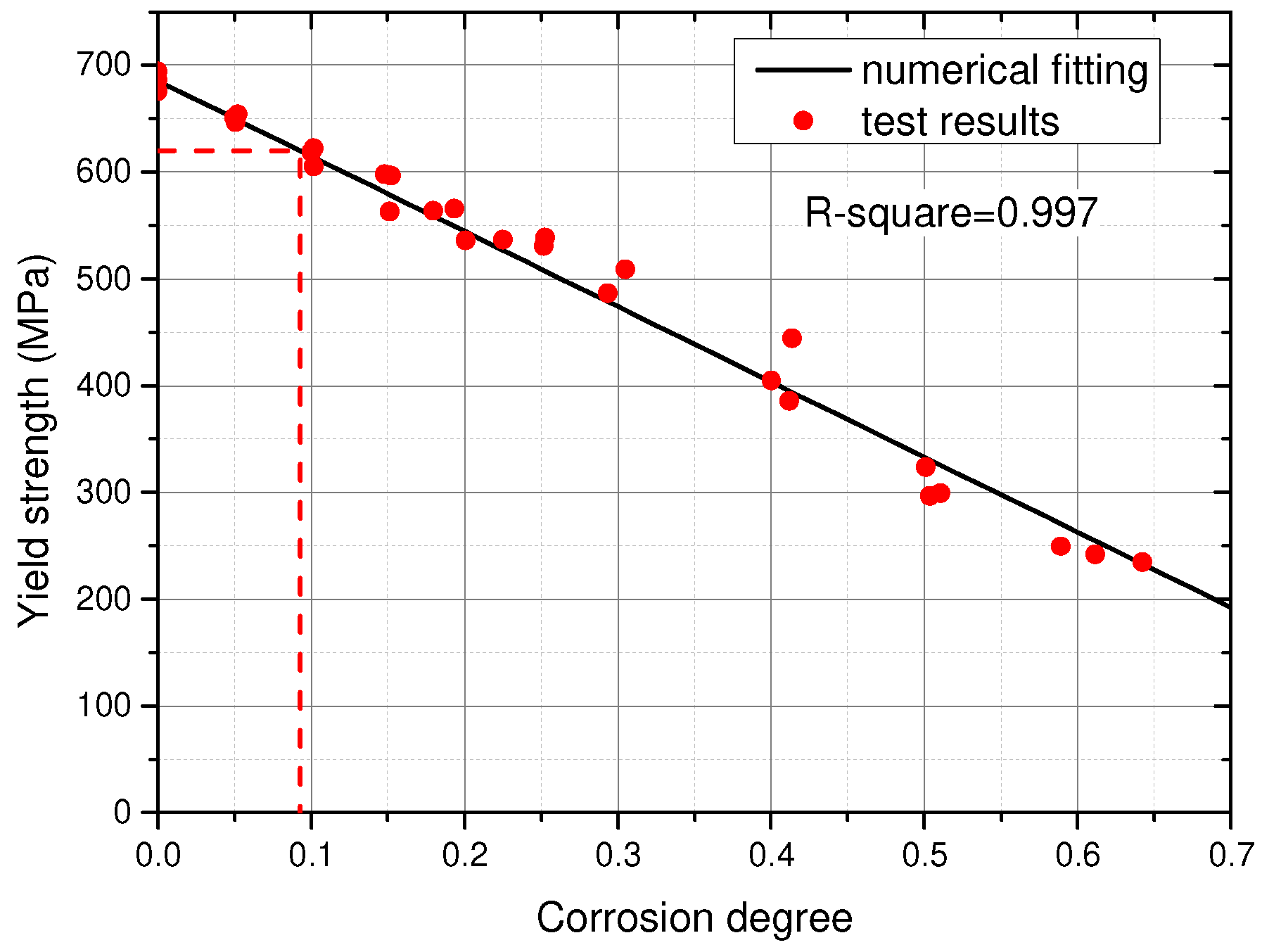
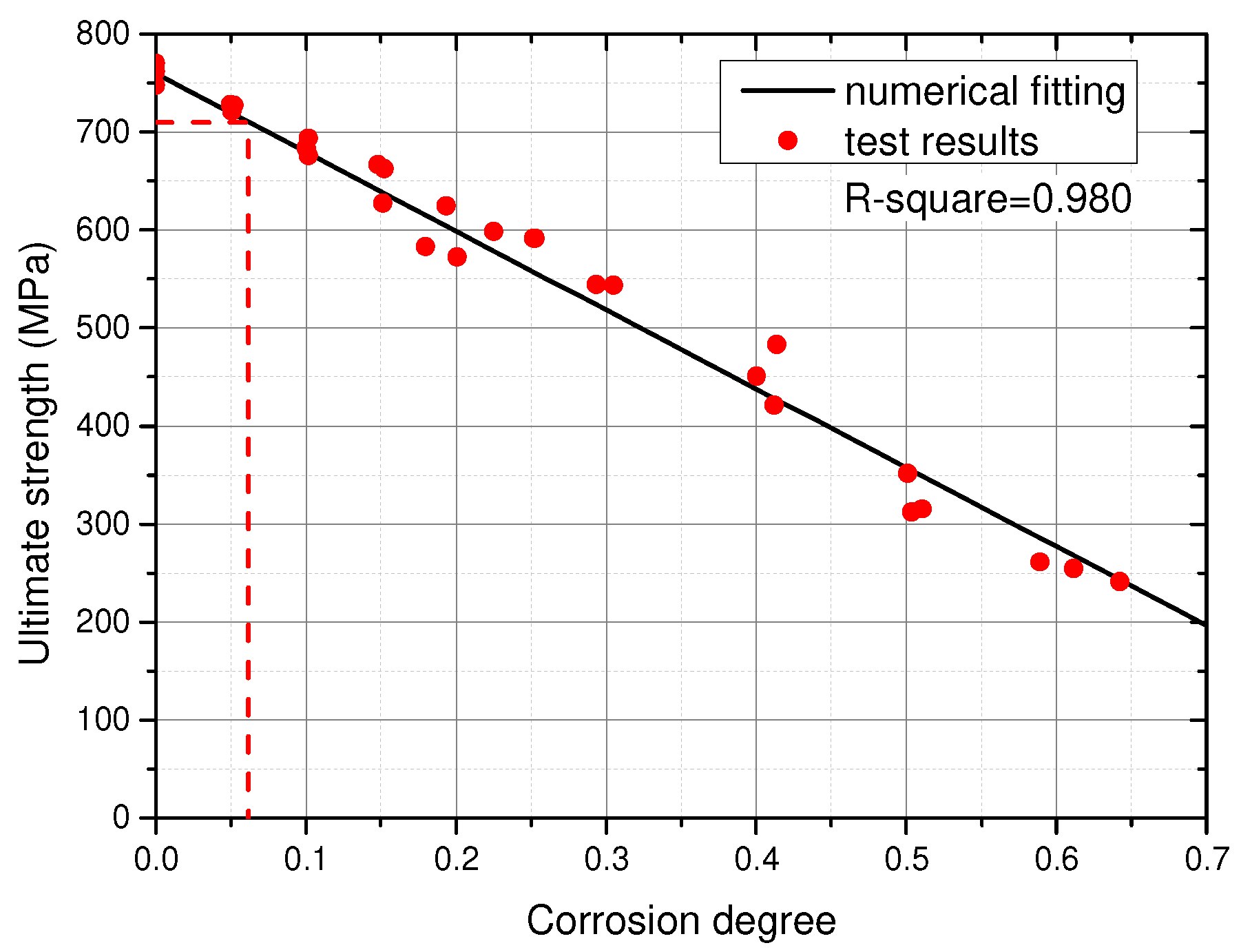
3.4. Simplified Constitutive Model
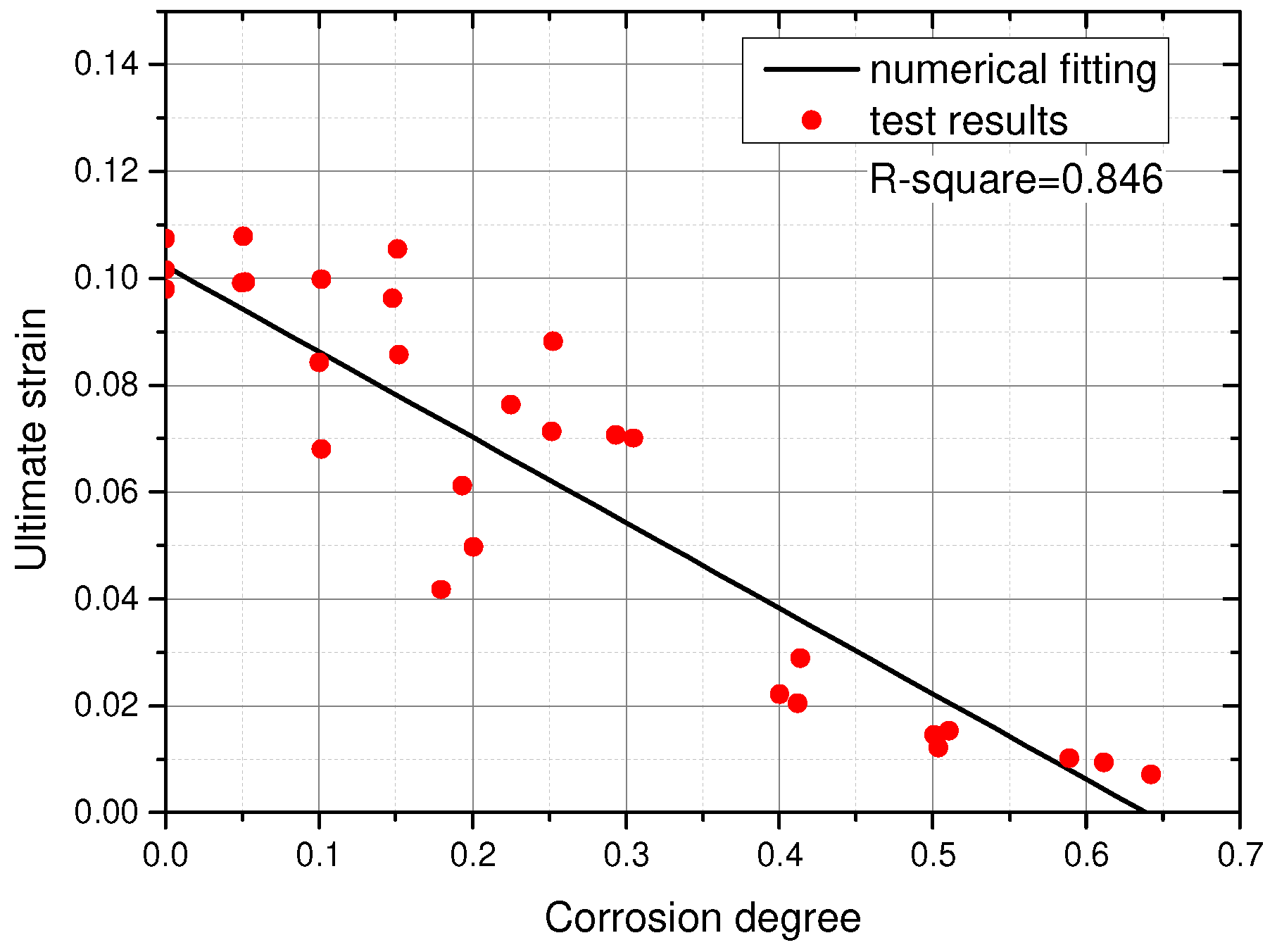
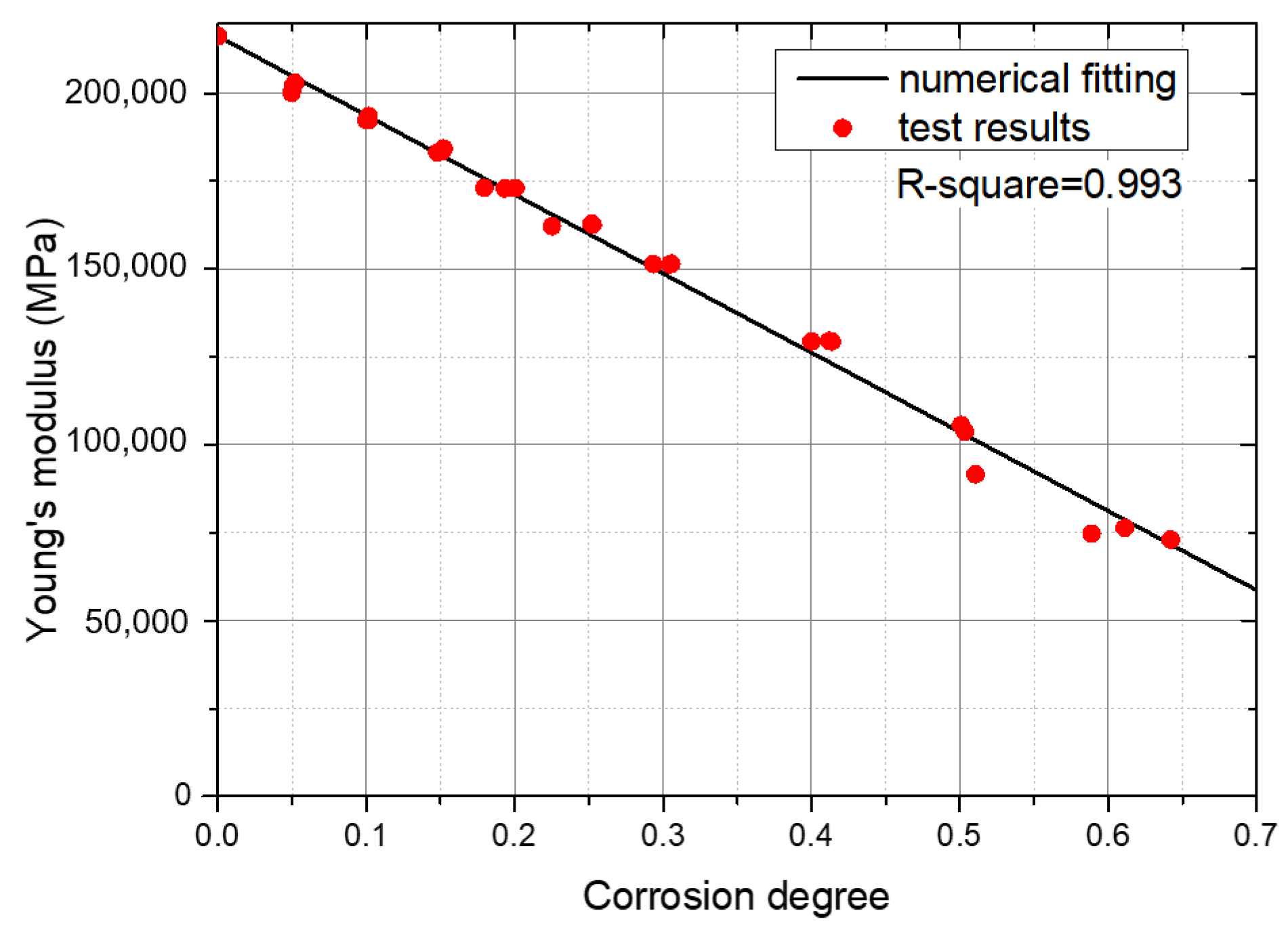
3.4.1. Relationship between Corrosion Degree and Characteristic Point
3.4.2. Comparison with Other Test Results
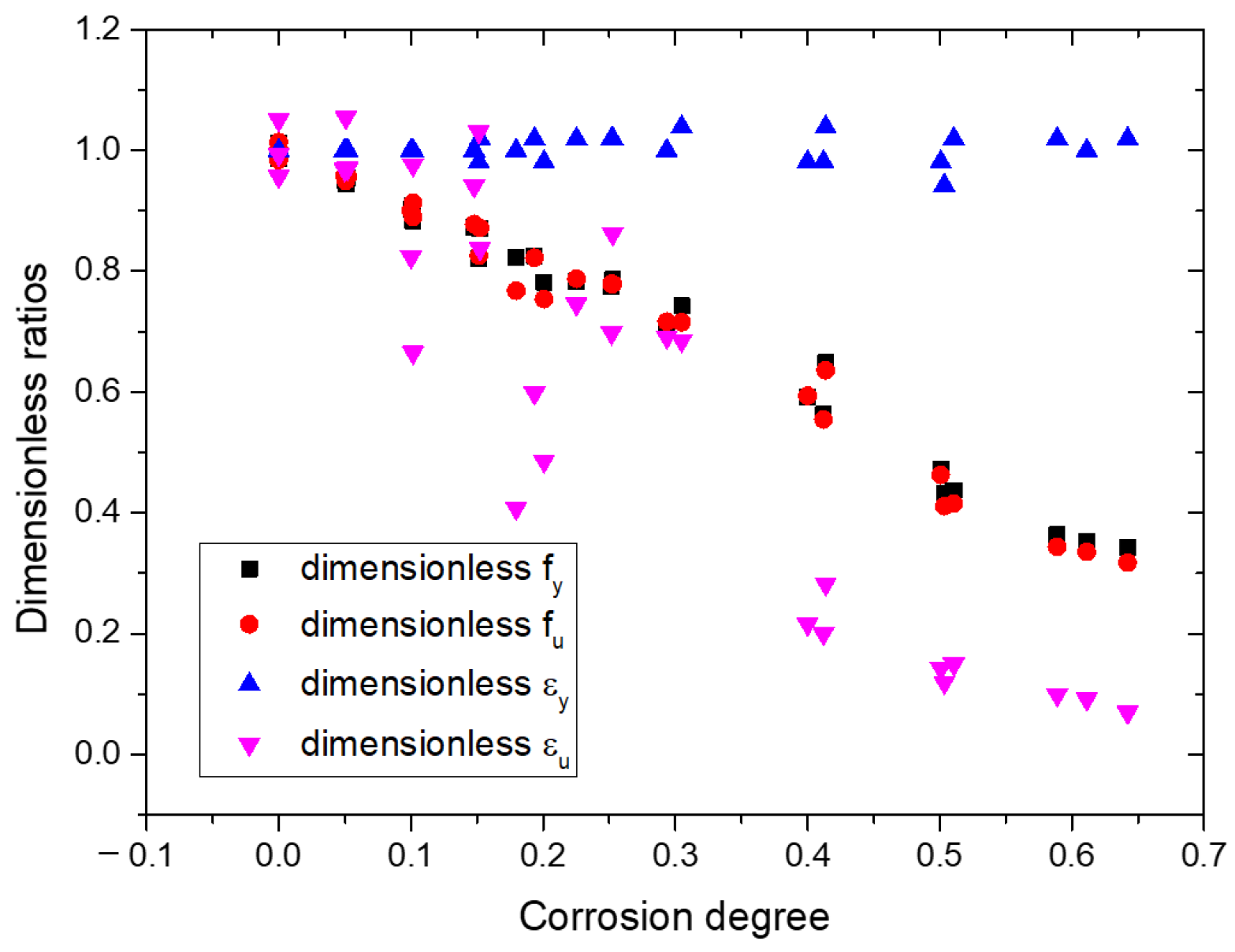
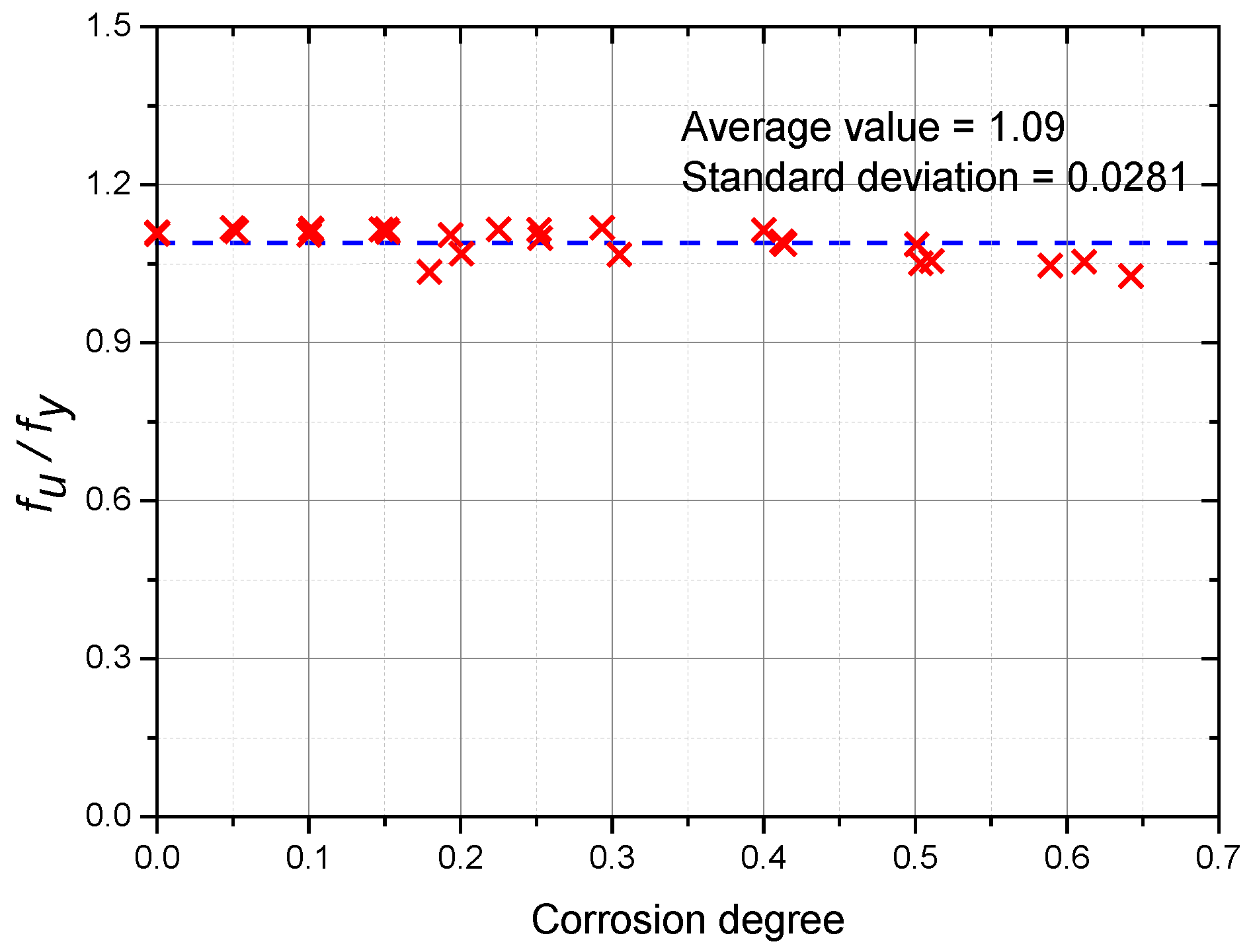
3.5. fu/fy and εu/εy
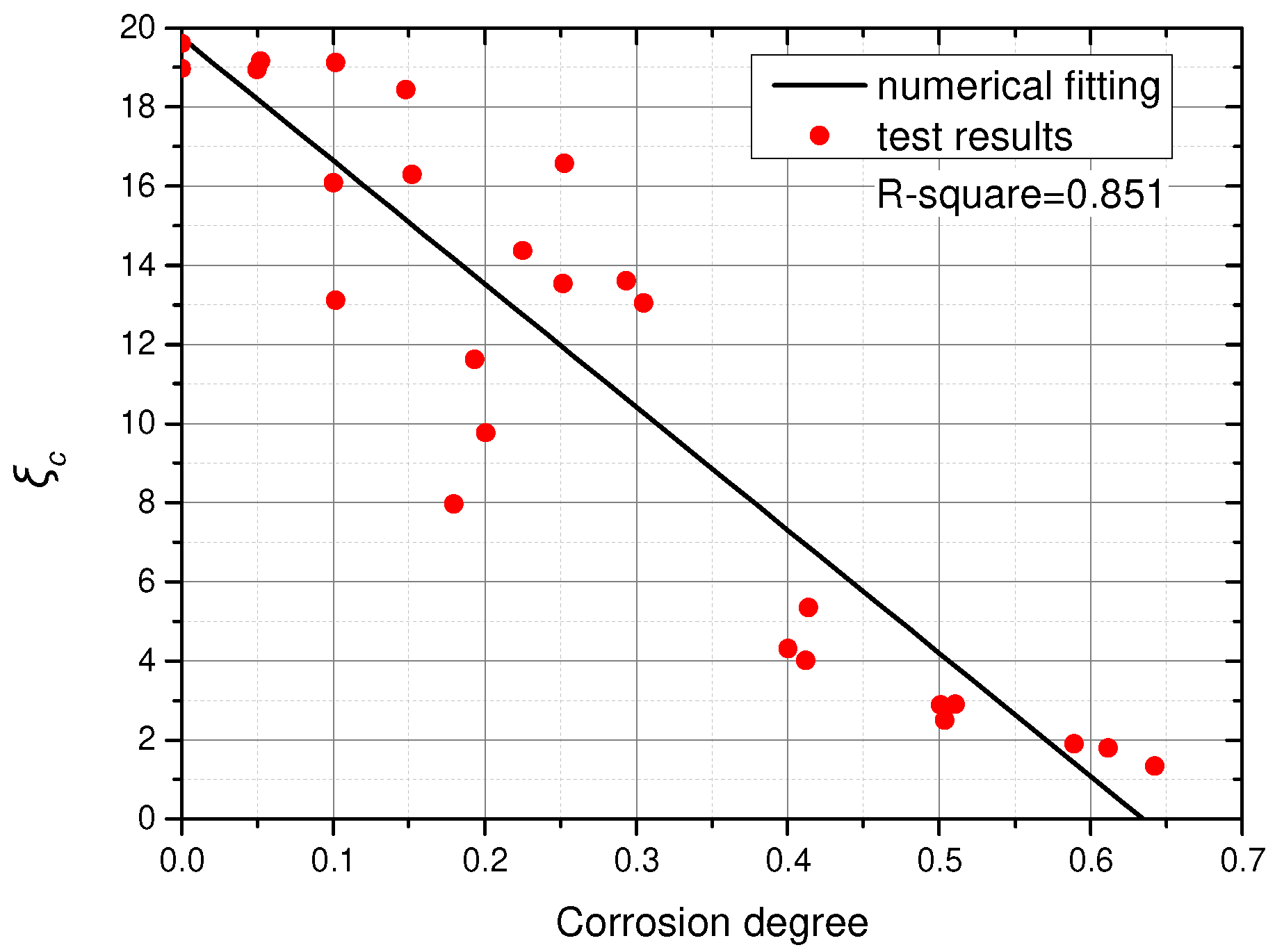
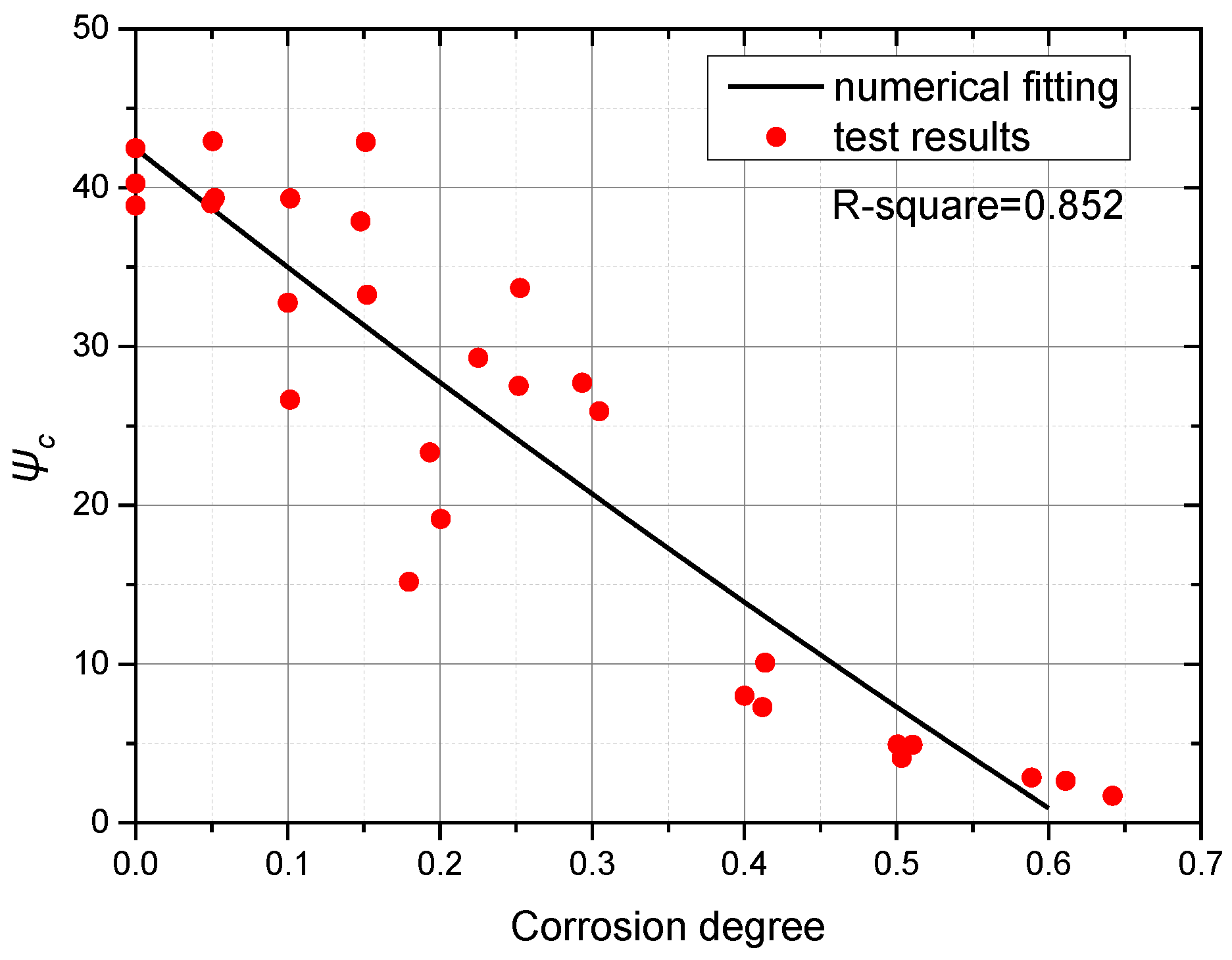
3.6. Energy Indexes
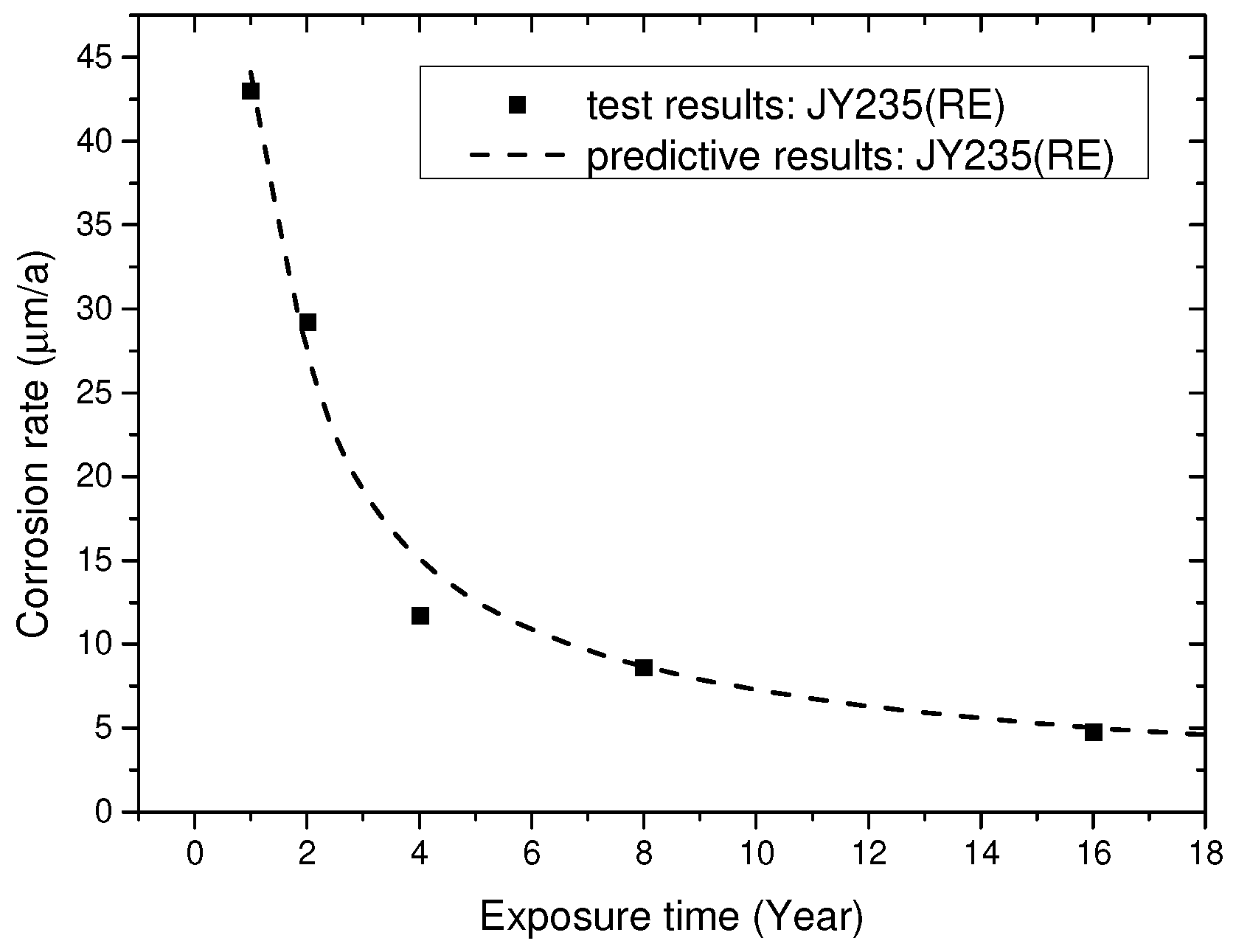
3.7. Forecast of Mechanical Properties
4. Conclusions
- The electrochemical accelerated corrosion test was conducted in the study to obtain Q620 HSS specimens with different corrosion degrees (ρ = 0%, 5%, 10%, 15%, 20%, 25%, 30%, 40%, 50% and 60%). When the corrosion degree was comparatively low (5~20%), reductions in the width and thickness kept almost the same along the length, which indicated that the corrosion was approximately uniform. When the corrosion degree was comparatively large (25~60%), the corrosion became more and more non-uniform. The weak area occurred in the middle portion of the specimen, which had an adverse effect on ductility of Q620 HSS;
- The tensile coupon test was conducted to study the mechanical performance of corroded Q620 HSS specimens. After considering the test results, there was no clear yield plateau in the stress–strain curves of corroded Q620 HSS specimens. With the increment in corrosion degree, the fy, fu, εu and E decreased, correspondingly. The effect of corrosion on the εy could be ignored;
- After the tensile coupon test, failure performances of corroded Q620 HSS specimens were obtained. For the Q620 HSS specimen without corrosion, the obvious necking occurred in the fracture area, which indicated a ductile failure. With the increment in corrosion degree, the necking was weakened. With the non-uniform corrosion, plastic deformation was confined to the weak area in the middle portion, which reduced the ductile property of Q620 HSS specimens with different corrosion degrees. The stress concentration caused by the non-uniform corrosion resulted in the earlier fracture;
- The simplified constitutive model consisting of the nominal yield point (εy, fy) and the ultimate point (εu, fu) was proposed to quantify mechanical performance of corroded Q620 HSS. After numerical fitting, the relationships between corrosion degree and mechanical properties were clarified through Equations (4)–(7). The degradation coefficients of fy and fu are 1.028 and 1.059, respectively. Considering that the degradation coefficient of the idealized uniform corrosion was 1, the adverse effect of the non-uniform corrosion in this study was larger than that of the idealized uniform corrosion. Because the degradation coefficients 1.566 > 1.059 > 1.028, the corrosion effect on εuc was more severe than that on fyc and fuc. A comparison in mechanical properties among mild steels and HSSs with different corrosion methods was conducted, where it transpired that the effects of corrosion on the mechanical properties of Q235 mild steel, Q460, Q550 and Q620 HSSs were different from each other;
- Indexes fy/fu, εu/εy, κ and ψ were selected to clarify the effects of corrosion on the ductile property of Q620 HSS with different corrosion degrees. Based on the test results, the effect of corrosion on the index fy/fu was weak and could be ignored. With increments in corrosion degree, the εu/εy, κ and ψ decreased, correspondingly. The corrosion had an adverse effect on the ductile property of Q620 HSS. After numerical fitting, Equations (11), (14) and (15) were suggested to clarify the corrosion effect on the indexes εu/εy, κc and ψc;
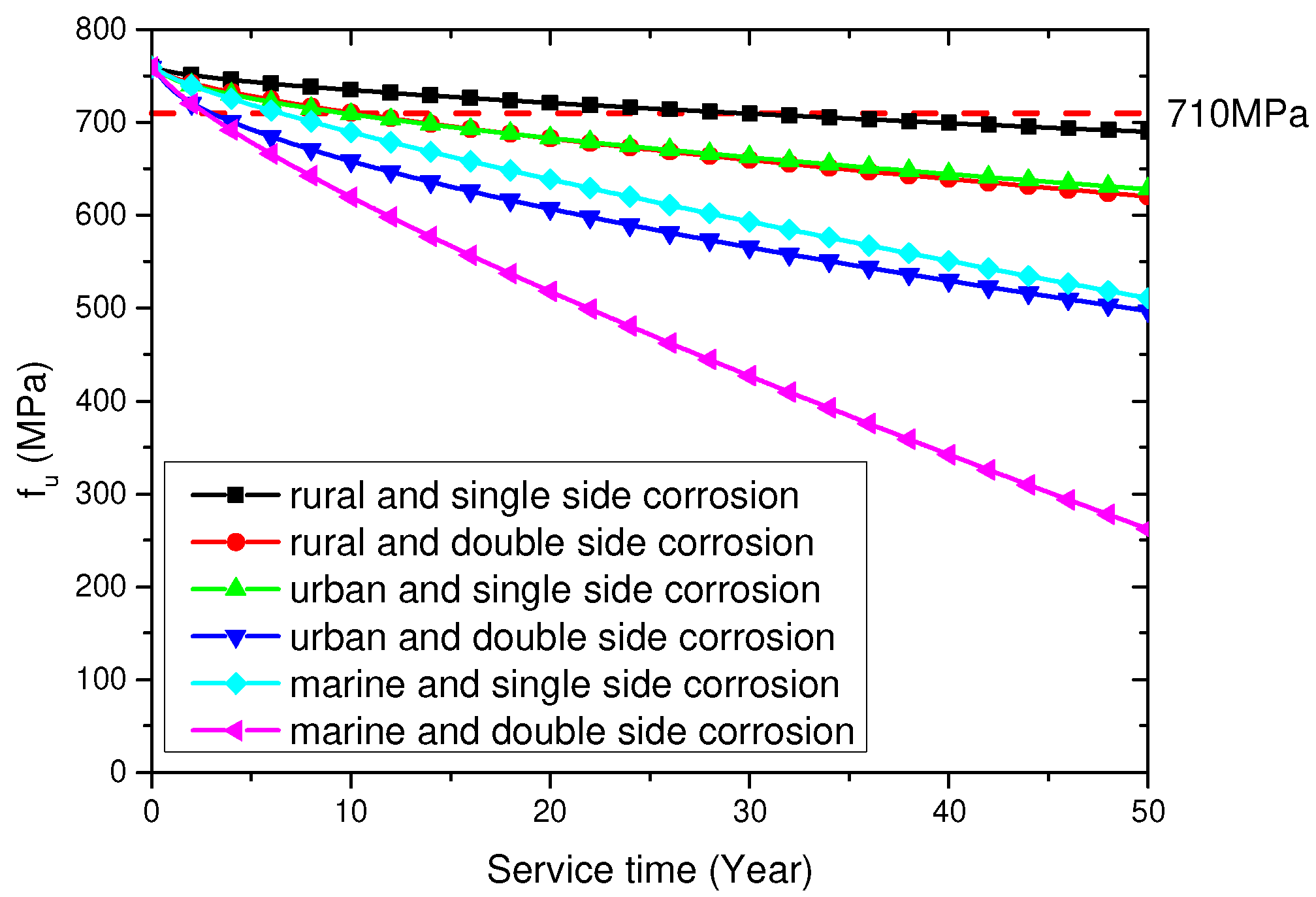
- Combining with investigations on corrosion rates, the relationship between service time, service environment, corrosion form and strength properties of Q620 HSS with five thickness were discussed. Based on the test results of corrosion rates for structural steel in Beijing, the service life of Q620 HSS was discussed. The decreases in strength properties of Q620 HSS serving in a marine environment were much more severe than those of Q620 HSSs serving in rural and urban environments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hua, J.; Yang, Z.; Zhou, F.; Hai, L.; Wang, N.; Wang, F. Effects of exposure temperature on low–cycle fatigue properties of Q690 high–strength steel. J. Constr. Steel Res. 2022, 190, 107159. [Google Scholar] [CrossRef]
- Hua, J.; Wang, F.; Xue, X.; Ding, Z.; Sun, Y.; Xiao, L. Ultra-low cycle fatigue performance of Q690 high-strength steel after exposure to elevated temperatures. J. Build. Eng. 2022, 57, 104832. [Google Scholar] [CrossRef]
- Hua, J.; Xue, X.; Huang, Q.; Shi, Y.; Deng, W. Post-fire performance of high-strength steel plate girders developing post-buckling capacity. J. Build. Eng. 2022, 52, 104442. [Google Scholar] [CrossRef]
- Xiao, Y.; Xue, X.Y.; Sun, F.F.; Li, G.Q. Intermediate transverse stiffener requirements of high-strength steel plate girders considering postbuckling capacity. Eng. Struct. 2019, 196, 109289. [Google Scholar] [CrossRef]
- Xiao, Y.; Xue, X.Y.; Sun, F.F.; Li, G.Q. Postbuckling shear capacity of high-strength steel plate girders. J. Constr. Steel Res. 2018, 150, 475–490. [Google Scholar] [CrossRef]
- Wang, W.; Liu, T.; Liu, J. Experimental study on post-fire mechanical properties of high strength Q460 steel. J. Constr. Steel Res. 2015, 114, 100–109. [Google Scholar] [CrossRef]
- Sun, F.F.; Xue, X.Y.; Xiao, Y.; Le, Y.M.; Li, G.Q. Effect of welding and complex loads on the high-strength steel T-stub connection. J. Constr. Steel Res. 2018, 150, 76–86. [Google Scholar] [CrossRef]
- Wang, W.; Li, G.Q.; Ge, Y. Residual Stress Study on Welded Section of High Strength Q460 Steel after Fire Exposure. Adv. Steel Constr. 2015, 11, 150–164. [Google Scholar] [CrossRef]
- Wang, Y.-B.; Lyu, Y.-F.; Li, G.-Q.; Liew, J.R. Behavior of single bolt bearing on high strength steel plate. J. Constr. Steel Res. 2017, 137, 19–30. [Google Scholar] [CrossRef]
- Ban, H.; Shi, G.; Shi, Y.; Bradford, M.A. Experimental investigation of the overall buckling behaviour of 960MPa high strength steel columns. J. Constr. Steel Res. 2013, 88, 256–266. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, H.; Xian, L.; Liu, H. Tensile strength of Q345 steel with random pitting corrosion based on numerical analysis. Thin-Walled Struct. 2020, 148, 106579. [Google Scholar] [CrossRef]
- Wang, F.; Hua, J.; Xue, X.; Wang, N.; Yao, Y. Effects of Polyoxymethylene Fiber on Mechanical Properties of Seawater Sea-Sand Concrete with Different Ages. Polymers 2022, 14, 3472. [Google Scholar] [CrossRef] [PubMed]
- Hua, J.; Wang, F.; Xue, X.; Fan, H.; Yan, W. Fatigue properties of bimetallic steel bar: An experimental and numerical study. Eng. Fail. Anal. 2022, 136, 106212. [Google Scholar] [CrossRef]
- Hua, J.; Yang, Z.; Xue, X.; Huang, L.; Wang, N.; Chen, Z. Bond properties of bimetallic steel bar in seawater sea-sand concrete at different ages. Constr. Build. Mater. 2022, 323, 126539. [Google Scholar] [CrossRef]
- Hua, J.; Fan, H.; Xue, X.; Wang, F.; Chen, Z.; Huang, L.; Wang, N. Tensile and low-cycle fatigue performance of bimetallic steel bars with corrosion. J. Build. Eng. 2021, 43, 103188. [Google Scholar] [CrossRef]
- Hua, J.; Wang, F.; Wang, N.; Huang, L.; Hai, L.; Li, Y.; Zhu, X.; Xue, X. Experimental and numerical investigations on corroded stainless-clad bimetallic steel bar with artificial damage. J. Build. Eng. 2021, 44, 102779. [Google Scholar] [CrossRef]
- Wang, F.; Hua, J.; Xue, X.; Ding, Z.; Lyu, Y.; Liu, Q. Low-cycle fatigue performance of bimetallic steel bar considering the effect of inelastic buckling. Constr. Build. Mater. 2022, 351, 128787. [Google Scholar] [CrossRef]
- Hua, J.; Wang, F.; Xue, X.; Ding, Z.; Chen, Z. Residual monotonic mechanical properties of bimetallic steel bar with fatigue damage. J. Build. Eng. 2022, 55, 104703. [Google Scholar] [CrossRef]
- Hua, J.; Yang, Z.; Wang, F.; Xue, X.; Wang, N.; Huang, L. Relation between the Metallographic Structure and Mechanical Properties of a Bimetallic Steel Bar after Fire. J. Mater. Civ. Eng. 2022, 34, 04022193. [Google Scholar] [CrossRef]
- Hua, J.; Wang, F.; Xue, X. Study on fatigue properties of post-fire bimetallic steel bar with different cooling methods. Structures 2022, 40, 633–645. [Google Scholar] [CrossRef]
- Shi, Y.; Luo, Z.; Zhou, X.; Xue, X.; Xiang, Y. Post-fire performance of bonding interface in explosion-welded stainless-clad bimetallic steel. J. Constr. Steel Res. 2022, 193, 107285. [Google Scholar] [CrossRef]
- Hua, J.; Wang, F.; Xiang, Y.; Yang, Z.; Xue, X.; Huang, L.; Wang, N. Mechanical properties of stainless-clad bimetallic steel bars exposed to elevated temperatures. Fire Saf. J. 2022, 127, 103521. [Google Scholar] [CrossRef]
- Hua, J.; Fan, H.; Yan, W.; Wang, N.; Xue, X.; Huang, L. Seismic resistance of the corroded bimetallic steel bar under different strain amplitudes. Constr. Build. Mater. 2021, 319, 126088. [Google Scholar] [CrossRef]
- Hua, J.; Wang, F.; Yang, Z.; Xue, X.; Huang, L.; Chen, Z. Low-cycle fatigue properties of bimetallic steel bars after exposure to elevated temperature. J. Constr. Steel Res. 2021, 187, 106959. [Google Scholar] [CrossRef]
- Shi, Y.; Luo, Z.; Zhou, X.; Xue, X.; Li, J. Post-fire mechanical properties of titanium–clad bimetallic steel in different cooling approaches. J. Constr. Steel Res. 2022, 191, 107169. [Google Scholar] [CrossRef]
- Nakai, T.; Matsushita, H.; Yamamoto, N. Effect of pitting corrosion on strength of web plates subjected to patch loading. Thin-Walled Struct. 2006, 44, 10–19. [Google Scholar] [CrossRef]
- Ahn, J.-H.; Cheung, J.-H.; Lee, W.-H.; Oh, H.; Kim, I.-T. Shear buckling experiments of web panel with pitting and through-thickness corrosion damage. J. Constr. Steel Res. 2015, 115, 290–302. [Google Scholar] [CrossRef]
- Wen, Z.; Wei, X.; Xiao, L.; He, K. Experimental evaluation of the shear buckling behaviors of corrugated webs with artificial corrosion pits. Thin-Walled Struct. 2019, 141, 251–259. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Soares, C.G. Effect of corrosion severity on the ultimate strength of a steel box girder. Eng. Struct. 2013, 49, 560–571. [Google Scholar] [CrossRef]
- Yao, Y.; Yang, Y.; He, Z.; Wang, Y. Experimental study on generalized constitutive model of hull structural plate with multi-parameter pitting corrosion. Ocean Eng. 2018, 170, 407–415. [Google Scholar] [CrossRef]
- Ahn, J.-H.; Kainuma, S.; Kim, I.-T. Shear failure behaviors of a web panel with local corrosion depending on web boundary conditions. Thin-Walled Struct. 2013, 73, 302–317. [Google Scholar] [CrossRef]
- Blikharskyy, Y.; Selejdak, J.; Kopiika, N. Corrosion Fatigue Damages of Rebars under Loading in Time. Materials 2021, 14, 3416. [Google Scholar] [CrossRef] [PubMed]
- Lipiński, T. Roughness of 1.0721 steel after corrosion tests in 20% NaCl. Prod. Eng. Arch. 2017, 15, 27–30. [Google Scholar] [CrossRef]
- Taylor, C.D.; Gale, J.D.; Strehblow, H.H.; Philippe, M. An Introduction to Corrosion Mechanisms and Models; Wiley: New York, NY, USA, 2015; pp. 1–34. [Google Scholar] [CrossRef]
- Sharifi, Y.; Paik, J.K. Ultimate strength reliability analysis of corroded steel-box girder bridges. Thin-Walled Struct. 2011, 49, 157–166. [Google Scholar] [CrossRef]
- Wang, R.; Shenoi, R.A.; Sobey, A. Ultimate strength assessment of plated steel structures with random pitting corrosion damage. J. Constr. Steel Res. 2018, 143, 331–342. [Google Scholar] [CrossRef]
- Rahgozar, R. Remaining capacity assessment of corrosion damaged beams using minimum curves. J. Constr. Steel Res. 2009, 65, 299–307. [Google Scholar] [CrossRef]
- Saad-Eldeen, S.; Garbatov, Y.; Parunov, J.; Kodvanj, J.; Saad-Eldeen, S.; Soares, C.G. Experimental assessment of tensile strength of corroded steel specimens subjected to sandblast and sandpaper cleaning. Mar. Struct. 2016, 49, 18–30. [Google Scholar] [CrossRef]
- Nakai, T.; Matsushita, H.; Yamamoto, N. Effect of pitting corrosion on the ultimate strength of steel plates subjected to in-plane compression and bending. J. Mar. Sci. Technol. 2006, 11, 52–64. [Google Scholar] [CrossRef]
- Ok, D.; Pu, Y.; Incecik, A. Computation of ultimate strength of locally corroded unstiffened plates under uniaxial compression. Mar. Struct. 2007, 20, 100–114. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, N.; Wu, J.; Gao, Y.; Sun, Q. Shear capacity of steel plates with random local corrosion. Constr. Build. Mater. 2020, 239, 117816. [Google Scholar] [CrossRef]
- Xiao, L.; Peng, J.; Zhang, J.; Ma, Y.; Cai, C. Comparative assessment of mechanical properties of HPS between electrochemical corrosion and spray corrosion. Constr. Build. Mater. 2020, 237, 117735. [Google Scholar] [CrossRef]
- Xue, X.Y.; Zhou, X.; Shi, Y.; Xiang, Y. Ultimate shear resistance of S600E high-strength stainless steel plate girders. J. Constr. Steel Res. 2021, 179, 106535. [Google Scholar] [CrossRef]
- Hua, J.; Wang, F.; Huang, L.; Wang, N.; Xue, X. Experimental study on mechanical properties of corroded stainless-clad bimetallic steel bars. Constr. Build. Mater. 2021, 287, 123019. [Google Scholar] [CrossRef]
- Wu, X.; Ye, D.; Li, H.; Yu, H. Corrosion characteristics of S23043 duplex stainless steel bars. Constr. Build. Mater. 2018, 178, 135–143. [Google Scholar] [CrossRef]
- Lee, H.-S.; Cho, Y.-S. Evaluation of the mechanical properties of steel reinforcement embedded in concrete specimen as a function of the degree of reinforcement corrosion. Int. J. Fract. 2009, 157, 81–88. [Google Scholar] [CrossRef]
- GB/T 228-2010; Metallic Materials—Tensile Testing—Part 1:Method of Test at Room Temperature. China Standard Press: Beijing, China, 2010. (In Chinese)
- Xiao, L.F.; Peng, J.X.; Zhang, J.R.; Cai, C.S. Mechanical properties of corroded high performance steel specimens based on 3d scanning. Adv. Steel Constr. 2019, 15, 129–136. [Google Scholar] [CrossRef]
- Gathimba, N.; Kitane, Y. Effect of surface roughness on tensile ductility of artificially corroded steel plates. J. Constr. Steel Res. 2021, 176, 106392. [Google Scholar] [CrossRef]
- GB/T 16545-2015; Corrosion of Metals and Alloys—Removal of Corrosion Products from Corrosion Test Specimens. China Standard Press: Beijing, China, 2015. (In Chinese)
- Zhou, X.; Xue, X.; Shi, Y.; Xu, J. Post-fire mechanical properties of Q620 high-strength steel with different cooling methods. J. Constr. Steel Res. 2021, 180, 106608. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, R.; Song, G. Post-fire mechanical properties of Q460 and Q690 high strength steels after fire-fighting foam cooling. Thin-Walled Struct. 2020, 156, 106983. [Google Scholar] [CrossRef]
- Amraei, M.; Skriko, T.; Björk, T.; Zhao, X.-L. Plastic strain characteristics of butt-welded ultra-high strength steel (UHSS). Thin-Walled Struct. 2016, 109, 227–241. [Google Scholar] [CrossRef]
- GB/T 1591-2018; High Strength Low Alloy Structural Steels. China Standard Press: Beijing, China, 2018. (In Chinese)
- Weizhou, S.; Lewei, T.; Yiyi, C.; Zigang, L.; Kai, S. Experimental study on influence of corrosion on behavior of steel material and steel beams. J. Build. Struct. 2012, 33, 53–60. (In Chinese) [Google Scholar]
- Yang, C. The Seismic Performance and Vulnerability Research of Corroded Steel Frame Structure in Acidic Air Environment; Xi’an University of Architecture and Technology: Xi’An, China, 2015. (In Chinese) [Google Scholar]
- Zheng, S.; Zhang, X.; Wang, X.; Cheng, Y.; Sun, L. Experimental research on seismic behaviors of multi-aged steel frame columns in the offshore atmospheric environment, Tumu Gongcheng Xuebao/China. Civ. Eng. J. 2016, 49, 69–77. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, W. Experimental Study on Influence of Corrosion on Static and Fatigue Performance of High Performance Steel Specimens; Changsha University of Science and Technology: Changsha, China, 2017. (In Chinese) [Google Scholar]
- Tang, F.; Lin, Z.; Chen, G.; Yi, W. Three-dimensional corrosion pit measurement and statistical mechanical degradation analysis of deformed steel bars subjected to accelerated corrosion. Constr. Build. Mater. 2014, 70, 104–117. [Google Scholar] [CrossRef]
- Paik, J.K.; Kim, S.K.; Lee, S.K. Probabilistic corrosion rate estimation model for longitudinal strength members of bulk carriers. Ocean Eng. 1998, 25, 837–860. [Google Scholar] [CrossRef]
- Zhi, Y.; Yang, T.; Fu, D. An improved deep forest model for forecast the outdoor atmospheric corrosion rate of low-alloy steels. J. Mater. Sci. Technol. 2020, 49, 202–210. [Google Scholar] [CrossRef]














| Element | Ti | C | Si | Mn | Nb | P | S | V | Ni | Cr | Cu | Mo | B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| wt.% | 0.09 | 0.07 | 0.10 | 1.71 | 0.003 | 0.012 | 0.001 | 0.001 | 0.02 | 0.02 | 0.02 | 0.001 | 2 |
| Number | ρ (%) | E (MPa) | fy (MPa) | fu (MPa) | fye (MPa) | fue (MPa) | εy | εu | fu/fy | εu/εy |
|---|---|---|---|---|---|---|---|---|---|---|
| S0-1 | 0 | 216,347 | 694.21 | 770.08 | 694.21 | 770.08 | 0.0052 | 0.1075 | 1.11 | 20.67 |
| S0-2 | 0 | 216,162 | 675.61 | 747.59 | 675.61 | 747.59 | 0.0052 | 0.0979 | 1.11 | 18.98 |
| S0-3 | 0 | 216,188 | 686.13 | 761.31 | 686.13 | 761.31 | 0.0052 | 0.1016 | 1.11 | 19.61 |
| S5-1 | 5.07 | 202,088 | 646.86 | 721.23 | 681.41 | 759.74 | 0.0052 | 0.1079 | 1.11 | 20.83 |
| S5-2 | 4.97 | 200,110 | 651.09 | 727.56 | 685.14 | 765.61 | 0.0052 | 0.0991 | 1.12 | 18.95 |
| S5-3 | 5.21 | 202,952 | 654.12 | 726.94 | 690.07 | 766.89 | 0.0052 | 0.0993 | 1.11 | 19.17 |
| S10-1 | 10.15 | 192,322 | 605.42 | 676.10 | 673.82 | 752.47 | 0.0052 | 0.0681 | 1.12 | 13.12 |
| S10-2 | 10.01 | 192,381 | 618.72 | 683.55 | 687.54 | 759.59 | 0.0052 | 0.0843 | 1.10 | 16.09 |
| S10-3 | 10.16 | 193,571 | 622.60 | 693.71 | 693.01 | 772.16 | 0.0052 | 0.0999 | 1.11 | 19.13 |
| S15-1 | 15.21 | 184,316 | 596.52 | 662.22 | 703.53 | 781.01 | 0.0053 | 0.0857 | 1.11 | 16.29 |
| S15-2 | 15.13 | 183,518 | 562.66 | 627.36 | 662.96 | 739.20 | 0.0051 | 0.1055 | 1.11 | 20.80 |
| S15-3 | 14.79 | 183,089 | 598.13 | 666.81 | 701.94 | 782.55 | 0.0052 | 0.0963 | 1.11 | 18.44 |
| S20-1 | 20.06 | 173,076 | 535.76 | 572.74 | 670.20 | 716.46 | 0.0051 | 0.0497 | 1.07 | 9.77 |
| S20-2 | 19.34 | 172,918 | 565.80 | 624.87 | 701.47 | 774.69 | 0.0053 | 0.0612 | 1.10 | 11.61 |
| S20-3 | 17.96 | 173,131 | 563.81 | 583.28 | 687.24 | 710.97 | 0.0052 | 0.0417 | 1.03 | 7.97 |
| S25-1 | 25.18 | 162,940 | 530.91 | 591.78 | 709.59 | 790.94 | 0.0053 | 0.0714 | 1.11 | 13.54 |
| S25-2 | 25.26 | 162,613 | 538.74 | 591.74 | 720.83 | 791.73 | 0.0053 | 0.0882 | 1.10 | 16.58 |
| S25-3 | 22.52 | 162,154 | 536.65 | 598.36 | 692.64 | 772.27 | 0.0053 | 0.0763 | 1.11 | 14.37 |
| S30-1 | 29.35 | 151,442 | 486.58 | 544.20 | 688.71 | 770.27 | 0.0052 | 0.0707 | 1.12 | 13.61 |
| S30-2 | 30.47 | 151,352 | 509.12 | 543.39 | 732.23 | 781.52 | 0.0054 | 0.0701 | 1.07 | 13.05 |
| S30-3 | 30.56 | 151,526 | - | - | - | - | - | - | - | - |
| S40-1 | 40.01 | 129,415 | 405.05 | 451.14 | 675.20 | 752.02 | 0.0051 | 0.0221 | 1.11 | 4.31 |
| S40-2 | 41.37 | 129,422 | 444.45 | 483.14 | 758.05 | 824.06 | 0.0054 | 0.0289 | 1.09 | 5.35 |
| S40-3 | 41.21 | 129,562 | 385.68 | 421.26 | 655.92 | 716.42 | 0.0051 | 0.0205 | 1.09 | 4.01 |
| S50-1 | 50.34 | 103,777 | 296.91 | 312.04 | 597.89 | 628.35 | 0.0049 | 0.0122 | 1.05 | 2.50 |
| S50-2 | 50.08 | 105,616 | 323.58 | 351.53 | 648.20 | 704.19 | 0.0051 | 0.0146 | 1.09 | 2.88 |
| S50-3 | 51.06 | 91,625 | 299.03 | 315.49 | 611.01 | 644.65 | 0.0053 | 0.0153 | 1.06 | 2.90 |
| S60-1 | 64.21 | 73,025 | 234.82 | 240.99 | 656.11 | 673.34 | 0.0053 | 0.0071 | 1.03 | 1.34 |
| S60-2 | 58.88 | 74,779 | 249.62 | 261.20 | 607.05 | 635.21 | 0.0053 | 0.0101 | 1.05 | 1.91 |
| S60-3 | 61.12 | 76,374 | 241.92 | 254.79 | 622.22 | 655.32 | 0.0052 | 0.0094 | 1.05 | 1.80 |
| Study | Type | Accelerated Corrosion Test | νy | νu | νE |
|---|---|---|---|---|---|
| Present study | Q620 HSS | electrochemically | 1.028 | 1.059 | 1.041 |
| Zhang [58] | Q460 HSS | electrochemically | 0.925 | 1.050 | 1.216 |
| Zhang [58] | Q550 HSS | electrochemically | 0.832 | 0.812 | 1.196 |
| Shi et al. [55] | Q235 mild steel | neutral salt spray | 0.9852 | 0.9732 | - |
| Cheng [56] | Q235 mild steel | acid salt spray | 0.802 | 0.955 | 0.836 |
| Zheng et al. [57] | Q235 mild steel | neutral salt spray | 0.9684 | 0.9438 | 0.8913 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, X.; Hua, J.; Wang, F.; Wang, N.; Li, S. Mechanical Property Model of Q620 High-Strength Steel with Corrosion Effects. Buildings 2022, 12, 1651. https://doi.org/10.3390/buildings12101651
Xue X, Hua J, Wang F, Wang N, Li S. Mechanical Property Model of Q620 High-Strength Steel with Corrosion Effects. Buildings. 2022; 12(10):1651. https://doi.org/10.3390/buildings12101651
Chicago/Turabian StyleXue, Xuanyi, Jianmin Hua, Fei Wang, Neng Wang, and Shuang Li. 2022. "Mechanical Property Model of Q620 High-Strength Steel with Corrosion Effects" Buildings 12, no. 10: 1651. https://doi.org/10.3390/buildings12101651
APA StyleXue, X., Hua, J., Wang, F., Wang, N., & Li, S. (2022). Mechanical Property Model of Q620 High-Strength Steel with Corrosion Effects. Buildings, 12(10), 1651. https://doi.org/10.3390/buildings12101651











