Study on Parameters’ Influence and Optimal Design of Tuned Inerter Dampers for Seismic Response Mitigation

Abstract

In this paper, parameter analyses of a tuned inerter damper (TID) are carried out based on the displacement mitigation ratio. The optimal design of TID based on the closed-form solution method is carried out and compared with the fixed-point method. Meanwhile, applicable conditions of two methods are discussed in wider range of values of objective function under different inherent damping ratios. Finally, seismic responses of SDOF system with TID are carried out, which verifies the feasibility of the closed-form solution optimization method. Compared with the fixed-point method, the inherent damping ratio of the original structure is considered in the closed-form solution method, and the optimal damping ratio of a TID is smaller than that of the fixed-point method under same displacement mitigation ratio. The parameters’ combination of a TID designed by the fixed-point method obtains a vibration mitigation effect with a larger damping ratio by cooperating with the deformation enhancement effect of the inerter, which may make the vibration mitigation effect of the TID lower than that of the VD in structures with large inherent damping ratios. However, the deformation enhancement effect on the damping element of the inerter can be fully used by using the closed-form solution method. Better applicability and robustness are shown in closed-form solution method. Under the same displacement mitigation ratio, the damping ratio of a TID obtained by using the closed-form solution method is about one tenth of that obtained by using the fixed-point method, which can realize the lightweight design of the TID.

1. Introduction

Buildings, lifelines, bridges and other structures have high vulnerability to ground motions or fluctuating wind [1,2,3], especially for super high structures, steel-frame buildings [4], and transmission towers [5]. The main reason is that the vibration frequencies of the structures are close to the predominant frequency of external excitation [6], resulting in the vibration amplification of the structure [7]. Hence, much research has studied reinforcement measures or energy dissipation devices for vibration mitigation, as well as the design methods of these devices for the vibration control of different structures [8,9]. At present, tuned mass damper (TMD) is the most widely used [10] in the fields of electronics, machinery, building, and so on [11]. Other devices for vibration control used in practice, such as traditional isolation systems [12,13], include isolation bearings, e.g., elastomeric [14] or wire rope isolators [15], are installed at the bottom of the structures as in the case of traditional base-isolated buildings [16] or rigid blocks [17]. Some electronic and mechanical equipment has much higher requirements for the accuracy and robustness of vibration control than structures, and buildings and other structures are exposed to the external environment for a long time [18]. Many super-high-rise structures adopt the TMD design scheme. However, in order to achieve a certain vibration control effect, TMD requires larger size and volume [19]. However, from the perspective of economy and applicability [20], this is unrealistic for most structures, such as light space truss structures, because structures of this type are quite flexible and it is difficult to realize large-scale vibration mitigation measures based on TMD. Thus, it is necessary to design a lightweight and efficient damper which is easily designed and has little impact on the original structure, such as an inerter-based damper. A scheme that uses inerter-based dampers to suppress these vibrations [21,22,23]—including in some special structures, such as transmission lines [24], tall buildings [25], and transformer-bushing systems [26], will be satisfactory.

Vibration control technologies based on inerters have been developed based on electromechanical similarity theory [27]. Compared with TMDs, the inerter-based damper can control the inertial force at the two terminals directly. Moreover, the inerter element can effectively enlarge the small apparent mass through converting the translational motion into rotary motion such as with a ball screw. In 2001, Smith [28] put forward the concept of inerter elements and gave the basic forms of ball screw inerter elements and rack and pinion inerter elements and designed hydraulic inerter elements in 2013 [29]. Subsequently, shock absorbers such as tuned viscous mass dampers (TVMD) and tuned inerter dampers (TID) were proposed. The design method of inerter systems is also studied. Ikago et al. [30] derived a closed-form formula for TVMD optimization design based on fixed-point theory. Pan et al. [31] considered the natural damping of the original structure and the cost of the inerter-based damper and make up for the deficiency of fixed-point theory. Then, they proposed the design method of an SPIS-II inerter-based damper based on stochastic response mitigation ratio [32]. Hwang et al. [33] proposed a rotation inerter system connected with a toggle brace based on a ball screw. It is shown that the system can be effectively used in the structure with small drift. Zhang et al. [34,35] applied the inerter damper system to high-rise structures such as chimneys and wind power towers and proved the effectiveness of the inerter-based damper in high-rise structures. Gao et al. [36] put forward an optimum design method of viscous inerter damper (VID) based on the feedback control theory. De Domenico and collaborators [37,38,39,40,41,42,43,44,45,46,47] proposed the optimal design methods of inerter-based TMD systems for seismic response mitigation. Although some scholars have used the inerter-based damper in practical engineering [48], most of the research on the inerter-based damper is still in the stage of theoretical analysis, and only a few scholars have proposed the connection mode and design method of the inerter system be applied in building structures [49]. Xie et al. [50,51] put forward a cable-bracing inerter system (CBIS) and showed that it is easy to install and can effectively control displacement and acceleration of a structure. Wang et al. [52] put forward a new tuned inerter negative stiffness damper (TINSD) based on the fixed-point method which is more effective than the TID, TVMD, and INSD in reducing the dynamic response of structures.

At present, many design methods [31,53] are based on Den Hartog’s tuning theory [54] of dynamic absorbers, which does not consider the inherent damping of the original structures and the excitation properties. Moreover, the design methods do not consider the target or demanded performance of the primary structure. Pan et al. [32] proposed a parameter optimization method that considers the inherent damping ratio and control cost for an T structure with an inerter system, such as TVMD. The vibration response mitigation ratio of a structure based on H_∞ norm or H₂ norm [16,55,56] is also used in parametric optimization of inerter systems. Meanwhile, the vibration mitigation effect of inerter systems, such as TIDs, is inferior to that of some traditional or ordinary dampers, such as viscous damper (VD), under some optimum parameters obtained based on the fixed-point method. Many parameter design methods of inerter systems have been proposed in previous research, such as using multi-objective optimization. However, these design methods are used in specific conditions; applicable conditions of these methods should be discussed in a wider range of values of objective functions or boundary conditions. Therefore, it is necessary to discuss the applicability of current design methods of inerter systems.

In this paper, the motion control equations of the single-degree-of-freedom (SDOF) system with a typical inerter damper, the tuned inerter damper (TID), are established in Section 2. Parameter analyses of the TID are carried out based on the displacement mitigation ratio in Section 3. At the same time, the parameter optimization design of TIDs based on the closed-form solution method is carried out and compared with the fixed-point method. Applicable conditions of two methods are discussed in a wider range of values of objective function under different inherent damping ratios. Finally, seismic responses of the SDOF system with the TID are carried out, which verifies the feasibility of the closed-form solution optimization method in Section 4. Applicability of the two design methods to structures with different inherent damping ratios is discussed, as are the value ranges of invalid parameters of the TID by comparison with the mitigation performance of VD under identical damping ratios. The research in this paper can provide reference for the selection of design methods of inerter systems.

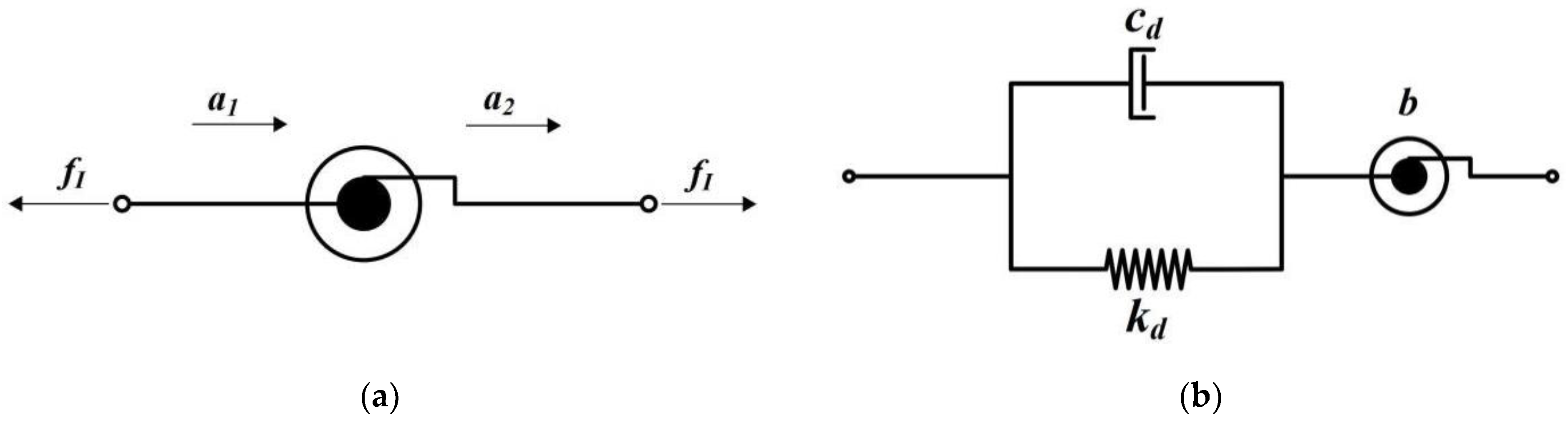
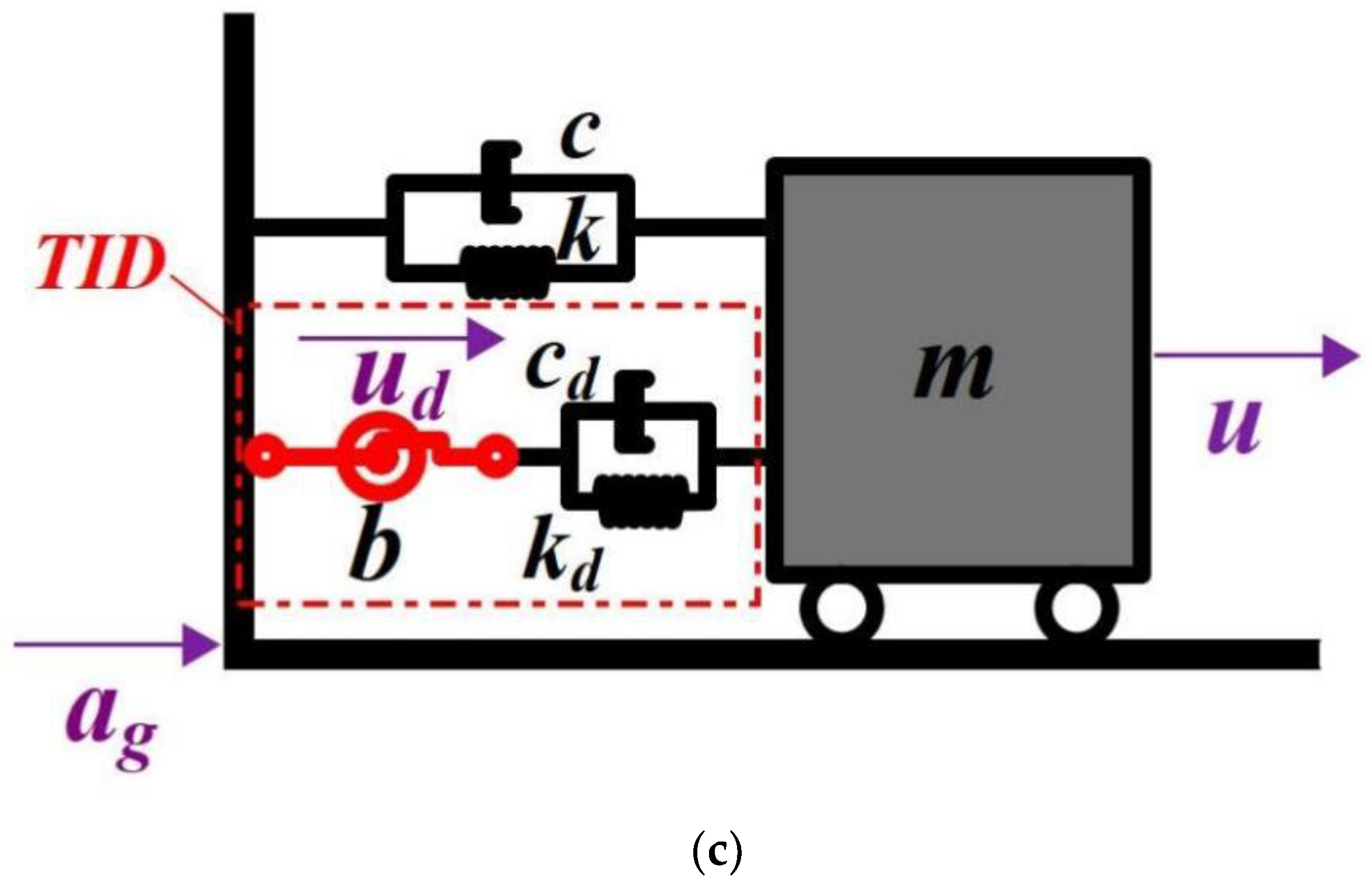
2. Motion Control Equation of TID System

Equation (1) is the output force of an inerter element when its two ends have different accelerations. Hence, the output of the inerter element is also directly proportional to the relative acceleration at two terminals, which can be shown as:

$$f_I=b\left(a_2-a_1\right)$$

(1)

where f_I is the output force of the inerter element, a₁ and a₂ are the accelerations at terminals, and Figure 1a is the mechanical model of the inerter element. The inerter element is the same as the mass element and cannot dissipate energy by itself. It is generally used in combination with a damping element, such as a viscous damper. Figure 1b shows the mechanical model of the TID, and the TID is a series-parallel layout inerter system composed of inerter, damping element, and stiffness elements. Where k_d, c_d, and b are the stiffness, damping, and inertance of the TID. The mechanical model of the SDOF system with TID is shown in Figure 1c, and m, k, c are the mass, stiffness, and damping of the original structure.

Equation (2) is the motion control equation of SDOF with TID:

$$\left\{\begin{array}{c}m\ddot{u}+c\dot{u}+ku+k_d\left(u-u_d\right)+c_d\left(\dot{u}-{\dot{u}}_d\right)=-m{a}_g\\ b\left({\ddot{u}}_d+a_g-a_g\right)=k_d\left(u-u_d\right)+c_d\left(\dot{u}-{\dot{u}}_d\right)\end{array}\right.$$

(2)

where u and u_d are the displacement responses of SDOF and the TID, and a_g is the ground acceleration. Dimensionless parameters are defined at the same time as follows:

$${\zeta }_0=\frac{c}{2m{\omega }_0},{\omega }_0=\sqrt{\frac{k}{m}},\mu =\frac{b}{m},\zeta =\frac{c_d}{2m{\omega }_0},\kappa =\frac{k_d}{k}$$

(3)

where ζ₀ and ω₀ are the damping ratio and circular frequency of the original structure; κ, μ, and ζ are the stiffness ratio, inerter–mass ratio and damping ratio of the TID. Rewrite Equation (2) into dimensionless form as:

$$\left\{\begin{array}{c}\ddot{u}+2{\zeta }_0{\omega }_0\dot{u}+{\omega }_0{}^{2}u+\kappa {\omega }_0{}^2\left(u-u_d\right)+2\zeta {\omega }_0\left(\dot{u}-{\dot{u}}_d\right)=-a_g\\ \mu \left({\ddot{u}}_d+a_g-a_g\right)=\kappa {\omega }_0{}^2\left(u-u_d\right)+2\zeta {\omega }_0\left(\dot{u}-{\dot{u}}_d\right)\end{array}\right.$$

(4)

The Laplace transform of Equation (4) can be obtained:

$$\left\{\begin{array}{c}{s}^{2}U+2{\zeta }_0{\omega }_{0}sU+{\omega }_0{}^{2}U+\kappa {\omega }_0{}^2\left(U-U_d\right)+2\zeta {\omega }_{0}s\left(U-U_d\right)=-A_g\\ \mu s^2\left(U_d+A_g-A_g\right)=\kappa {\omega }_0{}^2\left(U-U_d\right)+2\zeta {\omega }_{0}s\left(U-U_d\right)\end{array}\right.$$

(5)

where s = iΩ, Ω is the excitation frequency of ground motion, U, U_d, and A_g are the laplace transforms of u, u_d, and a_g. Then, the displacement response transfer function (frequency response function, FRF) of SDOF with TID H_U of can be obtained by solving the linear Equation (5):

$$H_U=\frac{U}{A_g}=-\frac{s^2\mu +2s\zeta \omega +\kappa {\omega }^2}{s^4\mu +2s^3\left(\zeta +\zeta \mu +{\zeta }_0\mu \right)\omega +s^2\left(4\zeta {\zeta }_0+\kappa \mu +\kappa +\mu \right){\omega }^2+2s\left(\zeta +\kappa \zeta \right){\omega }^3+\kappa {\omega }^4}$$

(6)

Assuming that the seismic excitation is a stationary white noise process, and according to the Parseval’s theorem, the displacement response root mean square (RMS) σ_U of the original structure with a TID is:

$${\sigma }_U=\sqrt{{\int }_{-\infty }^{+\infty }{\left|H_U\right|}^2{S}_0\mathrm{d}s}$$

(7)

where S₀ is the power spectral density of white noise. The mitigation ratio of the RMS of displacement response of the original system with and without a damper can be compared to measure the effect of the shock absorber, namely, the displacement mitigation ratio. For an SDOF system with a viscous damper (VD) and a TID, the closed-form solutions of the structural displacement mitigation ratios J_VD and J can be obtained by using the James integral formula:

$$J_{VD}=\frac{{\sigma }_{U_{VD}}({\zeta }_0)}{{\sigma }_U{}_{{}_0}({\zeta }_0)}=\sqrt{\frac{{\zeta }_0}{{\zeta }_0+{\zeta }_0}},J=\frac{{\sigma }_U}{{\sigma }_{U_0}}=\frac{I_4}{I_2}$$

(8)

$$J=\sqrt{\frac{{\zeta }_0^2\left({\kappa }^2{\mu }^2+4\mu {\zeta }^2+4\kappa \left(\mu +1\right){\zeta }^2\right)+{\zeta }_0\zeta \left({\mu }^2+{\kappa }^2{\left(\mu +1\right)}^2-\kappa \mu \left(\mu +2\right)+4{\zeta }^2\left(\mu +1\right)\right)+4\kappa \mu \zeta {\zeta }_0^3}{\zeta {\zeta }_0\left(-2\kappa \mu +{\mu }^2+{\kappa }^2{\left(\mu +1\right)}^2+4{\zeta }^2\left(\mu +1\right)\right)+{\zeta }_0^2\left({\kappa }^2{\mu }^2+4\mu {\zeta }^2+4\kappa \left(\mu +1\right){\zeta }^2\right)+{\mu }^2{\zeta }^2+4\kappa \mu \zeta {\zeta }_0^3}}$$

(9)

where σ_U0 and σ_UVD are the RMS of displacement responses of the original structure with and without VD, I₄ and I₂ are the fourth-order and second-order James formula analytical solutions. It can be seen from Equation (9) that J_VD and J have nothing to do with the white noise excitation amplitude. The smaller the displacement mitigation ratio, the better the vibration mitigation effect of the TID, so J can be used as the main performance index for parametric analysis and optimization.

3. Parametric Analysis

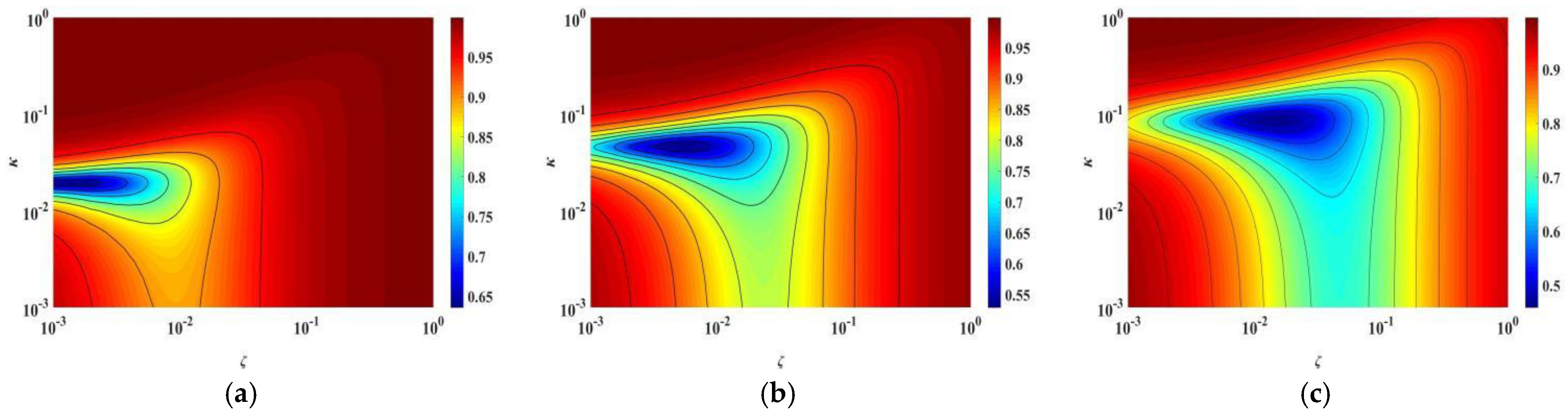
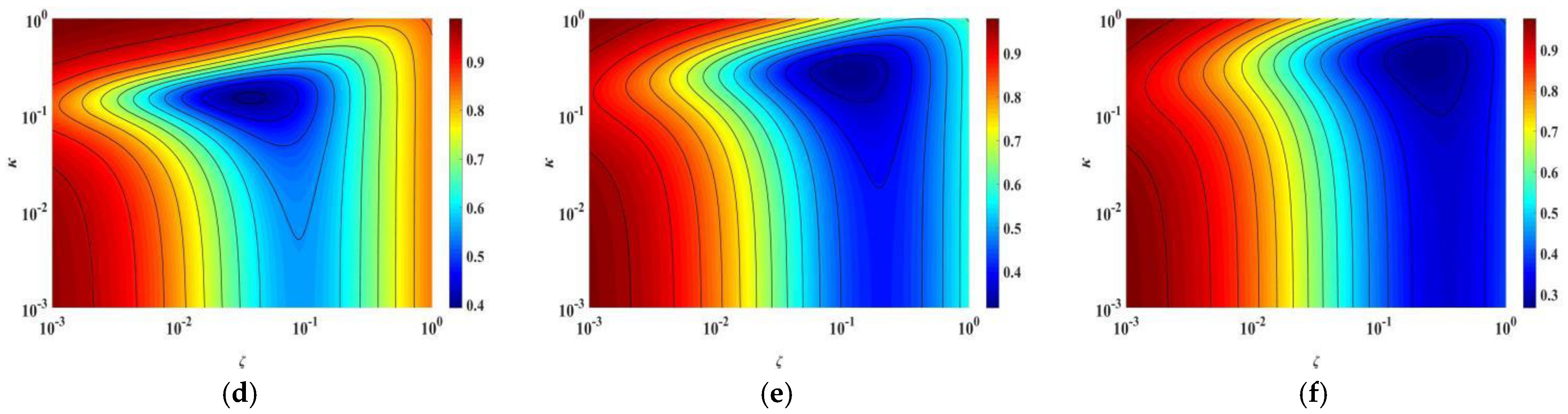
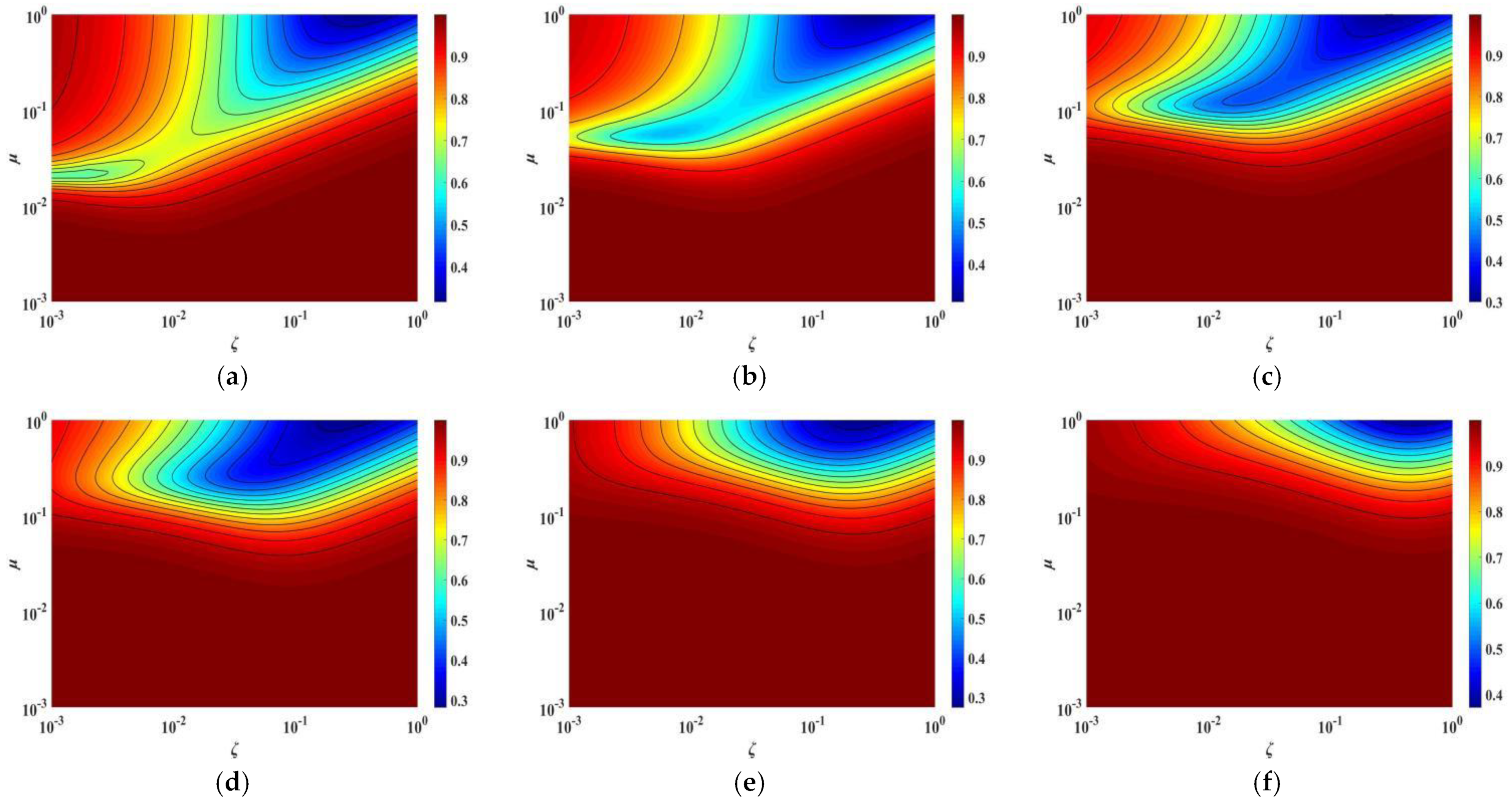
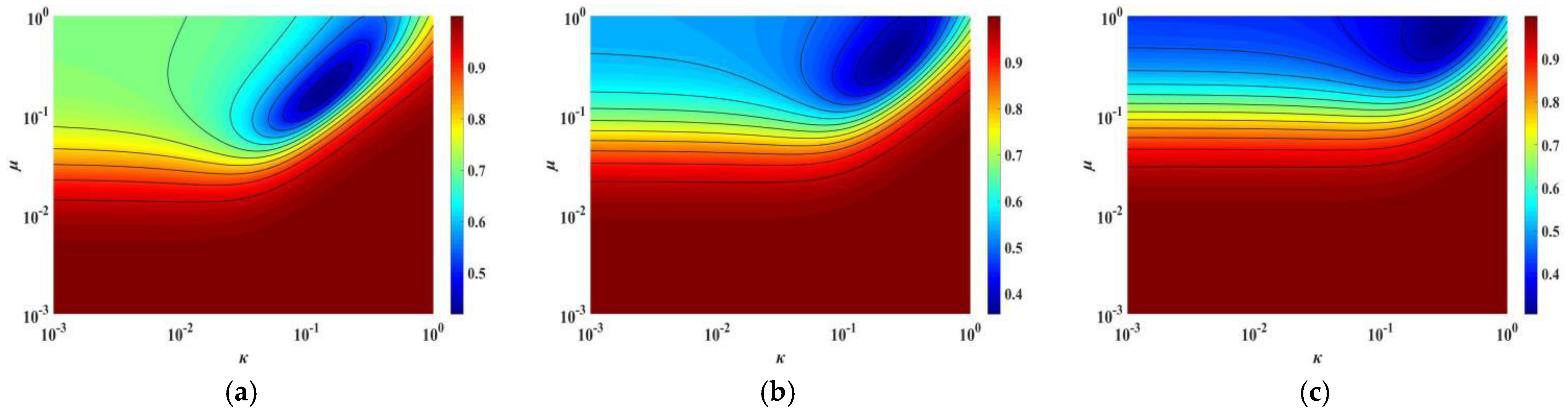
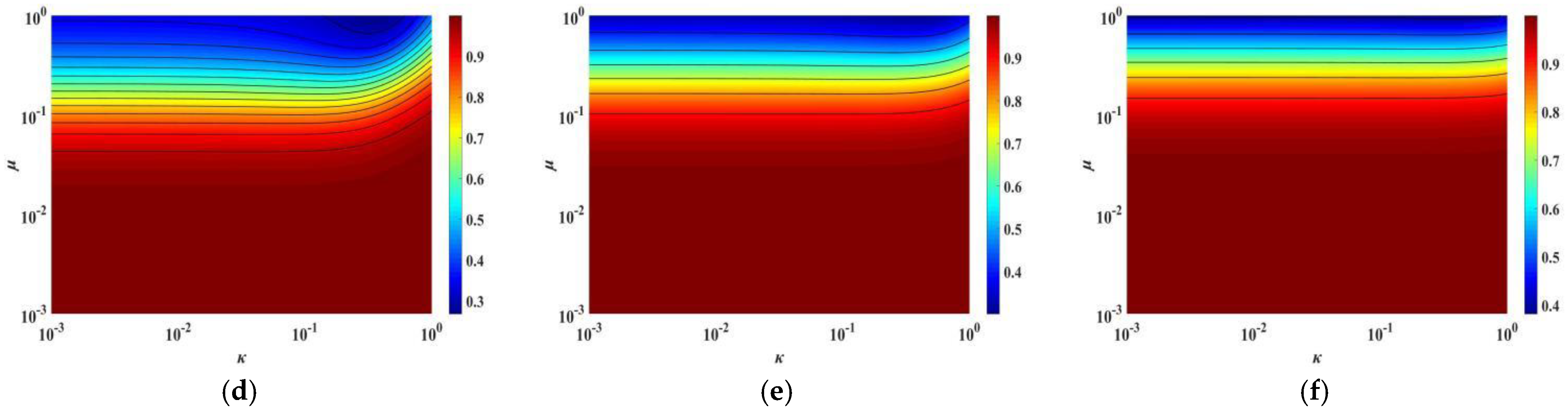
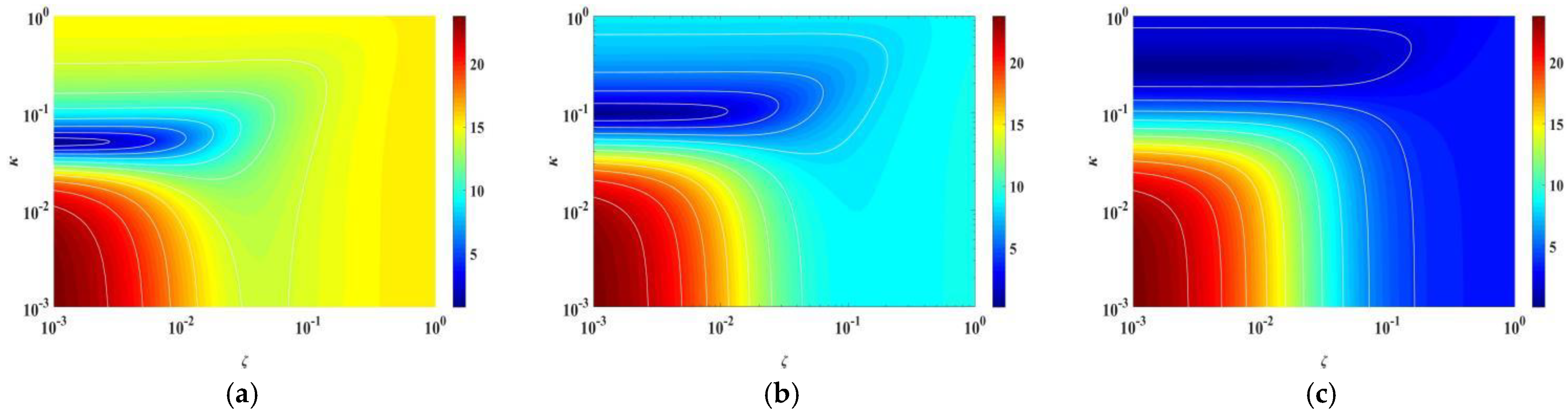
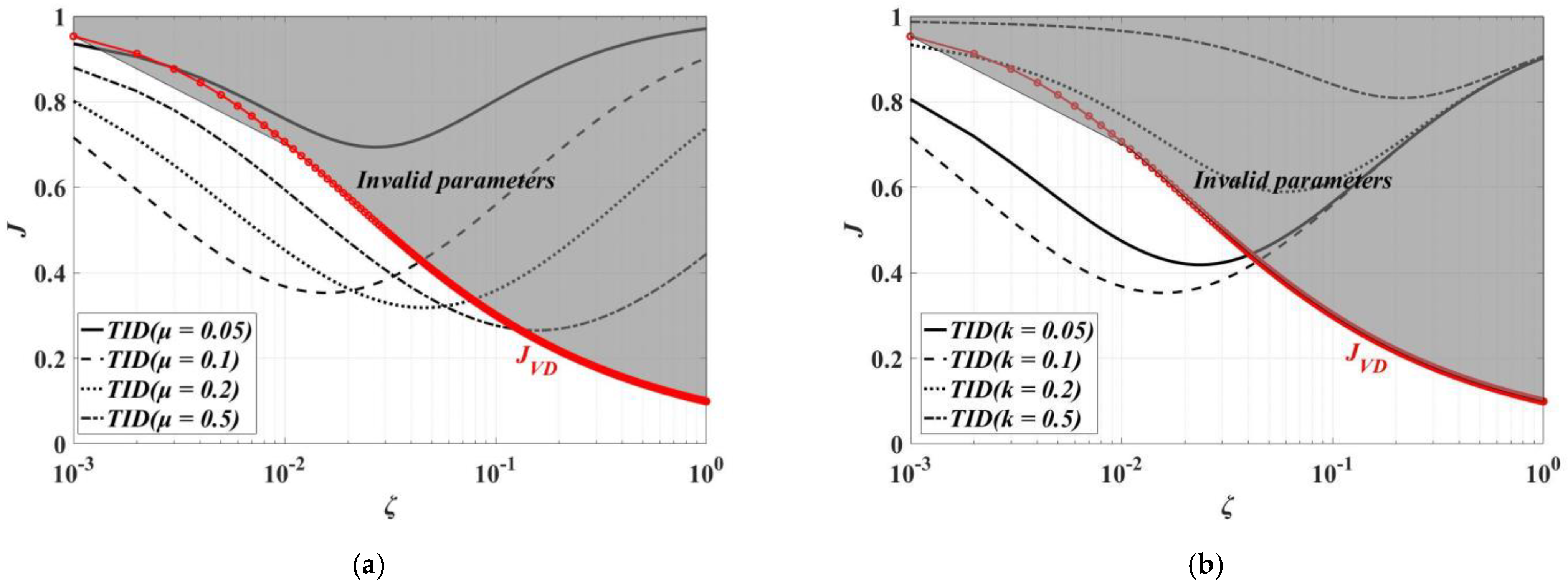
3.1. Parametric Analysis of TID Based on Closed-Form Solution J

The closed-form solution of the displacement mitigation ratio based on stochastic response is taken as the parametric analysis index, and the inerter–mass ratio (μ), the damping ratio (ζ), and the stiffness ratio (κ) are selected to carry out the parametric analysis of the TID. The inherent damping ratio (ζ₀) of the original structure is assumed to be 0.02. The displacement mitigation ratio of the SDOF system with TID is related to three parameters of the TID, and it is quite difficult to see the trends of J with variations of three parameters simultaneously. In order to determine the optimal design parameters quickly, one parameter should be fixed and the variable trends of the other two parameters can be observed. In the parametric analysis, the ranges of parameters of the inerter–mass ratio (μ), the damping ratio (ζ), and the stiffness ratio (κ) are all 0.001 to 1. The values of μ, κ, and ζ are fixed as 0.02, 0.05, 0.1, 0.2, 0.5, and 1, respectively, and the continuous variable trends of the other two parameters except the fixed values within 0.001 to 1 are studied. At the same time, the contour plots are drawn as shown in Figure 2, Figure 3 and Figure 4, and the area of the dark blue area in the Figure is defined as the optimal solution range.

It can be seen from Figure 2 that with increasing μ, the lowest point moves to the upper-right part of the overall contour, indicating that the optimal stiffness ratio (κ) and damping ratio (ζ) are positively correlated with the inerter–mass ratio (μ). In addition, no matter how much the inerter–mass ratio (μ) is fixed, the lowest point will appear in the contour plot, indicating that there always exists an optimal combination of stiffness ratio (κ) and damping ratio (ζ) within the parameter range. Figure 3 shows that the position of the lowest point is basically stable at the upper-right of the contour with increasing κ, but the optimal solution range gradually decreases (the dark blue area). When κ is fixed as 0.02, 0.2, and 0.1, the minimum of J (J_min) is 0.35, 0.30, and 0.39, respectively, indicating that J_min first decreases and then increases with the increasing κ. However, the fluctuation of J_min is not obvious in general. As shown in Figure 4, when the value of ζ is within [0, 0.2], the optimal solution range increases gradually. When ζ = 0.2, J_min reaches the minimum value of 0.29—but when the value of ζ is in [0.2, 1]—the optimal solution range becomes smaller, and J_min also increases, indicating that the vibration mitigation effect of the TID decreases at the same time. With increasing ζ, the variable trends of the contour become gentle and are only correlated with μ but have no connection to the value of κ. At the same time, with increasing μ, κ, and ζ, the cost of the TID will increase simultaneously. Figure 2, Figure 3 and Figure 4 are only the analytical solution of Equation (9). It is difficult to achieve a damping ratio (ζ) greater than 0.2 in practical engineering. The smaller values of J, μ, κ, and ζ should be determined simultaneously.

Figure 5 shows the maximum frequency response function (FRF) of original structural displacement with a TID under different μ. It can be seen from Figure 2 and Figure 5 that the optimal solution ranges of the contour will be small under small inerter–mass ratios (μ) whether it is the response under harmonic excitation or the stochastic response, and the difficulty of optimization increases accordingly.

Moreover, compared with the viscous damper (VD), the different topological connection forms of the inerter elements in the SDOF system can enhance the deformation of the viscous damping element and improve the energy dissipation ratio. Therefore, a new index of the damping effect of the TID is proposed by comparing J_VD and J, namely, inerter-enhanced energy dissipation coefficient η:

$$\eta =\frac{{\sigma }_U{}_0\left({\zeta }_0\right)-{\sigma }_U\left({\zeta }_0,\zeta ,\kappa ,\mu \right)}{{\sigma }_U{}_0\left({\zeta }_0\right)-{\sigma }_U{}_{VD}\left({\zeta }_0,\zeta \right)}$$

(10)

where η is under the same additional damping ratio, the damping element with inerter element has higher deformation effect. When η is greater than 1, it shows that the inerter can strengthen the energy dissipation of the structure, and it can be used as an index to evaluate the economy and robustness of the TID. Figure 6 shows the 3D contour plots of η under different inerter–mass ratio μ.

It can be seen from Figure 6 that there always exist ranges of less than 1 (below the light green surface) in the contour plot. This means that the damping effect of the TID may be worse than VD under some specific value of optimal design parameter (κ, μ, and ζ) combinations. Figure 7 shows that the vibration mitigation effect of the TID is lower than VD under some specific ranges of damping ratio (J > J_VD) (invalid parameters in the shaded part). This will cause loss of the value of adding an inerter element. Hence, the vibration mitigation effect of the designed parameters of the TID should be compared with the VD after parameter optimization.

3.2. Parameter Optimization of TID by Using Closed-Form Solution Method

The design parameters of the TID can be determined by the fixed-point method. Based on the Den Hartog fixed-point theory [54], Pan et al. [16] deduced the design equation of the SDOF structure with TID. After the inerter–mass ratio is determined, the stiffness ratio and damping ratio can be obtained by the following formulas:

$$\kappa =\frac{\mu }{\left(1+\mu \right)2},\zeta =\frac{\mu }{2\left(1+\mu \right)}\sqrt{2+\frac{1}{2+\mu -\sqrt[]{\mu 2+\mu }}}$$

(11)

However, the inherent damping ratio and external excitation characteristics of the original structure are not considered in the fixed-point theory, and other performance demands of the original structure, such as displacement of the original structure, cannot be considered. At the same time, all three parameters cannot be optimized simultaneously by using the fixed-point method.

For this reason, when TID parameters are designed, the main performance of the original structure should be considered first, and the target mitigation ratio can be determined according to the performance demands of different structures. The extreme conditions are used for parameter optimization at the same time, namely:

$$J=J_t,\frac{\partial J}{\partial \kappa }=0,\frac{\partial J}{\partial \zeta }=0$$

(12)

where J_t is the target displacement mitigation ratio of the original structure. It is difficult to realize the installation of a TID in practical engineering under a high damping ratio. Therefore, the constraint condition of Equation (12) is to meet the target mitigation ratio (J_t) and the damping ratio is simultaneously determined to be as small as possible to meet the practical engineering requirements. This is called the closed-form solution method in this paper. After the optimal solution of the damping ratio is obtained, J_t should also be smaller than the displacement mitigation ratio of the VD system (J_VD) under the same damping ratio, namely, Formula (13). If Formula (13) is not satisfied, that is J_t > J_VD, the vibration mitigation effect of the TID is lower than the VD, and the design parameters are invalid parameters correspondingly.

$$J_t\le J_{VD}$$

(13)

The inerter–mass ratio obtained by the closed-form solution method is also used in the fixed-point method as additional tuning condition, and then the optimal damping ratio and optimal stiffness ratio of the fixed-point method are obtained by using Formula (11).

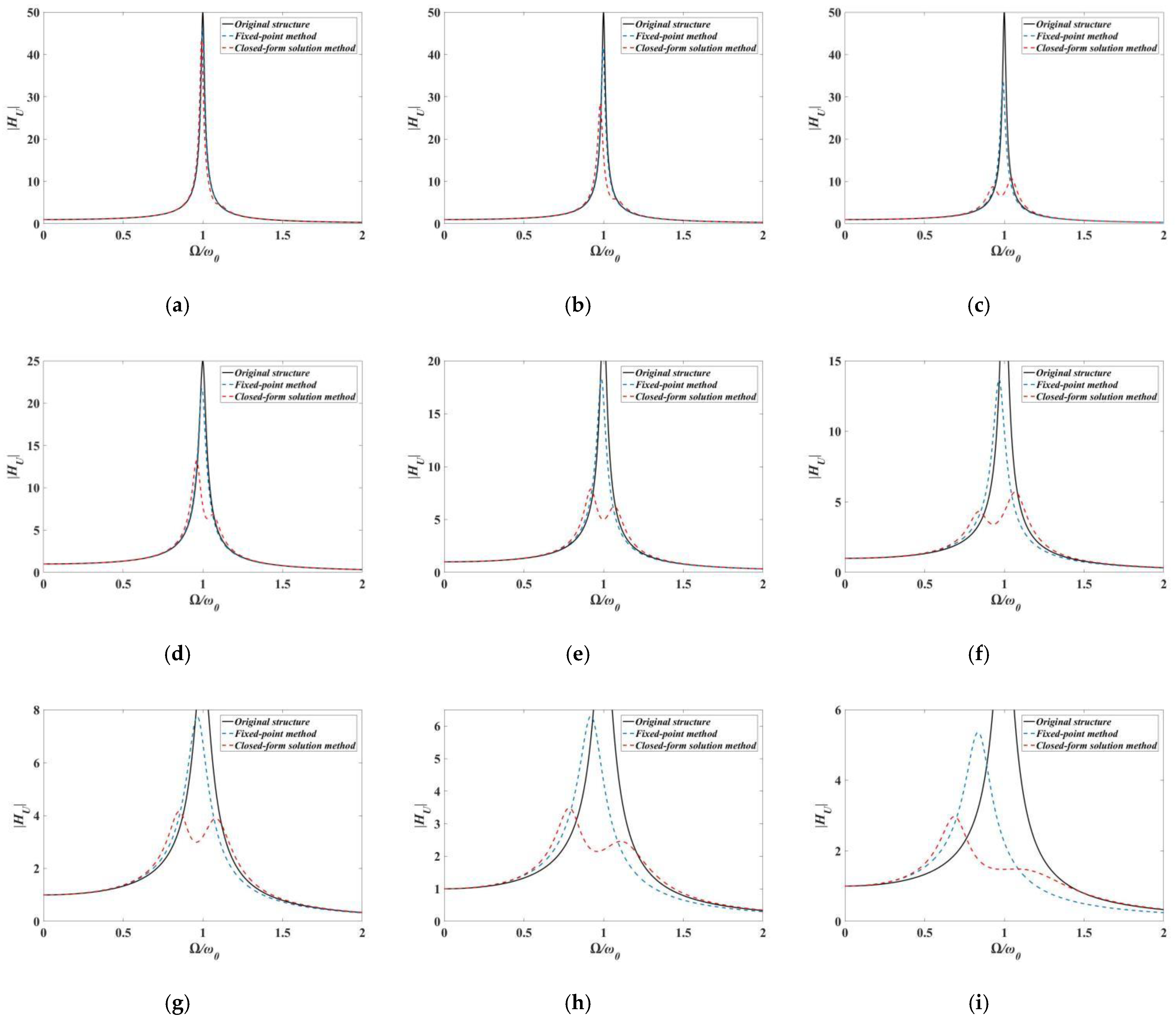
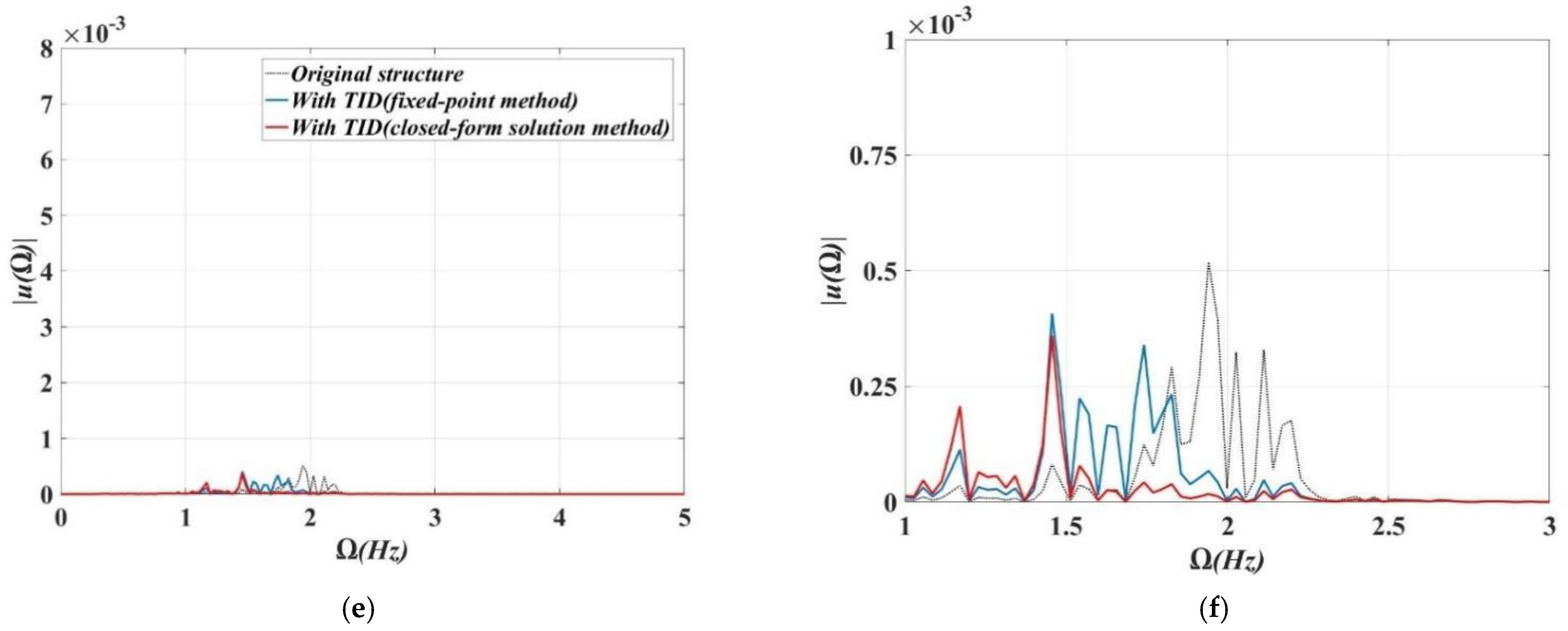
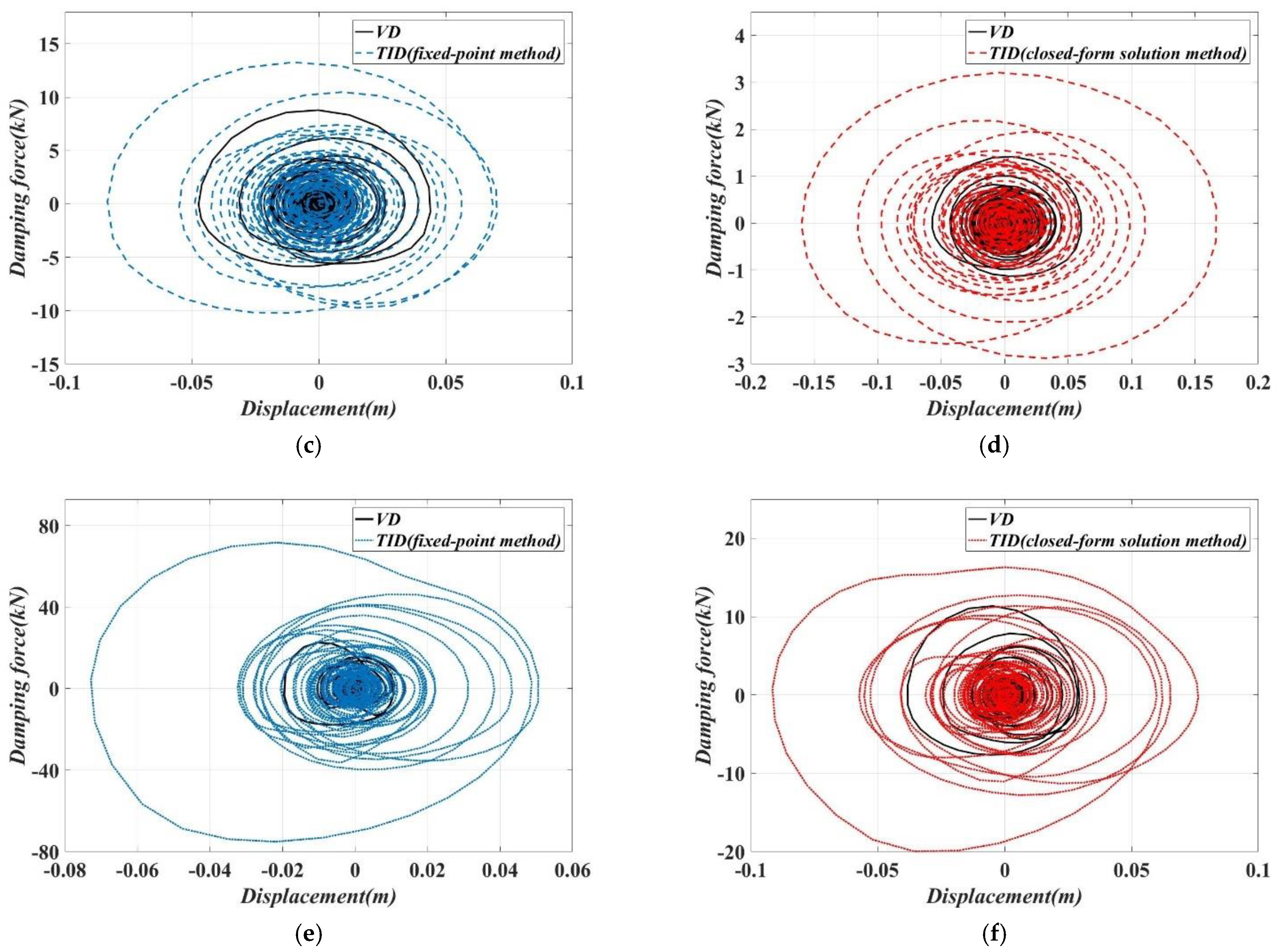
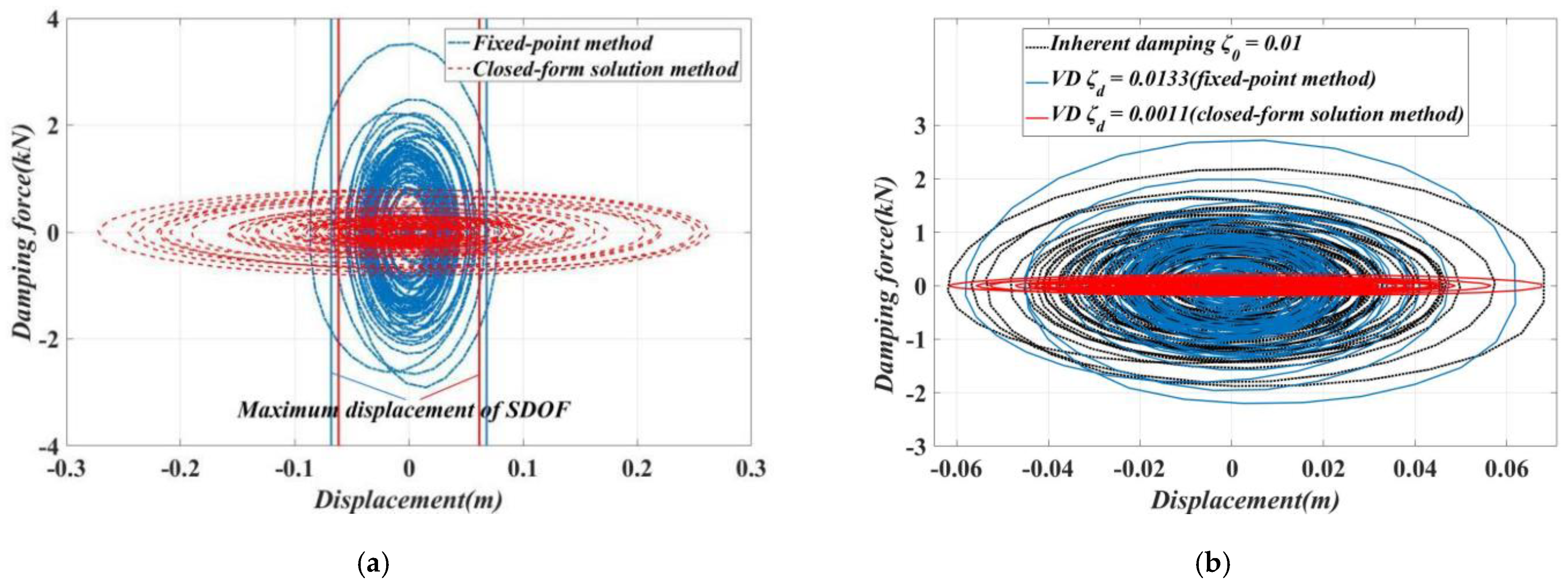
3.3. Applicability Analysis of Closed-Form Solution Method and Fixed-Point Method

In this paper, the optimization designs of different original structures with inherent damping ratios (ζ₀ is considered to be 0.01, 0.02, and 0.05) are carried out.

Table 1. Designed parameters of TID and J_VD with different optimal methods.

ζ0	Closed-Form Solution Method					Fixed-Point Method
	Jt	μ	κ	ζ	JVD	μ	κ	ζ	JVD
0.01	0.7	0.0026	0.0031	0.0001	0.9901	0.0026	0.0025	0.0020	0.9117
	0.6	0.0065	0.0073	0.0003	0.9860	0.0065	0.0073	0.0052	0.8104
	0.5	0.0165	0.0156	0.0010	0.9528	0.0165	0.0160	0.0134	0.6541
0.02	0.7	0.0100	0.0105	0.0005	0.9873	0.0100	0.0098	0.0080	0.8445
	0.6	0.0256	0.0250	0.0020	0.9532	0.0256	0.0243	0.0210	0.6984
	0.5	0.0647	0.0533	0.0071	0.8589	0.0647	0.0570	0.0554	0.5151
0.05	0.7	0.0608	0.0533	0.0068	0.9381	0.0608	0.0541	0.0521	0.6991
	0.6	0.1559	0.1267	0.0264	0.8089	0.1559	0.1167	0.1462	0.5048
	0.5	0.3935	0.2705	0.0934	0.5905	0.3935	0.2027	0.4508	0.3160

shows the optimization parameter values of the TID and the J_VD of the VD under the same damping ratio. It can be seen from Table 1 that the damping ratio (ζ) of the TID obtained by the closed-form solution method is always smaller than the fixed-point method, and the J_VD obtained is always greater than J_t, indicating that the TID design parameters obtained by the closed-form solution method are effective parameters which can achieve the effect of enhancing damping. However, when the inherent damping ratio (ζ₀) of the original structure is equal to 0.05, the design parameters of the TID obtained by using the fixed-point method are invalid, indicating that the fixed-point method is not suitable for structures with large inherent damping ratios (blue font in Table 1).

Figure 8 shows the displacement transfer function of the SDOF structure for the two optimization methods. It can be seen from Figure 8 that the TID vibration mitigation effect obtained by using the fixed-point method is significantly lower than that of the closed-form solution method, and only the resonance response of the original structure can be controlled under the fixed-point method, which is similar to the VD. The optimal parameters of the TID by using the closed-form solution method can expand the frequency domain of displacement control effect and that it is no longer limited to narrow-band control. The displacement response in the near-circular frequency of the original structure or even a wider range can be controlled, which is more obvious when considering a larger inherent damping ratio.

Figure 9 shows the range of the TID invalid parameters under the two optimization methods, and the shaded part in Figure 8 represents the ranges of invalid parameters (J_t > J_VD). It can be seen from Figure 8 that when the inherent damping ratio (ζ₀) of the original structure is 0.01 and 0.02, the TID design parameters obtained by the closed-form solution are all effective. When ζ₀ is 0.05, the closed-form solution fails when J is within [0.25, 0.4]. When J is within [0.25, 0.4], as the inherent damping ratio of the original structure increases, the effect of the TID becomes closer to that of the VD, indicating that the vibration mitigation effect of the TID is worse. The range of invalid parameters increases to [0.17, 0.6] as ζ₀ increases to 0.1. The TID design parameter combination obtained by the fixed-point method has no invalid parameters only when ζ₀ is 0.01. The invalid ranges of parameters under other inherent damping ratios all exist, and the invalid ranges are larger than those found by using the closed-form solution method. Within the range of effective design parameters of the TID, the positions of curves of equivalent J_VD obtained by the closed-form solution method are always above those of the fixed-point method, indicating that the cost of the closed-form solution method is lower than that of the fixed-point method. That is, the optimal damping ratio (ζ_opt) of TID obtained by the closed-form solution method is smaller than that by the fixed-point method.

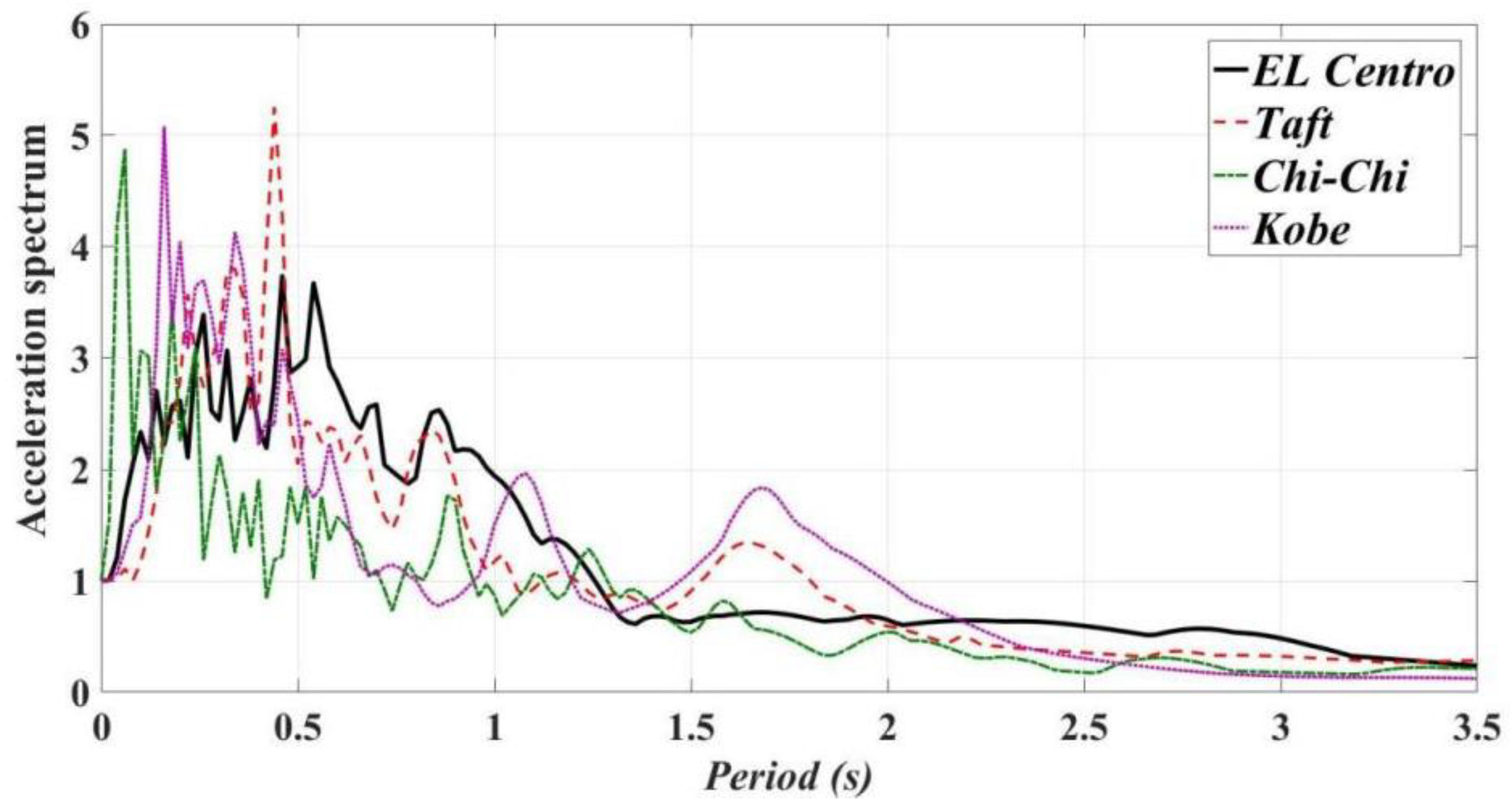
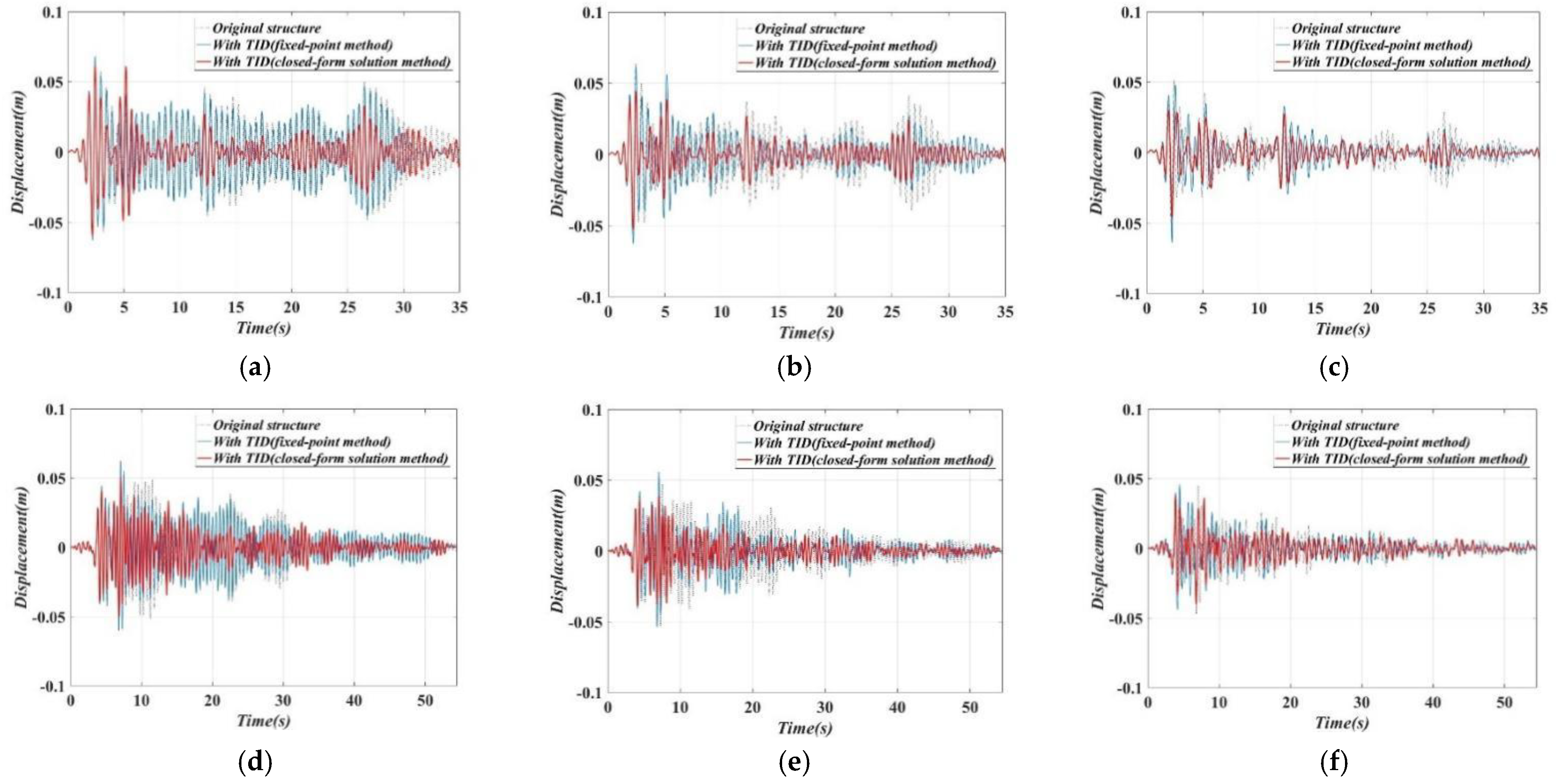
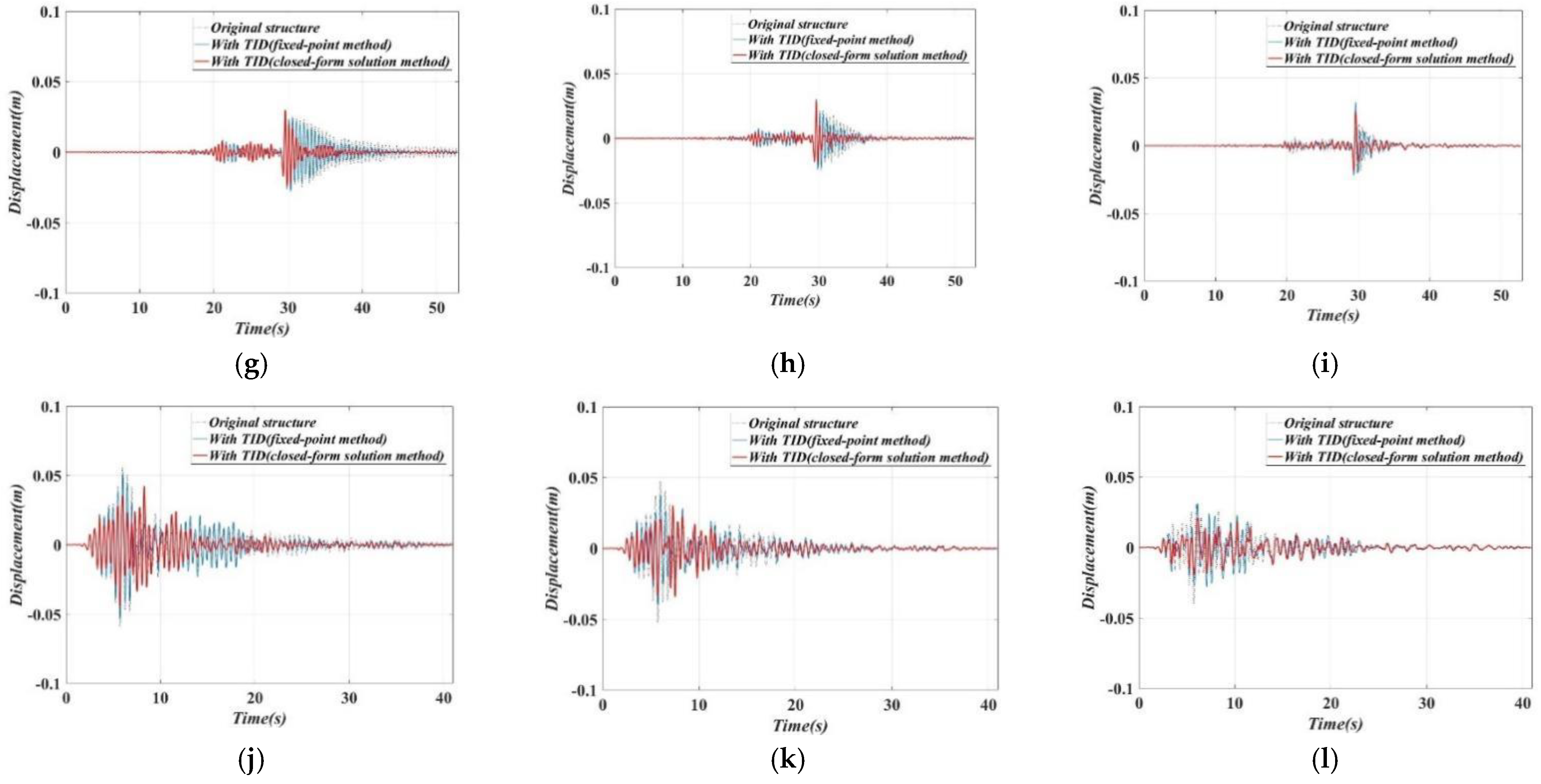
4. Seismic Responses

In order to verify the vibration mitigation effect of the TID and parameter optimization results, 0.5 is taken as the target displacement mitigation ratio J_t, the seismic responses of the SDOF system with TID under ground motions are carried out, and the TID parameters obtained by the two optimization methods were compared. The original structural mass is m = 1 × 10⁴ kg, stiffness k = 1.57 × 10³ kN/m, and the inherent damping ratio ζ₀ is taken as 0.01, 0.02, and 0.05.

EL Centro record, Taft record, Chi-Chi record, and Kobe record are selected, and Figure 10 is the acceleration response spectrum of the four records. At the same time, different dominant frequencies of records are selected four including low frequency, high frequency and many components such as El Centro record. Figure 11 is the displacement time history response of the SDOF system under four records. It can be seen from Figure 11 that the vibration control effects of the TID parameters obtained by using the closed-form solution on the structure are better than those obtained by using the fixed-point method under the ground motions with different predominant frequencies, indicating that the design method of the TID based on the closed-form solution method has better robustness. As the seismic response of the structure progresses, the vibration control effects of the TID in the later stage become better, indicating that a stable vibration state of the original structure can be quickly brought under control by the TID. Figure 12 shows the Fourier amplitude spectrum of the displacement response of the SDOF system under the excitation of the EL Centro record. It can be seen from Figure 12 that the TID parameters obtained by the closed-form solution method can be tuned to match all high-amplitude regions of ground motion. The control frequency domain is wider than that of the fixed-point method, and the controlled displacement amplitude decreases significantly at the fundamental frequency of the original structure. The spectral curve has no obvious peaks or corresponding frequencies, which also corresponds to the steady and low seismic response in the time history curves.

Figure 13 shows the hysteresis loops of damping elements of the TID and VD with the same damping ratio under the excitation of EL Centro record. The corresponding TID design parameters are shown in Table 1. It can be seen from Figure 13 that, under the same damping ratio, the deformation and damping force of the damping element of the TID are both greater than those of the VD, and the overall energy dissipation effect is better than that of the VD. Compared with the hysteresis loops of the TID and VD with the same damping ratio under the two optimization methods, it can be seen that the hysteresis loop areas of the VD corresponding to the fixed-point method increase with the increase of the inherent damping ratio, while the corresponding to closed-form solution method decreases. These show that the design parameters of the fixed-point method are relatively conservative, a larger damping ratio is selected for energy dissipation, and the damping force is 4–5 times that of the closed-form solution method. However, the damping deformation enhancement characteristics of the inerter system are not obvious by using the combination of designed parameters obtained by the fixed-point method. At the same time, the inherent damping ratio of the original structure is not considered in the fixed-point method, which will cause a detuning effect. The inherent damping ratio of the original structure is not considered in the closed-form solution method, so the damping deformation enhancement characteristics of the inerter system can be brought into full play and the same vibration control effect as the fixed-point method is achieved with a smaller damping coefficient.

Figure 14 shows the hysteresis loops of the damping element of the TID by using different optimization methods under the excitation of EL Centro record. It can be seen from Figure 14a that the damping coefficient of the TID obtained by using the fixed-point method is much higher than that obtained by the closed-form solution method. Although a high damping coefficient will increase the damping force and increase the energy dissipation effect, the cost of the TID will increase dramatically. However, the damping deformation enhancement characteristics of the inerter system found using the closed-form solution method are about three times higher than those found using the fixed-point method. Hence, the damping element of the TID obtained by the closed-form solution method still has effective energy dissipation. Figure 14b shows the energy dissipation effect of inherent damping ratio and the equivalent VD obtained by the two methods. The optimal damping ratio of the TID obtained by the closed solution method is much smaller, which is 11% of the damping ratio obtained by using the fixed-point method and 8.3% of the inherent damping ratio. From Figure 14a, we can see that the maximum displacements of the main structure with a TID are nearly identical using two optimal design methods; however, the additional damping ratio of the TID designed by the closed-form solution method is considerably smaller compared to that of the fixed-point method. The damping enhancement effect of the inerter element can be fully utilized when employing the proposed performance-demand-based design approach. The designed parameters of the TID obtained by the closed-form solution method can not only meet the performance demands of the structures with different inherent damping ratio, but the engineering cost is also greatly reduced, achieving a lightweight design of the TID at the same time.

5. Conclusions

In this paper, the motion control equations of the SDOF system with TID are established. The inerter–mass ratio, damping ratio, and stiffness ratio are analyzed based on the displacement mitigation ratio of stochastic response, and the parameter optimization design of the TID based on the closed-form solution method are also carried out compared with the fixed-point method. Additionally, applicable conditions of the two methods are discussed in a wider range of values of objective function under different inherent damping ratios. Finally, seismic responses are carried out on the SDOF system with TID, which verifies the feasibility of the closed-form solution optimization method. The main conclusions are as follows:

• The investigation on the variation patterns of invalid designed parameters of TIDs under different inherent damping ratios indicates that compared with the fixed-point method, better applicability and robustness are shown in closed-form solution method.
• The displacement mitigation ratio could be used as a target during the determination of design parameters of the TID, which meets the structural design concept based on performance demand.
• Nearly identical performances of main structures with TID can be realized using two optimal design methods; however, the additional damping ratio of the TID designed by the closed-form solution method is considerably smaller compared to that of the fixed-point method. The damping enhancement effect of the inerter element can be fully utilized when employing the proposed performance demand-based design approach.
• Considering the lower additional damping ratio and inerter–mass ratio, applications of the TID designed by the closed-form solution method can be extended and its installation made more flexible. The corresponding verification experiment study must be conducted in the near future.